Похожие презентации:
Основные сведения о матрицах. Операции над матрицами
1.
ЛекцияТема: «Основные сведения о
матрицах.
Операции над матрицами»
12.09.2021
1
2.
12.09.20212
3.
Применение матричногоисчисления
Матричное исчисление положено в основу
математического аппарата квантовой и
статической механики, квантовой
физики, химии, радиоэлектроники.
Одно из первых направлений в квантовой
механике, заложенное Гейзенбергом, даже
носило название
МАТРИЧНОЙ МЕХАНИКИ.
12.09.2021
4
4.
Матричноеисчисление значительно
упрощает описание электромагнитных
процессов в цепях
Матричное исчисление облегчает
решение системы линейных уравнений
Матричное исчисление широко
применяется при анализе электронных
схем
12.09.2021
5
5.
Матричноеисчисление играет большую
роль в решении ряда прикладных задач.
На нем базируется теория колебаний в
электрических, акустических и
механических системах, где
фундаментальное значение имеют
характеристические уравнения,
собственные значения и собственные
векторы.
12.09.2021
6
6.
Кзадачам линейной алгебры
сводятся многочисленные
алгоритмы обработки
экспериментальных данных,
минимизации линейных форм,
различные задачи теории
прочности, упругости и
пластичности.
12.09.2021
7
7.
1. Основные сведения о матрицах.Определение: Система m n действительных чисел
(или элементов матрицы), расположенных в
прямоугольную таблицу из m строк и
n столбцов, называется матрицей
a11 a12 ... a1n
a 21 a 22 ... a 2 n
A
. . . .
a a ... a
mn
m1 m 2
12.09.2021
8
8.
Матрицу можно записывать коротко:в виде
A aij 1 i m,
или в виде
где
12.09.2021
a ij
1 j n
A a ij ,
- элемент данной матрицы
9
9.
Элементы матрицы a ij образуют столбцы истроки.
Первый индекс i указывает номер строки,
а второй j – номер столбца, на пересечении
которых и стоит элемент a ij.
12.09.2021
10
10.
Например, элементa 23 матрицы
2 2 10
A 0 5 2
3 2 5
находится на пересечении второй строки и
третьего столбца
и равен a23 2
Элемент
12.09.2021
a13 10
11
11.
(ai1 , ai 2 ,..., ain )Набор
называют i ой строкой матрицы A .
Набор
a1 j
a2 j
a называют
3j
...
a
мj
j ым
столбцом.
12.09.2021
12
12.
Если хотят указать размер матрицы,то пишут
A,
m n
это означает, что в матрице
и
столбцов.
n
12.09.2021
m строк
13
13.
2 2 6Например, матрица B
8 0 2
имеет порядок m n 2 3
B .
, т.е. 2
3
Элемент b22 данной матрицы равен (?)
12.09.2021
14
14.
МОЛОДЦЫ!Верно, b22 0
12.09.2021
15
15.
Типы матриц1. Если матрица содержит только одну строку – это
вектор-строка (или строчная матрица).
Например, матрица C 3 7 2
1 3
имеет порядок
m n 1 3
2. Если один столбец – это вектор-столбец (или
столбцевая матрица).
7
имеет порядок
Матрица 2D
1
8
12.09.2021
m n 2 1
16
16.
3. Если m n , то матрица называетсяквадратной, а число m n – ее порядком.
Элементы a11 , a 22 ,..., a nn квадратной матрицы
называются диагональными и образуют главную
диагональ матрицы.
12.09.2021
17
17.
4. Матрица, у которой все элементы, кромедиагональных, равны 0, называется диагональной и
записывается в виде
Diag n (a11 , a 22 ,..., a nn )
Например,
12.09.2021
2 0 0
С 0 3 0
3 3
0 0 1
18
18.
5. Диагональная матрица виданазывается
единичной
и обозначается
или
12.09.2021
1 0 0
0 1 0
E
0 0 1
1, если i j
E ij , где ij
0, если i j
E Diag n (1,1,...,1)
19
19.
6. Нулевая матрица (0) размера m n есть матрица этогоразмера, все элементы которой равны нулю:
0 0 0
( 0) 0 0 0
0 0 0
7. Если нули будут под главной диагональю или над главной
диагональю, то матрица называется треугольной:
1 1 1
- 3 0 0
K 0 - 2 6 , L - 5 1 0
0 0 1
4 7 2
12.09.2021
20
20.
Определение. Две матрицы равны, если равныэлементы, стоящие на одинаковых местах (при
этом число строк и столбцов должно быть
одинаковым). То есть размеры и элементы двух
равных матриц совпадают.
12.09.2021
21
21.
2. Операции над матрицамиОперации над матрицами определяются с
помощью операций над их элементами.
1. Сложение матриц. Суммой двух матриц
A и B с одинаковым количеством строк и
столбцов называется матрица C, элементы
которой определяются равенством,
cij aij bij
12.09.2021
i 1 m, j 1 n
22
22.
Например,6 -1 0
- 6 6 2
, B
A
2 - 2 1
1 0 -4
6 ( 6 ) 1 6 0 2 0 5 2
.
C A B
2 1 2 0 1 ( 4 ) 3 - 2 - 3
12.09.2021
23
23.
ЗамечаниеСтрого говоря, операции вычитания
матриц одного порядка А и В как
таковой не существует.
Разность двух матриц по сути есть
сумма матрицы А и матрицы В,
предварительно умноженной на
минус единицу: A B A ( 1) B
12.09.2021
24
24.
Произведением матрицы A на числоназывается матрица, у которой каждый
элемент равен произведению
соответствующего элемента матрицы
A на число : A aij
если A aij , то, по определению
для любого R
2.
12.09.2021
25
25.
Например, если-1 1 3
A
4 0 2
2
то
-1 1 3 - 2 2 6
B 2A 2 *
4 0 2 8 0 4
12.09.2021
26
26.
3. Произведением матрицы A, имеющей m строк иq столбцов, на матрицу B , имеющую q строк и
n столбцов, называется матрица C , имеющая m
строк и n столбцов, у которой элемент c ij равен
сумме произведений элементов i-ой строки
матрицы A и j-ого столбца матрицы B:
q
cij aik bkj ,
k 1
12.09.2021
27
27.
ЗАМЕЧАНИЕ:1) если число столбцов первой матрицы и число
строк второй матрицы не совпадают, то
произведение не определено, т. е. не существует.
2) размерность полученной матрицы быстро
определяется с использованием записи:
A B C
m q
12.09.2021
q n
m n
28
28.
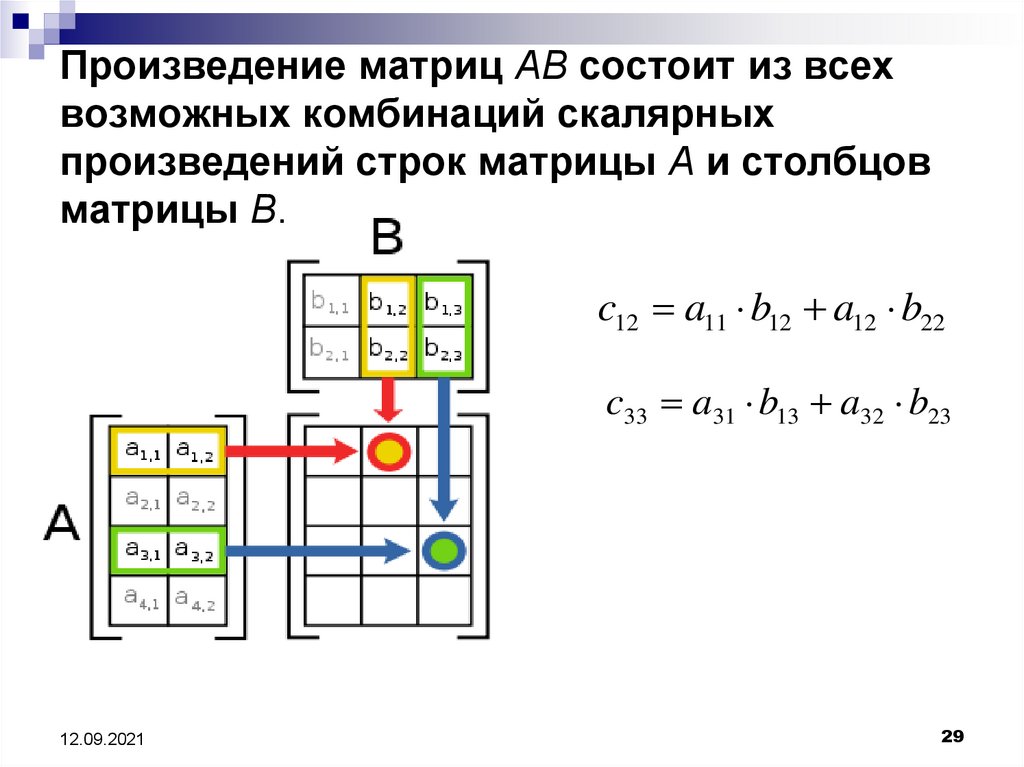
Произведение матриц AB состоит из всехвозможных комбинаций скалярных
произведений строк матрицы A и столбцов
матрицы B.
c12 a11 b12 a12 b22
c33 a31 b13 a32 b23
12.09.2021
29
29.
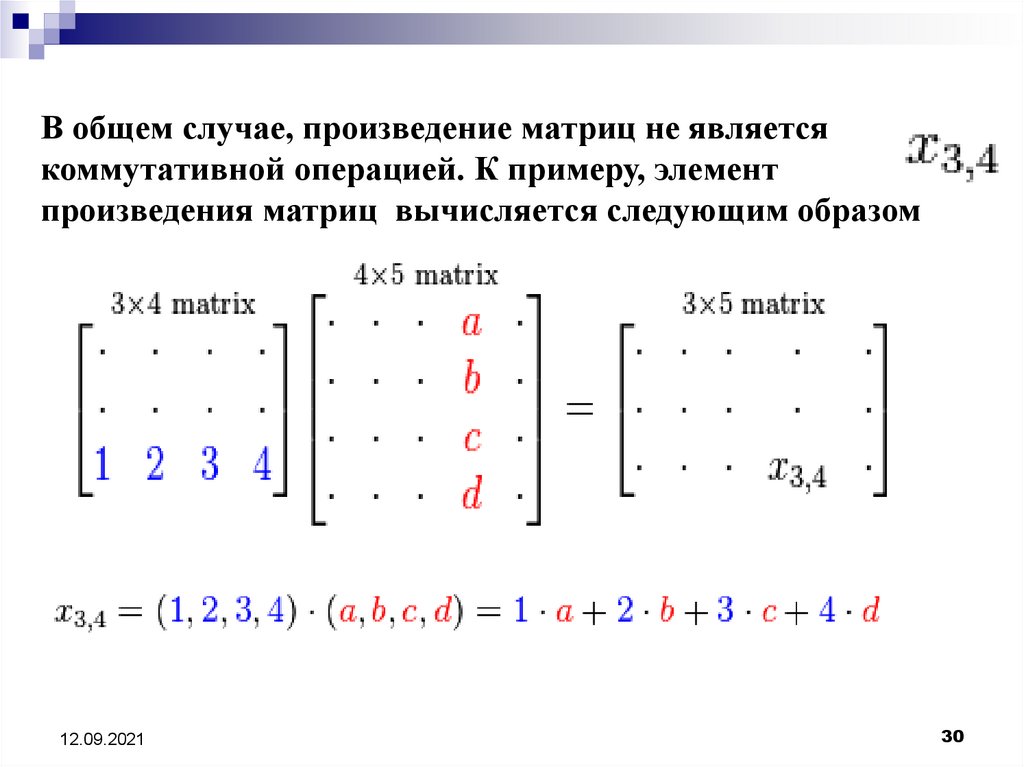
В общем случае, произведение матриц не являетсякоммутативной операцией. К примеру, элемент
произведения матриц вычисляется следующим образом
12.09.2021
30
30.
12 1
2 0 6
Например,
, B
, C 2 .
A
3 4
5 3 1
3
Найти произведение 1) A B и 2) B C
РЕШЕНИЕ
1)Укажем размеры заданных матриц:
2 1
,
A
2 2
3 4
2 0 6
,
B
2 3
5 3 1
2) Произведение матриц
1 3
A B D
d11 d12
B D
A
2 2 2 3
2 3
d 21 d 22
12.09.2021
C
1
2 .
3
существует:
d13
.
d 23
31
31.
3)Найдём элементы матрицы D:d 11 2
d 12 2
d 13 2
d 21 3
d 22 3
d 23 3
12.09.2021
2
2 ( 2) ( 1) 5 9
1
5
0
2 0 ( 1) ( 3) 3
1
3
6
1 2 6 ( 1) 1 11
1
2
3 ( 2) 4 5 14
4
5
0
3 0 4 ( 3) 12
4
3
6
4 3 6 4 1 22
1
32
32.
4) Запишем матрицу D:9 3 11
.
A B D
2 2 2 3
2 3
14 12 22
12.09.2021
33
33.
5)1
2 0 6
2
B C M
2 3 3 1
2 1
5 3 1 3
2 ( 1) 0 2 6 3 2 0 18 38
.
5 ( 1) ( 3) 2 1 3 5 6 3 8
12.09.2021
34
34.
4. Умножение на единичную матрицу.Единичная матрица обладает
замечательным свойством, а
именно:
умножение
квадратной матрицы любого
порядка
на
соответствующую
единичную
матрицу
не
меняет матрицу.
.
12.09.2021
35
35.
Замечание:для
произвольной
матрицы
и единичной матрицы
переместительный
закон
умножения
выполняется.
Это
свойство и объясняет ее название
«единичная»:
при
умножении
матриц она обладает таким же
свойством, как число 1 при
умножении чисел.
A E E A A
12.09.2021
36
36.
5. Транспонирование матрицТранспонированной к матрице A a
T
называется матрица An m , в которой
строки и столбцы поменялись
местами.
Например, если
m n
1 2 3
, то
A
3 2 1
12.09.2021
ij
1 3
T
A 2 2
3 1
37
37.
6. Возведение в степеньПусть m – натуральное число. Для любой
квадратной матрицы А степенью m матрицы A
называется матрица
A A A ... A
m
m
12.09.2021
раз
38
38.
3. Свойства алгебраическихопераций над матрицами
1. Свойства операций сложения
1. A ( B C ) ( A B ) C (ассоциативность сложения)
2. A B B A
(коммутативность сложения)
3. А+ 0 A
для любой матрицы А того же размера,
что и нулевая матрица 0 .
4. Для любой матрицы А существует матрица A aij ,
для которой A ( A) 0 .
2. Свойства операции умножения.
1. A( BC ) ( AB)C
(ассоциативность умножения)
2. Равенство AB BA выполняется не всегда, то есть
умножение матриц некоммутативное.
12.09.2021
39
39.
1 13 -1
и В
Например, для матриц A
3 1
-1 2
3 - 1 1 1 3 1 1 3 3 1 - 1 1
A B
- 1 2 3 1 - 1 1 2 3 - 1 1 2 1
0 2
5 1
1 1 3 -1 1 3 1 ( 1) 1 (-1) 1* 2 2 1
B A
3 1 -1 2 3 3 1 (-1) 3 (-1) 1 2 8 -1
A B B A
12.09.2021
40
40.
3. Дистрибутивность. Для любых матриц A, B, C, A1, B1, C1 , укоторых определены соответственно операции сложения и
умножения, A( B C) AB AC, ( A1 B1 )C1 A1C1 B1C1
4. Умножение матрицы на число.
1) ( A B ) A B
2) ( ) A A A
3) ( AB) ( A) B A( B )
4) ( A) ( ) A
5. Свойства операции транспонирования
1) ( A ) A
2) ( A) A
3) ( A B ) A B
4) ( AB) B A
12.09.2021
41
41.
ЛИТЕРАТУРАМатематики
шутят
12.09.2021
42
42.
ЛИТЕРАТУРА1.
2.
Пискунов Н.С. Дифференциальное и
интегральное исчисление. Т.II. Гл.XXI §§2,3,4
Данко П.Е. и др. Ч.I, Гл.IY, §2
12.09.2021
43








































 Математика
Математика








