Похожие презентации:
Алгебраические выражения
1. Тема: «Повторение: алгебраические выражения»
2. Цели:
вспомнить и закрепить методы работы салгебраическими выражениями:
• правила раскрытия скобок
• правила умножения одночлена на
многочлен и многочлена на многочлен
• формулы сокращенного умножения
• разложение многочлена на множители
• действия над рациональными дробями;
3. Задачи урока:
• вспомнить и применить при решениитренировочных упражнений
вышеперечисленные правила работы с
алгебраическими выражениями.
4. 1) Правила раскрытия скобок
Пример 1 5а (4с 3b) 5a 4c 3b5а 1 (4с 3b) 5a 4c 3b
Пример 2 5а (4с 3b) 5a 4c 3b
5а 1 (4с 3b) 5a 4c 3b
Общее правило раскрытия в скобках
(a b) c ac bc
5. Устные примеры:
2a 3b 5c 4 8a 12b 20c1
(8 x 3) 4 x 1,5
2
7 x 3(2 x 1,5) 4( x 3) 3x 7,5
6. 2) Правило умножения одночлена на многочлен
2) Правило умножения2
2
2
a
b
a
2
ab
b
одночлена на
2
2
2
a
b
a
2
ab
b
многочлен
Пример 3
2
x (x 1) x x
а 2 b 2 (a b)(a b)
a 3 b3 a b a 2 ab b 2
a 3 b3 a b a 2 ab b 2
2a (3 4a ) 6a 8a
Правило умножения многочлена на
многочлен
Пример 4 x 1 x 2 x 2 x 2 x 2 x 2 x 2
2
3
2
5
2x y x y 2x yx 2x y y 2x x y y
2
2
3
2
2
2
3
2
2
7. 3) Формулы сокращенного умножения
Карточка №1(3a 1) 9a 6a 1
2
2
x 64 ( x 4)( x 4 x 16)
3
2
a b 2 a 2 2ab b 2
a b 2 a 2 2ab b 2
a 3 b3 a b a 2 ab b 2
а 2 b 2 (a b)(a b) a 3 b3 a b a 2 ab b 2
8. 3) Формулы сокращенного умножения
Карточка №2(5 y 4 x) 25 y 40 yx 16 x
2
2
2
169a с (13a с)(13a с)
2
2
a b 2 a 2 2ab b 2
a b 2 a 2 2ab b 2
a 3 b3 a b a 2 ab b 2
а 2 b 2 (a b)(a b) a 3 b3 a b a 2 ab b 2
9. 3) Формулы сокращенного умножения
Карточка №325a 64b (5a 8b)(5a 8b)
2
2
x 8 ( x 2)( x 2 x 4)
3
2
a b 2 a 2 2ab b 2
a b 2 a 2 2ab b 2
a 3 b3 a b a 2 ab b 2
а 2 b 2 (a b)(a b) a 3 b3 a b a 2 ab b 2
10. Соедините линиями задания и ответы:
24
2
1)( n 2 mn m 2 )( m n)
3
9
3
2) x 6 6 x 3 y 4 9 y 8
1) x 2 64
2)( a 2 2b) 2
3)( x 3 3 y 4 ) 2
4) 4 a 4 a b b
6
3 2
3)(8 x)( x 8)
4
5)(0,3c 0,2d )(0,3c 0,2d )
6)100 x y 20 xy
2
7)( a 10b)
2
2
8)(3 a )(9 6a a )
2
8 3
m n3
27
10)(10m 2 4n 3 )(10m 2 4n 3 )
9)
4)100m 4 80n 3 m 2 16n 6
5)9 a 3
6)0,09c 2 0,04d 2
7)a 4 4a 2b 4b
8)( 2a 3 b 2 ) 2
9)100а 2 20ab b 2
10)(10 x y ) 2
11. 4) Разложение на множители
• Ответить на вопрос: что общего вприведенных ниже примерах?
2
2
2
2
2
8
x
y
16
x
8
x
y
8
x
2
8
x
( y 2)
Пример 5
Пример 6
Пример 7
4a 2b 2 1 (2ab 1)(2ab 1)
mx my 6 x 6 y m( x y ) 6( x y ) ( x y )( m 6)
Пример 8 9 x 2 25 x 6 9( x 3)( x 2 ) ( x 3)(9 x 2)
9
D 841, x1 3, x2
2
9
Ответ: в ответах получаются произведения.
12. Определение.
• Представление многочлена в виде произведения двухили нескольких многочленов называют разложением
на множители.
• Назвать, исходя из данных примеров, методы
разложения многочлена на множители.
• А) вынесение общего множителя за скобки
• Б) способ группировки
• В) с помощью формул сокращенного умножения
• Г) формула разложения на множители квадратного
трехчлена.
ax 2 bx c a( x x1 )( x x2 )
13. 5) Действия над рациональными дробями
• Сокращение дроби( x 3) x x 3
( x 5) x x 5
• Сумма и разность дробей
5a
6
5a 6
a 8
a 8 a 8
5a
6
5a 6
a 8 a 8
a 8
14. Сумма и разность дробей с разными знаменателями
b 8a 8
b 8
a 8
5a(b 8) 6(a 8)
5a
6
(a 8)(b 8)
a 8 b 8
5a(b 8) 6(a 8)
5a
6
(a 8)(b 8)
a 8 b 8
15.
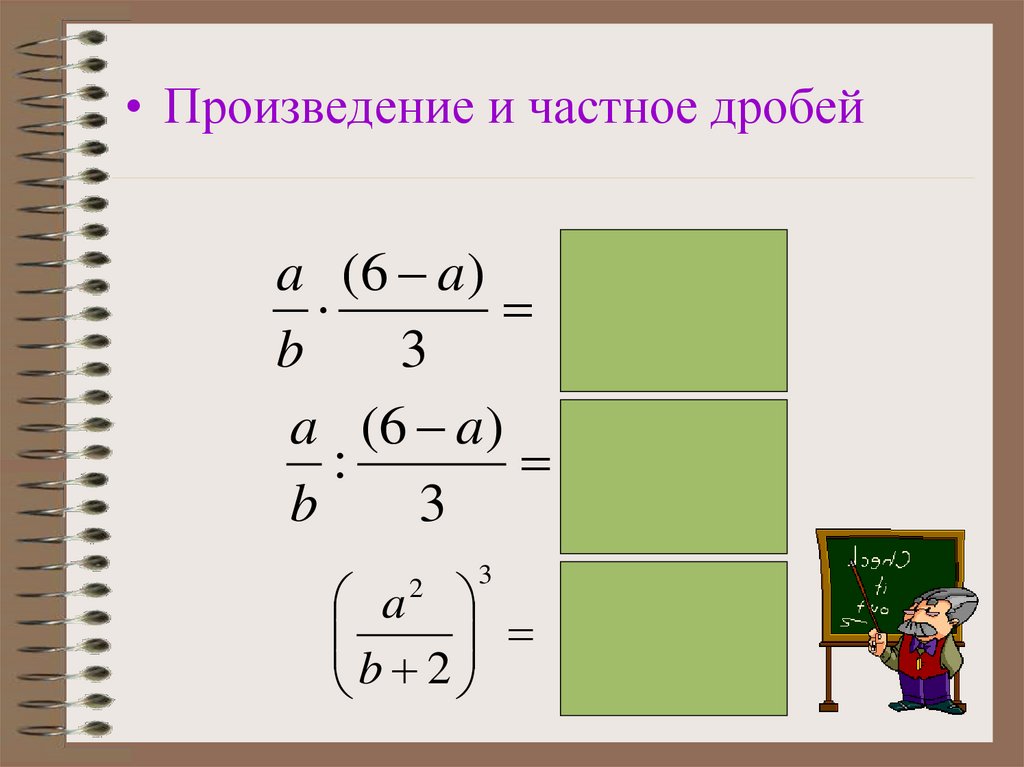
• Произведение и частное дробейa (6 a )
a (6 a )
3b
b
3
a (6 a )
3a
:
b
3
b (6 a )
3
6
a
a
2
(b 2 )
b 2
2
16. Задание. Рассмотреть решение примера и найти ошибки
xxx 33 x x 3 3 x
3 3 x x 3 3 x x3 (3x 3) x x3 3
( x 3)
2
x 3 x 3 2x 2 9
22 9
2
x
x
9
x 9 x 3 x 3 x 9
( x 3)
2
2
2
2
2
(
x
3
)(
x
6
x
9
x
6
x
9
)
2
x
18
2( x 3)( x 3)
2( x 3)
2
2
2
2
( xx 39))( x ( x3
)( 3x)( x3 ) 3)( x 3)( x 9)( x 3)
( x 9)(
22
2
xx 93
17. 4. Тренировочные упражнения № 1000(а, в, д, ж), 1004(а, в, д)
• 1 вариант - №1000(а, ж)а)( x 2 y)( x 2 y) 4 y 2 x 2 4 y 2 4 y 2 x 2
ж)(3x 4 y) 2 (2 x 7 y)(4 x 2 y) x 2 30 y 2
• 2 вариант - №1000(в, д)
в)(5x 1) 2 10 x 25x 2 1
д)(m 2n)(m2 2mn 4n 2 ) 6n3 m3 2n 2
18.
• Ответы выбрать из предложенныхвыражений на слайде:
( x 5 y)
2
(2a c)(4a 2ac c )
2
2
( x 5 y)( x 5 y)
2
2
(2a c)(4a 2ac c )
(3b 4c)(3b 4c) ( x 5 y )( x 5 y )
2
2
(2a c)(4a 2ac c )
2
a(3b 4c)(3b 4c)
a(3b 4c)
2
2
19. №2 Упростите выражение:
x( x 6) 2( x 8)2
( x 8) 16
x 2 6 x 2 x 16
x 2 8 x 16
( x 4)( x 4)
x 4
2
2
x 16 x 64 16 x 16 x 48 ( x 12)( x 4) x 12
x 2 8 x 16 0
D 0, x 4
x 2 16 x 48 0
D 64, x1 12, x2 4
20. №3 Упростите выражение:
xy3 x 4 x y x 2 xy y 22
5
4
2
y 4 x y x y x xy y
x( y 3 x 3 ) ( x y )( x 2 xy y 2 ) ( x y )( x 2 xy y 2 )
4
4
2
2
y( y 4 x )
( x y )( x xy y )
x( y 3 x 3 )( x 3 yx 2 x 2 y xy2 xy2 y 3 x 3 x 2 y x 2 y xy2 y 2 x y 3 )
4
4
3
3
y ( y 4 x )( x y )
x(4 x 2 y 2 y 3 )
2 xy(2 x 2 y 2 )
2x
y( y 4 4 x 4 )
y ( y 2 2 x 2 )( y 2 2 x 2 ) y 2 2 x 2
21. 5. Итог урока
1)(15a ...) 2 ...... 144 x 22)(... 3 xy) 2 ... 24 xy ...
3)(... b 2 )(b 2 ...) 25 b 4
4)(17 ...)(17 ...) 289 9a 2
5) x 3 ...0,125 ( x...0,5)( x 2 0,5 x 0,25)
18a 3b 4
6)
...
2
12 ab
a 2 ...
a 2
7)
3a ...
3
4...
2
4
8)... x y :
3x 3
x
22. Проверяем!
1)(15a 12 x) 2 225a 360ax 144 x 22)( 4 3 xy) 2 16 24 xy 9 x 2 y 2
3)(5 b 2 )(b 2 5) 25 b 4
4)(17 3a )(17 3a ) 289 9a 2
5) x 3 0,125 ( x 0,5)( x 2 0,5 x 0,25)
2b 2
3
a
18a b
6)
12ab
2
a 4 a 2
7)
3
3a 6
4 y3
8)12 x y :
3x
3 4
2
2
2
4
x
3
23. Домашнее задание:
1. Вынесите общий множитель за скобки:а. 3х + 2ху
б. 3x 2 12 x;
2. Разложите на множители способом группировки:
ab 2a b 2 2b;
3. Разложите на множители с помощью формул сокращенного
умножения:
а. 4 x 2 9;
б. 9у2 + 48у + 64
4. Сократите дробь с помощью формул сокращенного умножения:
а) 15 52y ;
9 y
б) m 24mn 24n .
2
2
m 4n
5. Решите уравнение, разложив левую часть на множители: x 3 64 x 0.
6. Разложите на множители и найдите значение выражения, используя
разность квадратов: 5072 - 4932























 Математика
Математика