Кинематика

1.

Кинематика
Механическое
движение
– это изменение
Механическое
движение
– стр.7 положения
тела относительно других тел с течением времени.
Основная задача механики – определить положение тела в
любой момент времени.

2.

Кинематика
Кинематика
Кинематика––это
этораздел
разделмеханики
механики,стр.9
который отвечает
на вопрос: КАК движется тело? Причем причины :
почему так? нас не интересуют. При этом тело
рассматривается как материальная точка
Материальная точка – тело, размерами которого
можно пренебречь по сравнению с расстояниями в
рассматриваемой задаче.
Материальной точкой тело можно считать если:
•Его размеры малы по сравнению с пройденным
расстоянием

3.

Кинематика
Поступательное движение – это движение тела, при
котором траектории всех его точек одинаковы.

4.

Кинематика
В
∆r
А
Траектория – линия, по которой движется тело.
Путь – длина траектории.
Перемещение – вектор соединяющий начальное и
конечное положение тела.

5.

Чтобы определить положение тела в любой момент времени
необходима система отсчета.
Система отсчета состоит из:
•Тела отсчета
•Системы координат
•Прибора для измерения времени
Если тело отсчета выбрано, то положение точки
относительно него можно задать с помощью координат или
радиус-вектора. Всегда выбираются оси системы координат
и сама система так, чтобы было легче решить задачу.

6.

х x( t )
y y( t )
A( x ; y )
r r( t )
r x; y

7.

Умножение вектора на скаляр
F1 F0 a
F0
a 0
F2
F1
F1 F0 a
F0
F2 F0 b
b 0
F2 F0 b

8.

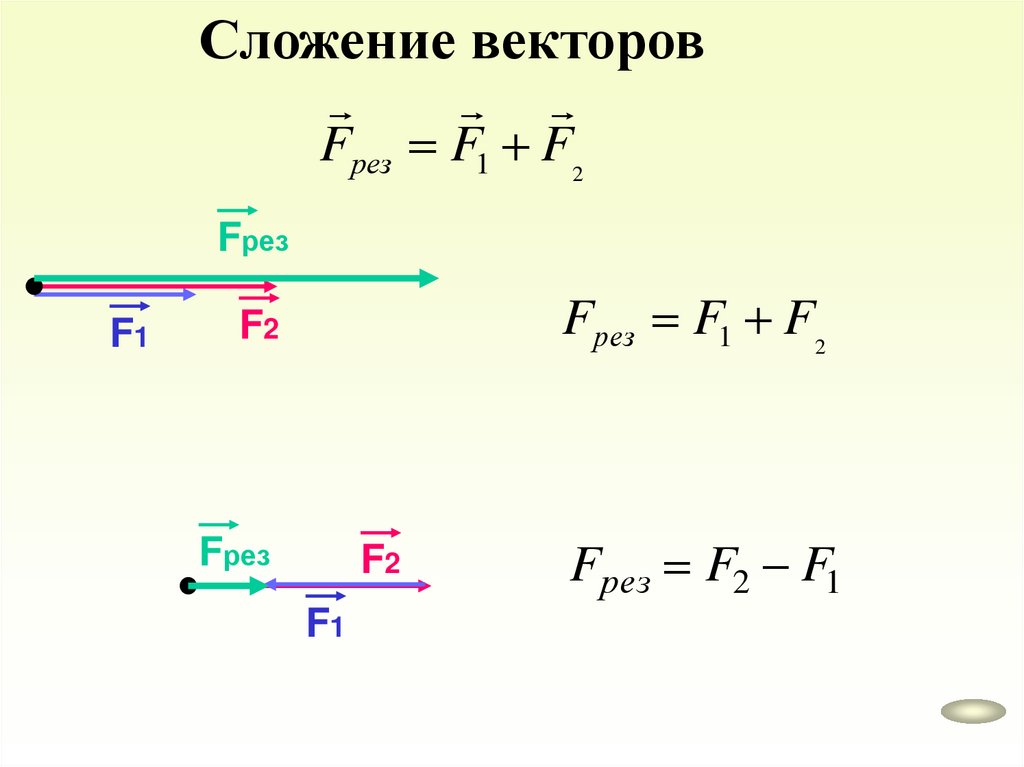
Сложение векторов
Fрез F1 F2
Fрез
F1
Fрез F1 F2
F2
Fрез
F2
F1
Fрез F2 F1

9.

Сложение векторов
Fрез F1 F2
F2
F1
Fрез
F2 Fрез
F1
Fрез F12 F22

10.

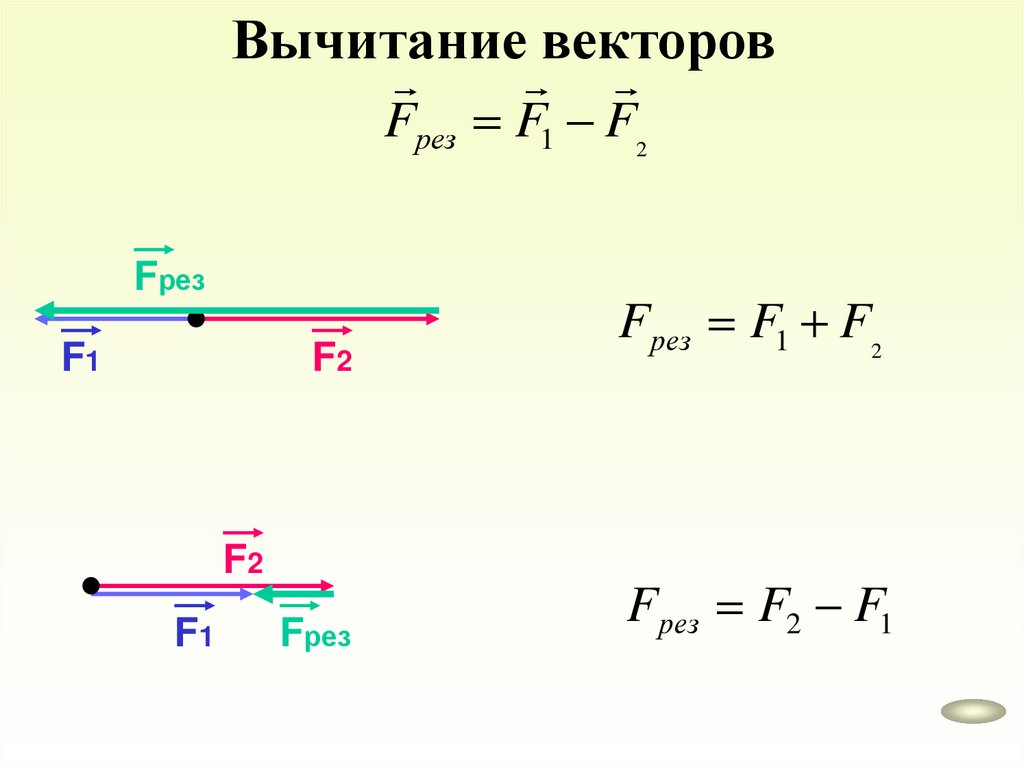
Вычитание векторов
Fрез F1 F2
Fрез
F1
F2
Fрез F1 F2
Fрез
Fрез F2 F1
F2
F1

11.

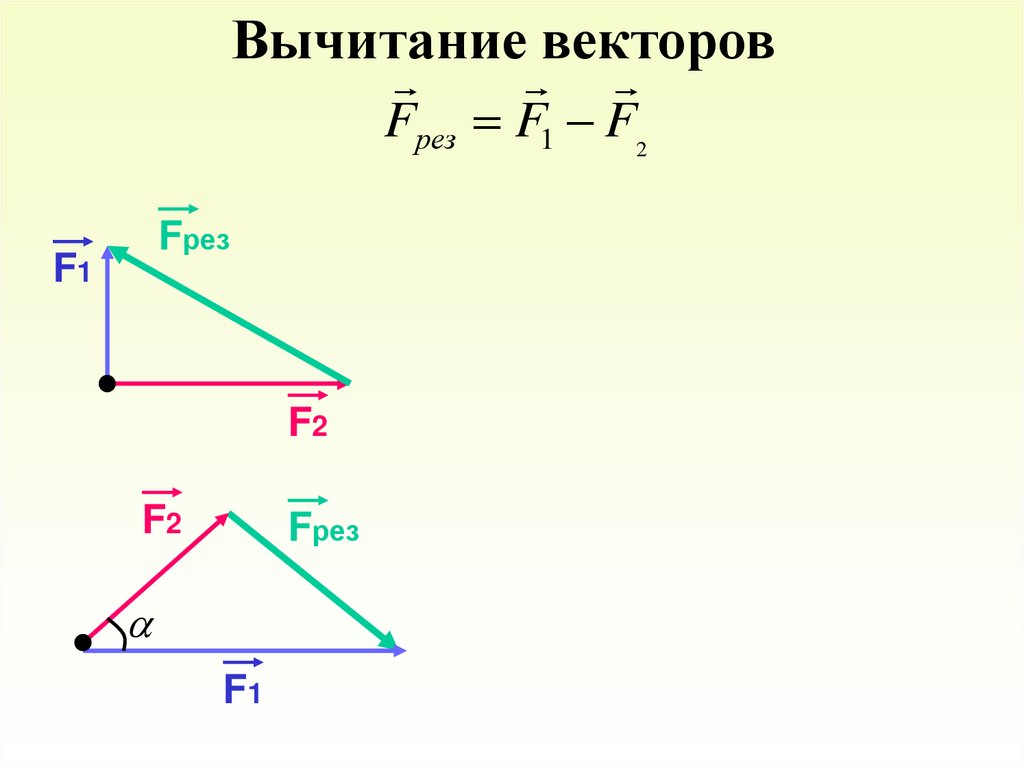
Вычитание векторов
Fрез F1 F2
Fрез
F1
F2
F2
Fрез
F1

12.

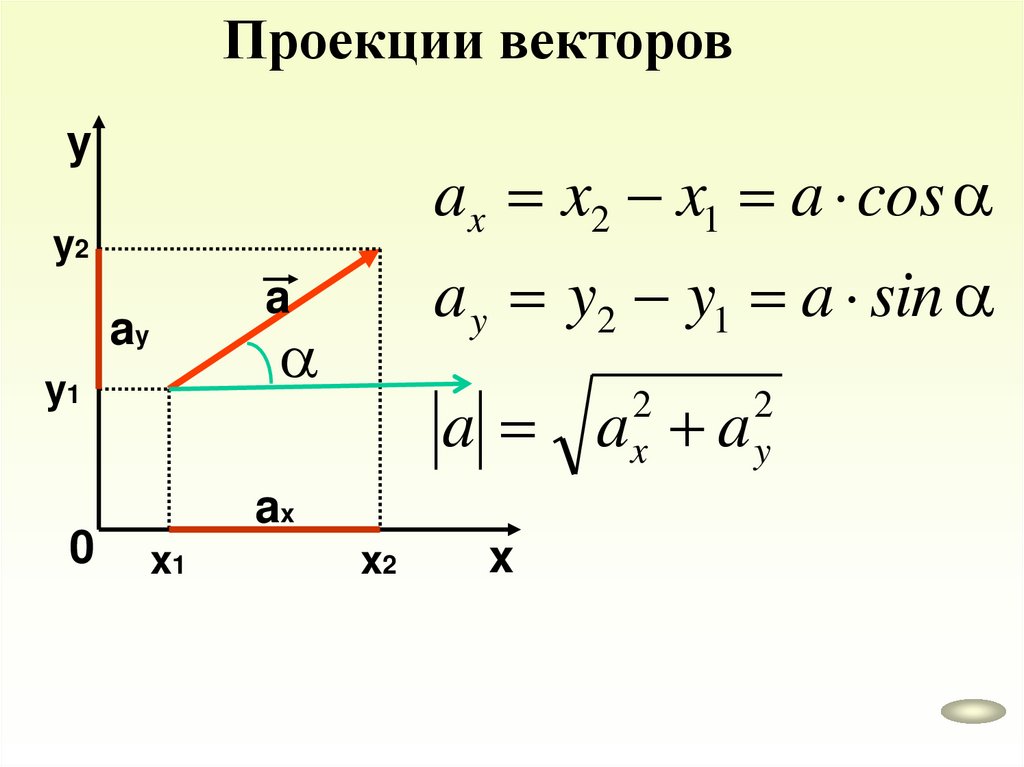
Проекции векторов
y
ax x2 x1 a cos
y2
ay
y1
0
a y y2 y1 a sin
a
a a a
2
x
ax
x1
x2
x
2
y

13.

Важнейшие характеристики
движения материальной
точки: скорость и ускорение.

14.

Прямолинейное и равномерное
движение тела
Равномерное движение – это такое движение при
котором тело за любые равные промежутки времени
проходит одинаковые пути.
Скоростью равномерного прямолинейного движения
тела называется величина,
r r
t
t
r

15.

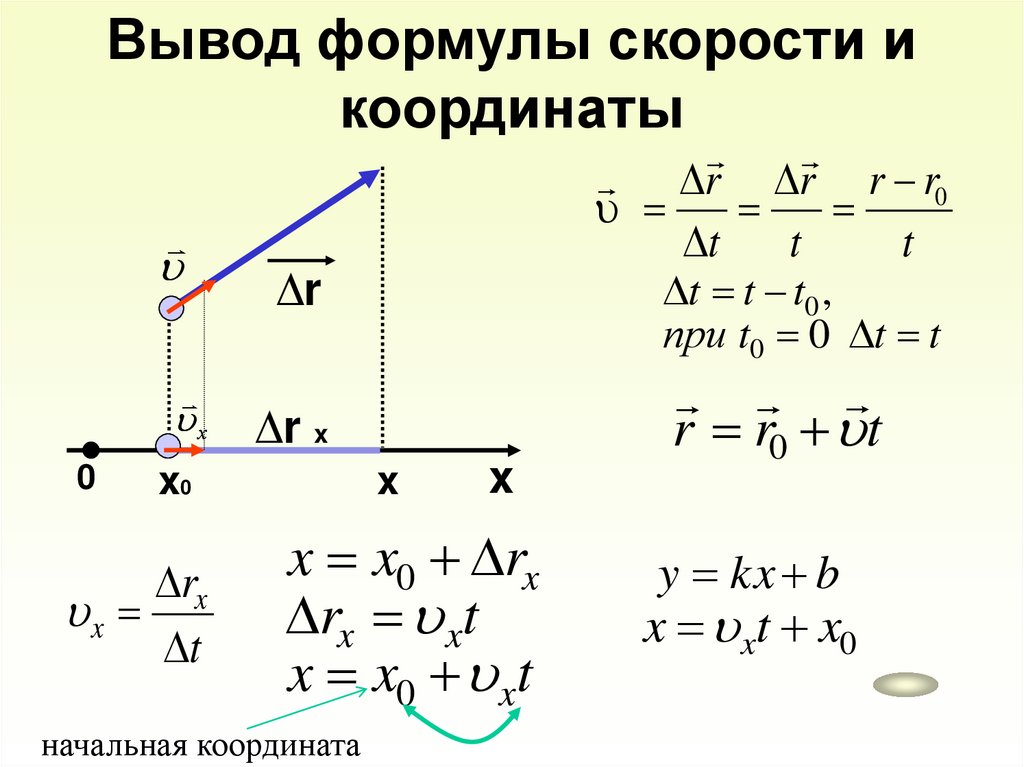
Вывод формулы скорости и
координаты
r r r r0
t
t
t
х
0
t t t0 ,
при t0 0 t t
∆r
∆r x
x0
rx
x
t
x
x
x x0 rx
rx xt
x x0 xt
начальная координата
r r0 t
y kx b
x xt x0

16.

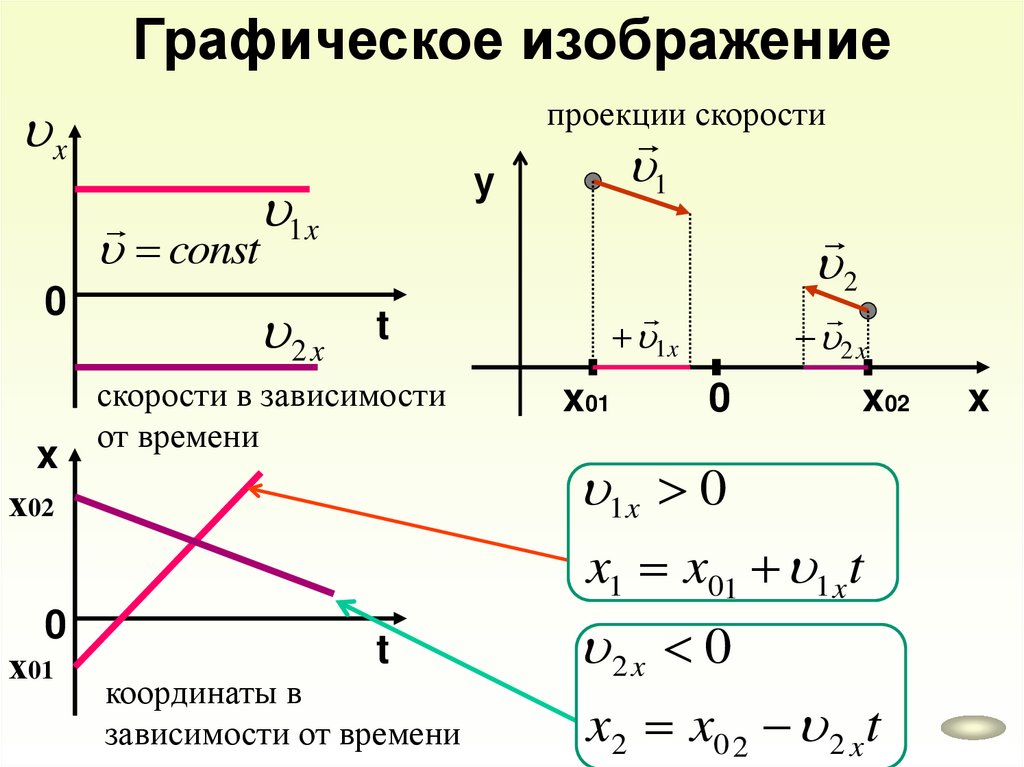
Графическое изображение
x
проекции скорости
1
у
1x
const
0
x
2 x
х02
1x
t
скорости в зависимости
от времени
2
x01
2 x
0
x02
1x 0
x1 x01 1 x t
0
х01
t
координаты в
зависимости от времени
2 x 0
x2 x0 2 2 x t
x

17.

Как посчитать перемещение:
r r r0
S y rу y y y0
Перемещение тела за время ∆t это есть
или S x rx x x x0
x
графический способ
по формуле
x
rx x t
∆rх
0
t0
t
t
Перемещение тела за время ∆t
равно площади фигуры под
графиком зависимости скорости
от времени.

18.

Мгновенная скорость
Ни одно тело не движется все время с
постоянной скоростью.
Если тело проходит различные расстояния за
одни и те же интервалы времени, то тело
движется неравномерно.
Неравномерное движение может быть как
прямолинейным, так и криволинейным.

19.

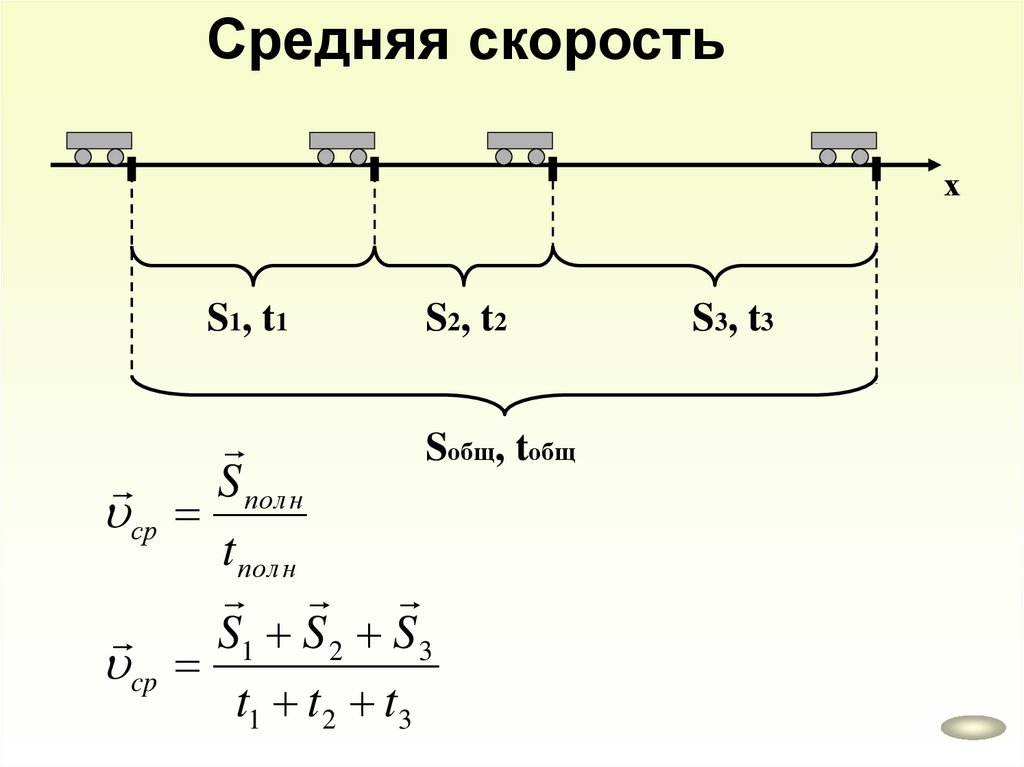
Средняя скорость
х
S1, t1
S2, t2
Sобщ, tобщ
S пол н
ср
t пол н
S1 S 2 S 3
cp
t1 t 2 t3
S3, t3

20.

Чтобы полностью описать неравномерное
движение точки, надо знать ее положение и
скорость в каждый момент времени.
Скорость в данный момент времени называется
мгновенной скоростью.
Мгновенная скорость рассматривается при
любом неравномерном движении.

21.

Любую траекторию всегда можно
представить как виде множества маленьких
прямолинейных участков, причем если
рассматривать очень маленькие участки, на
которых скорость не успевает меняться, то
можно каждый из этих участков
рассматривать как участок с равномерным
прямолинейным движением.

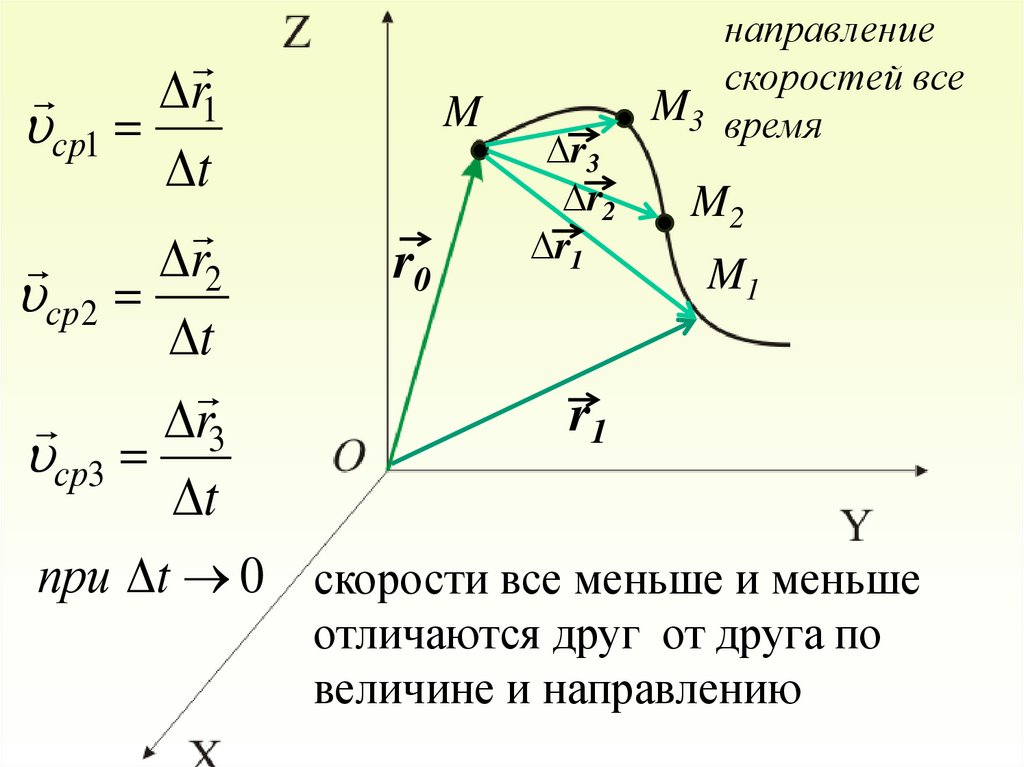
22.

r1
ср1
t
r2
ср 2
t
r3
ср3
t
M
r0
∆r3
∆r2
∆r1
направление
скоростей все
M3 время
M2
M1
r1
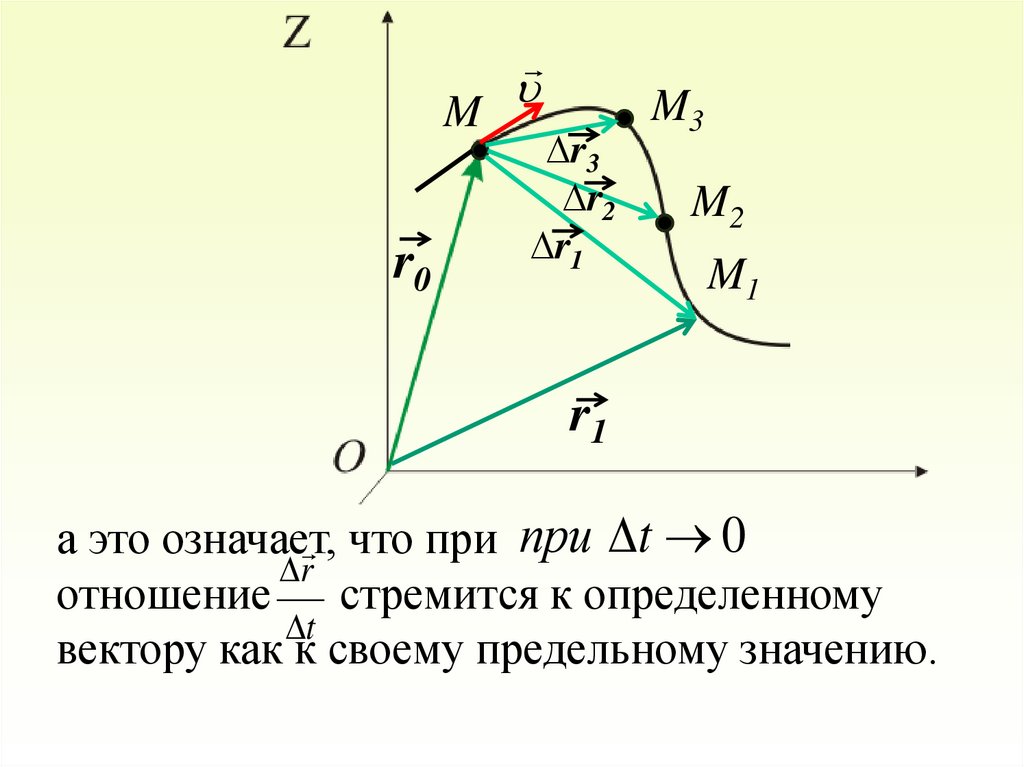
при t 0 скорости все меньше и меньше
отличаются друг от друга по
величине и направлению

23.

M
r0
∆r3
∆r2
∆r1
M3
M2
M1
r1
а это означает,
что при при t 0
r
отношение стремится к определенному
t
вектору как к своему предельному значению.

24.

Мгновенная скорость точки есть
величина, равная пределу отношения
перемещения к промежутку времени, в
течение которого это перемещение
произошло, при стремлении
последнего к нулю.
r
мгн. , при t 0
t
предел
r
м гн. lim
,
t 0 t

25.

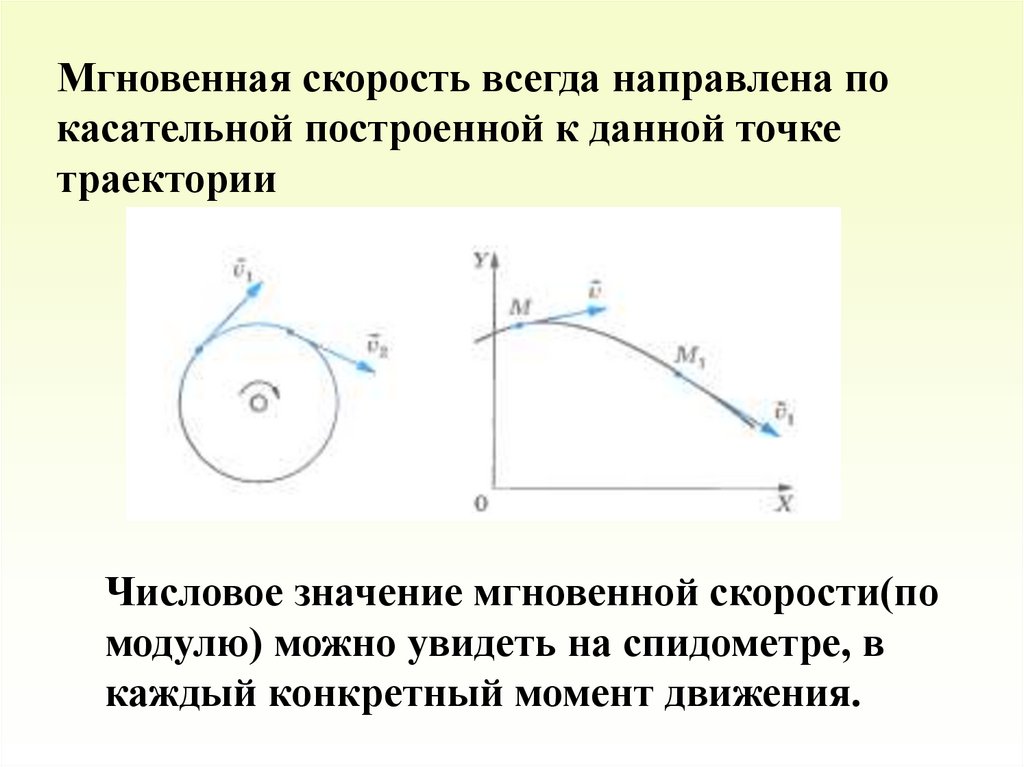
Мгновенная скорость всегда направлена по
касательной построенной к данной точке
траектории
Числовое значение мгновенной скорости(по
модулю) можно увидеть на спидометре, в
каждый конкретный момент движения.

26.

Ускорение
Ускорение - это быстрота изменения скорости
со временем

27.

Ускорение
Ускорение – величина, равная отношению
изменения скорости к промежутку времени,
за которое это изменение произошло, при
условии что последнее стремиться к нулю.
0
a
t
при t 0
м
м
с
а 2
с
с

28.

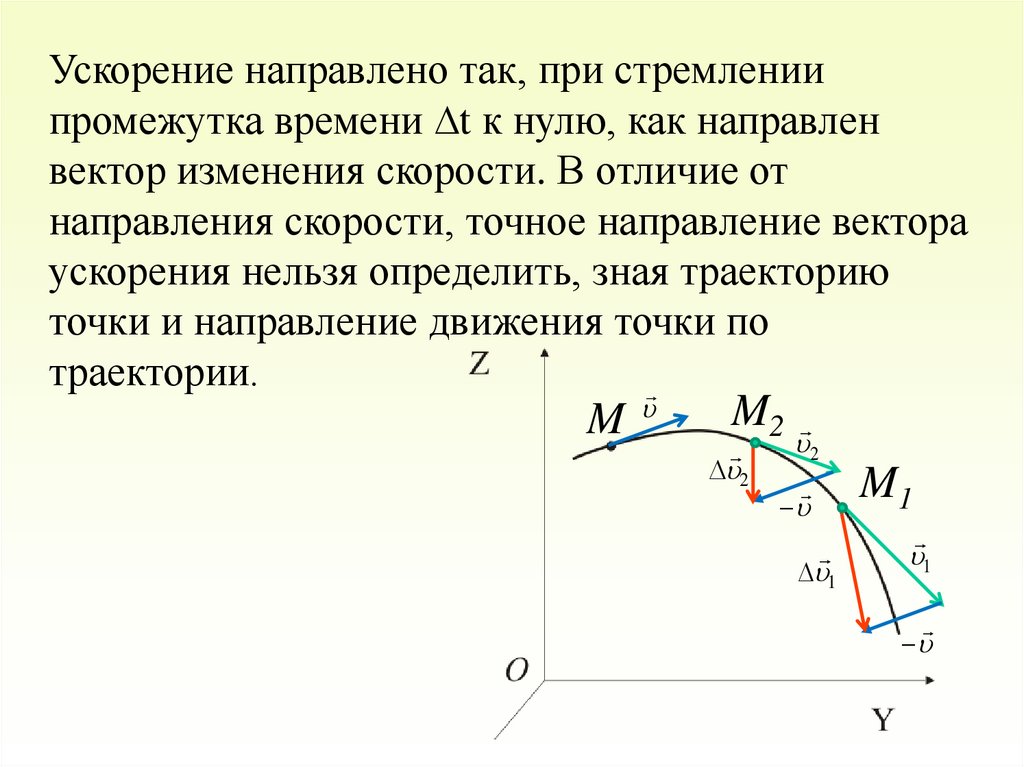
Ускорение направлено так, при стремлении
промежутка времени ∆t к нулю, как направлен
вектор изменения скорости. В отличие от
направления скорости, точное направление вектора
ускорения нельзя определить, зная траекторию
точки и направление движения точки по
траектории.
M
M2
2
2
1
M1
1

29.

Движение с ускорением можно
разделить на два вида: движение с
постоянным ускорением, когда модуль и
направление вектора ускорения не
меняются со временем, и движение с
переменным ускорением, когда
ускорение со временем меняется по
модулю или по направлению.

30.

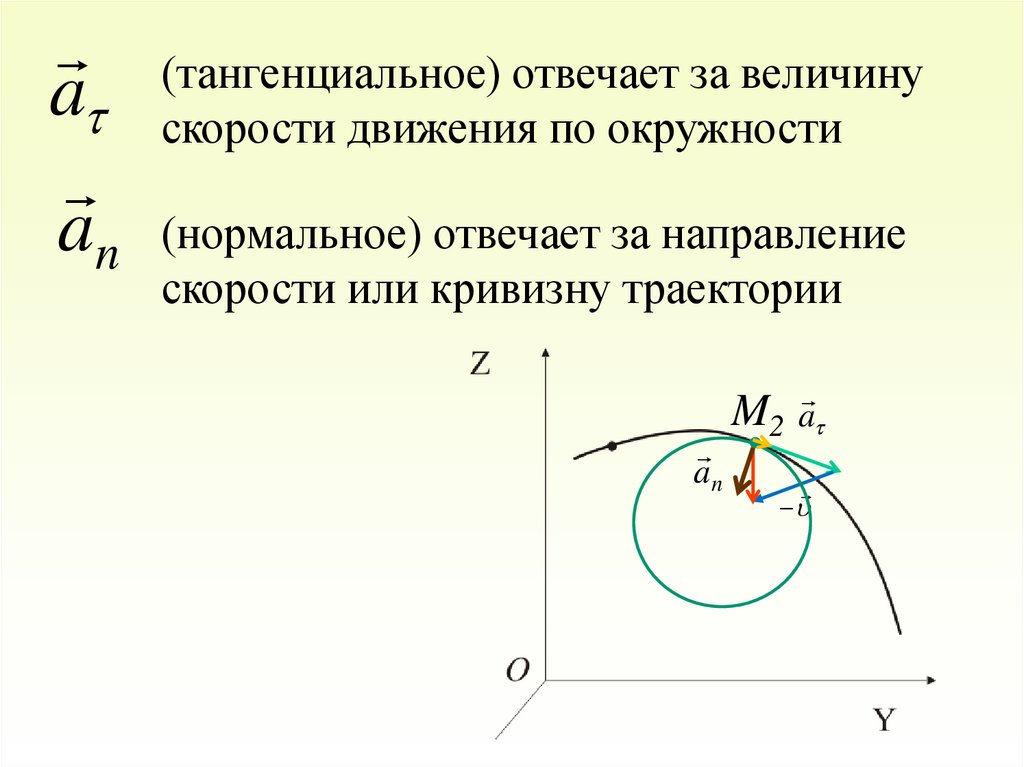
(тангенциальное) отвечает за величину
a скорости движения по окружности
an (нормальное) отвечает за направление
скорости или кривизну траектории
an
M2 a

31.

Прямолинейное движение с
постоянным ускорением
Равноускоренное движение – это движение с постоянным
ускорением, при котором модуль скорости увеличивается.
(a=const)
Равнозамедленное движение – это движение с
постоянным ускорением, при котором модуль скорости
уменьшается. (a=const)
0 0 0
a
, при t 0 0
t t 0
t
t
0
a
0 a t
t

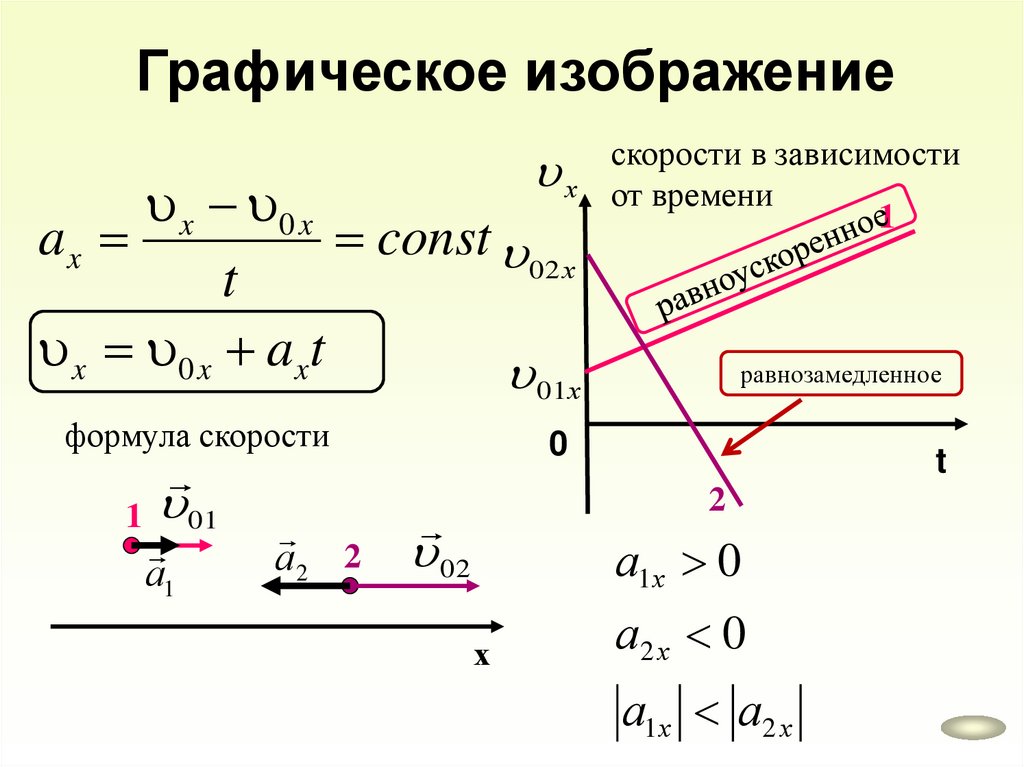
32.

Графическое изображение
ускорения:
x 0 x
ax
const
t
ax
0
ax 0
t
ax 0

33.

Графическое изображение
х
x 0 x
ax
const 02 х
t
x 0 x a x t
скорости в зависимости
от времени
1
равнозамедленное
01х
формула скорости
0
1 01
а1
а2 2
t
2
02
а1х 0
х
а2 х 0
а1х а2 х

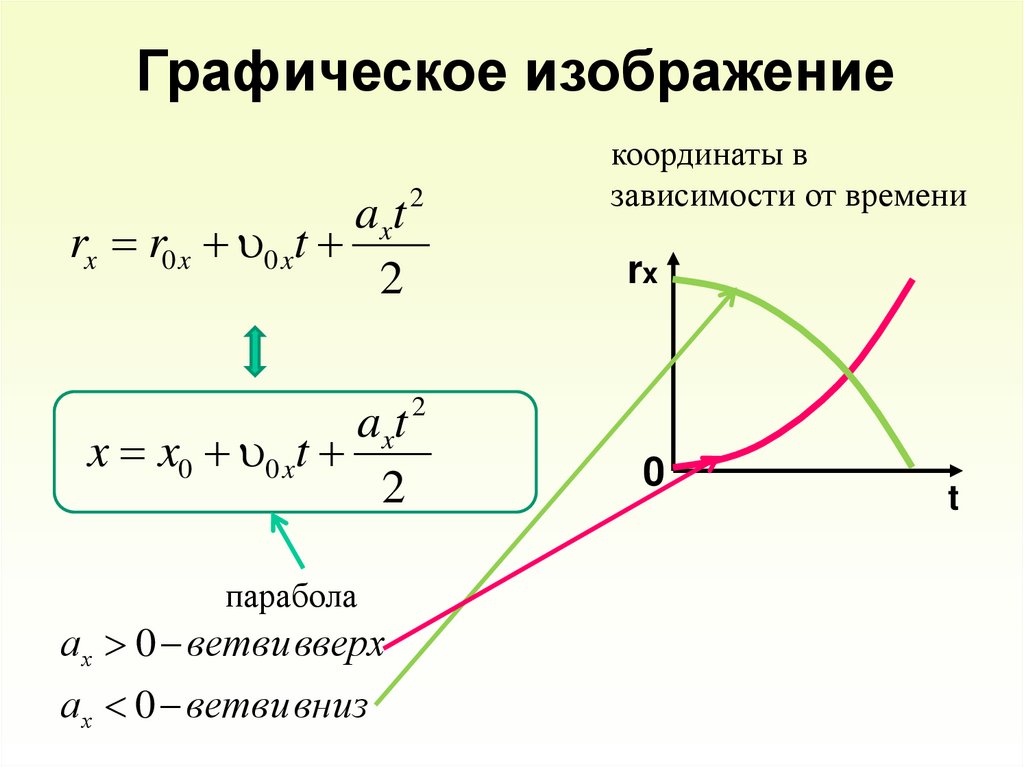
34.

Графическое изображение
axt
rx r0 x 0 xt
2
2
a xt 2
x x0 0 xt
2
парабола
ах 0 ветви вверх
ах 0 ветви вниз
координаты в
зависимости от времени
rx
0
t

35.

Как посчитать перемещение:
х
под графиком скорости –
фигура-трапеция ( в данном
случае)
х
по формуле
axt
rx 0 xt
2
axt
S x x x0 0 xt
2
rx
0 х
0
t0
2
t
t
Перемещение тела за время ∆t
равно площади фигуры под
графиком зависимости скорости
от времени.
2

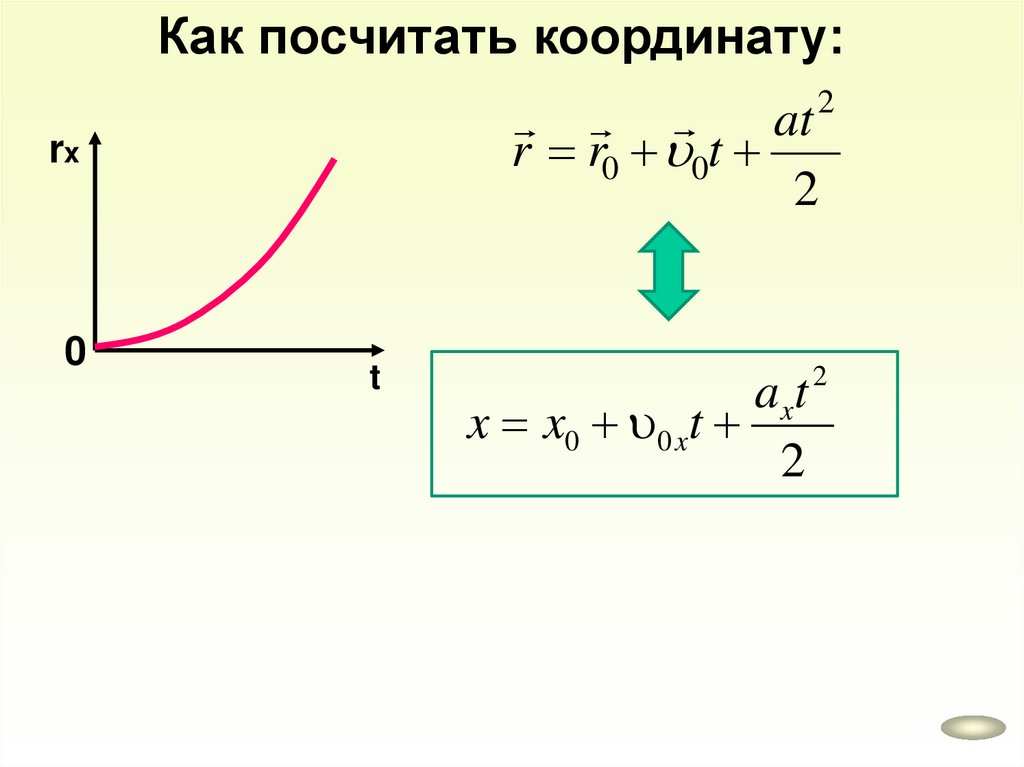
36.

Как посчитать координату:
at 2
r r0 0t
2
rx
0
t
a xt
x x0 0 xt
2
2

37.

Свободным падением называется
движение тела, обусловленного
притяжением Земли, при отсутствии
начальной скорости и сопротивления
среды(например, воздуха)
Все тела с одной и той
же высоты свободно
падают с одной и той
же скоростью, за одно и
то же время, не
зависимо от их массы

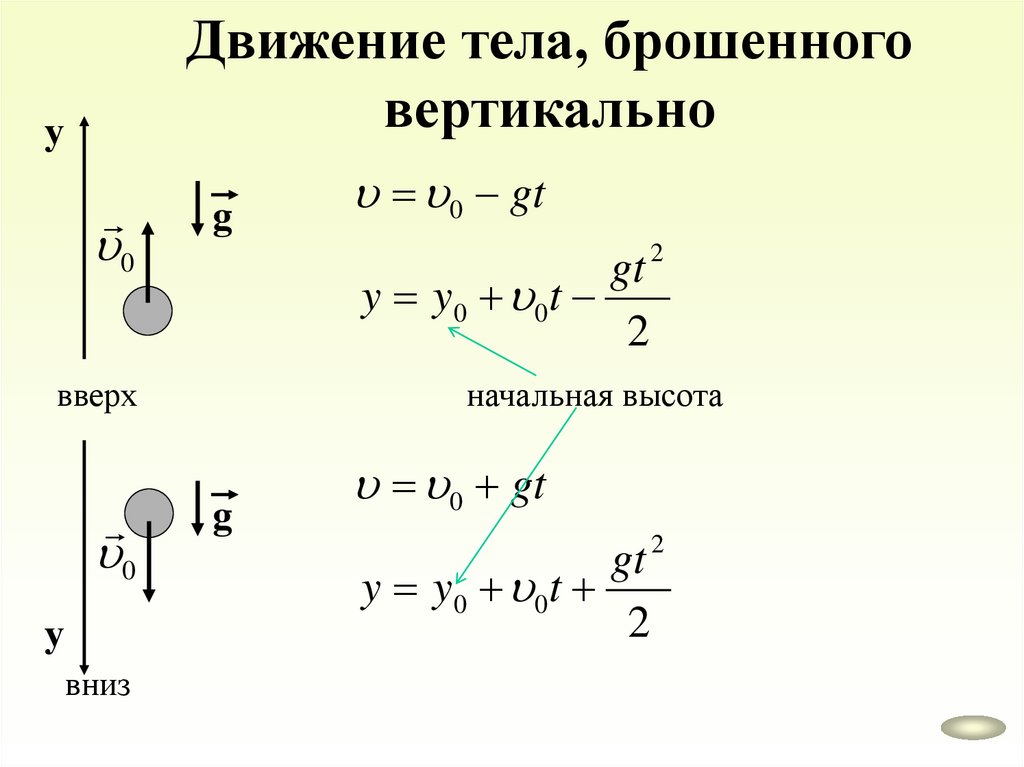
38.

Движение тела, брошенного
вертикально
у
0
g
gt 2
y y0 0t
2
вверх
0
у
вниз
0 gt
начальная высота
g
0 gt
gt 2
y y0 0t
2

39.

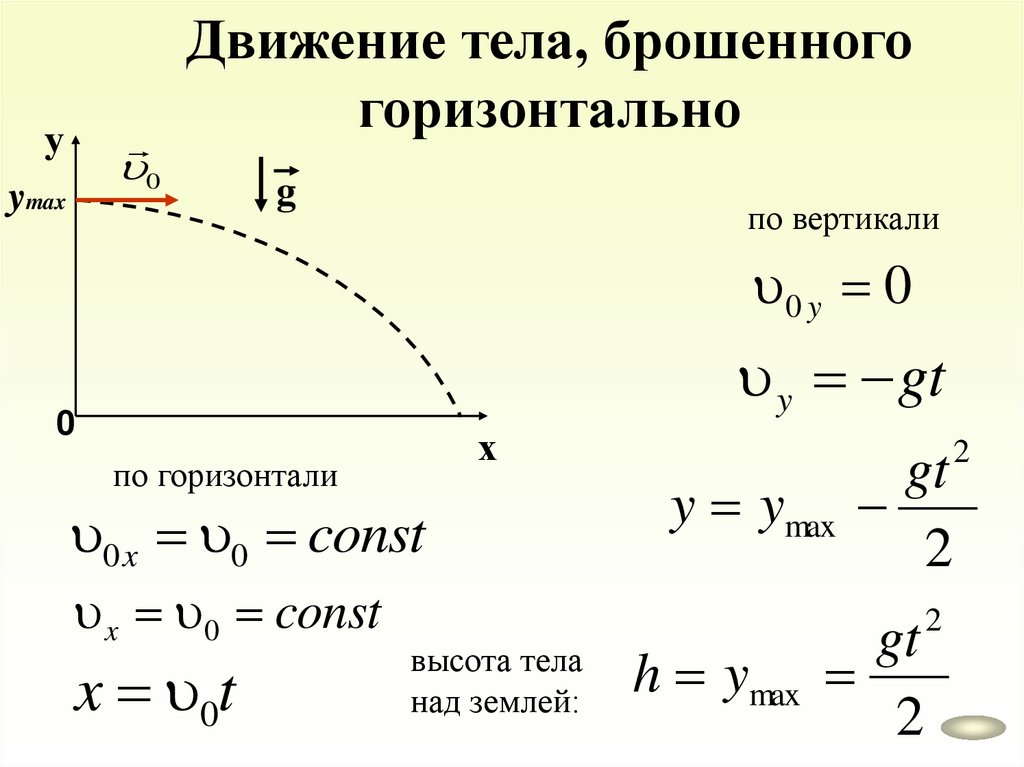
Движение тела, брошенного
горизонтально
у
0
ymax
g
по вертикали
0 y 0
y gt
0
х
по горизонтали
0 x 0 const
x 0 const
x 0t
высота тела
над землей:
gt
y ymax
2
gt
h ymax
2
2
2

40.

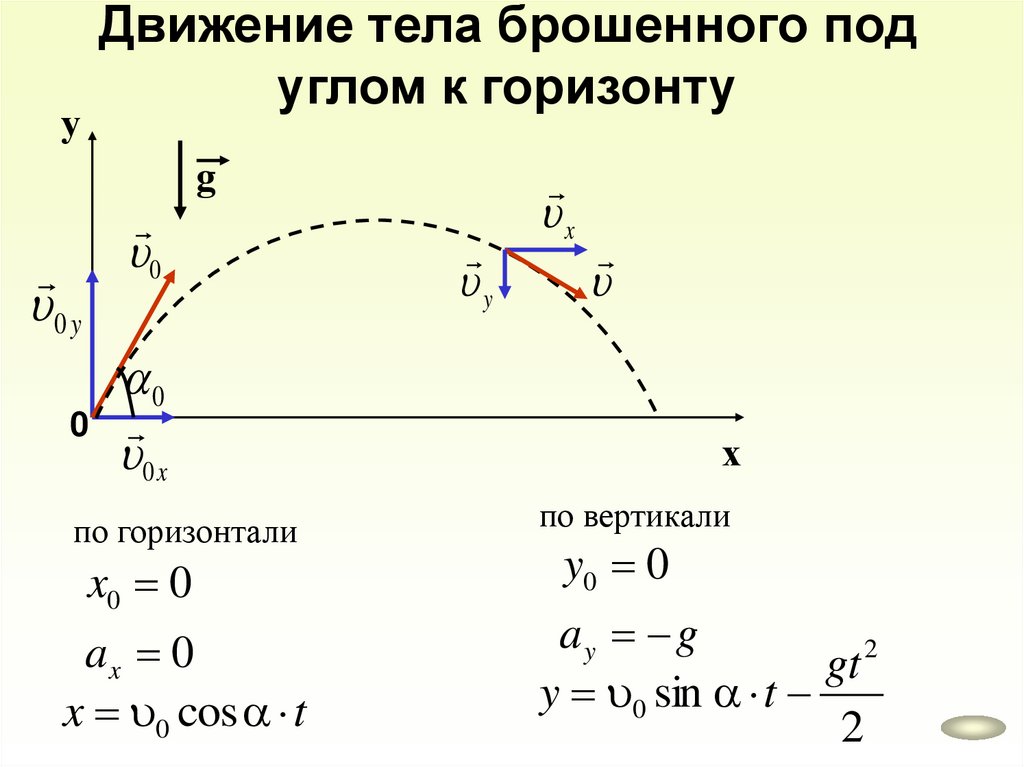
Движение тела брошенного под
углом к горизонту
у
g
0
0 y
0
y
x
0
0 x
по горизонтали
x0 0
ax 0
x 0 cos t
х
по вертикали
y0 0
ay g
2
gt
y 0 sin t
2

41.

Равномерное движение тела по
окружности
0
1 2 3 ...
const
1
R
2
4
3
1 2 3
const

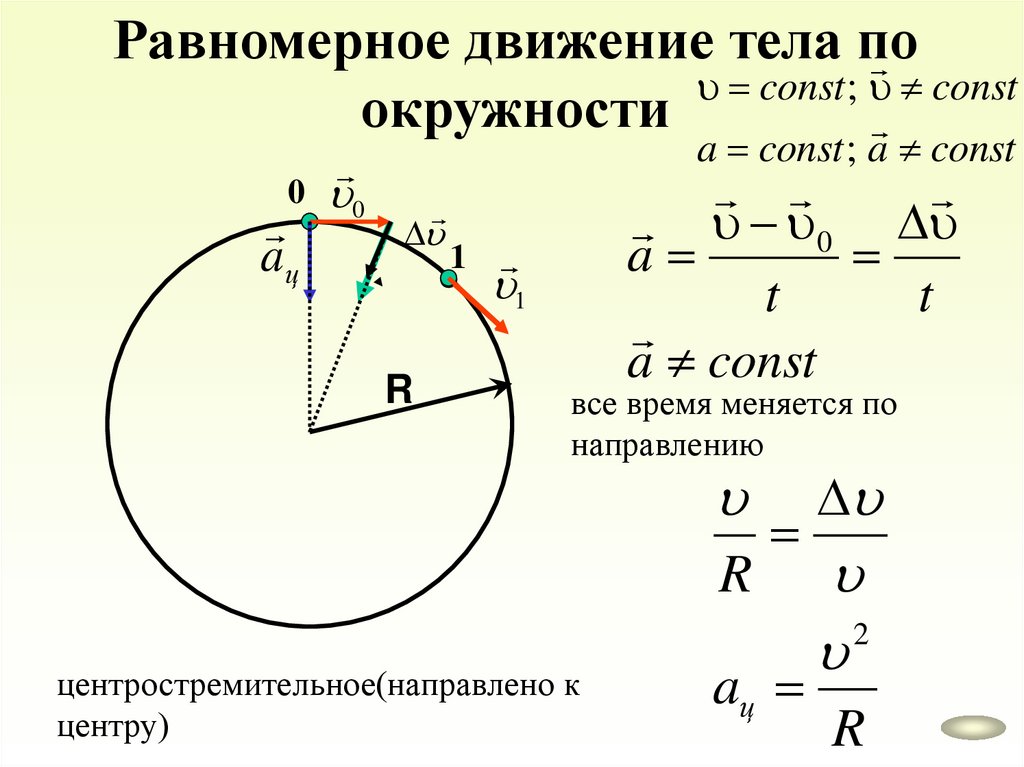
42.

Равномерное движение тела по
const ; const
окружности
a const ; a const
0 0
aц
R
1
1
0
a
t
t
a const
все время меняется по
направлению
R
центростремительное(направлено к
центру)
aц
2
R