Похожие презентации:
Механика. Часть 1. Лекция 2. Кинематика точки. Способы задания движения
1.
Национальныйисследовательский
Томский политехнический
университет
Часть 1
Комплект слайд-лекций для технических
специальностей университета
2.
доктор физико-математических наук,профессор кафедры
Теоретической и прикладной механики
Томского политехнического университета
3.
Кинематика точки.Способы задания движения.
4.
КИНЕМАТИКАКИНЕМАТИКА изучает движение
тел с геометрической точки зрения,
без рассмотрения причин
вызывающих изменение этого
движения, то есть сил
5. Кинематика точки
1. ТРАЕКТОРИЯТраектория движения точки- это
непрерывная неизменяемая линия,
включающая в себя точки
пространства, которые
последовательно занимает точка в
процессе движения
6.
7.
8.
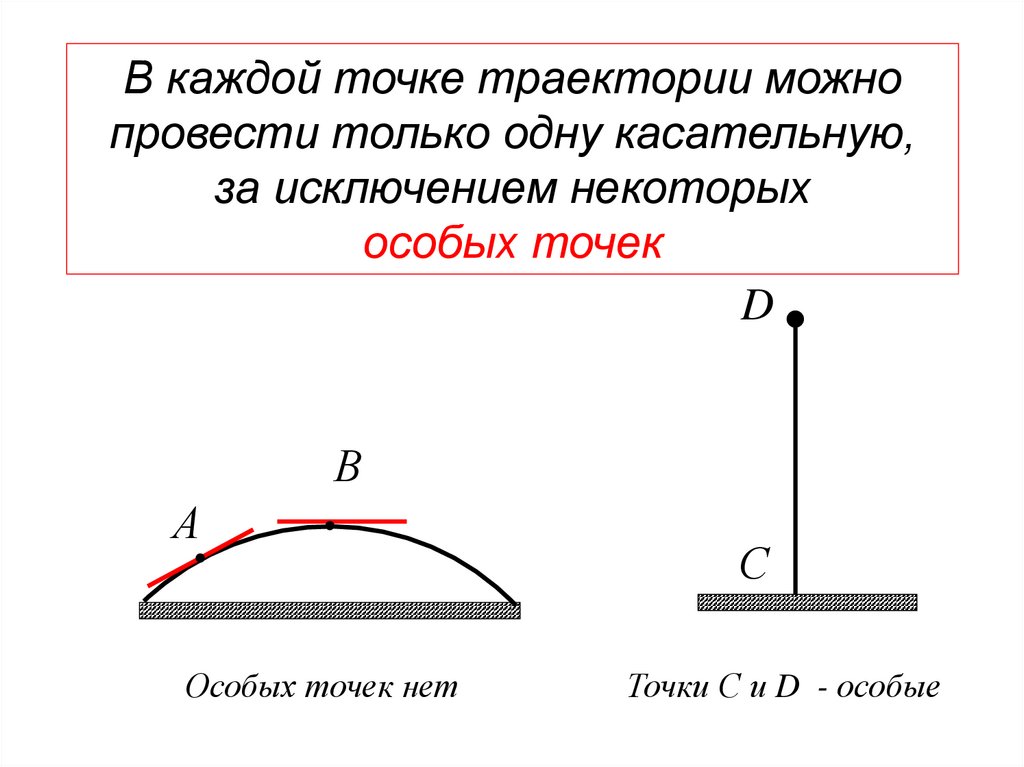
В каждой точке траектории можнопровести только одну касательную,
за исключением некоторых
особых точек
D
В
А
Особых точек нет
С
Точки С и D - особые
9.
Основная задача кинематикисостоит
в том, чтобы при помощи уравнений,
определяющих закон движения точки,
или системы точек, найти все
кинематические характеристики
движения:
•траектории различных
точек,
•их скорости,
•ускорения
•и т.д.
10. 2. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
Определить (задать) движение точки –значит определить (задать) ее положение
относительно выбранной системы
отсчета в любой момент времени.
Существует три способа задания
движения точки:
• естественный
• координатный
• векторный
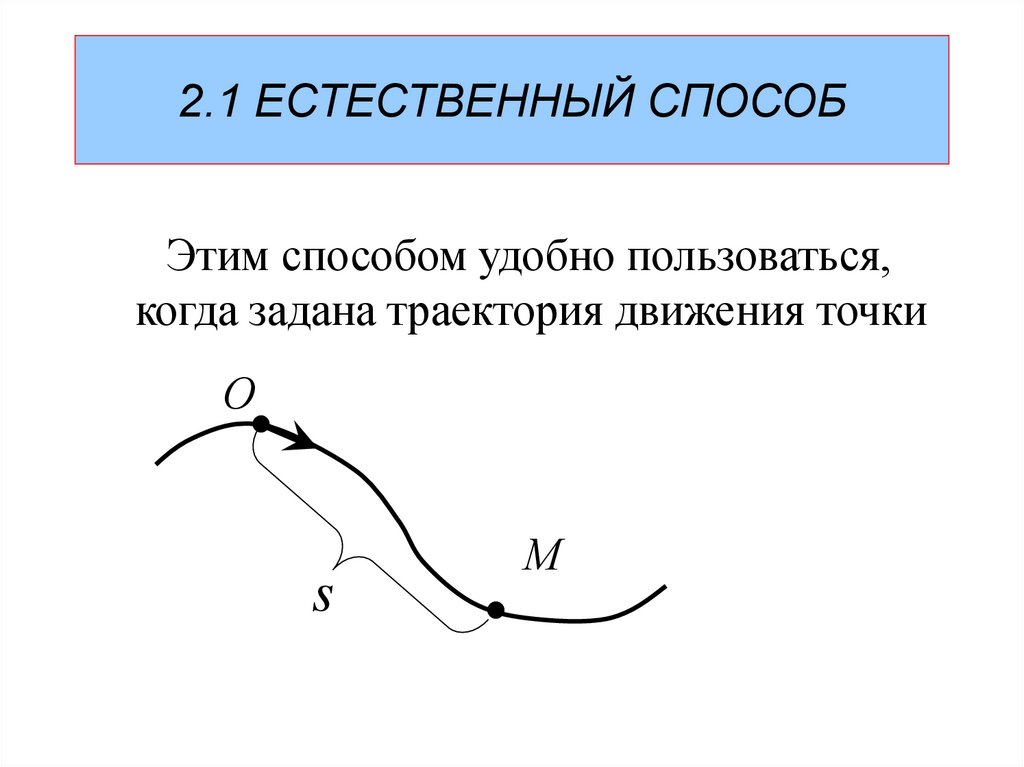
11. 2.1 ЕСТЕСТВЕННЫЙ СПОСОБ
Этим способом удобно пользоваться,когда задана траектория движения точки
О
М
12.
2.1 ЕСТЕСТВЕННЫЙ СПОСОБЭтим способом удобно пользоваться,
когда задана траектория движения точки
О
s
М
13.
Следует различать понятия:• «пройденный путь»
• «перемещение»
• «дуговая (естественная)
координата» - s
14.
Следует различать понятия:• «пройденный путь»
• «перемещение»
• «дуговая (естественная)
координата» - s
s s t
- закон движения точки
s(t) – функция однозначная, непрерывная,
дифференцируемая
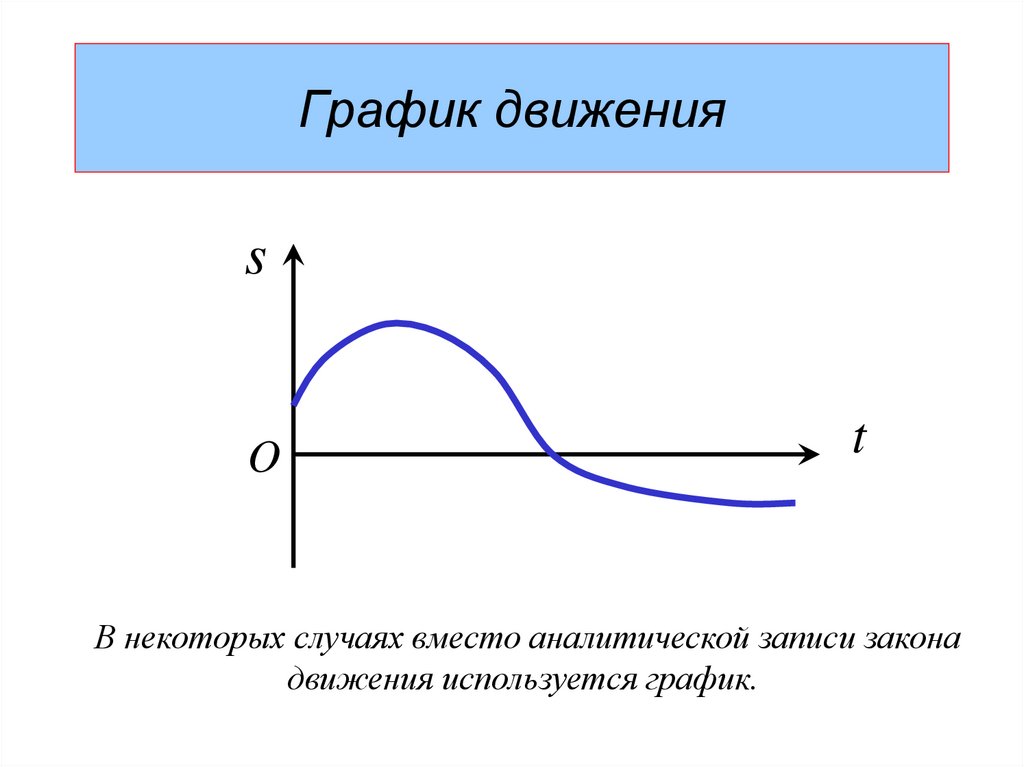
15. График движения
sO
t
В некоторых случаях вместо аналитической записи закона
движения используется график.
16. 2.2 Координатный способ
Виды координатных систем:• декартова прямоугольная
• цилиндрическая (полярная)
• сферическая
• и т.д.
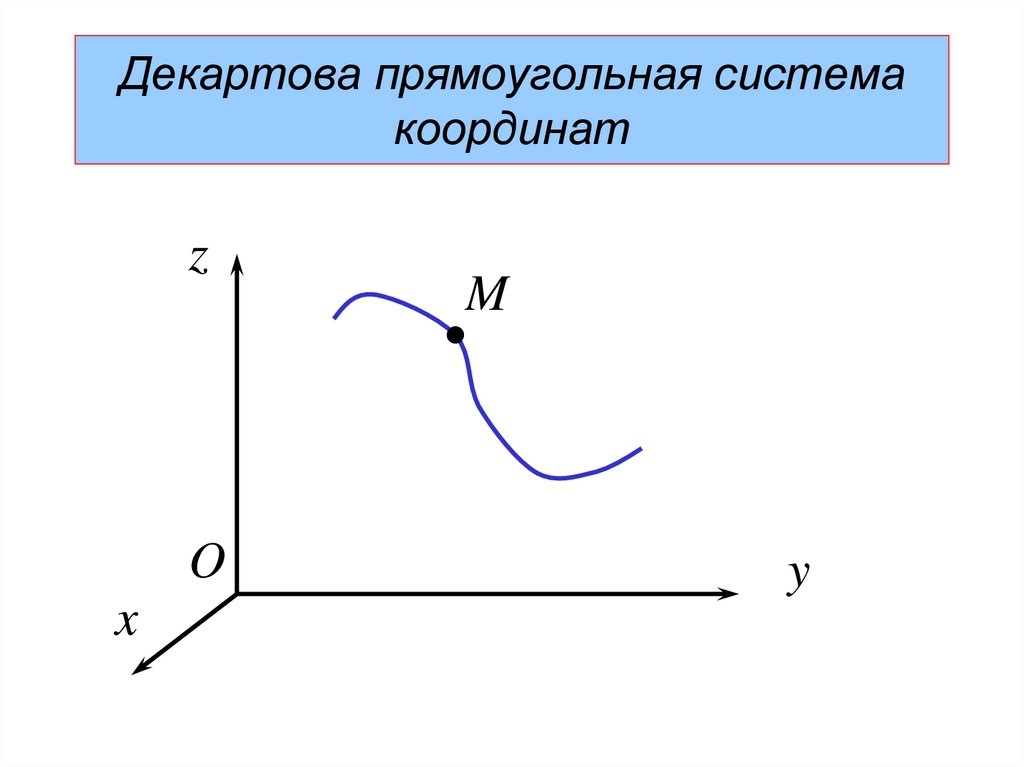
17. Декартова прямоугольная система координат
zO
x
M
y
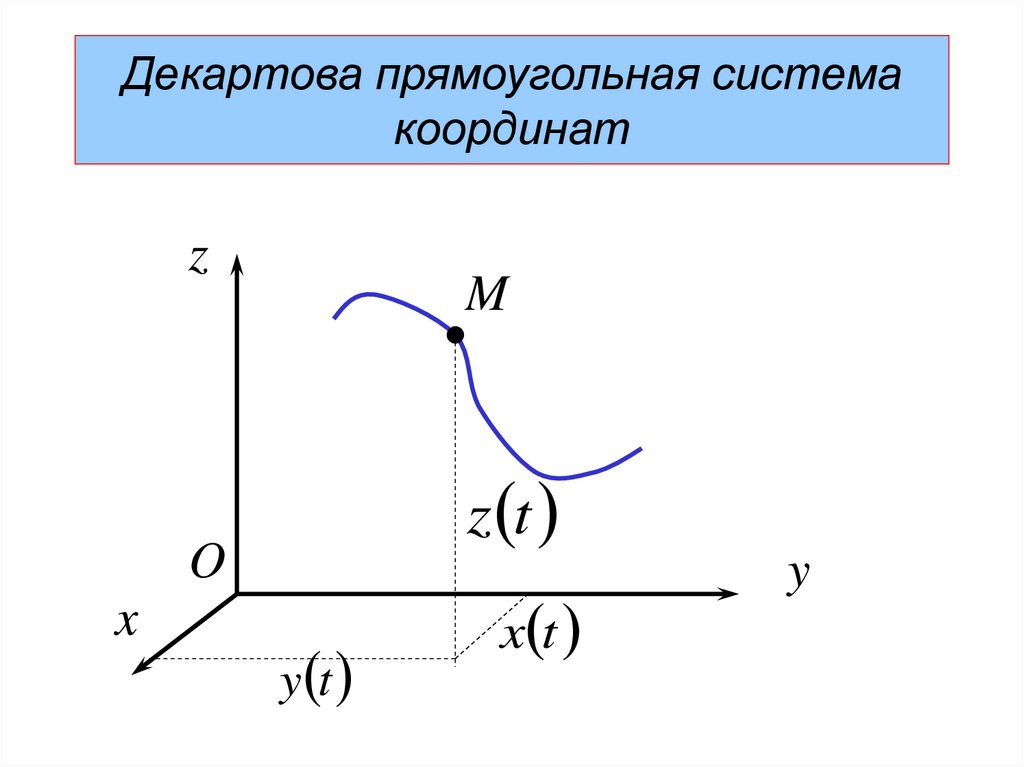
18.
Декартова прямоугольная системакоординат
z
M
z t
O
x
y t
x t
y
19. Уравнения движения:
x x ty y t
z z t
(1)
20. ПРИМЕР:
Точка совершает движение согласноуравнениям:
x 6 3t
y 4t
Определить уравнение траектории
точки М.
(2)
21. РЕШЕНИЕ:
yt ;
4
x 6 0 ,75 y
22.
РЕШЕНИЕ:y
t ;
4
x 6 0 ,75 y
y
O
6
x
8
Траекторией точки является полупрямая линия.
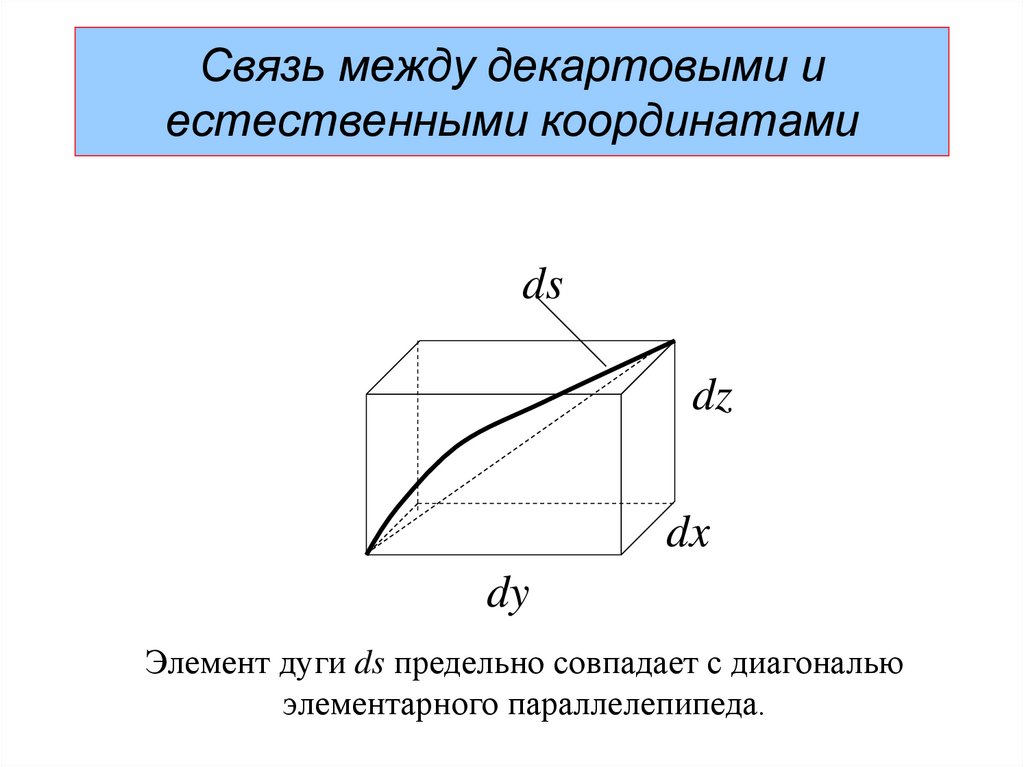
23. Связь между декартовыми и естественными координатами
dsdz
dx
dy
Элемент дуги ds предельно совпадает с диагональю
элементарного параллелепипеда.
24.
Связь между декартовыми иестественными координатами
ds
dz
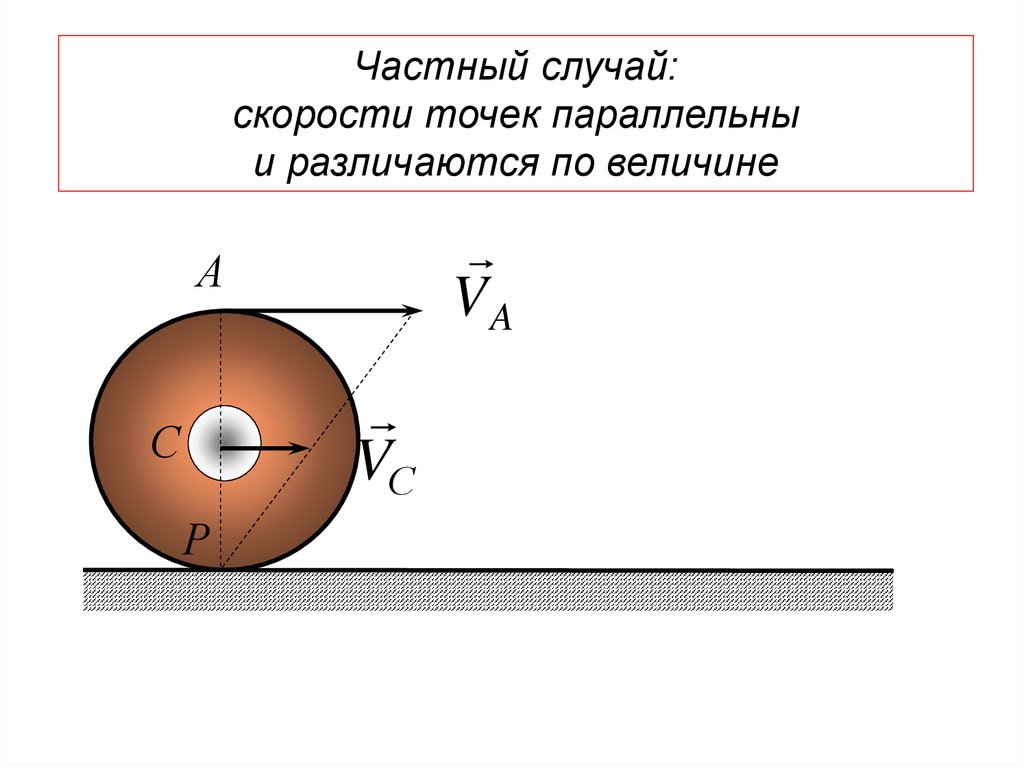
dx
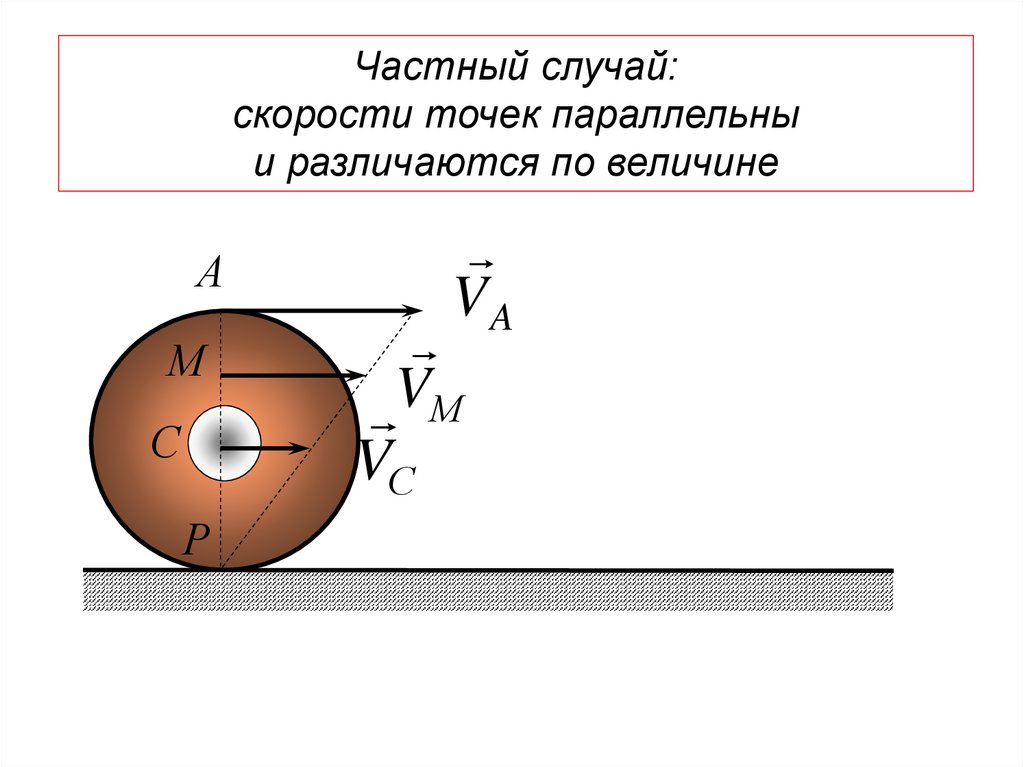
dy
ds dx dy dz
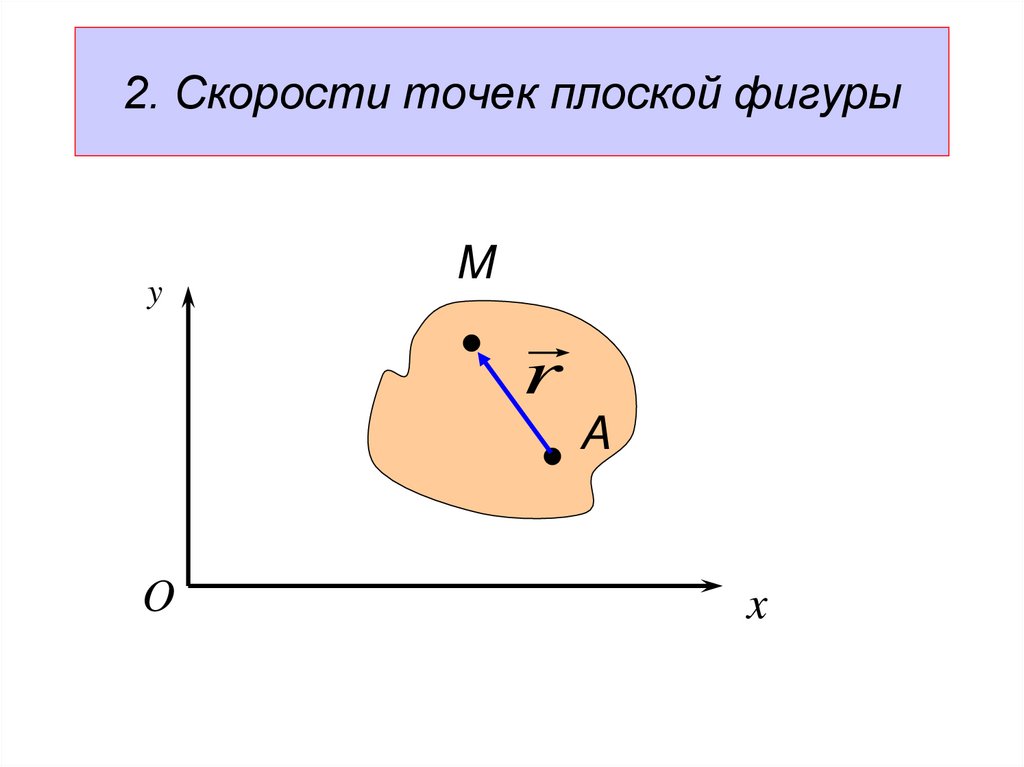
2
2
2
2
25.
dxdx dt ;
dt
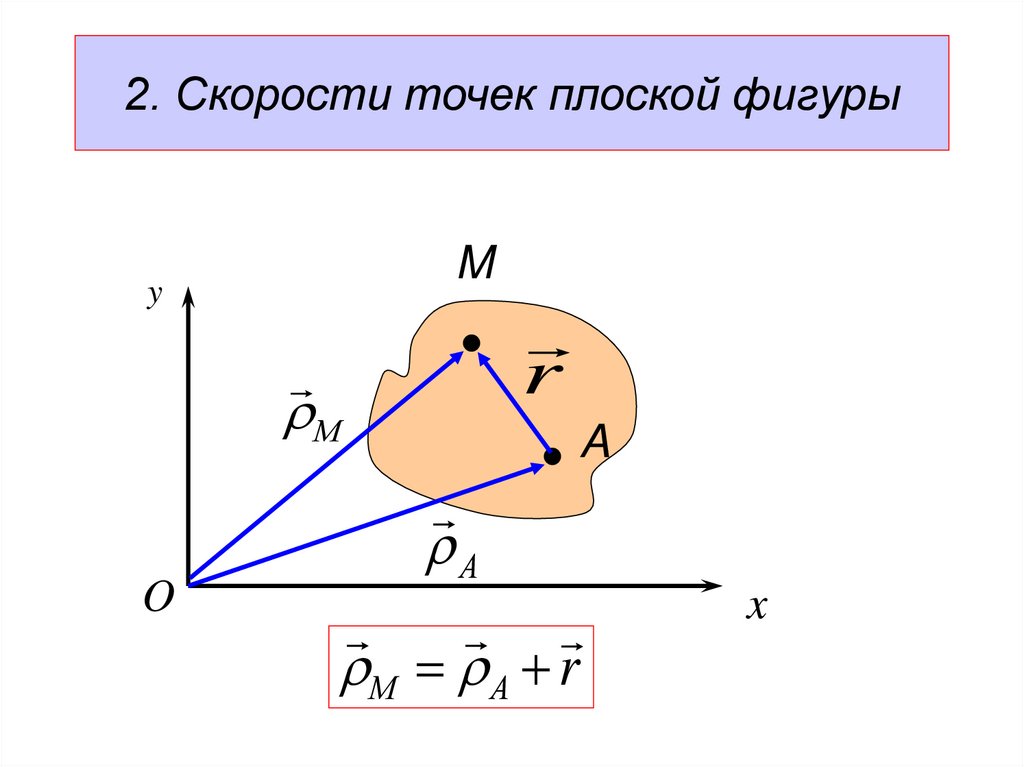
dy
dy dt ;
dt
dz
dz dt
dt
26.
dxdx dt ;
dt
dy
dy dt ;
dt
2
2
dz
dz dt
dt
2
dx dy dz
ds dt
dt dt dt
(3)
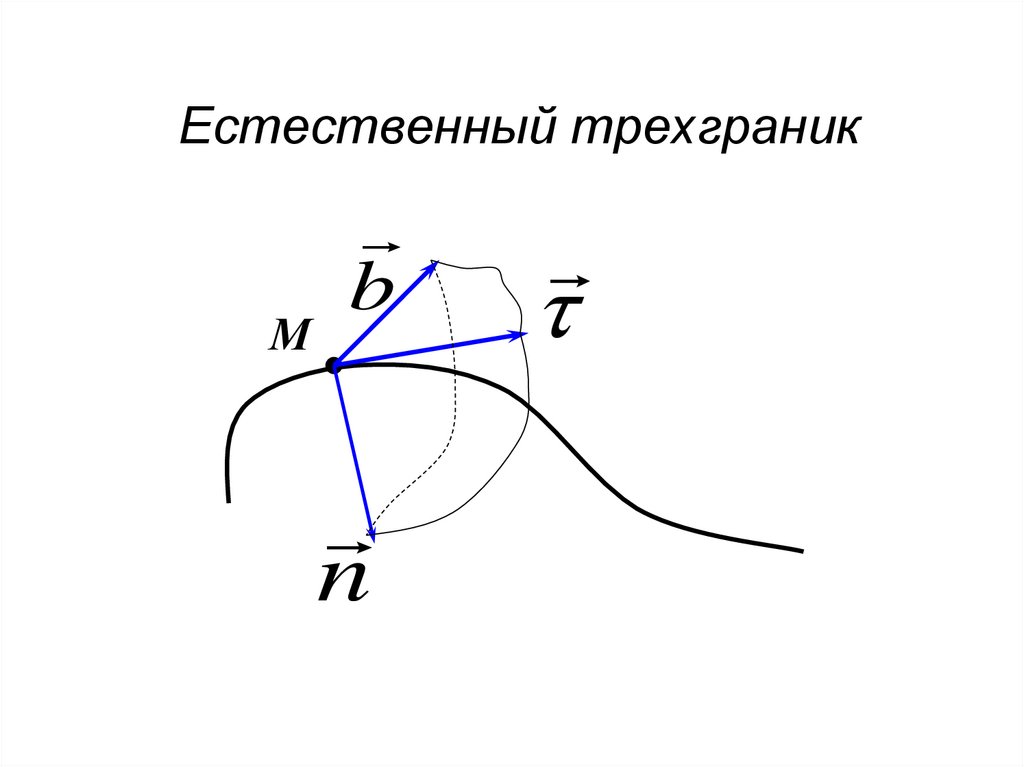
27.
dxdx dt ;
dt
dy
dy dt ;
dt
2
dz
dz dt
dt
2
2
dx dy dz
ds dt
dt dt dt
s
2
2
(3)
2
dx dy dz
dt s0
dt dt dt
(4)
28.
Частный случай:если подкоренное выражение не зависит
от времени:
2
2
2
dx dy dz
s t s0 (5)
dt dt dt
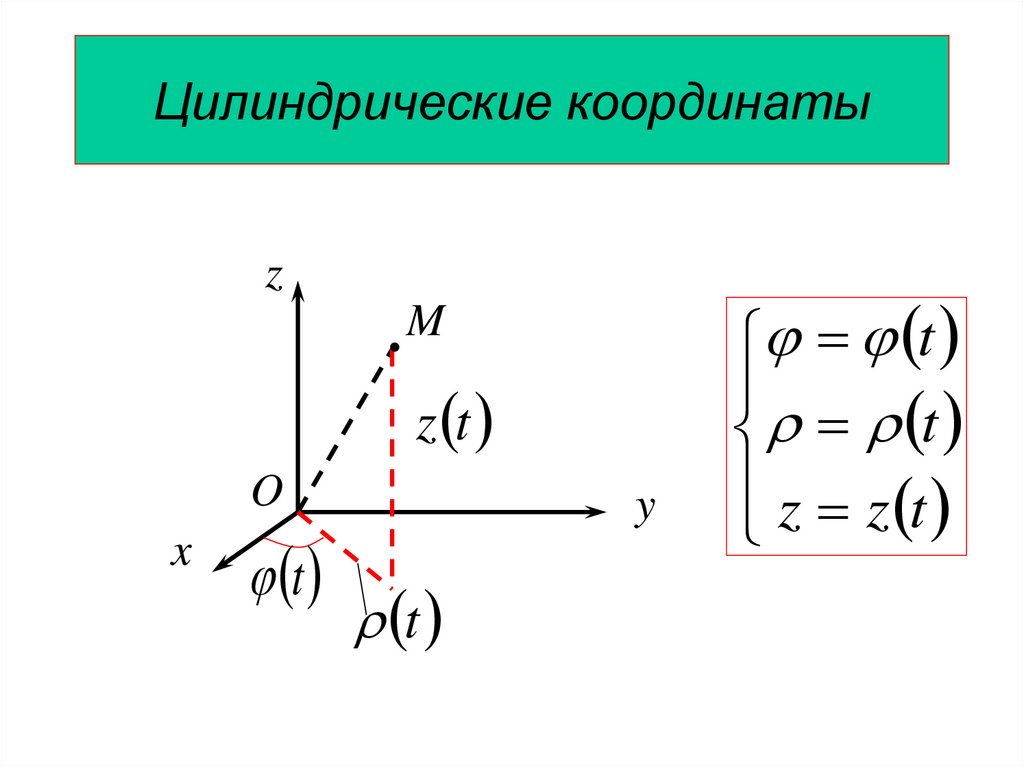
29.
Цилиндрические координатыz
M
z t
O
x
t
y
t
t
t
z z t
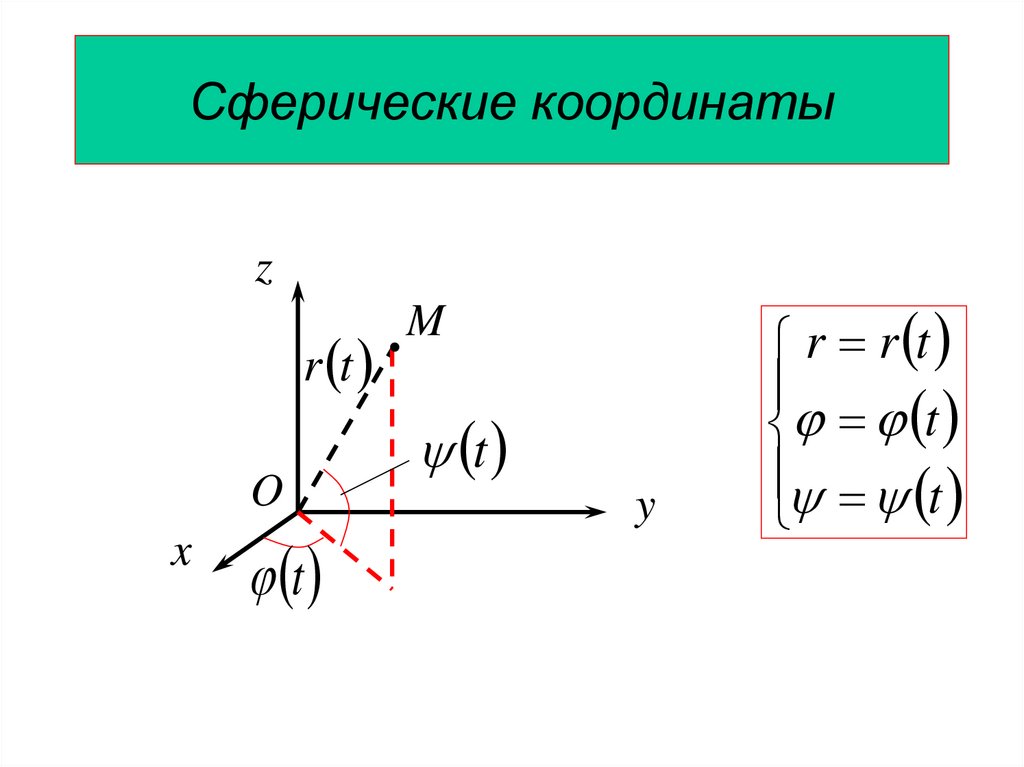
30. Сферические координаты
zr t
O
x
t
M
t
y
r r t
t
t
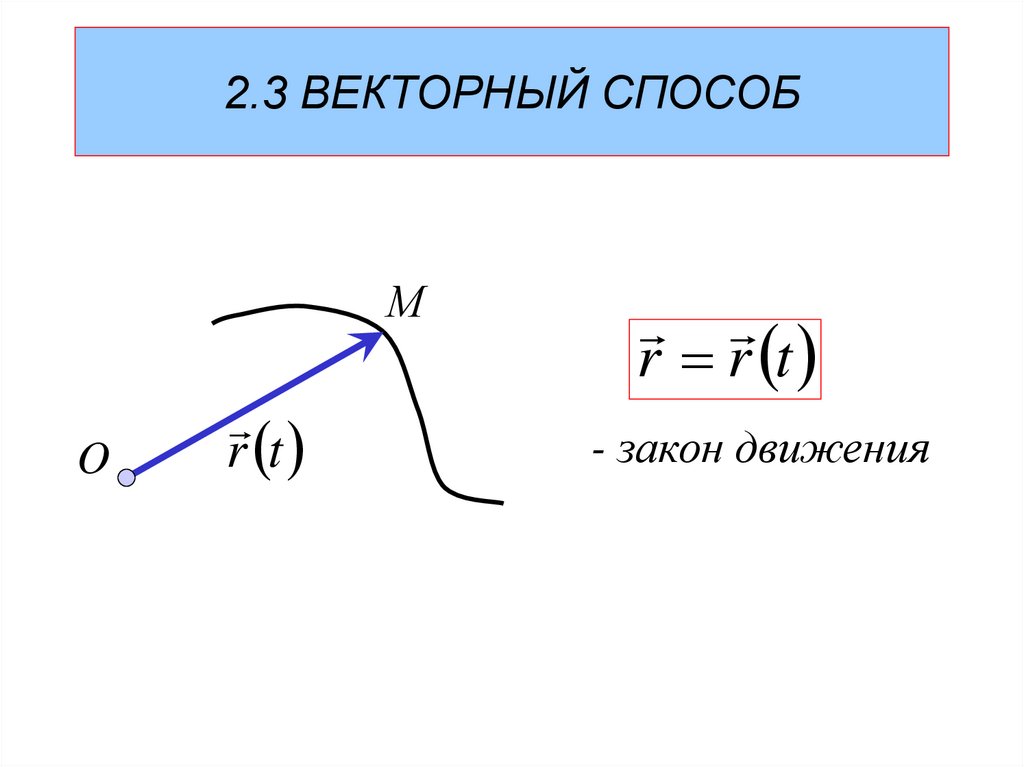
31. 2.3 ВЕКТОРНЫЙ СПОСОБ
МO
r t
r r t
- закон движения
32.
2.3 ВЕКТОРНЫЙ СПОСОБМ
O
r t
r r t
- закон движения
Связь с декартовыми координатами:
r xi yj zk
33. ПРИМЕР:
Закон движения точки задан в виде:2
r 2ti 5 j 3t k
(7)
Записать закон движения точки в координатной форме.
34.
ПРИМЕР:2
r 2ti 5 j 3t k
x 2t
y 5
2
z 3t
(7)
35.
После просмотра и конспектирования слайд-лекциинеобходимо прочитать указанные страницы
учебников и дополнить конспект наиболее важными
сведениями
1. Тарг С.М. Краткий курс теоретической механики:
Учеб. для втузов.- 10-е изд. – М: ВШ, 1986. С. 9599.
36.
Скорость точки.37.
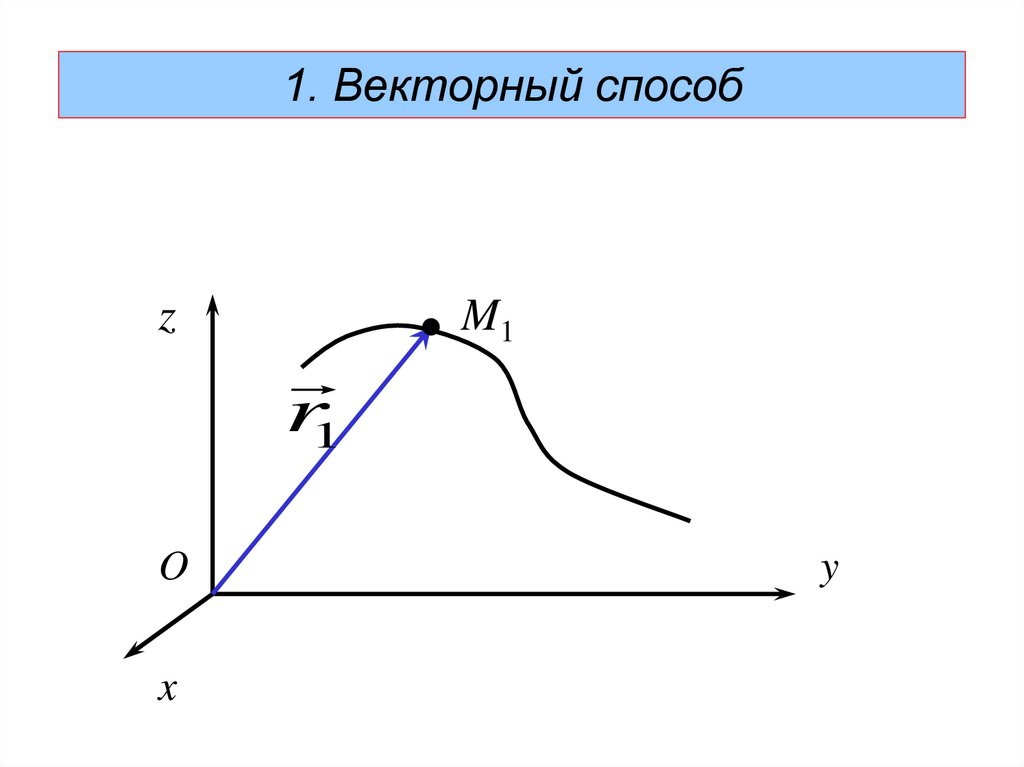
1. Векторный способz
O
x
r1
M1
y
38.
1. Векторный способz
M1
r1
O
x
r2
M2
y
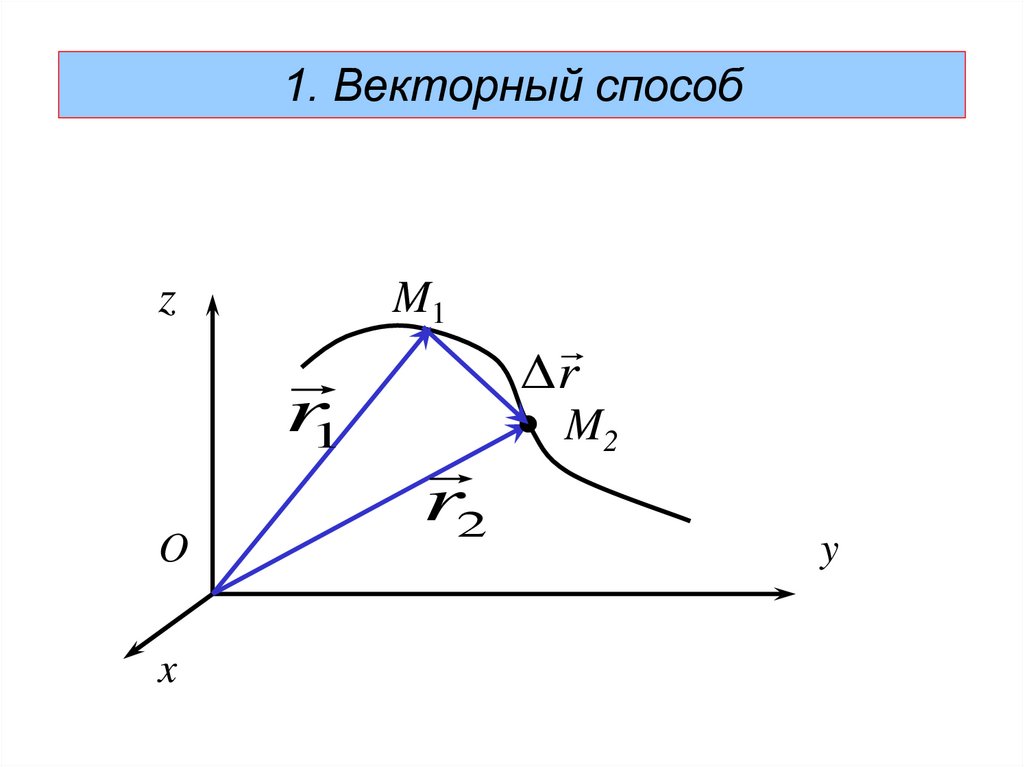
39.
1. Векторный способz
M1
r1
O
x
r2
Δr
M2
y
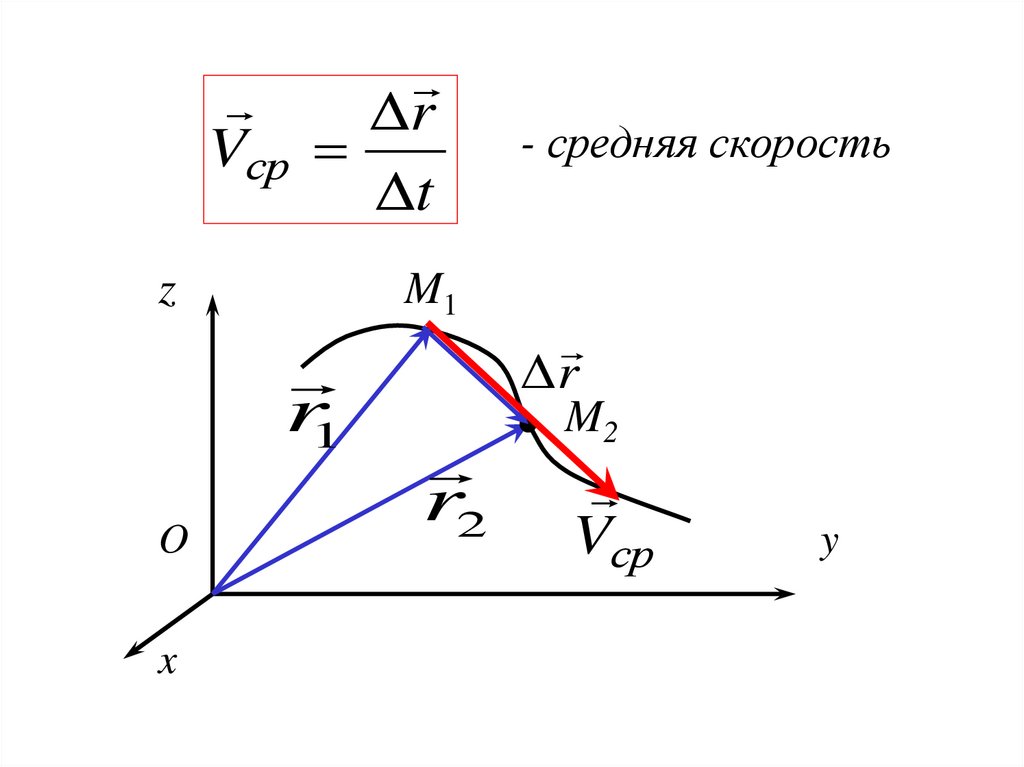
40.
ΔrVср
Δt
z
M1
r1
O
x
r2
- средняя скорость
Δr
M2
Vср
y
41.
Совершим предельный переход приt 0
Получим значение скорости в данный момент
времени (мгновенную скорость):
r d r
V lim
dt
t 0 t
(1)
42.
V направлен по касательнойВектор скорости
к траектории движения точки.
z
M
r
O
x
V
y
43.
ОПРЕДЕЛЕНИЕ:Скорость точки в данный момент
времени есть вектор, определяемый как
производная по времени радиус-вектора,
характеризующего ее движение.
dr
V
dt
(2)
44.
2. Естественный способТак как
то
dr ds
dr
ds
V
dt
dt
(3)
45.
3. Координатный способТак как
то
r xi yj zk
dr dx dy dz
V
i
j k
dt dt
dt
dt
dx
Vx
;
dt
dy
Vy
;
dt
dz
Vz
;
dt
(4)
46.
Координатный способМодуль скорости:
V
2
2
2
Vx V y Vz
x y z
2
2
2
Направляющие косинусы вектора скорости:
Vy
cos V , j
;
V
Vx
cos V , i ;
V
Vz
cos V , k ;
V
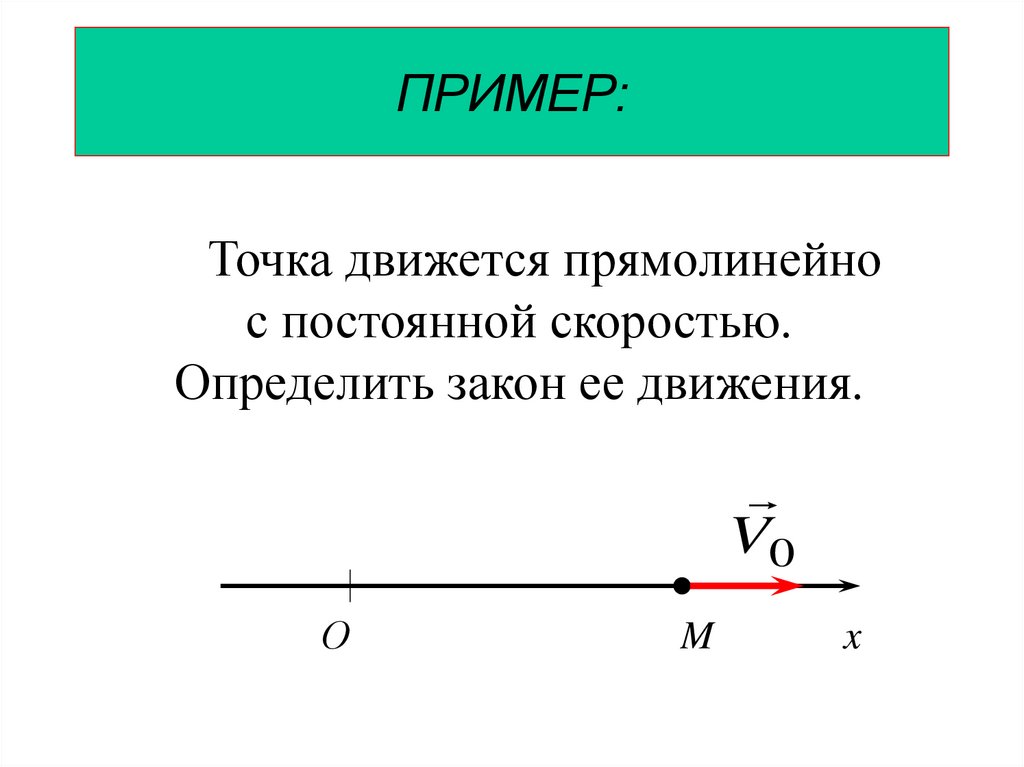
47.
ПРИМЕР:Точка движется прямолинейно
с постоянной скоростью.
Определить закон ее движения.
V0
О
M
x
48.
dxV0 ;
dt
dx V0 dt
интегрируем
x V0t C
При
t 0
x x0
поэтому
x V0t x0
- линейный закон движения
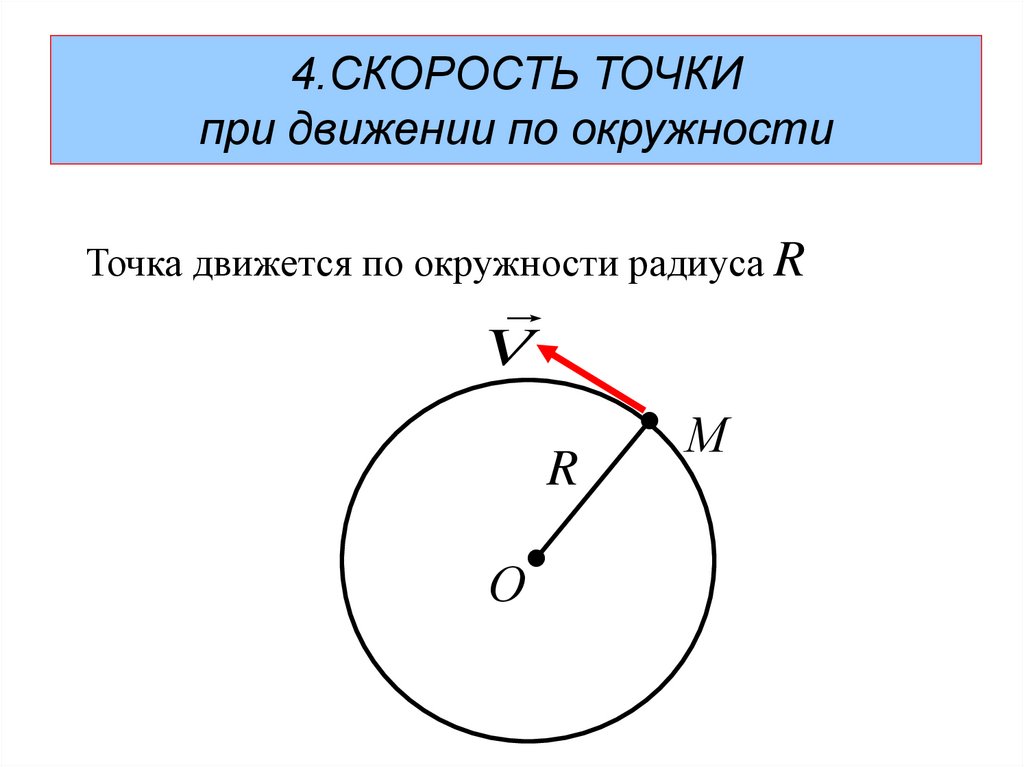
49.
4.СКОРОСТЬ ТОЧКИпри движении по окружности
Точка движется по окружности радиуса R
V
R
О
М
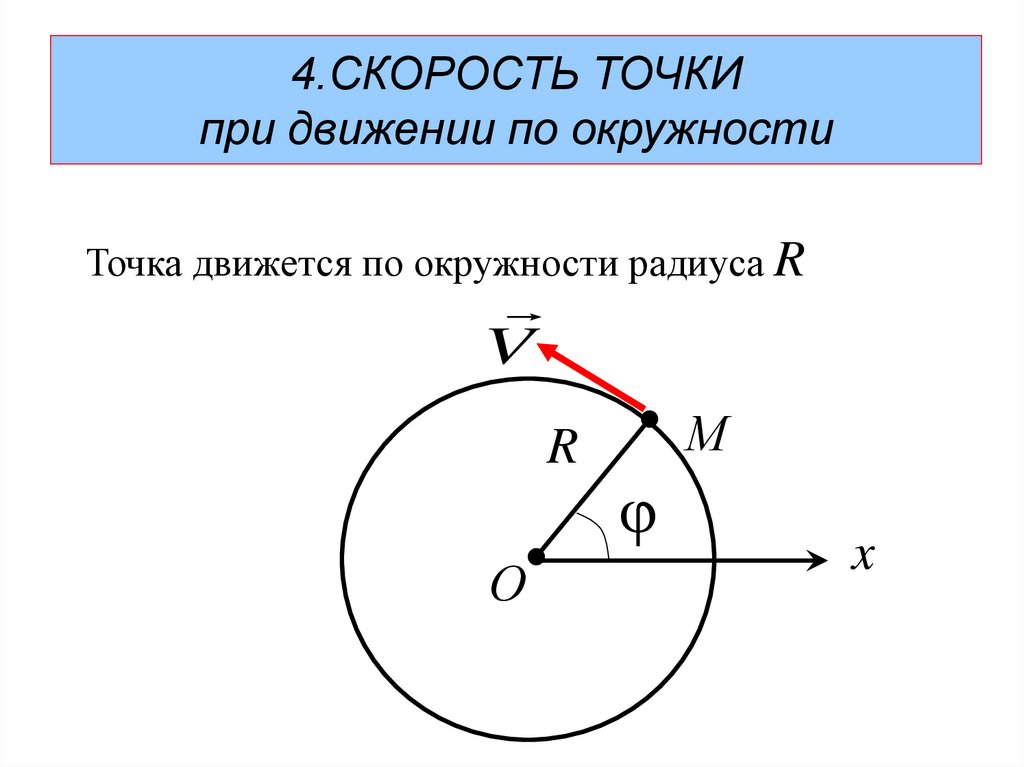
50.
4.СКОРОСТЬ ТОЧКИпри движении по окружности
Точка движется по окружности радиуса R
V
R
О
М
φ
x
51.
dsV ; ds R dφ ;
dt
dφ
dφ
V R ;
ω;
dt
dt
ω - угловая скорость
Формула Эйлера:
Период обращения:
V ωR
2 πR 2 π
T
ωR
ω
(5)
(6)
52.
6.ТЕОРЕМАо сложении скоростей
Законы Ньютона сформулированы для движения точки
по отношению к инерциальным системам отсчета. Для
определения кинематических параметров точки при
движении относительно произвольно движущейся
системы отсчета вводится теория сложного движения.
Сложным называют движение точки по отношению к
двум или нескольким системам отсчета.
53.
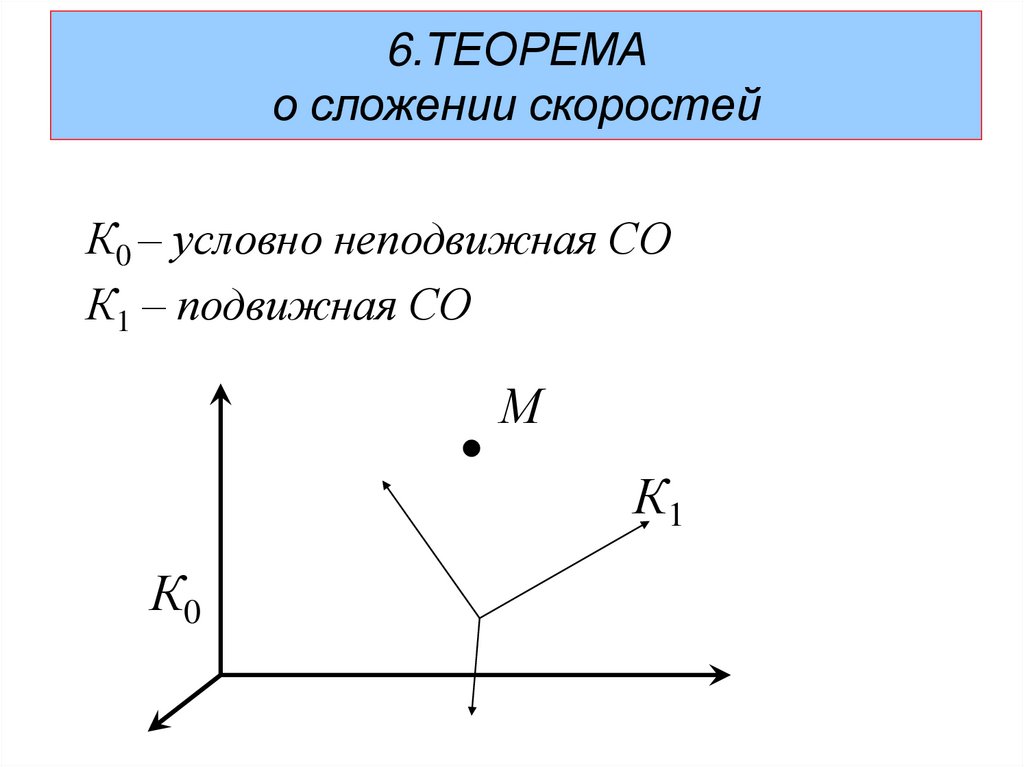
6.ТЕОРЕМАо сложении скоростей
К0 – условно неподвижная СО
К1 – подвижная СО
М
К1
К0
54.
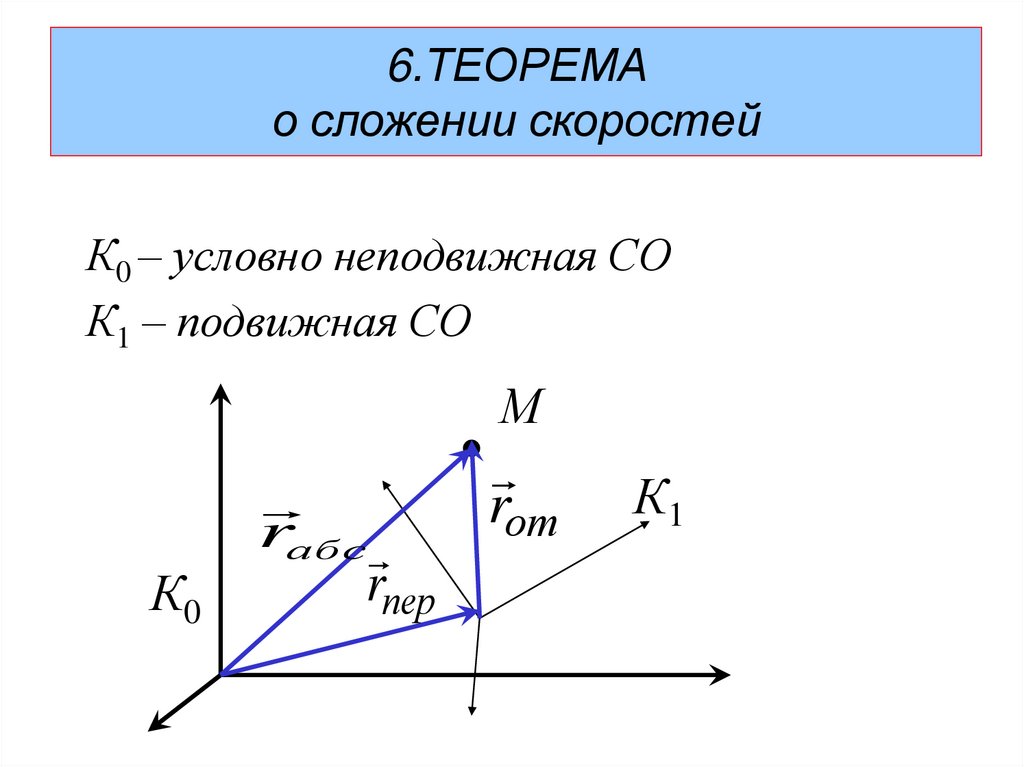
6.ТЕОРЕМАо сложении скоростей
К0 – условно неподвижная СО
К1 – подвижная СО
М
К0
rабс
rпер
rот
К1
55.
rабс rот rперVабс Vот Vпер
(10)
56.
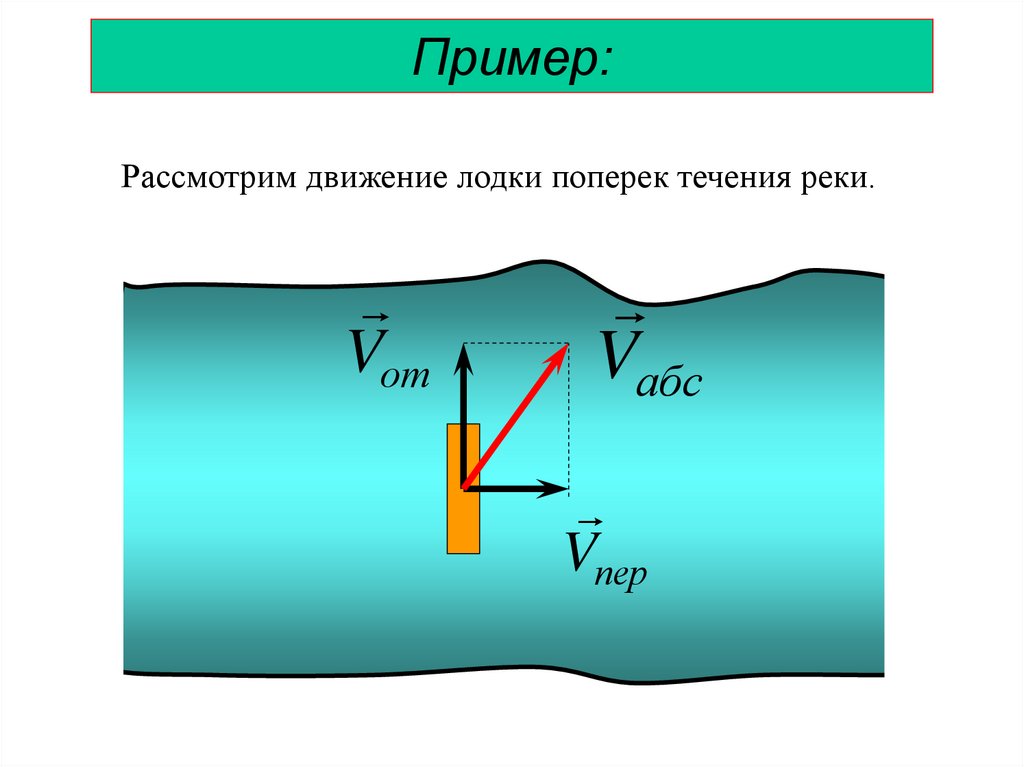
Пример:Рассмотрим движение лодки поперек течения реки.
Vот
Vабс
Vпер
57.
Пример:Лодка совершает сложное движение, которое возникает
в результате сложения относительного и переносного
движений.
58.
После просмотра и конспектирования слайд-лекциинеобходимо прочитать указанные страницы
учебников и дополнить конспект наиболее важными
сведениями
1. Тарг С.М. Краткий курс теоретической механики:
Учеб. для втузов.- 10-е изд. – М: ВШ, 1986. С. 99100.
59.
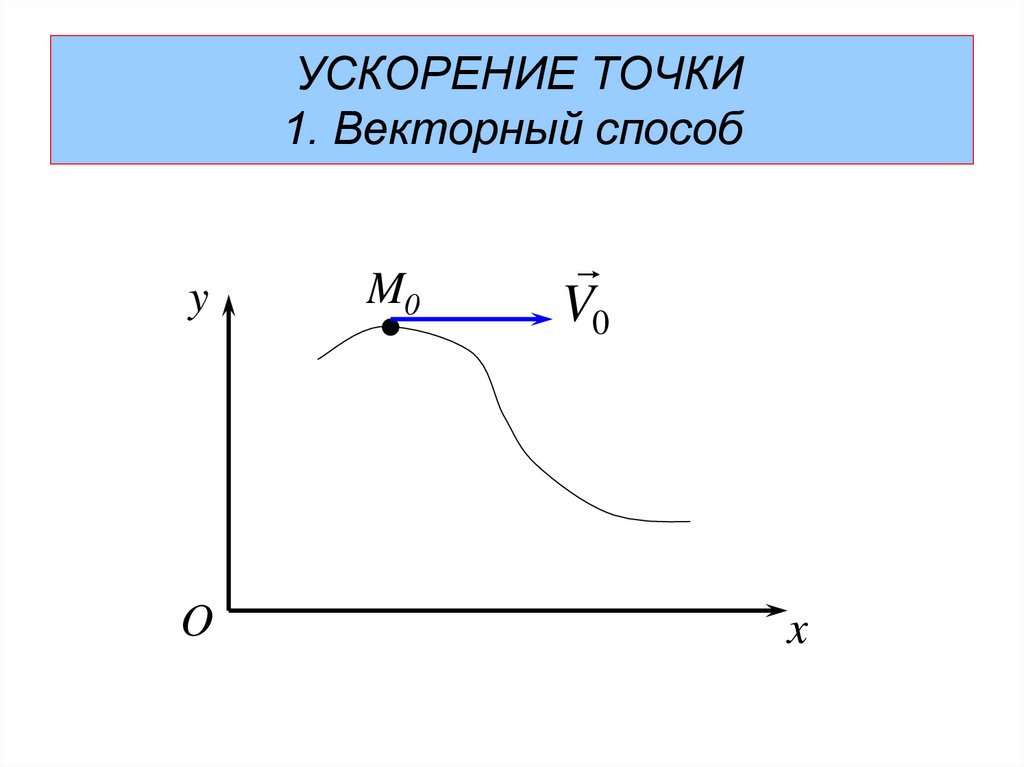
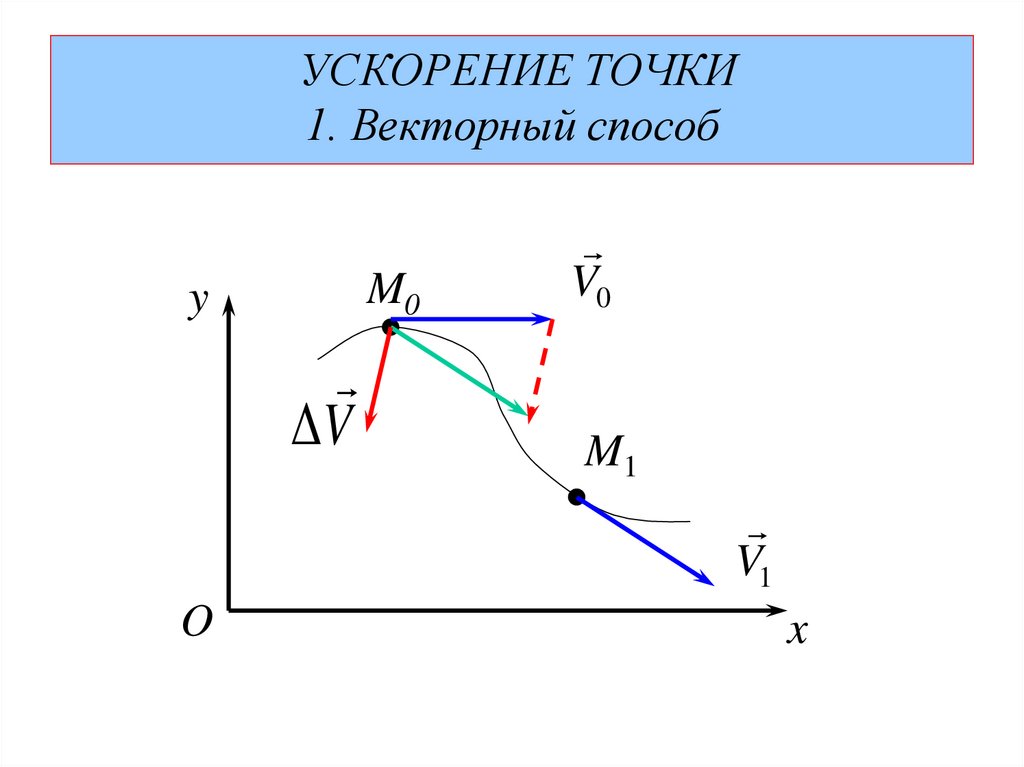
Ускорение точки.60. УСКОРЕНИЕ ТОЧКИ 1. Векторный способ
yO
M0
V0
x
61.
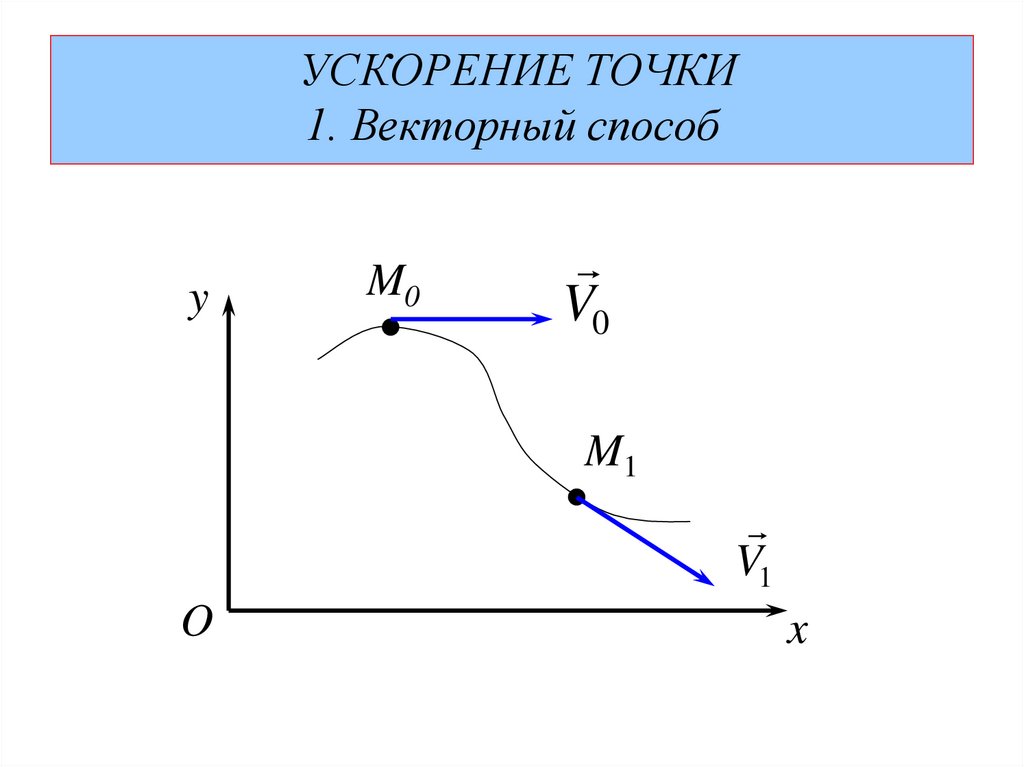
УСКОРЕНИЕ ТОЧКИ1. Векторный способ
y
M0
V0
M1
V1
O
x
62.
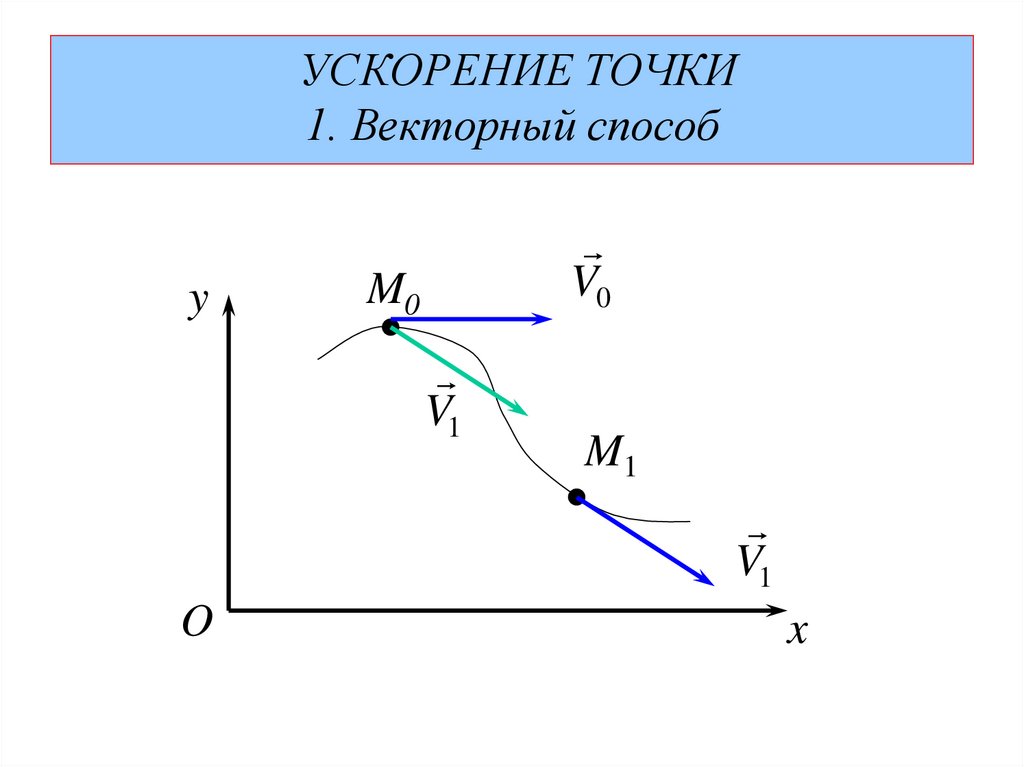
УСКОРЕНИЕ ТОЧКИ1. Векторный способ
y
V0
M0
V1
M1
V1
O
x
63.
УСКОРЕНИЕ ТОЧКИ1. Векторный способ
M0
y
ΔV
V0
M1
V1
O
x
64.
r r t - закон движения точкиV0 V t0 -скорость точки в положении М0
V1 V t0 t -скорость точки в положении М1
65.
r r t - закон движения точкиV0 V t0 -скорость точки в положении М0
V1 V t0 t -скорость точки в положении М1
V V1 V0 ; t t1 t0
V -среднее ускорение точки на отрезке
aср
t пути М0 М1
66.
VdV
a lim
t 0 t
dt
Мгновенное ускорение точки:
2
d r
dV
a
2
dt
dt
(1)
67. 2. Координатный способ
r xi yj zk2
2
2
d y
d z
d r d x
a 2 2 i 2 j 2 k
dt
dt
dt
dt
2
68.
2d x
dVx
;
a x 2 x
dt
dt
2
dVy
d y
;
a y 2 y
dt
dt
2
d z
dVz
.
a z 2 z
dt
dt
(2)
69.
iМодуль вектора ускорения:
a
2
2
2
ax a y az
Направление вектора ускорения:
ax
cos a , i ;
a
ay
cos a , j ;
a
az
cos a , k
a
(3)
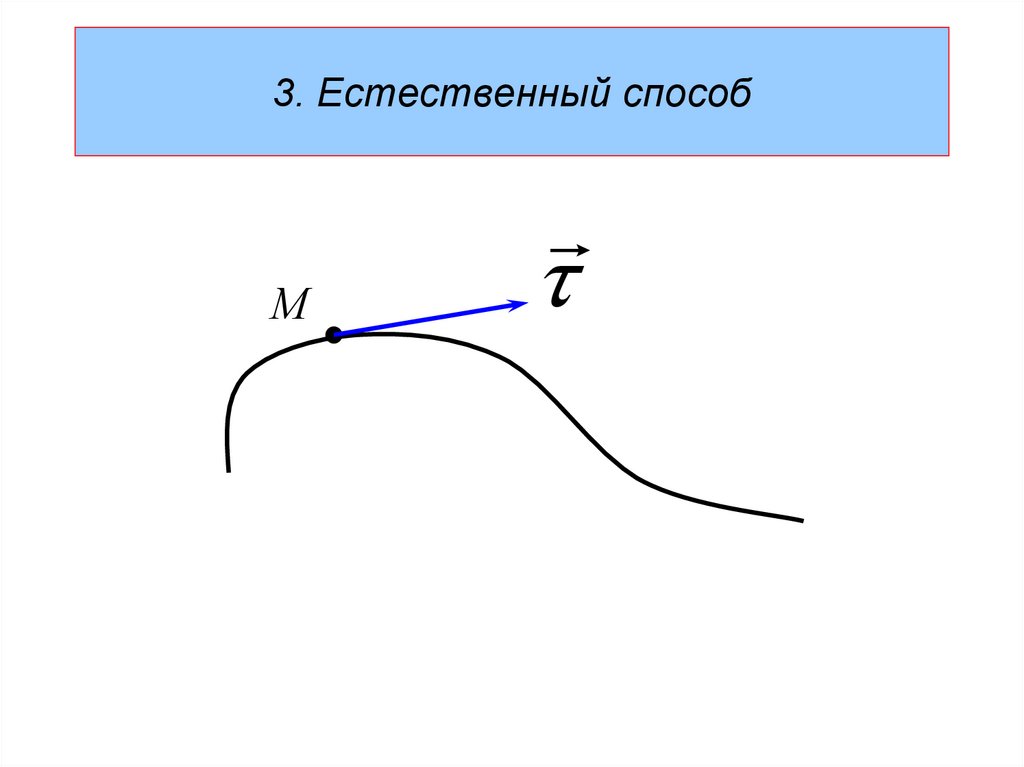
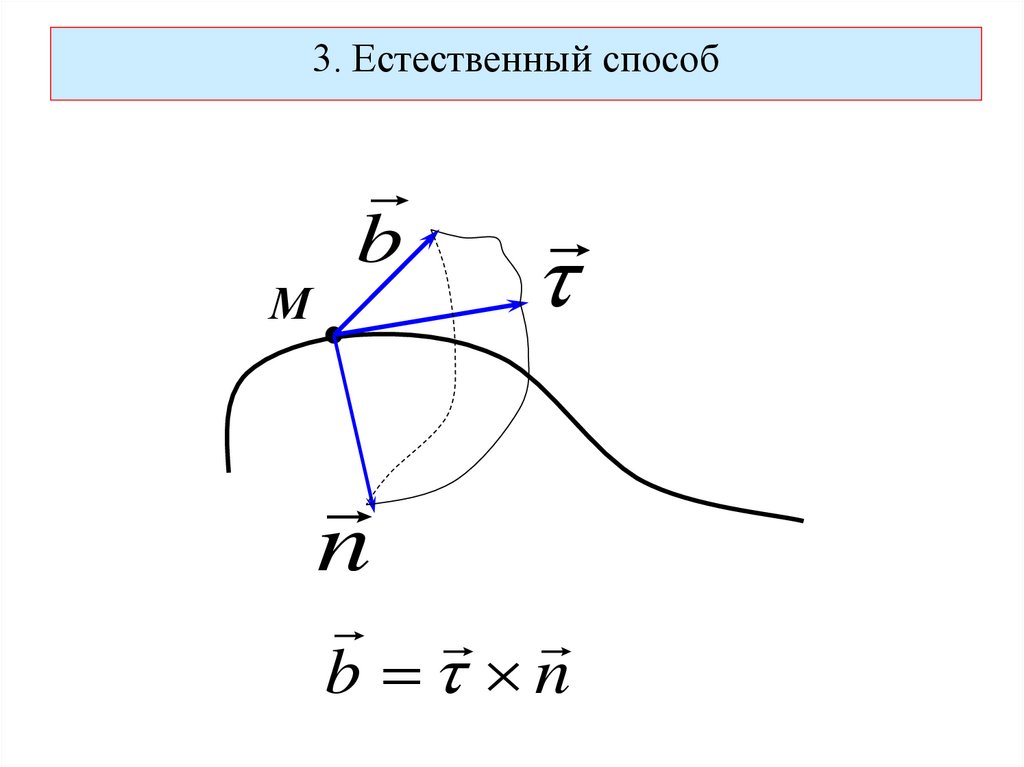
70. 3. Естественный способ
М71.
3. Естественный способМ
n
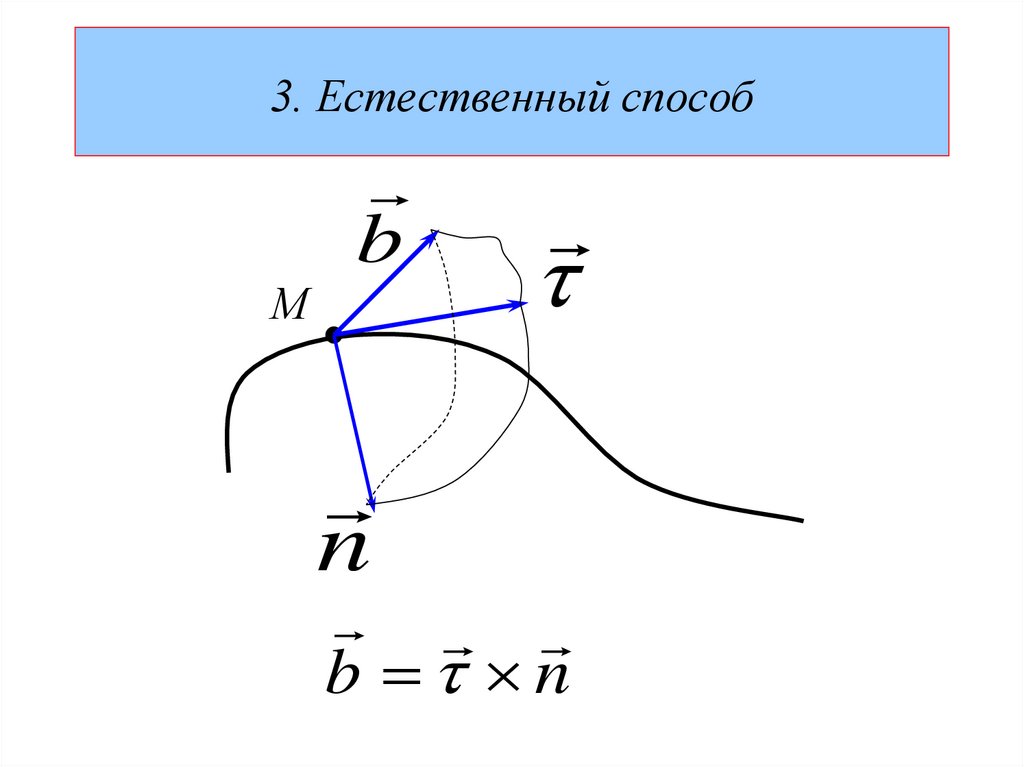
72.
3. Естественный способb
М
n
b n
73.
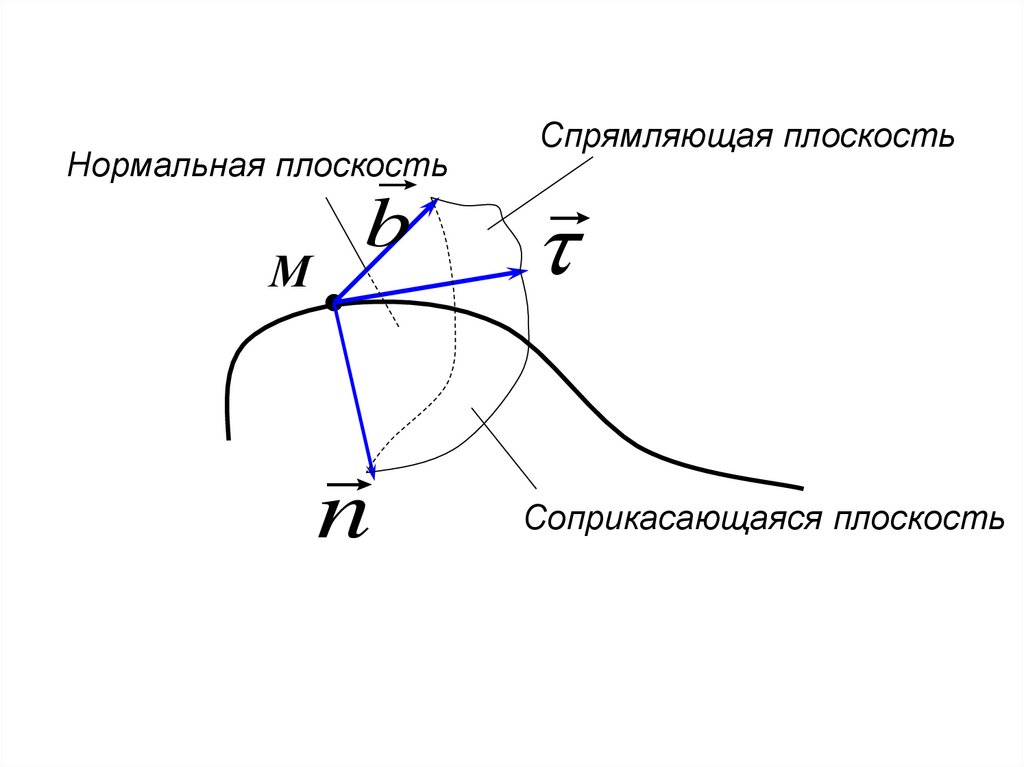
bНормальная плоскость
М
n
Спрямляющая плоскость
Соприкасающаяся плоскость
74.
Лекционная видеодемонстрация(дважды кликнуть по значку)
или выделить гиперссылку, кликнуть правой
кнопкой мыши, выбрать «Открыть
гиперссылку» и нажать левую кнопку мыши
Естественный трехгранник –
YouTube
www.youtube.com/watch?v=GLs2ZtPqsV
A
75.
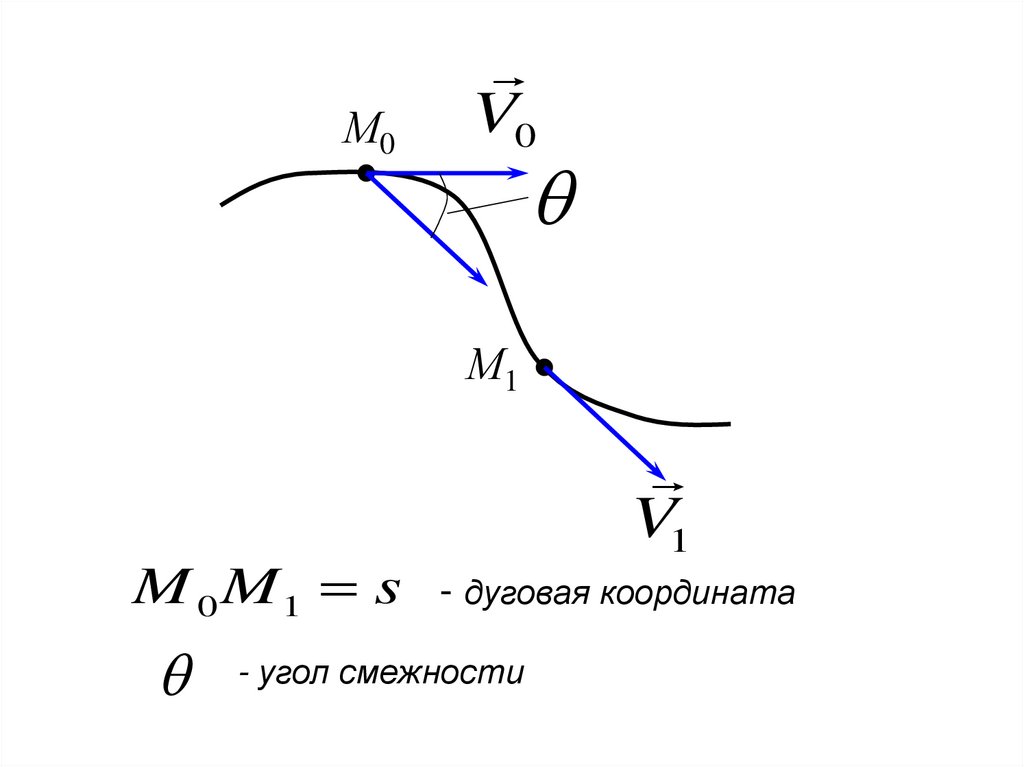
М0V0
М1
M 0 M1 s
V1
- дуговая координата
- угол смежности
76.
d- кривизна кривой
k
ds
1
ds
- радиус кривизны в данной точке
k
d
77.
V Vd
dV dV
a
V
dt dt
dt
(4)
d d d ds V (примем
n
n n без вывода)
где
dt
dt
ds dt
Формула (4)
принимает
вид (5):
2
dV V
a
n
dt
(5)
78.
Тангенциальное (касательное) ускорение:dV
a
dt
(6)
Нормальное ускорение:
an
V
2
(7)
Бинормальное ускорение:
ab 0
79.
aan
a
dV V
dt
2
a
2
a an
2
2
2
(8)
80. 4. Сложное движение точки. Теорема Кориолиса
Ранее рассматривали теорему о сложениискоростей:
Vабс Vотн Vпер
(9)
81.
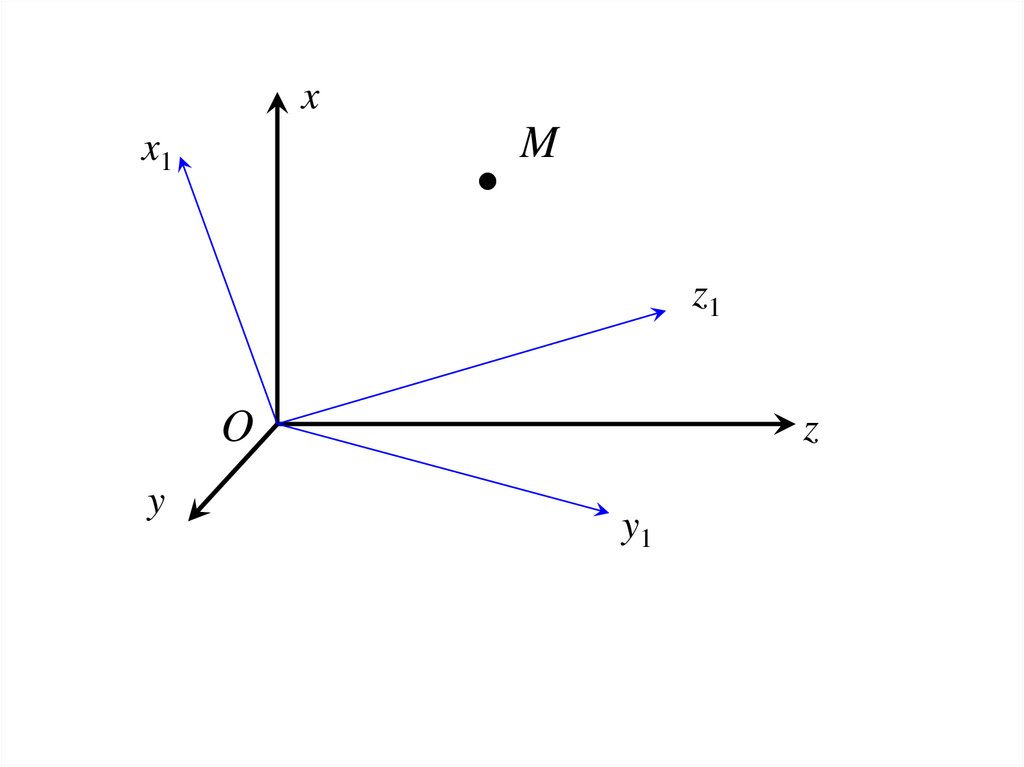
xM
x1
z1
O
y
z
y1
82.
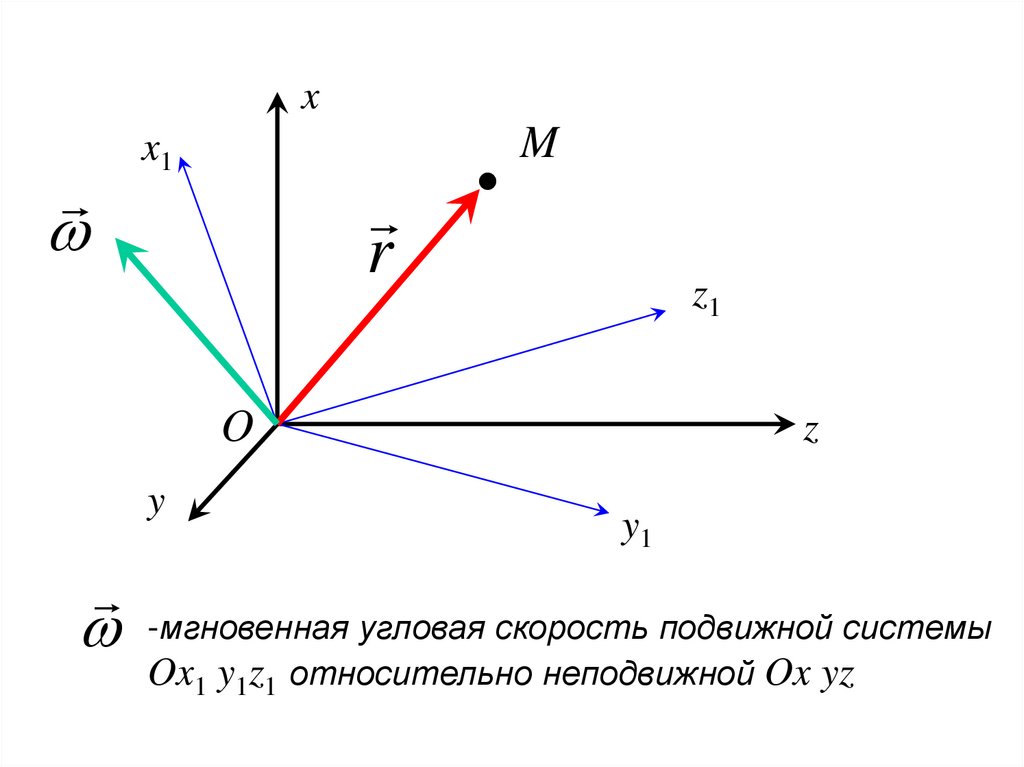
xM
x1
r
z1
O
y
z
y1
-мгновенная угловая скорость подвижной системы
Ox1 y1z1 относительно неподвижной Ox yz
83.
dr -приращение радиус-вектора в системе Oxyz~ -приращение радиус-вектора в системе Ox y z
1 1 1
dr
84.
dr -приращение радиус-вектора в системе Oxyz~ -приращение радиус-вектора в системе Ox y z
1 1 1
dr
dr
-абсолютная производная
dt
~
dr
-локальная (относительная) производная
dt
85.
drVабс
dt
(10)
~
dr
Vотн
dt
(11)
Vпер r
(12)
86.
Vабс Vотн Vпер~
dr d r
r
dt
dt
(13)
87.
Vабс Vотн Vпер~
dr d r
r
dt
dt
Аналогично для любого вектора с :
~
dc d c
c
dt
dt
(13)
(14)
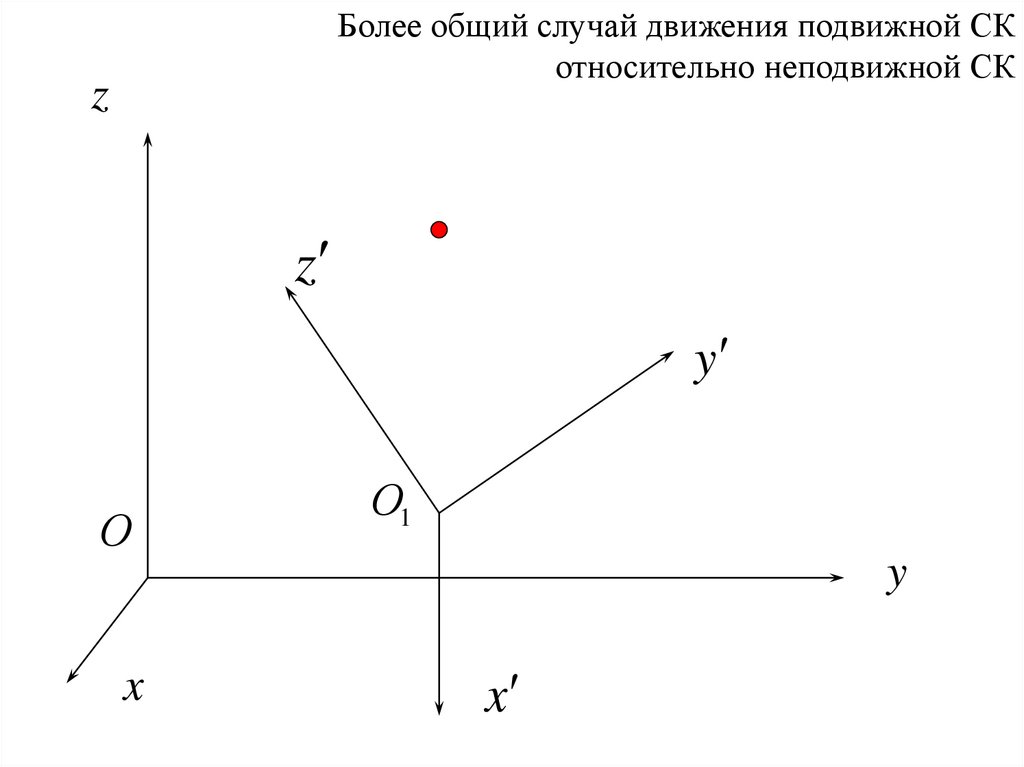
88.
Более общий случай движения подвижной СКотносительно неподвижной СК
z
z
y
О
x
О1
y
x
89.
Vот нz
М
аот н
z
y
О
x
О1
y
x
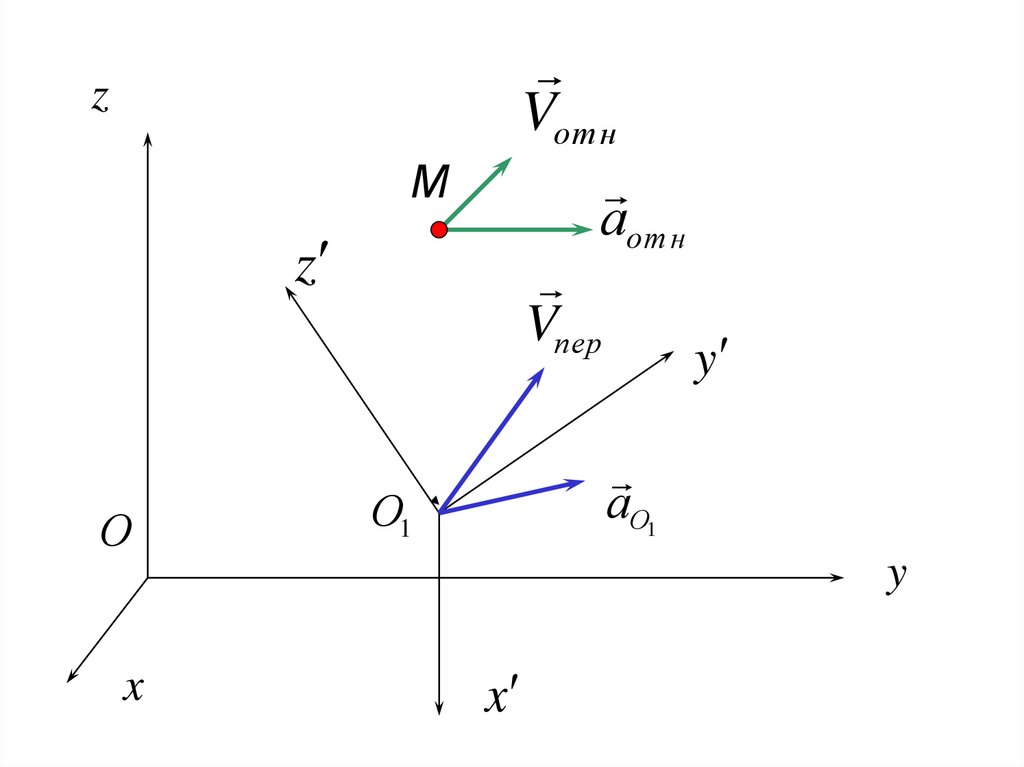
90.
Vот нz
М
аот н
z
О
x
Vпер
y
аО1
О1
y
x
91.
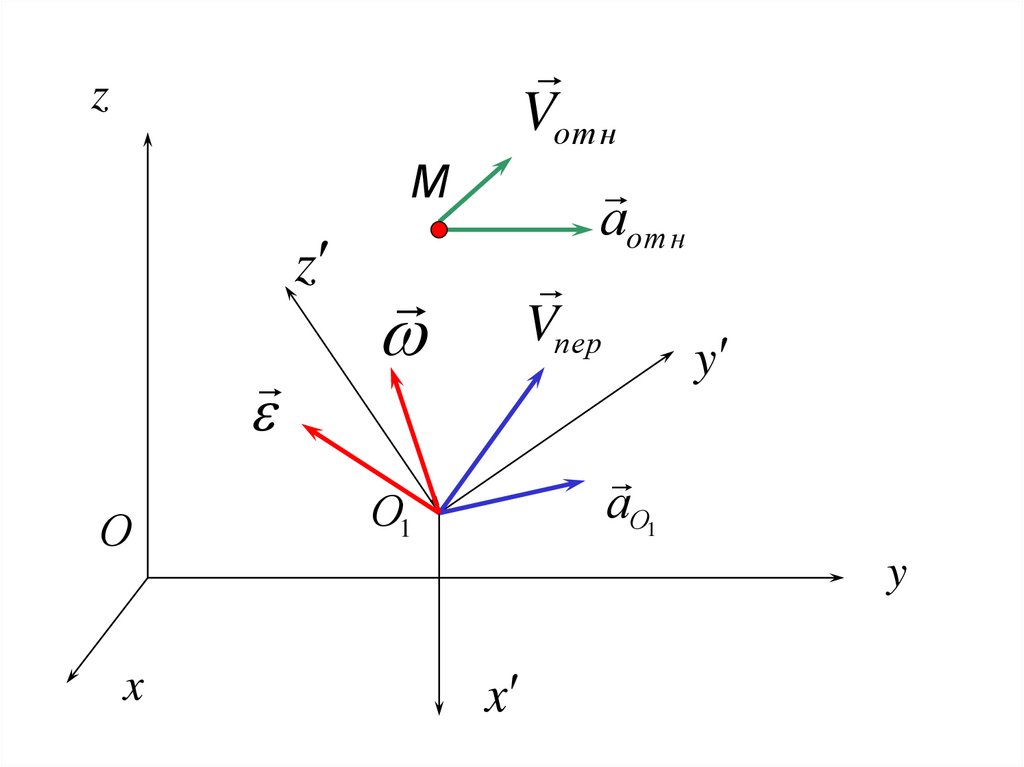
Vот нz
М
z
О
x
аот н
Vпер
y
аО1
О1
y
x
92. Теорема Кориолиса
aабс aотн апер акор(15)
93.
Теорема Кориолисаaабс aотн апер акор
~
~2
d Vот н d r
aот н
dt
dt 2
(15)
(16)
aпер a01 r r (17)
aкор 2 Vотн
(18)
94.
Теорема КориолисаАбсолютное ускорение
точки при сложном
движении
складывается из
относительного,
переносного и
кориолисова
ускорений.
Гаспар-Гюстав Кориолис
(1792-1843)
95.
После просмотра и конспектирования слайдлекции необходимо прочитать указанныестраницы учебников и дополнить конспект
наиболее важными сведениями
1. Тарг С.М. Краткий курс теоретической
механики: Учеб. для втузов.- 10-е изд. – М:
ВШ, 1986. С. 100-103.
96.
Кинематикаабсолютно твердого тела.
97. КИНЕМАТИКА абсолютно твердого тела
Абсолютно твердым телом (АТТ) называетсятакая механическая система, в которой
расстояние между любыми двумя точками
неизменно.
98.
Геометрические связи:M 1M 2 const
M 1M 3 const
M 2 M 3 const
М1
М2
М3
99. 1. Простейшие движения АТТ
Простейшими называются поступательное ивращательное (вокруг закрепленной оси)
движения твердого тела.
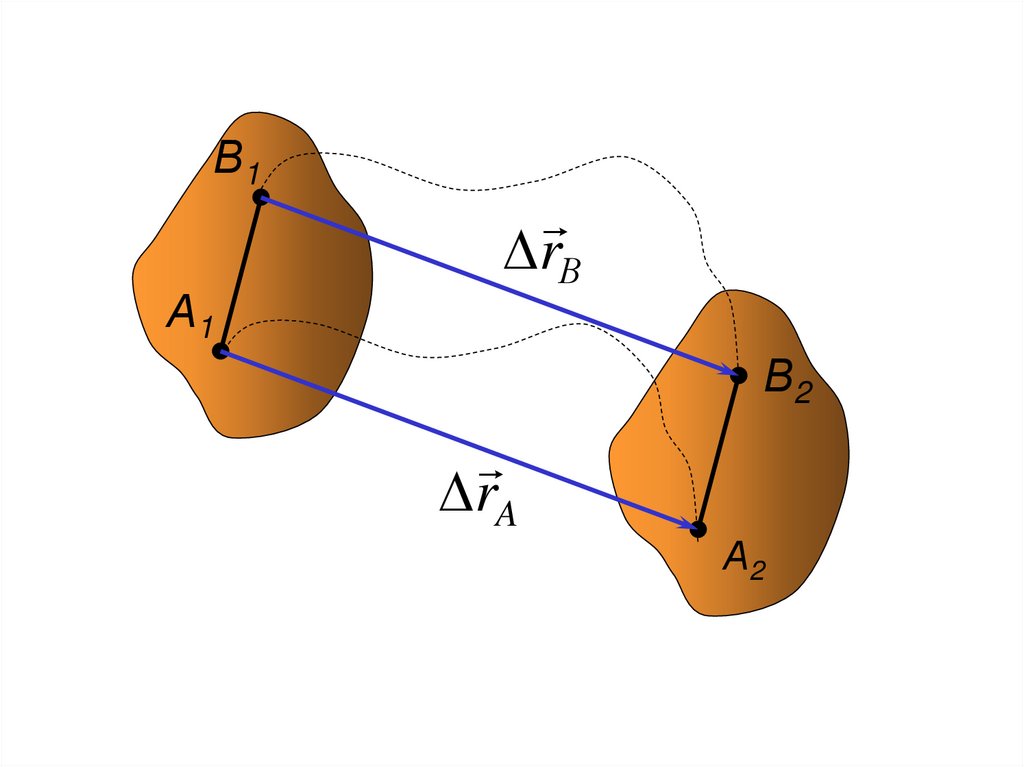
100. 1.1 Поступательное движение АТТ
Поступательным называют такое движениеАТТ, при котором любая прямая проведенная
в теле во все время движения остается
параллельной самой себе.
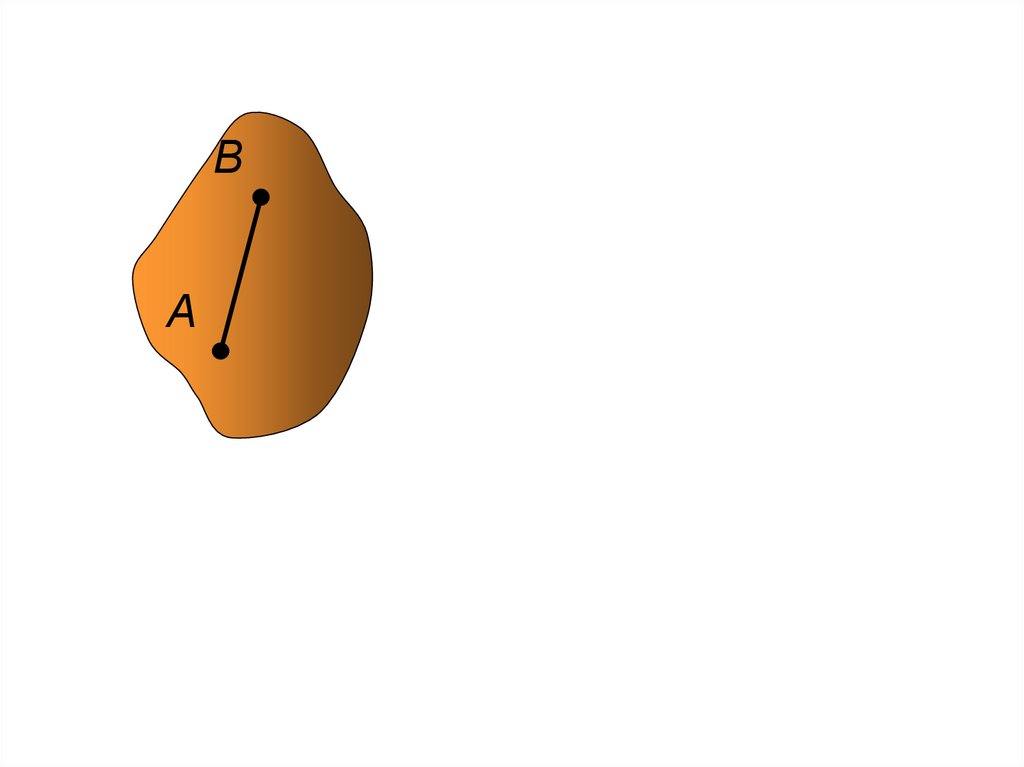
101.
ВА
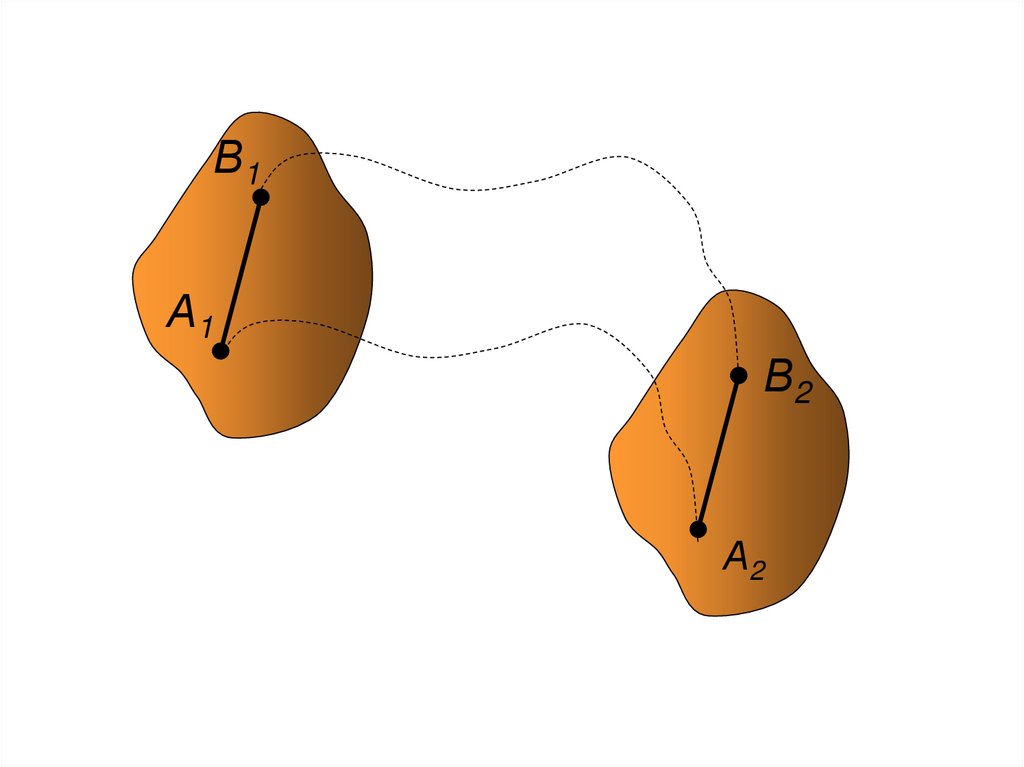
102.
В1А1
В2
А2
103.
В1А1
rВ
В2
rA
А2
104.
rA rBrA rB
t
t
VA VB
a A aB
105. Выводы:
1. При поступательном движении АТТ все его точкиописывают одинаковые траектории и в любой
момент времени имеют одинаковые скорости и
ускорения.
2. Поступательное движение АТТ вполне
определяется движением одной из его точек.
Следовательно изучение поступательного
движения АТТ сводится к кинематике точки.
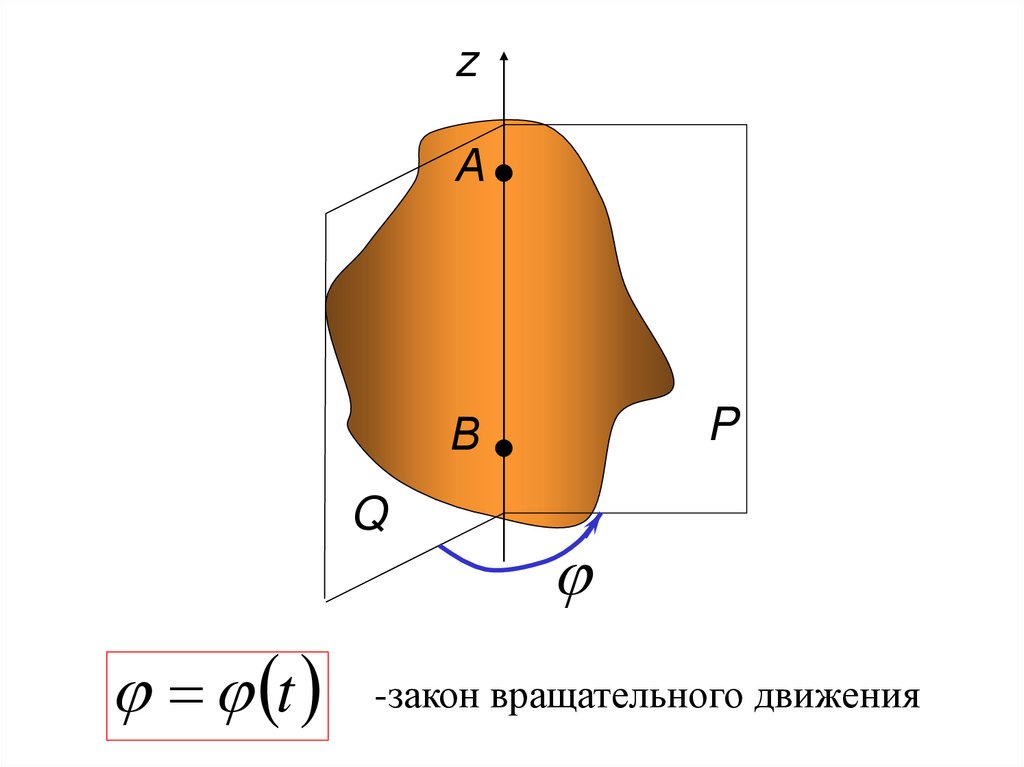
106.
1.2 Вращение твердого тела вокругзакрепленной оси
Если АТТ движется так, что две его точки,
например А и В, остаются неподвижными, то
движение тела называется вращательным, а
прямая АВ – осью вращения.
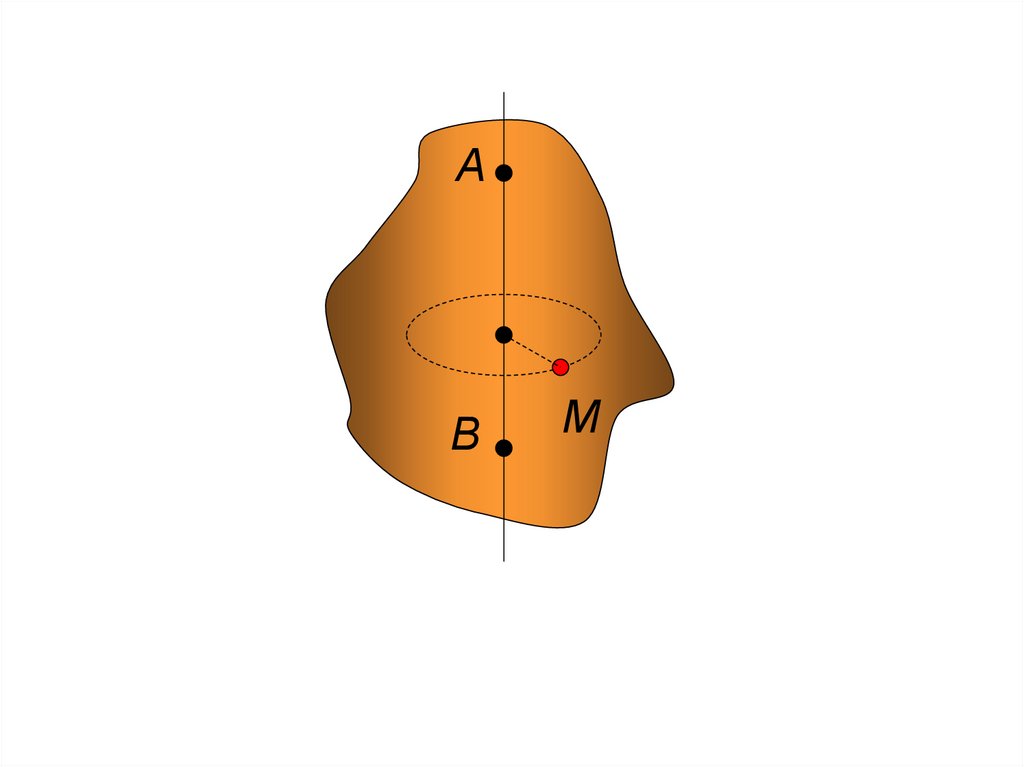
107.
108.
АВ
М
109.
zА
P
В
Q
t
-закон вращательного движения
110.
dt
- угловая скорость
dt
d
- угловое ускорение
dt
111. Частные случаи:
Случай 1:const ;
0 t
0
(1)
112.
Случай 2:const
d
dt
113.
Случай 2:const
d
dt
0 t
(2)
t
0 0t
2
2
(3)
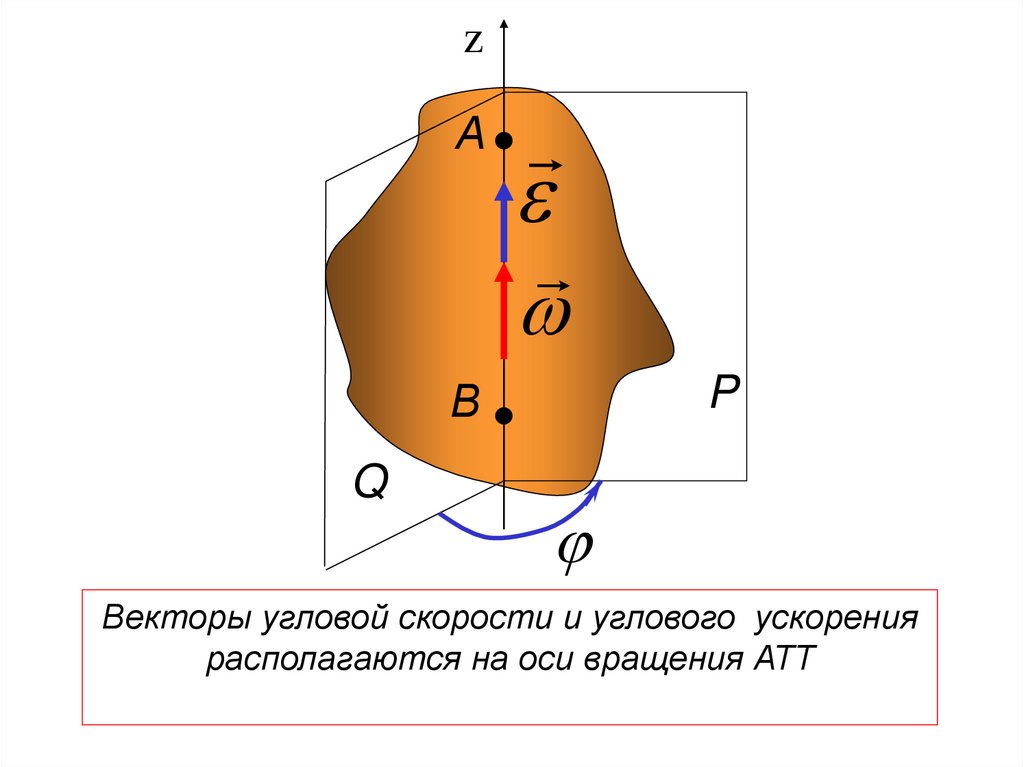
114.
zА
P
В
Q
Векторы угловой скорости и углового ускорения
располагаются на оси вращения АТТ
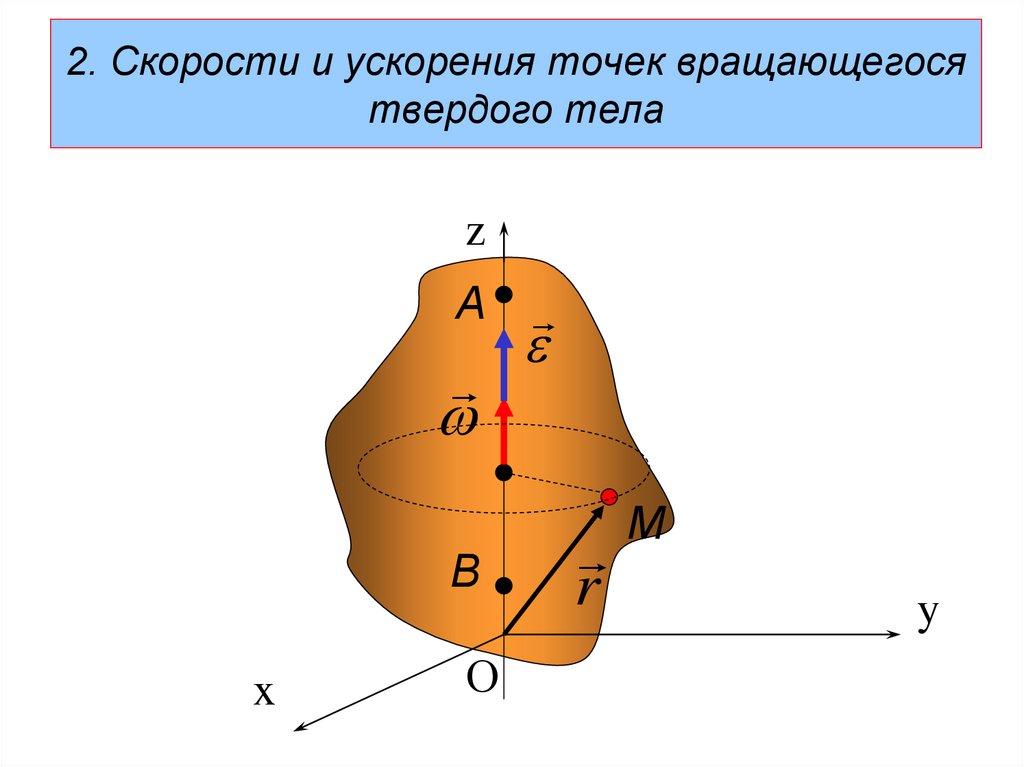
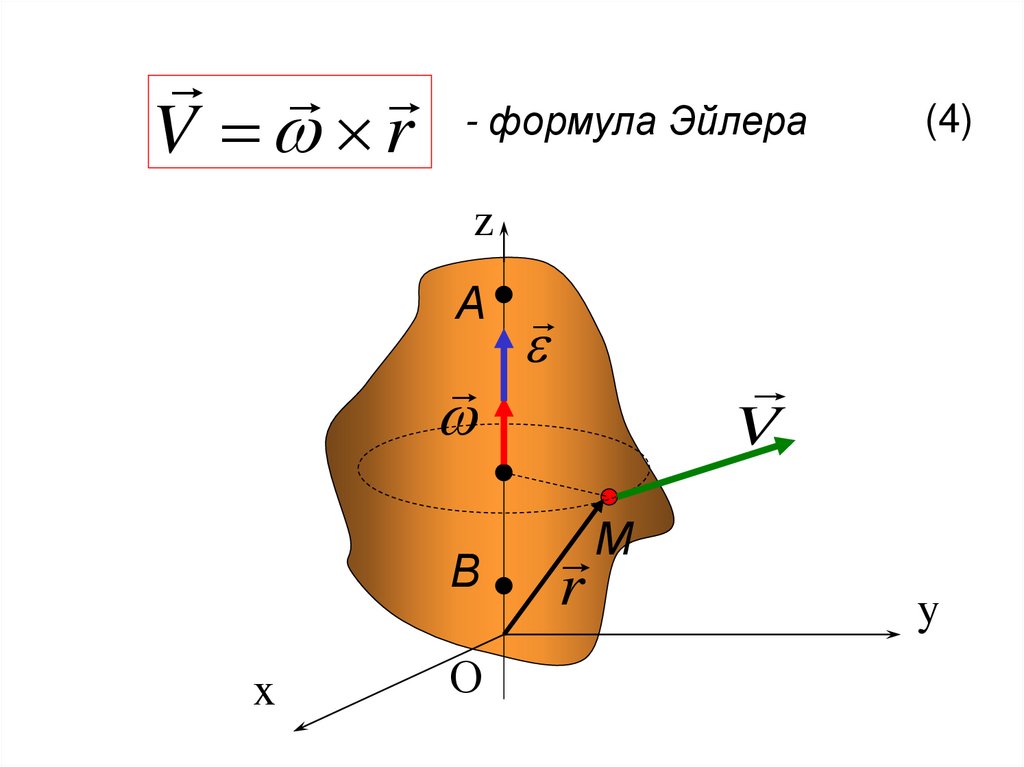
115. 2. Скорости и ускорения точек вращающегося твердого тела
zА
В
x
О
r
М
y
116.
формулаЭйлера
V r
(4)
z
А
В
x
О
V
М
r
y
117.
iV r x
x
j
k
i
y z
y
z
Проекции скорости на координатные оси:
Vx y z z y
Vy z x x z
V y x
x
y
z
(5)
118.
Вычислим ускорение точки М:dV d r
a
dt
dt
d dr
r
dt
dt
r V
119.
Составляющие ускорения в проекциина естественные оси:
а r V
(6)
120.
Составляющие ускорения в проекциина естественные оси:
а r V
(6)
r aвр -вращательное ускорение (7)
(касательное, тангенциальное)
-осестремительное
V r aос (нормальное)
(8)
ускорение
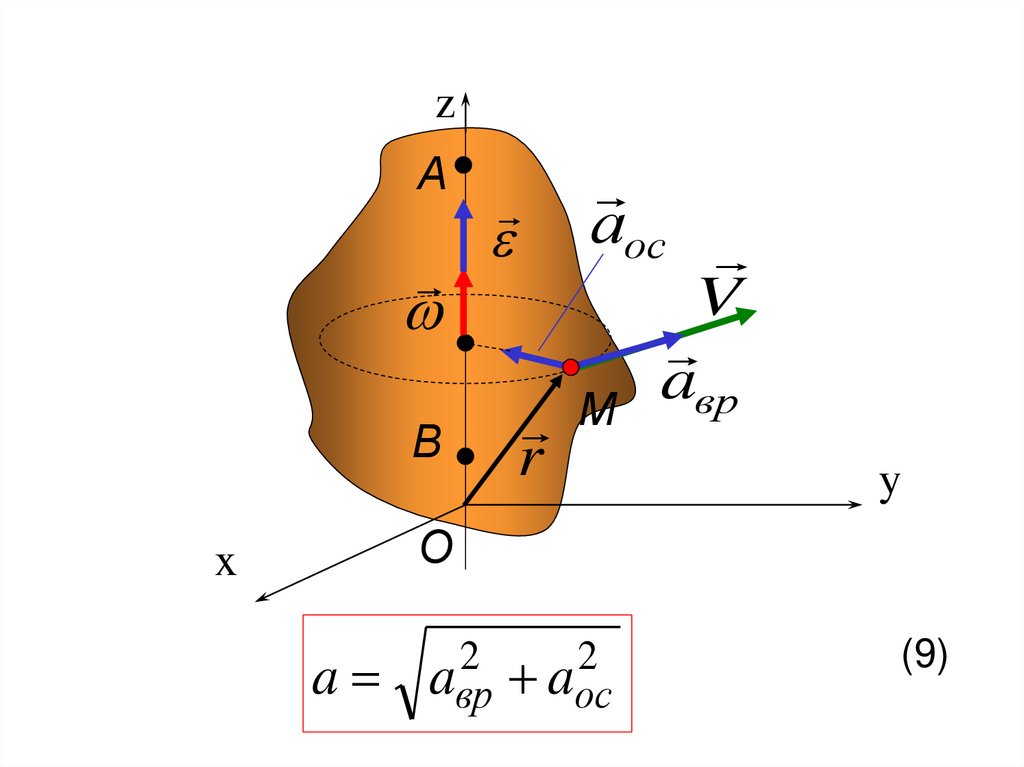
121.
zА
В
аос
V
a
вр
М
r
y
О
x
a
2
2
aвр aос
(9)
122.
После просмотра и конспектирования слайдлекции необходимо прочитать указанныестраницы учебников и дополнить конспект
наиболее важными сведениями
1. Тарг С.М. Краткий курс теоретической
механики: Учеб. для втузов.- 10-е изд. – М:
ВШ, 1986. С. 117-126.
123.
Плоскопараллельное движениетвердого тела
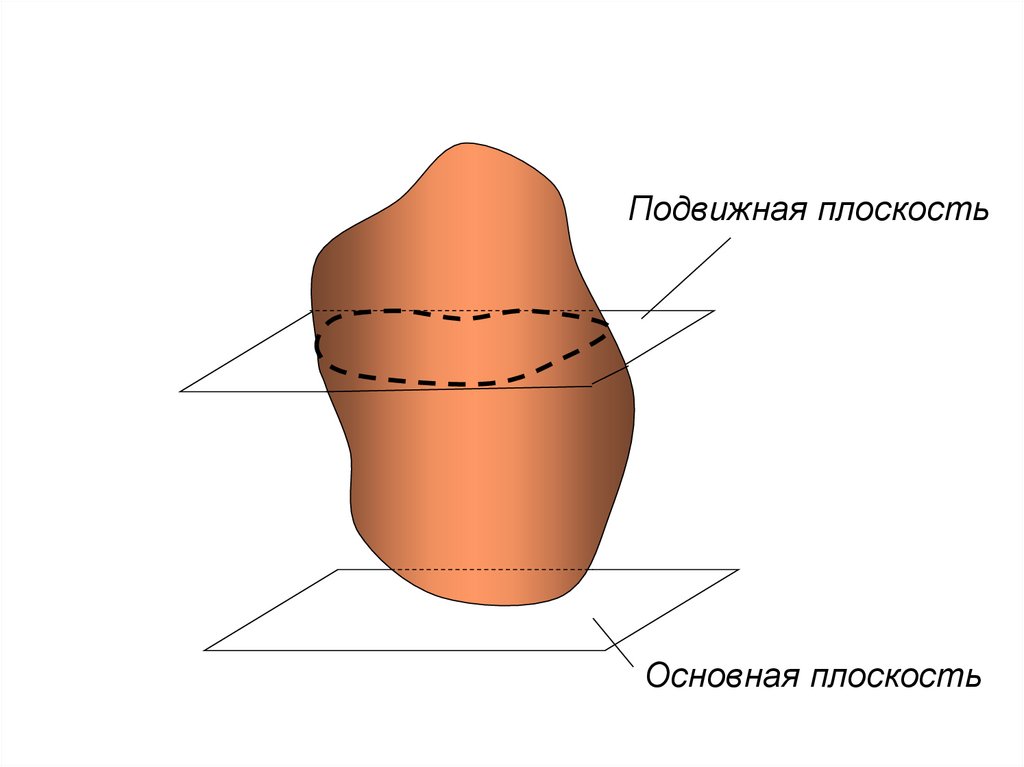
124. 1. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ АТТ
Плоскопараллельным (плоским) называется такоедвижение АТТ, при котором все его точки движутся
параллельно какой-нибудь неподвижной (основной)
плоскости
125.
Подвижная плоскостьОсновная плоскость
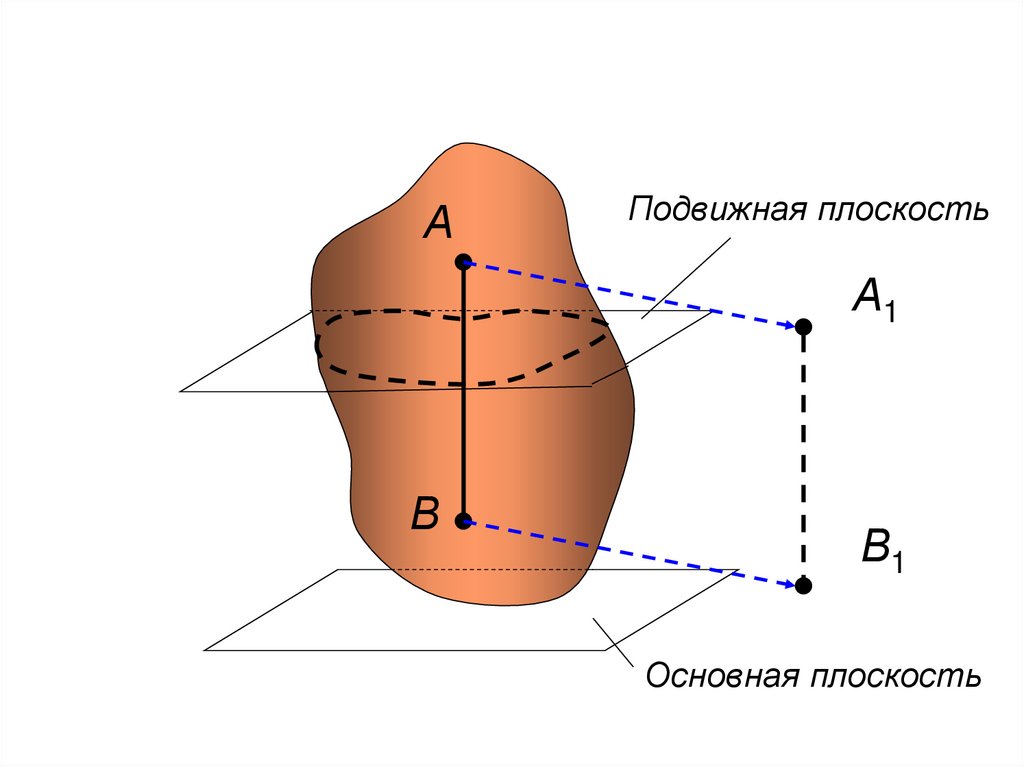
126.
АПодвижная плоскость
А1
В
В1
Основная плоскость
127. Примеры плоского движения:
- Качение колеса без поворотов- Движение шестерней в зубчатой передаче
- Движение шатуна и кривошипа в
кривошипно-шатунном механизме
128.
129. Вывод:
Рассмотрение плоскопараллельного движения АТТсводится к изучению движения неизменяемой
плоской фигуры в ее плоскости
130.
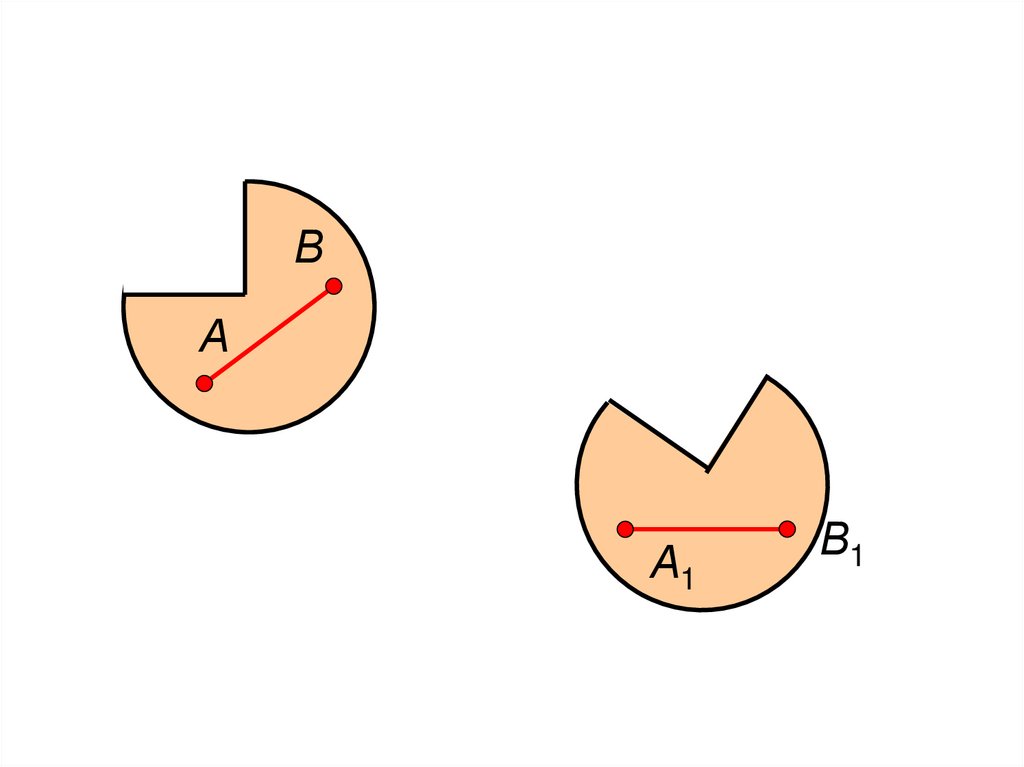
Общий случай плоскопараллельного движения131. Теорема 1:
Всякое перемещение плоской фигуры в ееплоскости может быть составлено из поступательного
перемещения и поворота вокруг произвольного центра
(полюса).
132.
Разложение движения на поступательнуюи вращательную составляющие
133.
ВА
А1
В1
134.
ВА
В
А1
В1
135.
ВА
В
А1
А
В1
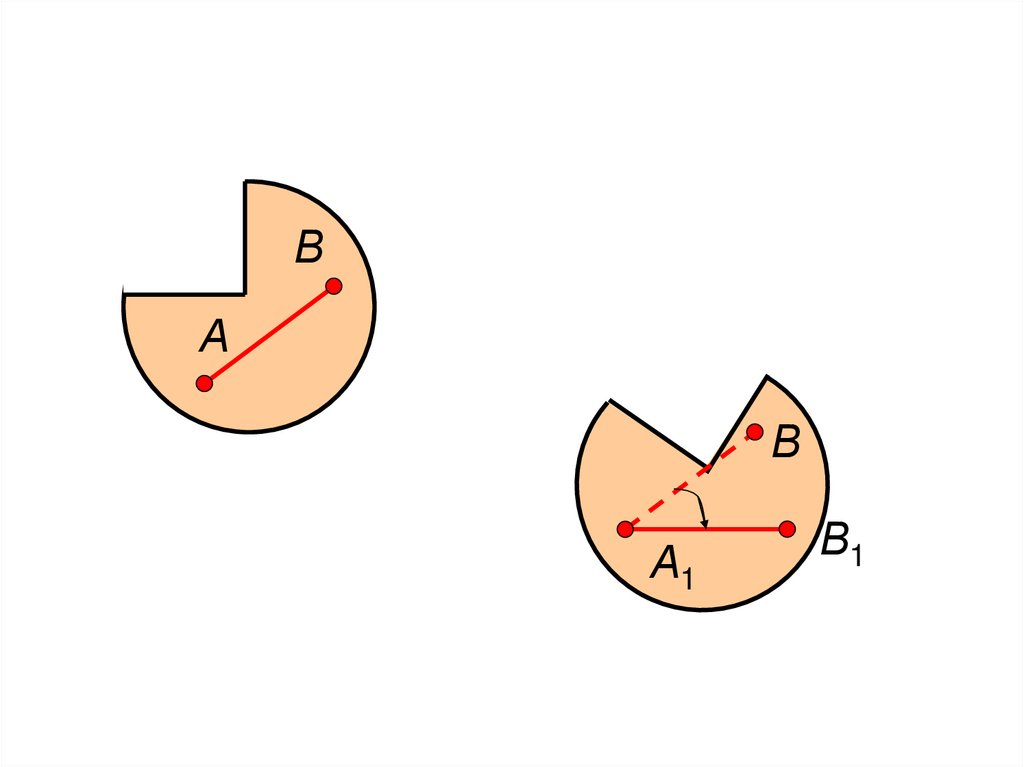
136. Вывод:
Поступательная составляющая движениязависит от выбора полюса, а вращательная –
нет.
Можно выбрать такой полюс, для которого
поступательная составляющая движения
вообще отсутствует. Такой полюс называется
центром конечного вращения.
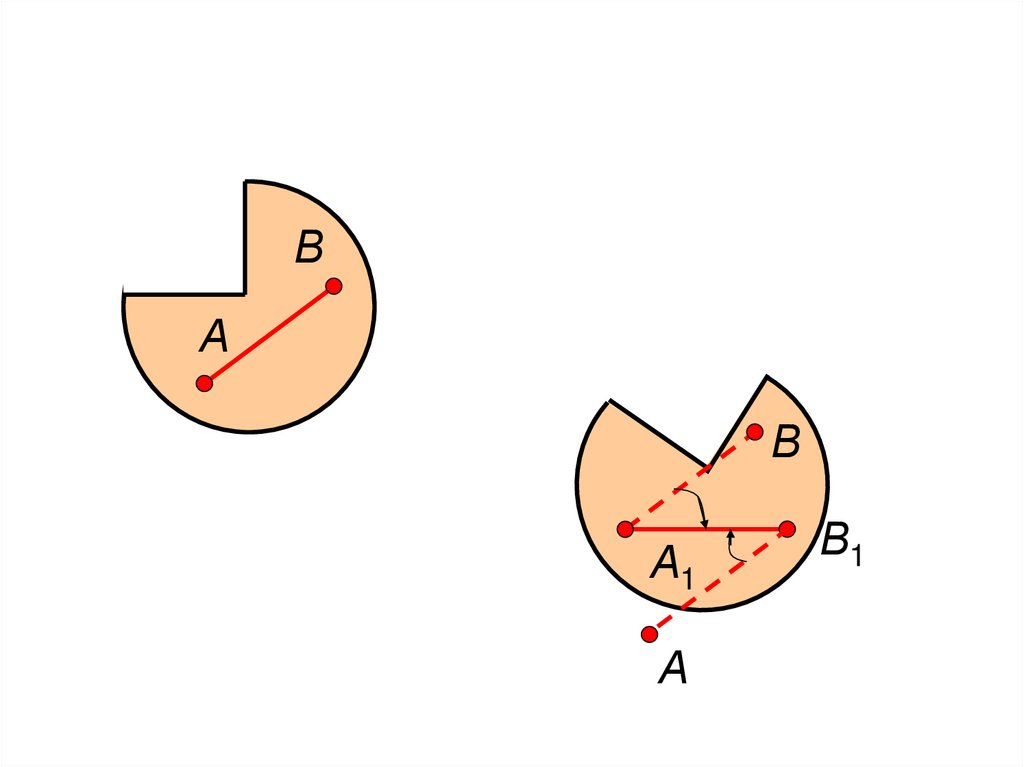
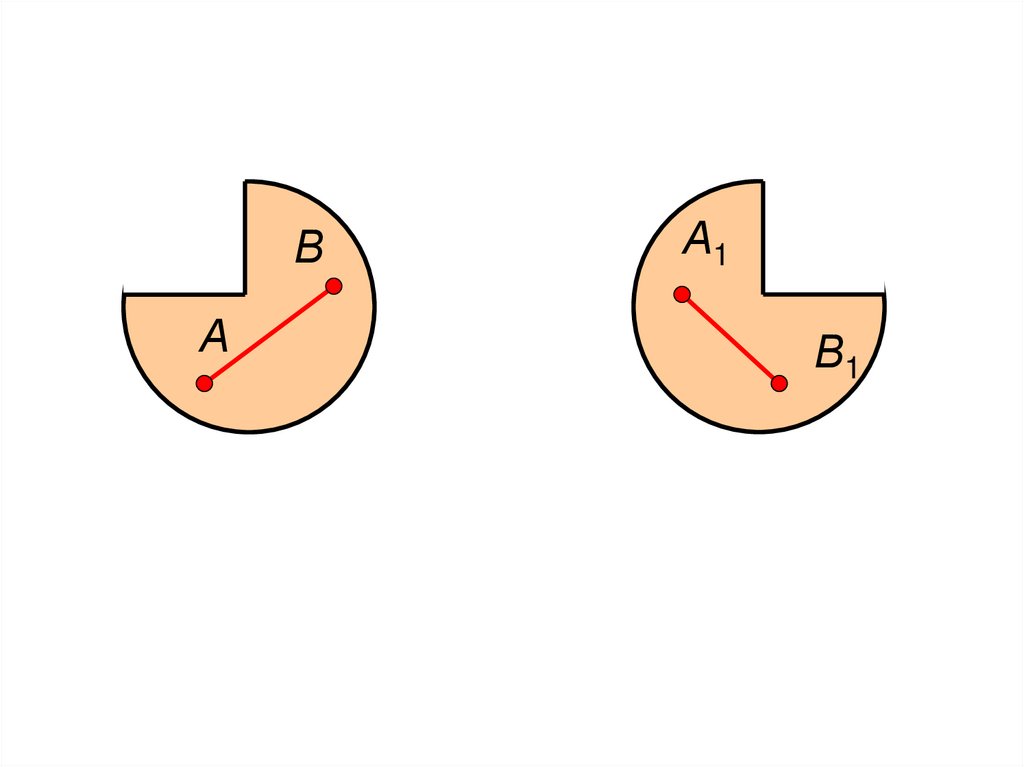
137.
ВА
А1
В1
138.
ВА
А1
В1
139.
ВА
А1
В1
140.
ВА
А1
В1
141.
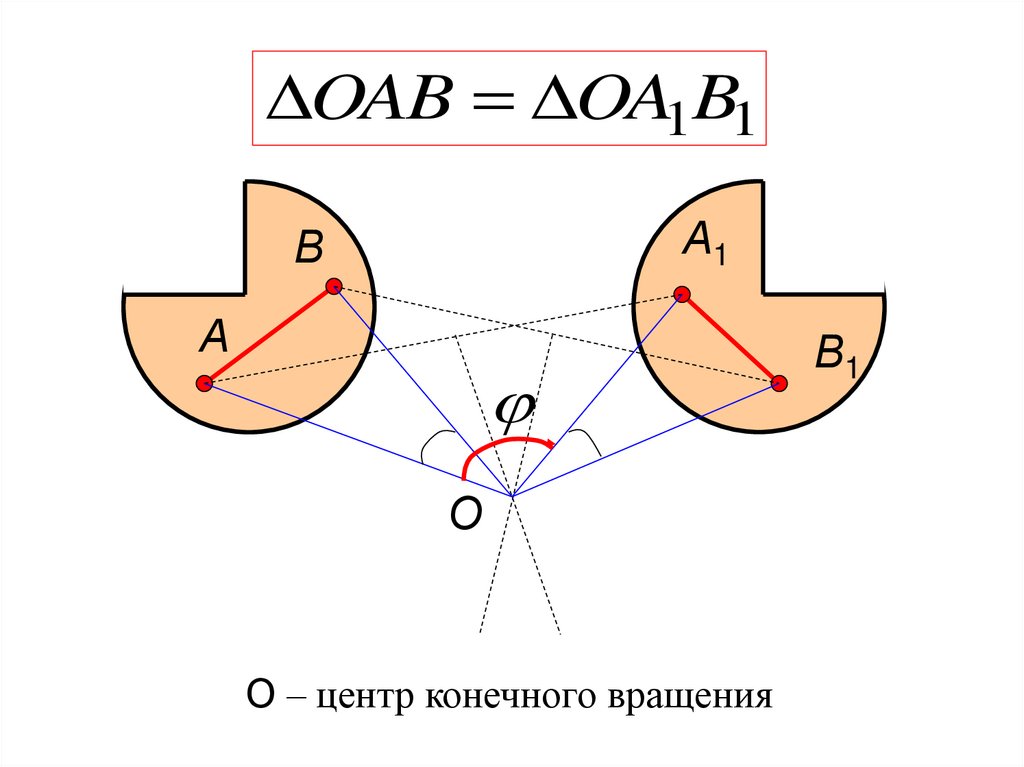
OAB OA1B1А1
В
А
О
О – центр конечного вращения
В1
142. Следствие:
Всякое непоступательное движение плоскойфигуры в ее плоскости можно рассматривать
как непрерывную последовательность
бесконечно малых поворотов вокруг
мгновенных центров вращения.
Величина угловой скорости фигуры в данный
момент времени называется
мгновенной угловой скоростью вращения.
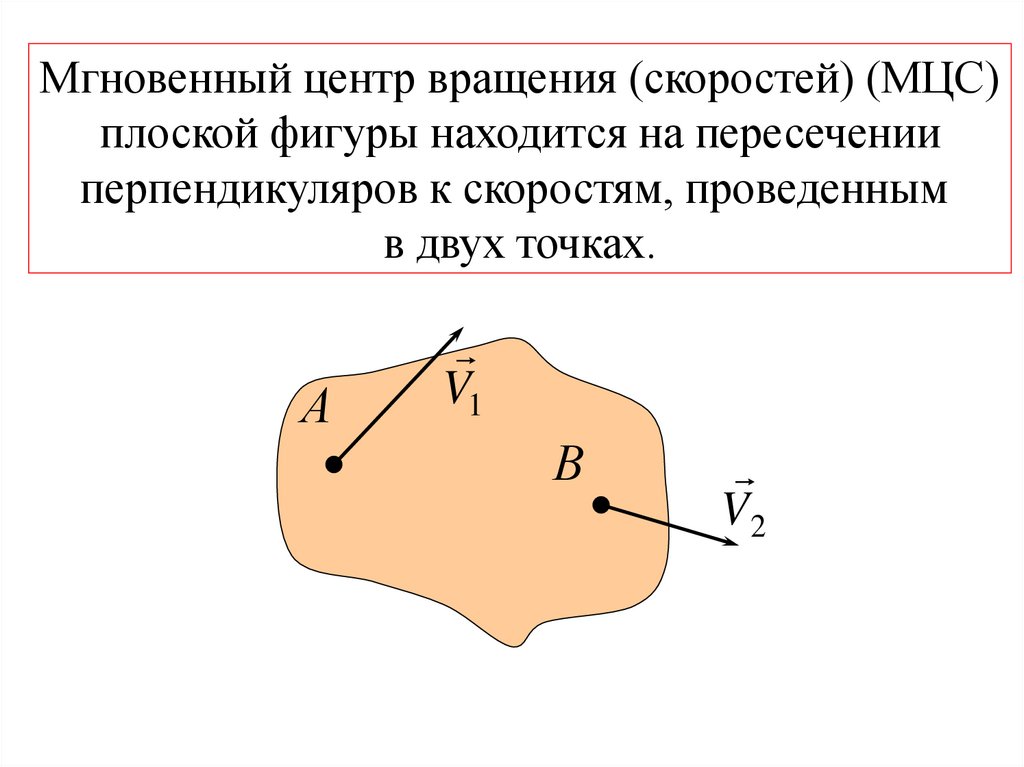
143.
Мгновенный центр вращения (скоростей) (МЦС)плоской фигуры находится на пересечении
перпендикуляров к скоростям, проведенным
в двух точках.
144.
Мгновенный центр вращения (скоростей) (МЦС)плоской фигуры находится на пересечении
перпендикуляров к скоростям, проведенным
в двух точках.
А
V1
В
V2
145.
Мгновенный центр вращения (скоростей) (МЦС)плоской фигуры находится на пересечении
перпендикуляров к скоростям, проведенным
в двух точках.
А
V1
В
Р
V2
146.
Частный случай:скорости точек параллельны
и различаются по величине
VA
А
VС
С
Р
147.
Частный случай:скорости точек параллельны
и различаются по величине
А
М
С
Р
VA
V
М
VС
148.
Замечание:Величина скорости точки плоской фигуры
при плоскопараллельном движении
пропорциональна расстоянию точки от МЦС
VМ MP
149. 2. Скорости точек плоской фигуры
yM
r
A
O
x
150.
2. Скорости точек плоской фигурыM
y
М
O
r
A
А
М А r
x
151.
d M d A d rdt
dt
dt
152.
d M d A d rdt
dt
dt
d M
VM
dt
153.
d M d A d rdt
dt
dt
d M
VM ;
dt
d A
VA ;
dt
154.
d M d A d rdt
dt
dt
d M
VM ;
dt
d A
VA ;
dt
dr
r VMA
dt
155.
d M d A d rdt
dt
dt
d M
VM ;
dt
d A
VA ;
dt
dr
r VMA
dt
VM VA VMA
156.
ТЕОРЕМАо скоростях точек плоской фигуры
Скорость любой точки плоской фигуры
находится
как векторная сумма скорости произвольного
центра и скорости данной точки при движении
вокруг этого центра
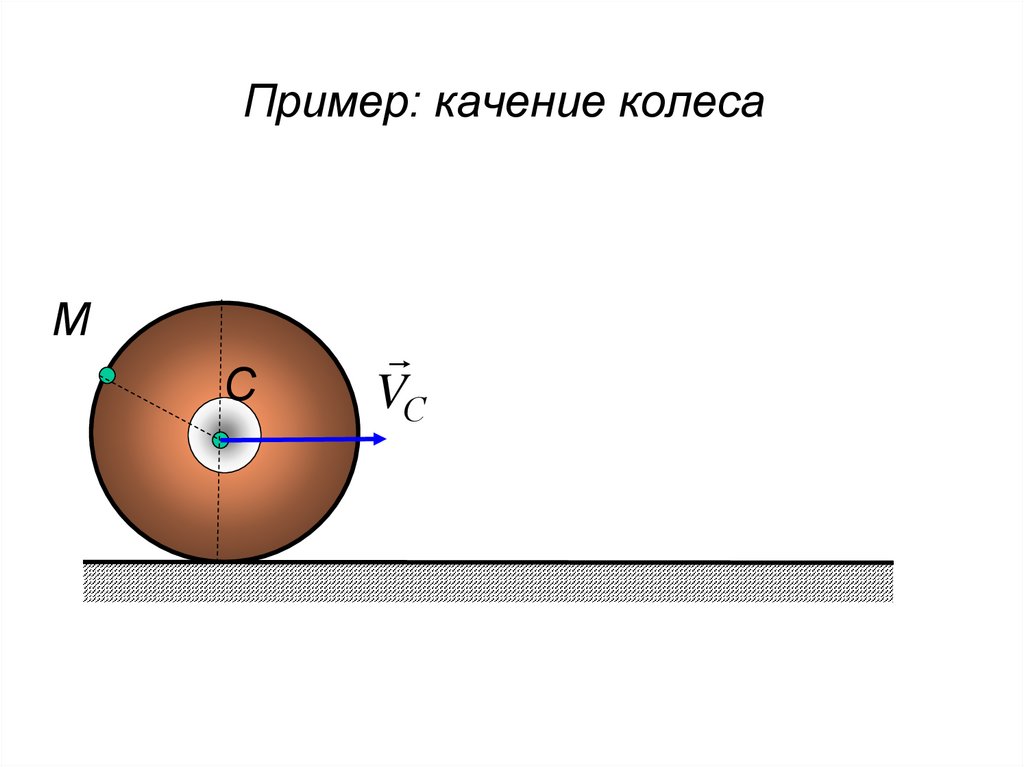
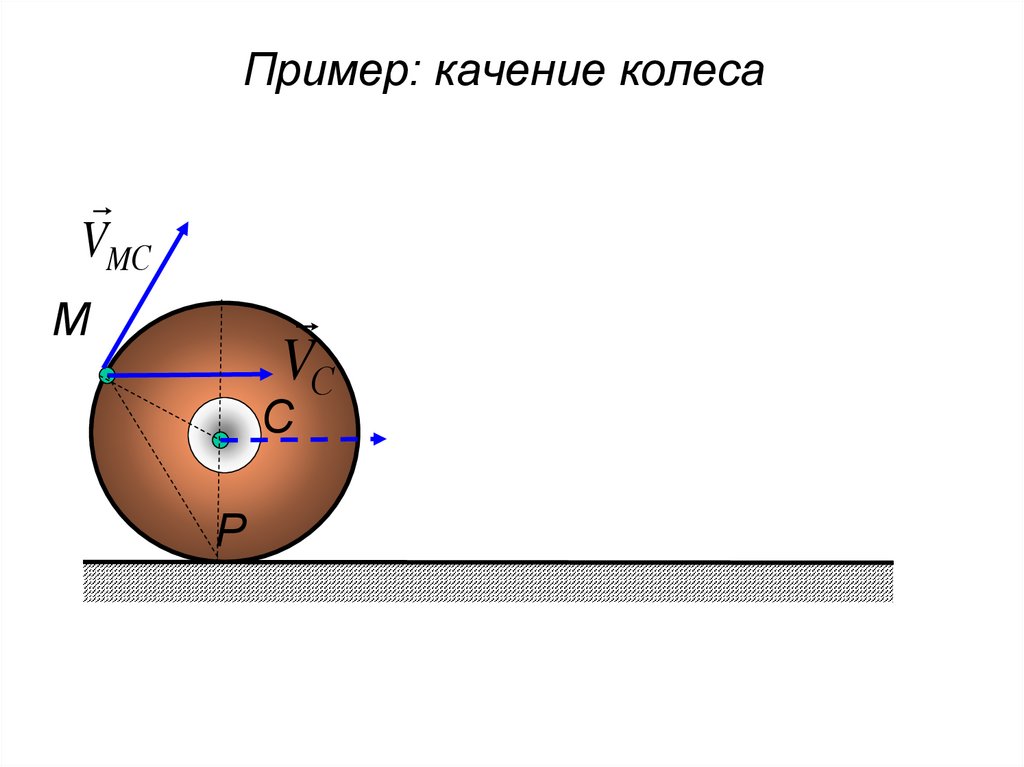
157. Пример: качение колеса
МС
VС
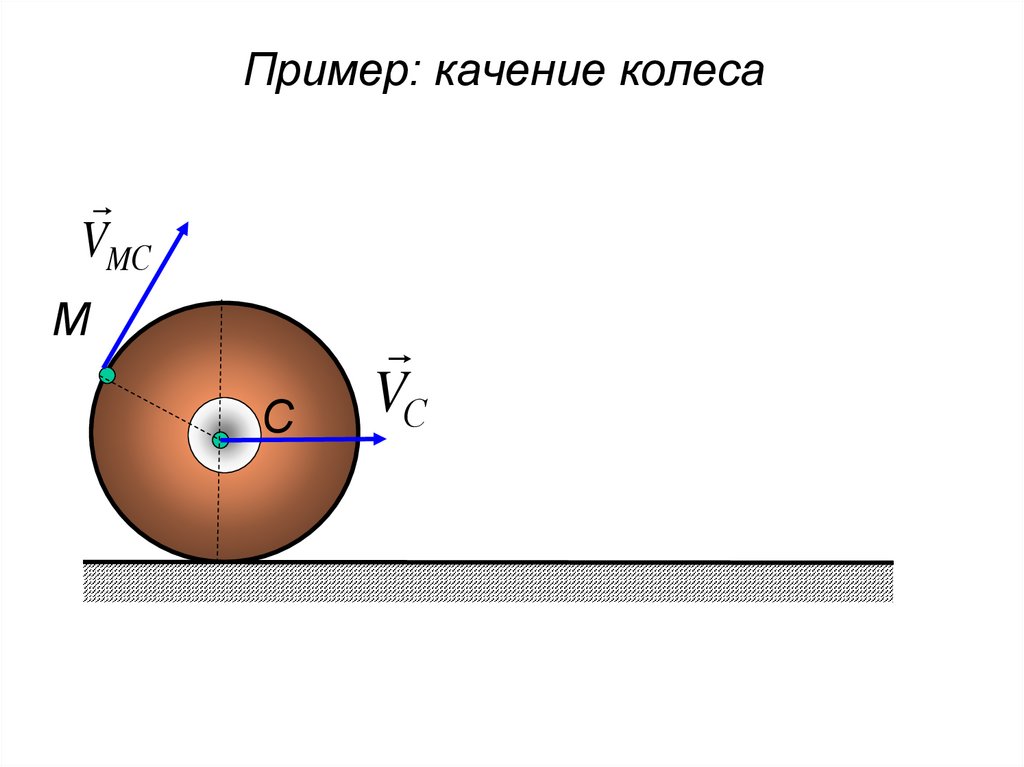
158.
Пример: качение колесаVMС
М
С
VС
159.
Пример: качение колесаVMС
VС
М
С
Р
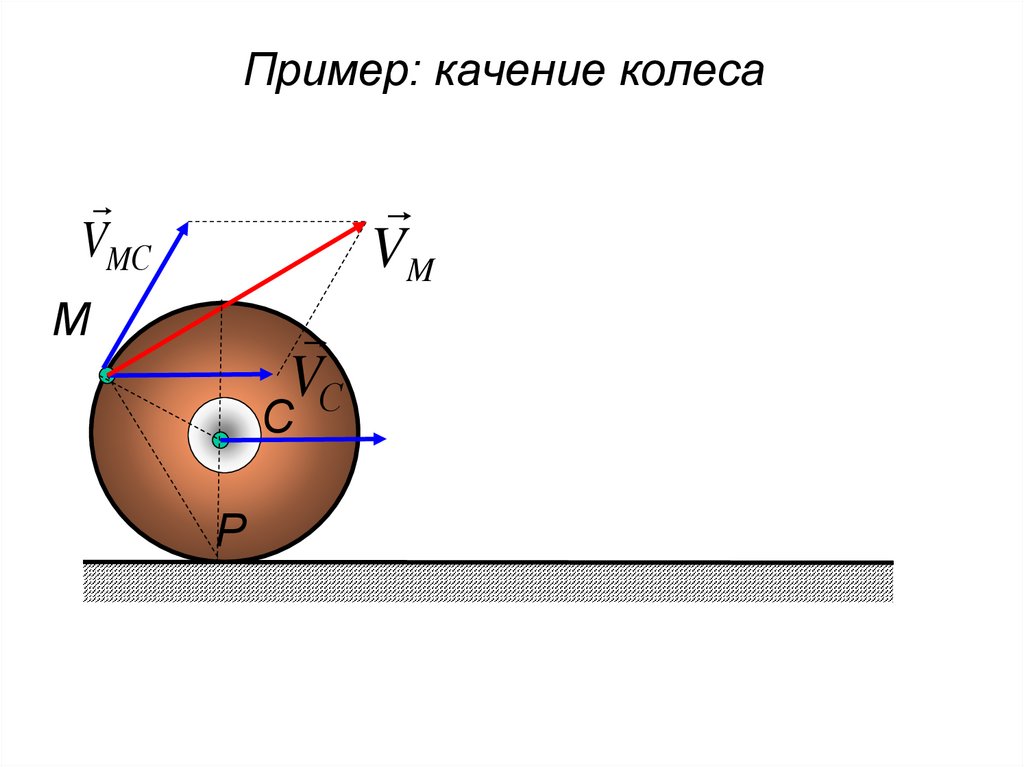
160.
Пример: качение колесаVM
VMС
М
VС
С
Р
161. Теорема о проекциях скоростей
Проекции скоростей концов неизменяемогоотрезка на его направление равны
между собой.
162.
VAА
В
VВ
163. 3. Ускорения точек плоской фигуры
VM VA VMA VA r164.
3.Ускорения точек плоской фигурыVM VA VMA VA r
dVM dVA d dr
r
dt
dt
dt
dt
165.
Так какdVA
a A - ускорение центра А
dt
d
dt
- угловое ускорение плоской фигуры
dr -скорость точки М при движении
r
вокруг центра А
dt
166.
2aM a A r r
вр цс
aM a A аМА аМА
aM a A аМА
167. Вывод:
Ускорение точки плоской фигуры приплоскопараллельном движении
геометрически складывается из ускорения
выбранного полюса и ускорения, которое
получает точка при вращении фигуры
вокруг полюса.
168.
После просмотра и конспектирования слайд-лекциинеобходимо прочитать указанные страницы
учебников и дополнить конспект наиболее важными
сведениями
1. Тарг С.М. Краткий курс теоретической
механики: Учеб. для втузов.- 10-е изд. – М:
ВШ, 1986. С. 127-147.
169.
Динамика материальной точки170.
Динамика изучает механическое движениематериальных тел в зависимости от
действующих на них сил.
171. Законы динамики
Первый закон Ньютона(закон инерции):
Системы отсчета (СО), в которых
материальная точка находится в покое или
движется прямолинейно и равномерно, если
все действующие на нее силы
скомпенсированы (уравновешены),
называются инерциальными.
172.
Второй закон Ньютона (основной):В инерциальной СО ускорение,
приобретаемое материальной точкой
постоянной массы, прямо пропорционально
действующей на точку силе и обратно
пропорционально ее массе.
F
a
m
(1)
173.
Третий закон Ньютона(«действия-противодействия»):
В инерциальной системе отсчета при
взаимодействии двух тел на них действуют
силы одинаковые по модулю и
противоположные по направлению.
174. Дифференциальные уравнения движения точки
1. Векторная формаd r
m 2 F
dt
2
(3)
n
где F Fi -главный вектор действующих
i 1
на точку сил
175. 2. Координатная форма
В проекции на прямоугольные координатные оси:d x
m dt 2 Fx
2
d y
Fy
m
2
dt2
m d z F
z
2
dt
2
(4)
176.
3. Естественный способb
М
n
b n
177.
bНормальная плоскость
М
n
Спрямляющая плоскость
Соприкасающаяся плоскость
178. Естественный трехграник
Мb
n
179.
Лекционная видеодемонстрация(дважды кликнуть по значку)
(или выделить гиперссылку, кликнуть правой
кнопкой мыши, выбрать «Открыть гиперссылку» и
нажать левую кнопку мыши)
Естественный трехгранник – YouTube
www.youtube.com/watch?v=GLs2ZtPqsVA
180.
Тангенциальное (касательное) ускорение:2
dV
d s
a
2
dt
dt
(5)
Нормальное ускорение:
an
V
2
(6)
181.
Дифференциальные уравнения в естественной форме:d s
m
F
2
dt
V2
m
Fn
2
(7)
182.
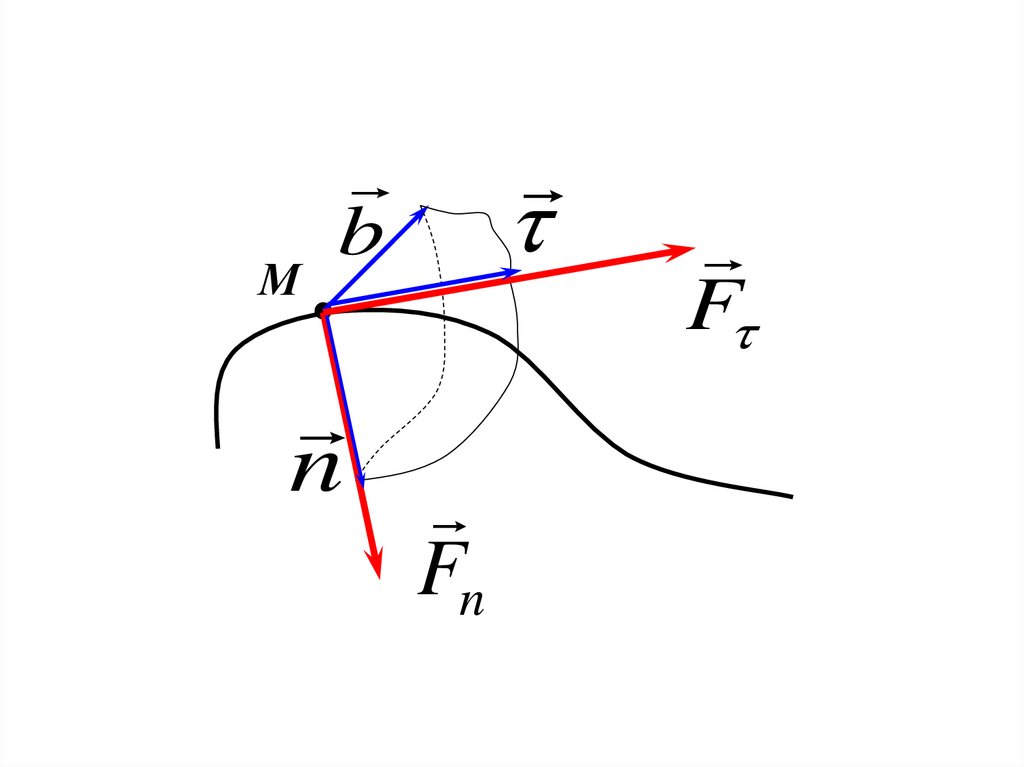
Мb
n
Fn
F
183.
Основные задачи динамики точкиПервая (прямая) задача:
Определение действующей силы по заданному
закону движения точки известной массы
Вторая (обратная) задача:
Определение закона движения точки определенной
массы под действием заданных сил при известных
начальных условиях
184.
Таким образом, первая задача динамики сводитсяк дифференцированию закона движения точки
по времени и, поэтому всегда разрешима.
Решение второй задачи динамики требует
интегрирования дифференциальных уравнений
движения и, поэтому не всегда разрешима
аналитически.
185.
После просмотра и конспектирования слайд-лекциинеобходимо прочитать указанные страницы
учебников и дополнить конспект наиболее важными
сведениями
Тарг С.М.
Краткий курс теоретической
механики: Учеб. для втузов.- 10-е изд. – М:
ВШ, 1986. С. 180-201.
Рекомендованные учебники и учебные пособия выложены в
информационном модуле














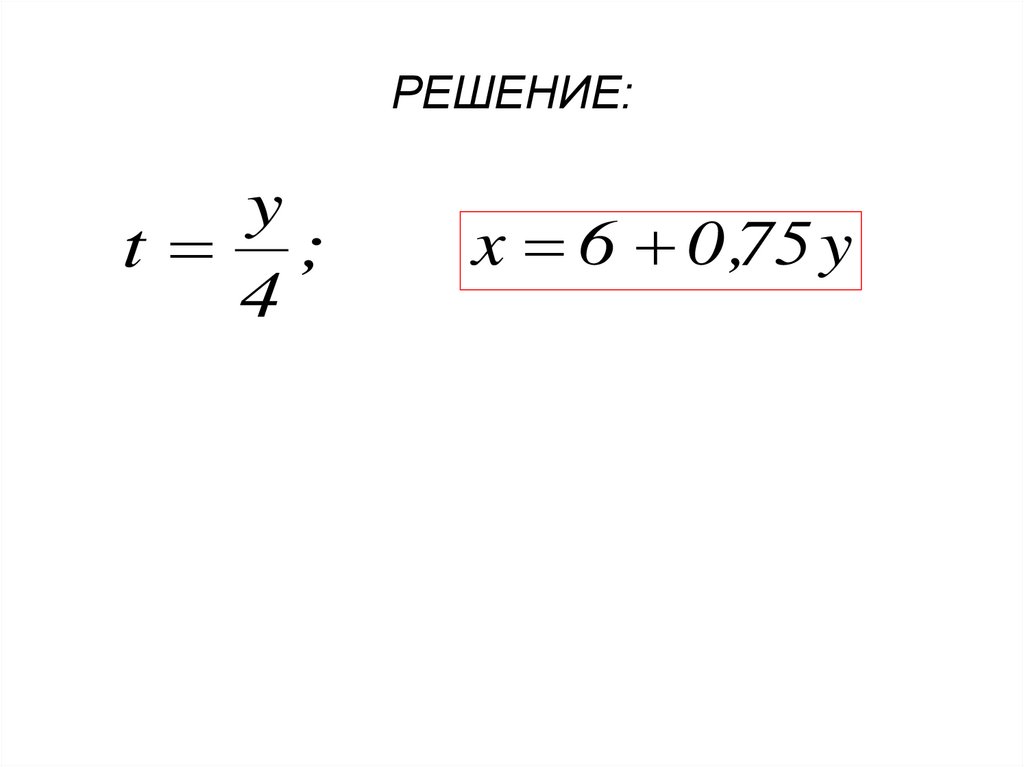


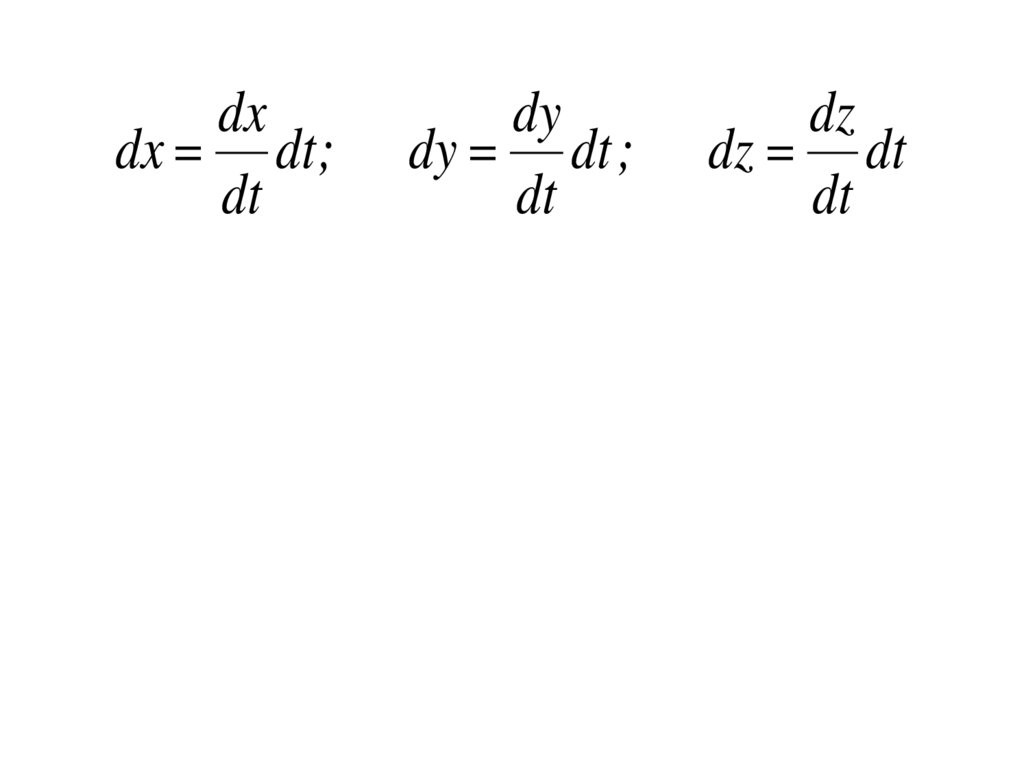
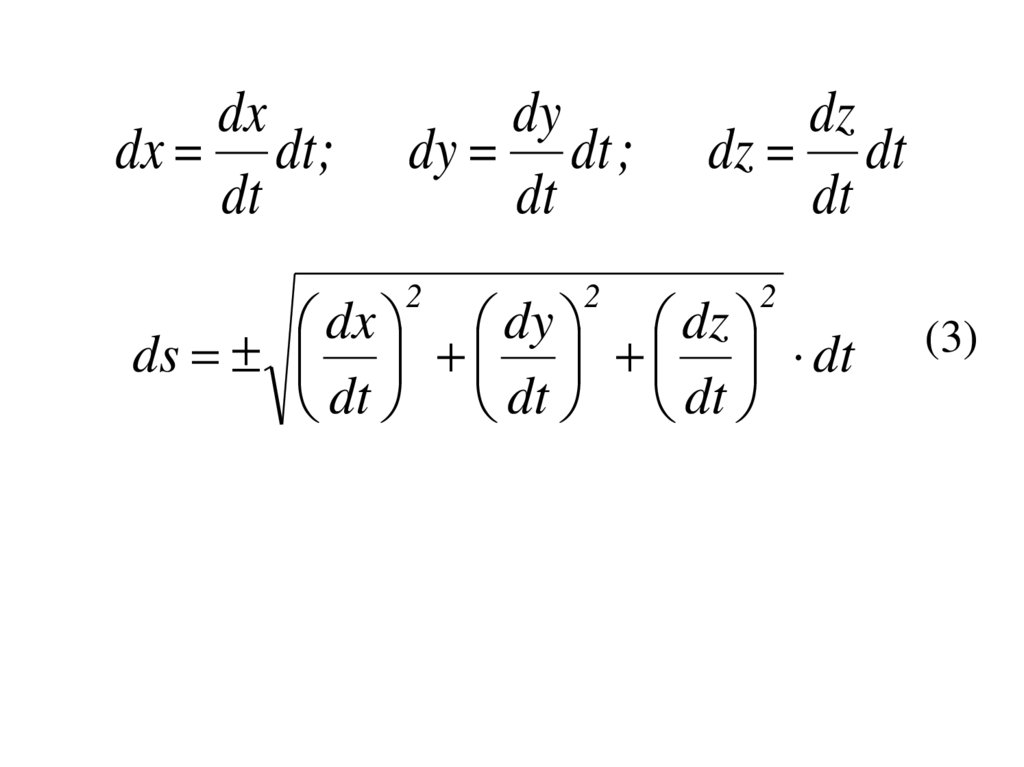
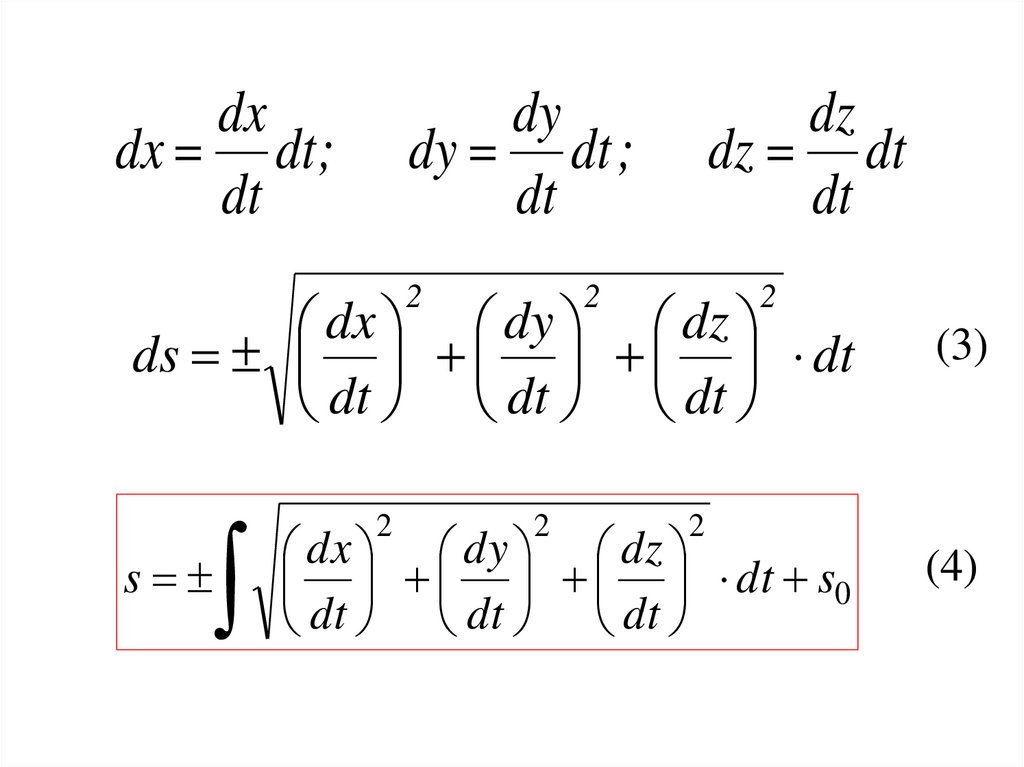
















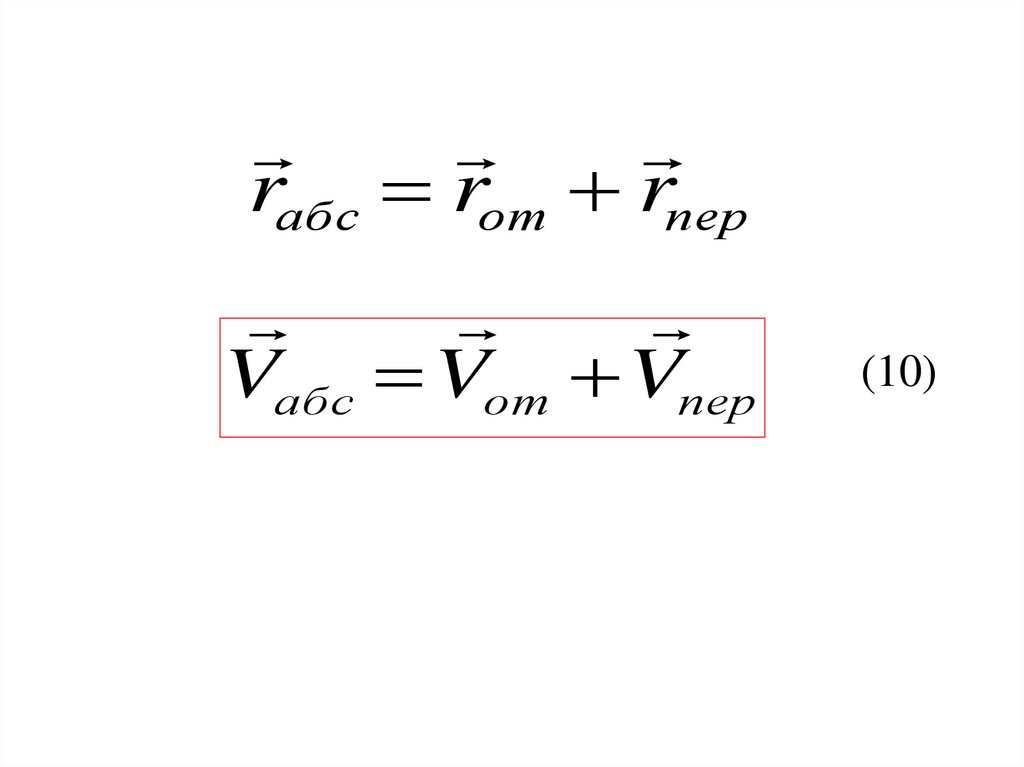






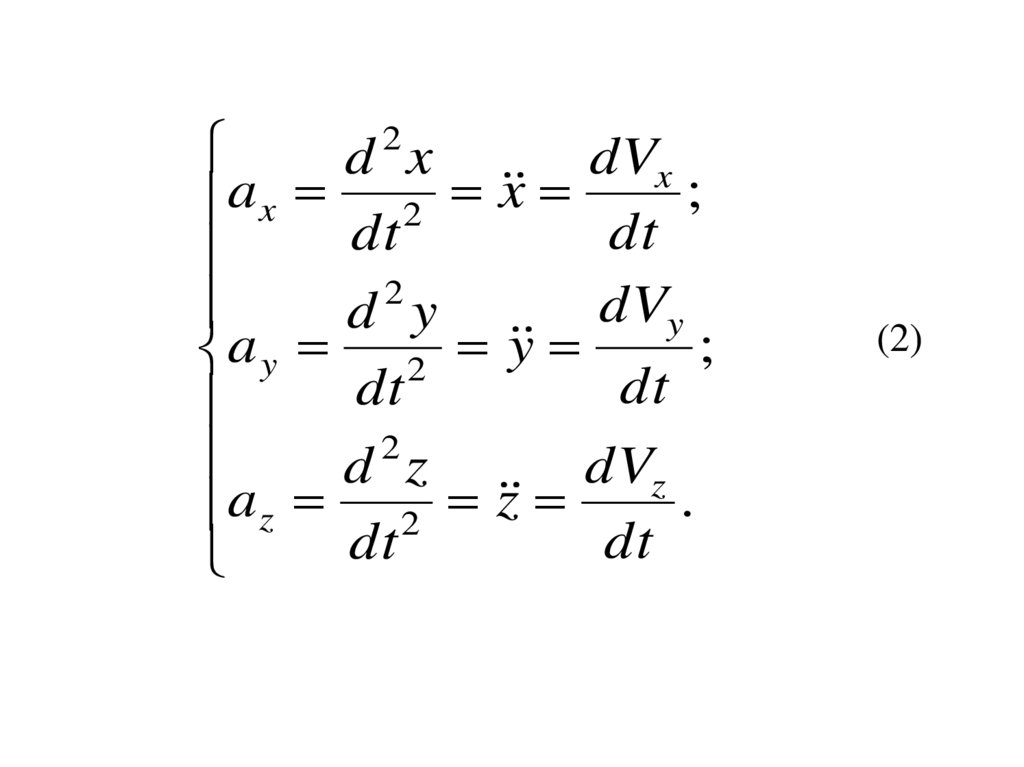
























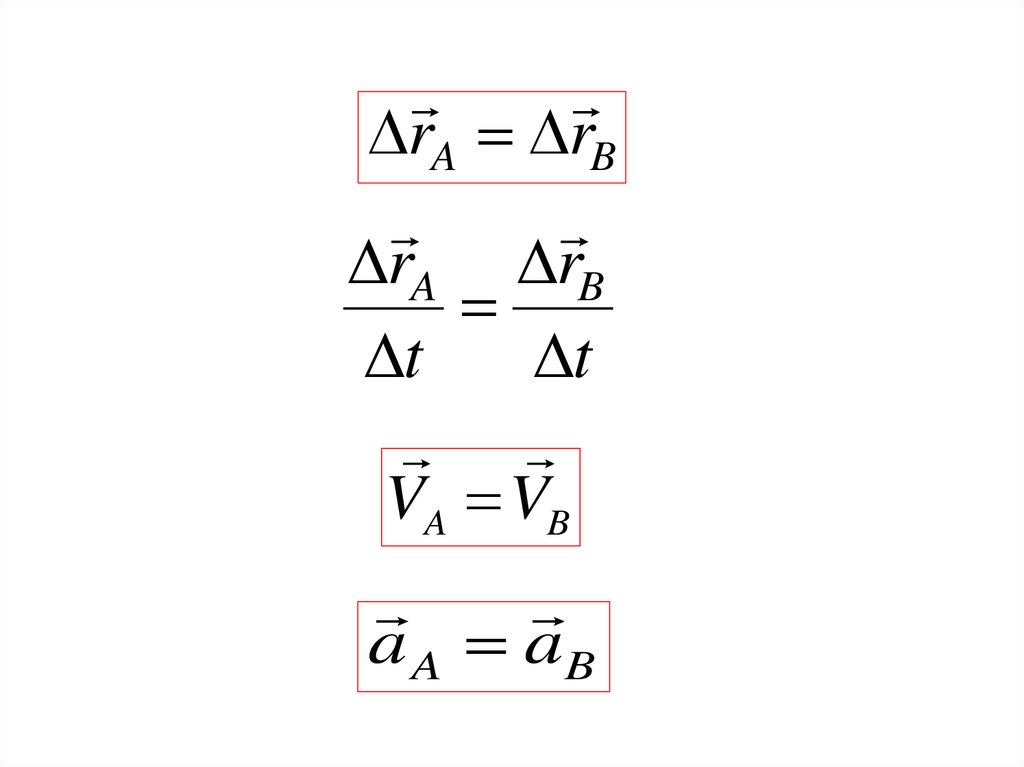




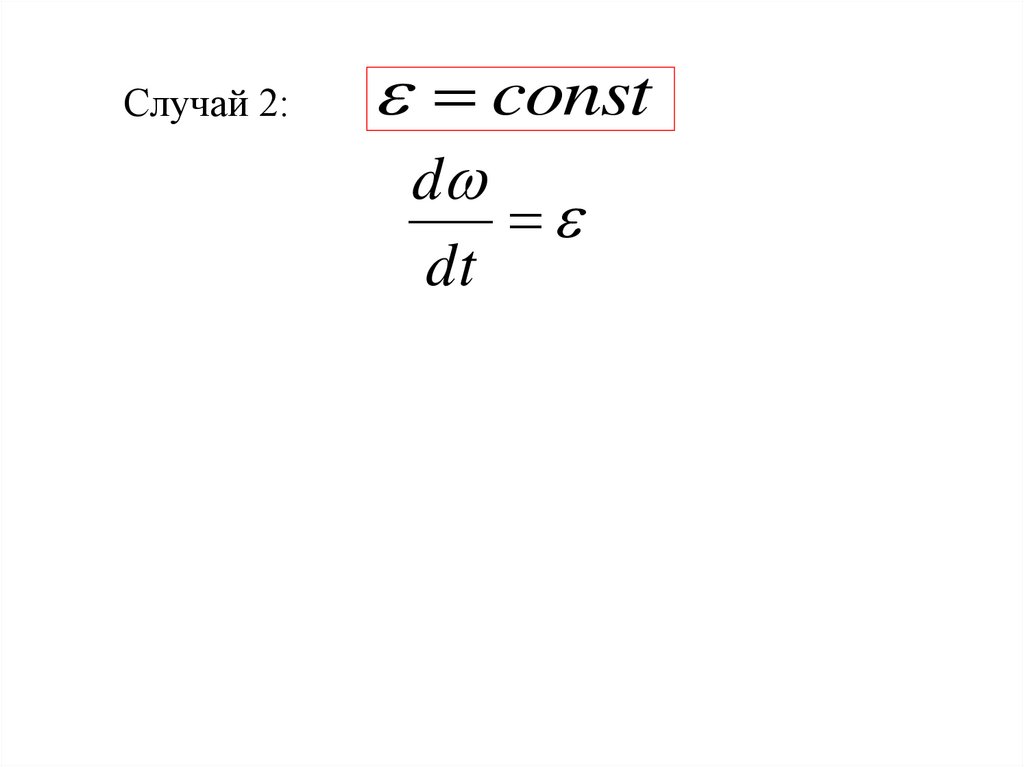























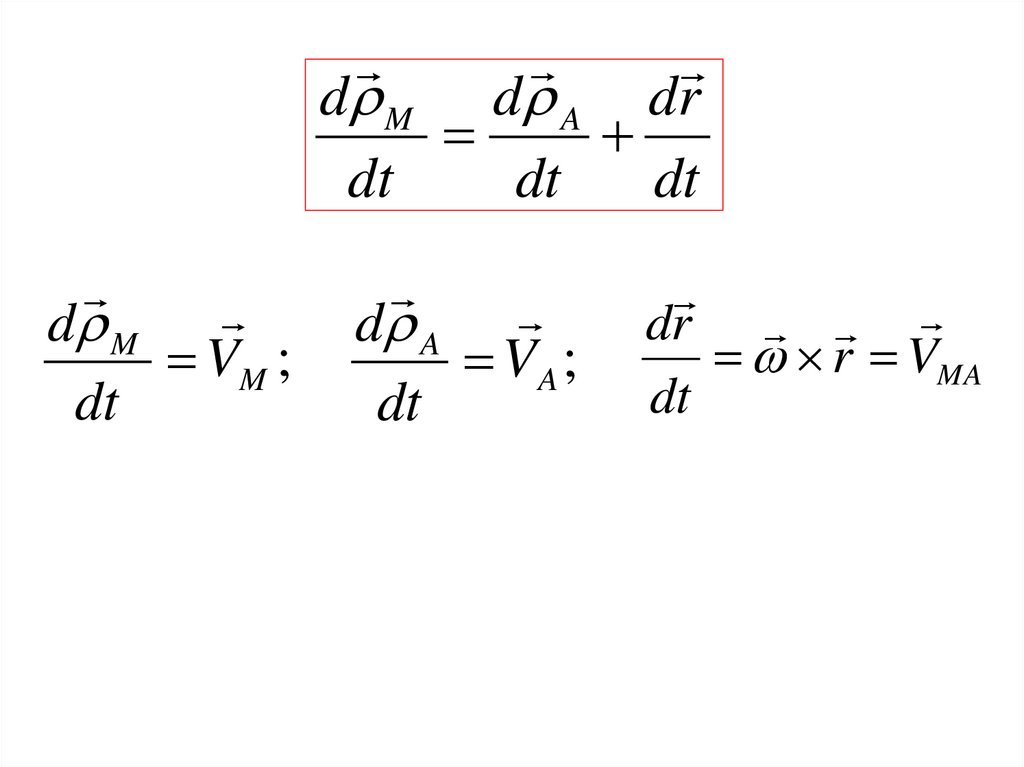
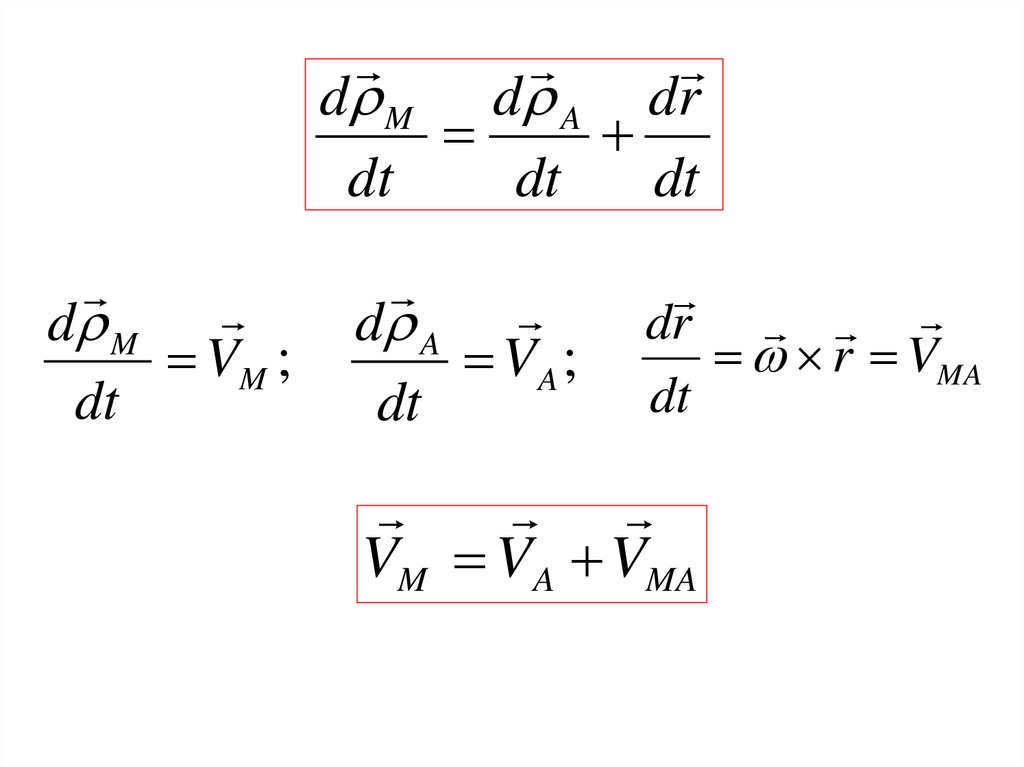






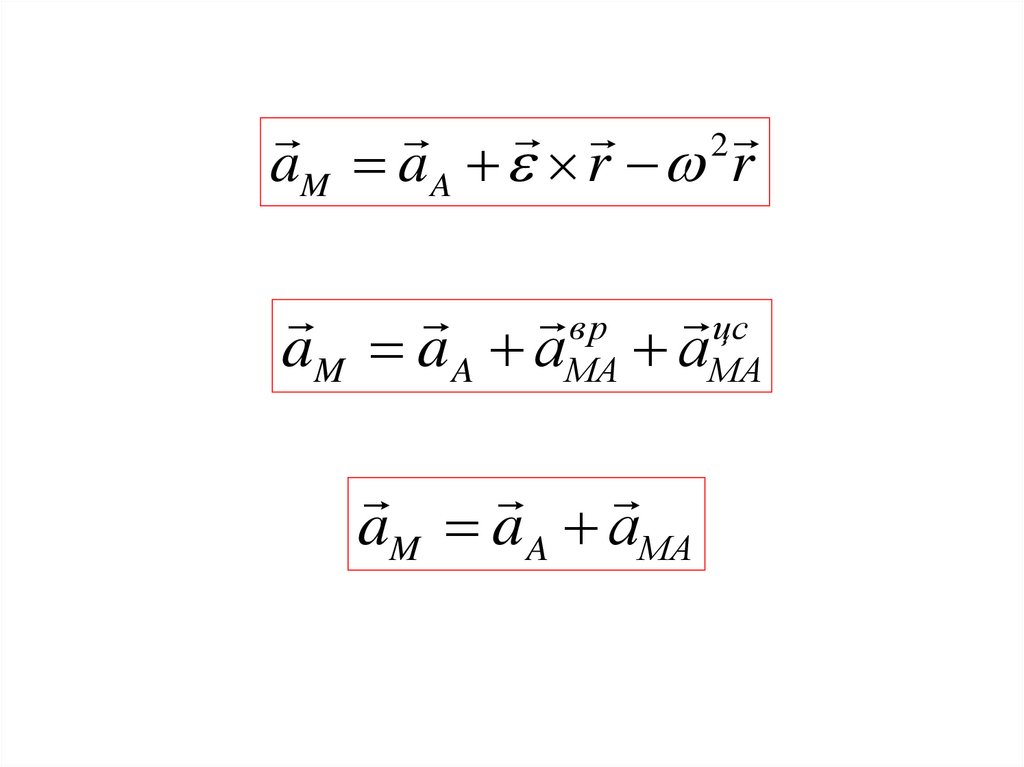















 Физика
Физика Механика
Механика








