Похожие презентации:
Математическая статистика
1. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
2.
• Математическая статистика –раздел математики, который изучает математические методы
систематизации, обработки и использования статистических
данных для научных и практических выводов.
• Характерной чертой нашего времени является проникновение
математических методов анализа и обработки в такие науки,
которые традиционно считались не поддающиеся
математизации.
• Например, в гуманитарные и в частности в лингвинистику.
• Доктор философских наук Р.Т. Пиотровский отмечает: «Для
быстрого изучения иностранного языка надо прежде всего знать
модальные слова (т.е. наиболее часто встречающиеся) и
несложные грамматические правила, и поэтому математизация
языковедения в значительной части основана на статистике».
3.
• Известно, что язык представляет собоймножество
• слов (до 200000). Какие же слова изучать в
первую очередь? Конечно, модальные!
• 10 наиболее часто встречающихся слов
составляют 15-25 % любого текста;
30 слов - 30-40 %;
100 слов – 50 %;
1000 слов – 75 %.
• Частотные словари помогают быстро изучить
иностранный язык.
4.
• Статистическими данными называются сведения очисле объектов, обладающих теми или иными
признаками.
• В процессе изучения статистического изучения
исходных данных выявляются статистические
закономерности, имеющие силу ( т.е. распространяющиеся) для всей массы объектов и явлений.
• Однако законы эти обнаруживаются лишь тогда,
когда мы изучаем явления не по отдельности, а в
большом числе, т.е. когда мы изучаем массовые
явления.
• Математическая статистика основана на массовых
явлениях и базируется на теории вероятности.
5. Исходные термины и понятия
• Случайной величиной называют переменную величину,зависящую от различных случайных обстоятельств.
• Случайные величины могут быть
• - прерывными (дискретными);
• - непрерывными.
• Случайная величина называется прерывной, если она может
принимать только конечное или счетное количество раз.
• Например, количество машин на автостоянке.
• Случайная величина является непрерывной, если
• изучаемый признак меняется непрерывно, т.е. может принимать
любые значения (целые и дробные) в определенном промежутке.
Например, высота рельефа на изучаемом участке.
6.
Генеральная совокупность – это вся подлежащая
изучению совокупность (т.е. все исходные данные),
состоящая из бесчисленного ( множества) количества
членов.
• На практике для изучения генеральной совокупности
используют выборку, в результате которой получают
статистическую совокупность.
• Элементами совокупности называются отдельные
значения, входящие в состав совокупности.
• Объемом совокупности называется число ее
элементов.
• Обозначение:
• «N» - в генеральной совокупности;
• «n» - в статистической совокупности.
7.
Статистическая совокупность представляетсобой беспорядочный ряд наблюдений. Их
необходимо упорядочить. Для этого используются
приемы вариационной статистики, которые
необходимо освоить в данном курсе.
1.
2.
3.
4.
5.
6.
Вариационный ряд и его виды.
Графическое изображение вариационных рядов.
Форма статистических распределений.
Статистические характеристики вариационного
ряда.
Моменты вариационного ряда.
Оценка точности и надежности статистик
вариационного ряда.
8. Вариационный ряд и его виды
Пусть из генеральной совокупности извлечена
выборка. Причем
• Х1 наблюдалось n1 раз;
• Х2 наблюдалось n2 раз;
• Хк наблюдалось nк раз.
• Хi - называются вариантами (или говорят, что
варианты возможные значения признака.
• А последовательность вариант, записанных в
возрастающем (убывающем) порядке называется
вариационным рядом.
9.
Размер Штрихлевобувика
Частота
ni
Накопленная
частота
Частость, Накопленная
Wi
частость
35
5
5
10,0
10,0
36
8
13
16,0
26,0
37
15
28
30,0
56,0
38
12
40
24,0
80,0
39
6
46
12,0
92,0
40
4
50
8,0
100,0
10.
• Частота (ni) – число указывающее сколько раз то илииное значение признака встречается в статистической
совокупности.
• Частость (wi) – частное от деления частоты на объем
совокупности.
wi = ni / n 100, %
• Накопленные частоты (частости) результаты
последовательного суммирования частот (частостей)
всех вариантов или интервалов.
11.
• Вариационные ряды делятся на прерывные(дискретные) и непрерывные (интервальные).
• В прерывном ряде изучаемый признак может
принимать только конкретные отдельные
значения.
• При непрерывном варьировании признака
возможные его значения задаются
интервалами
• «от…..до» Интервалы принято называть
классами.
• В общем виде интервальный ряд
представляется таблицей распределения.
12. Мощность пласта Красный 2 на участке шахтного поля Верхнекамского месторождения (Соликамск)
Интервалы мощности, мСередина
интервала
Частота
2,9 – 3,3
ni
Накопленная
частота
Частость,
Wi,%
Накопленная
частость
3,1
2
2
2,9
2,9
3,3 -3,7
3,5
11
13
15.9
18,8
3,7 – 4,1
3,9
8
21
11,6
30,4
4,1 – 4,5
4,3
11
32
15,9
46,3
4,5 -4,9
4,7
16
48
23,2
69,5
4,9- 5,3
5,1
11
59
15,9
85,4
5,3 – 5,7
5,7 -6,1
5,5
5,9
6
4
65
69
8,7
5,9
94,1
100,0
13. Определение ширины интервала
• Когда выполняют упорядочивание интервальныхвариационных рядов, то особое внимание уделяют
правильности определения ширины интервала.
• Правильно выбранная ширина интервала позволяет
обнаружить скрытые закономерности исследуемого
признака и оптимизировать процесс вычисления
Ширину интервала рассчитывают по формуле:
Xmax - Xmin
∆ = --------------1 + 3,2 lg n
где Xmax, Xmin максимальное и минимальное
значение случайной величины в статистической
совокупности;
n – объем совокупности.
Начало первого интервала определяют Xmin - ∆/2
14. 2. Графическое изображение вариационных рядов
• Геометрическая иллюстрация статистических данныхпридает им - наглядность,
- упрощает их анализ.
• Применяется несколько способов графического
изображения вариационных рядов. Выбор зависит
от вида ряда (прервный или непрерывный) и от
поставленной цели.
• Рассмотрим 4 вида графиков:
• - полигон;
• - гистограмму;
• - кумулятивную кривую (сокращенно кумуляту);
• - огиву.
• Графики строят в прямоугольной системе
координат.
15. Полигон интервального ряда
• Этот график представляет собой ломаннуюлинию, которая замыкается на оси абцисс.
• По оси абцисс откладывают середины
интервалов.
• По оси ординат – частоты или частости,
которые относят к середине интервалов.
• Полученные точки соединяют ломанной
линией.
• Чтобы график был замкнутым,
вариационный ряд с обеих сторон
дополняют интервалами с частотами
равными нулю.
16.
ωi, %n=96
25
Частость, %
20
15
10
5
0
0,1
0,3
0,5
0,7
0,9
1,1 1,3
1,5
1,7
Середины интервалов
Рис. 1. Полигон
1,9
2,1
2,3
хi
17. Гистограмма
• Гистограмма используется только дляизображения интервальных рядов. Отличие
гистограммы от полигона состоит в том, что
по оси абцисс откладывают не точки,
соответствующие середине интервалов, а
отрезки, равные ширине интервалов.
• На этих отрезках строят прямоугольники,
высоты которых равны частостям
соответствующих интервалов.
• Получается ступенчатая фигура –
прямоугольная диаграмма.
18.
, 0 025
20
Частость, %
15
10
5
0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
Границы интервалов
1,6
Рис. 2 - Границы интервалов
1,8
2,0
2,2
хi
19. Кумулята
Кумулята применяется для графического изображения дискретных (прерывных) и непрерывных
(интервальных ) рядов. Это интегральный график.
• Для его построения используют интервалы, как и
для построения гистограммы- они откладываются по
оси абцисс, а накопленные частости откладывают
по оси ординат.
• Началу первого интервала соответствует 0-ая
частота.
• Накопленные частости относятся к правым верхним
границам интервалов.
20.
n=96, %
i
100
Накопленная частость, %
90
80
70
60
50
40
30
20
10
0
0,2
0,4
0,6
0,8 1,0
1,2
1,4
1,6
Границы интервалов
Рис. 3. Кумулята
1,8
2,0
2,2
хi
21. Огива
Огива применяется также для графического
изображения дискретных и интервальных рядов. Это
тоже интегральный график.
При построении огивы по оси абцисс откладывают
накопленные частости, по оси ординат интервалы.
Т. е. при построении огивы меняются ролями оси
абцисс и ординат.
На практике чаще используют кумуляту, чем огиву.
• На всех графиках показывают объем совокупности
(n). Он является показателем представителем
выборки, а, следовательно, и надежности
полученных результатов.
22.
хin=96
2,2
Границы интервалов
2,0
1,8
1,6
1,4
1,2
1,0
0,8
0,6
0,4
0,2
0
10
20
30
40
50
60
70
80
Накопленная частость, %
Рис. 4. Огива
90
100
, %
i
23. 3. Форма статистических распределений
• Под формой статистического распределенияпонимается вид его графика - полигона или
гистограммы.
• Формы графиков могут быть весьма разнообразными. В первую очередь их можно разделить на
• - симметричные и
• - несимметричные.
• Распределение считается симметричным, если
частоты (частости) любых двух вариантов,
равноотстоящих от среднего варианта, равны между
собой.
• Однако на практике такого совпадения почти не
бывает.
• И за симметричные принимают распределения, в
которых частоты (частости) вариантов,
равноотстоящих от среднего отличаются
незначительно.
24.
Частота niСимметричное
распределение
_
Xi
25. Асимметричные распределения
Их распределяют на 3 вида:
- умеренно асимметричные или скошенные;
- крайне асимметричные;
- U- образные распределения.
Для умеренно асимметричных различают :
- левосторонную асимметрию (отрицательную)
- правосторонную асимметрию (положительную).
Умеренно асимметричные характеризуются тем, что
у них частоты вариантов, равноудаленных от
наибольшей частоты, все время больше (или все
время меньше) соответствующих частот с другой
стороны от указанной частоты.
26.
Умеренно
ассиметричные
27.
_Xi
28. Крайне асимметричные распределения
• Они характеризуются тем, что наибольшуючастоту имеет наибольший или наименьший
вариант, а остальные частоты медленно
убывают или возрастают. Т. е. снижение
(увеличение) частот происходит в одну
сторону.
29.
Крайнеассиметричные
ni
0
_
Xi
30.
Крайнеассиметричные
ni
0
_
Xi
31. U- образные распределения
• При таком распределении частоты сначаламедленно убывают, а затем, достигнув
наименьшего значения, начинают медленно
возрастать.
32.
U-образноераспределение
ni
_
Xi
33.
• В математической статистике установлено, чтопричиной возникновения асимметрии является
неоднородность совокупности. т.е. возможное
смешение двух или нескольких совокупностей из
различных генеральных совокупностей.
• Поэтому при анализе той или иной совокупности
необходимо быть заранее уверенным в ее
однородности. Иначе можно сделать неверные
выводы.
• Итак, составление таблиц распределения
• и построение графиков распределения является
первым шагом к раскрытию закономерностей
поведения изучаемой случайной величины.
34. 4. Статистические характеристики вариационного ряда
• После того, как собранный материал представлен ввиде вариационного ряда, приступают к анализу
полученных данных.
• Для этого определяют в первую очередь статистические характеристики вариационного ряда. И уже на
их основе судят о закономерностях распределе-ния
изучаемого признака.
Основные статистические характеристики, чаще
всего используемые на практике:
• 1 группа – центральные величины вариационного
ряда;
• 2 группа – показатели вариации.
35. Центральные величины вариационного ряда
• - Мода.x
i
• Средняя арифметическая
• - Медиана.
• - Средняя арифметическая определяется для
прерывного ряда по формуле:
m
x n
x1n1 x2 n2 xn nm i 1
x
n1 n2 nm
n
i i
36.
Для интервальных (непрерывных) рядов, если n великоm
x
Если n мало, то
x n
i
i 1
i
n
x
x
i
n
Средняя арифметическая выражается в тех же
единицах, что и наблюдаемые значения.
37.
• Медианой называется вариант, приходящий-ся насередину ранжированного ряда.
• Медиану непрерывного (интервального)
распределения вычисляют по формуле:
n m 1
ni
2 i 1
M e x0
nm
• где: ∆ - ширина интервала;
n – объем совокупности,
количество данных;
=
• х 0 – начальное значение интервала, в котором
содержится медиана;
• m 1
ni
• i 1 – сумма частот, предшествующих медианному
интервалу;
m – частота медианного интервала.
n
38.
• Модой называется наиболее часто встречающийсявариант.
• Модой прерывного (дискретного) ряда является
вариант, которому соответствует наибольшая частота
(частость).
• При интервальном распределении можно лишь
указать вариант, содержащий моду и приближенно
вычислить по формуле:
(ni ni 1 )
M 0 x0
(ni ni 1 ) (ni ni 1 )
• где: х 0 – начальное значение модального интервала;
– частота модального интервала;
• ni – частота интервала предшествующего
ni 1
модальному;
– частота интервала следующего за модальным.
ni 1
39.
• Мода выявляет то значение признака, около которогогруппируется большая часть объема совокупности.
• При симметричном распределении все характеристики центральных величин совпадают.
• Среднее арифметическое = медиане = моде.
40. Показатели вариации
• Простейшим измерителем вариации признакаявляется размах
R = Хmax – Хmin.
• Это разность между наибольшим и наименьшим
значениями случайной величины в статистической
совокупности. Размах является приближенной мерой
изменчивости.
• На практике больший интерес представляет
рассеяние (разброс) около средней арифметической,
для характеристики которого используют 4
показателя:
• -среднее абсолютное отклонение (d);
• -дисперсия ( 2)
• -среднее квадратическое отклонение (σ);
• -коэффициент вариации (V).
41.
• Среднее абсолютное отклонение• Для прерывных рядов
n
| x x |
i
d i 1
n
• Для непрерывных рядов
m
| x x |
d i 1
i
n
• m – число интервалов;
• x - середина i-го интервала
i
• ni - количество данных в интервале.
42.
• Дисперсия• Для прерывных рядов
n
2
2
(
x
x
)
i 1
n
• Для непрерывных рядов
m
(x x) n
2
2
i 1
i
n
i
43.
• Среднее квадратическое отклонение• Для прерывных рядов
n
2
(
x
x
)
i 1
n
• Для непрерывных рядов
m
2
(
x
x
)
ni
i
i 1
n
44.
• Коэффициент вариацииV 100%
x
• На практике чаще всего из 4-х рассмотренных
показателей используют
• среднее квадратическое отклонение (σ), оно
характеризует абсолютную изменчивость случайной
величины и
• коэффициент вариации (V), он характеризует
относительную изменчивость случайной величины.
45. Моменты вариационногоряда
Из всего множества моментов рассмотрим только
условные, начальные и центральные моменты
вариационного ряда.
При большом количестве данных расчет статистических характеристик становится громоздким,
поэтому для быстроты вычислений предложено
несколько упрощенных методов.
Один из них – метод моментов.
Рассмотрим его на примере.
В результате опробования эксплуатационного блока
золоторудного месторождения получены данные
содержания золота в г/т. Они представлены в
таблице в виде интервального ряда.
46.
• Распределение содержания золота в пробах (г/т)классы
xi
ni
аi
ni ai
ni a i2
0-3
3–6
6–9
9 – 12
12 - 15
15- 18
18 -21
21 - 24
1.5
4,5
7,5
10,5
13,5
16,5
19,5
22,5
35
10
9
3
1
1
1
60
-1
0
+1
+2
+3
+4
+5
+6
-35
0
+9
+6
0
+4
+5
+6
-5
+35
0
+9
+12
0
+16
+25
+36
133
47.
• В 4-м столбце проставляются порядковые номераклассов. Для этого сначала выбирают нулевой класс.
• Вверх от нулевого класса записываются номера со
знаком минус (-),
• Вниз – со знаком плюс (+).
• Затем производится вычисление произведений ni a.
• Нулевой класс выбирают с таким расчетом, чтобы
n
a
i
i была минимальной.
48.
• Расчет условных моментов производится поформулам:
• Первый условный момент
ni αi
γ1
n
• Второй условный момент
2
n
α
i i
γ2
n
• Третий условный момент
=
3
n
а
i i
γ3
n
• Четвертый условный момент
4
n
а
i i
γ4
n
49.
• Используя значения 1-го и 2-го условных моментов• рассчитаем статистические характеристики
вариационного ряда:
• среднее арифметическое X
• среднее квадратическое отклонение (σ ).
х с 1
где: с – середина интервала нулевого класса;
∆ - ширина интервала;
σ=
Δ
2
γ 2 γ1
50.
• Начальный момент к-го порядкаn
k
x
i
k i 1
n
k
i
• где x
• При к=1
- отдельное значение случайной величины.
n
x
1 i 1
n
i
x
• начальный момент 1-го порядка равен средней
арифметической.
51.
• Центральный момент к-го порядкаn
k
(
x
x
)
i
k i 1
n
• Центральный момент 1-го порядка равен нулю.
n
1
(
x
x
)
i
1 i 1
n
0
• Центральный момент 2-го порядка – дисперсия.
n
2
(
x
x
)
i
2 i 1
n
2
52.
• Нормированный моментk
rk k
• 3-ий нормированный момент используется для
количественной оценки асимметрии распределения
3
А 3
• Для приближенной оценки асимметрии распределения можно использовать другую более простую
формулу
x Mo
A
53.
• А – безразмерная величина.• Знаки (+ или -) указывают на характер асимметрии.
• Левосторонняя – со знаком (-); правосторонняя со
знаком (+).
• Практически распределение считается
симметричным, если соблюдается следующее
условие
| A|
3
mA
• Ошибка показателя ассимметрии
mA
6
n
54.
• Кроме асимметрии кривые распределения могутиметь разную форму вершин:
• -высоковершинные;
• - низковершинные;
• -узковершинные;
• -широковершинные.
• Крутость вершин распределения оценивается
эксцессом, который представляет собой четвертый
нормированный момент.
4
Е 4
• Удобнее пользоваться модифицированной
формулой
4
Е 3
4
55.
Если Е>0 – распределение высоковершинное.
Если Е<0 – распределение низковершинное.
Если Е=0 распределение близко к нормальному.
При | E |
mE
3
• Ошибка показателя эксцесса
24
mЕ
n
• Между начальным и центральными моментами
вариационного ряда существуют простые
алгебраические соотношения
2 2 ( 1 )
2
3 3 3 1 2 2( 1 )
4 4 4 1 3 6( 1 ) 2 3( 1 )
2
4
3
56. 6. Оценка точности и надежности статистических характеристик вариационного ряда
• Статистическая совокупность является выборкой изгенеральной совокупности, поэтому статистические
характеристики вариационного ряда являются
приближенной оценкой соответствующих характеристик генеральной совокупности.
• Разницы между значениями характеристик
выборочной и генеральной совокупностей
представляют собой ошибки статистических характеристик вариационного ряда.
57.
х хo m xd d o md
o m
V Vo mV
• где
x , d , ,V- статистические характеристики
выборочной совокупности;
xo , d o , o ,Vo
-соответственно математиче-ское
ожидание,среднее абсолютное отклонение, среднее
квадратическое отклонение, коэффициент вариации
случайной величины в генеральной совокупности.
58.
• В виду того, что значения статистик в генеральнойсовокупности зачастую не известны, для оценки
точности выборочных статистик используют выборочное среднее квадратическое отклонение (σ).
• Расчет абсолютных ошибок выборочных статистик
производится по формулам:
• - ошибка средней арифметической
t
• При n>30
mx
• -при n<30
mx
n
t
n 1
• - ошибка среднего квадратического отклонения
m
t
2n
59.
• - ошибка среднего абсолютного отклоненияt
md 1,07
2n
• - ошибка коэффициента вариации
• при малых его значениях
mV
tV
2n
• При больших его значениях
tV
V 2
mV
0,5 (
)
100
n
• где t –вероятностный коэффициент, он характеризует
надежность результатов
60.
• Наиболее часто применяемые значения вероятностного коэффициента приведены в таблице.Р
0,68
0,95
0,99
0,997
t
1
2
2,58
3
61.
• Истинные значения характеристик записываются вследующем виде
xo x m x
o m
d o d md
VO V mV
• либо
62.
• Интервальная оценка статистик генеральнойсовокупности случайной величины.
• С принятой вероятностью можем утверждать, что
истинные значения данных статистик не выйдут за
доверительные границы.
x m x xo x m x
m o m
d md d o d md
V mV VO V mV
63.
• Относительные ошибки выборочных статистиквычисляются по формулам:
mx
Mx
100%
x
M
m
100%
md
Md
100%
d
mV
MV
100%
V
• Они характеризуют надежность результатов.
64. Законы распределения случайных величин
1. Общие сведения
2. Законы распределения
2.1. Нормальный закон
3. Аппроксимирование эмпирического распределения теоретическим законом
3.1 Подбор закона
3.2. Проверка гипотезы
3.3. Критерии согласия
4. Аппроксимирование эмпирического распределения
нормальным законом
4.1. Приближенная проверка гипотезы о нормальном
распределении случайной величины
4.2. Строгая проверка гипотезы
65. 1. Общие сведения
• Целью любого исследования являетсяпрактическое использование его
результатов.
• Достигается это чаще всего путем
открытия законов, по которым происходят
те или иные явления, протекает тот или
иной технологический процесс.
• Знание законов позволяет прогнозировать
события и управлять технологическими
процессами, т.е. избегать излишних
материальных затрат и экономить время в
нашей практической деятельности.
• Поэтому изучение любой случайной
величины по данным выборки направлено
прежде всего на выявление ее закона
распределения.
66.
• Что же понимается под статистическим закономраспределения случайной величины?
• В результате наблюдений мы получаем опытные
(эмпирические) данные, т.е. выборку из генеральной
совокупности. После статистической обработки этих
данных мы получаем вариационный ряд. Его
графическое изображение в виде полигона принято
называть эмпирической кривой распределения.
• Установлено, что по мере увеличения числа
наблюдений и уменьшения величины интервалов
полигон распределения (или гистограмма)
приближается к плавной кривой, которую называют
кривой распределения.
• Кривые распределения являются графической
формой выражения законов распределения
случайной величины.
67.
• полигонω i,%
Кривая
распределения
n
∆х
∞ }ω
0
Pi
i
Эмпирическая
кривая
Х
68.
• кумулята∑ω i,
%
Кривая
распределения
n
∆х
∞ }ω
0
i
Pi
Эмпирическая
кривая
Х
69.
• Прежде, чем дать определение законураспределения случайной величины,
познакомимся с некоторыми понятиями
теории вероятностей.
• Теория вероятностей – математическая
дисциплина, основанная на интуитивном
представлении вероятностей появления
объекта или события.
• Вероятность – количественное выражение
возможности того, что данное событие
произойдет. Ее принято обозначать «Р» и
выражать в долях единицы.
70.
• Вероятность появления событийР,
дол
.
ед.
Событие (А)
Возможность
появление
невозможно
Название
невозможное
событие Р(А)
1
Обязательно
Достоверное
произойдет
событие Р(А)
>0 Может произойти Случайное событие
<1 или не произойти
0<P(A)<1
0
71.
• Законом распределения прерывной (дискретной)величины называется всякая функция, устанавливающая связь между возможными значениями
случайной величины и соответствующими им
вероятностями.
• P =f(x)
• Для непрерывной случайной величины можно вести
речь лишь о вероятности того, что случайная
величина примет значение, заключенное в определенном интервале ее изменения.
• Решить эту задачу позволяет функция, характеризующая плотность вероятности.
Рi
Р
x
72.
• где Р - средняя вероятность, приходящаяся наединицу длины интервала;
• Рi
- вероятность попадания значений непрерывной
случайной величины в интервал
.
х
• Относительная плотность распределения
wi
Рi
x
• При n
i i
x 0
• Получаем выражение функции в общем виде
P = f(x)
• Эта функция характеризует плотность вероятности в
точке и является одной из форм закона
распределения непрерывной случайной величины.
73.
• Функцию f(x) называют дифференциальной функциейраспределения или дифференциальным законом
случайной величины.
• Ее основные свойства:
• - функция всегда положительная
f ( x) 0
• - площадь, ограниченная кривой распределения и
осью абцисс, равна 1
f ( x)dx 1
• Распределение случайной величины можно
охарактеризовать и другим способом, а именно с
помощью кумуляты, или интегральной кривой
распределения.
74.
n
i i
x 0
wi
Pi
x
x
w P
i
i
Р характеризует вероятность того, что значение
i
случайной величины,
F ( x) F ( x x a )
• где F (x ) - накопленная вероятность;
• F ( x xa ) - символ, обозначающий вероятность того,
что наблюдаемое значение (х) будет меньше или
равно заданному (x a ).
75.
• В общем виде предыдущую формулу принятовыражать через дифференциальную функцию f(x) в
следующем виде
F ( x) f ( x)dx
• Функция F(x) называется интегральной функцией
распределения или интегральным законом
распределения случайной величины.
• Основные свойства этой функции:
• 1. Всегда положительная F ( x) 0
• 2. Поскольку вероятность не может принимать
значения больше 1, 0 F ( x ) 1
• 3. Предельные значения функции:
x F ( x) 1
• При x F ( x) 0, при
76.
• 4. Так как F(x) – неубывающая функция, то приF
(
x
)
F
(
x
)
и
2
1
2
1
• Из этого свойства вытекает важное следствие:
• Вероятность того, что случайная величина примет
значение, лежащее в интервале между x1 и x 2
• равно разности значений F ( x2 )и F ( x1 )
x x
P( x1 x x2 ) F ( x2 ) F ( x1 )
77. 2. Законы распределения
• Существует множество законов распределенияслучайной величины, такие как
• - нормальный;
• - логарифмически–нормальный;
• - закон Пуассона;
• - закон Максвелла;
• - биноминальный.
• Три закона занимают особое место в теории
статистики. Это биноминальный, нормальный изакон
Пуассона.
• Биноминальный закон известен с 1700 года, его
открытие связано с именем Якова Бернулли.
78.
• Нормальный закон открыт в конце 18 века и связан сименами Лапласа и Гаусса.
• Закон Пуассона открыт в 1837 году Симеоном Деки
Пуассоном.
• Эти 3 закона являются классическими, т.к. остальные
законы можно свести к этим 3-ем путем
соответствующих преобразований. Наиболее
распространенным является нормальный закон. Он
чаще других используется при статистических
исследованиях.
• 2.1. Нормальный закон
• Строгое математическое обоснование нормальный
закон получил в трудах П.Л. Чебышева, А.А. Маркова
и А.М. Ляпунова.
79.
• В трудах доказывается, что если варьированиеслучайной величины происходит под воздействием
большого числа независимых (или мало зависимых )
факторов, причем влияние каждого из них
незначительно по сравнению с совокупным воздействием остальных факторов, то распределение
случайной величины подчиняется нормальному закону.
Дифференциальная функция нормального
распределения выражается следующей формулой
f ( x)
1
2
e
( x M )2
2 2
• где σ - среднее квадратическое отклонение случайной
величины;
• М – математическое ожидание;
• Х – частное значение;
- постоянные величины.
.....и.....е
80.
• Величиныи М называют параметрами распределения.
• Графическое изображение дифференциальной функции
представляет собой кривую колоколообразной формы,
симметрично расположенную относительно
вертикальной прямой из точки х=М и ассимптотически
приближающуюся к оси абцисс по обе стороны от
максимума.
• Величину (М) называют центром распределения.
• Основные свойства нормальной кривой распределения
• 1. Центральные величины распределения совпадают
(математическое ожидание = моде = медиане).
81.
распределения• График нормального закона распределения
случайной величины
fx
M
x
82.
• 2. Кривая имеет один максимум при х=М, он равен1
2
• 3. При х ветви кривой ассимптотически
• приближаются к оси абцисс.
• 4. Изменение (М) при σ= const приводит к
смещению кривой распределения вдоль оси абцисс.
• 5. σ– характеризует форму кривой распределения.
• С уменьшением σ кривая вытягивается вверх в
центре и быстрее приближается к оси абцисс при
удалении от центра.
• При увеличении σ кривая становится плоской,
растягиваясь вдоль оси абцисс.
83.
• При нормальном распределении основная массанаблюдений группируется около М (центра
распределения) или средней арифметической ( х).
• В интервале
68%
2 95%
3 99,7%
• Практически при нормальном распределении вся
совокупность укладывается в интервал 3 .
• В этом заключается правило 3-х сигм, которое имеет
широкое практическое приложение в технике.
84.
• Рассмотрим интегральную функцию нормальногораспределения.
F ( x)
1
2
e
( x M )2
2 2
dx
• На практике величину F(x) определяют через
функцию Лапласа, т.к. существует специальная
таблица значений этой функции.
1
F ( x) (t ) 1
2
(t )
2
t
e
2
0
t2
2
dt
• где t – нормированное отклонение случайной
x M
величины
t
85.
• Функция(t ) обладает следующим свойством
( t ) (t )
• Теоретическое и практическое значение нормального
закона состоит в том, что он является предельным.
• Во многих случаях законы распределения случайных
величин могут быть приведены к нормальному путем
определенной трансформации случайной величины.
86. 3. Аппроксимирование эмпирического распределения теоретическим законом
• Суть аппроксимации состоит в том, чтобы установить наиболее вероятный закон распределенияслучайной величины на основе эмпирического распределения. Сводится оно к решению двух задач:
• 1. Подбор закона.
• 2. Проверка правильности принятого решения.
• 3.1. Подбор закона
• Производится путем последовательного принятия
гипотез относительно характера распределения
случайной величины. Так как нормальный закон
наиболее распространен в природе и наиболее
изучен в математической статистике, то в первую
очередь следует убедиться : не подчиняется ли
эмпирическое распределение изучаемой случайной
величины нормальному закону.
87.
• Приняв ту или иную гипотезу о характере распределения случайной величины, т.е. выбрав теоретический закон, выражают функции теоретического закона через параметры эмпирического распределения.• Затем производят расчет теоретической кривой
распределения (теоретических частот).
• После этого приступают к решению 2-ой задачи – к
проверке принятой гипотезы.
• 3.2. Проверка гипотезы
• Сводится к тому, чтобы установить является ли
различие между эмпирической и теоретическими
кривыми распределения существенными или
случайными. Для этого производят сравнение
эмпирических и теоретических частот в одних и
тех же интервалах.
88.
• Различие между ними может быть вызвано либо тем,что принятая гипотеза не верна, т.е. несоответ-ствие
закономерно. Либо действием случайных факторов
на параметры эмпирического распределения, т.е.
несоответствие случайно. В последнем случае
принятую гипотезу отвергать нет оснований. Можно
утверждать, что рассматриваемое эмпирическое
распределение соответствует принятому в качестве
гипотезы теоретическому закону.
• Решить этот вопрос позволяют критерии согласия.
• 3.3. Критерии согласия
• Их существует несколько. Используем критерий
согласия Пирсона. Он основан на определении
89.
2• величины
, которая вычисляется по формуле:
0 2
(
n
n
2
i
i )
0
n
i 1
i
m
ni - частота i-го интервала эмпирического
распределения случайной величины;
0
n i - частота i-го интервала теоретического
распределения случайной величины;
m - число интервалов.
2
Величина является случайной величиной.
При пользовании критерием Пирсона обязательным
условием является требование:
Частот в интервалах должно быть не менее 5.
Если их меньше, то такие интервалы следует
объединить с соседними.
90.
• Порядок расчета и использования критерия Пирсона• 1. По эмпирическим (опытным) данным подобрать
теоретический закон, найти параметры выбранного
закона.
• 2. Определить теоретические частоты (при наличии
малых частот в интервалах эти интервалы объединить с соседними).
2
• 3. Вычислить величину критерия Пирсона ( ).
• 4. Определить число степеней свободы (к) по
формуле:
• K= m – s,
• где m – число интервалов;
s - число параметров эмпирического
распределения, использованных при вычислении
теоретических частот.
91.
2• Используя полученные значения
и (к) найти
2
• соответствующую вероятность Р( ) по таблице
2
вероятностей для
.
6. Сформулировать вывод, исходя из принципа
применения критерия согласия.
2
• Если Р(
) > 0,1, то расхождения между
эмпирическими и теоретическими частотами следует
считать несущественными, а эмпирическое
распределение согласующимся с теоретическим.
• В противном случае расхождения являются не
случайными и избранный закон отвергается.
92. 4. Аппроксимирование эмпирического распределения нормальным законом
• Первоначально выполняется приближенная оценкасоответствия эмпирического распределения
нормальному закону.
• 4.1. Приближенная проверка гипотезы о нормальном
распределении случайной величины
• Порядок следующий
• 1. Визуальная оценка симметричности эмпирической
кривой (сравнение ее с нормальной кривой).
• 2. Сравнение центральных величин эмпирического
распределения.
| M0 x |
3,то
если
х Ме М0
| x Me |
• закон нормальный.
93.
• 3. Оценка формы эмпирической кривой при помощипоказателей асимметрии и эксцесса
|E|
| A|
• Если
3 , то закон
3
mE
mA
нормальный
• 4. Оценка эмпирического распределения по коэффициенту вариации (у нормального закона V< 50%).
• 5. Интервальная оценка эмпирического распределения базируется на том, что при нормальном
распределении основная масса данных группируется
около математического ожидания (М).
• Обычно гипотезу о нормальном распределении
принимают при выполнении следующего условия
x 2
S Wi 0,95
x 2
94.
i ,%25
х 2 0,91 2 0,4 0,11
х 2 0,91 2 0,4 1,71
20
1 2
0,2 7,3
h1
0,95 3,6
2
2
7,3 15,6
S 2 2 3 h2
1 11,4
2
2
S1
S3
3 4
15,6 22,9
h3
1 19,2
2
2
S4
4 5
22,9 16,7
h4
1 19,8
2
2
S5
5 6
16,7 14,6
h5
1 15,6
2
2
S6
6 7
14,6 10,4
h6
1 12,5
2
2
S7
7 8
10,4 6,2
h7
1 8,3
2
2
S8
8 9
6,2 4,2
h8
1 5,2
2
2
15
10
1 , 71
95 ,6
i
5
0 ,11
S5
S6
S7
S8
h8
h7
h6
h5
5
6
7
8
9
h3
0
S4
h4
3
4
h2
1
2
S3
h1
S1 S2
0,1 0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9 2,1 2,3
2
0,11
2
0,91
1,71
Рис. 6 - Графический способ определения площадей
хi
95.
• При выполнении больше перечисленных условийпринимают гипотезу о нормальном распределении и
приступают к строгой проверке гипотезы. Если же
приближенная оценка дает отрицательный результат, то подбирают другой подходящий закон, исходя
из особенностей изучаемой случайной величины.
• 4.2. Строгая проверка гипотезы
• Приняв гипотезу о нормальном распределении
случайной величины выражают функции нормального закона через параметры эмпирического
распределения, подставляя вместо
хи σ
96.
• их численные значения.F ( x)
1
e
2
f ( x)
1
2
( xi x ) 2
e
2 2
( xi x ) 2
2 2
dx
• Затем при помощи этих выражений производят
расчет теоретических частот. Для практических целей
используют таблицы функций Лапласа.
f (t )
1
2
e
t2
2
(t )
2
t
e
2
t2
2
dt
0
• t - нормированное отклонение случайной величины
(вероятностный коэффициент)
t
xi x
97.
• Методика расчета теоретических частот• при помощи интегральной функции
• Ранее рассматривались свойства интегральной
функции. Из 4-го свойства вытекало следующее
следствие.
• Вероятность того, что случайная величина примет
х2
значение, лежащее в интервале между х1и
• равна разности значений F ( x2 )и F ( x1 )
P( x1 x x2 ) F ( x2 ) F ( x1 )
• Этим следствием воспользуемся для расчета
теоретических частот
i x
i x
1
0
ni n [ (
2
) (
)]
98.
0i
• n - теоретическая частота i-го интервала;
• n – объем совокупности;
• i - правая граница i-го интервала;
• i -левая граница i-го интервала.
• Расчеты удобно выполнять в формуляре.
• Теоретические частоты сравниваются с эмпирическими, производится вычисление:
2
• - критерия Пирсона ( );
• - число степеней свободы (к).
• Для нормального закона s =3 ( x , , n)
2
• В таблице вероятностей по вычисленным и (к)
2
• находится Р(
) и на основании ее делается
заключение о существенности или случайности
расхождения между эмпирической и теоретической
кривой распределения случайной величины.
99.
Формуляр для расчета теоретических частот и критериясогласия Пирсона 2
Интервалы
x
( i i ) ni i
t
(t )
(t )
i x x
i x ( i x )
i
(
) ( )
x
(
i
nio (t )
n
2
(ni nio ) 2
nio
ni nio
)
100.
• Теория погрешностей101. Задачи теории погрешностей
• Выполнение геодезических работ связано с различногорода измерениями. Известно, что всякие измерения
сопровождаются неизбежными ошибками.
• И как бы не совершенствовались приборы и инструменты, методика измерений, ошибки остаются.
• Поэтому геодезист д. разработать такую методику
выполнения работ, при которой ошибки не превышали
бы предельно допустимых, заложенных в нормативные
документы.
102.
• Для этого специалисту необходимо уметь решатьследующие задачи:
• - организовать измерения так, чтобы их результаты не
содержали ошибок, превышающих допустимые;
• - оценить точность полученных результатов;
• - из полученных результатов измерений вычислить
наиболее надежное значение;
• - оценить точность полученного наиболее надежного
результата.
• Для решения всех перечисленных задач требуется знать
свойства случайных ошибок, уметь устанавливать
закономерности возникновения и накопления ошибок.
• Научная дисциплина, которая занимается этими
вопросами, называется «Теория ошибок и способ
наименьших квадратов».
103.
• Сущность и виды геодезических измерений• Под измерением какой-либо величины понимают ее
сравнение с однородной величиной, принятой за единицу
меры.
• Любые измерения выполняются при наличии и
взаимодействии следующих элементов, участвующих в
процессе измерений:
• - объект измерений;
• - наблюдатель;
• - инструменты, которыми производятся измерения;
• - методика измерений;
• - внешняя среда, в которой производятся измерения.
• Совокупность элементов называют
условиями измерений.
104.
• Существующие виды измерений в геодезической практикевыделим в 3 группы.
1. По способу получения
результатов
2. По возникновению
ошибок
3. По количеству
1. Прямые
1. Зависимые
1. Необходимые
2. Косвенные
2. Не зависимые
2. Избыточные
3. Связанные условиями
3. Равноточные
4. Не связанные
условиями
4. Неравноточные
105.
• Прямые измерения – такие, при которых искомыйрезультат получается из непосредственного
сравнения измеряемой величины с единицей
измерения.
• Косвенные, когда искомый результат находится по
функциональным зависимостям через другие
непосредственно измеренные величины.
• Связанные условиями- это измерения, для которых
заранее известно, что их истинные значения должны
удовлетворять определенным теоретическим
требованиям.
• Не связанные условиями – измерения, для которых
не существует теоретических условий.
• Зависимые – такие, у которых ошибки одного
измерения связаны с ошибками другого.
106.
• Независимые – такие, у которых ошибки одного измеренияне влияют на ошибку другого.
• Равноточные – такие, у которых сохраняются все условия
измерений во время всего процесса съемки.
• Неравноточные – такие, у которых изменяется хотя бы
одно из условий измерений.
• Необходимые – такие, которые дают возможность
получить одно единственное значение каждой из искомых
величин.
• Избыточные – такие, которые выполнены помимо
необходимых.
• Выполнение избыточных измерений в геодезии
обусловлено:
- контролем измерений;
- повышением точности измерений.
107. Погрешности измерений. Их классификация.
Под погрешностью результата измерений понимаютразность
xi X ,
где x i - измеренное значение искомой величины;
Х ее истинное значение.
Погрешности измерений возникают в результате
суммы элементарных ошибок и являются
неизбежными.
В зависимости от природы образования погрешности
делят на 3 группы:
1) грубые;
2) систематические;
3) случайные.
108.
• Грубыми называются ошибки, выходящими за пределыточности. Предельной называют наибольшую ошибку,
равную утроенной средней квадратической ошибке.
Причины: небрежность, -усталость,
- рассеянность.
• Грубые ошибки обнаруживаются при повторных
измерениях и исключаются из результатов измерений.
• Систематические ошибки – это те, которые при повторных
измерениях одной и той же величины остаются
постоянными со знаком (+) или (-) или закономерно
изменяются.
• Причины возникновения – условия измерений.
Систематические ошибки стараются исключить из результатов измерений устранением причин возникновения, либо
введением поправок с обратным знаком.
• Случайные ошибки – явление неизбежное. Они возникают
под влиянием множества факторов.
109.
• Случайные ошибки имеют разные величины и знаки,изменяются случайным образом при повторных измерениях одной и той же величины. Они подчиняются
статистическим закономерностям массовых случайных
явлений. Их численное значение устанавливают путем
многократных измерений определяемой величины и
используют для оценки точности конечных результатов.
• Свойства случайных погрешностей
• 1. По абсолютной величине случайные погрешности не
могут превосходить определенного предела (3 m).
• 2. Погрешности положительные и равные им по величине
отрицательные встречаются одинаково часто.
• 3. Малые по абсолютной величине погрешности
встречаются чаще.
• 4. Среднее арифметическое из погрешностей при
неограниченном числе измерений стремится к нулю.
lim
lim 1 2 .... n 0.....при...n
n
n
110. Числовые характеристики точности измерений
• Погрешности определяют в абсолютных и относительныхвеличинах.
• К абсолютным относятся:
• - средняя арифметическая, она определяется по формуле:
| | | |
| |
i
n
i
n
• -средняя квадратическая погрешность, она определяется
по формуле Гаусса:
m
2
i
n
• Это основная мера точности в теории ошибок.
4
| | m
5
111.
• Вероятная ошибка (r) – это такое значение случайнойвеличины при данных условиях равноточных
измерений, по отношению к которому число ошибок
больших ее по абсолютной величине равно числу
ошибок меньших.
r =2/3m
• Предельная ошибка – это такое абсолютное
значение случайной ошибки, которого не может
превзойти ни одна из истинных ошибок данного ряда.
• Ошибки, большие предельной, считаются грубыми.
112. Математическая обработка ряда равноточных измерений
• Равноточными называются измерения, при выполнениикоторых совокупность условий наблюдений не изменяется.
• В геодезии часто обрабатывают результаты измерений
одной и той же величины (х1, х2 … хn).
• Если получен ряд результатов равноточных измерений, то
требуется произвести их математическую обработку.
• Она состоит из вычислений:
• - среднего арифметического значения измеренной
величины;
• - средней квадратической погрешности отдельного
измерения;
• - средней квадратической погрешности среднего
арифметического.
113.
• Среднее арифметическое значение определяется поформуле:
х1 х 2 ... х n x
х
n
n
• Рассмотрим доказательство того, что среднее арифмети• ческое является наиболее надежным значением из данного
ряда равноточных измерений.
• Есть результаты равноточных измерений х1, х2…..хn.
• Истинное значение величины Х.
• Разность между измеренными и истинным значением дает
истинную случайную погрешность.
1 x1 X
2 x2 X
n xn X
114.
х Х n• Затем разделим каждый член полученного равенства на n
x X
• Обозначим
n
n
x x
n
n
х - среднее арифметическое из данного ряда равноточных
измерений;
- среднее арифметическое из истинных случайных
ошибок результатов данного ряда измерения.
• Согласно принятым обозначениям формула примет вид
х Х
115.
• На основании 4-го свойства случайных погрешностейможно утверждать, что среднее арифметическое из
погрешностей при неограниченном числе измерений
стремится к нулю.
lim
lim 0.....при....n
n
x X
• Тогда при n
• т. е при неограниченном возрастании числа измерений
среднее арифметическое из результатов равноточных
измерений одной и той же величины стремится к
истинному значению этой величины.
• Среднее арифметическое из данного ряда равноточных
измерений принимается за наиболее надежное значение
и при конечном числе измерений, так как и в этом случае
происходит компенсация случайных ошибок
• и полученный результат надежнее характеризует
действительные размеры объекта.
116.
• Для расчета среднего арифметического используютупрощенную формулу. Рассмотрим ее вывод.
• Возьмем некоторое значение из данного ряда,
обозначим (хо), оно называется приближенным.
Обычно его берут равным минимальному значению.
• Найдем уклонения измеренных величин от
приближенного х х
о
1
1
х 2 хо 2
х n xo n
• Сложим левые и правые части равенств
х хо n
• Разделим каждый член уравнения на n и получим
x xo n
n
n
n
x xo
n
117.
• Пример.№ п/п
Х, м
1
2
3
4
5
6
,мм
+3
+5
+2
+4
0
+4
= 18
27,483
27,485
27,482
27,484
27,480
27,484
Хо= 27,480
0,018
х х
27,480
27,483
о
n
6
118. Свойства уклонений от среднего арифметического
• Результаты многократных измерений одной и той жевеличины будут отличаться от их среднего
арифметического на разности
1 х1 х
2 х2 х
n xn x
• Докажем, что алгебраическая сумма уклонений от
среднего арифметического для данного ряда равноточных измерений равна нулю при любом числе n.
• Это первое свойство.
• Сложим уравнения, получим
х х n
119.
• Разделим на nx x n
n
• Получим
n
n
x x 0,..т.е..... 0
n
• 2-ое свойство.
• Сумма квадратов уклонений данного ряда
измеренных величин от среднего арифметического
всегда будет меньше суммы квадратов уклонений
измеренных величин от любого числа х не равного
среднему арифметическому
vv
• Для доказательства используем ряд равноточных
измерений. Определим уклонения от какого-либо
o
значения
x
120.
• Получимх1 х 1
о
х2 х 2
о
хn x n
o
• Найдем разность равенств
( х1 х ) ( х1 х о ) 1 1
( х2 х ) ( х2 х 0 ) 2 2
( хn x ) ( xn x o ) n n
• Раскроем скобки и после преобразований получим
х х 1 1
о
х х 2 2
о
х х n n
о
Обозначим постоянную величину
х х
о
121.
• Тогда1 1
2 2
n n
2 1
2
1
• Возведем равенства в квадрат
2
2
1
2 2
n2 2 n 2 n2
2
2
2
• И сложим 2 n
n
• Известно 0 тогда
2
2
2
• Отсюда следует
vv
2
2
2
2
2
122.
• 3-е свойство.• Сумма квадратов уклонений от среднего арифметического
всегда меньше суммы квадратов истинных погрешностей.
• Составим 2 ряда разностей.
• 1 ряд – погрешности измерений ( x1, x2,…. хn) от их
истинного значения (X).
x X
1
1
2 x2 X
n xn X
• 2 ряд уклонения измеренных величин ( x1, x2,…. хn) от
среднего арифметического ( х )
1 х1 х
2 х2 х
n xn x
123.
• Найдем разности этих равенств1 1 ( x1 X ) ( x1 x )
2 2 ( x2 X ) ( x2 x )
n n ( xn X ) ( xn x )
• Преобразуем –
1 1 ( x X )
2 2 (x X )
n n (x X )
• Возведем в квадрат обе части
21 12 2 1 ( x X ) ( x X ) 2
22 22 2 2 ( x X ) ( x X ) 2
2n n2 2 n ( x X ) ( x X ) 2
• Сложим
• Так как
2( x X ) ( x X ) 2 n
0
124.
( x X ) 2 n• то уравнение примет вид
• После преобразований
• Тогда очевидно, что
( x X ) 2 n
• Предыдущее уравнение представим в следующем
виде
( x X ) 2 n
• Разделим его на n
(x X )
2
n
• Разность
х Х
m 2
n
- истинная погрешность
= средней квадратической
n
погрешности по формуле Гаусса.
125.
• А среднее из всех возможных квадратов истиннойn
• погрешности среднего арифметического будет являться
квадратом средней квадратической погрешности
среднего арифметического
2
m
m
n
2
x
• Тогда в уравнении ( x X ) 2 n
• произведем соответствующую замену и получим
2
m
m n
n
n
2
m (n 1)
2
m
n 1
• Это формула Бесселя, немецкого астронома и
геодезиста.
126.
• Средняя квадратическая погрешность данного рядаравноточных измерений равна корню квадратному из
суммы квадратов уклонений от арифметической
средины, деленной на число избыточных измерений.
• Средняя квадратическая погрешность среднего
арифметического по уклонениям от него определится по
формуле:
mx
• или
(n 1)n
mx
m
n
127.
• Рассмотрим пример.2
2
8
64
+3,2
10,24
17,08
0
0
-4,8
23,04
3
17,14
6
36
+1,2
1,44
4
17,10
2
4
-2,8
7,84
5
17,18
10
100
+5,2
27,04
6
17,11
3
9
-1,8
3,24
№
п/п
хi
1
17,16
2
х 0 =17,08
=29см
=213 +0,2см =72,84
2
2
128.
• Среднее арифметическое х х 17,08 м 29см 17,1283 м0
n
6
хокр 17,128 м
• Среднее округленное
• Ошибка округления хокр х 17,128 17,1283 0,0003 м
• Контроль:
n ( 0,0003) 6 0,0018м
n 213 296 72,83
2
2
2
2
• Средняя квадратическая погрешность результата
измерения:
72,83 3,8cм 0,038 м
m
n 1
6 1
Средняя квадратическая погрешность среднего
арифметического
mx
m
n
0,038
6
0,016 м
129. Математическая обработка ряда неравноточных измерений
• В геодезии часто встречаются неравноточные измерения. Они обусловлены изменением условий измерений.• Результаты неравноточных измерений обладают
различной степенью надежности. И поэтому при
определении наиболее надежного из ряда таких
неравноточных измерений нельзя воспользоваться
просто арифметической срединой. На окончательный
результат более точные измерения должны оказывать и
большее влияние.
• Значит при определении окончательного значения
должно учитываться достоинство каждого измерения.
Его выражают весом.
• Весом называют степень доверия к результату
измерения, выраженную числом.
130.
• Между весом и средней квадратической погрешностьюсуществует следующая взаимосвязь: чем меньше средняя
квадратическая погрешность какого-нибудь измерения, тем
больше его вес.
• Исходя из этого за веса результатов измерений принимают
величины обратно пропорциональные квадратам соответствующих им средних квадратических погрешностей.
• Пусть некоторая величина измерялась неравноточно n раз.
• Получим результаты
x1 , x2 ,....xn
• Их средние квадратические
m1 , m2 ,....mn
• погрешности соответственно
• равны
• Веса этих измерений могут
• быть выражены
1
1
1
P1 2 ,...P2 2 ,........Pn 2
m1
m2
mn
131.
• Вес – величина относительная, т.е. он даетпредставление о точности результата измерения
только при сравнении с весами других результатов.
• Поэтому выражения весов можно записать в
следующем виде:
c2
c2
c2
P1 2 ;...P2 2 ;......Pn 2
m1
m2
mn
• где с - коэффициент пропорциональности.
• Он может быть любым, но обязательно одинаковым
для выражения всех весов результатов данного ряда
измерений.
• Коэффициент (с) подбирают таким, чтобы придать
весам удобные для расчетов численные значения.
132.
• При расчете весов должны быть выполнены 2 условия:• - средние квадратические погрешности m, по которым
определяются веса, д.б. вычислены из достаточно
большого числа наблюдений (не менее 8);
• - из результатов измерений д.б. исключены
систематические погрешности.
• Свойства весов
• 1. Отношение весов двух измерений обратно
пропорционально квадратам средних квадратических
погрешностей измерений.
P1 m22
c2 c2
P1 : P2 2 : 2 ...... 2
P2 m1
m1 m2
• 2. Отношение весов не изменится, если их
увеличивать или уменьшать в одинаковое число раз.
133.
• Из определения веса следует, что равноточныеизмерения имеют равные веса.
• Найдем вес среднего арифметического.
2
с
• Вес отдельного измерения равен
P
m
• Вес среднего арифметического равен
• Составим соотношение весов
Px mi2
2
Pi m x
m
• Но m x
, тогда Px
m2n
n
2 n
Pi
2
i
i
с2
Px
2
mx
m
• Но если примем вес отдельного измерения Рi= 1 при
условии равноточных измерений m1 m2 ..... mn m
2
2
2
• то, следовательно, P m 1;....P m 1;......P m 1
1
m2
2
m2
n
m2
134.
• ТогдаPx
n
1
• Вес арифметической средины равен числу (n), показывающему из скольки равноточных измерений с весами,
равными единице, получена данная арифметическая
средина.
• Определение весовой арифметической средины
производят по формуле:
P1 x1 P2 x 2 ... Pn x n Px
x
P
P1 P2 ... Pn
• Весовая средняя арифметическая равна сумме
произведений каждого неравноточного измерения на
его вес, разделенной на сумму весов.
• Для упрощения расчетов используют рабочую формулу,
в которой выделяются приближенные значения (хо) из
измеренных величин
P1 1 P2 2 .... Pn n
P
x xo
xo
P
P1 P2 ... Pn
135.
1 , 2 ,..... n• Где
- уклонения измеренных величин от
х0 ;
приближенного значения
• P1 , P2 ,.....Pn
- веса соответствующих измеренных
• величин x1 , x2 ,....xn
Ошибка единицы веса
Известны результаты неравноточных измерений
x1 , x2 ,....xn
m1 , m2 ,....mn
P1 , P2 ,.....Pn
c2
c2
c2
P1 2 ;...P2 2 ;......Pn 2
m1
m2
mn
Пусть среди этого ряда имеется некоторое
измерение, вес которого равен единице
i тое
Pi 1
136.
• Получимc2
2
2
1
,......
отсюда
.....
с
m
i
mi2
• Т.е. коэффициент (с) есть средняя квадратическая
погрешность измерения, вес которой равен единице.
• В отличие от СКП других измерений, веса которых не
равны единице, она обозначается через ( ) и
называется ошибкой единицы веса.
с 2 mi2 2
• Заменяем (с) ошибкой единицы веса и получим
P1
• Или
2
2
1
m
.....P2
2
m
2
2
......Pn
2
mn2
m1 P1 m2 P2 mn Pn
m1
P1
;......m2
P2
;.......mn
Pn
137.
• Следует иметь ввиду, что в данном ряде неравноточныхизмерений может не быть фактического измерения, вес
которого равен 1. Можно условно принять некоторое
фиктивное измерение с весом =1 и с ним сравнивать
надежность всех остальных результатов.
• Ошибка единицы веса через истинные погрешности
данного ряда неравноточных измерений вычисляется по
формуле:
Р
n
• где i - истинная погрешность данного ряда
неравноточных измерений.
138.
• Свойства уклонений от арифметической средины• 1 свойство. Сумма произведений соответствующих весов
на уклонения от арифметической средины равна 0 при
любом числе измерений.
• Доказательство.Найдем уклонения результатов измерений
от средневесового.
х х
1
1
2 х2 х
n xn x
• Умножим обе части уравнений на веса соответственно
P1 , P2 ,.....Pn
и получим
1 P1 x1 P1 xP1
2 Р2 х2 Р2 хР2
n Pn xn Pn xPn
139.
• Сложим равенства, получим суммарное уравнениеР хР х Р
• Подставим вместо
х
• Тогда
Рх
Р
Рх
Р Рх Р ,.....тогда.. Р 0
Р
• 2-е свойство. Сумма произведений соответствующих
весов на квадраты уклонений от арифметической
средины всегда меньше суммы произведений весов на
квадраты уклонений от любого числа, не равного
арифметической средине.
Р P
2
2
140.
• 3-е свойство. Сумма произведений соответствующихвесов на квадраты уклонений от арифметической
средины всегда меньше суммы произведений весов
на квадраты истинных погрешностей
P P
2
2
• Ошибка единицы веса вычисляется по уклонениям от
арифметической средины по формуле:
P
2
n 1
- уклонение от арифметической средины;
• n- число неравноточных измерений.
2
• Контроль:
P
P P
P 2 P 2
P
• Средняя квадратическая погрешность арифметической средины рассчитывается по формуле:
mx
P
141. Оценка точности функций измеренных величин
• Вспомним о косвенном виде измерении. Это такиеизмерения, при которых искомая величина находится
по функциональным зависимостям через другие
непосредственно измеренные величины.
• Так как непосредственные (прямые измерения сопровождаются ошибками, то и значение вычисленной
функции будет определено с ошибкой.
• Рассмотрим функцию общего вида.
Y F ( X 1 , X 2 ,... X n )
Х 1 , Х 2 ,..... Х-n истинные значения независимых
• где
величин (аргументов);
• m1 , m2 ,....mn - соответственно их средние
квадратические ошибки.
• Для определения аргументов выполнены
соответствующие ряды непосредственных измерений.
142.
• Формула для вычисления средней квадратическойпогрешности функции общего вида следующая:
2
2
2
F 2
F 2 F 2
2
mn
m1
m2 ....
mY
X 1
X 2
X n
• Квадрат средней квадратической ошибки функции
общего вида независимых величин равен сумме
произведений квадратов частных производных
функции по каждому аргументу на квадраты средних
квадратических ошибок соответствующих аргументов.
• На практике значения производных в этой формуле
вычисляются при подстановке в них измеренных
аргументов, т.к. изменение частных производных F
X
i
• в пределах от.. Х i ...до... Х i i xi не окажет
существенного влияния на точность вычисления
средней квадратической ошибки.
2
2
2
F 2
F 2 F 2
2
mn
m1
m2 .....
m y
x1
x 2
x n
143. Функции частного вида
• Функция произведения непосредственно измеренногоаргумента на постоянный коэффициент.
Y aX
• Средняя квадратическая ошибка произведения
постоянной величины на непосредственно измеренный
аргумент равна произведению этой постоянной на
среднюю квадратическую ошибку аргумента.
m y am
• Пример. Длина окружности ( 2 r d ) измерена с
погрешностью m d
. Средняя квадратическая
погрешность определения длины окружности равна
mC md
144.
• Линейная функцияУ a1 X 1 a2 X 2 .... an X n
• Квадрат средней квадратической ошибки функции
общего вида равен сумме произведений квадратов
коэффициентов на квадраты средних квадратических
ошибок соответствующих аргументов.
m y2 a12 m12 a22 m22 ... an2 mn2
• Если измерения равноточные
m1 m2 ..... mn m
• то
m m a
2
y
2
2
145.
• Функция алгебраической суммы нескольких слагаемыхY X 1 X 2 ... X n
• Квадрат средней квадратической ошибки
алгебраической суммы нескольких слагаемых равен
сумме квадратов средних квадратических ошибок.
m y2 m12 m22 ... mn2
• Если измерения равноточные
• то
2
2
my m n
m1 m2 ..... mn m ,
146. Вес функций измеренных величин
• Чтобы определить веса функций воспользуемсяформулами определения СКП функций и понятием веса.
• Обозначим вес функции Ру, а вес аргумента Рi.
• Тогда вес фунции будет определяться по формуле:
Ру
2
m y2
• Вес аргументов по формуле:
P1
2
2
1
m
.....P2
2
m
2
2
......Pn
2
mn2
• Из этих соотношений СКП функции и аргументов
соответственно
my
Py
m1
P1
;......m2
P2
;.......mn
Pn
147.
• Рассмотрим определение весов для различных функций.• СКП Функции общего вида
2
2
2
F 2
F 2 F 2
2
mn
mY
m1
m2 ....
X 1
X 2
X n
• Заменим в этой формуле СКП функции и аргументов
выше приведенными соотношениями и получим
2
F 2 2
F 2 2
F 2 2
( )
(
)
... (
)
Ру
x1 P1
x 2 P2
x n Pn
• Произведем сокращение и получим
1
F 2 1
F 2 1
F 2 1
( )
(
)
.... (
)
Py
x1 P1
x 2 P2
x n Pn
• Величина, обратная весу функции общего вида, равна
сумме произведений квадратов частных производных
по каждому аргументу на величины, обратные весам
соответствующих аргументов.
148.
• Функции частного вида:• 1)СКП функции произведения непосредственно
измеренного аргумента на постоянный коэффициент
m y am
• Величина обратная весу функции произведения
постоянного коэффициента на аргумент равна
произведению квадрата коэффициента на величину
обратную весу аргумента
1
2 1
• 2) СКП линейной функции
Py
a
P
m y2 a12 m12 a22 m22 ... an2 mn2
• Величина, обратная весу линейной функции, равна сумме
произведений квадратов постоянных коэффициентов на
величины, обратные весам аргументов
1
2 1
2 1
2 1
a1
a2
.. a n
Py
P1
P2
Pn
149.
• 3) СКП функции алгебраической суммы несколькихслагаемых
m m m ... m
2
y
2
1
2
2
2
n
• Величина, обратная весу функции алгебраической
суммы аргументов, равна сумме величин обратных
весам аргументов.
1
1
1
1
...
Py P1 P2
Pn
150.
• Оценка точности по разностям двойныхравноточных измерений
• В геодезической практике часто встречаются случаи, когда
одна и та же величина измерена независимо дважды. Т.е.
выполнены двойные измерения однородных величин.
• Как использовать эти результаты для оценки точности
измерений?
• Пусть имеем двойные равноточные измерения n величин.
x1 , x2 ,....xn
x1I , x 2I ,....x nI
• Составим их разности.
x1 x d1
I
1
x2 x2I d 2
x n x nI d n
151.
• Если бы измерения были абсолютно точными и несодержали систематических ошибок, то каждая
разность двойных измерений di ,была бы равна нулю.
• Т.е. Xi –Xi=0,
• Где Xi – истинное значение искомой величины.
• Следовательно, нуль есть истинное значение каждой
разности двух измерений, а
• di – измеренное значение этой разности.
• Определим расхождение между измеренным
значением разности и ее истинным значением.
d1 0 d1
d2 0 d2
dn 0 dn
• Отсюда вытекает, что d1, d2,…dn являются истинными
погрешностями.
152.
• Используя формулу, в которой определение СКПпроизводится по истинным погрешностям
2
m
n
• можно вычислить среднюю квадратическую
погрешность разности
d
m
2
d
n
• Так как в паре два равноточных измерения то СКП
одного измерения определится по формуле:
d
m
2
2n
• СКП среднего арифметического из двух измерений
равно
mx
m
2
153.
• В разностях двойных измерений может присутствоватьсистематическая погрешность. На ее наличие указывает
• - преобладание одного знака в разностях;
• - неравенство нулю величины d 0 при значительном
n
числе n;
• - при несоблюдении условия
| d |
| d | 2,5
n
• Если систематические погрешности обнаружены, то их
• надо исключить из разностей. Для этого определяют
величину систематической погрешности, приходящуюся
на одну разность. d
n
do
• Вычтем это значение из всех разностей.
d1 d 0 d1I
d 2 d 0 d 2I
d n d 0 d nI
154.
• Так как величина do – есть среднее арифметическое, томожно ( d I ) рассматривать как уклонение от него.
• Доказательство.
• Сложим равенства. Получим d d n d I
0
d d
• Подставим вместо do равное ему соотношение
d
I
d n d
• Отсюда
n
n
d 0
I
• Таким свойством обладает только уклонение от
среднего арифметического. Тогда применив формулу
Бесселя можно записать СКП разности
dIdI
md
n 1
dIdI
m
СКП одного измерения
2(n 1)
o
155. Оценка точности по результатам двойных неравноточных измерений.
• Даны результаты двойных неравноточных измерений.x .и..x .....x .и..x ......x .и..x
I
1
• Их веса соответственно
II
1
I
2
II
2
I
n
II
n
P1I .и..P1II .....P2I .и..P2II ......PnI .и...PnII
• Определим разности двойных результатов
x1I x1II d1
x2I x2II d 2
x nI x nII d n
• Перед нами функция алгебраической суммы слагаемых
1
1
1
Р2 Р1
1
Р у Р1 Р2
или
Ру
Р1 Р2
156.
• Веса разностей могут быть записаныI
1
I
2
II
1
PnI PnII
Pd n I
Pn PnII
II
2
P P
Pd 2 I
P2 P2II
• Рассматривая разности d1,d2,…dn с весами Pd ,..Pd ,......Pd
• на основание формулы, определяющей ошибку единицы
веса
P 2
P P
Pd1 I
P1 P1II
1
2
n
• Ошибку единицы веса можно записать
Pd1 d12 Pd 2 d 22 ....Pd n d n
n
P d
2
d
n
• Если двойные измерения будут попарно равноточны, т.е.
I
II
I
II
I
II
P1 P1 P1 ......P2 P2 P2 ......Pn Pn Pn
Pn
P1
P2
Pd1 .....Pd 2 ......Pd n
2
2
2
n
157.
• Тогда ошибка единицы веса (при отсутствии в разностяхсистематических погрешностей) определяется по формуле:
Pd
2
2n
• В разностях результатов двойных равноточных измерений
могут присутствовать систематические ошибки.
• Критерием их наличия является не выполнение условия
| Pd d | 2,5
| Pd d |
Pd
• Следует из разностей исключить систематическую
Pd d
погрешность, величина которой определяется
0
P
I
d1 d 0 d1
d 2 d 0 d 2I
d n d 0 d nI
158.
• Ошибка единицы ( при наличии в разностях двойныхнеравноточных измерений систематических погрешностей) определяется по формуле:
Pd d
I
I
2( n 1)
• Средняя квадратическая погрешность одного измерения
• равна
mi
Pi
• Средняя квадратическая погрешность среднего результата
равна
mx
2 Pi
159.
• Контроль вычислений при наличии в результатахсистематических погрешностей.
• Двойные равноточные
• 1.
d I n
2
d
d I d I d 2
n
• 2. Двойные неравноточные
Pd P
I
2
Pd
Pd I d I Pd 2 P
160. Геодезические методы проведения государственного земельного контроля
• Основные задачи геодезических методов проведениягосударственного земельного контроля
• 1. Контроль местоположения земельного участка.
• 2. Контроль площади земельного участка.
• Обе поставленных задачи могут быть решены одними и теми же
методами при условии, что имеется единая система координат, в
которой определяются координаты поворотных точек границы
земельного участка.
• Будем считать, что на контролируемой территории существует
отвечающая необходимым требованиям опорная межевая сеть.
Вынос проектов земельных участков в натуру и определение
координат поворотных точек границ проводилось относительно
точек ОМС с требуемой соответствующими инструкциями
точностью. В этом случае координаты граничных точек получены с
нормативной средней квадратической погрешностью mt .
161.
• Далее, предположим, проводятся контрольные определениякоординат граничных точек, при этом используются точки той же
ОМС, и измерения выполняются по той же методике. Тогда СКП
контрольного определения также будет иметь то же значение
mt
• Расхождение между документальными значениями координат и
контрольными вычисляют по формуле:
f t ( X док Х контр ) 2 (У док У контр ) 2
• Принимая во внимание положения теории погрешностей, можем
утверждать, что допустимое предельное расхождение между
этими координатами может быть рассчитано по формуле:
пред 2,5mt 2 3,5mt
162.
• Если выполняется неравенство вида f t пред• то можно утверждать, что координаты граничных
точек соответствуют документальным данным.
• При выполнении неравенства противоположного
смысла, т.е. f t пред, можно утверждать, что
фактические координаты точек границ земельного
участка не соответствуют правоустанавливающим
документам. Причины такого расхождения должны
быть определены конкретно для каждого случая на
месте.
163.
• Вопросы соответствия площади по документам и площадиизмеренной при выполнении контроля решаются
примерно по той же схеме. Прежде всего, по координатам,
полученным в результате контрольных измерений,
вычисляют площадь земельного
участка по формуле
n
Рконтр 0,5 x k ( y k 1 y k 1 )
k 1
• и сравнивают ее с площадью, записанной в
правоустанавливающих документах f P
t
контр
. Р
• Предельно допустимое расхождение может быть
вычислено по формуле:
• где m p
пред 2,5m p 2 3,5m p
СКП вычисления площади.
док
164.
• Для расчета этой величины может быть использована формула:m p mt
1 K 2
P
2K
• , где К – коэффициент вытянутости участка.
• При условии, что f p пред , можно считать, что фактическая
• площадь земельного участка соответствует
правоустанавливающим документам. В противном случае
необходимо на месте делать соответствующие выводы.
• Однако, указанная методика проведения контроля возможна
только при наличии определенных условий, которые будут
изложены ниже. В случае не выполнения этих условий
проведение полноценной геометрической экспертизы любого
земельного участка представляется проблематичной.
165.
Условия качественного проведениягеометрической экспертизы земельного участка
Наличие опорной межевой сети (ОМС) на территории кадастрового
округа (района), созданной в единой системе координат (государственной или местной). При этом местная система координат должна иметь ключи перехода в государственную систему координат для
координатной стыковки границ кадастрового округа (района).
Плотность и точность создания ОМС должна обеспечивать
оперативное и качественной определения местоположения границ
земельных участков.
Наличие нормативно – технических документов, жестко
регламентирующих работ по созданию ОМС, в том числе
финансировании, проектировании, построении, поддержание ее в
рабочем состоянии.
Наличие ведомства (организации), полностью отвечающей за
ведение работ по построению и контролю за состоянием ОМС
Наличие нормативно – технических документов, жестко
регламентирующих порядок проведения работ по определению
координат точек границ земельных участков.








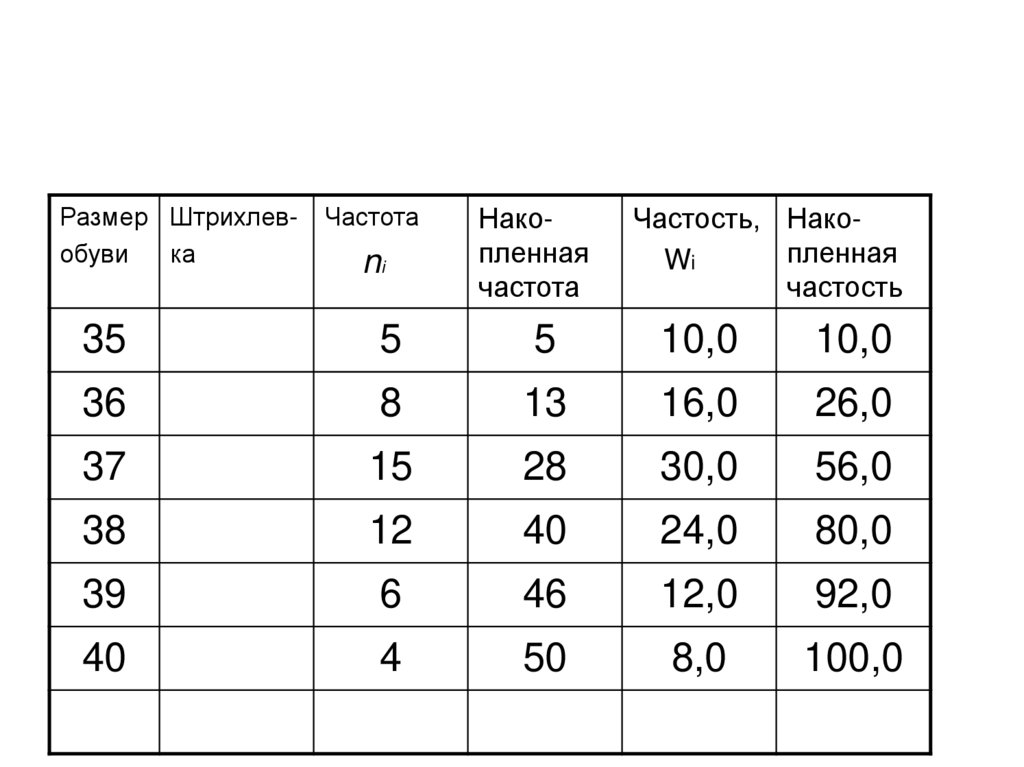

















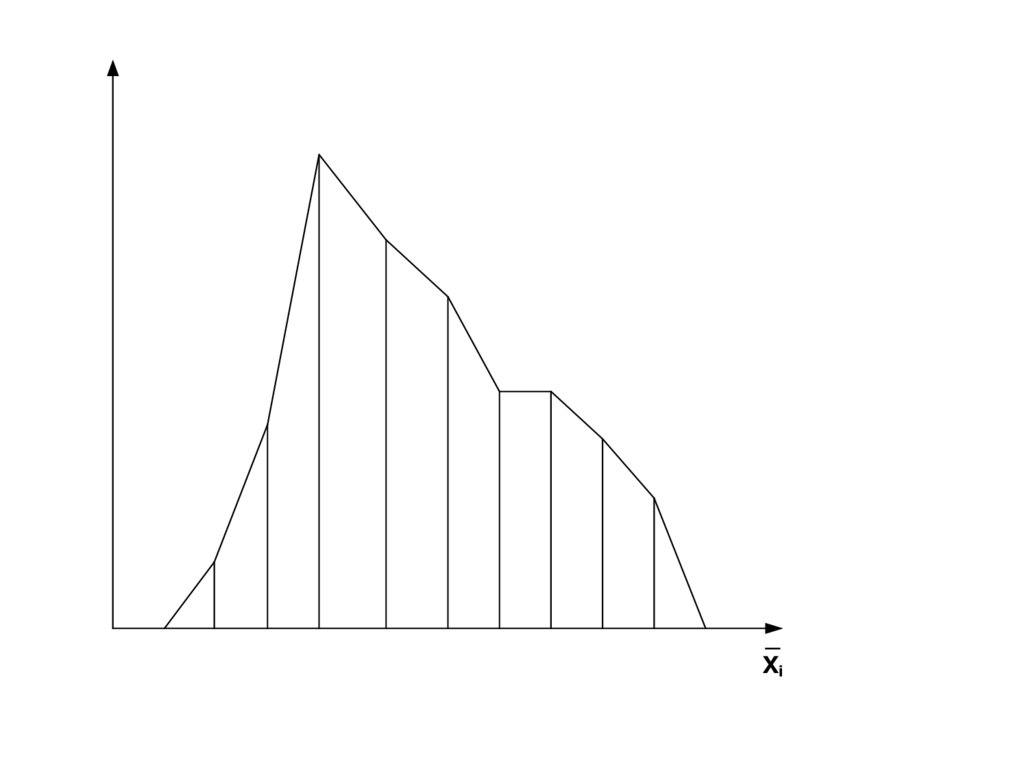







































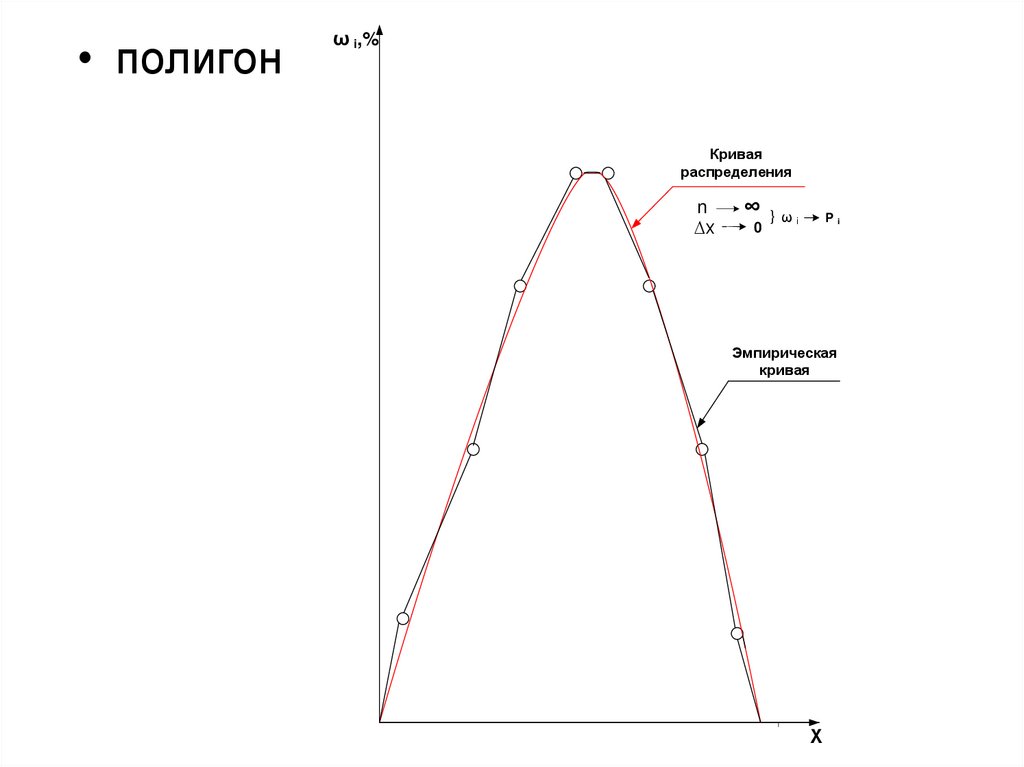













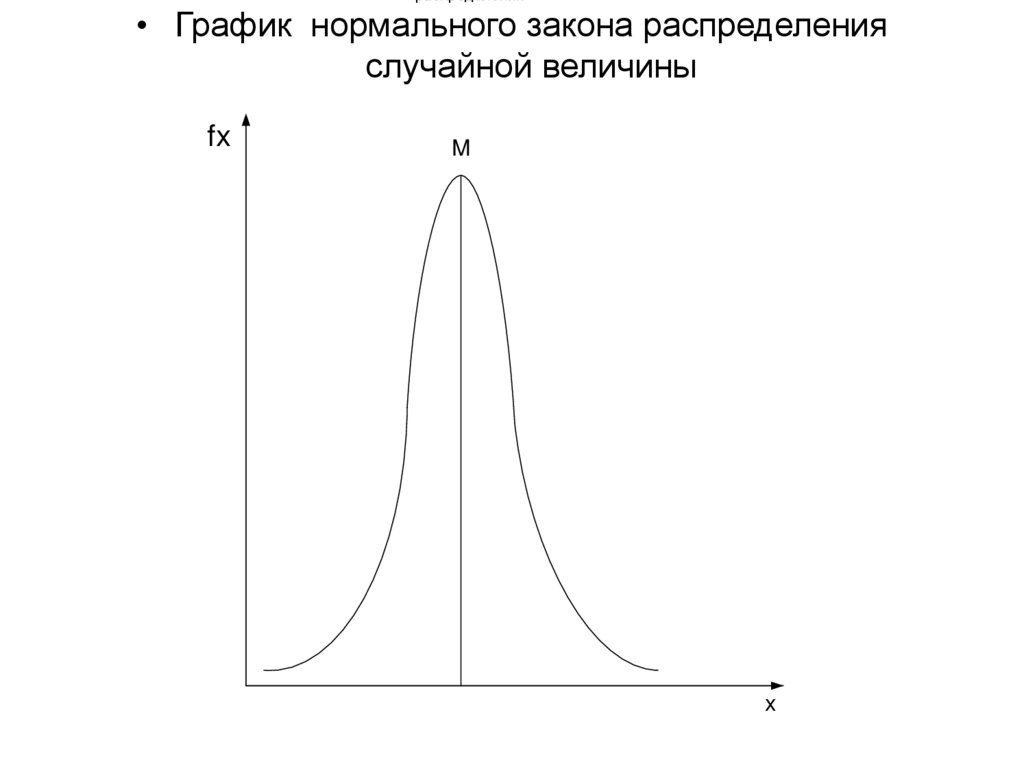




















































































 Математика
Математика








