Математическая статистика

1. Математическая статистика

Статистика – математическая
теория, позволяющая познать мир
через опыт
В. Томпсон

2. Введение

Математическая
статистика
–
наука,
изучающая методы обработки результатов
наблюдений массовых случайных явлений,
обладающих статистической устойчивостью и
закономерностью, с целью выявления этой
закономерности.
Задачи математической статистики:
указать способы отбора и группировки
статистических сведений, полученных в
результате наблюдений;
разработать методы анализа статистических
данных в зависимости от целей исследования.

3. методы анализа статистических данных в зависимости от целей исследования:

оценка неизвестной вероятности события;
оценка неизвестной функции распределения;
оценка параметров распределения;
проверка статистических гипотез о виде
неизвестного распределения или о величине
параметров распределения, вид которого
известен.

4. Генеральная совокупность и выборка

Выборочной совокупностью (выборкой)
называется совокупность случайно отобранных
объектов.
Генеральной совокупностью называется
совокупность объектов, из которых производится
выборка.
Объемом совокупности (выборочной или
генеральной) называется число объектов этой
совокупности.
Обозначение N – объем генеральной
совокупности;
n – объем выборочной совокупности.

5. Способы отбора

1.Отбор, не требующий расчленения:
простой, бесповторный
с повторениями
2.Отбор, при котором вся генеральная совокупность
делится на части
Механический; типический; серийный
Простой – отбор, при котором объекты извлекаются
из совокупности по одному.
Механический – генеральная совокупность
«механически» делится на группы. Выборка
производится с каждой из групп.
Типический – объекты выбирают не из всей
совокупности, а из каждой ее типической части.
Серийный – объекты отбираются не по одному, а
сериями, которую подвергают сплошному
обследованию.

6.

Для того, чтобы по данным выборки можно
было судить об интересующем нас
признаке генеральной совокупности,
нужно чтобы выборка правильно
представляла пропорции генеральной
совокупности, т.е. выборка должна быть
репрезентативной (представительной). В
силу закона больших чисел можно
утверждать, что выборка будет
репрезентативной, если каждый объект
отобран случайно и если все объекты
имеют одинаковую вероятность попасть в
выборку.

7. Статистическое распределение выборки

Пусть из генеральной совокупности извлечена
выборка, причем значения
х1
наблюдается n1 раз;
х2
n2 раз;
хk
……………….
nk раз
Причем ni = n – объем выборки
Обычно значения х1 , х2 , …, хk называются
вариантами.
Числа n1 , n2 , …, nk называются их частотами.
Если варианты ранжированы по возрастанию,
такое представление называется вариационным
рядом.

8.

На телефонной станции проводились
наблюдения над числом Х – неправильных
соединений в минуту. Наблюдения в течение
часа дали следующие результаты:
3; 1; 3; 1; 4; 2; 2; 4; 0; 3; 0; 2; 2; 0; 2; 1;
4; 3; 3; 1; 4; 2; 2; 1; 1; 2; 1; 0; 3; 4; 1; 3;
2; 7; 2; 0; 0; 1; 3; 3; 1; 2; 4; 2; 0; 2; 3; 1;
2; 5; 1; 1; 0; 1; 1; 2; 2; 1; 1; 5

9. после ранжирования и группировки данных получаем следующий массив:

0; 0; 0; 0; 0; 0; 0; 0; 1; 1; 1; 1;
1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1;
1; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2;
2; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 3;
3; 3; 3; 4; 4; 4; 4; 4; 4; 5; 5; 7

10. Относительная частота варианты

Относительной частотой варианты хi
называется отношение частоты ni этой
варианты к объему всей выборочной
совокупности n числа наблюдений к
объему выборки.
Wi=ni/n
Статистическим распределением называют
перечень вариант и соответствующих им
частот или относительных частот.

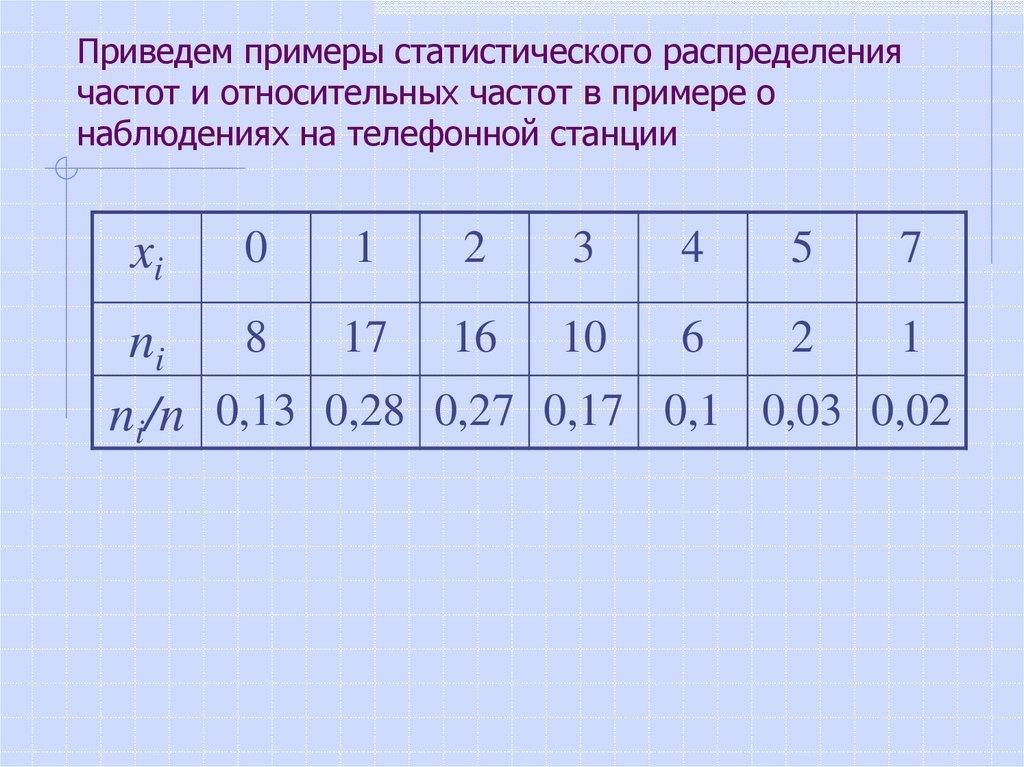
11. Приведем примеры статистического распределения частот и относительных частот в примере о наблюдениях на телефонной станции

xi
0
1
2
3
4
5
7
8
17 16 10
6
2
1
ni
ni/n 0,13 0,28 0,27 0,17 0,1 0,03 0,02

12. Простейшие характеристики вариационного ряда

Опр. 1 Варианта, имеющая наибольшую
частоту называется модой
Обозначение М0.
Опр. 2 Варианта, которая делит
вариационный ряд на две части, равные по
числу вариант, называется медианой
Обозначение mе.
- если число вариант n нечетно, т.е.
n=2k+1, то mе=хk+1;
- если число вариант четно, т.е. n=2k, то
mе=(хk+ хk+1)/2

13.

Опр.3 Размахом варьирования R
называется разность между наибольшей
и наименьшей вариантами:
R=xmax- xmin
Замечание. Размах является
простейшей характеристикой рассеяния
вариационного ряда.

14.

В случае достаточно большого объема выборочных
данных или в случае, когда наблюдается непрерывный
признак составляется интервальное статистическое
распределение. Для этого:
располагают значения xi по возрастанию;
весь интервал разбивают на k последовательных
непересекающихся интервалов;
подсчитывают числа ni – количество попавших
значений xi в каждый интервал.
Составляется таблица, которая называется
интервальным статистическим распределением.
xi ; xi+1
x1 ; x2
x2 ; x3
...
xk-1 ; xk
ni
n1
n2
...
nk

15.

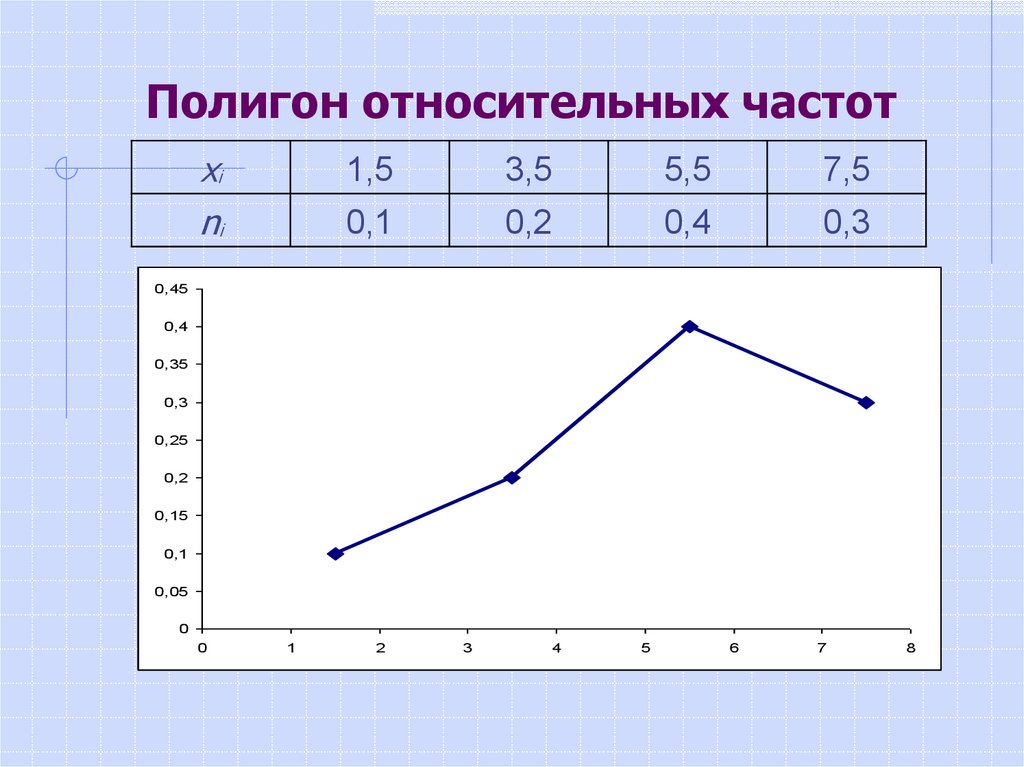
Наглядным изображением статистического ряда
распределения служат полигон и гистограмма.
Полигон частот (относительных частот)–
ломаная линия, соединяющая точки с координатами
(xi;ni) (с координатами (xi ;ni/n)).
Гистограмма относительных частот –
ступенчатая фигура, состоящая из
прямоугольников, основаниями которых служат
интервалы, длиной h , а высотой – величины wi /h.
(площадь такой фигуры равна 1).
Гистограммой частот называется
ступенчатая фигура, состоящая из
прямоугольников, основаниями которых служат
интервалы, длиной h , а высотой – величины ni/h.
(площадь такой фигуры равна объему выборки).

16. Полигон относительных частот

xi
ni
1,5
3,5
5,5
7,5
0,1
0,2
0,4
0,3
0,45
0,4
0,35
0,3
0,25
0,2
0,15
0,1
0,05
0
0
1
2
3
4
5
6
7
8

17. Гистограмма частот

ni
ni/h
5;10
4
10;15 15;20 20;25 25;30 30;35 35;40
6
16
36
24
10
4
0,8
1,2
3,2
7,2
4,8
2
0,8

18. Эмпирическая функция распределения

Эмпирической функцией распределения
(функция
распределения выборки) называется
функция F*(x), определяющая для
каждого
значения x относительную частоту события X<x.
F*(x)=nx/n;
где nx – число вариант, меньше x, n – объем
выборки.
Свойства
множество значений [0;1]
неубывающая: если x2> x1 , то F*(x2)> F*(x1),
если x1 – наименьшая варианта, F*(x1)=0
если xk – наибольшая, то F*(x2)=1.

19.

В отличие от эмпирической функции,
функция F(x) генеральной совокупности
называется теоретической. Различия
между ними состоят в том, что F(x)
определяет вероятность события X<x, а
F*(x) – относительную частоту.

20. Точечные оценки параметров распределения

Точечной называют оценку, определяющуюся
одним числом.
Пусть требуется изучить количественный признак
генеральной совокупности. Допустим, удалось
установить, какое имеется распределение. Тогда
возникает задача оценки параметров данного
распределения.
Однако чаще всего экспериментатору не известен
вид распределения, т.к. он обладает только
данными выборки и тогда для оценки параметров
нужно найти зависимость этих параметров от
наблюдаемых величин.

21. Требования к точечным оценкам

Несмещенности – математическое
ожидание оценки должно быть равно
оцениваемому параметру;
Эффективности – оценка при
заданном объеме выборки n должна
иметь наименьшую дисперсию;
Состоятельности – при n→∞ оценка
по вероятности, должна стремиться к
оцениваемому параметру.

22. Генеральная и выборочная средние

Опр. 1. Генеральной средней
называется среднее
арифметическое значений генеральной совокупности.
1 N
x г xi
N i 1
в случае, когда все значения признака различные
и
1 N
xг
nx
N
i i
i 1
в случае, когда среди значений
признака есть
одинаковые
Если рассматривать значения генеральной
совокупности, как значения случайной величины, то
M(x) xг

23.

Опр.2 Выборочной средней называется среднее
арифметическое значений выборки.
Пусть имеется выборка объема n. Тогда
выборочная средняя равна:
n
1
xв хi
n i 1
n
1
xв ni хi
n i 1
Выборочная средняя по данным одной
выборки есть определенное число.

24.

Если извлекать другие выборки такого
же объема из генеральной
совокупности, то выборочная средняя
меняется от выборке к выборке.
Как правило, генеральная средняя
является неизвестной, но её можно
оценить по выборочной средней.

25.

Пусть из генеральной совокупности извлечена
повторная выборка объема n со значениями
признака
х1, х2, …хn
(не уменьшая общности будем считать, что эти
значения различны)
Пусть генеральная средняя неизвестна и
требуется её оценить по данным выборки. В
качестве оценки генеральной совокупности
принимают выборочную среднюю:
x1 ... xn
xв
n

26.

Убедимся, что xв - несмещенная
оценка, т.е. покажем, что
M ( xв ) xг
Будем рассматривать xв как случайную
величину; значения признака х1, х2, …хn
как независимые случайные величины
Х1…Хn. Так как эти величины одинаково
распределены, они имеют одинаковое
математическое ожидание, которое
обозначим а.

27.

Из теории вероятностей известно
M ( X 1 ) ... M ( X n )
M (Xв)
a
n
…….(*)
Т.к. каждая из величин имеет то же
распределение, что и вся генеральная
совокупность, то числовые характеристики
этих случайных величин и генеральной
совокупности одинаковые, т.е.
……… (**)
M ( X ) xг a

28.

Из (*) и (**) следует
M ( xв ) xг
Это, в свою очередь, означает, что xв
является несмещенной оценкой
генерального среднего (математического
ожидания)

29. Групповые и общие средние

Предположим, что все значения
количественного признака Х разбиты на
несколько групп. В этом случае каждую группу
можно рассматривать как отдельную
совокупность.
Опр. 3. Групповой средней называется среднее
арифметическое значений признака,
принадлежащих группе.
Опр. 4 Общей средней называется среднее
арифметическое значений признака,
принадлежащих всей совокупности.

30.

Зная групповые средние и объемы групп,
можно найти общую среднюю.
Теорема 5. Общая средняя равна средней
арифметической групповых средних,
взвешенных по объемам групп
x
n x
i i
i
n

31.

Из формулы (*) можно получить выражение для
величины стоящей в числителе дроби, которое в
дальнейшем нами будет использоваться при
изложении теории
n x x n xn
i
i
С другой стороны, из формулы
x
n x
i i
i
n
получаем:
n x nx
i i

32.

Опр. 6 Отклонением называется
разность между значением признака и
общей средней
Теорема 7. Сумма произведений
отклонений на соответствующие частоты
равна нулю.
Следствие 8. Среднее значение
отклонений равно нулю

33.

Опр.9 Генеральной дисперсией называется
среднее арифметическое квадратов отклонений
значений генеральной совокупности от их
среднего значения.
1
Dг ( xi x г ) 2 ;
N i 1
N
N
Dг N i ( xi x г )
2
N;
i 1
Опр. 10 Выборочной дисперсией называется
среднее арифметическое квадратов отклонений
наблюдаемых значений выборки от их среднего
значения
n
1 n
2
2
Dв ( xi x в )
Dв ni ( xi x в ) n
n i 1
i 1

34.

Кроме дисперсий для характеристики
рассеивания значений генеральной
(выборочной) совокупности вокруг
генерального (выборочного) среднего
пользуются еще одной характеристикой –
генеральным (выборочным) средним
квадратическим отклонением, которое
определяется как корень квадратный из
дисперсии.

35.

Выборочная дисперсия (выборочное среднее
квадратическое отклонение) является смещенной
оценкой генеральной дисперсии, поэтому для
более точных расчетов обычно используют
исправленную выборочную дисперсию
n
S
Dв
n 1
2
или
k
1
2
s
ni ( xi xв )
n 1 i 1
2

36.

исправленное среднее квадратическое
отклонение
n (x x )
s
i
i
n 1
в
2

37.

Если все значения количественного
признака разбиты на k групп, то
рассматривая каждую группу как
самостоятельную совокупность, можно
найти групповые межгрупповую и
внутригрупповую дисперсии.

38.

Определение 11.
Внутригрупповой дисперсией
называется средняя арифметическая
групповых дисперсий, взвешенная по
объемам групп:
1 m
Dвнгр
N i Dгр
n i 1
где N i объем группы ; n - объем всей
совокупности

39.

Определение 12.
Межгрупповой дисперсией
называется дисперсия групповых
средних относительно общей средней:
D межгр
2
N i xi x
n
1 m
i 1
где xi - групповая средняя i группы ,
x - общая средняя

40.

Определение 13.
Общей дисперсией называют
дисперсию значений признака всей
совокупности относительно общей
средней.
Пример