Производная функции. Дифференциал и его приложение к приближенным вычислениям

1.

Тема 2.1. Производная функции.
Дифференциал и его приложение к
приближенным вычислениям.

2.

План.
► 1 Приращение аргумента. Приращение
функции.
► 2. Определения производной.
► 3. Вычисление производных.
► 4. Правила дифференцирования.
► 5. Дифференцирование функции
► 6. Геометрический и механический смысл
производной
► 7. Признаки возрастания и убывания
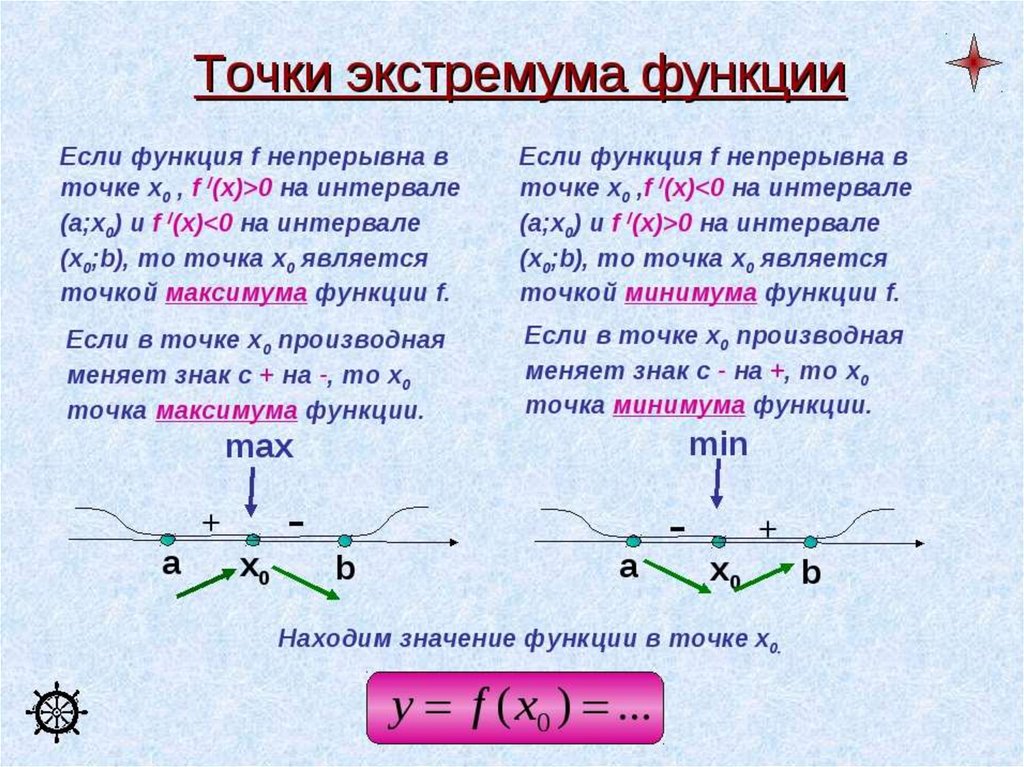
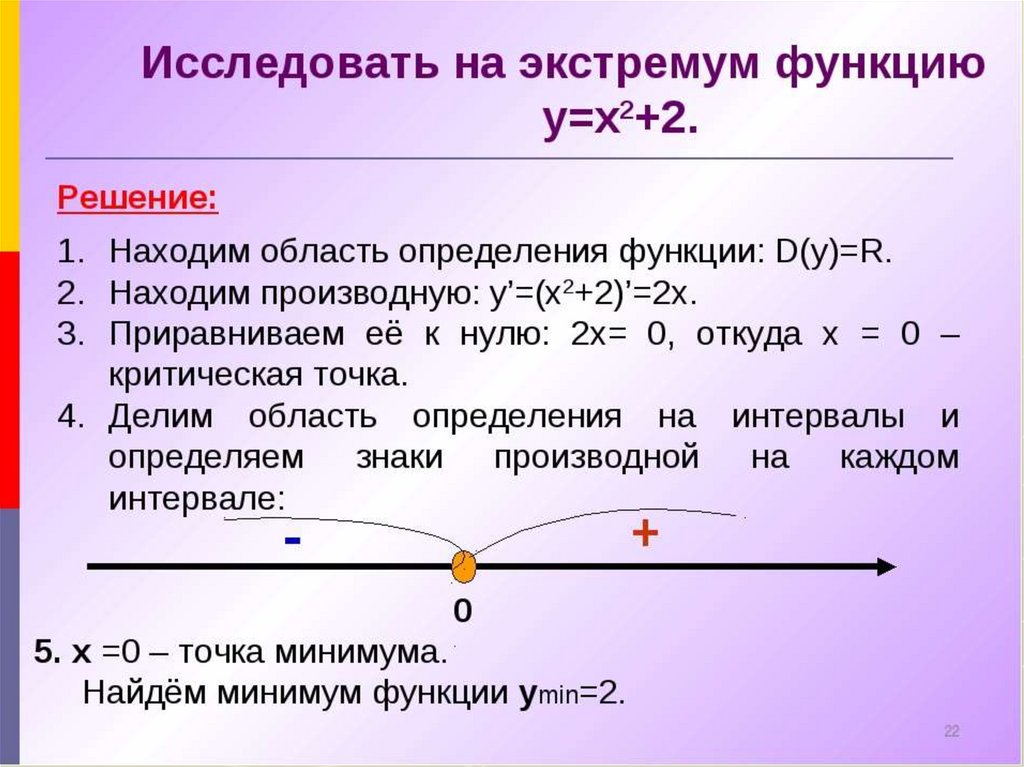
► 8. Экстремум функции.

3.

Опр. 1. Пусть ф-я y f (x ) определена в точках х0
и х1. Разность х1-х0 называют приращением
аргумента (при переходе от точки х0 к х1), а
разность f ( x1 ) f ( x0 ) называют
приращением функции.
Приращение аргумента обозначают x(читают:
дельта икс).
Приращение функции обозначают y или f.
Итак, x1 x0 x, значит, x1 x0 x
f ( x1 ) f ( x0 ) y(или f ) , значит
y f ( x0 x) f ( x0 )

4.

Пример 1.
Найти приращение функции у=х2 при переходе от точки х0=1
к точке:
а) х=1,1;
Решение
f(1)=12=1,
f(1,1)=(1,1)2=1,21
б) х=0,9
Решение
f(1)=12=1,
f(0,9)=(0,9)2=0,81
y f (1,1) f (1)
y f (0,9) f (1)
1,21 1 0,21
0,81 1 0,19
Обратите внимание на полученный в примере ответ: приращение функции
может быть и положительным и отрицательным числом, так что не
истолковывайте термин «приращение» как «прирост».
Опр*. Функция непрерывна в точке х=а, если в точке х=а выполняется
следующее условие: если ,
то

5.

Пример 2.
Для функции у=х2 найти:
а) приращения функции при
переходе от фиксированной
точки х к точке х + x ;
б) предел отношения
приращения функции к
приращению аргумента при
условии, что приращение
аргумента стремится к нулю
Решение.
f(x)=х2
Решение.
y
2 x x ( x ) 2
lim
lim
x 0 x
x 0
x
lim ( 2 x x) 2 x
f ( x x) ( x x) 2
y f ( x x) f ( x)
( x x) x ( x 2 x x
2
2
2
( x) 2 ) x 2 2 x x ( x) 2
Итак, y 2 x x ( x)
2
x 0
При вычислении предела мы
учитывали, что х - фиксированная
точка (const), x – переменная,
стремящаяся к нулю.
y
2x
Итак, lim
x 0 x

6.

2. Определения производной.
Опр. 2. Пусть функция y f (x)определена в точке
х и в некоторой точке ее окрестности. Дадим
аргументу х приращение x, такое, чтобы не
выйти из указанной окрестности. Найдем y
соответствующее приращение функции
и
составим отношение y . Если существует
x
предел этого отношения при x 0, то указанный
предел называют производной функции y f (x)
f (x. )
в точке х и обозначают
Итак,
y
lim
x 0
x
f ( x)
иногда производную обозначают
y

7.

Если функция y f (x) имеет производную
в точке х, то ее называют
дифференцируемой в точке х. Процедуру
отыскания производной функции y f (x)
называют дифференцированием
функции y f (x) .
Формулами дифференцирования
обычно называют формулы для отыскания
производных конкретных функции.

8.

3. Вычисление производных. Таблица производных
Функция
y xn
y
y
x
1
x
Производная
Производная
y nx n 1
1
y
2 x
y cos x
1
x2
y ctgx
y
y arcsin x
y
x
y arccos x
y
1
x ln a
y arctgx
y
1
x
y arcctgx
y
y
y ax
y a x ln a
y e
y e
x
Функция
y log a x
y
y ln x
y
y sin x
y cos x
y tgx
y sin x
1
y
cos 2 x
1
sin 2 x
1
1 x2
1
1 x2
1
1 x2
1
1 x2

9.

Правила дифференцирования.
Правило 1. Если функция y f (x) и y g (x) имеют
производную в точке х, то и их сумма имеет производную в
точке х, причем производная суммы равна сумме
производных.
( f ( x) g ( x)) f ( x) g ( x)
(производная суммы равна сумме производных)
Например, ( x 2 sin x) 2 x cos x
Правило 2. Если функция y f (x) имеет производную в
точке х, то функция y kf (x) имеет производную в точке
х,
причем.
(постоянный множитель можно вынести за знак
производной)
Например, (5 x 2 ) 5( x 2 ) 5 2 x 10 x
(kf ( x)) k f ( x)

10.

Правило 3. Если функция y f (x) и y g (x ) имеют производную
в точке х, то и их произведение имеет производную в
точке х, причем
( f ( x) g ( x)) f ( x) g ( x) f ( x) g ( x)
(производная произведения двух ф-ий равна сумме двух слагаемых; первое
слагаемое есть произведение производной первой ф-ии на вторую ф-ию, а
второе слагаемое есть произведение первой ф-ии на производную второй ф-ии)
Например, (( 2 x 3) sin x) (2 x 3) sin x (2 x 3) (sin x)
2 sin x (2 x 3) cos x
Правило 4. Если функция y f (x) и y g (x ) имеют производную в
точке х и в этой точке g ( x ) 0 , то и частное f ( x ) имеет производную
в точке х, причем
g ( x)
f ( x)
f ( x) g ( x) f ( x) g ( x)
2
g
(
x
)
g
( x)
( x 2 ) (5 4 x) x 2 (5 4 x) 2 x(5 4 x) x 2 ( 4) 10 x 4 x 2
2
2
(5 4 x)
(5 4 x)
(5 4 x) 2
5 4x
Например, x 2