Похожие презентации:
Приложение дифференциала к приближенным вычислениям
1. Приложение дифференциала к приближенным вычислениям.
2.
Дифференциалом функции y = f(x)называется произведение
производной функции на
приращение аргумента.
dy = f'(x) x = f'(x) dx
3. Дифференциалы высшего порядка
d f ( x) fn
(n)
( x)dx
n
y ln sin 3x d y ?
1
2
2
y (ln sin 3x)
(sin 3x)
2
sin 3 x
2 sin 3 x(sin 3 x) 2 sin 3 x 3 cos 3 x
6Ctg3x
2
2
sin 3 x
sin 3 x
6 3
18
y (6Ctg3x)
2
2
sin 3x sin 3x
18
2
2
d y
dx
2
sin 3 x
Пример
2
2
4.
Геометрический смысл дифференциалау
f(x)=f(x0+∆x)
∆f(x0)
∆y
dy
f(x0)
х
0
х0
∆x
x=x0+∆x
5.
При достаточно малом x df(x)≈Δf(x)f ( x0 ) f ( x0 x) f ( x0 )
f ( x0 x) f ( x0 ) f ( x0 )
f ( x0 x) f ( x0 ) df ( x0 )
- формула для вычисления
приближенного значения
функции
6.
Найти приближенное значение функциии ее приращение в точке х = 2,01
x 0,01
x0 2
f ( x) 5 x 3 2 x 3
I. Найти приращение функции Δf(x0)
f ( x0 ) df ( x0 ) f ' ( x0 )dx f ' ( x0 ) x 58 0,01 0,58
f ' ( x) 15x 2 2
f ' (2) 15 4 2 58
II. Найти приближенное значение функции
f ( x0 x) f ( x0 ) df ( x0 )
df (2) 0,58
f (2) 5 8 2 2 3 39
f (2 0,01) 39 0,58 39,58
Точное значение
f(2,01)=39,583005
7. Приближенное вычисление степени.
x x0 xf ( x) x n
f ( x0 x) f ( x0 ) df ( x0 )
( x0 x) x d ( x 0 ) x0n nx0n 1dx x0n nx0n 1 x
n
n
0
n
( x0 x) n x0n nx0n 1 x
Пример:
(4,012) ? x0 4, x 0,012
2
(4 0,012) 4 2 4 0,012 16,096
2
Точное значение
f(4,012)=16,096144
2
1
n 2
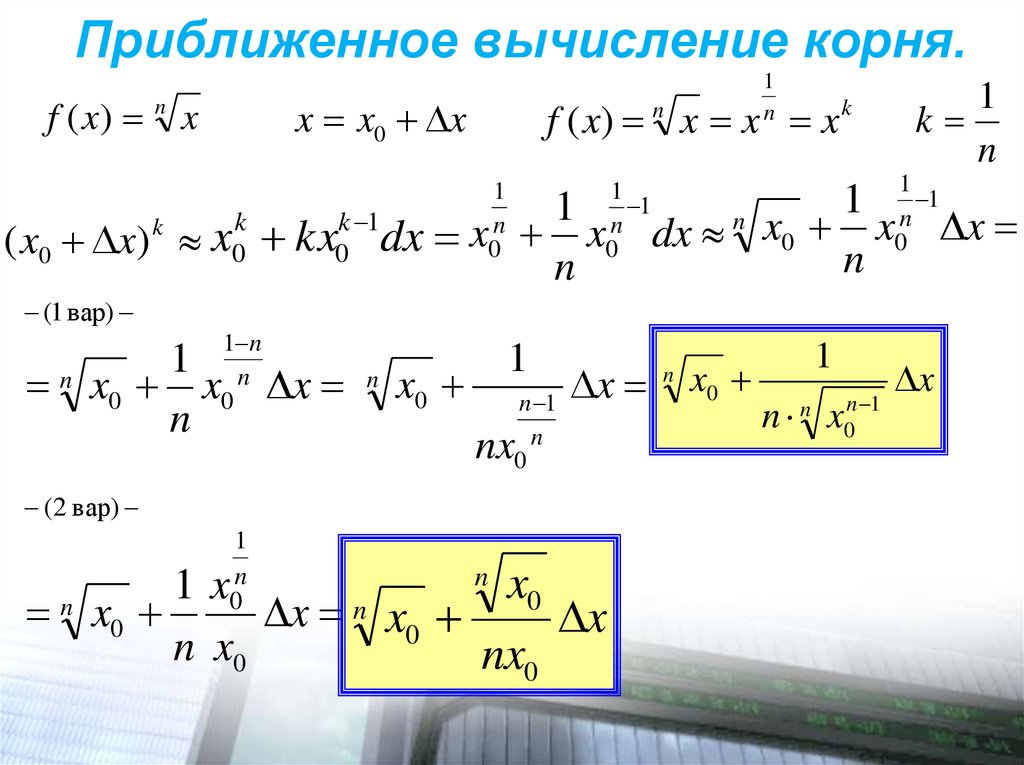
8. Приближенное вычисление корня.
f ( x)n
x x0 x
x
f ( x) x x x
n
1
n
0
1
1
n
0
1
k
k 1
k
( x0 x) x0 kx0 dx x x
n
(1 вар)
1 n
n
0
1
n
x0 x
n
x
n
x0
1
n 1
n
0
x
nx
(2 вар)
1
n
0
1
n
n x
x
1
0
n x0
x n x0
x
n x0
nx0
1
k
n
k
1
1
n
0
1
dx x0 x
n
n
n
x0
1
n n x0n 1
x
x
9. Приближенное вычисление корня.
nx0 x x0
1
n
n 1
0
n x
n
x
n
Пример:
1,006 ?
x
0
n
x0 x x0
x
nx0
n
x0 1
x 0.006
0,006
1 0,006 1
1 0,003 1,003
2 1
1,006 1,0029955
10. Пример
На сколько увеличится при нагреванииобъем шара радиуса R, если его радиус
удлинится на величину ΔR?
4 3
V R
3
Изменение (приращение) радиуса - ΔR
Изменение (приращение) объема- ΔV
4 3
4 2 2
R dR
V dV V ' dR ( R )' dR 4 R3 dR
3
3









 Математика
Математика








