Момент силы относительно центра и оси. Лекция 2С

1. Лекция 2С 1 Момент силы относительно центра и оси

1
Лекция 2С
Момент силы относительно центра и оси
1. Алгебраический момент силы относительно центра:
MO (F) = Fh = 2S OAB, где h – плечо силы F относительно
центра О. Знак + при действии момента против часовой
стрелки, знак минус – по часовой. [MO] = Нм.
2. Векторный момент силы относительно центра:
MO(F)
O
(1)
MO(F) = r F
Модуль момента силы: MO (F) = Frsin = Fh = 2S OAB.
Разложение момента силы по осям системы координат:
i
MO(F) = r F =
h
B
r
A
Рис. 1
j k
x y z = i(yFz – zFy) + j(zFx – xFz) + k(xFy – yFx)
Fx Fy Fz
Mx(F) = yFz – zFy ,
Проекции момента силы на оси координат =
моментам силы относительно осей координат:
My(F) = zFx – xFz,
(2)
Mz(F) = xFy – yFx.
Модуль момента силы:
M O (F ) M x2 M y2 M z2 ( yFz zFy ) 2 ( zFx xFz ) 2 ( xFy yFx ) 2
Направляющие косинусы:
cos M
My
Mx
M
, cos M
, cos M z .
MO
MO
MO
F

2.

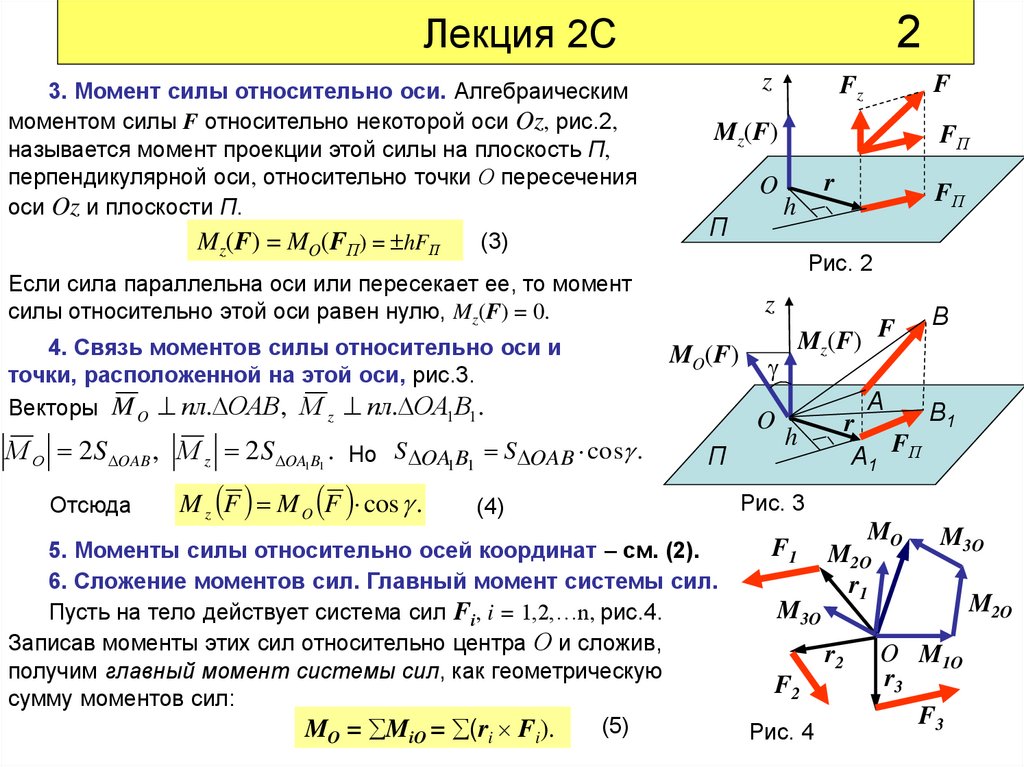
Лекция 2С
3. Момент силы относительно оси. Алгебраическим
моментом силы F относительно некоторой оси Oz, рис.2,
называется момент проекции этой силы на плоскость П,
перпендикулярной оси, относительно точки О пересечения
оси Oz и плоскости П.
(3)
Mz(F) = MO(FП) = hFП
2
z
Mz(F)
O
П
М О 2S OAB , М z 2S OA1B1 . Но S OA1B1 S OAB cos .
Отсюда
M z F M O F cos .
FП
r
FП
h
Рис. 2
Если сила параллельна оси или пересекает ее, то момент
силы относительно этой оси равен нулю, Mz(F) = 0.
4. Связь моментов силы относительно оси и
точки, расположенной на этой оси, рис.3.
Векторы M O пл. ОАВ , М z пл. ОА1 В1.
F
Fz
z
MO(F)
(4)
5. Моменты силы относительно осей координат – см. (2).
6. Сложение моментов сил. Главный момент системы сил.
Пусть на тело действует система сил Fi, i = 1,2,…n, рис.4.
Записав моменты этих сил относительно центра О и сложив,
получим главный момент системы сил, как геометрическую
сумму моментов сил:
(5)
MO = MiO = (ri Fi).
В
z
O
П
M (F) F
А
В1
r
F
А1 П
h
Рис. 3
F1
M3O
MO
M2O
r1
r2
F2
Рис. 4
M3O
M2O
O M1O
r3
F3

3.

Лекция 2С
3
Главный момент системы сил относительно оси z равен
алгебраической сумме моментов сил относительно этой оси:
Mz = Miz
Проецируя (5) на некоторую ось z, получим зависимость
MOcos(MO, z) = Mz
Проекция главного момента сил относительно некоторого центра на ось, проходящую
через этот центр, равна главному моменту сил относительно этой оси.
7. Условия равновесия системы моментов сил.
z
В векторной форме: MO = MiO = 0
В аналитической форме:
M3
Mx = Mix = 0; My = Miy = 0; Mz = Miz = 0.
M2
8. Главный момент плоской системы сил.
Главный момент плоской системы сил равен алгебраической
сумме моментов сил относительно оси z пл. П или центра О
пересечения оси z с плоскостью П, рис. 5.
M = M
z
F1
r1
П
F2
iz
F
Предельное равновесие: MB(Fi) = 0; G(AB/2) – Fh = 0. AB = 2Fh/G.
h
Коэффициент устойчивости kуст = Mудер / Mопр.
Выбор расстояния АВ: AB = 2kустFmaxh/G.
F3
Рис.5
9. Устойчивость тел на опрокидывание, рис. 6.
Mопр = Fh, Mудер = G(AB/2). Условие устойчивости: Mудер >Mопр.
M1
r3
O
r2
A
G
Рис.6
B

4.

Лекция 2С
4
Пара сил
B
1. Пара сил - система двух равных по величине параллельных сил,
направленных в противоположные стороны, рис.1; F1 = - F2 .
Пара сил – простейший объект механики. Плоскость расположения пары
– ее плоскость действия. Кратчайшее расстояние между силами пары
h называется плечом пары сил.
2. Алгебраический момент пары:
M = F1h = F2h Нм
F1
C
h
A
F2
Рис.1
D
Знак плюс берется при действии пары против часовой стрелки, минус – по часовой.
Модуль пары: M = F1h = F2h = SABCD – площадь параллелограмма ABCD.
3. Векторный момент пары: M = r F2 = -r F1
M
|M |= F2rsin = F2h
Вектор момента пары M направлен перпендикулярно плоскости
действия пары в сторону, откуда действие пары видно против
часовой стрелки, рис.2.
4. Свойства пары сил.
Теорема 1. Сумма моментов сил пары относительно
произвольной точки О равна моменту пары, рис. 3.
MO(F1) + MO(F2) = rA F1 + rB F2 = (rB – rA) F2 = r F2 = M
Следствие. Момент пары равен моменту одной из сил пары
относительно точки приложения другой силы. Следует принять
за точку О точку А или В.
r
A
F1
F2
h
С
B
Рис.2
F1
A
r
B
rA
O
F2
rB
Рис.3

5.

Лекция 2С
5
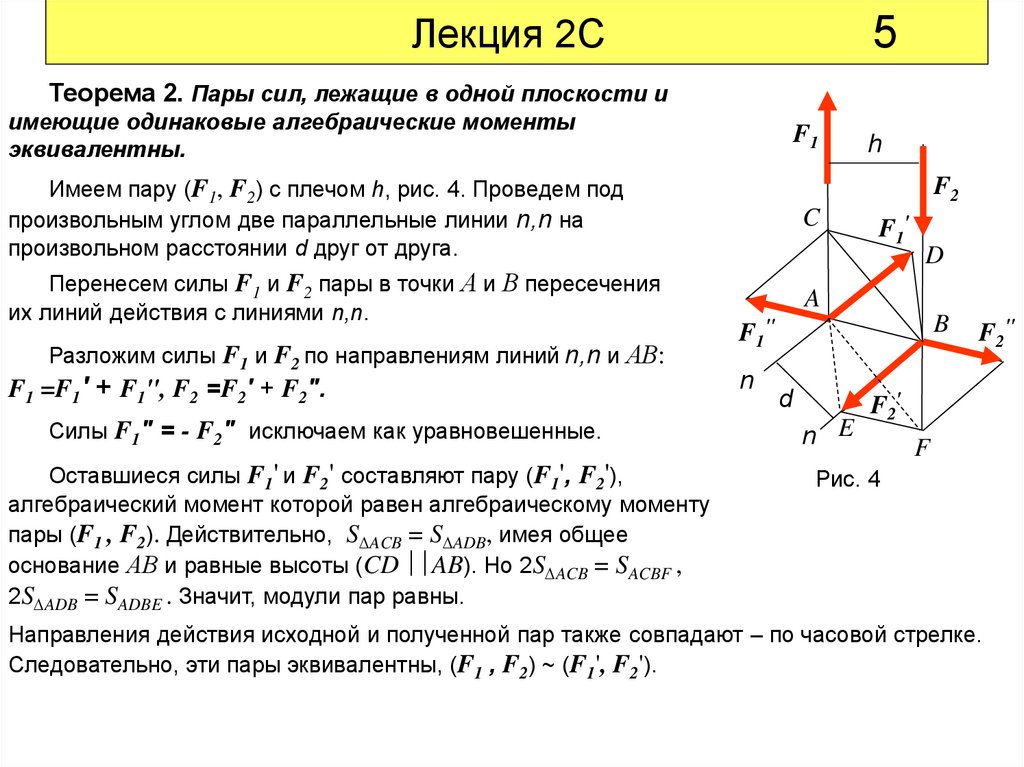
Теорема 2. Пары сил, лежащие в одной плоскости и
имеющие одинаковые алгебраические моменты
эквивалентны.
F1
Имеем пару (F1, F2) с плечом h, рис. 4. Проведем под
произвольным углом две параллельные линии n,n на
произвольном расстоянии d друг от друга.
C
Перенесем силы F1 и F2 пары в точки А и В пересечения
их линий действия с линиями n,n.
A
Разложим силы F1 и F2 по направлениям линий n,n и АВ:
F1 =F1' + F1", F2 =F2' + F2".
Силы F1" = - F2" исключаем как уравновешенные.
Оставшиеся силы F1' и F2' составляют пару (F1', F2'),
алгебраический момент которой равен алгебраическому моменту
пары (F1 , F2). Действительно, S ACB = S ADB, имея общее
основание АВ и равные высоты (CD AB). Но 2S ACB = SACBF ,
2S ADB = SADBE . Значит, модули пар равны.
h
F2
F1'
D
B
F1"
n
d
n E
F2"
F2'
F
Рис. 4
Направления действия исходной и полученной пар также совпадают – по часовой стрелке.
Следовательно, эти пары эквивалентны, (F1 , F2) ~ (F1', F2').

6.

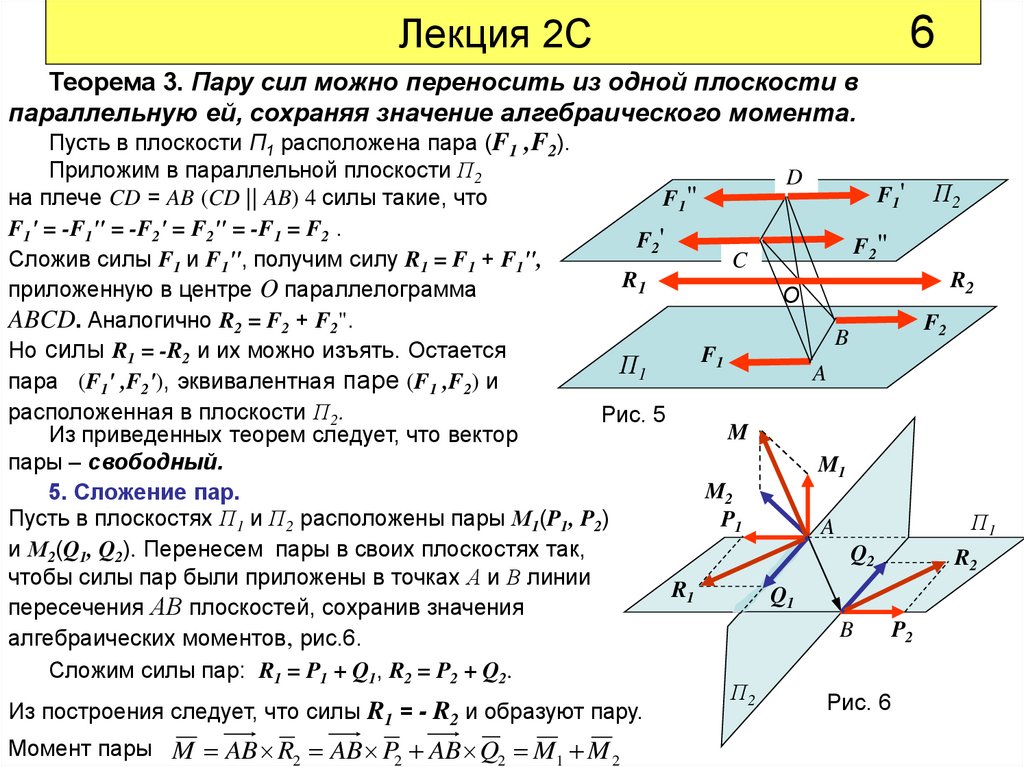
Лекция 2С
Теорема 3. Пару сил можно переносить из одной плоскости в
параллельную ей, сохраняя значение алгебраического момента.
Пусть в плоскости П1 расположена пара (F1 ,F2).
6
Приложим в параллельной плоскости П2
D
F1' П2
на плече CD = AB (CD || AB) 4 силы такие, что
F1 "
F1' = -F1" = -F2' = F2" = -F1 = F2 .
F2 '
F2 "
Сложив силы F1 и F1", получим силу R1 = F1 + F1",
C
R1
R2
приложенную в центре O параллелограмма
О
ABCD. Аналогично R2 = F2 + F2".
F2
B
Но силы R1 = -R2 и их можно изъять. Остается
F1
П1
A
пара (F1' ,F2'), эквивалентная паре (F1 ,F2) и
расположенная в плоскости П2.
Рис. 5
M
Из приведенных теорем следует, что вектор
пары – свободный.
M1
M2
5. Сложение пар.
Пусть в плоскостях П1 и П2 расположены пары М1(P1, P2)
P1
П1
A
и М2(Q1, Q2). Перенесем пары в своих плоскостях так,
Q2
R2
чтобы силы пар были приложены в точках А и В линии
R1
Q1
пересечения АВ плоскостей, сохранив значения
B
P2
алгебраических моментов, рис.6.
Сложим силы пар: R1 = P1 + Q1, R2 = P2 + Q2.
П2
Рис. 6
Из построения следует, что силы R1 = - R2 и образуют пару.
Момент пары M AB R2 AB P2 AB Q2 M1 M 2

7.

Лекция 2С
7
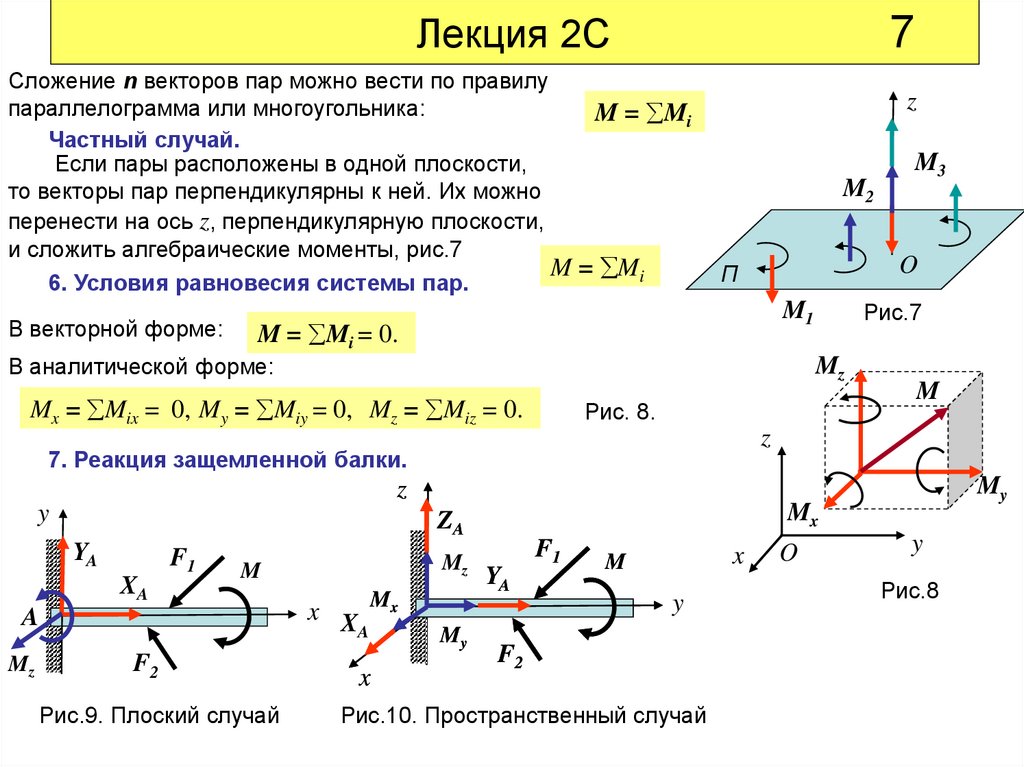
Сложение n векторов пар можно вести по правилу
параллелограмма или многоугольника:
M = Mi
Частный случай.
Если пары расположены в одной плоскости,
то векторы пар перпендикулярны к ней. Их можно
перенести на ось z, перпендикулярную плоскости,
и сложить алгебраические моменты, рис.7
M = Mi
6. Условия равновесия системы пар.
В векторной форме:
z
M2
O
П
Рис.7
M1
M = Mi = 0.
В аналитической форме:
Mz
Mx = Mix = 0, My = Miy = 0, Mz = Miz = 0.
M3
Рис. 8.
M
z
7. Реакция защемленной балки.
My
z
y
YA
F1
XA
Mz
M
A
Mz
Mx
ZA
F2
Рис.9. Плоский случай
x X
A
Mx
x
My
F1
YA
x
M
y
F2
Рис.10. Пространственный случай
O
y
Рис.8

8.

Лекция 2C
8
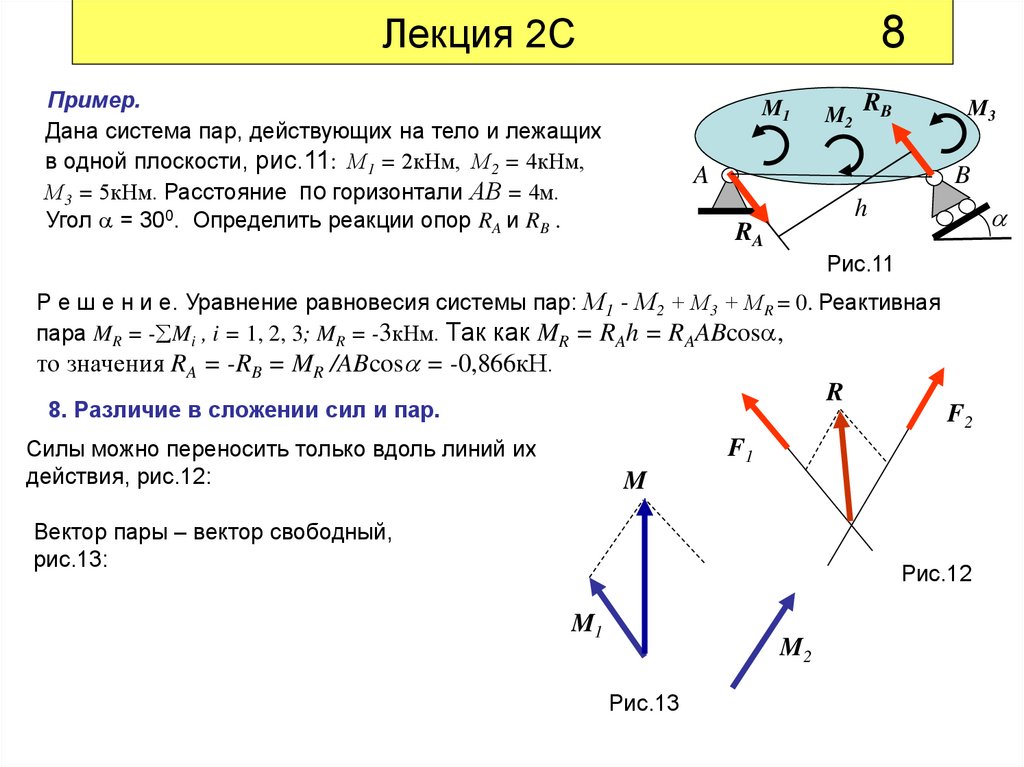
Пример.
Дана система пар, действующих на тело и лежащих
в одной плоскости, рис.11: М1 = 2кНм, М2 = 4кНм,
М3 = 5кНм. Расстояние по горизонтали АВ = 4м.
Угол = 300. Определить реакции опор RA и RB .
M1
M2
RB
M3
A
B
h
RA
Рис.11
Р е ш е н и е. Уравнение равновесия системы пар: М1 - М2 + М3 + МR = 0. Реактивная
пара MR = - Mi , i = 1, 2, 3; MR = -3кНм. Так как MR = RAh = RAABcos ,
то значения RA = -RB = MR /ABcos = -0,866кН.
R
8. Различие в сложении сил и пар.
Силы можно переносить только вдоль линий их
действия, рис.12:
F2
F1
M
Вектор пары – вектор свободный,
рис.13:
Рис.12
M1
M2
Рис.13