Момент силы. Лекция 1.3

1. МОМЕНТ СИЛЫ

Момент силы - это величина,
характеризующая вращательный
эффект производимый силой.

2. Момент силы относительно центра

B
MO ( F )
F
h
MO ( F ) F h;
α
СИ : MO ( F ) Н м;
A
r
OA r ;
O
MO ( F ) r F ;
(3.4)
r F F r sin α F r sin 180 α F h M O ( F ) ;
MO ( F ) 2S OAB ;
(3.5)

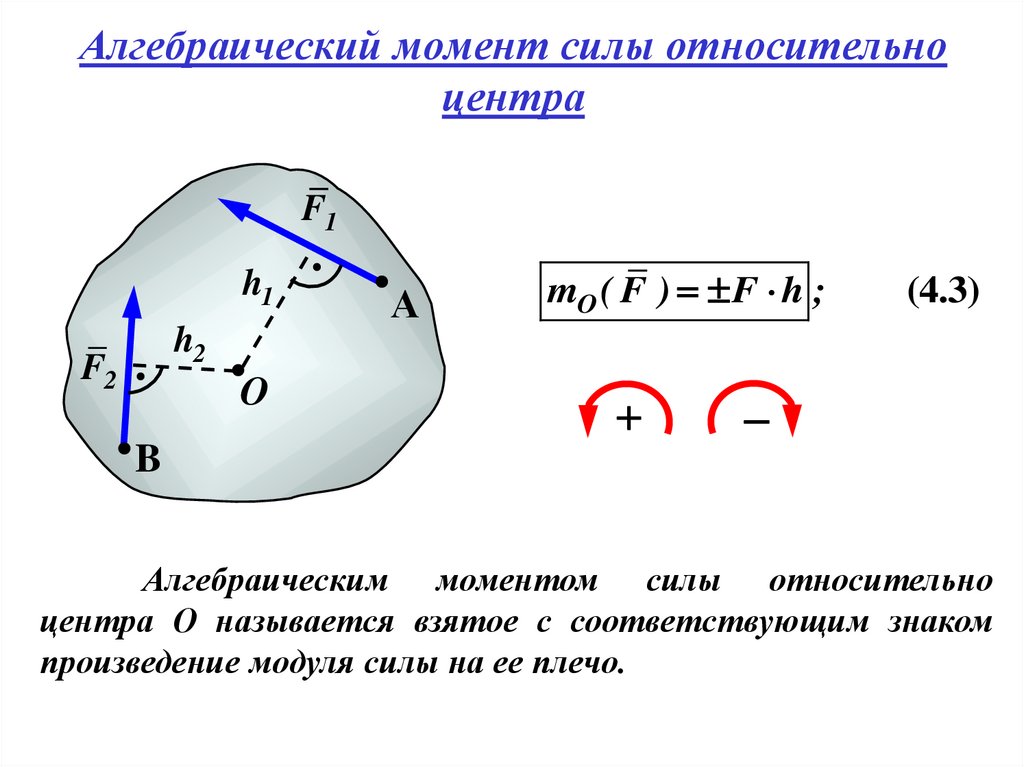
3. Алгебраический момент силы относительно центра

F1
h1
h2
F2
O
А
mO ( F ) F h ;
(4.3)
B
Алгебраическим моментом силы относительно
центра О называется взятое с соответствующим знаком
произведение модуля силы на ее плечо.

4.

h 0;
A
O
F
M O ( F ) 0;
Момент силы относительно центра равен нулю, если линия
действия силы проходит через этот центр.

5.

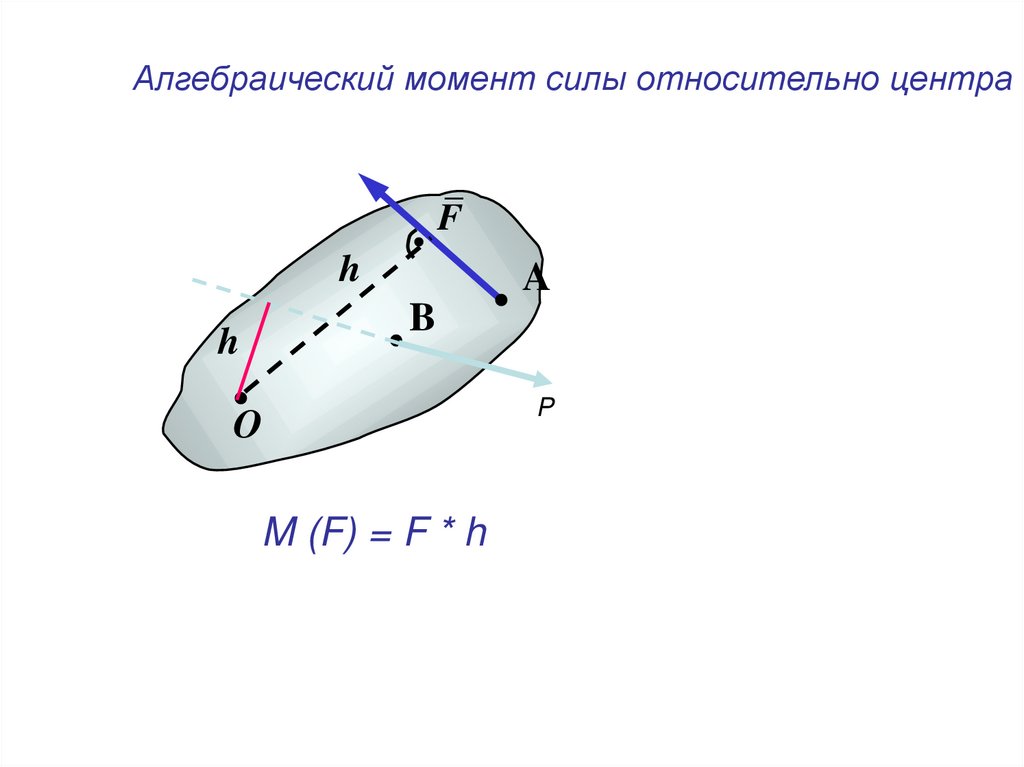
Алгебраический момент силы относительно центра
F
h
A
B
h
O
M (F) = F * h
P

6. Момент силы относительно оси

Z
MO ( F )
B
Мz
F α
h
A
r
Y
O
X
MO ( F ) 2S OAB ;
(3.5)
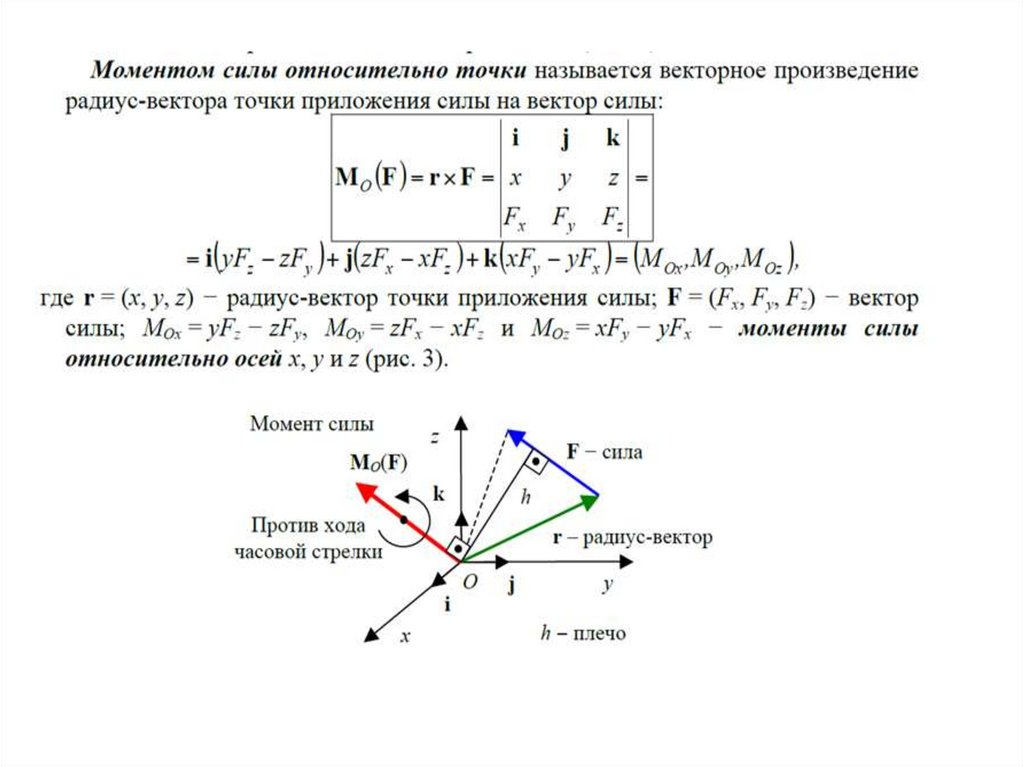
Проекция вектора М на некоторую ось z называется моментом силы F
относительно этой оси.

7.

8.

z
F
h
Fxy
M(F)=+ Fxy*h

9. Момент силы относительно оси

10. Иллюстрация понятия момента силы. Неподвижная ось - это голень. Чем дальше рука спортсмена относительно оси, тем легче сломать

ракетку.
Аугусто Куэртен.
Сидней,
Олимпийские игры
2001 г.
AP and Renters

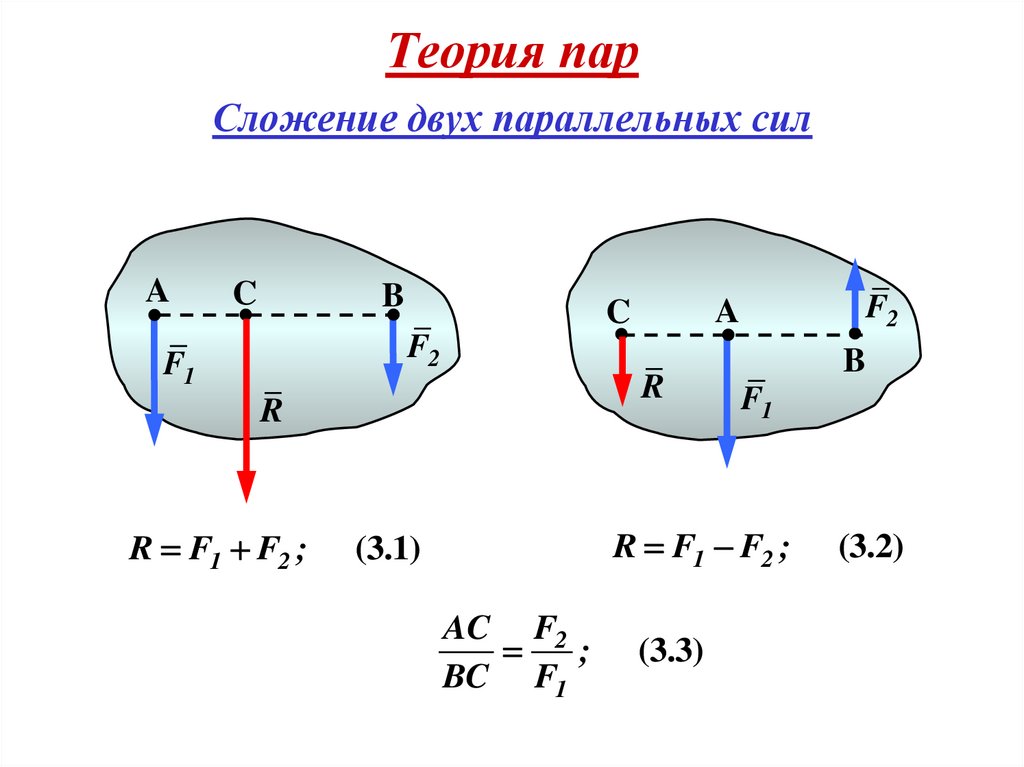
11. Теория пар

Сложение двух параллельных сил
A
C
B
F2
A
C
F2
F1
R
R
R F1 F2 ;
B
F1
R F1 F2 ;
(3.1)
AC F2
;
BC F1
(3.3)
(3.2)

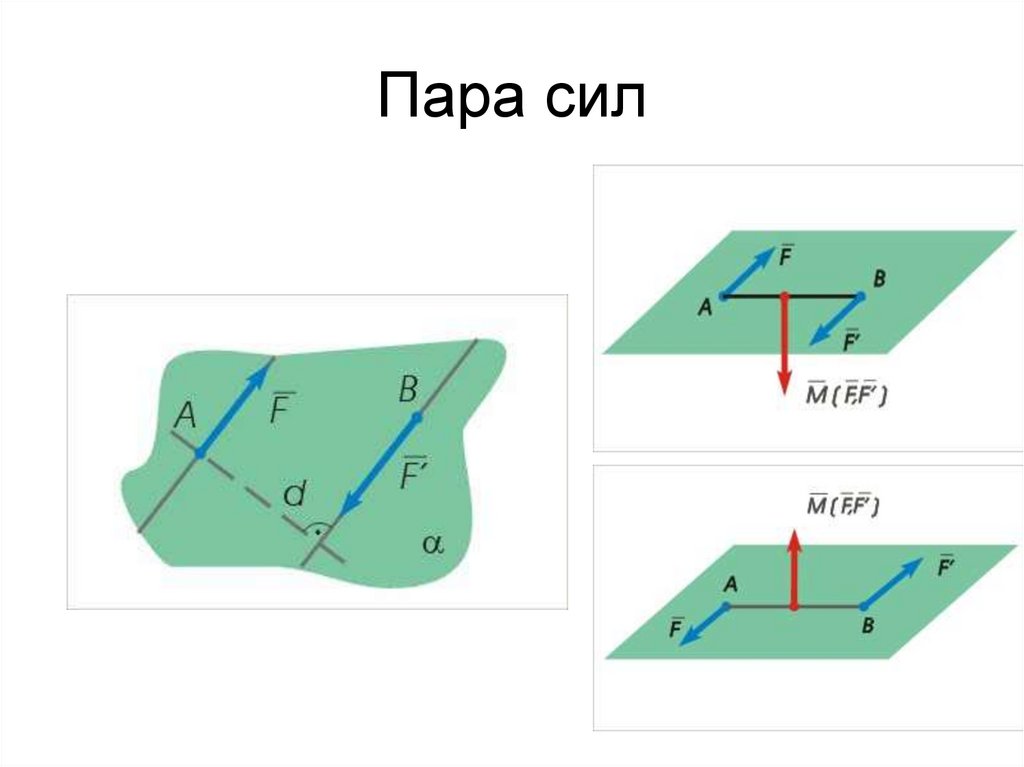
12. Пара сил и ее момент

Пара сил (пара) – совокупность двух параллельных, равных по
величине и направленных в противоположные стороны сил.
m
F F ;
B
d
F
d
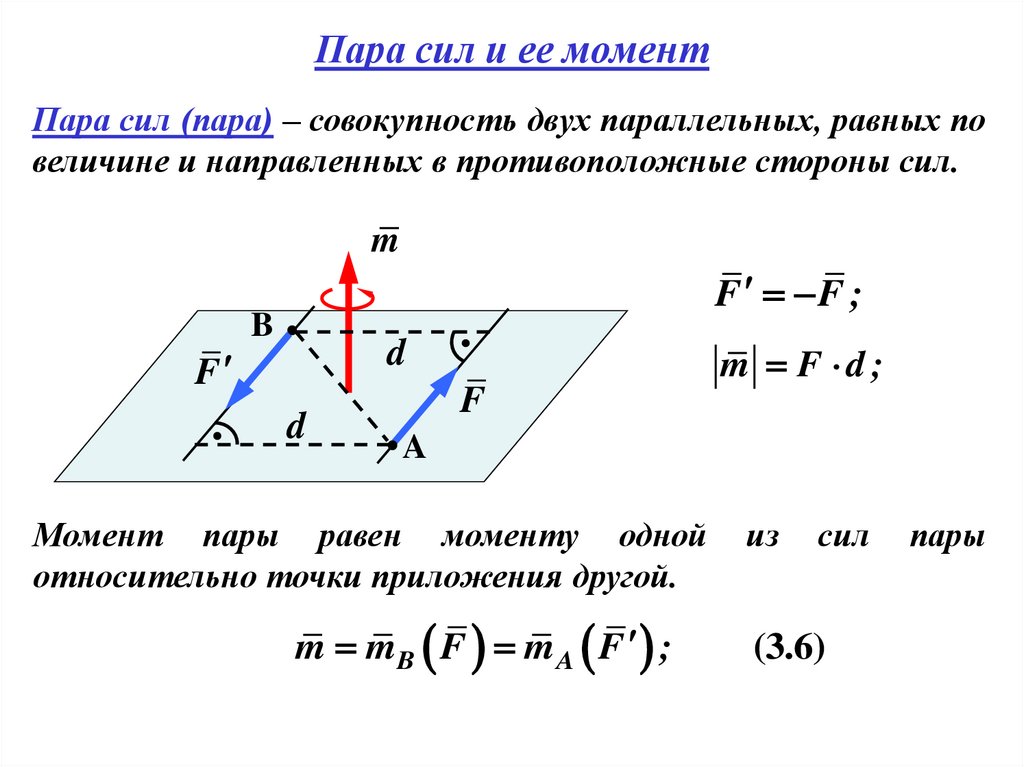
m F d;
F
A
Момент пары равен моменту одной
относительно точки приложения другой.
m mB F m A F ;
из
сил
(3.6)
пары

13. Пара сил

14. Свойства пары сил:

1. Не изменяя действия пары на твердое тело, пару можно
переносить в плоскости ее действия, произвольно меняя
модули сил и длину плеча пары, но сохраняя неизменный ее
момент и направление вращения.
2. Не изменяя действия пары на твердое тело, пару можно
переносить из данной плоскости в любую другую
плоскость, параллельную данной.
Основной характеристикой пары сил является ее момент.
Вектор-момент пары сил является свободным вектором.

15. Приведение системы пар к простейшему виду. Равновесие системы пар.

m1 ;m2 ; ...mn ;
n
M m1 m 2 ... mn mk ;
k 1
Система пар, действующих на абсолютно твердое
тело, эквивалентна одной паре с моментом, равным
геометрической сумме моментов слагаемых пар.
Для равновесия пространственной систем пар
необходимо и достаточно, чтобы момент результирующей
пары равнялся нулю.
n
M mk 0;
k 1
(3.7)

16.

n
mkx 0
k 1
n
mky 0 ;
k 1
n
mkz 0
k 1
z
(3.8)
n
mkz 0;
M1
Mk
y
k 1
n
Fk d k 0;
k 1
x
M2
К содержанию курса

17. Пара сил и ее момент

Пара сил (пара) – совокупность двух параллельных, равных по
величине и направленных в противоположные стороны сил.
m
F F ;
B
d
F
d
m F d;
F
A
Момент пары равен моменту одной
относительно точки приложения другой.
m mB F m A F ;
из
сил
(3.6)
пары

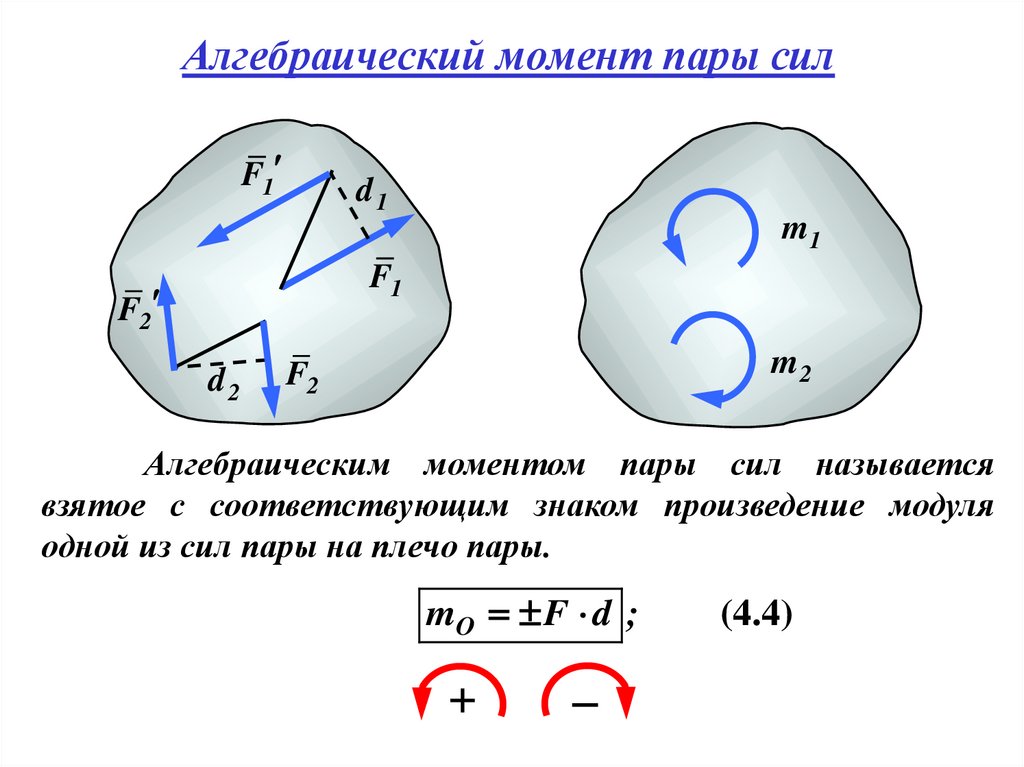
18. Алгебраический момент пары сил

F1
d1
m1
F1
F2
d2
m2
F2
Алгебраическим моментом пары сил называется
взятое с соответствующим знаком произведение модуля
одной из сил пары на плечо пары.
mO F d ;
(4.4)

19. Теоремы о парах

Теорема о сумме моментов сил пары.
Сумма
моментов
сил,
составляющих
пару,
относительно произвольного центра не зависит от выбора
этого центра и равна моменту самой пары .
O
mO F mO F
m
OA F OB F ;
F
B
F F ;
F
A
mO F mO F OA F OB F
OA OB F BA F m;

20. Свойства пары сил:

1. Не изменяя действия пары на твердое тело, пару можно
переносить в плоскости ее действия, произвольно меняя
модули сил и длину плеча пары, но сохраняя неизменный ее
момент и направление вращения.
2. Не изменяя действия пары на твердое тело, пару можно
переносить из данной плоскости в любую другую
плоскость, параллельную данной.
Основной характеристикой пары сил является ее момент.
Вектор-момент пары сил является свободным вектором.

21. Приведение системы пар к простейшему виду. Равновесие системы пар.

m1 ;m2 ; ...mn ;
n
M m1 m 2 ... mn mk ;
k 1
Система пар, действующих на абсолютно твердое
тело, эквивалентна одной паре с моментом, равным
геометрической сумме моментов слагаемых пар.
Для равновесия пространственной систем пар
необходимо и достаточно, чтобы момент результирующей
пары равнялся нулю.
n
M mk 0;
k 1
(3.7)

22. Теория пар