Нелинейные электрические цепи. Лекция №12

1. Лекция №12

Тема: Нелинейные
электрические цепи

2.

Тема лекции исключительно актуальна!!!

3. Учебные вопросы

1. Нелинейная электрическая цепь и её
преобразовательные свойства.
2. Классификация нелинейных резистивных
элементов и их характеристики.
3. Статические и дифференциальные параметры
резистивных нелинейных элементов.
4. Аппроксимация ВАХ нелинейных элементов.
5. Ток в нелинейном резисторе при воздействии
гармонического напряжения. Анализ
аналитическим методом.
6. Ток в нелинейном резисторе при воздействии
гармонического напряжения. Анализ
графическим методом.

4. Литература

1. Попов В.П. Основы теории
цепей: Учебник для вузов
спец. "Радиотехника".-М.:
Высшая школа, 2007 с. 275305.

5. В электротехнике, автоматике, электронике и радиотехнике широко применяются элементы электрических цепей, имеющие нелинейную

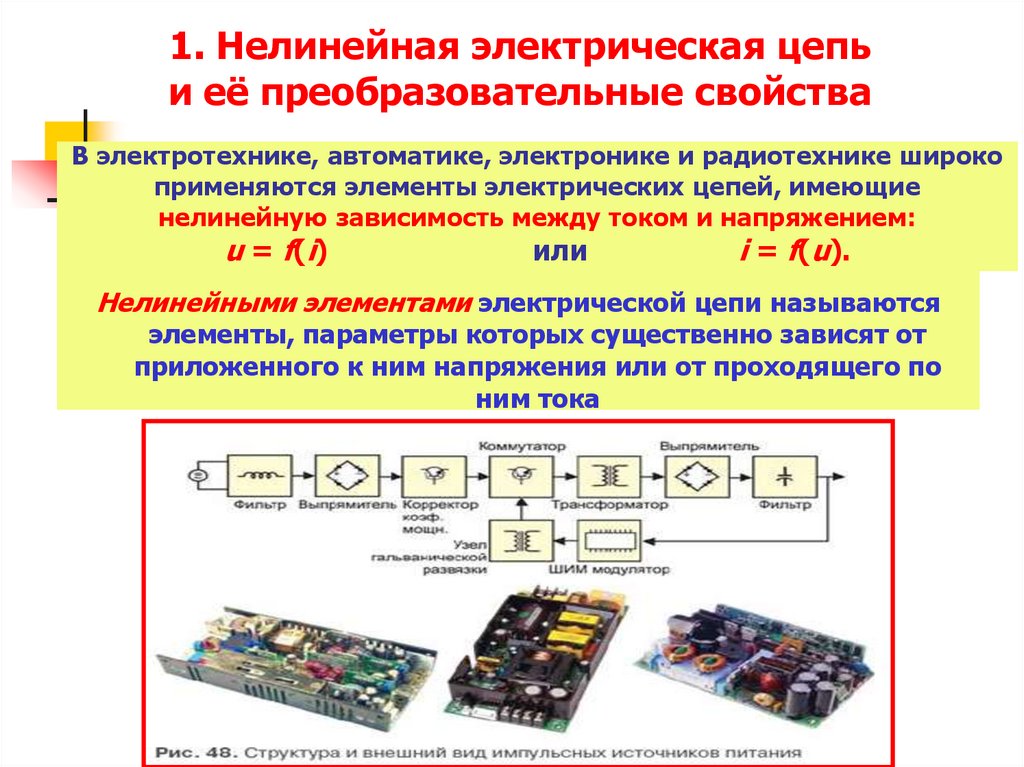
1. Нелинейная электрическая цепь
и её преобразовательные свойства
В электротехнике, автоматике, электронике и радиотехнике широко
применяются элементы электрических цепей, имеющие
нелинейную зависимость между током и напряжением:
u = f(i)
или
i = f(u).
Нелинейными элементами электрической цепи называются
элементы, параметры которых существенно зависят от
приложенного к ним напряжения или от проходящего по
ним тока

6.

В зависимости от типа
параметра различают
нелинейные
резистивные,
индуктивные и
емкостные элементы
Нелинейные элементы
описываются нелинейными
уравнениями или
соответствующими
нелинейными
вольтамперными i(u) (рис.
а), вебер-амперными (i)
(рис. б) и кулон-вольтными
q(u) (рис. в)
характеристиками
Нелинейная
электрическая цепь
- это цепь, которая
содержит хотя бы
один нелинейный
элемент.

7.

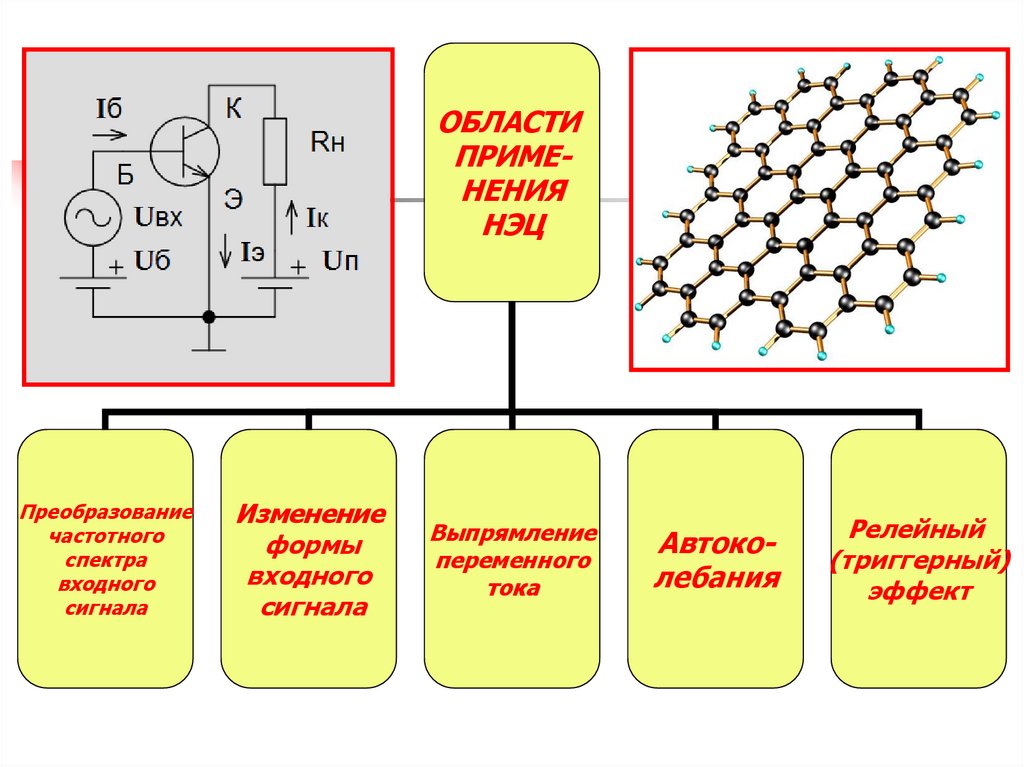
ОБЛАСТИ
ПРИМЕНЕНИЯ
НЭЦ
Преобразование
частотного
спектра
входного
сигнала
Изменение
формы
входного
сигнала
Выпрямление
переменного
тока
Автоколебания
Релейный
(триггерный)
эффект

8.

2. Классификация нелинейных резистивных
элементов и их характеристики
Статическая ВАХ – это зависимость тока, протекающего через нелинейный
резистивный элемент, от приложенного к нему напряжения в
установившемся режиме (или наоборот – зависимость падения
напряжения на элементе от протекающего через него тока).
В зависимости от числа внешних выводов различают нелинейные
двухполюсные элементы (резисторы с нелинейным сопротивлением,
электровакуумные и полупроводниковые диоды) и нелинейные
многополюсные элементы (транзисторы и тиристоры различных типов,
электровакуумные триоды и пентоды).

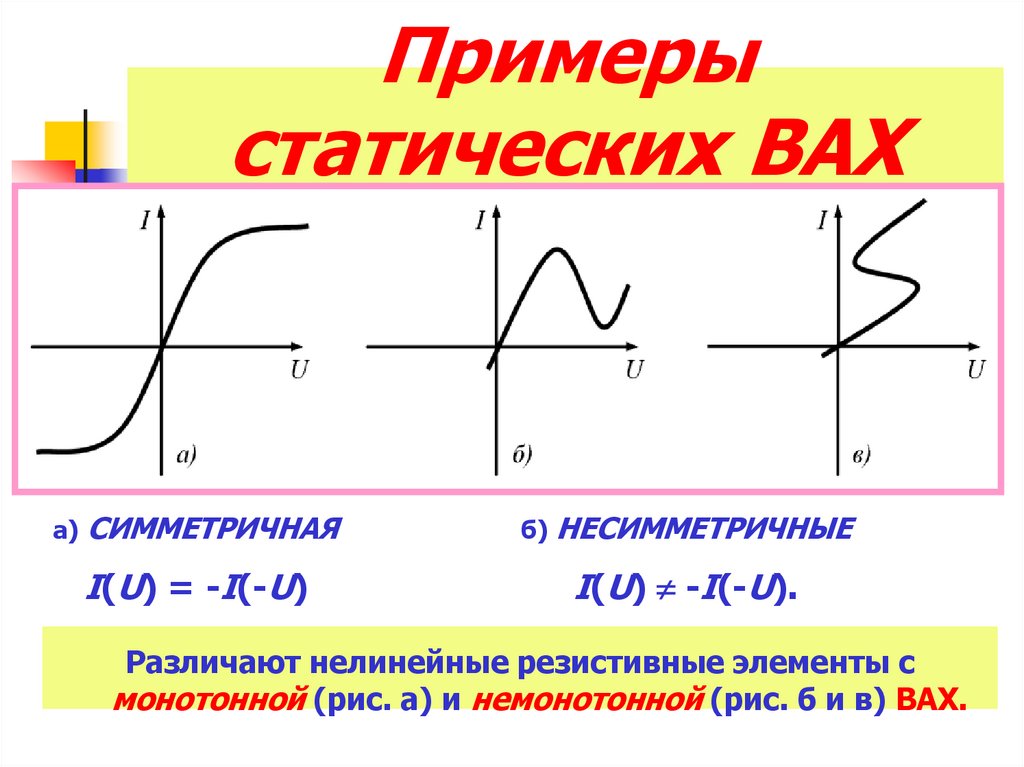
9. Примеры статических ВАХ

а) СИММЕТРИЧНАЯ
б) НЕСИММЕТРИЧНЫЕ
I(U) = -I(-U)
I(U) -I(-U).
Различают нелинейные резистивные элементы с
монотонной (рис. а) и немонотонной (рис. б и в) ВАХ.

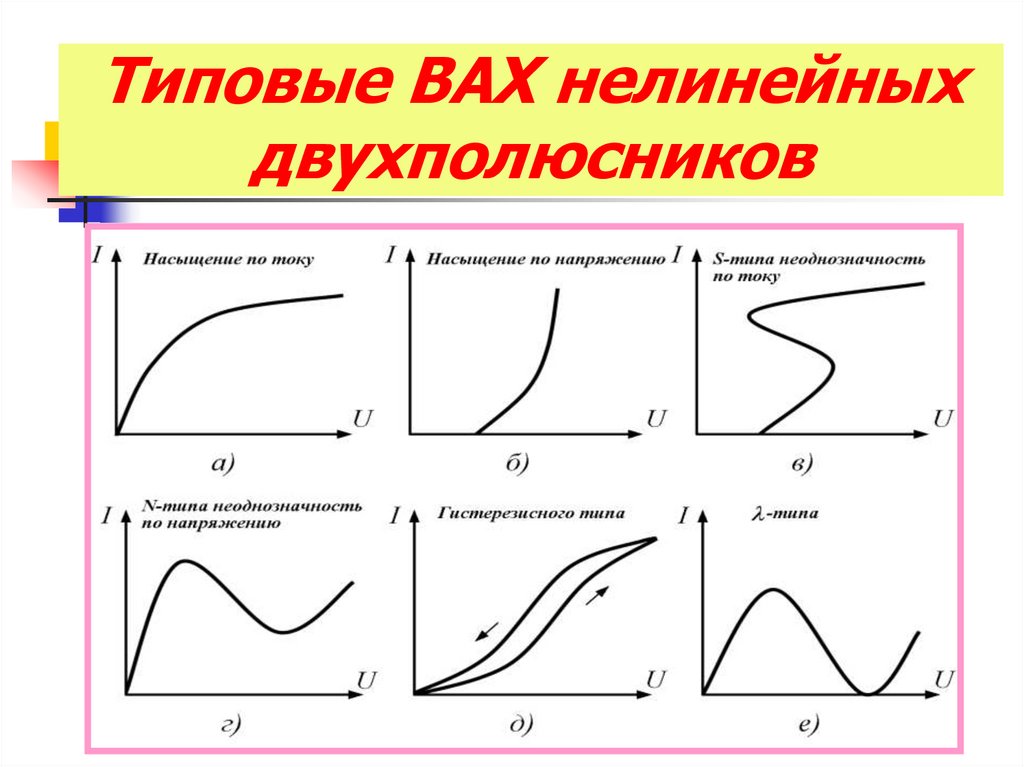
10. Типовые ВАХ нелинейных двухполюсников

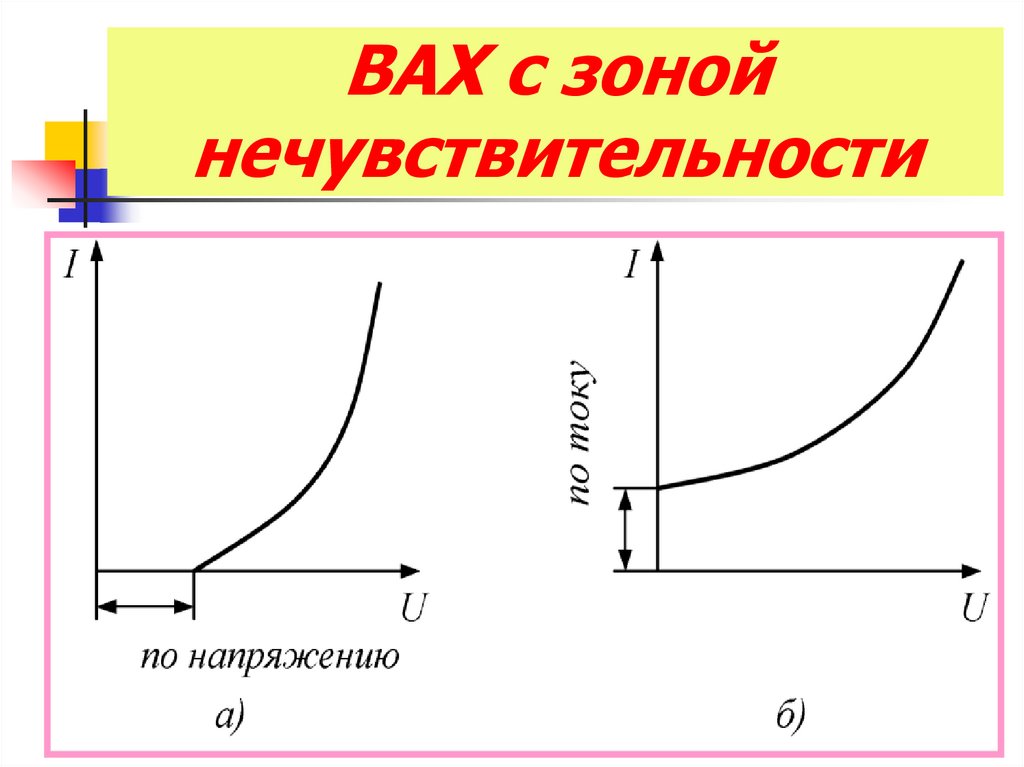
11. ВАХ с зоной нечувствительности

12. Управляемые нелинейные элементы:

а) неэлектрически управляемые
двухполюсники
Семейство ВАХ
термистора
б) электрически управляемые
элементы
Транзистор и его
выходные
характеристики

13. Резистивные нелинейные элементы и их ВАХ

Элемент,
графическое
обозначение
Вид ВАХ
1
2
Варистор
Характеристика
ВАХ
3
Симметричная
I(U) = -I(-U),
монотонная
dI
0
dU

14. Резистивные нелинейные элементы и их ВАХ (продолжение)

1
Электровакуумный диод
Неоновая лампа
2
3
Несимметричная,
монотонная ВАХ
(dI/dU) > 0
ВАХ с падающим
участком (dI/dU)
< 0,
несимметричная,
немонотонная,
S-типа

15. Резистивные нелинейные элементы и их ВАХ (продолжение)

1
2
3
Полупроводниковый диод
ВАХ
несимметричная,
монотонная
Туннельный
диод
ВАХ с
падающим
участком,
несимметричная
, немонотонная,
N-типа

16. Резистивные нелинейные элементы и их ВАХ (продолжение)

1
2
Фотодиод
Биполярный
транзистор
3
ВАХ
несимметрична,
монотонна, с
насыщением по
току.Сопротивле
ние зависит от
светового потока
Выходные ВАХ
ВАХ
несимметрична,
монотонна, с
насыщением по
току.
Iк = I(IБ, Uкэ)

17. Резистивные нелинейные элементы и их ВАХ (продолжение)

1
Тиристор
2
3
ВАХ
несимметрична
, немонотонна,
S-типа,
зависит от
напряжения на
управляющем
электроде

18. 3.1 Статические параметры

3. Статические и дифференциальные параметры
резистивных нелинейных элементов
3.1 Статические параметры
U0
R ст
ktg
I0
k
mu
mi
Статическое сопротивление – это
отношение напряжения к току в
данной точке ВАХ. Статическое
сопротивление – это сопротивление
нелинейного элемента постоянному
току.
Статическая проводимость
Io
1
1
Gст
ctg .
Rст U o k
есть величина, обратная
статическому
сопротивлению

19. 3.2 Дифференциальные параметры

U
Rдиф.
.
I
Дифференциальное сопротивление
– это предел отношения
приращения напряжения к
соответствующему приращению
тока при небольшом смещении
рабочей точки на ВАХ под
воздействием переменного
напряжения малой амплитуды:
Дифференциальное
сопротивление – это
сопротивление нелинейного
элемента переменному току
малой амплитуды.
U dU
Rдиф. lim
I 0 I
dI
1
(.) p
ktg ,
dI
1
S G диф
ctg
R диф dU k

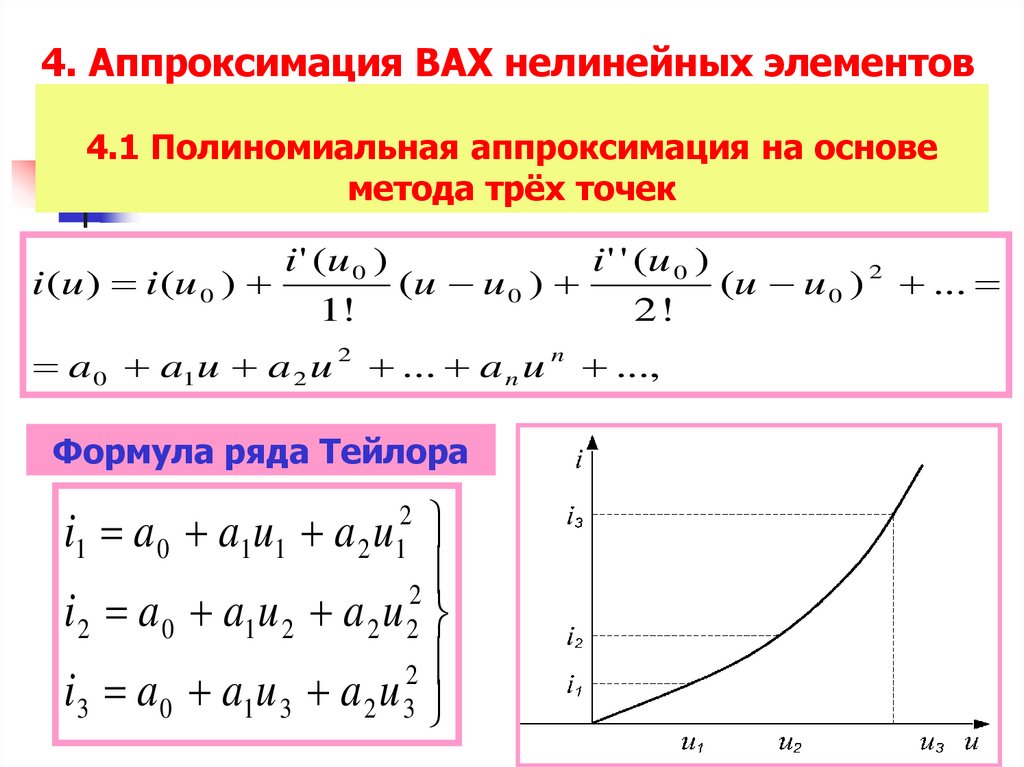
20. 4.1 Полиномиальная аппроксимация на основе метода трёх точек

4. Аппроксимация ВАХ нелинейных элементов
4.1 Полиномиальная аппроксимация на основе
метода трёх точек
i ' (u 0 )
i ' ' (u 0 )
i (u ) i (u 0 )
(u u 0 )
(u u 0 ) 2 ...
1!
2!
a 0 a1u a 2 u 2 ... a n u n ...,
Формула ряда Тейлора
i1 a 0 a1u1 a 2 u12
2
i 2 a 0 a1 u 2 a 2 u 2
2
i3 a 0 a1u 3 a 2 u 3

21. 4.2 Кусочно-линейная аппроксимация. Пример

22. Кусочно-линейная аппроксимация

i3 i2
i 2 i1
.
S1
, S2
u3 u 2
u 2 u1
1
u U 1
i
S1
1
u U 2
i
S2
при
i i 1 ,i 2
при
i i 2 ,i 3

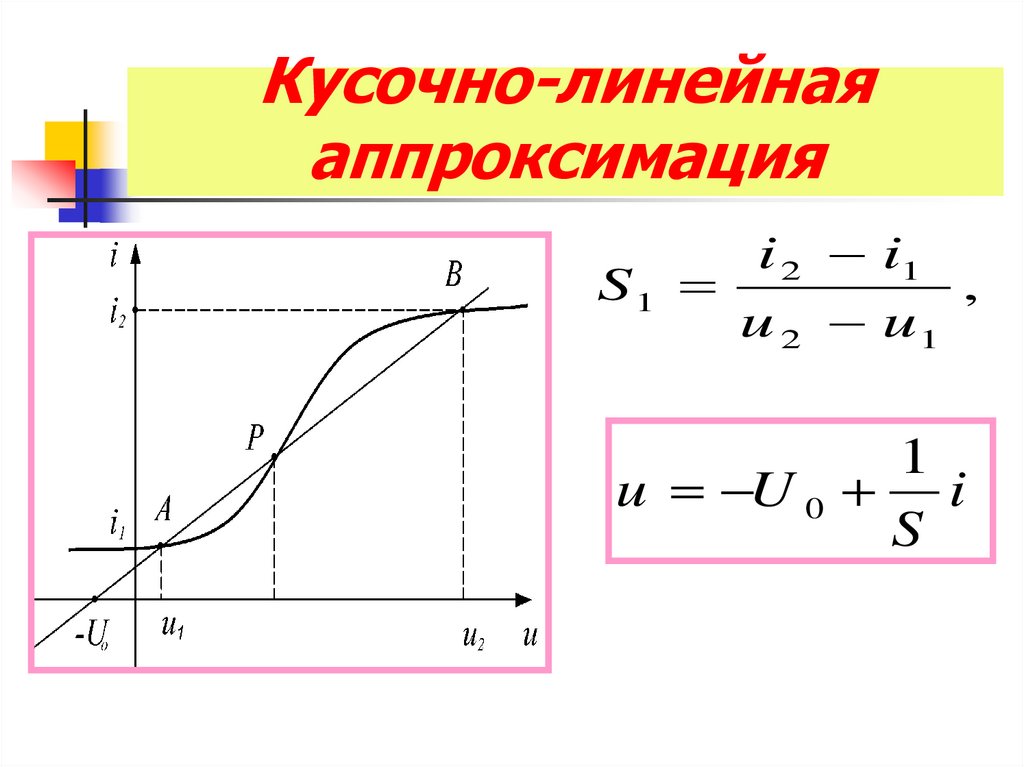
23. Кусочно-линейная аппроксимация

i 2 i1
S1
,
u 2 u1
1
u U 0 i
S

24. 5. ТОК В НЕЛИНЕЙНОМ РЕЗИСТОРЕ ПРИ ВОЗДЕЙСТВИИ ГАРМОНИЧЕСКОГО НАПРЯЖЕНИЯ. АНАЛИЗ АНАЛИТИЧЕСКИМ МЕТОДОМ

n
i a 0 a1u a 2 u ... a n u a k u k ,
2
u = Umcos t
n
k 0
2
4
a
U
a
U
2
2 m
a 2 (U m cos t )
(1 cos 2 t ); a4 (U m cos t ) 4 4 m (3 4 cos 2 t cos 4 t );
2
8
3
a
U
a5U m5
3
5
3 m
(10 cos t 5 cos 3 t cos 5 t )
a3 (U m cos t )
(3 cos t cos 3 t ); a5 (U m cos t )
16
4
n
i I0
k 1
1
3
5
2
4
6
I
a
a
U
a
U
a
U
I mk cos k t , 0 o 2 2 m 8 4 m 16 6 m ...;
1
1
15
I m 2 a 2U m2 a 4U m4 a 6U m6 ...;
2
2
32
I ь1 a1U m
U mn
1
2
n
a
U
.
n
m
n 1
3
5
a 3U m3 a 5U m5 ...;
4
8

25. Ток в нелинейном резисторе при воздействии гармонического напряжения

n
i I 0 I mk cos k t , Ток в нелинейном резисторе
k 1
при воздействии
гармонического напряжения
Выводы
1. Реакция нелинейного элемента на гармоническое
внешнее воздействие определенной частоты
представляет собой сумму постоянной составляющей I0 и
гармонических составляющих (гармоник) с частотами,
кратными частоте внешнего воздействия.
2. Основные гармоники напряжения и тока совпадают по
фазе, т.е. резистивный элемент потребляет только
активную мощность по первой гармонике.
3. Амплитуда k-й гармоники Imk зависит только от членов
полинома k-й и более высоких степеней.
4. Амплитуды четных гармоник и постоянная составляющая
определяется только членами полинома четных
степеней, а амплитуды нечетных гармоник – членами
полинома нечетных степеней.

26. Алгоритм анализа НЭЦ графическим методом

6. Ток в нелинейном резисторе при воздействии
гармонического напряжения. Анализ
графическим методом
Алгоритм анализа НЭЦ графическим
методом
1) для ti по графику функции u(t) найти
мгновенное значение внешнего
воздействия u(ti);
2) по ВАХ i(u) определить
соответствующие этим внешним
воздействиям мгновенные значения
реакции i(ti) на графике i = i(t).

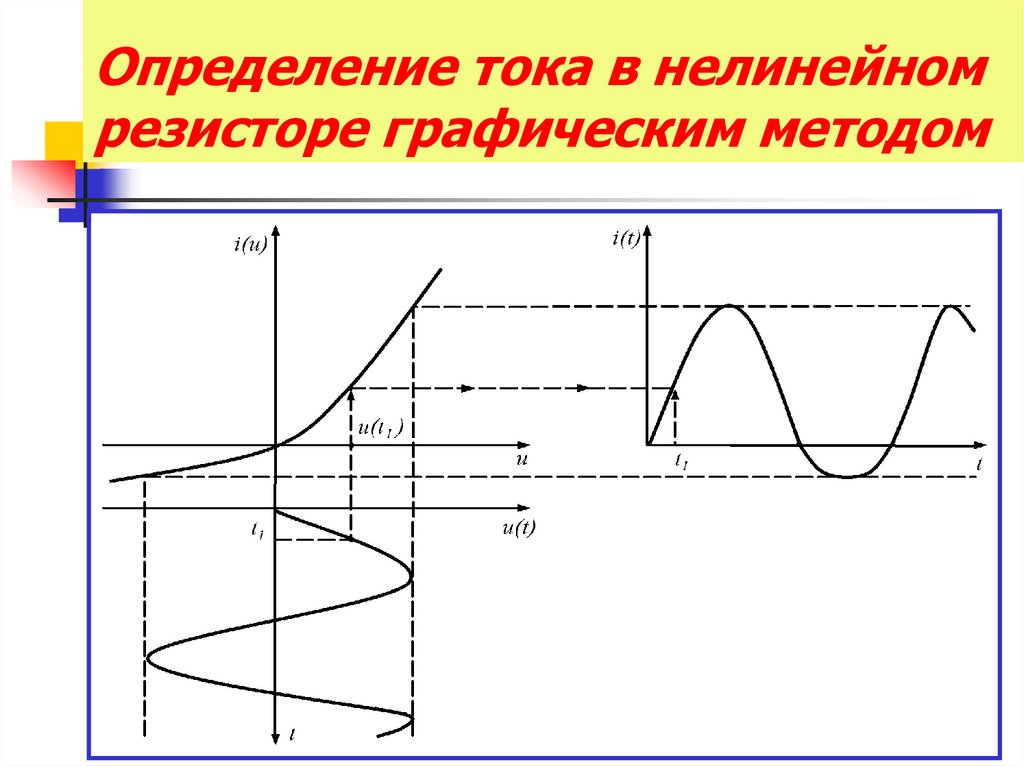
27. Определение тока в нелинейном резисторе графическим методом

28. Определение тока в нелинейном резисторе графическим методом с помощью служебной оси

Вывод: реакция нелинейной цепи на
гармоническое воздействие в общем случае не
является гармонической функцией времени.

29. Определение ВАХ нелинейного резистивного элемента