Принципы модуляции и демодуляции

1. ПРИНЦИПЫ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ

Кафедра «КРЭМС»
ПРИНЦИПЫ
МОДУЛЯЦИИ И
ДЕМОДУЛЯЦИИ
Зырянов
Юрий Трифонович
доктор технических наук
профессор

2.

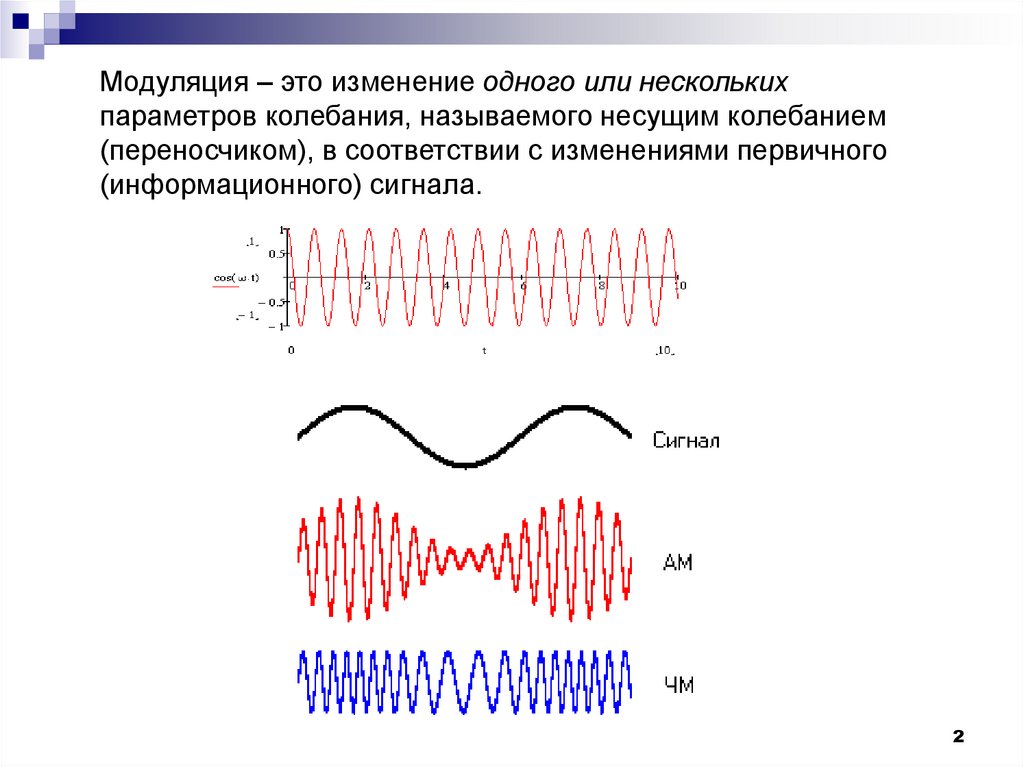
Модуляция – это изменение одного или нескольких
параметров колебания, называемого несущим колебанием
(переносчиком), в соответствии с изменениями первичного
(информационного) сигнала.
2

3.

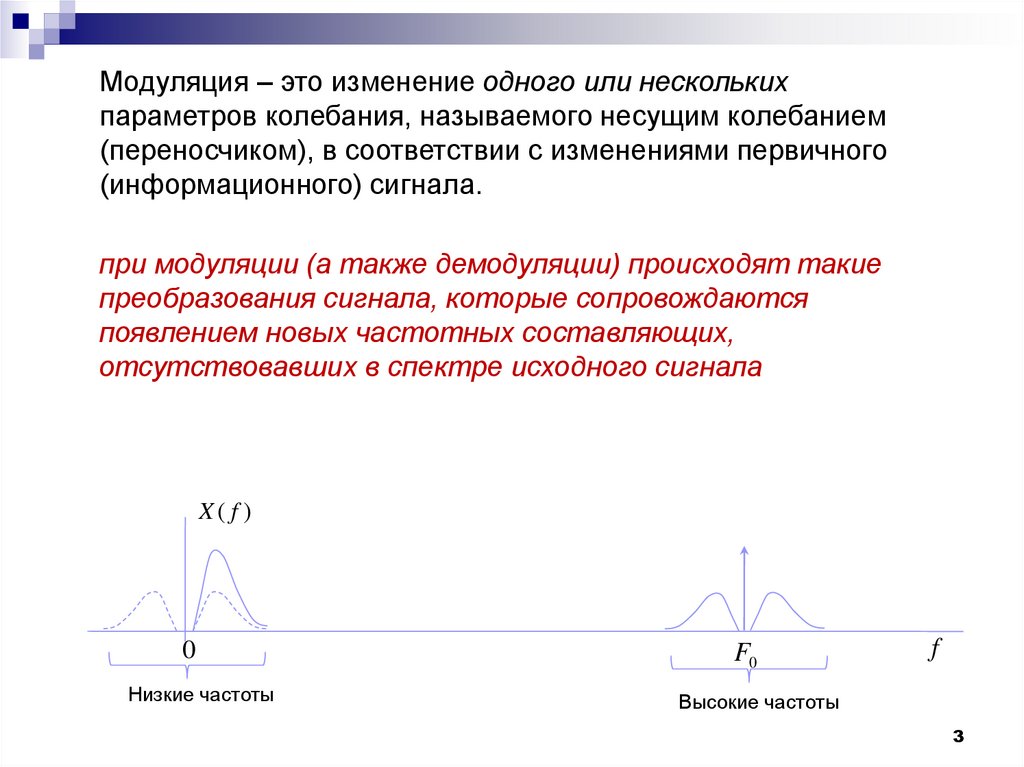
Модуляция – это изменение одного или нескольких
параметров колебания, называемого несущим колебанием
(переносчиком), в соответствии с изменениями первичного
(информационного) сигнала.
при модуляции (а также демодуляции) происходят такие
преобразования сигнала, которые сопровождаются
появлением новых частотных составляющих,
отсутствовавших в спектре исходного сигнала
X(f )
0
F0
Низкие частоты
Высокие частоты
f
3

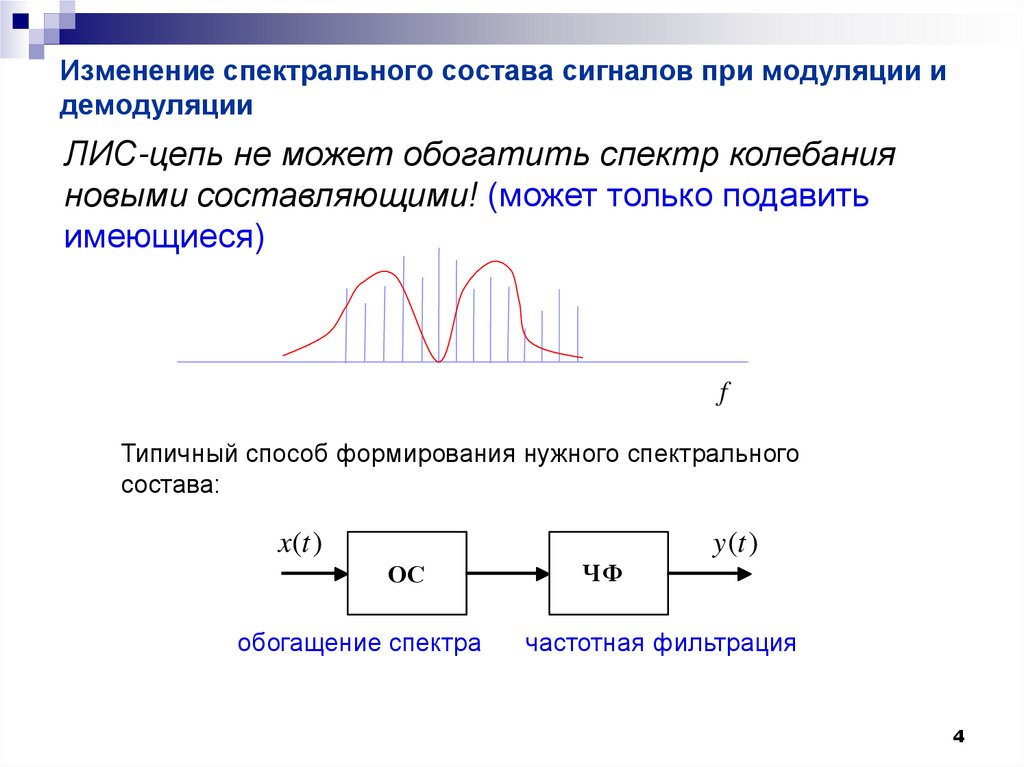
4. Изменение спектрального состава сигналов при модуляции и демодуляции

ЛИС-цепь не может обогатить спектр колебания
новыми составляющими! (может только подавить
имеющиеся)
f
Типичный способ формирования нужного спектрального
состава:
x(t )
y (t )
ОС
обогащение спектра
ЧФ
частотная фильтрация
4

5. Нелинейные элементы и их характеристики

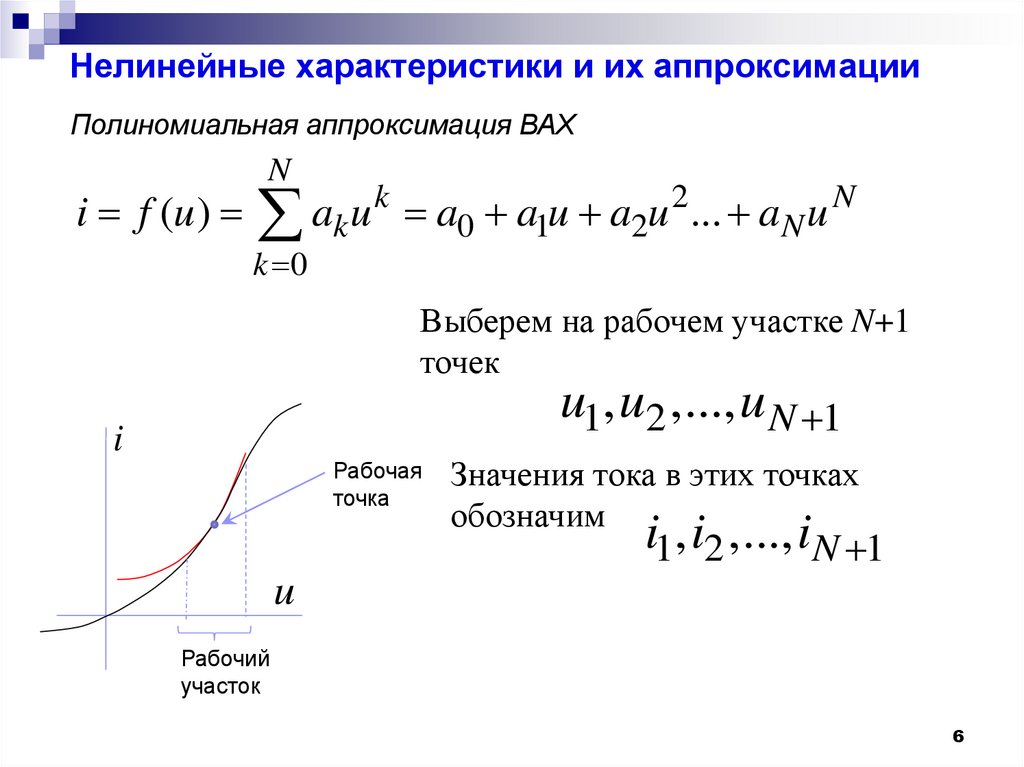
5

6. Нелинейные характеристики и их аппроксимации

Полиномиальная аппроксимация ВАХ
N
i f (u ) ak u k a0 a1u a2u 2 ... a N u N
k 0
Выберем на рабочем участке N+1
точек
u1, u2 ,..., u N 1
i
Рабочая
точка
Значения тока в этих точках
обозначим
i1, i2 ,..., iN 1
u
Рабочий
участок
6

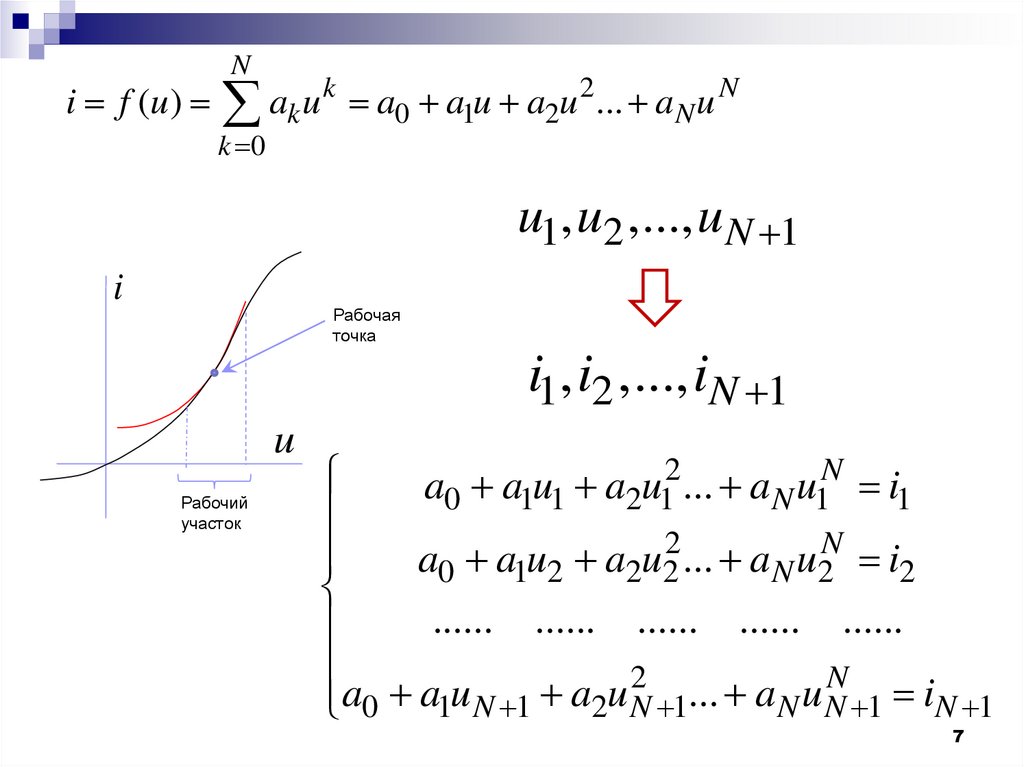
7.

N
i f (u ) ak u k a0 a1u a2u 2 ... a N u N
k 0
u1, u2 ,..., u N 1
i
Рабочая
точка
i1, i2 ,..., iN 1
u
Рабочий
участок
a0 a1u1 a2u12 ... a N u1N i1
a0 a1u2 a2u22 ... a N u2N i2
...... ...... ...... ...... ......
2
N
a
a
u
a
u
...
a
u
N N 1 iN 1
0 1 N 1 2 N 1
7

8.

Аппроксимация методом наименьших квадратов
N
i f (u ) ak u k a0 a1u a2u 2 ... a N u N
k 0
u1, u2 ,..., uM ; M N 1
i1, i2 ,..., iM
a0 a1u1 a2u12 ... a N u1N i1 1
a0 a1u2 a2u22 ... a N u2N i2 2
...... ...... ...... ...... ......
2
N
a
a
u
a
u
...
a
u
N N 1 iN 1 M
0 1 N 1 2 N 1
МНК:
M
min
k 1
2
k
8

9.

M
2
k min
k 1
a a u a u ... a u i min
M
0
k 1
1 k
2
2 k
N
N
k
2
k
a0 ,...aN
2
M
2
N
a0 a1uk a2uk ... a N uk ik 0, m 0, N
am k 1
M
2
N
a0 a1uk a2uk ... a N uk ik 0
k 1
M
2
N
a
a
u
a
u
...
a
u
0
1 k
2 k
N k ik uk 0
k 1
...... ...... ...... ...... ......
M
a0 a1uk a2uk2 ... a N ukN ik ukN 0
k 1
9

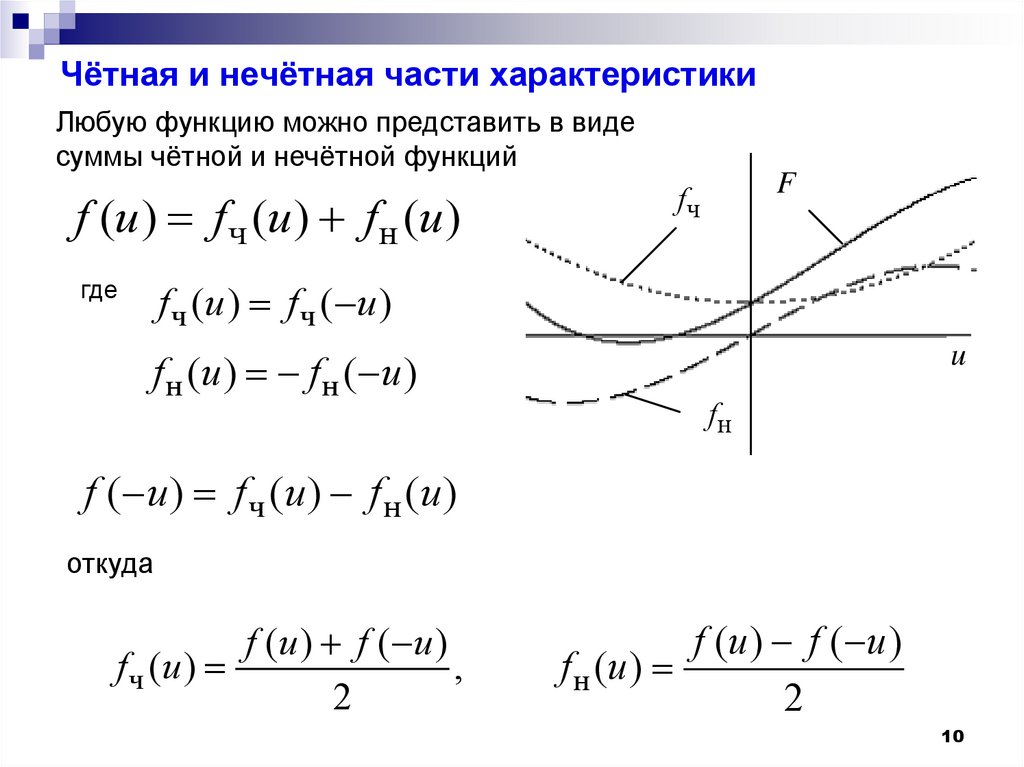
10. Чётная и нечётная части характеристики

Любую функцию можно представить в виде
суммы чётной и нечётной функций
f (u ) f ч (u ) f н (u )
где
F
fч
f ч (u ) f ч ( u )
fн (u ) fн ( u )
u
fн
f ( u ) f ч (u ) f н (u )
откуда
f (u ) f ( u )
f ч (u )
,
2
f (u ) f ( u )
f н (u )
2
10

11.

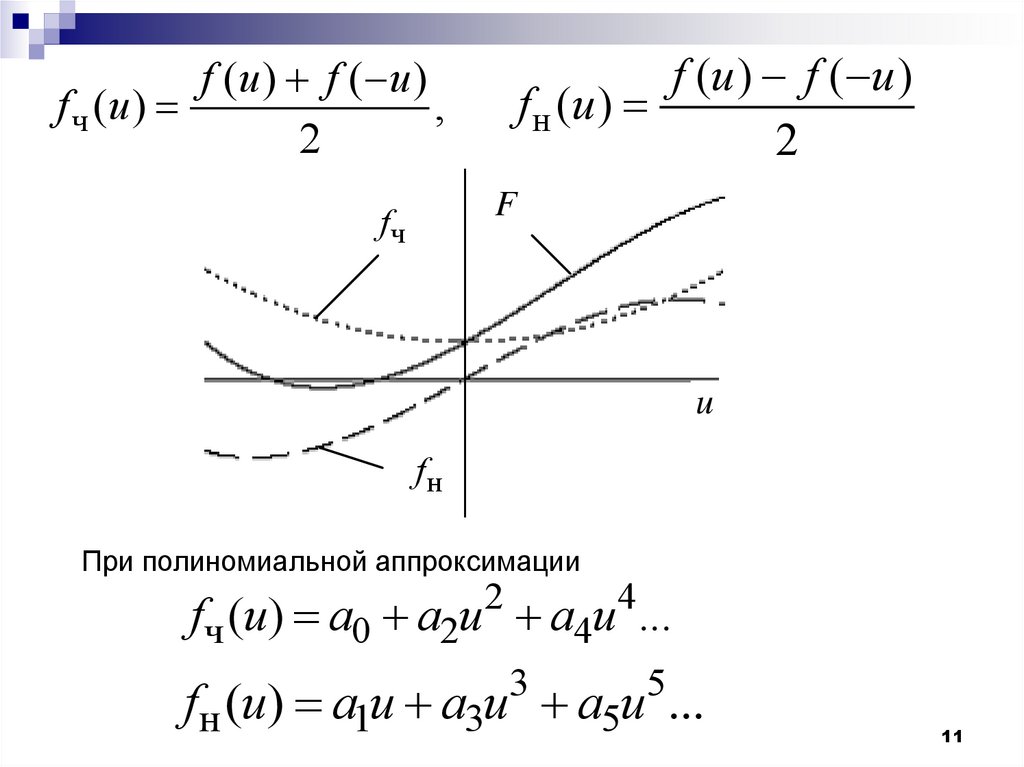
f (u ) f ( u )
f н (u )
2
f (u ) f ( u )
f ч (u )
,
2
F
fч
u
fн
При полиномиальной аппроксимации
2
4
fч (u) a0 a2u a4u ...
3
5
fн (u) a1u a3u a5u ...
11

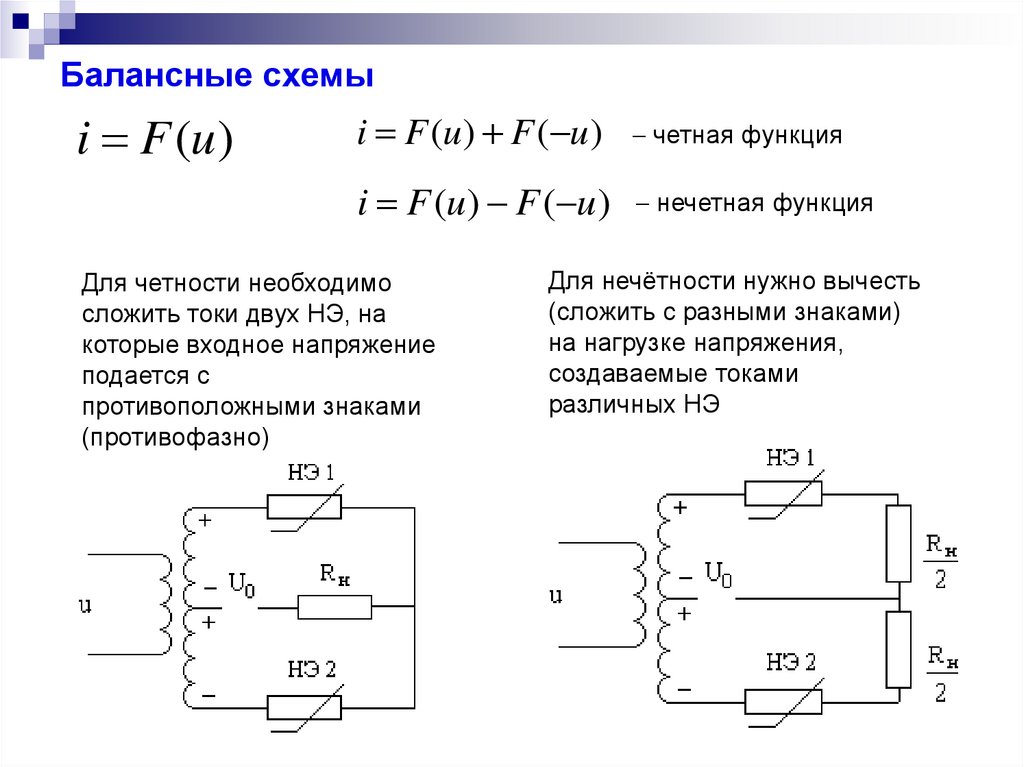
12. Балансные схемы

i F (u)
i F (u) F ( u)
четная функция
i F (u) F ( u) нечетная функция
Для четности необходимо
сложить токи двух НЭ, на
которые входное напряжение
подается с
противоположными знаками
(противофазно)
Для нечётности нужно вычесть
(сложить с разными знаками)
на нагрузке напряжения,
создаваемые токами
различных НЭ
12

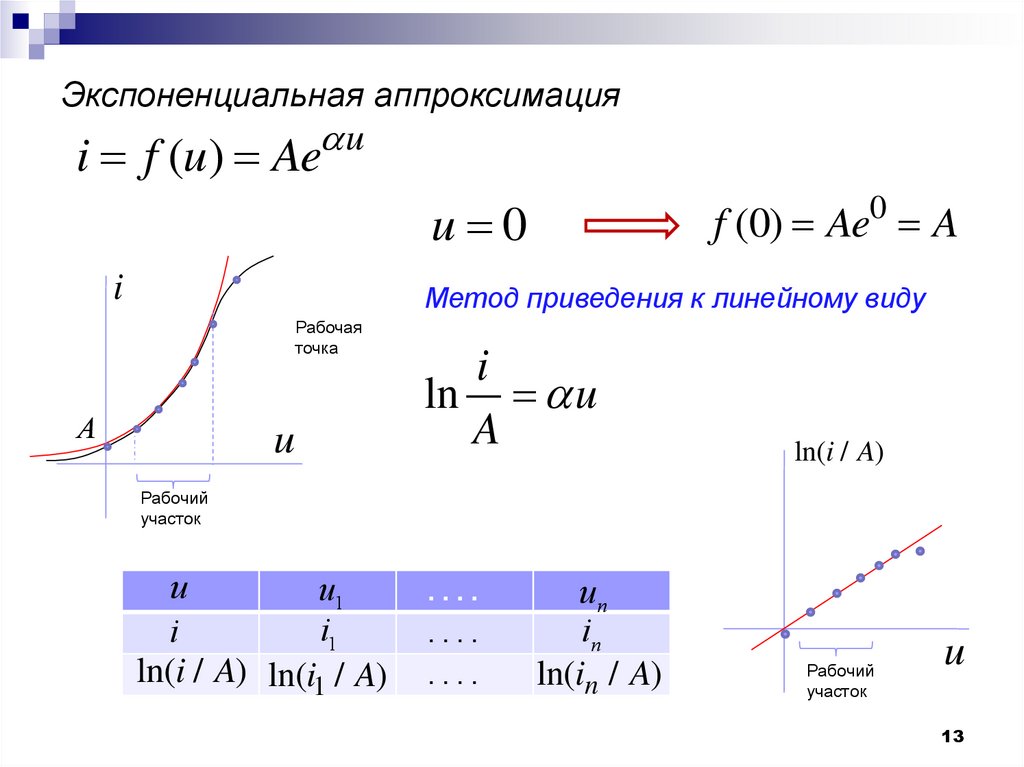
13. Экспоненциальная аппроксимация

u
i f (u) Ae
u 0
i
f (0) Ae0 A
Метод приведения к линейному виду
Рабочая
точка
A
u
i
ln u
A
ln(i / A)
Рабочий
участок
u
u1
i1
i
ln(i / A) ln(i1 / A)
....
....
....
un
in
ln(in / A)
Рабочий
участок
u
13

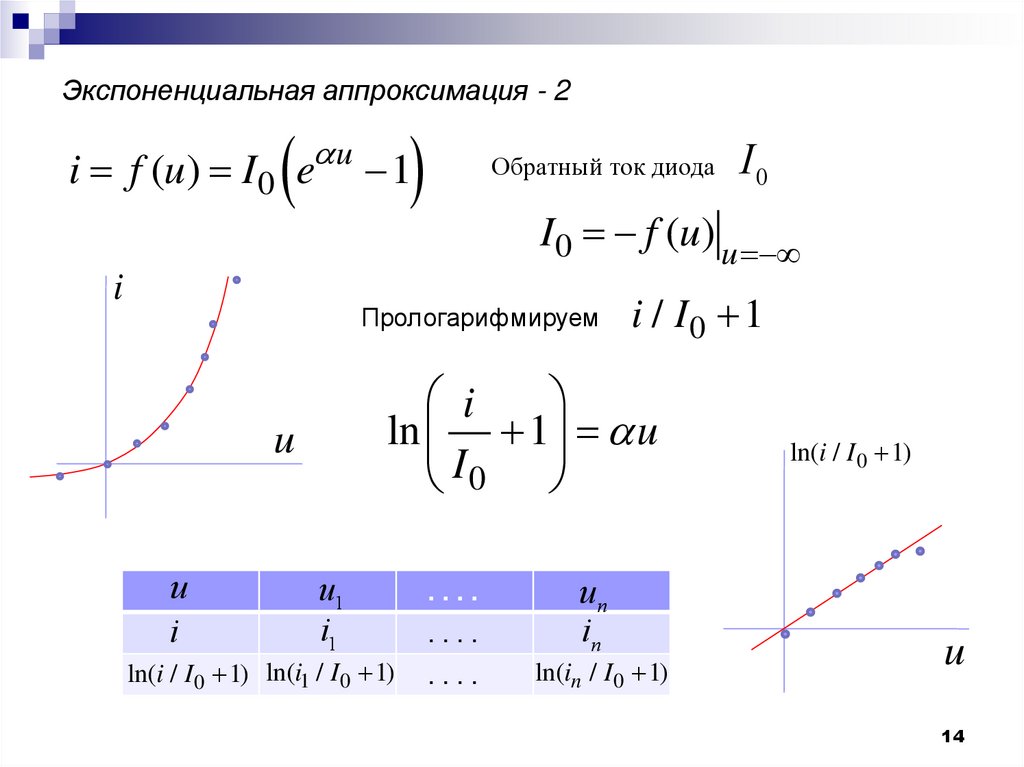
14. Экспоненциальная аппроксимация - 2

i f (u) I0 e u 1
i
Обратный ток диода
I0 f (u) u
Прологарифмируем
u
i
i / I0 1
i
ln 1 u
I0
u
u1
i1
ln(i / I 0 1) ln(i1 / I 0 1)
I0
....
....
....
un
in
ln(in / I 0 1)
ln(i / I 0 1)
u
14

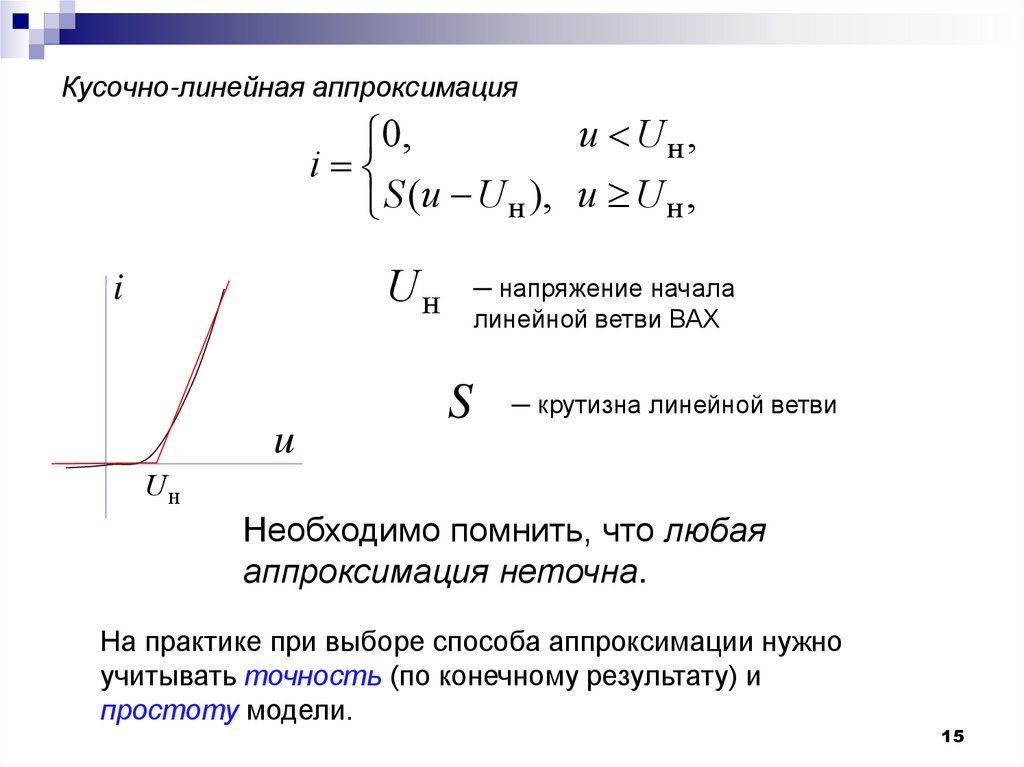
15. Кусочно-линейная аппроксимация

u Uн ,
0,
i
S (u U н ), u U н ,
U н ─ напряжение начала
i
линейной ветви ВАХ
u
S
─ крутизна линейной ветви
Uн
Необходимо помнить, что любая
аппроксимация неточна.
На практике при выборе способа аппроксимации нужно
учитывать точность (по конечному результату) и
простоту модели.
15

16. Воздействие гармонического колебания на нелинейный элемент

i a0 a1(u U0 ) a2 (u U0 )2... aN (u U0 ) N
u (t ) U 0 U m cos( 0t )
U 0 напряжение смещения для выбора р.т.
a1U m cos( 0t )
2 1 1
2
2
a2U m cos ( 0t ) a2U m cos 2( 0t )
2
3
3
a3U m cos ( 0t )
.....
2
кратные гармоники
n 0
n 0,1,2,..., N
16

17.

u (t ) U 0 U m cos( 0t )
i (t ) I 0 I1 cos( 0t 1) I 2 cos(2 0t 2 ) ...
... I N cos( N 0t N )
1
2 3
I 0 a0 a2U m a4U m4 ...
2
8
3
5
3
5
I1 a1U m a3U m a5U m
...
4
8
1
2 1
I 2 a2U m a4U m4 ...
2
8
1
5
3
5
I3 a3U m a5U m
...
4
16
17

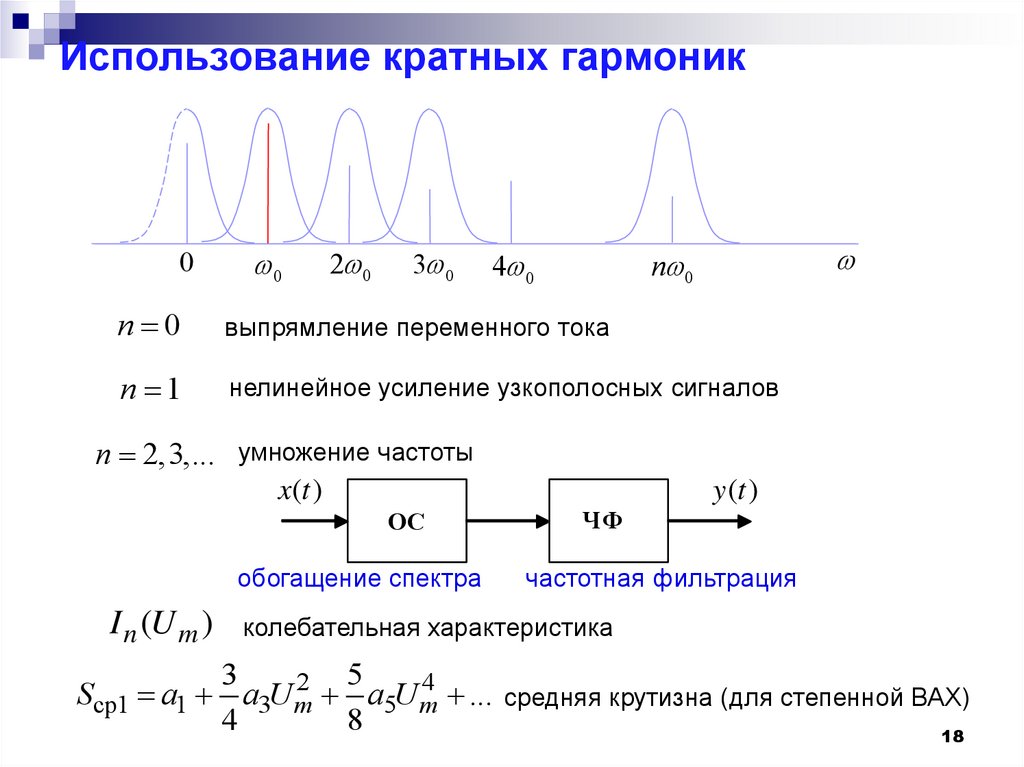
18. Использование кратных гармоник

0
0
2 0
3 0
n 0
4 0
n 0
выпрямление переменного тока
n 1
нелинейное усиление узкополосных сигналов
n 2,3,... умножение частоты
x(t )
ОС
обогащение спектра
I n (U m )
y (t )
ЧФ
частотная фильтрация
колебательная характеристика
3
5
Sср1 a1 a3U m2 a5U m4 ... средняя крутизна (для степенной ВАХ)
4
8
18

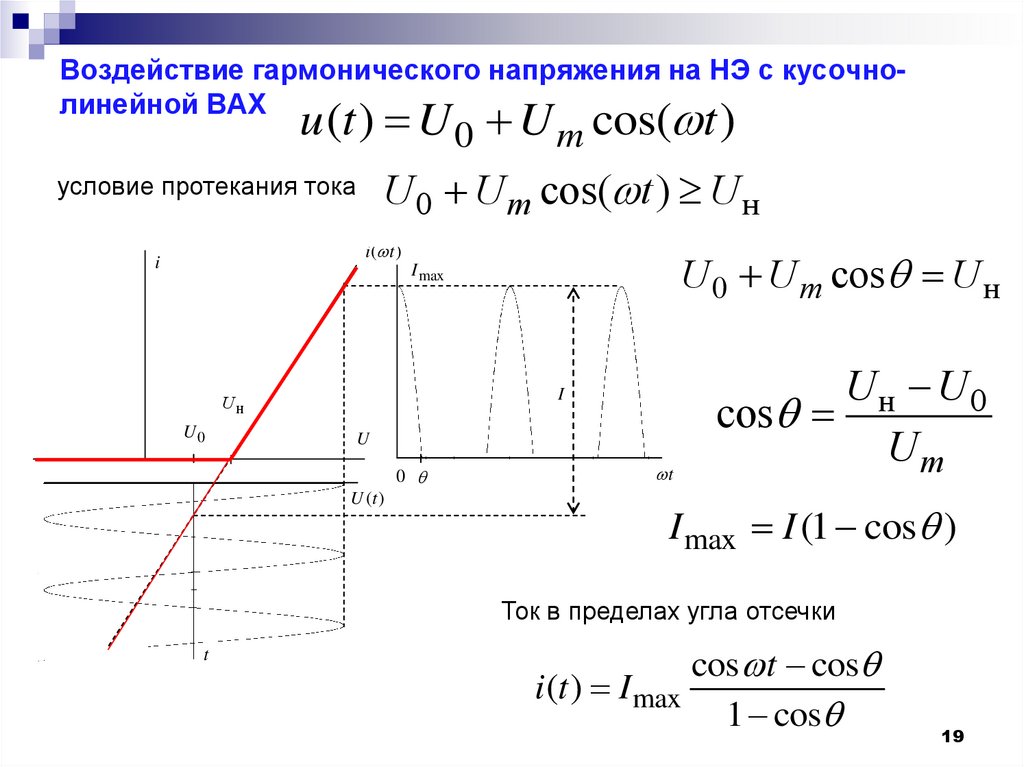
19. Воздействие гармонического напряжения на НЭ с кусочно-линейной ВАХ

Воздействие гармонического напряжения на НЭ с кусочнолинейной ВАХ
u (t ) U 0 U m cos( t )
условие протекания тока U U cos( t ) U
0
m
н
i ( t )
i
U 0 U m cos U н
I max
I
Uн
U0
U
0
U (t )
t
Uн U0
cos
Um
I max I (1 cos )
Ток в пределах угла отсечки
t
cos t cos
i (t ) I max
1 cos
19

20.

cos t cos
i (t ) I max
1 cos
разлагаем в ряд Фурье
i (t ) I 0 I1 cos t I 2 cos 2 t I 3 cos3 t ...
Коэффициенты ряда
I0
1
cos t cos
I
d t I max 0 ( );
max
2
1 cos
0 ( )
sin cos
(1 cos )
cos t cos
I1 I max
cos t d t I max 1( ); ( ) sin cos
1
1 cos
(1 cos )
1
In
1
I max
cos t cos
cos n t d t I max n ( );
1 cos
n ( )
2 sin n cos n cos n sin
n(n2 1)(1 cos )
20

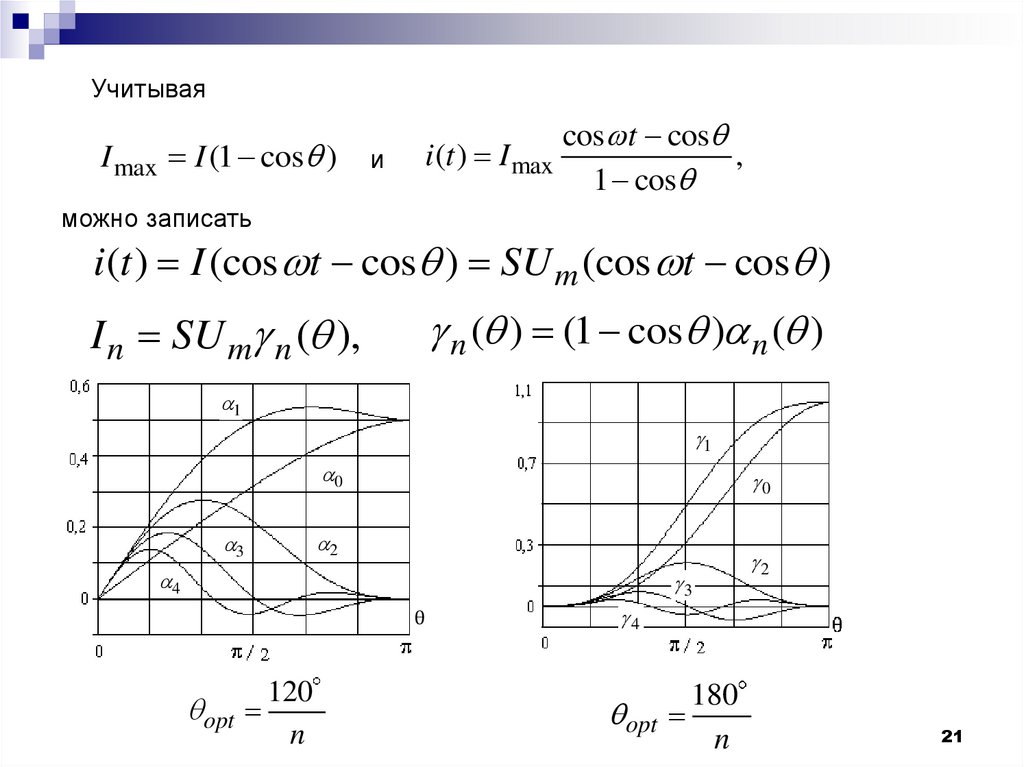
21.

Учитывая
I max I (1 cos )
cos t cos
i(t ) I max
,
1 cos
и
можно записать
i (t ) I (cos t cos ) SU m (cos t cos )
n ( ) (1 cos ) n ( )
I n SU m n ( ),
1
1
0
0
2
3
4
3
θ
opt
120
n
2
4
180
opt
n
21

22. Бигармоническое воздействие на НЭ

u (t ) U 0 U m1 cos( 1t 1) U m 2 cos( 2t 2 )
i a0 a1(u U0 ) a2 (u U0 ) ... aN (u U0 )
2
N
При возведении суммы гармонических составляющих в целые степени
будут получаться произведения согласно формуле бинома Ньютона
k
( a b)
k
m 0
Ckma k mb m
m k
Ck
m
k!
m!(k m)!
в спектре тока будут присутствовать комбинационные частоты вида
n1 1 n2 2
где порядок комбинационной частоты
n1 n2 N
22

23.

Например, если полином имеет степень 2, в спектре тока будут частоты
0, 1 , 2 , 1 2 , 1 2 , 2 1 , 2 2
Если полином имеет степень 3, в спектре тока будут частоты
0, 1 , 2 , 1 2 , 1 2 , 2 1 , 2 2 ,
1 2 2 , 2 1 2 , 1 2 2 , 2 1 2 ,
3 1 ,3 2
0 1
2
2 2
3 2
Нужно иметь в виду, что составляющие имеют различные амплитуды
23

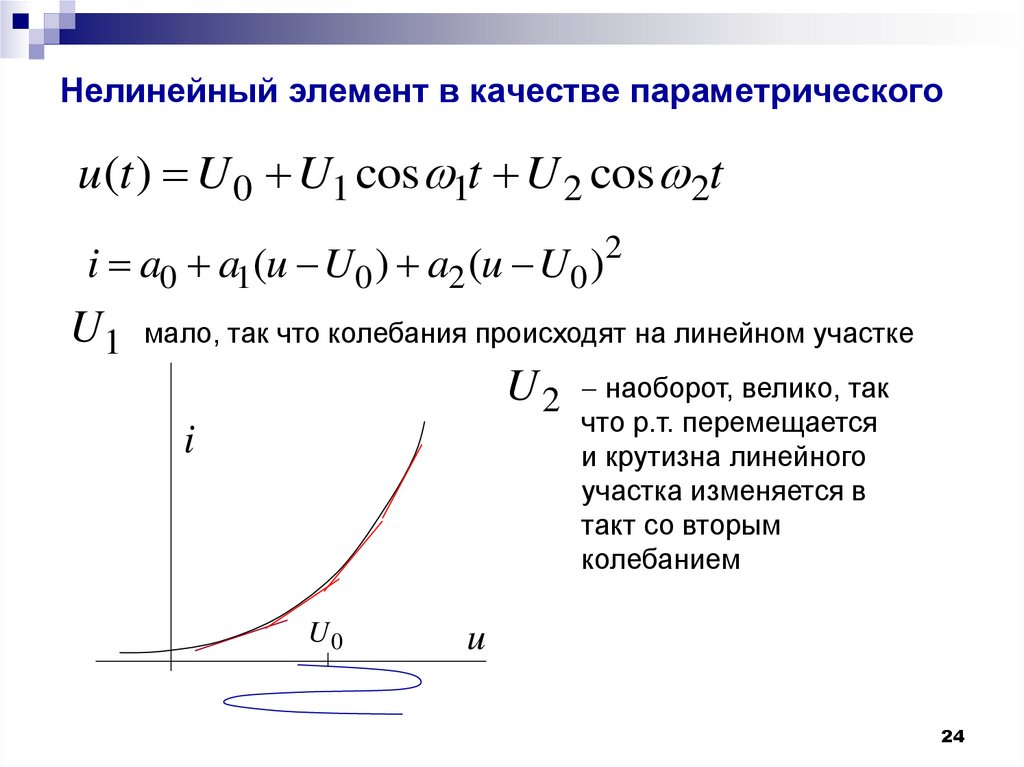
24. Нелинейный элемент в качестве параметрического

u (t ) U 0 U1 cos 1t U 2 cos 2t
i a0 a1(u U0 ) a2 (u U0 )2
U1 мало, так что колебания происходят на линейном участке
U 2 наоборот, велико, так
что р.т. перемещается
и крутизна линейного
участка изменяется в
такт со вторым
колебанием
i
U0
u
24

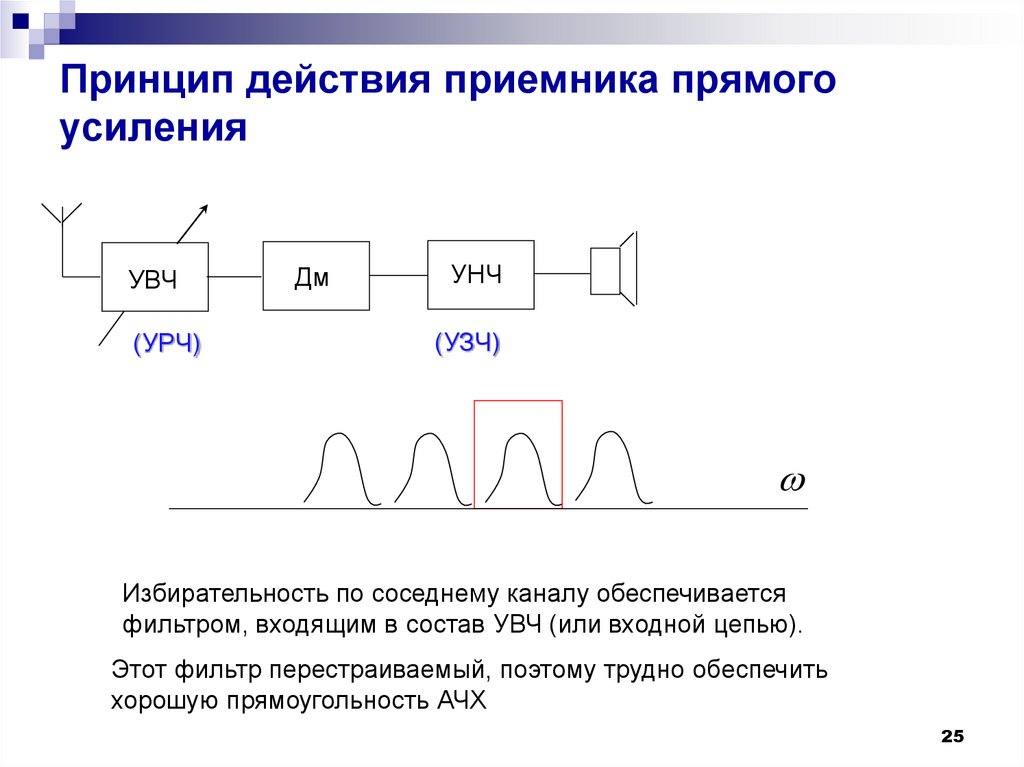
25. Принцип действия приемника прямого усиления

УВЧ
(УРЧ)
Дм
УНЧ
(УЗЧ)
Избирательность по соседнему каналу обеспечивается
фильтром, входящим в состав УВЧ (или входной цепью).
Этот фильтр перестраиваемый, поэтому трудно обеспечить
хорошую прямоугольность АЧХ
25

26. Принцип действия супергетеродинного приемника

Узкополосный ВЧ-сигнал слабый
x(t ) A(t )cos 0t (t ) A(t )cos (t )
Крутизна ПЧ (См) изменяется по закону
S (t ) S0 Sm cos гt
i(t ) A(t )cos 0t (t ) S0 Sm cos гt
УВЧ
ПЧ
УПЧ
Дм
УНЧ
Гет
г пр
26

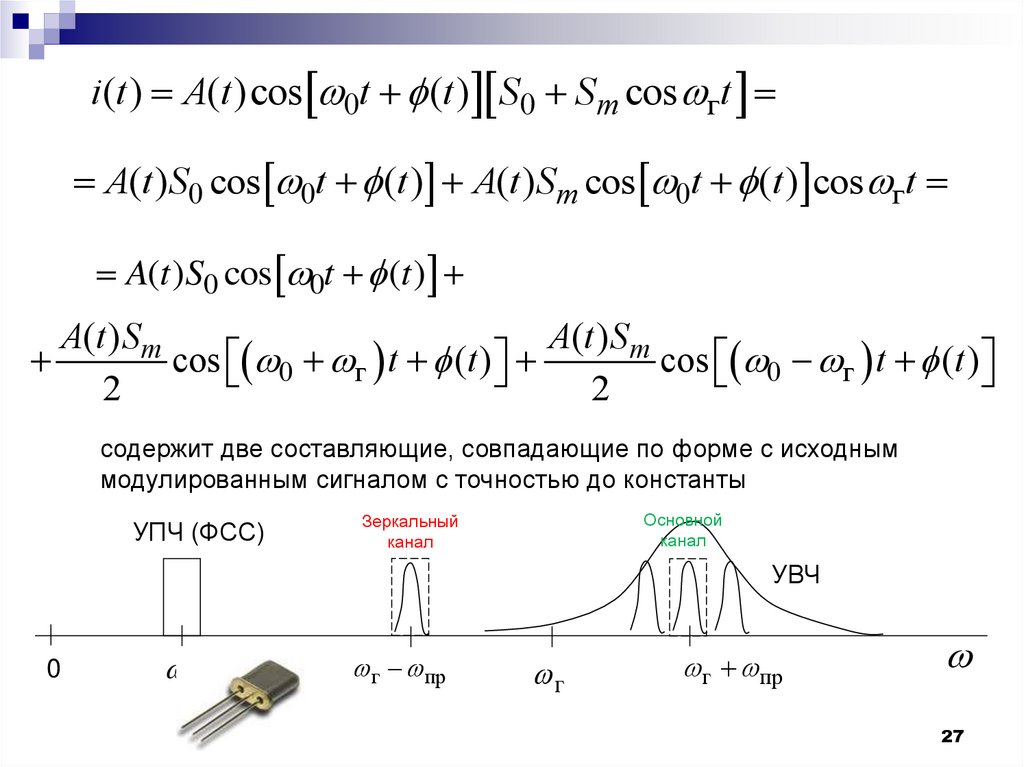
27.

i(t ) A(t )cos 0t (t ) S0 Sm cos гt
A(t )S0 cos 0t (t ) A(t )Sm cos 0t (t ) cos гt
A(t )S0 cos 0t (t )
A(t ) S m
A(t ) S m
cos 0 г t (t )
cos 0 г t (t )
2
2
содержит две составляющие, совпадающие по форме с исходным
модулированным сигналом с точностью до константы
УПЧ (ФСС)
Основной
канал
Зеркальный
канал
УВЧ
0
пр
г пр
г
г пр
27