Анализ прохождения сигналов через нелинейные цепи. Тема 8

1. ТЕМА 8 АНАЛИЗ ПРОХОЖДЕНИЯ СИГНАЛОВ ЧЕРЕЗ НЕЛИНЕЙНЫЕ ЦЕПИ

2. СВОЙСТВА И ХАРАКТЕРИСТИКИ ЭЛЕМЕНТОВ НЕЛИНЕЙНЫХ ЦЕПЕЙ

Параметры элементов нелинейных цепей (НЦ) зависят от
входного воздействия и происходящие в них процессы
описываются нелинейными дифференциальными уравнениями.
Нелинейные элементы (НЭ) НЦ характеризуются:
резистор – вольт-амперной характеристикой (ВАХ) i = f(U) =
= U / R(U);
конденсатор – вольт-кулонной характеристикой(ВКХ) q = f(U) =
= C(U) U;
индуктивность – ампер-веберной характеристикой (АВХ) Ф = f(i) =
= L(i) i.
Для НЦ её сопротивления постоянному току
и переменному току
dU
U
R~ Rдиф
dI U 0
I
U0
R
I0
U 0 U 0
как правило, отличаются.
(U0 и I0 – напряжение и ток в рабочей точке)

3. СВОЙСТВА И ХАРАКТЕРИСТИКИ ЭЛЕМЕНТОВ НЕЛИНЕЙНЫХ ЦЕПЕЙ

i
2
I2
I3
3
1
I1
I
0
U
U1
U
U2
U3 u
U
В
точке
1
сопротивление
постоянному
току
R==U1/I1,
сопротивление переменному току R~= U/ I>0;
В
точке
2
сопротивление
постоянному
току
R==U2/I2,
сопротивление переменному току R~= U/ I=0;
В
точке
3
сопротивление
постоянному
току
R==U3/I3,
сопротивление переменному току R~= U/ I<0.
Если характеристика НЦ снимается на постоянном токе, она
называется
статической,
а
если
на
переменном
–
дифференциальной (амплитудной).
При относительно “малой” амплитуде входного сигнала, не
выходящей за пределы линейных участков характеристик НЭ, НЦ
могут рассматриваться как линейные и исследоваться с
помощью линейных методов.

4. АППРОКСИМАЦИЯ ХАРАКТЕРИСТИК НЦ

Характеристики элементов НЦ, как правило, получают
экспериментальным путём в виде таблиц или графиков. Для
аналитических расчётов требуется процедура их представления в
виде формул, которая называется аппроксимацией. Она
используется также для упрощения сложных исходных формул.
Процедура аппроксимации разбивается на два этапа:
1 – выбор класса аппроксимирующей функции;
2 – определение коэффициентов аппроксимирующей функции.
На
практике
используются
следующие
классы
аппроксимирующих функций:
1 – кусочно-линейные функции вида y(x) = a0 + a1x;
2 – степенной полином y(x) = a0 + a1x + a2x2 +…+ anxn;
3 – экспоненциальный полином
y ( x) A1e a1x A2 e a2 x ... An e an x
4 – тригонометрические функции
y( x) A1cos( a1 x) A2cos(a2 x) ... An cos(an x)
5 – различные специальные функции (Бесселя и др.).

5. АППРОКСИМАЦИЯ ХАРАКТЕРИСТИК НЦ

На выбор класса аппроксимирующих функций влияет:
1 – режим работы НЭ. Различают режим “слабых” и “сильных”
сигналов;
2 – желаемая простота расчётной формулы;
3 – требуемая точность аппроксимации.
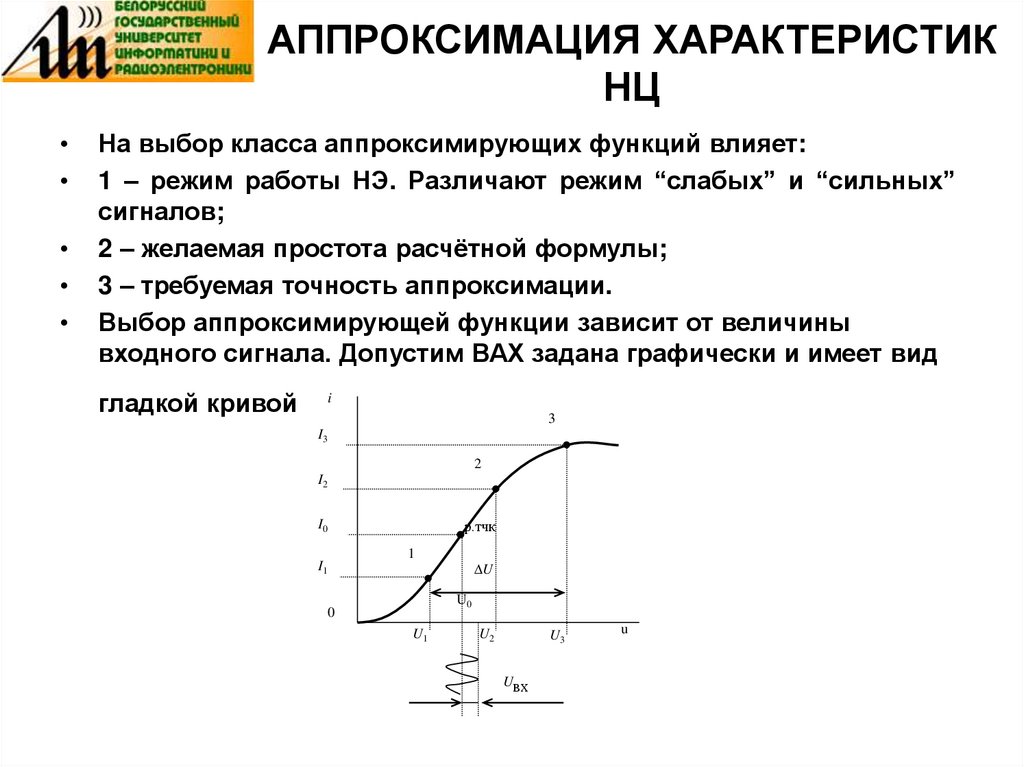
Выбор аппроксимирующей функции зависит от величины
входного сигнала. Допустим ВАХ задана графически и имеет вид
гладкой кривой
i
3
I3
2
I2
I0
р.тчк
1
I1
U
U0
0
U1
U2
U3
Uвх
u

6. АППРОКСИМАЦИЯ ХАРАКТЕРИСТИК НЦ

Если Uвх значительно
меньше
протяжённости
участка
аппроксимации U, такой режим называется “слабым” сигналом.
Постоянное напряжение U0 (напряжение смещения) задаёт
рабочую точку по постоянному току I0 .
В этом режиме чаще всего используется аппроксимация
степенным или экспоненциальным полиномом.
Если Uвх сравнимо или больше протяжённости участка
аппроксимации U, такой режим называется “сильным”
сигналом.
В этом режиме чаще всего используется аппроксимация
i
отрезками линий (кусочно-линейная).
I
н
3
U
2
I0
р.тчк
1
0
EЗ
U0
Uн
u
Uвх

7. АНАЛИЗ НЦ НА ПОСТОЯННОМ НАПРЯЖЕНИИ (ТОКЕ)

Анализ обычно проводится графически и реже аналитически. В
итоге преобразования любую сложную НЦ можно представить в
i
U
виде:
1
R
E/R
1
I = f(u2)
i
E
U2
ЛЦ эквивалентного
источника двухполюсника.
R(u)
р.тчк
Iр
нагрузочная
прямая
1
НЦ двухполюсника.
0
U2=Uр
а
U1
б
E
u
Графически решение осуществляется построением ВАХ I = f(U2) и
ВАХ (нагрузочной прямой) эквивалентного источника по двум
точкам: 1) U = E при i = 0; 2) U = 0 при i = E / R. Так как напряжение
на зажимах 1-1 общее для двух двухполюсников, то точка
пересечения их ВАХ даёт искомые значения рабочего напряжения
U1, U2 и тока Iр . Когда нелинейный двухполюсник составной, то
после определения его рабочей точки приходится определять
рабочие точки составляющих его элементов.

8. ПРОХОЖДЕНИЕ СИГНАЛА ЧЕРЕЗ БЕЗЫНЕРЦИОННУЮ НЦ

Пусть на вход НЦ с ВАХ i = f(u) воздействует сигнал U(t), спектр
которого Su(j ) известен, требуется определить спектр Si(j ) тока i(t).
На практике используется упрощённый спектральный метод. п
Полагают, что на вход НЦ воздействуют сигналы в виде:
– простейшего гармонического U(t) = Ucos( t)
– или сложного в виде суммы гармонических колебаний
U(t) = U1cos( 1t) + U2cos( 2t) +…+ Uncos( nt).
Пусть ВАХ задана степенным полиномом i(u) = a0 + a1u + a2u2 +…+ anun
и входной сигнал U(t) = U0 + Umcos( 1t), спектр которого состоит из
постоянной и гармонической составляющих.
U( )
I( )
Um
Im1
I0
U0
Im2
Im3
Imn
0
1
а
0
1 2 1
n 1
3 1
б

9. ПРОХОЖДЕНИЕ СИГНАЛА ЧЕРЕЗ БЕЗЫНЕРЦИОННУЮ НЦ

Подставим в выражение ВАХ в качестве напряжения значение U(t):
i (t ) a0 a1U 0 a1U m cos( 1t ) a2U 02 2a2U 0U m cos( 1t )
a2U m2 cos 2 ( 1t ) ... anU mn cos n ( 1t )
Для разложения в спектр тока НЦ применим тригонометрические
формулы кратных дуг (cosn(x) и sinn(x)).
cos 2 ( 1t )
1 1
cos( 2 1t )
2 2
cos 3 ( 1t )
3
1
cos( 1t ) cos(3 1t )
4
4
i(t ) I 0 I m1cos( 1t ) I m 2cos(2 1t ) I m3cos(3 1t ) ...
1
3
I 0 a0 a1U 0 a2U 02 a2U m2 a3U 03 a3U 0U m2 ...
2
2
3
I m1 a1U m 2a2U 0U m 3a3U 02U m a3U m3 ...
4
1
3
1
I m 2 a2U m2 a3U 0U m2 ...
I m 3 a3U m3 ...
2
2
4

10. ПРОХОЖДЕНИЕ СИГНАЛА ЧЕРЕЗ БЕЗЫНЕРЦИОННУЮ НЦ

U( )
I( )
Um
Im1
I0
U0
Im2
Im3
Imn
0
1
а
0
1 2 1
n 1
3 1
б
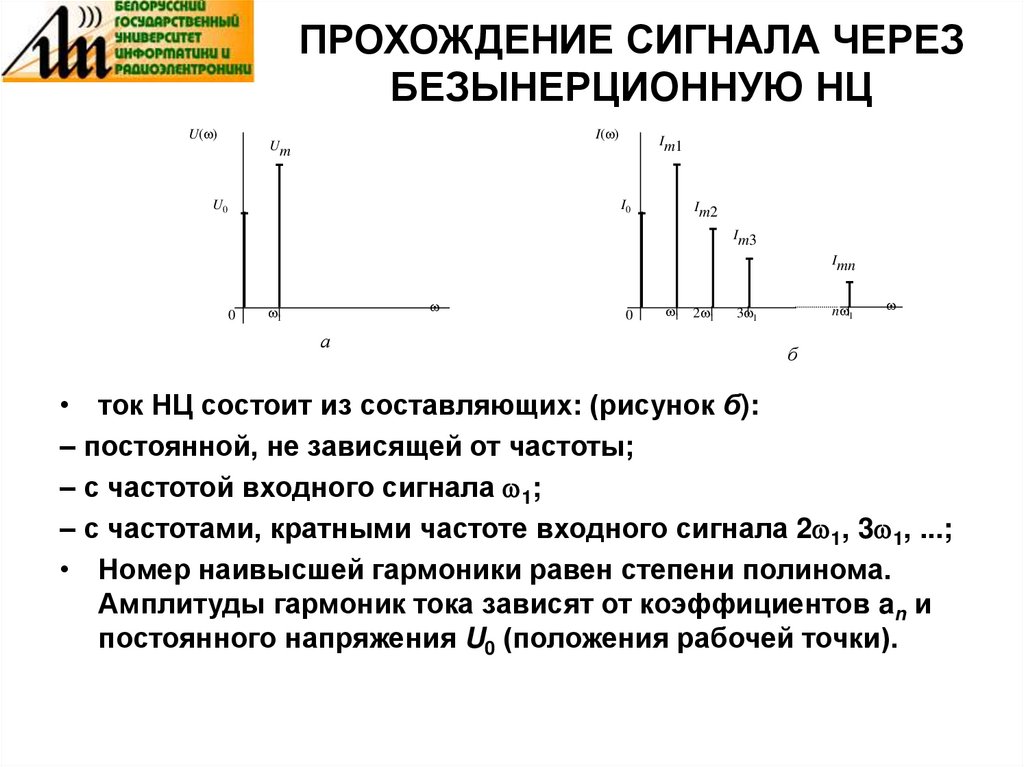
• ток НЦ состоит из составляющих: (рисунок б):
– постоянной, не зависящей от частоты;
– с частотой входного сигнала 1;
– с частотами, кратными частоте входного сигнала 2 1, 3 1, ...;
• Номер наивысшей гармоники равен степени полинома.
Амплитуды гармоник тока зависят от коэффициентов an и
постоянного напряжения U0 (положения рабочей точки).

11. ПРОХОЖДЕНИЕ СИГНАЛА ЧЕРЕЗ БЕЗЫНЕРЦИОННУЮ НЦ

Пусть задан входной сигнал U(t) = Um1cos( 1t) + Um2cos( 2t).
Его спектр состоит из двух гармонических составляющих.
ВАХ НЦ - в виде степенного полинома i(u) = a0 + a1u + a2u2 + … + anun.
используя
тригонометрические
формулы
кратных
дуг
и
произведений синусов и косинусов, разложим выражение тока в
спектр:
1
i (t ) a0 a1U m1cos( 1t ) a1U m 2 cos( 2t ) a2U m21
2
1
1
1
2
2
a2U m1cos( 2 1t ) a2U m 2 a2U m2 2 cos( 2 2t )
2
2
2
a2U m1U m 2 cos[( 1 2 )t ] a2U m1U m 2 cos[( 1 2 )t ]
3
3
a3U m3 1cos( 1t ) a3U m3 2 cos( 2t )
4
4
3
3
2
a3U m1U m 2 cos[( 2 1 2 )t ] a3U m1U m2 2 cos[( 2 2 1 )t ]
4
4
1
1
a3U m3 1cos(3 1t ) a3U m3 2 cos(3 2t ) ...
3
3

12. ПРОХОЖДЕНИЕ СИГНАЛА ЧЕРЕЗ БЕЗЫНЕРЦИОННУЮ НЦ

Ток НЦ состоит из составляющих (рисунок б):
– постоянной, не зависящей от частоты;
– с частотами входного сигнала 1, 2;
– с частотами, кратными частоте входного сигнала 2 1, 2 2, 3 1, 3 2 и т.д.;
– с комбинационными частотами 1 2, 2 1 2, 2 2 1, ….
Таким образом, спектр тока будет содержать составляющие с частотами
k 1 m 2
где ±k и ±m = 0, 1, 2, …, причём
Um
U( )
комбинационного
колебания.
I( )
k m n
Это число = N: порядок
.
1
Im1
Um2
0
1
2
I0
0
1 – 2
а
Im2
Imр
1
2
Imс
2 1
1 + 2
2 2
k 1
k 1 – m 2
б
m 2
k 1 + m 2

13. РЕЖИМ СИЛЬНОГО СИГНАЛА

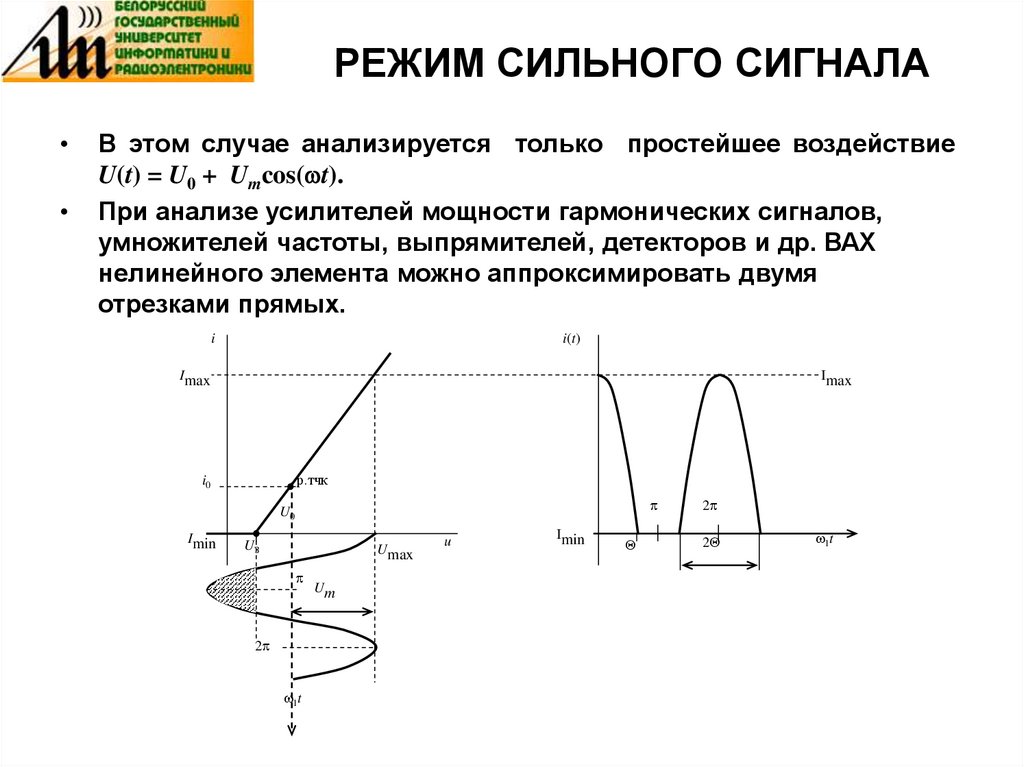
В этом случае анализируется только простейшее воздействие
U(t) = U0 + Umcos( t).
При анализе усилителей мощности гармонических сигналов,
умножителей частоты, выпрямителей, детекторов и др. ВАХ
нелинейного элемента можно аппроксимировать двумя
отрезками прямых.
i
i(t)
Imax
Imax
р.тчк
i0
U0
Imin
UЗ
Umax
2
1t
Um
u
Imin
2
2
1t

14. РЕЖИМ СИЛЬНОГО СИГНАЛА

Импульсы тока можно задать двумя параметрами: амплитудой
импульса Imax = S (Um + U0 – UЗ) и углом отсечки тока . (S -крутизна
участка ВАХ). Угол равен фазовому углу 1t (части периода), в
пределах которого протекает ток через НЭ, изменяясь от Imax до
Imin . Угол отсечки = 1t может принимать значения от 0 до
1800.
При 1t = ток i(t) = 0 и тогда S (U0 + Umcos( ) – UЗ) = 0, отсюда
получим
UЗ U0
cos( )
Um
при этом
Для угла
Imax = SUm[1 – cos( )].
1t получим
i(t ) I max
cos( 1t ) cos( )
1 cos( )
Спектр рассматриваемого сигнала весьма богат гармониками. Их
амплитуды можно определить, разложив выражение для тока в
ряд Фурье. Коэффициенты для гармоник (коэффициенты Берга)
n( ) обычно представляются в виде графиков.

15. РЕЖИМ СИЛЬНОГО СИГНАЛА

n( )
1( )/ 0( )
0,6
1/ 0
0,5
2
1
0,4
0
0,3
1
0,2
2
0,1
3
0
– 0,1
0
30
40
60
90
120
150
180
0
Существует так называемый оптимальный угол, при котором
амплитуда n-й гармоники будет максимальной. Он равен
1200
опт
n
При = 1800 будут только постоянная составляющая и гармоника
основной частоты (первая гармоника), а при = 900 – нечётные
гармоники, начиная с третьей, проходят через нуль, а к.п.д.
усилителя составляет 78,5 %.

16. МЕТОД РАСЧЕТА АМПЛИТУД ГАРМОНИК ПО ИЗВЕСТНОЙ ВАХ

В методе трех и пяти ординат используются формулы,
позволяющие выполнить анализ прохождения гармонического
сигнала через НЦ с известной ВАХ.
i
imax
i1
р.тчк
i0
i2
imin
Um
Umin
0,5Um
U0
0,5Um
u
Umax
С помощью формул трёх ординат можно рассчитать
приближённые значения постоянной составляющей и амплитуд
первой и второй гармоник тока НЦ. Они имеют вид
imax imin i0
I
;
0
4
2
imax imin
;
I1
2
I 2 imax imin i0 .
4
2

17. МЕТОД РАСЧЕТА АМПЛИТУД ГАРМОНИК ПО ИЗВЕСТНОЙ ВАХ

Формулы пяти ординат позволяют находить приближённые
значения постоянной составляющей и амплитуд первой, второй,
третьей и четвёртой гармоник тока НЦ. Они имеют вид
1
I
0 6 [imax imin 2(i1 i2 )];
1
I1 [imax imin (i1 i2 )];
3
1
I 2 (imax imin 2i0 );
4
1
I [i i 2(i i )];
1
2
3 6 max min
1
I
[imax imin 4(i1 i2 ) 6i0 ].
4
12
где imax , imin , i0 , i1 и i2 – токи, соответствующие максимальному и
минимальному значению напряжения входного сигнала,
напряжению постоянной составляющей и значениям, при
которых напряжение входного сигнала равно 0,5Um (Um –
амплитуда сигнала).

18. КОЭФФИЦИЕНТ ГАРМОНИК

Сигнал гармонической формы при прохождении через НЦ
искажается за счёт появления гармоник кратных частот. Эти
искажения (отличие формы выходного сигнала от
гармонической) оцениваются коэффициентом гармоник
(коэффициентом нелинейных искажений) по току или
напряжению:
I 22 1 I 32 1 ... I n2 1
kгI kниI
kниU
U
2
2 1
U
2
3 1
I 1
... U
2
n 1
U 1
100%
100%
U
n 2
U 1
2
n 1
100%
где U 1 и Un 1 – амплитуды напряжения 1-й и n-й гармоники на
выходе НЦ. Он принимает значения в пределах от 0 до .
На практике часто kГ определяют так:
2
(k'г = 0…1)
kг
kг
1 kг
2
kг
U
n 2
n 1
2
U
n 1
n 1

19. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗО-ВАНИЯ СИГНАЛОВ В НЦ

ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ В НЦ
• Пусть имеется некоторая НЦ и нагрузка. Имеются
следующие варианты.
Наименование
преобразования
Входной сигнал
Выходной сигнал
Нагрузка НЦ
(ЛЦ-фильтр)
1 Выпрямление
U(t)=U cos( t)
U= – постоянное на- ФНЧ (RC-фильтр с
пряжение
0 T )
2 Умножение частоты
U(t)=U cos( t)
U(t)=Un cos(n t)
3 Амплитудная модуляция
4 Детектирование
АМ-сигнала
U(t)=U cos( t)+
+U cos( t)
UАМ(t)=U cos( t)+
+0,5mU cos( )t
5 Преобразование
частоты
U(t)=Um1cos( 1t)+
+Um2cos( 2t)
6 Гетеродинирование
U(t)=Um1cos( 1t)+
+Um2cos( 2t), 1 2
ПФ (LC-контур с
0=n и узкой
2 0,7)
ПФ (LC-контур с
UАМ(t)=U cos( t)+
0= и 2 0,7 2 )
+0,5mU cos( )t
ФНЧ (RC-фильтр с
U(t)=U cos( t)
T 0 T , то есть
T T )
U(t)=Umcos( 1 2)t, ПФ (LC-контур с
"+" – вверх, "-"– вниз 0= 1 2 и узкой
2 0,7)
ПФ или ФНЧ (RCU(t)=Umcos( 1- 2)t,
фильтр с 0 T( 1- 2))