Похожие презентации:
§23. Непрерывность функции
1.
§23. Непрерывность функциип.1. Непрерывность функции в точке
Функция y f (x ) называется непрерывной в
точке a,, если существует предел функции в
этой точке и он равен значению функции в
этой точке.
lim f ( x ) f ( a )
x a
2.
lim x ?ax a
lim f ( x ) f ( a ) f lim x
x a
x a
Пример.
x 4
2
lim
x 2
x2 5x 6
lim
x 4
2
x 2 x 2 5 x 6
Самостоятельно: вычислить указанный
предел; привести еще 2 аналогичных примера.
3.
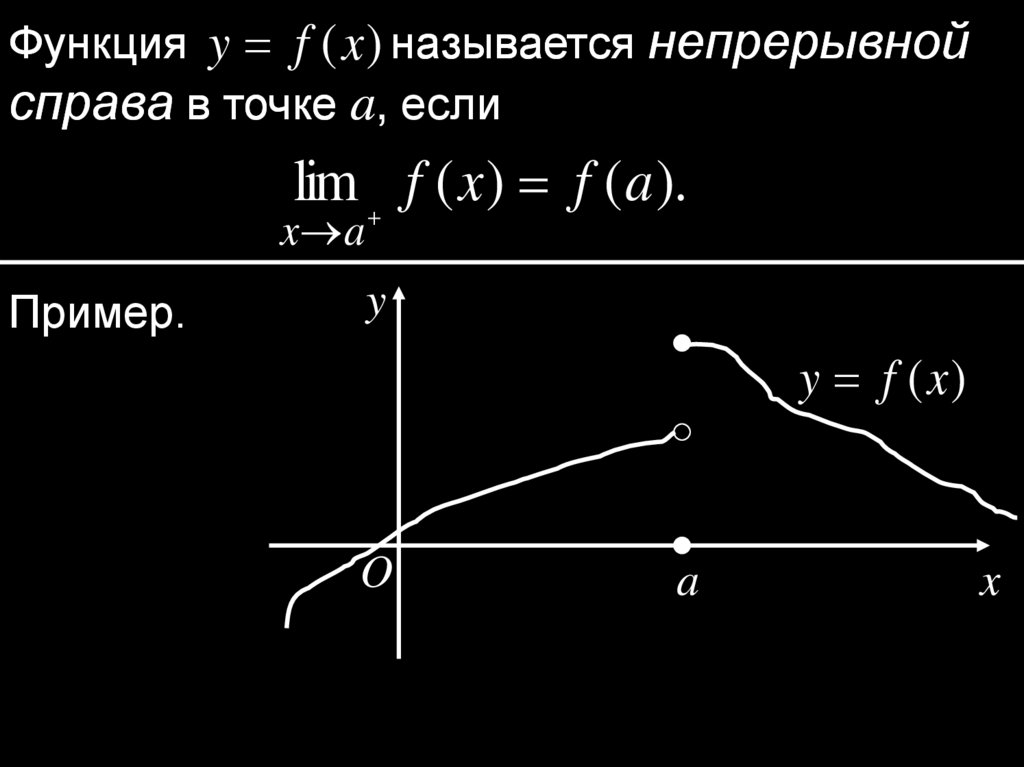
Функция y f (x ) называется непрерывнойсправа в точке a, если
lim f ( x ) f ( a ).
x a
Пример.
y
y f (x )
O
a
x
4.
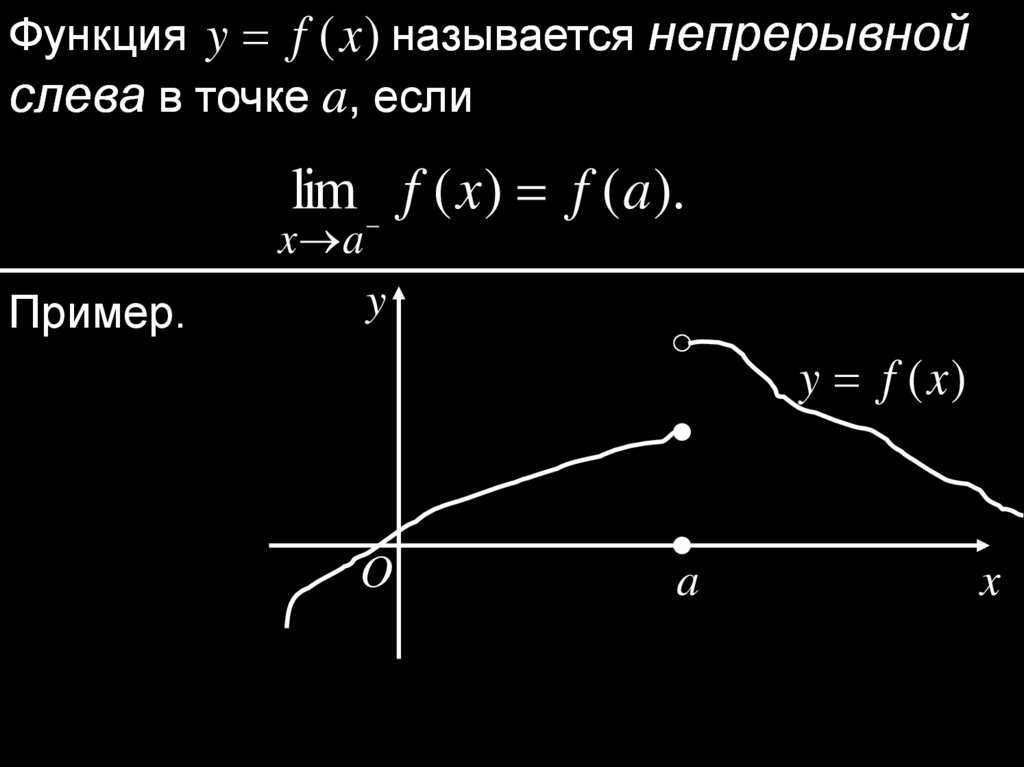
Функция y f (x ) называется непрерывнойслева в точке a, если
lim f ( x ) f ( a ).
x a
Пример.
y
y f (x )
O
a
x
5.
Пример. y [x ]y
2
1
-1 O
lim [ x ] 2
x 2
lim [ x ] 1
x 2
f ( 2) [ 2] 2
1
-1
2
3
x
6.
Теорема 1. Для того, чтобы функция f быланепрерывной в точке a
необходимо и достаточно, чтобы
она была непрерывной в точке a
справа и слева.
7.
lim f ( x ) f ( a ) limx a
x a 0
f ( x) f (a ) 0
x x a
y f ( x ) f ( a )
─ приращение
аргумента
─ приращение
функции
lim y 0
x 0
Функция f является непрерывной в точке а,
если ее приращение в этой точке есть БМФ.
8.
п.2. Основные теоремы онепрерывных в точке функций
Теорема 2. (Алгебраические свойства
непрерывных функций)
Пусть функции f (x ) и g (x ) непрерывны в
точке a.
Тогда, функции
f ( x ) g ( x ), f ( x ) g ( x ), f ( x ) g ( x ),
f ( x)
g (a) 0
g ( x)
также непрерывны в точке a.
9.
Теорема 3. (О непрерывности сложнойфункции)
Пусть функция y f (x ) непрерывна в точке x0 ,
функция z g ( y ) непрерывна в точке y0 .
Тогда, сложная функция
z g ( f ( x ))
непрерывна в точке x0 .
10.
Теорема 4. (О непрерывности обратнойфункции)
Пусть функция f : X Y непрерывна в точке
x0 X .
Тогда, если для функции f существует
обратная функция f 1 : Y X, то она
непрерывна в точке
y0 f ( x0 ).
11.
п.3. Точки разрыва и ихклассификация
Точками разрыва функции f называются те
точки, в которых функция f не является
непрерывной.
Точки разрыва
I род
точки
устранимого
разрыва
II род
точки
конечного
разрыва
12.
Точка x a называется точкой разрыва Iрода функции y f (x ), если в этой точке
существуют конечные (не равные )
односторонние пределы:
lim f ( x ),
x a
lim f ( x ).
x a
13.
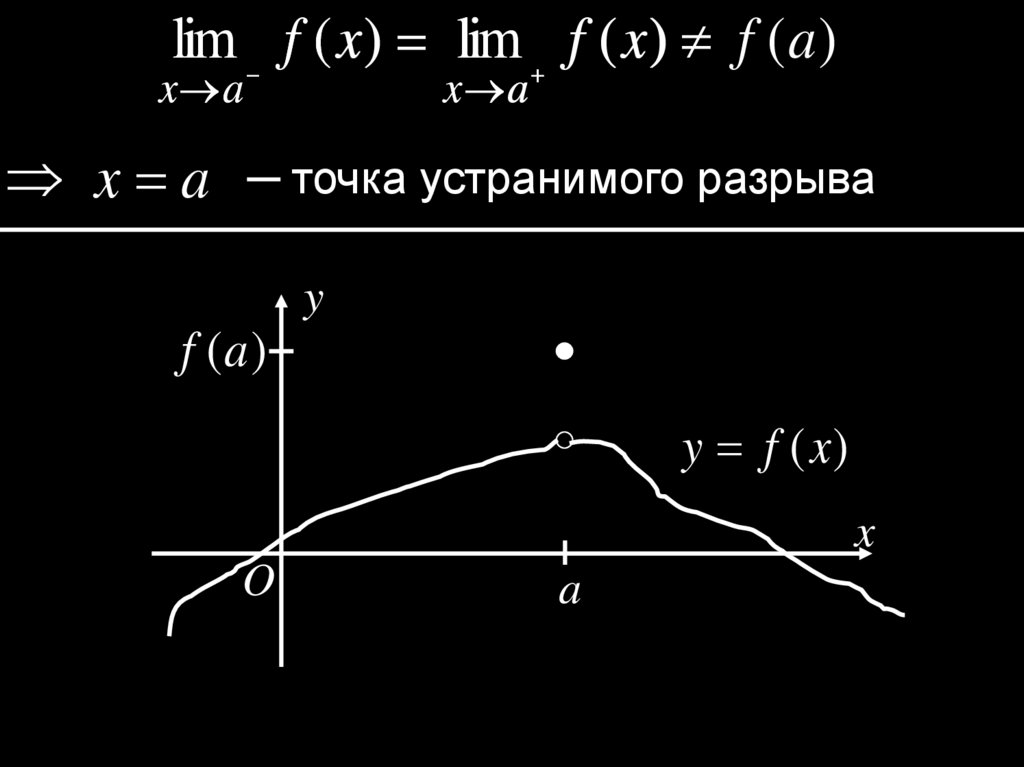
lim f ( x ) lim f ( x ) f ( a )x a
x a
x a ─ точка устранимого разрыва
y
f (a )
y f (x )
x
O
a
14.
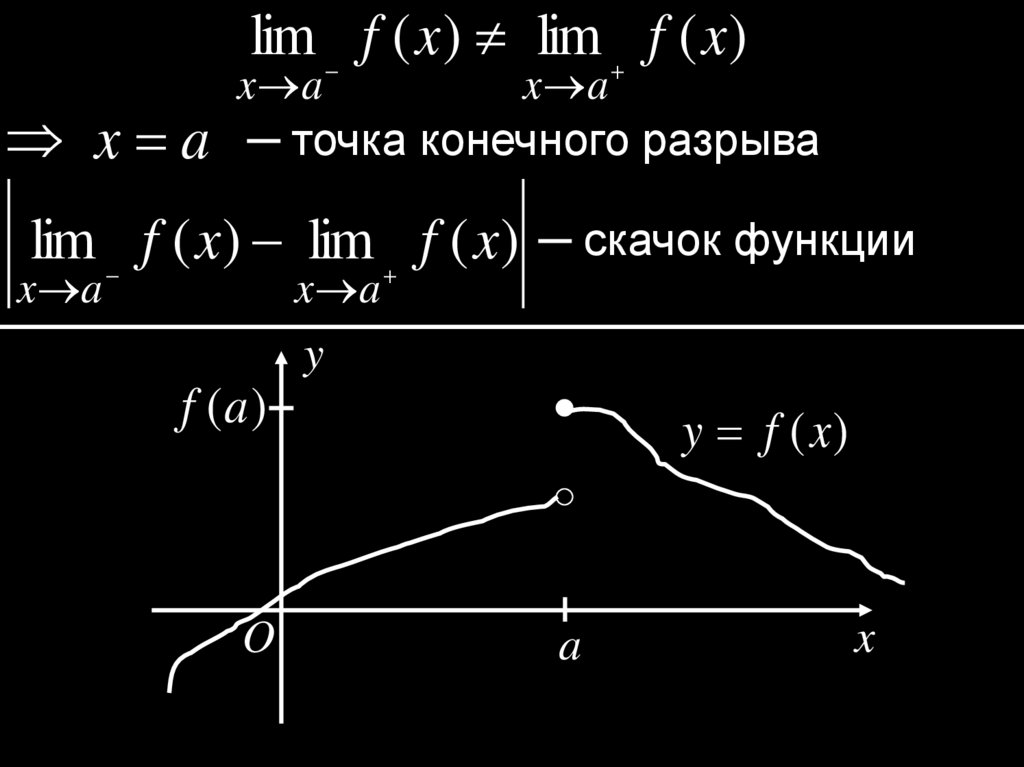
lim f ( x ) lim f ( x )x a
x a
x a ─ точка конечного разрыва
lim f ( x) lim f ( x) ─ скачок функции
x a
x a
y
f (a )
O
y f (x )
a
x
15.
Пример. y [x ]y
2
1
-1 O
lim [ x ] 2
x 2
lim [ x ] 1
x 2
f ( 2) [ 2] 2
1
-1
x 2
2
3
─ точка конечного
разрыва
lim [ x] lim [ x] 1 ─ скачок
x 2
x
x 2
функции
16.
Точка x a называется точкой разрыва IIрода функции y f (x ), если в этой точке
хотя бы один из односторонних пределов не
существует или равен бесконечности.
17.
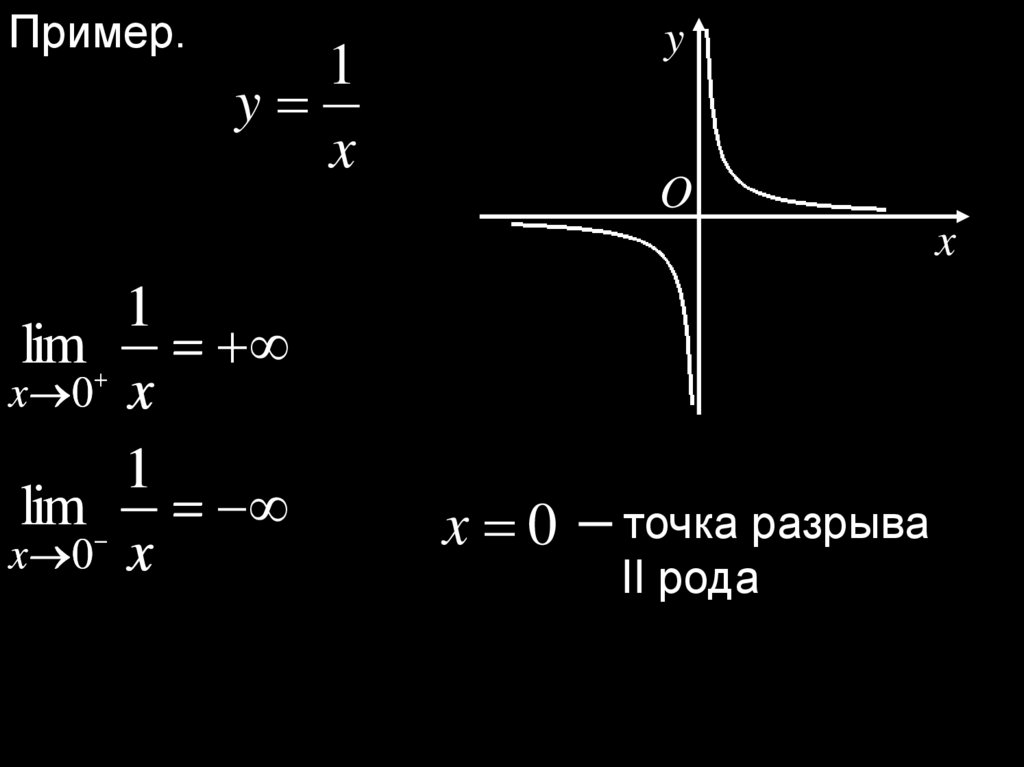
Пример.1
y
x
y
O
x
1
lim
x 0 x
1
lim
x 0 x
x 0 ─ точка разрыва
II рода
18.
п.4. Основные теоремы онепрерывных на отрезке функциях
Функция y f (x ) называется непрерывной
на отрезке [ a; b ], если она непрерывна в
каждой точке интервала ( a; b ), в точке x a
непрерывна справа, а в точке x bнепрерывна
слева.
19.
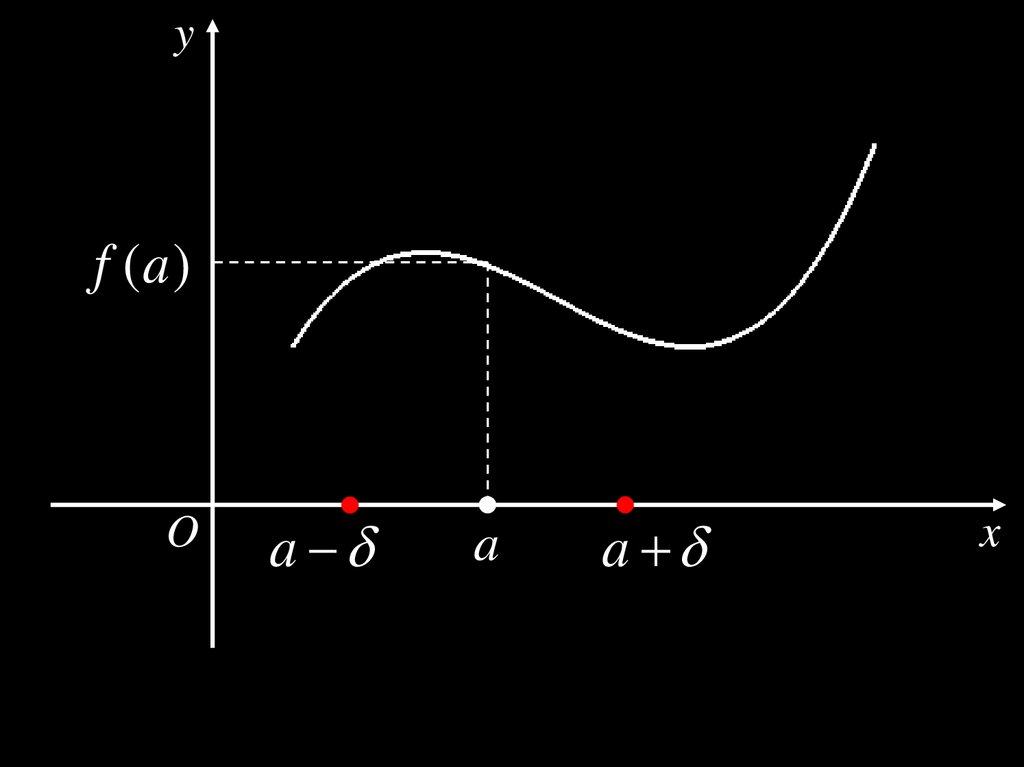
Теорема 5. (Об устойчивости знака)Пусть функция y f (x ) непрерывна в точке a
и f ( a ) 0. Тогда существует -окрестность
точки a такая, что в этой окрестности функция
y f (x ) имеет тот же знак, что и f (a ).
20.
yf (a )
O
a
a
a
x
21.
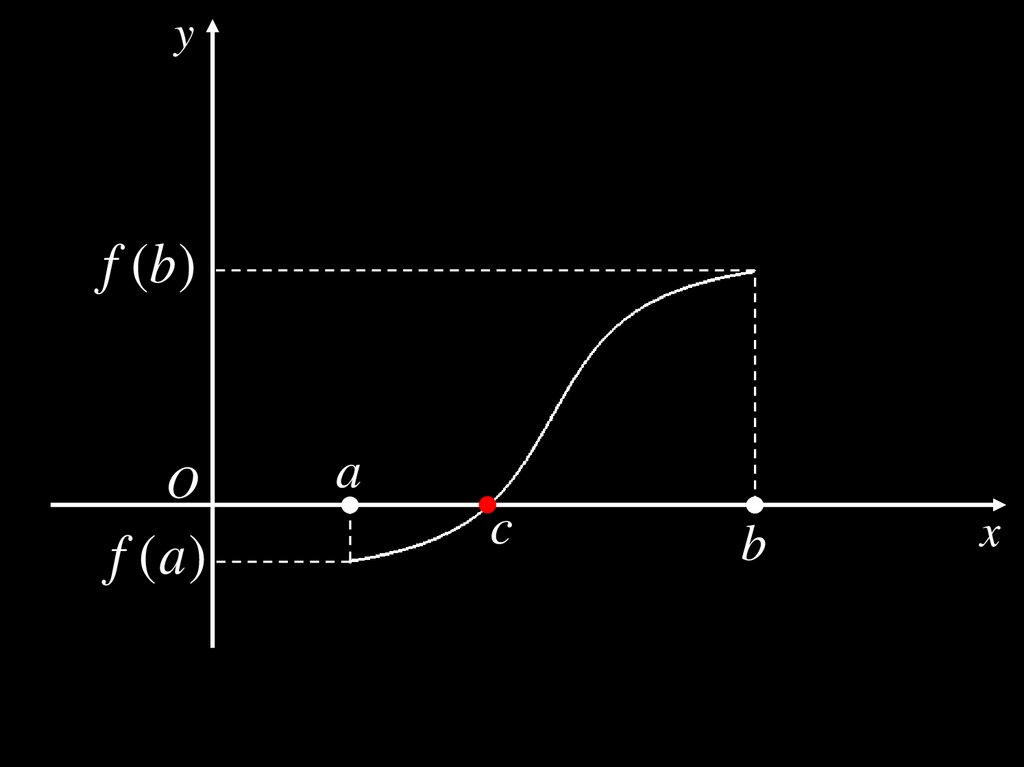
Теорема 6. (Первая теорема Больцано–Коши)Пусть
функция y f (x ) непрерывна на отрезке [ a; b ],
на концах отрезка принимает значения
разных знаков: f ( a ) f (b ) 0.
Тогда
c ( a; b ) :
f (c ) 0.
22.
yf (b )
O
f (a )
a
c
b
x
23.
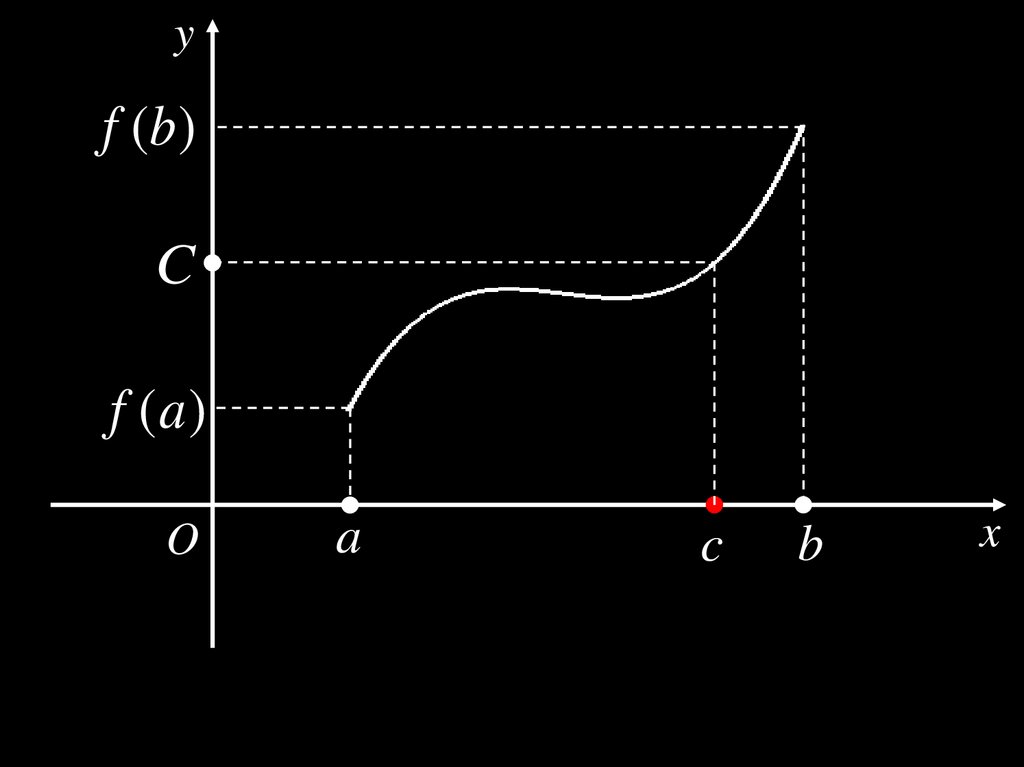
Теорема 7. (Вторая теорема Больцано–Коши)Пусть
функция y f (x ) непрерывна на отрезке [ a; b ],
f ( a ) f (b ),
f ( a ) C f (b ).
Тогда
c ( a; b ) :
f (c ) C .
24.
yf (b )
C
f (a )
O
a
c
b
x
25.
Теорема 8. (Первая теорема Вейерштрасса)Пусть
функция y f (x ) непрерывна на отрезке [ a; b ].
Тогда
она ограничена на этом отрезке.
26.
Теорема 9. (Вторая теорема Вейерштрасса)Пусть
функция y f (x ) непрерывна на отрезке [ a; b ].
Тогда
в некоторых точках этого отрезка она
достигает своего максимума и минимума.
, [ a; b ] :
max f ( x ) f ( )
x [ a ;b ]
min f ( x ) f ( )
x [ a ;b ]


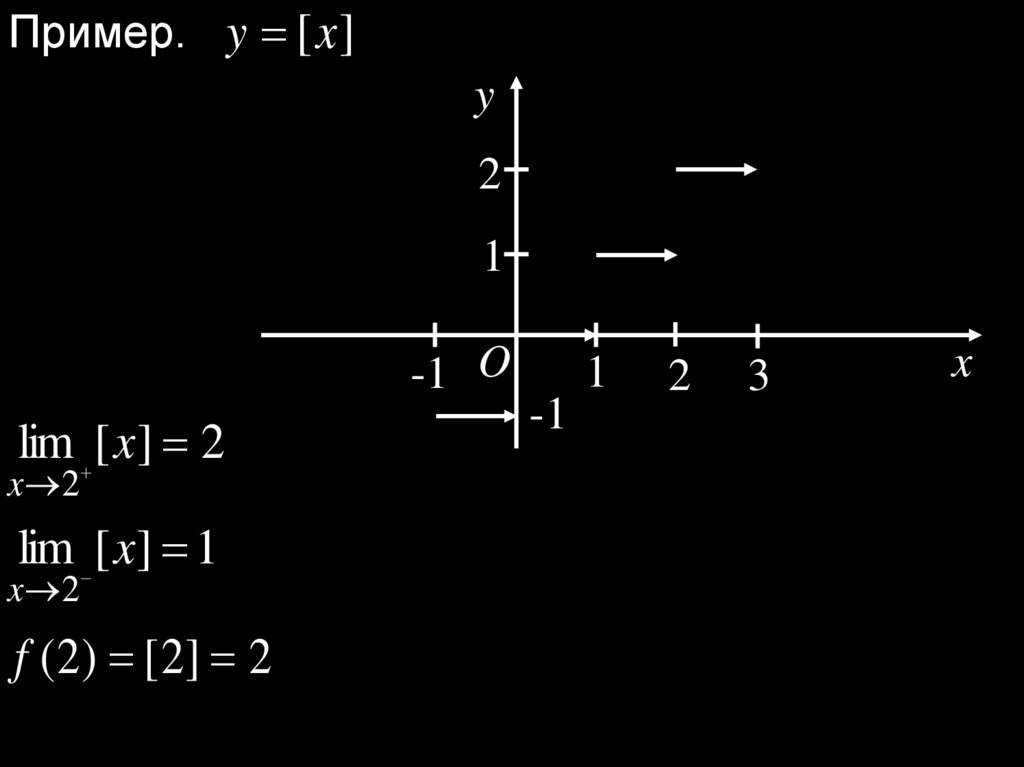














 Математика
Математика








