Основы теории пределов (глава 3)

1.

Глава 3
ОСНОВЫ ТЕОРИИ ПРЕДЕЛОВ

2.

V. Khudenko
2/24

3.

§ 1 Числовая последовательность и ее предел
Числовой последовательностью называется
функция натурального аргумента.
Обозначение: xn x1 , x2 , x3 ,..., xn ,...
Число x(n) называется общим членом
последовательности, а формула x n f ( n )
называется формулой общего члена
последовательности .
V. Khudenko
3

4.

4

5.

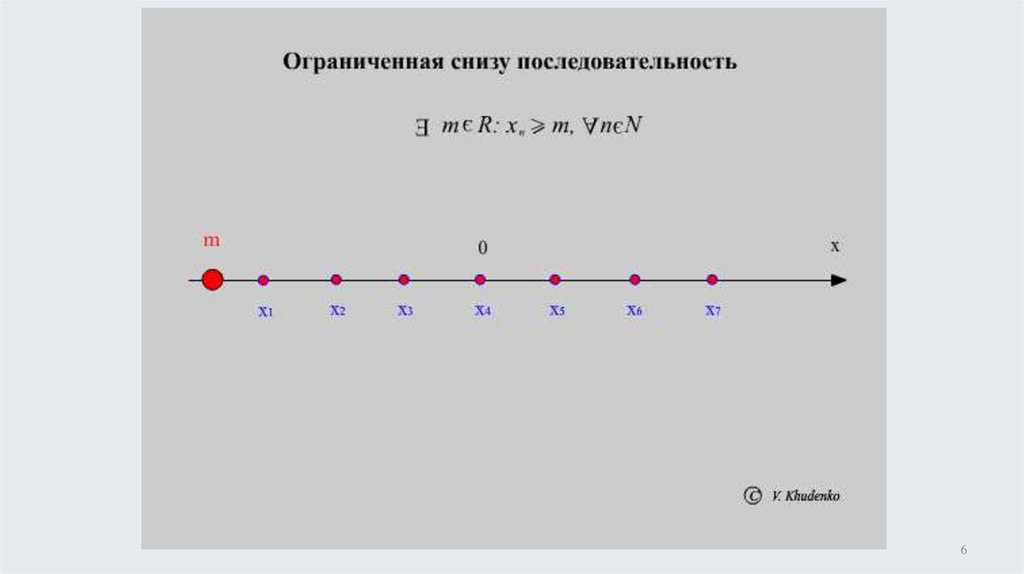
ограничена снизу на N m R : xn m, n N
5

6.

6

7.

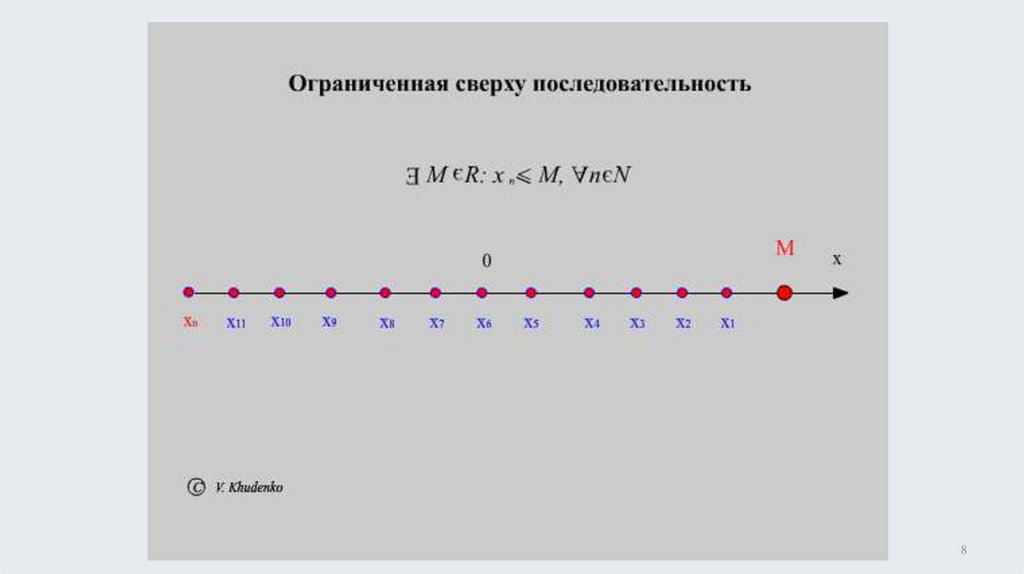
ограничена сверху на N
M R : xn M , n N
7

8.

8

9.

ограничена на N M , m R : m xn M , n N
9

10.

10

11.

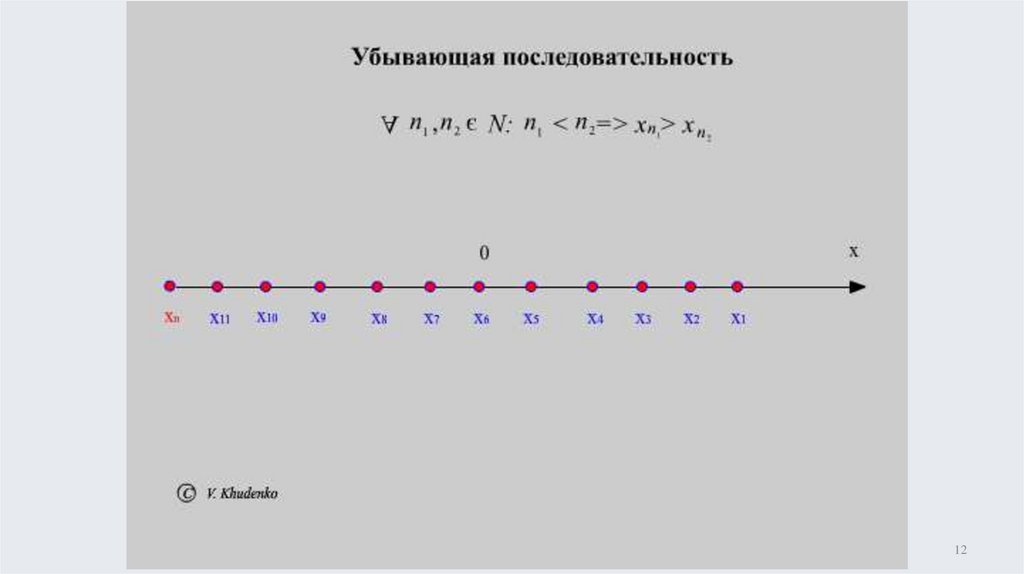
убывает на N n1 , n2 N : n1 n2 xn xn
1
2
11/24

12.

12

13.

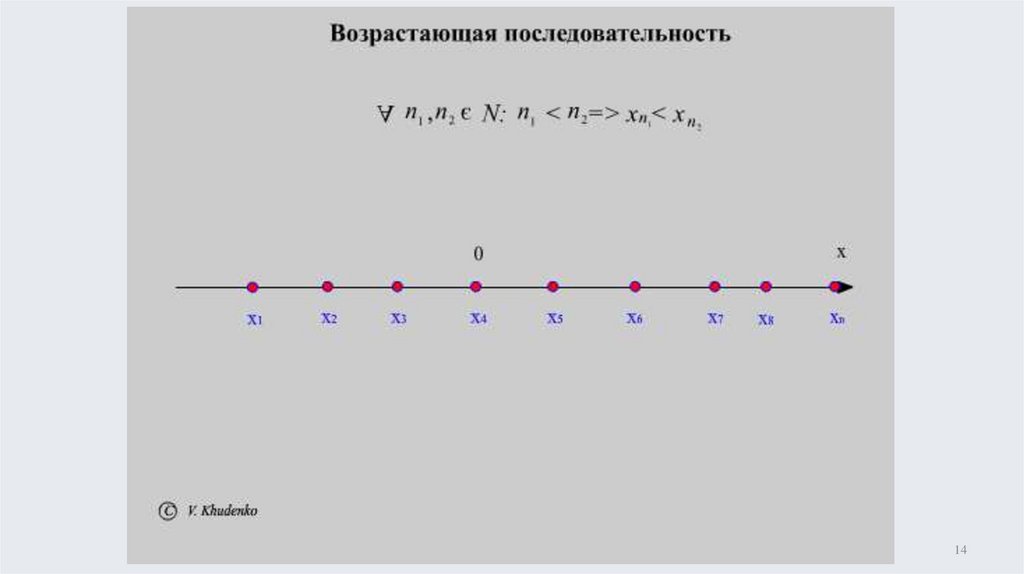
x - возрастает на N
n
1313/24

14.

14

15.

15

16.

Убывающие и возрастающие
последовательности называются
монотонными
Предел числовой последовательности
Понятие предела является одним из
фундаментальных в математике. На этом
понятии, как на фундаменте строится
здание математического анализа.
V. Khudenko
16

17.

Число а называется пределом числовой
последовательности , если для любого,
сколь угодно малого положительного числа
найдется такое натуральное число n ( ) ,
что для всех n n
члены этой
последовательности удовлетворяют
неравенству x n a
В этом случае говорят, что
последовательность имеет предел и пишут
0
0
lim x n a
n
lim xn a 0 n0 N : n n0 xn a
n
V. Khudenko
17

18.

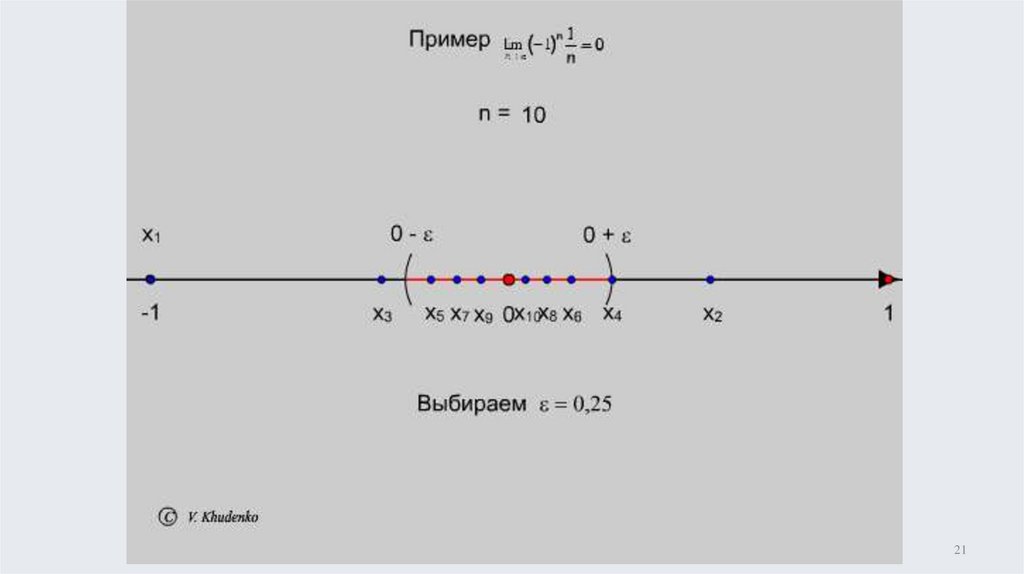
Последовательность, имеющую предел
называют сходящейся.
Эквивалентное определение
Число а называется пределом числовой
последовательности , если в любой сколь
угодно малой - окрестности числа а
содержатся все члены этой
последовательности, начиная с некоторого
числа n0
V. Khudenko
18

19.

19

20.

20

21.

21

22.

Свойства пределов последовательностей
Теорема 1. Если последовательность x
сходится, то она ограничена
n
lim x n a M R: x n M
n
Пусть x - сходящаяся последовательность.
По определению предела последовательности
n0 ,
0 существует натуральное число
что для любого n n выполняется неравенство
x a .
Тогда для 0 имеет место
неравенство: xn xn a a xn a a a
т.е. x a
n
0
n
n
22

23.

Пусть M max a , x1 , x2 ,..., xn
Тогда x M n N ,что и означает
ограниченность числовой
последовательности
Это только необходимый признак, например
n
1,1, 1,1,...
1
последовательность
ограниченная, но не сходящаяся.
Теорема 1.2. Если последовательность имеет
предел, то только один.
Предположим, что
lim xn a, lim xn b,
a
b
n
0
n
n
V. Khudenko
23

24.

Пусть для определенности a<b. Выберем
произвольное число >0 такое, что b 2 a
Рассмотрим окрестности точек а и b . По
выбору произвольного числа эти
окрестности не пересекаются
Из того факта, что точка а является пределом
последовательности следует, что все члены
последовательности (за исключением
конечного их числа) содержатся в
окрестности этой точки.
V. Khudenko
24

25.

Так как окрестности не пересекаются, то в
окрестности точки b содержатся только
конечное число членов
последовательности.
Получаем противоречие с предположением,
lim x b
что
.
Данное противоречие доказывает теорему.
Если встречается такая неограниченная
последовательность, что с возрастанием n
члены последовательности неограниченно
возрастают, то такие последовательности
называются бесконечно большими
n
V. Khudenko
n
25

26.

lim x n M R n0 N : n n0 x n M
n
V. Khudenko
26

27.

lim x n M R n0 N : n n0 x n M
n
V. Khudenko
27

28.

lim x n M R n0 N : n n0 x n M
n
V. Khudenko
28

29.

Числовую последовательность называют
бесконечно малой если ее предел равен
нулю.
lim x n 0 0 n0 N : n n0 x n
n
V. Khudenko
29

30.

30

31.

Свойства бесконечно малых и бесконечно
больших последовательностей
Терема 1.3. Сумма двух бесконечно малых
последовательностей есть бесконечно
малая последовательность.
lim xn 0
(1.1)
n
(1.2)
lim y n 0
n
2
2
0 n0 N n n0 выполняется
0 n1 N
V. Khudenko
n n1
yn
2
xn
2
(*)
(**)
31

32.

n* max n0 , n1
Обозначим
возьмем
тогда неравенства (*) и (**) будут
выполняться одновременно.
xn y n xn y n
2
2
n n
*
Мы получили, что для >0 существует
натуральное число n*, что для всех n>n*
Выполняется неравенство xn yn ,
следовательно, последовательность xn yn
является бесконечно малой.
V. Khudenko
32

33.

Теорема 1.4. Произведение бесконечно малой
последовательности на ограниченную
является бесконечно малой.
Пусть
(1.3)
lim xn 0
n
и n N yn M , M>0
По определению предела последовательности
для n n0
M
0, n0 N : n n0 xn
xn y n x n y n
V. Khudenko
M
M
M
33

34.

Следствие. Произведение двух бесконечно
малых последовательностей есть
бесконечно малая последовательность.
Теорема 1.5. Равносильны следующие два
утверждения:
1)Обратная к бесконечно малой
последовательности является бесконечно
большой последовательностью;
2) Обратная к бесконечно большой
последовательности является бесконечно
малой последовательностью
V. Khudenko
34

35.

1).Пусть , тогда
n0 N , n n0
По свойствам числовых неравенств получаем,
что для n n0 1 1
1
xn
M
1
0
M
xn
xn
M
1
xn
т.е последовательность
удовлетворяет
определению бесконечно большой
последовательности.
lim yn
2) Пусть
, следовательно,
n
M
1
0
n0 N ,
n n0
yn
1
по свойствам числовых неравенств
1
n n0 1 1
- бесконечно малая
y
y
n
V. Khudenko
n
yn
35

36.

Предел и неравенства
Теорема 1.5. Пусть x и yn
две
сходящиеся последовательности
lim xn a, lim yn b
причем
a b
n
n
тогда
n0 N , n n0 : xn yn
n
b a
2
Выберем
тогда окрестности
точек а и не будут пересекаться.
n1 N n n1 : xn a ,
n2 N n n2 : yn b ,
V. Khudenko
36

37.

Обозначим , n0 max n1 , n2 тогда начиная с
номера n0 будут выполняться неравенства
x n0 a b y n0
Замечание: Строгое неравенство в пределе
может в пределе перейти в нестрогое
неравенство.
1 1
для последовательности n 2 2 0
V. Khudenko
1
lim 2 0
n n
n
37