Похожие презентации:
Теплопередача. Понятия и определения
1.
Теплопередача2.
Целью освоения дисциплины является достижениеследующих компетенций на уровнях:
профессионально-специализированных:
- способен выполнять расчёты простых систем, деталей и узлов.
Формированию компетенций служит достижение следующих результатов образования:
знания:
на уровне представлений:
- основные законы теплопередачи в двигателях;
на уровне воспроизведения:
- методы анализа эффективности работы двигателей ЛА;
- расчет тепловых потоков
на уровне понимания:
- выполнения теплотехнических расчетов для эскизного проектирования оборудования;
умения:
теоретические:
- методы и алгоритмы анализа теплового режима двигателей ЛА
практические:
- проводить анализ работы тепловых машин и установок;
навыки:
- решения задач при проектировании теплового оборудования и энергетических узлов;
3.
4.
Литература• В. В. Нащокин. Техническая термодинамика и
теплопередача. М.: Высшая школа, 1980, 74 экз.
• В. В. Сахин. Исследование процессов теплообмена.
СПб.БГТУ "ВОЕНМЕХ" им. Д. Ф. Устинова, 2004, эл. рес.
• В. В. Сахин, В. Шалимов. Теплопередача. СПб.БГТУ
"ВОЕНМЕХ" им. Д. Ф. Устинова, 2003, эл. рес.
• В. В. Сахин, Е. М. Герлиман, Н. А. Брыков. Теплопередача
в примерах и задачах. СПб.БГТУ "ВОЕНМЕХ" им. Д. Ф.
Устинова, 2019, 84 экз.
• В. В. Сахин, Е. М. Герлиман, Н. А. Брыков. Теплопередача
в примерах и задачах. СПб.БГТУ "ВОЕНМЕХ" им. Д. Ф.
Устинова, 2019, эл. рес.
• Ю. А. Душин. . Термодинамика и тепло-массопередача.
СПб.БГТУ "ВОЕНМЕХ" им. Д. Ф. Устинова, 2008, эл. рес.
5.
6.
Понятия иопределения
7.
8.
Теплообмен (теплопередача)Это самопроизвольный, необратимый
процесс распространения теплоты в
пространстве, обусловленный
разностью температур.
Различают три элементарных вида
теплообмена: теплопроводность,
конвекцию и тепловые излучения.
9.
ТеплопроводностьЭто процесс переноса тепла,
осуществляемый в результате
непосредственного контакта
микрочастиц, обладающих
различной энергией.
10.
КонвекцияЭто процесс переноса теплоты
вследствие пространственного
перемещения макрообъемов
вещества с различной температурой.
Причем, внутри макрообъемов
осуществляется теплообмен
теплопроводностью.
11.
Тепловое излучениеЭто процесс переноса теплоты
посредством электромагнитного поля
с двойным взаимным превращением
– теплоты в энергию поля и энергии
поля в теплоту при поглощении.
Т.е. Т.И. осуществляется посредством
электромагнитных колебаний).
12.
Сложный теплообменЭто теплообмен,
осуществляемый в
результате одновременного
действия теплопроводности,
конвекции и излучения.
13.
Температурное полеЭто совокупность мгновенных
значений температуры во всех
точках пространства. Поле
температур является
скалярным полем, его
уравнение
Т = Т(х, у, z, )
14.
стационарный тепловой режимРежим теплообмена, при котором во всех
точках пространства температура не
изменяется во времени. В этом случае
температурное поле называется
стационарным (установившемся), ему
соответствует уравнение
Т=Т(х, у,z)
15.
Стационарное, двухмерное поле.Т= Т(х, у)
Одномерное стационарное поле.
Т = ƒ(х)
Одномерное нестационарное поле
Т = ƒ(х, )
16.
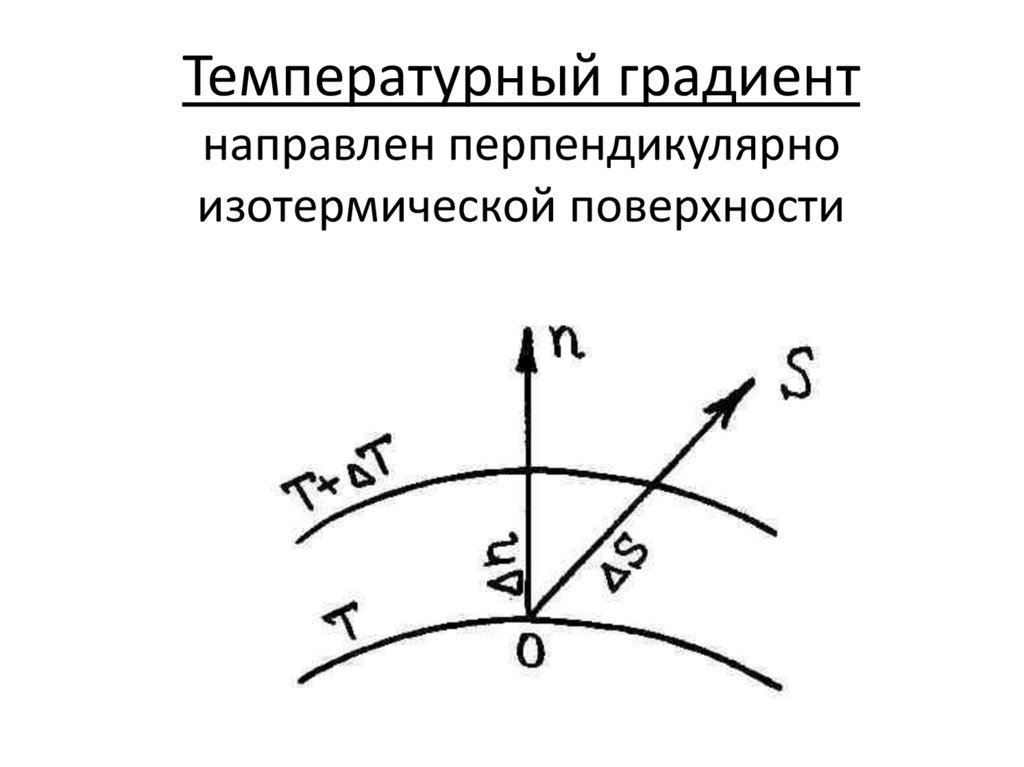
Изотермическая поверхностьЭто геометрическое
место точек пространства,
имеющих одинаковую
температуру
17.
Температурный градиентЭто физическая величина,
которая описывает, в каком
направлении и с какой
скоростью температура
меняется наиболее интенсивно
в определенном месте
18.
Температурный градиентнаправлен перпендикулярно
изотермической поверхности
19.
Температурный градиентЭто предел отношения разности
температур на изотермических
поверхностях ΔТ к расстоянию
между ними по нормали Δn:
T
T
grad T lim
n n 0 n
20.
Температурный градиентЭто вектор, определенный в каждой точке
температурного поля, направленный по
нормали к изотермической поверхности в
сторону увеличения температуры и
имеющий длину, равную производной от
температуры по направлению:
T
T
T
T
gradT
n0
i
j
k
n
x
y
z
21.
Температурный градиентявляется мерой интенсивности
изменения температуры.
Таким образом, скалярному полю
температур соответствует
векторное поле температурных
градиентов
22.
Тепловой потокЭто количество теплоты,
участвующее в теплообмене: Q, вт.
Плотность теплового потока
Это количество теплоты,
проходящее в единицу времени
через единицу площади: q, вт/м2
dQ
q
dF
23.
Плотность тепловогопотока q и тепловой поток
Q являются векторами,
направленными в
сторону уменьшения
температуры.
24.
Основной задачей расчетапроцессов теплообмена
является в конечном итоге,
выявление количественной
зависимости между
распределением
температуры и тепловыми
потоками.
25.
Раздел 1СТАЦИОНАРНАЯ
ТЕПЛОПРОВОДНОСТЬ
26.
Закон Фурье (1822 г.)дает связь поля температурных
градиентов и поля тепловых потоков.
Он устанавливает, что тепловой поток,
переносимый теплопроводностью,
пропорционален температурному
градиенту.
27.
Закон Фурьеq gra dT
Q gradT F
T
T
T
T
gradT
n0
i
j
k
n
x
y
z
28.
Коэффициент теплопроводностиλ Вт/(м0К).
Коэффициент λ это физический параметр,
характеризующий способность вещества
проводить теплоту.
Он численно равен количеству тепла,
проходящему через единицу
изотермической поверхности в единицу
времени по нормали к ней в сторону
уменьшения температуры при условии, что
градиент температуры в рассматриваемой
точке равен 1 К/м.
29.
Зависимость λ =λ(Т)Для большинства веществ зависимость
λ =λ(Т)
имеет линейный характер.
У газов, а также твердых теплоизоляторов и
огнеупорных материалов при увеличении
температуры λ возрастает, у других
(большинства чистых металлов и
жидкостей) убывает.
30.
Численные значения коэффициентатеплопроводности
• Для газов λ = 0,05 ÷ 0,5Вт/(м0К);
• Для капельных жидкостей λ =0,07÷0,7 Вт/(м0К);
• Для диэлектриков λ = 0,02 ÷ 0,3 Вт/(м0К);
• Для металлов λ = 2 ÷ 450 Вт/(м0К).
• Вещества,
имеющие
коэффициент
теплопроводности
λ≤0,25
Вт/(м0К)
используются в качестве теплоизоляторов для
снижения тепловых потерь, для тепловой
защиты.
31.
32.
33.
34.
35.
Дифференциальноеуравнение
теплопроводности
36.
Допущения:• 1) среда – однородная и изотропная;
• 2) внутренние источники тепла
отсутствуют;
• 3) конвекция отсутствует (среда
неподвижная);
• 4) физические параметры среды (ρ, с,
λ) постоянны
37.
К выводу дифференциальногоуравнения теплопроводности
dQ = dQх + dQу + dQz
dQi = dQi’ - dQi"
38.
Внутренняя энергия выделенногообъема
может изменяться только за счет
теплообмена с окружающей средой
dU = dQ,
где dU – изменение внутренней энергии
элемента за время dτ, Дж;
dQ – количество теплоты, которым
элемент обменивается с окружающей
средой за то же время, Дж.
39.
Величина dQ является суммой трехслагаемых, которые выражают тепловые
потоки, поступающие в элемент (или из него)
по направлению осей координат X, Y, Z
dQ = dQх + dQу + dQz
40.
Каждое из слагаемых можно представить какразность между потоками, входящими в
элемент
и
выходящими
из
него
в
соответствующем направлении.
dQx = dQx' - dQx" ,
где dQx' – количество теплоты, вошедшего в
элемент среды за время dτ в направлении
оси Х;
dQх" – количество теплоты, вышедшее из
элемента в том же направлении за тот же
промежуток времени;
dQх – количество теплоты, пошедшее на
изменение
внутренней
энергии
элемента за счет теплового потока,
направленного вдоль оси Х;
41.
dQ = q dF dτ,Температуры на гранях имеют
значение
на левой (вход):
Т
на правой (выход):
T
T
dx
x
42.
Исходя из закона Фурьеq gra dT
Q gradT F
T
T
T
T
gradT
n0
i
j
k
n
x
y
z
получаем:
43.
TdQ x
dydzd
x
T
dQ x T
dx dydzd
x
x
2
T
dQ x dQ x dQ x 2 dVd
x
44.
Аналогично получаем dQпо осям Y и Z.
Далее, суммируя их,
получаем общее
количество теплоты,
затраченное на изменение
температуры объема dV.
45.
T T TdQ dQx dQy dQz 2 2 2 dVd
x y z
2
2
2
T
T
dU c dM d c dV d
46.
22
2
T
T T T
c dV
d 2 2 2 dVd
y
z
x
T
T T T
2 2 2
c x
y
z
2
2
2
T T T
T x 2 y 2 z 2
2
2
2
2
47.
Дифференциальноеуравнение
теплопроводности
T
2
a T
48.
Коэффициенттемпературопроводности
a
c
49.
коэффициенттемпературопроводности
м2/с
Характеризует теплоинерционные
свойства вещества, т.е. его
способность с той или иной скоростью
изменять свою температуру при
подводе или отводе тепла, является
физическим параметром вещества.
50.
Дифференциальноеуравнение Фурье
относится к числу общих
уравнений. Чтобы получить из
бесконечного множества решений
единственное, отвечающее
конкретным условиям задачи,
необходимы дополнительные
условия – условия однозначности
решения.
51.
Условияоднозначности
52.
Условия однозначности (единственности)решения состоят из величин, учитывающих
индивидуальные различия процессов, т.к.
развитие процесса зависит от:
• физических характеристик
рассматриваемой системы,
• состояния системы к моменту
возникновения процесса,
• особенностей воздействия внешней среды.
53.
Условия однозначности• геометрические, характеризующие форму и
размеры системы, в которой протекает
процесс;
• физические,
учитывающие
физические
параметры среды (λ, ρ, с и т.д.)
• начальные
(временные),
описывающие
распределение температуры в начальный
момент времени;
• граничные,
отражающие
влияние
окружающей среды на процесс.
54.
55.
Способы задания однозначностиI рода:
,
Т= Т( х, у, z, );
II рода:
q = q( х, у, z, );
III рода (твердая стенка – жидкость):
Tc
Tc Tж ТВ
или
n c
Tc
Т с Т ж
ТВ
n c
IV рода (твердая стенка – твердая стенка):
T1
T2
1
2
n c
n c
56.
Теплопроводностьплоской стенки
57.
58.
59.
Дифференциальное уравнениетеплопроводности (выведено ранее)
T
2
a T
60.
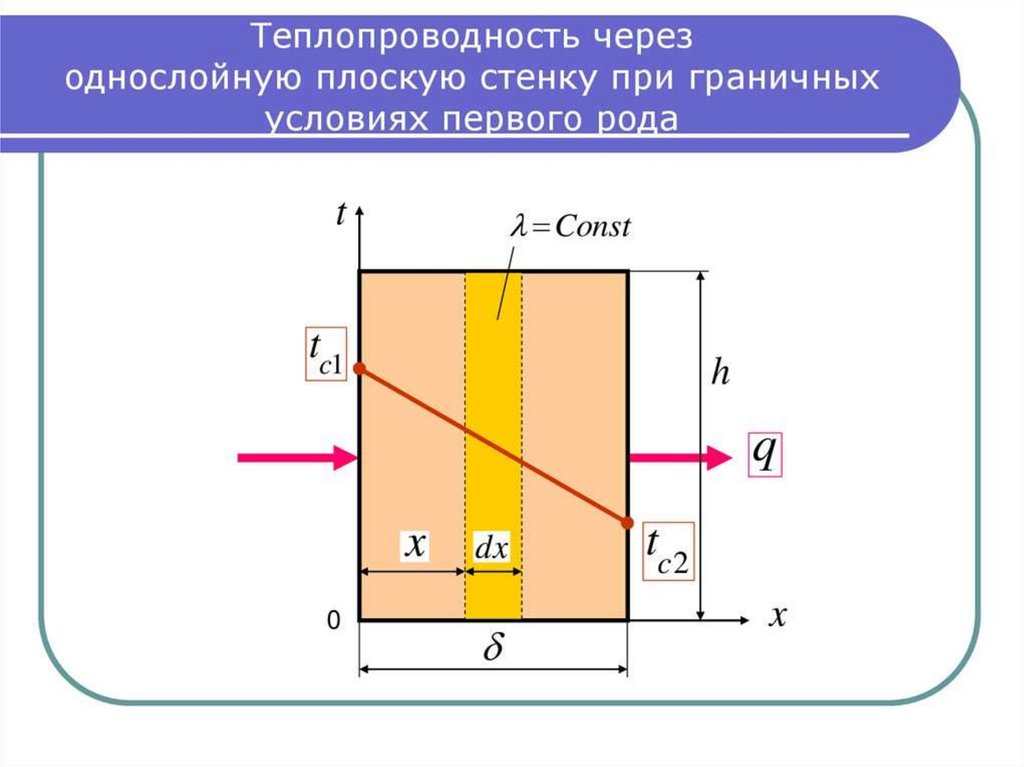
Теплопроводность плоскойоднослойной стенки
Температурное поле стационарное, одномерное:
Первое интегрирование:
Второе интегрирование:
dT
C1 ;
dx
d 2T
0
2
dx
dT C1dx
T C1 x C2
T T1
T1 T2
x
61.
T1 T2dT
q
C1
dx
q T1 T2
62.
Теплопроводность многослойнойплоской стенки
n
1
2
q T1 T2 T2 T3 ... Tn Tn 1
1
2
n
1
T1 T2 q
1
2
T2 T3 q
2
n
Tn Tn 1 q
n
n
1 2
n
i
T1 Tn 1 q
... q
n
i 1 i
1 2
q
T1 Tn 1
i
i 1 i
n
i
Tn T1 q
i 1 i
n
63.
Теплопередача через плоскуюстенку
q 1 Tж1 Т с1
q 2 Tc 2 Tс 2
q Tc1 Tc 2
64.
частные температурные напорыTж1 Т с1 q
1
Т с 2 Tж 2 q
1
Tc1 Tc 2 q
1
1
Tж1 Т ж 2 q
1 2
1
2
65.
Tж1 Т ж 2q
К Т ж1 Т ж 2
1
1
1
К
2
RT
1
1
1
R 1 RT 2 R 3
K
1 2
1
1
1 2
1
Tc1 Tж1 q
1
1
;
n
1
i
Tc 2 T ж 2 q
Tж1 q
2
1 i 1 i
1
66.
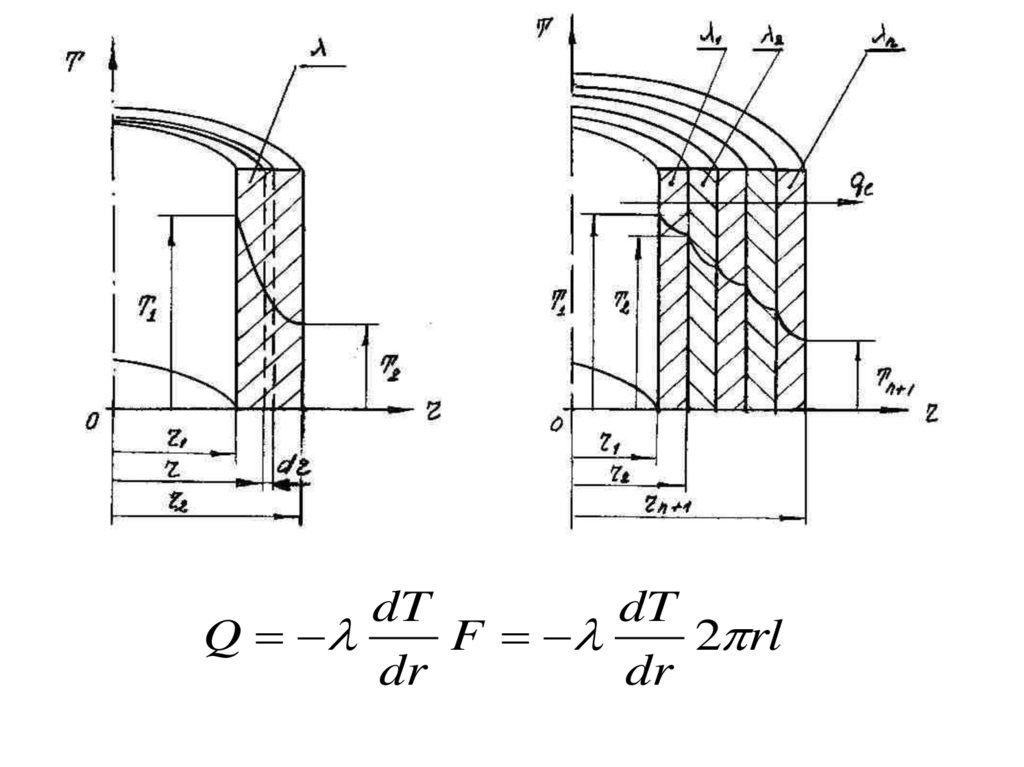
Теплопроводностьцилиндрической
стенки
67.
dTdT
Q
F
2 rl
dr
dr
68.
Для однослойной цилиндрической стенки:Q
dT
q l 2 rl
l
dr
q l dr
dT
2 r
ql
ql
T
ln r C
2
2
r2
ln
r1
1
T1 T2
69.
Для многослойной цилиндрической стенкиql
T1 Tn 1
2
ql
n
i 1
ri 1
ln
i
ri
1
2 (T1 Tn 1 )
n
i 1
ri 1
ln
i
ri
1
ql
Tn T1
2
n
i 1
ri 1
ln
i
ri
1
70.
Теплопередачачерез
цилиндрическую
стенку
71.
72.
ql 1 2 r1 Tж1 Т с12 Т с1 Т с 2
ql
1 r1
ln
r2
ql 2 2 r2 Tc 2 Tж 2
73.
ql 1Т ж1 Т с1
2 1r1
ql 1 r2
Tc1 Tc 2
ln
2 r1
ql 1
Tc1 Tж 2
2 2 r2
74.
ql 11 r2
1
Tж1 Т ж 2
ln
2 1r1 r1 2 r2
1 1 r2
1
K l
ln
r
r
r
11
1
2 2
1
2 Т ж1 Т ж 2
q l K l 2 (Tж1 Т ж 2 )
Rl
75.
11 r2
1
Rl
ln
1 r1 r1 2 r2
n
1
1 ri 1
1
Rl
ln
1 r1 i 1
ri
2 r2
ql 1
Tc1 Tж1
2 1 r1
n
ql 1
ql 1
1 ri 1
Tж 2
Tc 2 T1
ln
2 1 r1 i 1
ri
2 2 r2
76.
Тепловаяизоляция.
Критический
радиус изоляции.
77.
78.
rизr2
1
1
1
1
Rl
ln
ln
R к1 RТ 1 RТ 2 R к 2
1 r1 1 r1 из
r2 2 rиз
из
rкр.из
2
λиз ≤ α2 r2
rкр из ≤ α2 r2
79.
Теплопроводностьсферической
стенки
80.
81.
Для однослойной стенкиdT
dT
2
Q
F
4 r
dr
dr
Q dr
dT
4 r 2
Q 1
1
Т1 Т 2
4 r1 r2
82.
Q4 T1 T2
1
1
1
r1 r2
Q 1
1
Т Т2
4 r1 r2
83.
Для многослойной стенкиQ
4 T1 Tn 1
n
1 1
1
r
r
i
1
i 1
i 1
Q
Т n T1
4
n
i 1
1 1 1
i r1 rn
84.
Теплопередачачерез
сферическую
стенку
85.
Q 1 4 r Tж1 Т с12
1
Q
4 Tc1 Tc 2
1 1 1
r1 r2
Q 2 4 r Tc 2 Tж 2
2
2
Q4
4 Т ж1 Т ж 2
1
1 1 1
1
1 r1 r1 r2 2 r2
4 Tж1 Т ж 2
K cp 4 Tж1 Т ж 2
Rcp
86.
11 1 1
1
Rcp
1 r1 r1 r2 2 r2
1
1 1
1
1
Rcp
1 r1 i 1 i ri ri 1 2 r2
n
Q 1
Tc1 Tж1
2
4 1 r1
Q 1
Tc 2 Tж 2
4 2 r2
87.
Радиус критической изоляции шара88.
Нестационарнаятеплопроводность
89.
Понятие«нестационарная
теплопроводность»
90.
При нестационарном тепловомрежиме
температурное
поле
изменяется во времени.
Нестационарность
тепловых
процессов
обуславливается
изменением внутренней энергии тела
и всегда связана с явлением его
прогрева или охлаждения.
91.
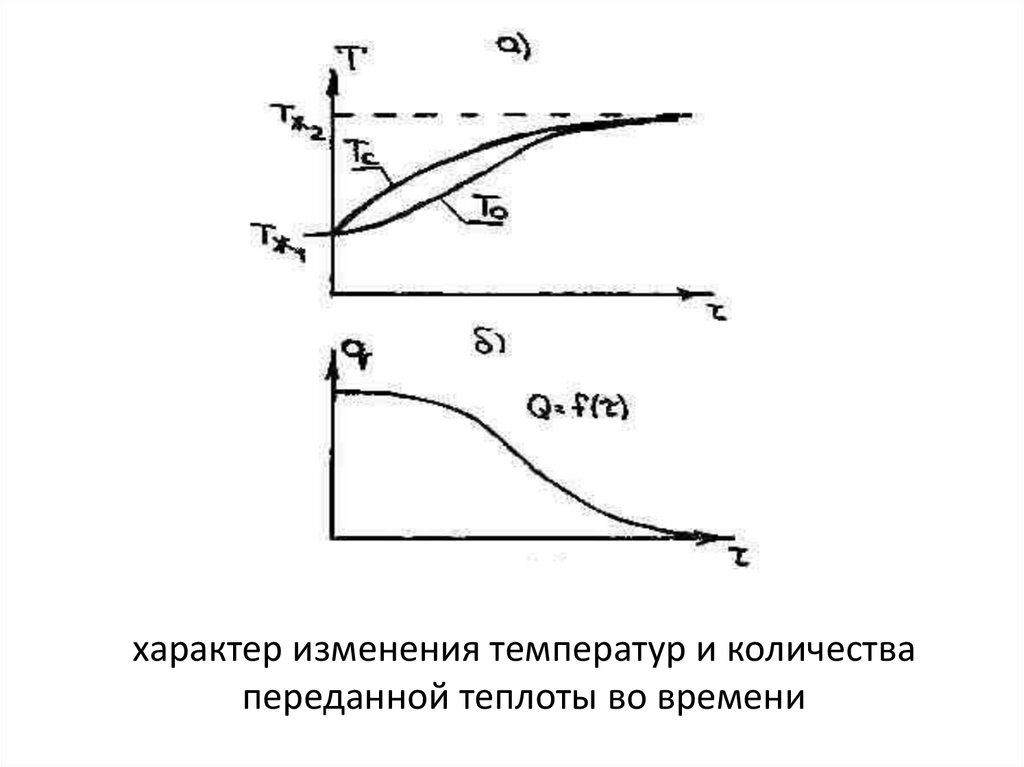
характер изменения температур и количествапереданной теплоты во времени
92.
Рассмотрим процесс теплопередачичерез стенку.
Пусть
вначале
процесс
был
стационарным, температура горячей жидкости
Т'ж1, холодной Т''ж2, стенок Т''с1 и Т''с2 (рис. а).
Если теперь изменить режим, например, сразу
резко изменить (увеличить) температуру
горячей среды Т"ж1, то на некоторое время
процесс
становится
нестационарным.
Температурная кривая Т'ж1 - Т''ст1 - Т'ст2 - Т"ж2
будет изменяться до тех пор, пока снова не
установится стационарный режим Т''ж1 - Т''ст1 Т''ст2 - Т"ж2 .
Изменение во времени Тс1 и Тс2
отдельно представлено на рис. б.
О характере изменения во времени
количества
передаваемой
теплоты
для
рассматриваемого случая дают представление
кривые на рис. б. Здесь Q' и Q" – тепловые
потоки при стационарных режимах, Q1 и Q2 –
тепловые потоки через горячую и холодную
поверхности при нестационарном режиме.
93.
Нестационарный тепловой процесс всегда связан сизменением внутренней энергии тела и им
обуславливается.
Так как скорость изменения энергии прямо
пропорциональна способности материала проводить
теплоту (то есть коэффициенту теплопроводности λ) и
обратно пропорциональна его аккумулирующей
способности (то есть, объемной теплоемкости cρ), то в
целом
скорость
теплового
процесса
при
нестационарном
режиме
определяется
коэффициентом температуропроводности :
а
c
94.
В задачах нестационарной теплопроводности выделяюттри характерных режима.
I режим. Начальный. Охватывает начало процесса, когда
существенно влияние начальных условий, при этом характерной
особенностью
является
распространение
температурных
возмущений в пространстве и захват все новых и новых слоев
тела. Скорость изменения температуры в отдельных точках при
этом различна, поле температур сильно зависит от начального
состояния, которое, вообще говоря, может быть различным.
II режим. Регулярный. С течением времени влияние
начальных
неравномерностей
(условий)
сглаживается
и
относительная скорость изменения температуры во всех точках
становится постоянной.
III режим. Стационарный. По прошествии длительного
времени – аналитически по истечении бесконечного времени,
наступает
третий,
стационарный
режим,
характерной
особенностью которого является постоянство температур во
времени. Если при этом температура во всех точках одинакова и
равна температуре окружающей среды, то это состояние
теплового равновесия.
95.
Решитьзадачу
нестационарной
теплопроводности
–
значит
найти
зависимость изменения температуры и
количества тепла для любой точки тела.
Такие зависимости могут быть получены:
- аналитическим способом,
- экспериментальными способами
- методами численного моделирования
(путем решения дифференциального
уравнения теплопроводности).
96.
Расчет нагрева иостывания
термически
тонких тел
97.
Наиболеепростым
но
достаточно
часто
распространенным является случай, когда удельное
тепловое сопротивление теплоотдачи 1/α от греющей
среды к телу значительно больше термического
сопротивления переноса теплоты теплопроводностью
внутри тела от его поверхности к середине δ/λ, то есть
α <<λ/δ
где
δ –половина толщины тела (пластины) или радиус
(шара и цилиндра), а для тел сложной формы – половина
наибольшего линейного размера.
При выполнении данного условия тело называют
термически тонким.
98.
В каждый момент времени температура Т внутри такого тела успеваетвыровняться за счет интенсивного переноса теплоты теплопроводностью.
Таким образом, величина Т зависит только от времени и не зависит от
координат.
Рассмотрим термически тонкое тело произвольной формы, объемом
V, все точки которого охлаждаются за счет теплоотдачи с одинаковой
скоростью dТ/dτ. За время dτ тело отдает количество теплоты:
dT
dQ c V
d
d
dQ F T Tж d
c VdT F (T Tж )d
99.
T Tжd
F
d
c V
F
ln
C
c V
Согласно начальным условиям: при τ = 0
T 0 Tж 0
C ln 0
100.
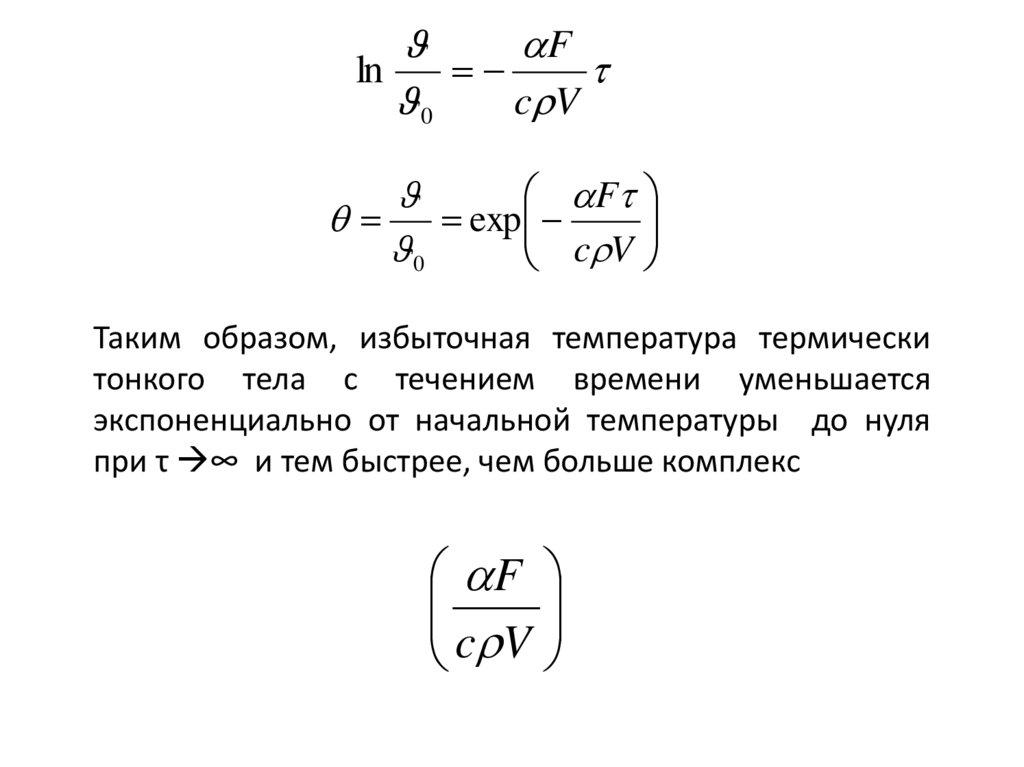
Fln
0
c V
F
exp
0
c V
Таким образом, избыточная температура термически
тонкого тела с течением времени уменьшается
экспоненциально от начальной температуры до нуля
при τ ∞ и тем быстрее, чем больше комплекс
F
c V
101.
Регулярный тепловой режим102.
ln ln( T Tж ) т СС е
т
**
m [1/сек] – темп охлаждения (нагревания).
Характеризует интенсивность охлаждения
(нагревания) тела. *
103.
Изменение температуры как функция временипри охлаждении тела
104.
Применим уравнение (**) к двумпроизвольным моментам времени τ’ и τ”
и, исключив постоянную С, получим
ln ln
m









































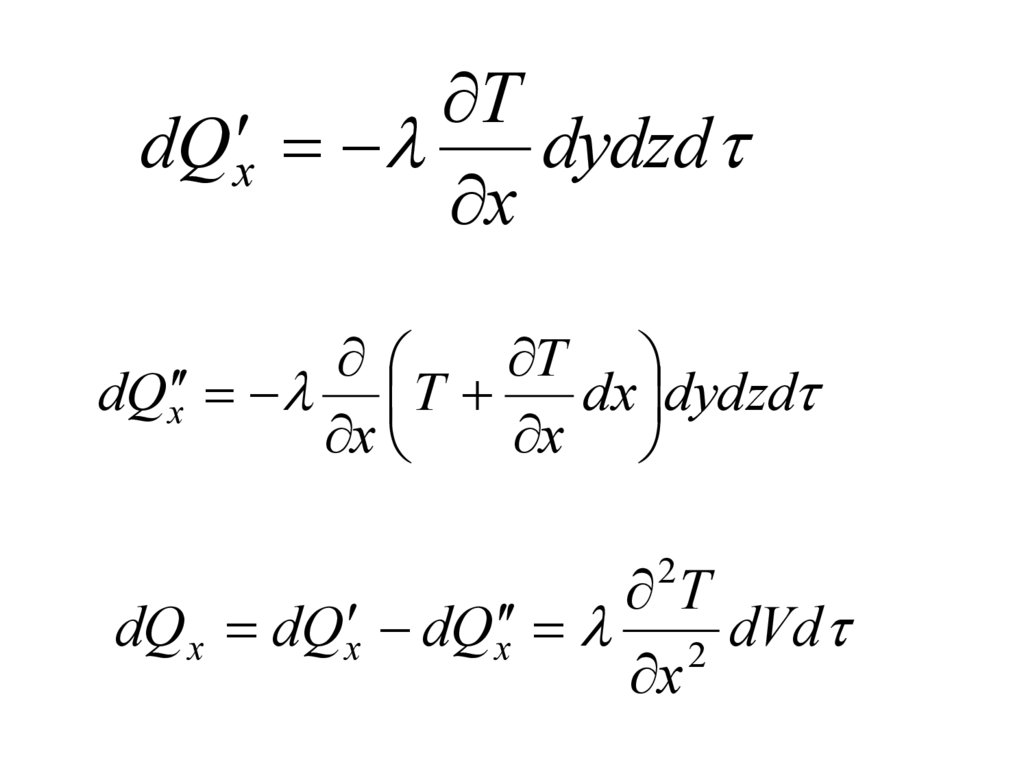



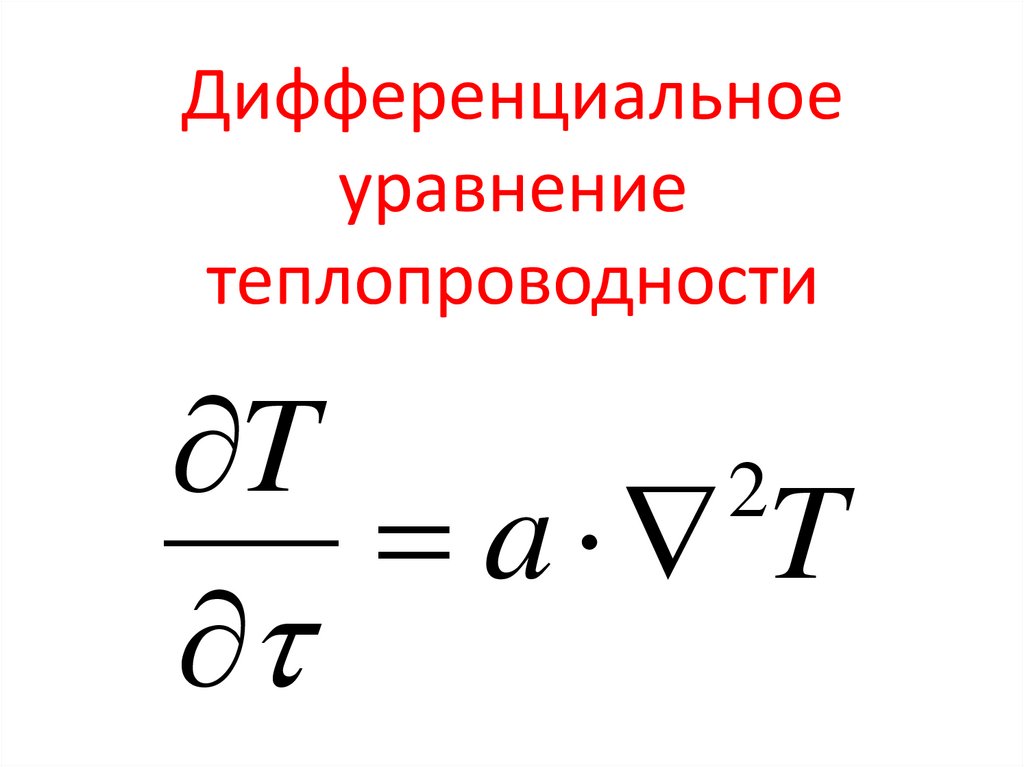
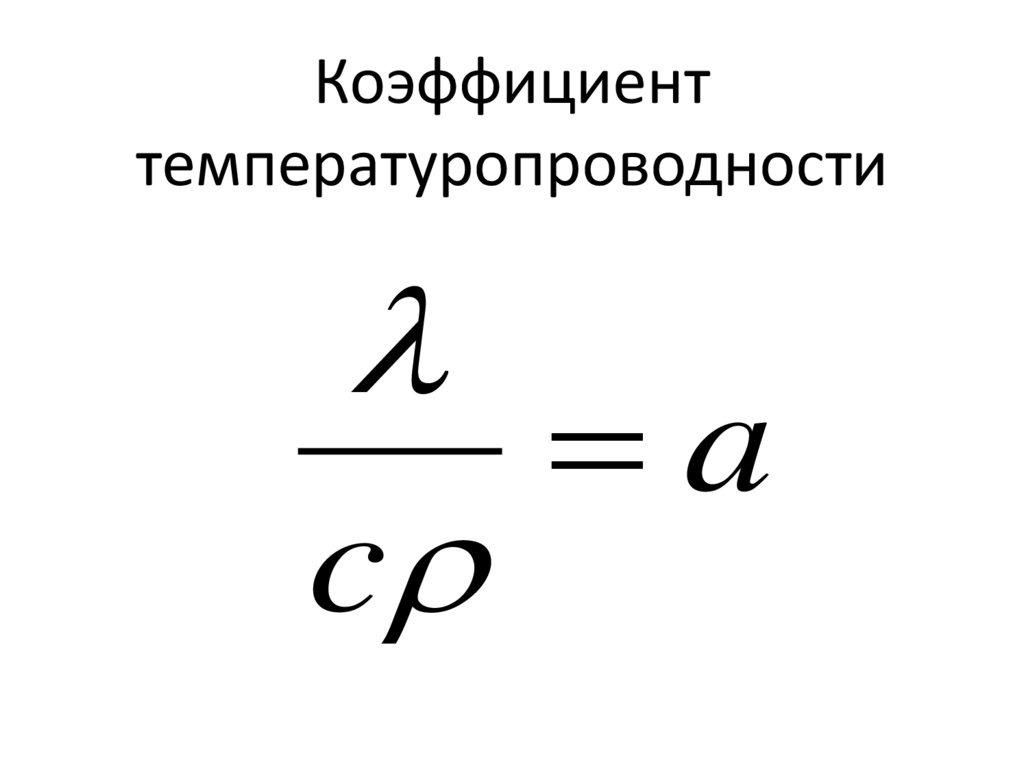






















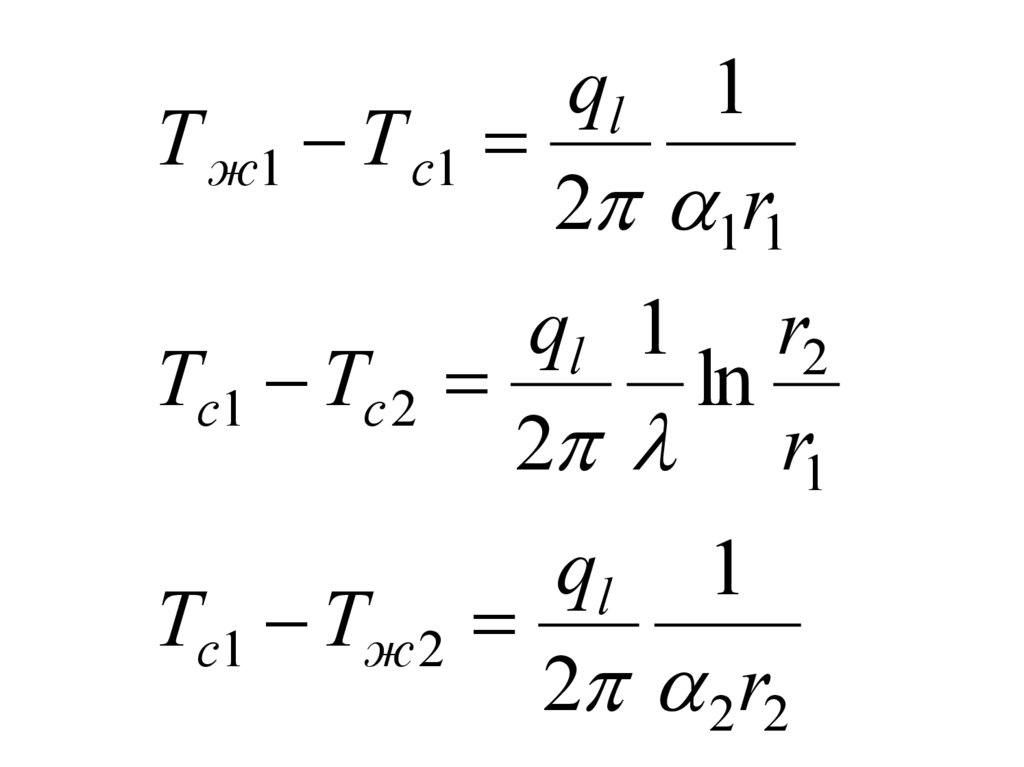

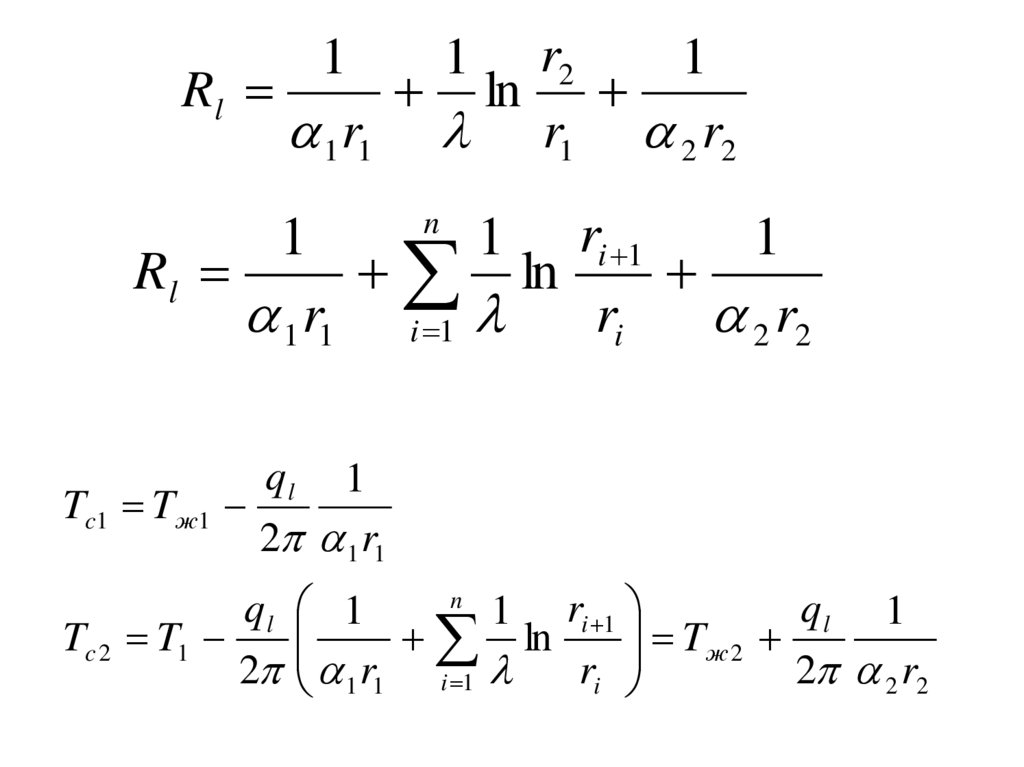


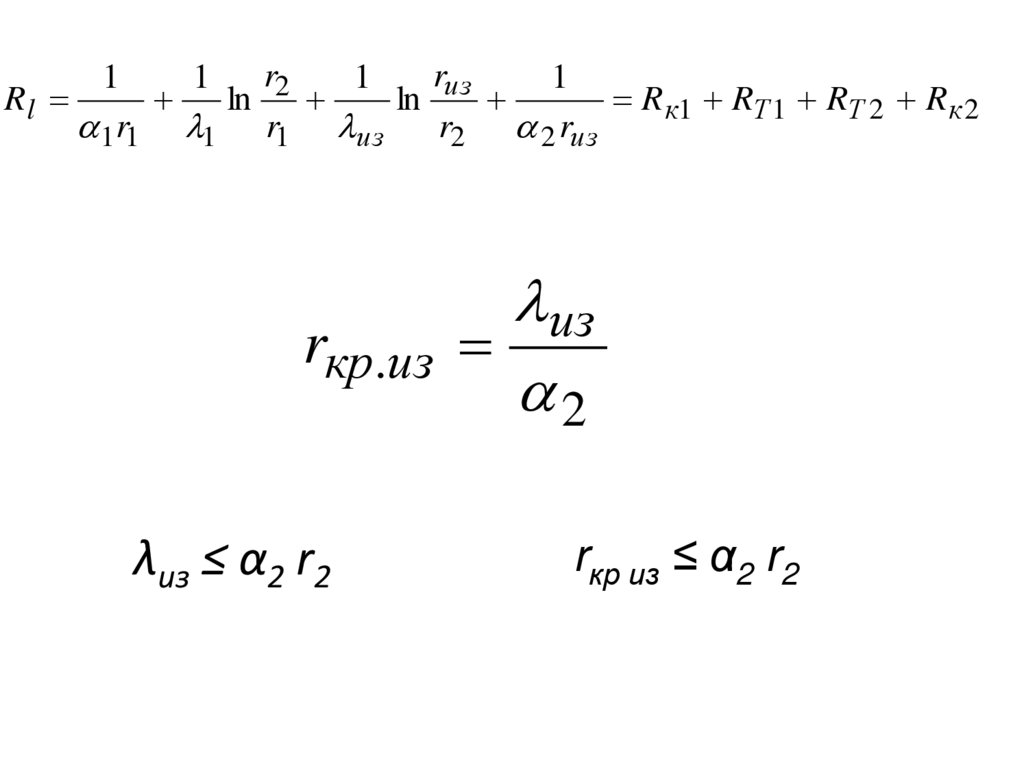





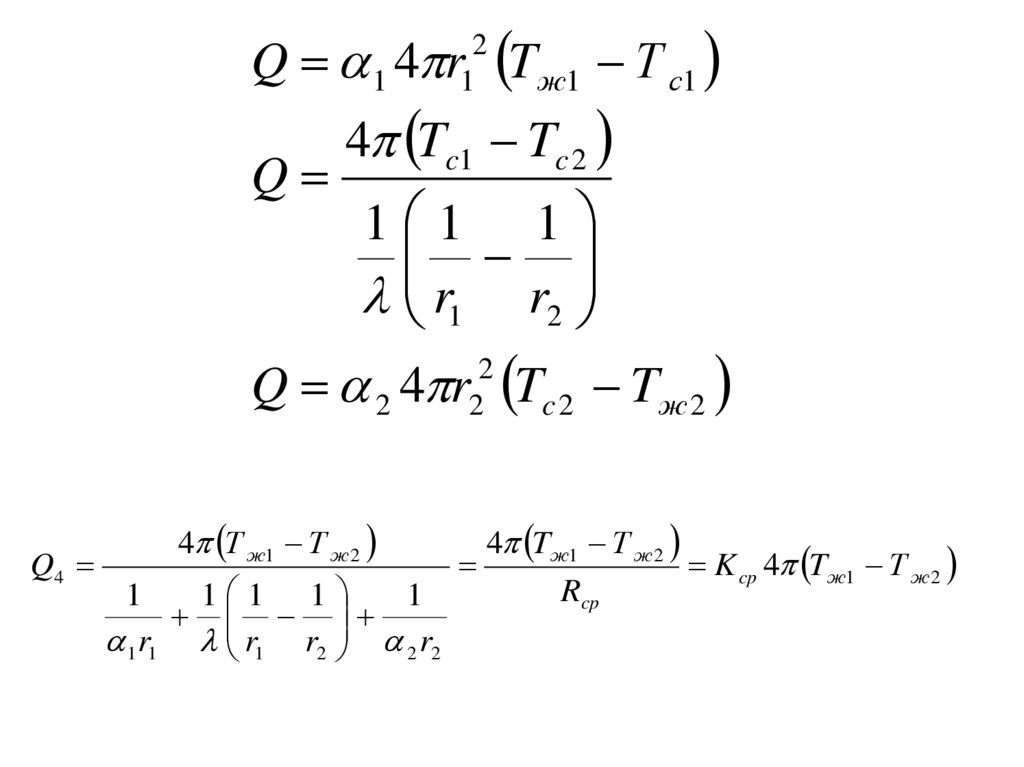












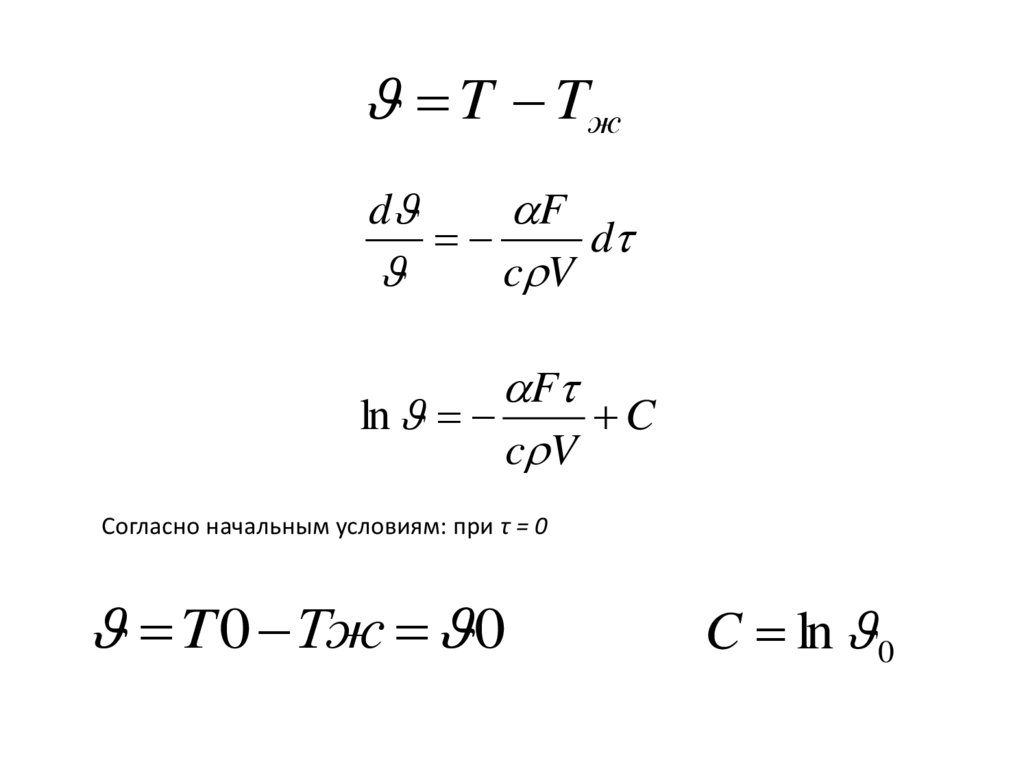


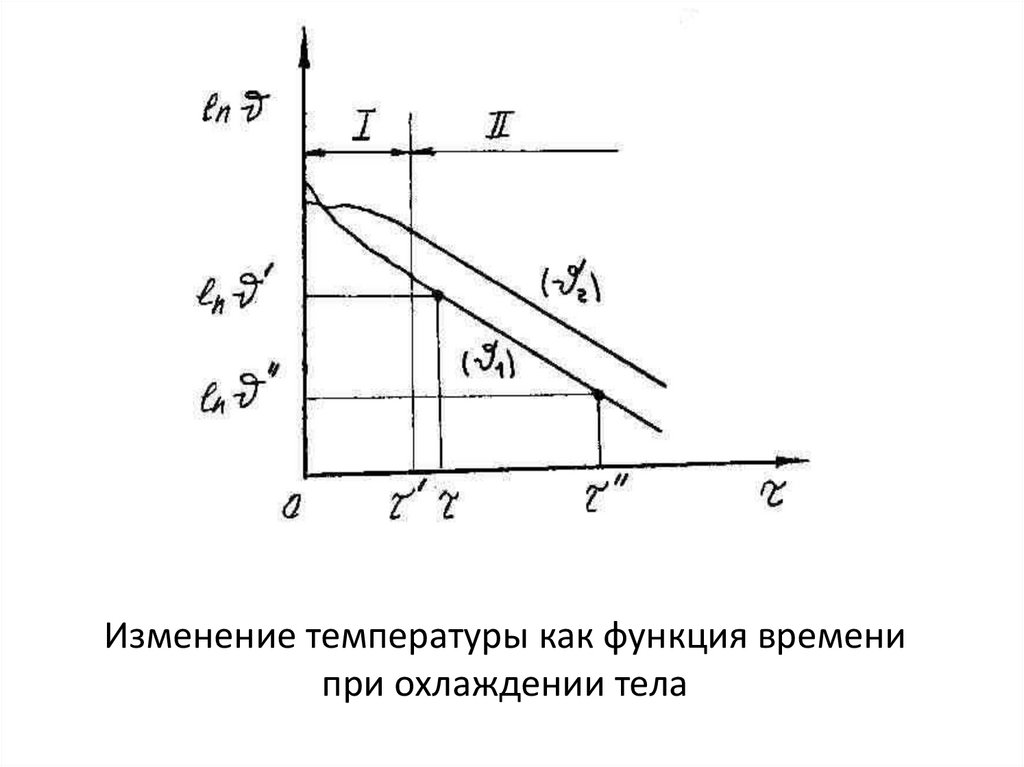




 Физика
Физика








