Похожие презентации:
Системы массового обслуживания (СМО)
1. Системы массового обслуживания (СМО)
2.
СМОфункционирование состоит в обслуживании
требований.
Входной поток
требований
СМО
Выходной поток
обслуженных
требований
СМО
требования
Очереди
Приборы
обслуживания на обслуживание
Теория систем массового обслуживания ~
Теория очередей
3.
Показатели СМО1. Среднее количество требований, которые СМО
обслуживает за единицу времени,
2. Средний процент требований, которые не были
обслужены,
3. Вероятность того, что пришедшее в систему
требование будет принято на обслуживание,
4. Среднее время ожидания требования в очереди,
5. Закон распределения времени ожидания,
6. Среднее количество требований в очереди,
7. Закон распределения числа требований в очереди,
8. Коэффициент загрузки прибора обслуживания,
9. Среднее
количество
приборов
занятых
обслуживанием.
4.
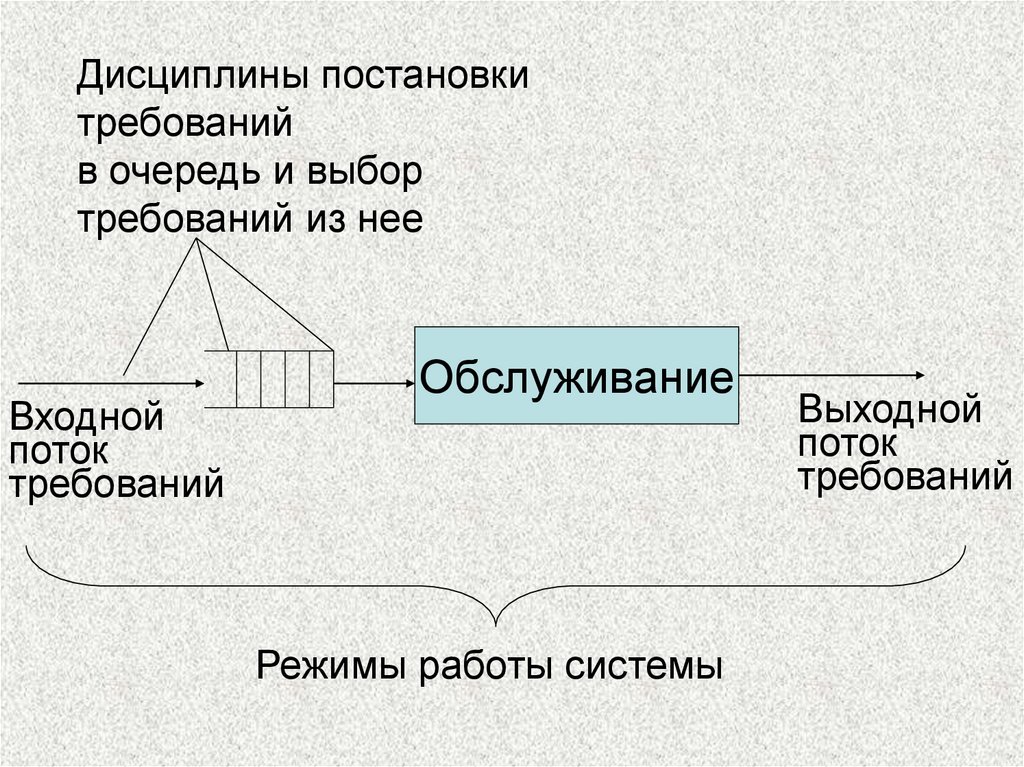
Дисциплины постановкитребований
в очередь и выбор
требований из нее
Входной
поток
требований
Обслуживание
Режимы работы системы
Выходной
поток
требований
5.
Входной поток требованийПуассоновский (простейший) поток
( t ) k t
Pk (t )
e , k 0, t 0
k!
èíòåíñèâíî ñòü ïîòîêà
(êîëè÷åñòâî òðåáîâàíèé â åäèíèöó âðåìåíè ).
T
t
F (t ) P, T t âåðîÿòíîñò
ü òîãî , ÷òî T t
6.
F (t ) 1 P0 ,( t ) 0 t
t
P0
e
e
,
0!
F (t ) 1 e t , t 0,
Ïëîòíîñòü
f(t) e - t
f (t )
f (t )
t
t
7.
Свойства пуассоновского потокастационарность
отсутствие
последствий
ординарность
Стационарность: вероятность прихода определенного
количества требований за время t зависит только от
длины t и λ.
Отсутствие последствия: вероятность прихода
определенного количества требований за промежуток
t зависит от числа требований, поступивших в систему
(предистории).
Ординарность
Поток ординарен, если невозможен приход двух и
Более требований одновременно.
8.
Поток Эрланга (ПЭ)ПЭ 1-го порядка (пуассоновский)
t
ПЭ 2-го порядка
t
ПЭ 3-го порядка
t
9.
Дисциплины обслуживанияочередей
FIFO
LIFO
Random
Выходной
поток требований
Выходной
поток обслуженных
требований
Выходной
поток не обслуженных
требований
10.
Правила обслуживания требованийОбслуживание
в СМО
одноканальное
многоканальное
Дисциплины
обслуживания
без приоритета
с приоритетом
11.
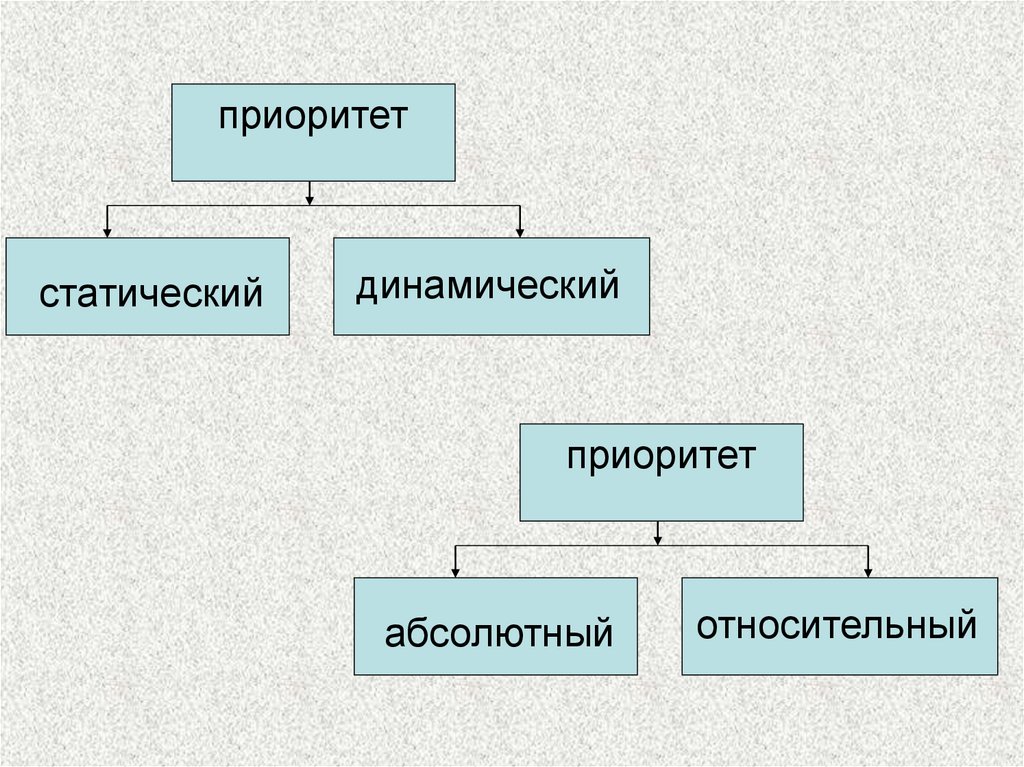
приоритетстатический
динамический
приоритет
абсолютный
относительный
12.
Типы моделей СМОX/Y/Z
где X - распределение времени прибытия требований,
Y - распределение времени обслуживания,
Z - количество приборов.
Например,
M/M/1
G/G/m
D/D/1
M/G/1
где М - марковский процесс,
D - дискретный процесс,
G - произвольное распределение.
13.
Закон сохранения стационарной очереди(формула Литтла)
количество
требований
12
(t )
N(t)
10
8
6
4
2
(t )
(t )
0
(t ) - случайный процесс прихода требований за промежуток
(0, t),
(t ) - выходной поток требований из системы на промежутке
(0, t),
(t ) - общая «работа» (произведение количества требований
на время их пребывания в СМО за промежуток (0, t)),
N (t ) (t ) (t )
14.
(t )(t )
èíòåíñèâíî
ñòü ïîñòóïëåíè
ÿ òðåáîâàíèé ,
t
(t)
T(t)
ñðåäíåå âðåìÿ ïðåáûâàíèÿ òðåáîâàíèé â
t
ñèñòåìå çà âðåìÿ (0, t),
N t tTt ,
lim t ,
t
T lim Tt ,
t
N T .
N lim N t ,
t












 Математика
Математика








