Марковские системы массового обслуживания

1. МАРКОВСКИЕ СМО

Системы массового обслуживания относятся к
марковским системам, если они описываются с
помощью дискретных марковских цепей.
Для анализа марковских СМО можно применять
аналитические методы решения

2. СЛУЧАЙНЫЕ ПРОЦЕССЫ (ЦЕПИ)

3. МАРКОВСКИЕ ЦЕПИ

4. Уравнения Чемпмена – Колмогоpова

5. ГРАФ СОСТОЯНИЙ ЦЕПИ

Маpковские процессы удобно изображать в виде графа
состояний (переходов):
1/5
2
1
1/2
4/5
2/5
3/5
J
3
1/2
Рис. 3.4. Граф состояний
2
0
5
1
0
5
1 0
2
3
5
4
5
1
2
Около каждой вершины записываются соответствующее
состояние En, а около дуги Pij – вероятность перехода .

6. ГРАФ ПЕРЕХОДОВ ПУАССОНОВСКОГО ПОТОКА ЗАЯВОК

Обозначим состояния E0 , E1 , E2 , … – появление нулевого
числа заявок, одной заявки, двух заявок и т.д. в течение
интервала времени (0,t) .
Для простейшего потока вероятность не появления заявки на
интервале dt: P0(dt) = (1 – λdt ).
Вероятность появления одной заявки: P1(dt) = λdt.
1– dt
1– dt
dt
dt
E0
1– dt
E1
dt
E2
Рис. 3.5. Граф переходов пуассоновского потока

7. ОДНОКАНАЛЬНАЯ СМО С ОЖИДАНИЕМ

Рассмотрим процесс обслуживания клиентов на почте.
Входной поток событий (появление клиента на почте) при
определенных ограничениях можно принять за простейший
(стационарный, ординарный, без последействия).
При определенных условиях время обслуживания клиентов на
почте распределено по экспоненциальному закону, и,
следовательно, формируемый выходной поток клиентов будет
обладать свойствами пуассоновского.
Дисциплина очереди: без приоритетов. Кроме того, клиент,
вставший в очередь на обслуживание, не покинет ее до тех
пор, пока требование не будет удовлетворено.

8. ЗАКОНЫ ОБСЛУЖИВАНИЯ. АППРОКСИМАЦИЯ ПОКАЗАТЕЛЬНЫМ ЗАКОНОМ

f1
f2
t
f
3
t1
.
t2
t3
А).
Гистограмма
и
экспоненциальный
закон
распределения
времени
обслуживания клиентов на
почте (марки и конверты,
заказные
письма,
почтовые
переводы).

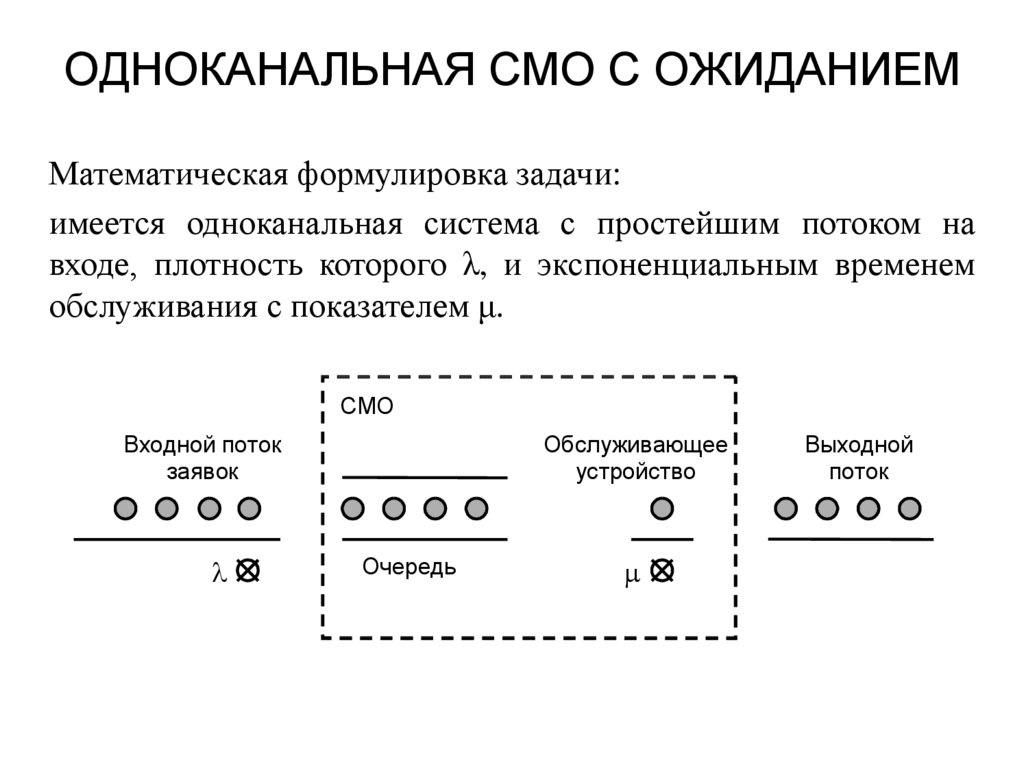
9. ОДНОКАНАЛЬНАЯ СМО С ОЖИДАНИЕМ

Математическая формулировка задачи:
имеется одноканальная система с простейшим потоком на
входе, плотность которого λ, и экспоненциальным временем
обслуживания с показателем μ.
СМО
Входной поток
заявок
Обслуживающее
устройство
Очередь
Выходной
поток
заявок

10. ОДНОКАНАЛЬНАЯ СМО С ОЖИДАНИЕМ

En – состояние системы, когда в ней находится n заявок.
На малом интервале времени (t, t+dt) могут произойти
следующие переходы с соответствующими вероятностями:
• E0 E0 с вероятностью (1 – λdt) ;
• En En+1 с вероятностью λdt ;
• En En-1 (n > 0) с вероятностью μdt ;
• En En (n > 0) с вероятностью (1 – λdt – μdt) .
1 – dt
E0
1 – dt – dt
dt
dt
E1
1 – dt – dt
dt
dt
E2
dt
dt

11. ОДНОКАНАЛЬНАЯ СМО С ОЖИДАНИЕМ

Матрица переходов одноканальной СМО
E0
E1
E2
E3
E0 1 dt
dt
0
0
E1 dt 1 ( + ) dt
dt
0
J
E2 0
dt
1 ( + ) dt dt
E
Уравнения вероятностей состояний получаются из матрицы
переходов
P(t+dt) = P (t)J ,
или
P0 (t dt ) (1 dt ) P0 (t ) dtP1 (t )
Pn (t dt ) dtPn 1 (t ) [1 ( )dt ]Pn (t ) dtPn 1 , n 1, 2, ... .

12. ОДНОКАНАЛЬНАЯ СМО С ОЖИДАНИЕМ

После преобразований получим
P0 (t dt) P0 (t )
= P0 (t ) + P1 (t ),
dt
Pn (t dt) Pn (t ) = P (t ) ( )P (t ) μ P (t ) , n=1, 2, ....
n 1
n
n+1
dt
или при
dt 0
dP0 (t )
dt = P0 (t ) + P1 (t ),
dPn (t ) = P (t ) ( )P (t ) μ P (t ) , n=1, 2, ... .
n 1
n
n+1
dt
Получена система линейных дифференциальных уравнений
Колмогорова .

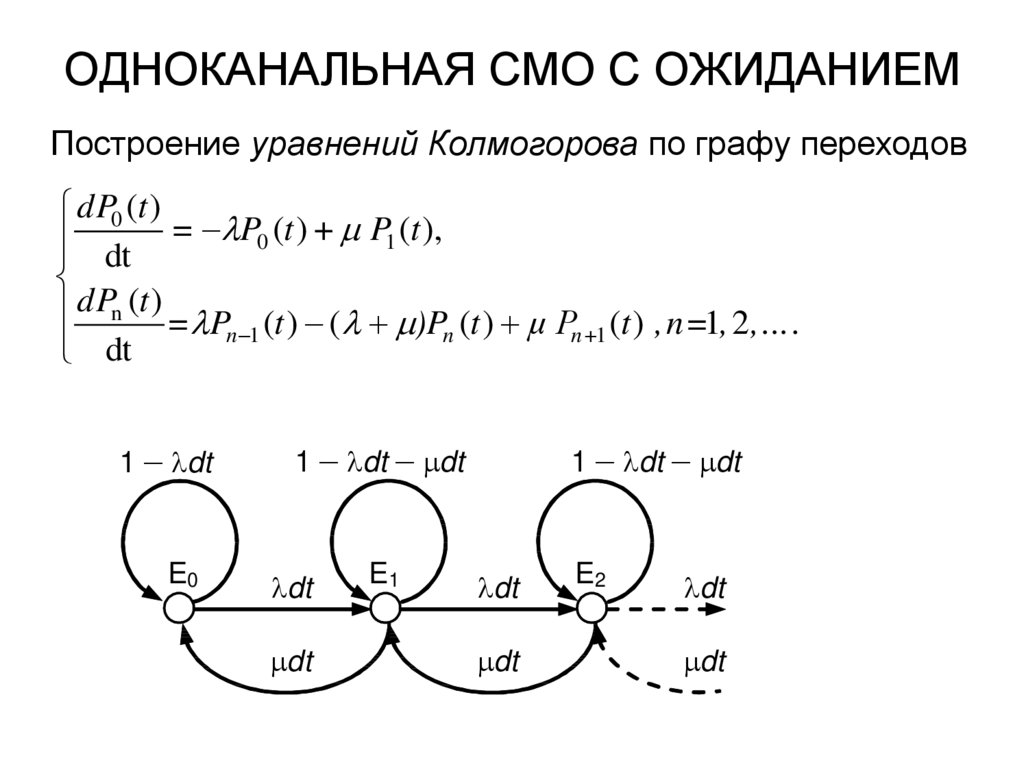
13. ОДНОКАНАЛЬНАЯ СМО С ОЖИДАНИЕМ

Построение уравнений Колмогорова по графу переходов
dP0 (t )
dt = P0 (t ) + P1 (t ),
dPn (t ) = P (t ) ( )P (t ) μ P (t ) , n=1, 2, ... .
n 1
n
n+1
dt
1 – dt
E0
1 – dt – dt
dt
dt
E1
1 – dt – dt
dt
dt
E2
dt
dt

14. ОДНОКАНАЛЬНАЯ СМО С ОЖИДАНИЕМ

Система уравнений Колмогорова
может быть решена,
например, при начальных условиях
P0(0)=1; Pn(0)=0, n=1,2,3,...
В результате будут получены временные характеристики
вероятностей состояний:
P (t ) ( P0 (t ), P1 (t ), P2 (t ), , Pk (t ), )
Если система устойчива, при t ∞ возникнет стационарный
режим, характеризующийся установившимся (финальным)
распределением вероятностей состояний.
Обозначим Ψ =