Похожие презентации:
Преобразование графиков тригонометрических функций
1.
2.
Пусть задан график функции y = f(x)Преобразование вида y = kf(x)
Преобразование вида y = f(x) + b
Преобразование вида y = f(x – a)
Преобразование вида y = f(mx)
Преобразование вида y = |f(x)|
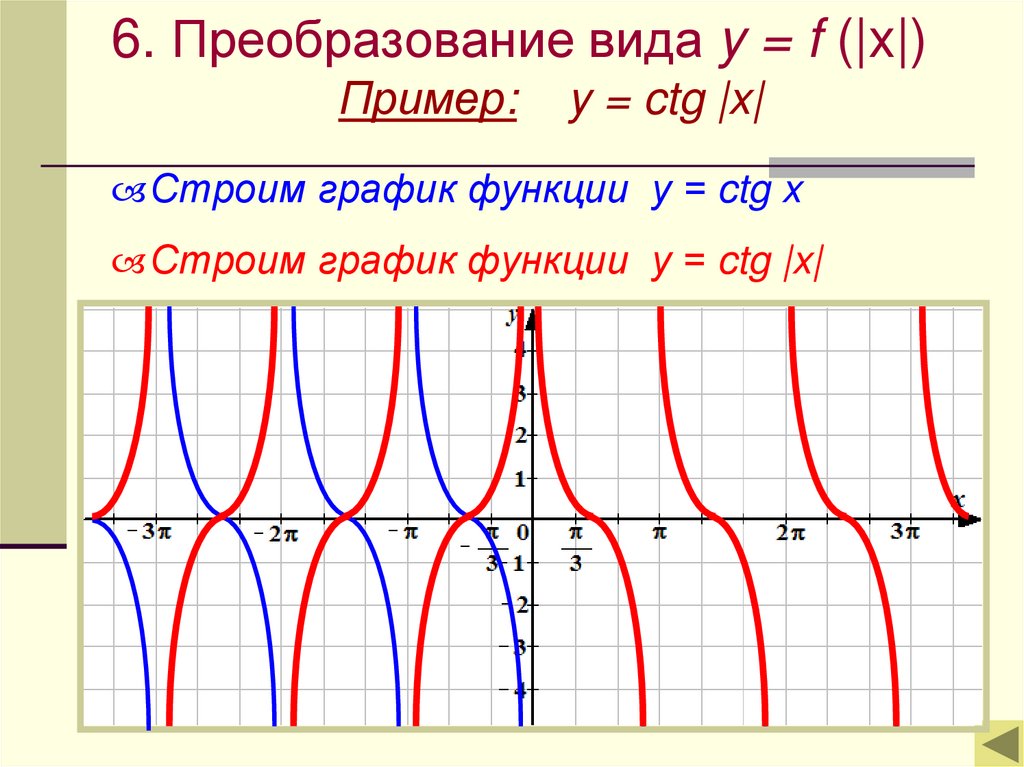
Преобразование вида y = f(|x|)
3.
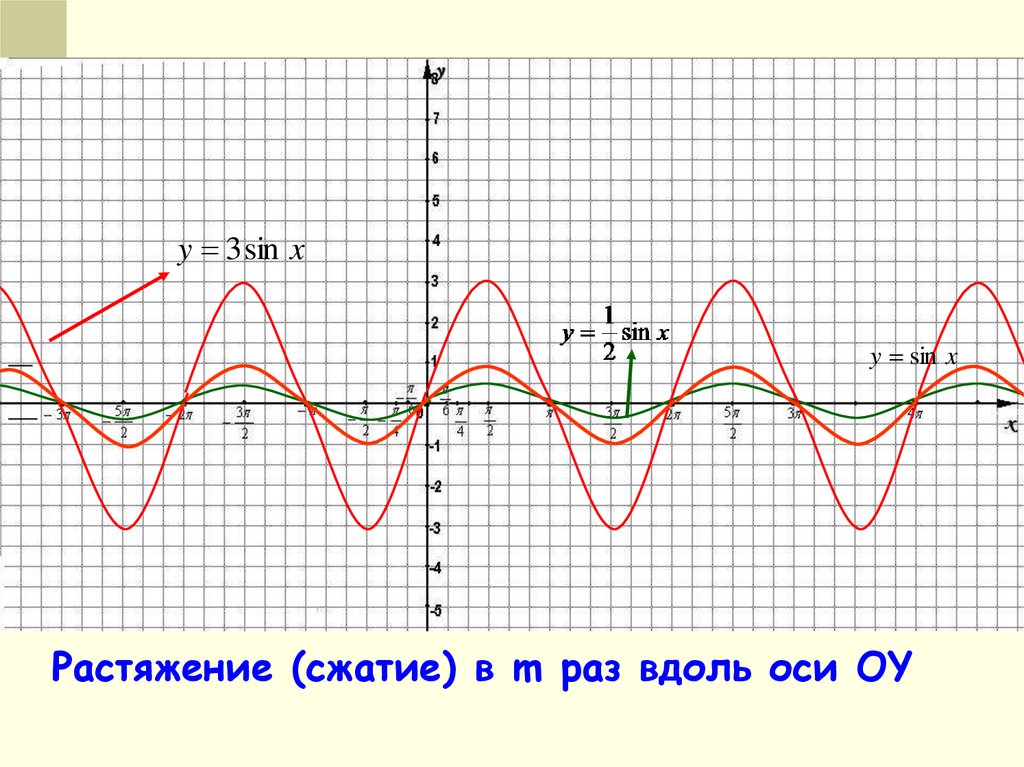
1. Преобразование вида y = kf(x)— Это растяжение (сжатие) в k раз
графика функции y = f(x)
вдоль оси ординат
Если , |k| > 1, то
происходит
Растяжение
Сжатие
Если , |k| < 1,
то происходит
4.
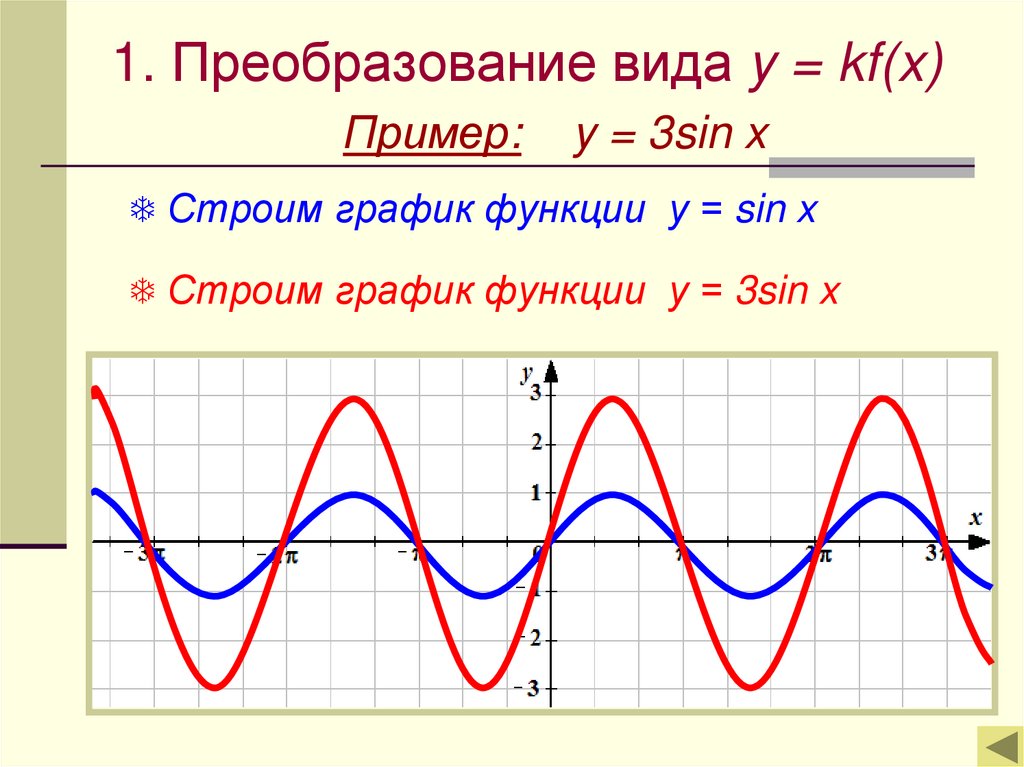
1. Преобразование вида y = kf(x)Пример:
y = 3sin x
Строим график функции у = sin x
Строим график функции у = 3sin x
5.
2. Преобразование вида y = f(x) + b— Это параллельный перенос
графика функции y = f(x) на b единиц
вдоль оси ординат
Если b > 0, то
происходит
смещение
Если b < 0, то
происходит
смещение
6.
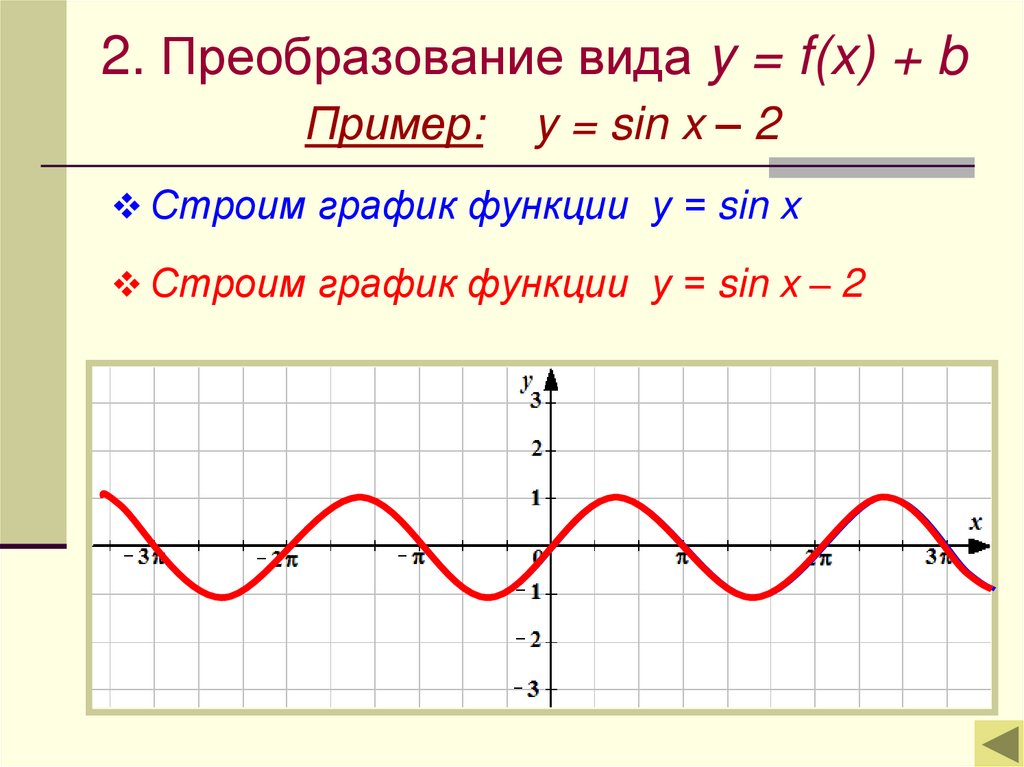
2. Преобразование вида y = f(x) + bПример:
y = sin x – 2
Строим график функции у = sin x
Строим график функции у = sin x – 2
7.
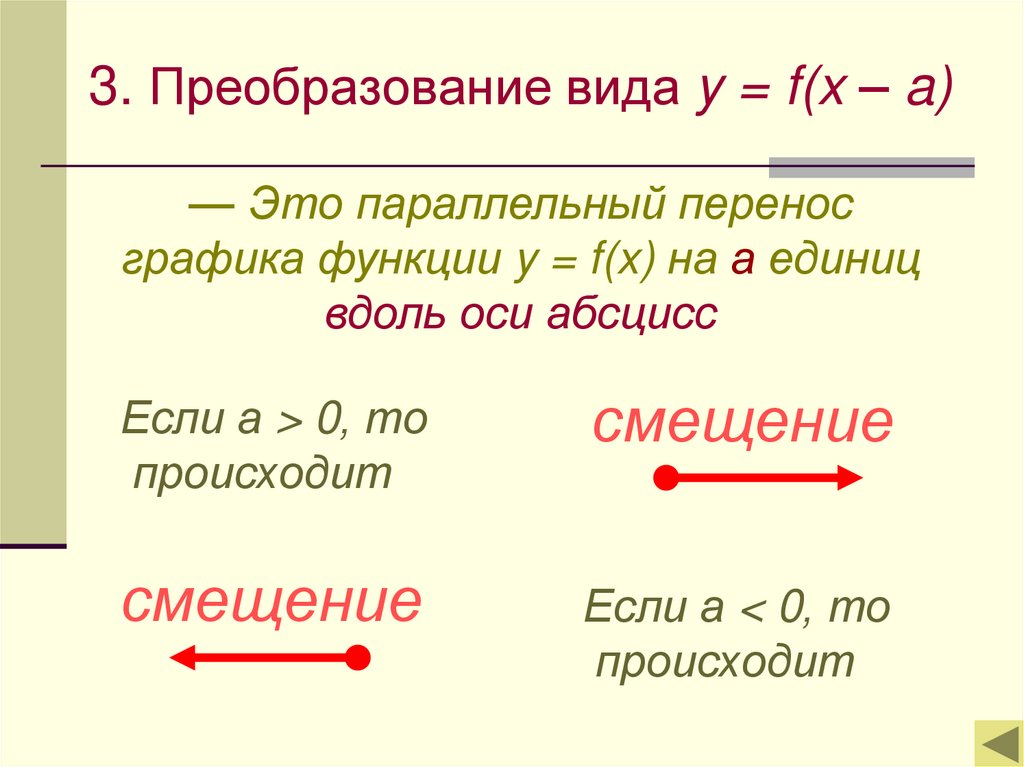
3. Преобразование вида y = f(x – a)— Это параллельный перенос
графика функции y = f(x) на а единиц
вдоль оси абсцисс
Если а > 0, то
происходит
смещение
смещение
Если а < 0, то
происходит
8.
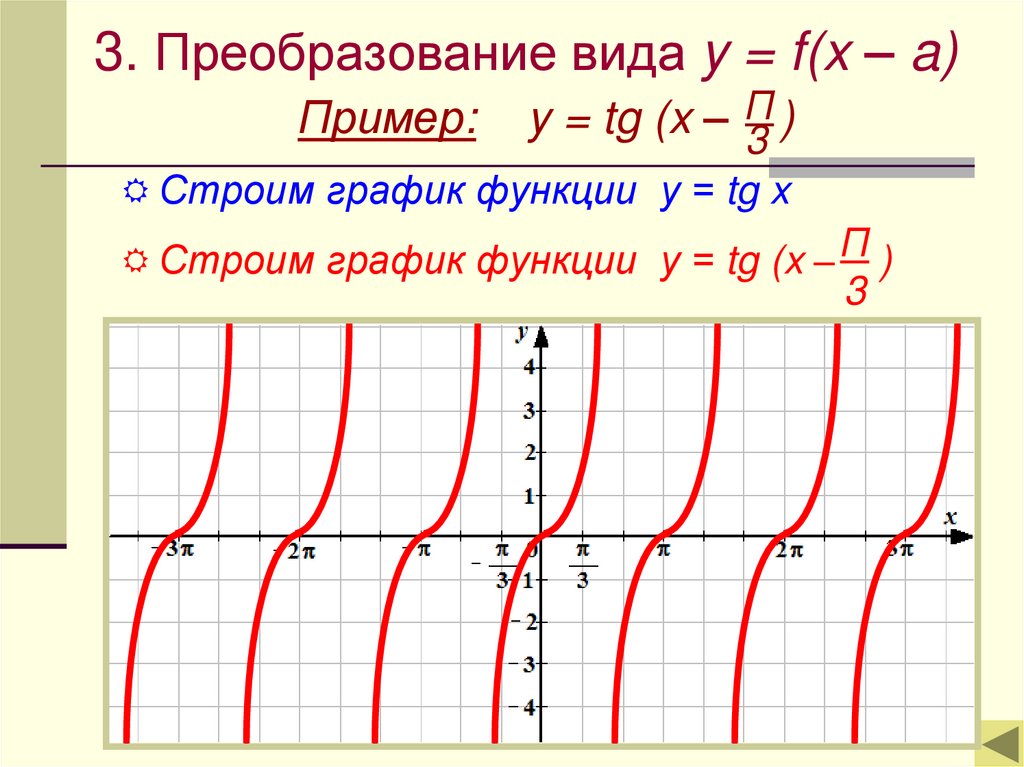
3. Преобразование вида y = f(x – a)Пример:
y = tg (x – Π
)
3
Строим график функции у = tg x
Строим график функции у = tg (x – Π )
3
9.
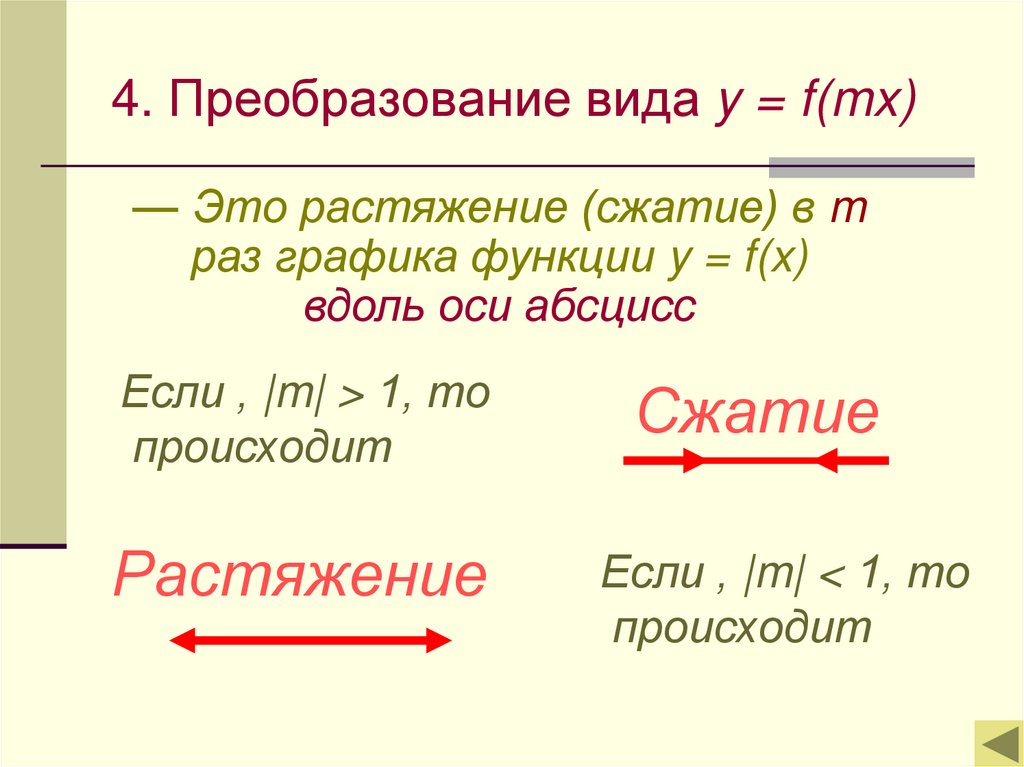
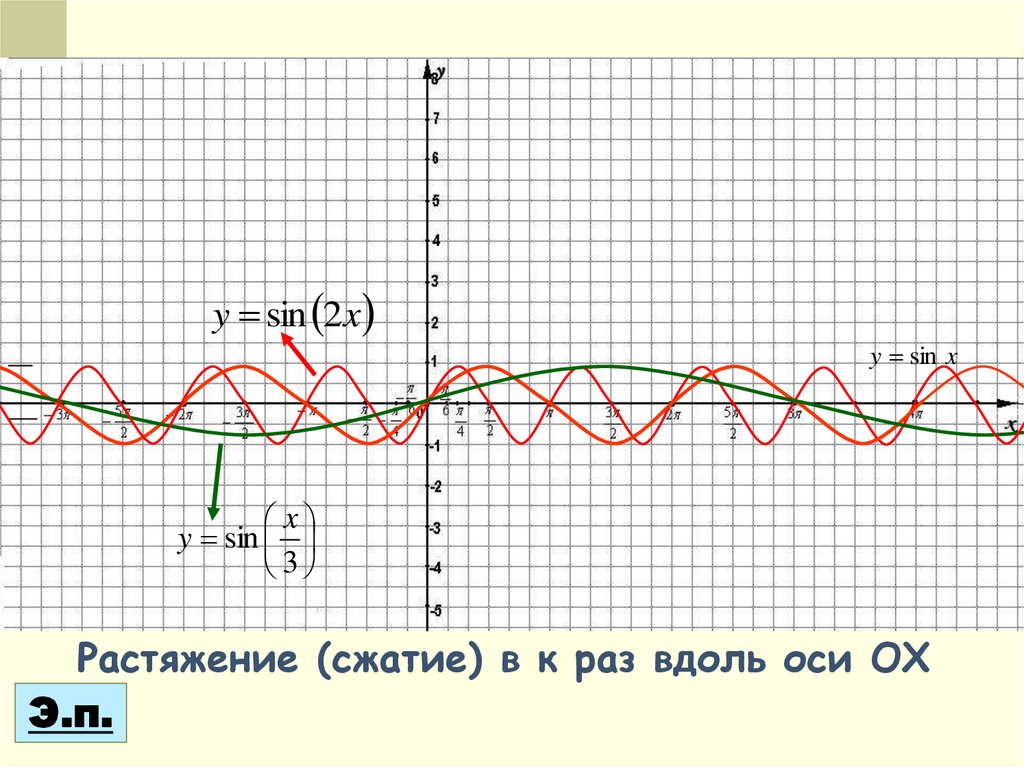
4. Преобразование вида y = f(mx)— Это растяжение (сжатие) в m
раз графика функции y = f(x)
вдоль оси абсцисс
Если , |m| > 1, то
происходит
Сжатие
Растяжение
Если , |m| < 1, то
происходит
10.
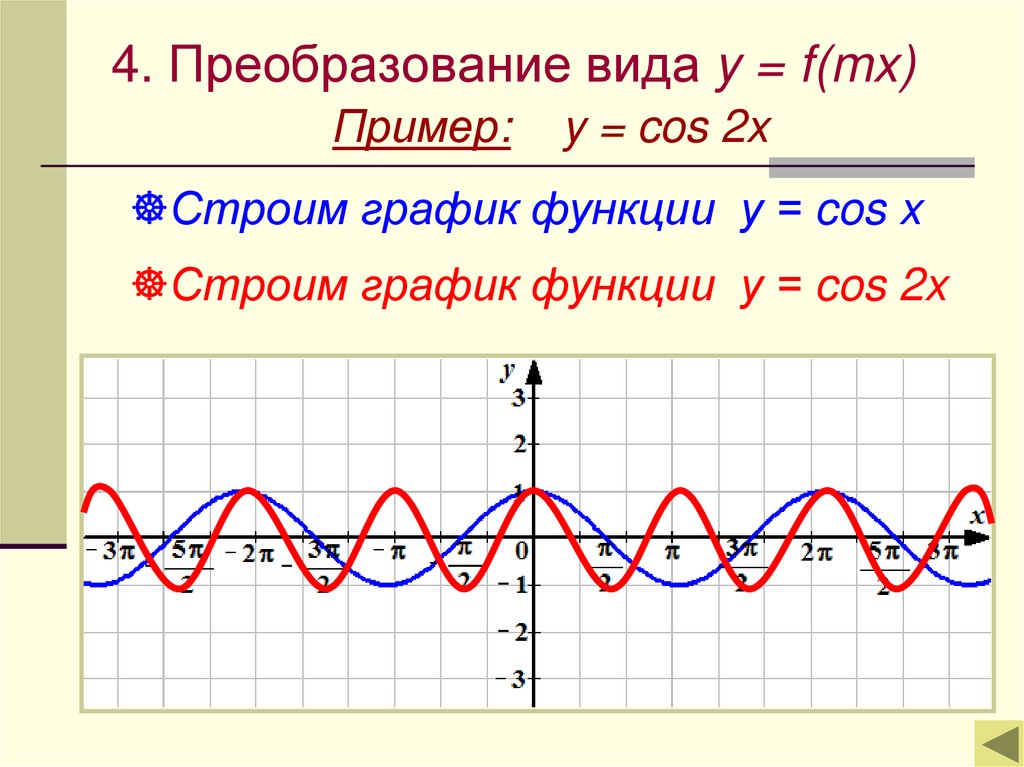
4. Преобразование вида y = f(mx)Пример:
y = cos 2x
Строим график функции у = cos x
Строим график функции у = cos 2x
11.
5. Преобразование вида y = |f(x)|— Это отображение нижней части графика
функции y = f(x) в верхнюю полуплоскость
относительно оси абсцисс
с сохранением верхней части графика
у
y = |f(x)|
y = f(x)
х
0
12.
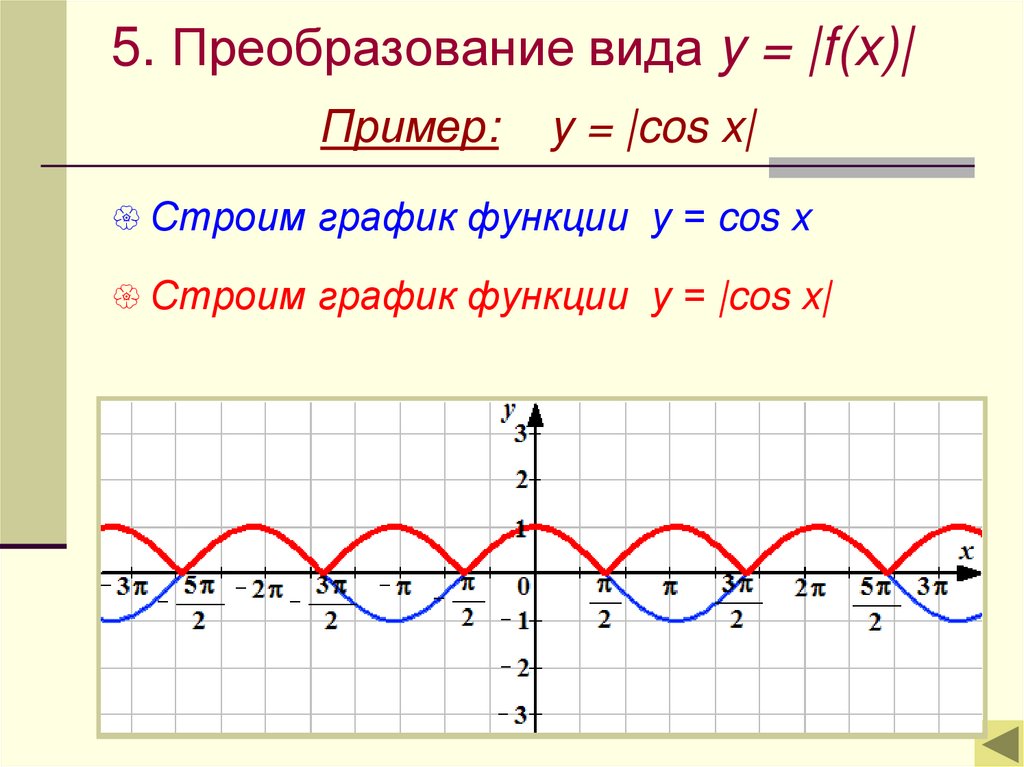
5. Преобразование вида y = |f(x)|Пример:
y = |cos x|
Строим график функции у = cos x
Строим график функции у = |cos x|
13.
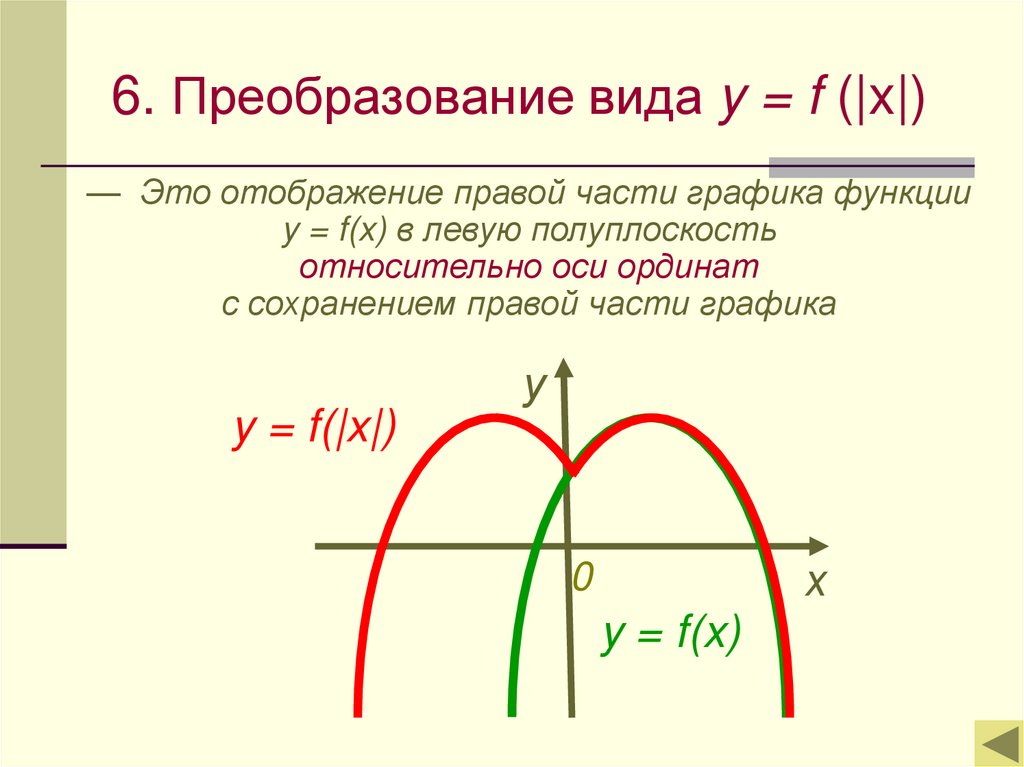
6. Преобразование вида y = f (|x|)— Это отображение правой части графика функции
y = f(x) в левую полуплоскость
относительно оси ординат
с сохранением правой части графика
у
y = f(|x|)
х
0
y = f(x)
14.
6. Преобразование вида y = f (|x|)Пример:
y = ctg |x|
Строим график функции у = ctg x
Строим график функции у = ctg |x|
15.
y 3 sin xy sin x
Растяжение (сжатие) в m раз вдоль оси OY
16.
y sin 2xy sin x
x
y sin
3
Растяжение (сжатие) в к раз вдоль оси OX
Э.п.
17.
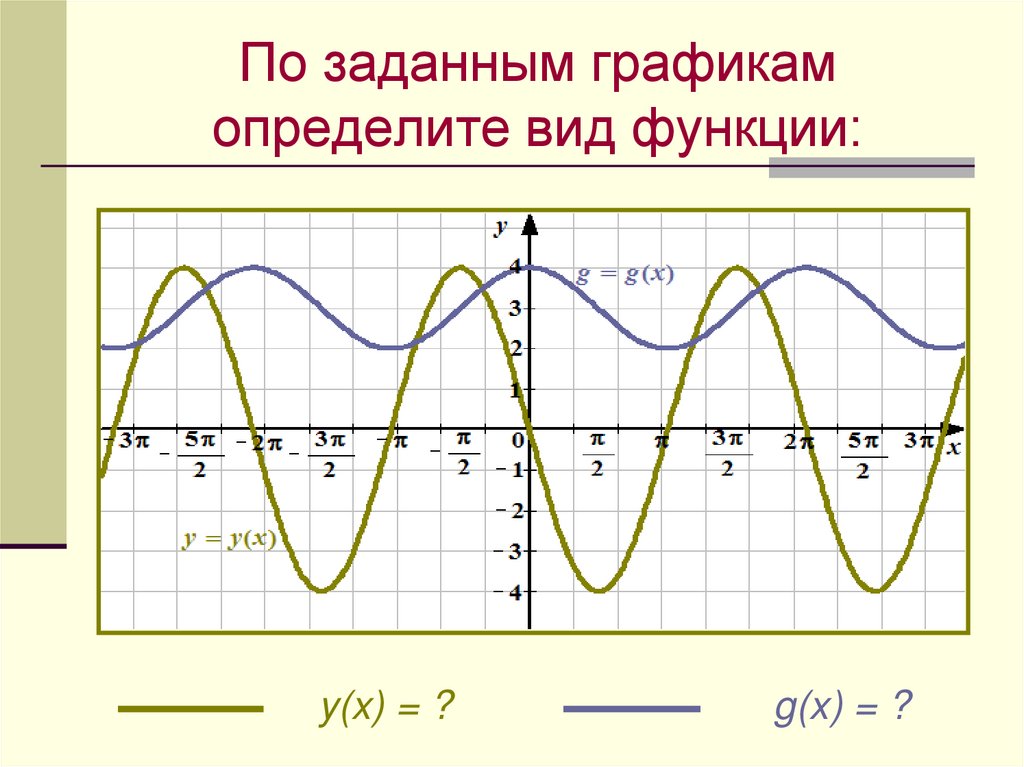
По заданным графикамопределите вид функции:
y(x) = ?
g(x) = ?
18.
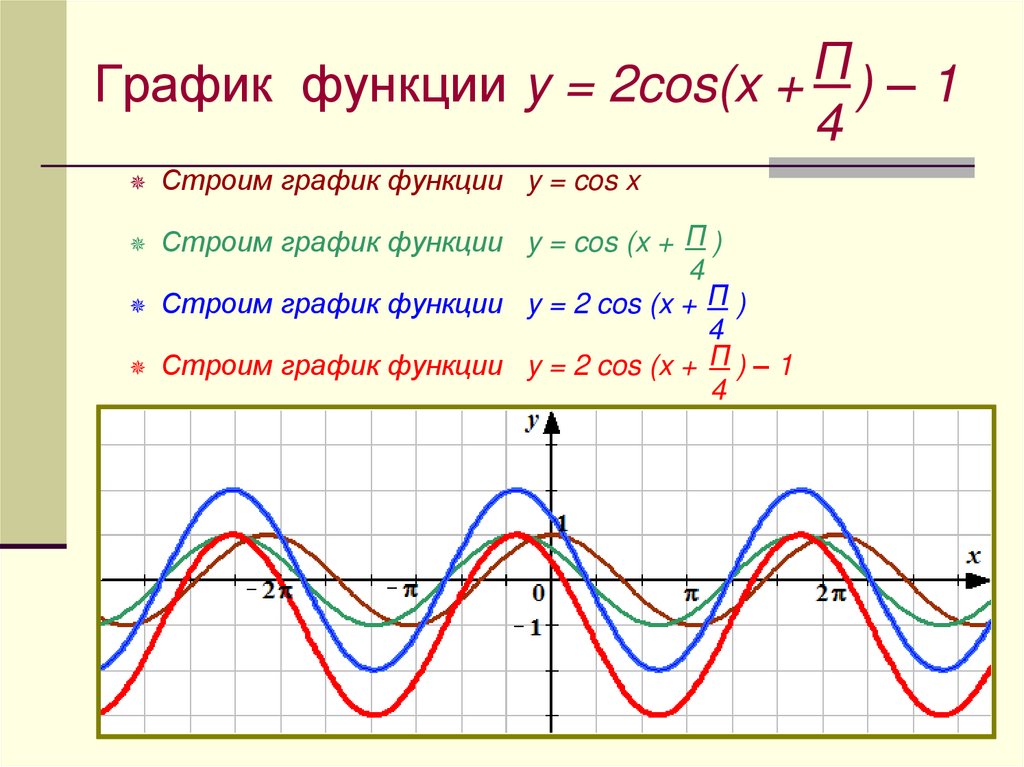
ΠГрафик функции y = 2cos(x + ) – 1
4
Строим график функции
y = cos x
y = cos (x + Π )
4
Строим график функции y = 2 cos (x + Π )
4
Строим график функции y = 2 cos (x + Π ) – 1
4
Строим график функции
19.
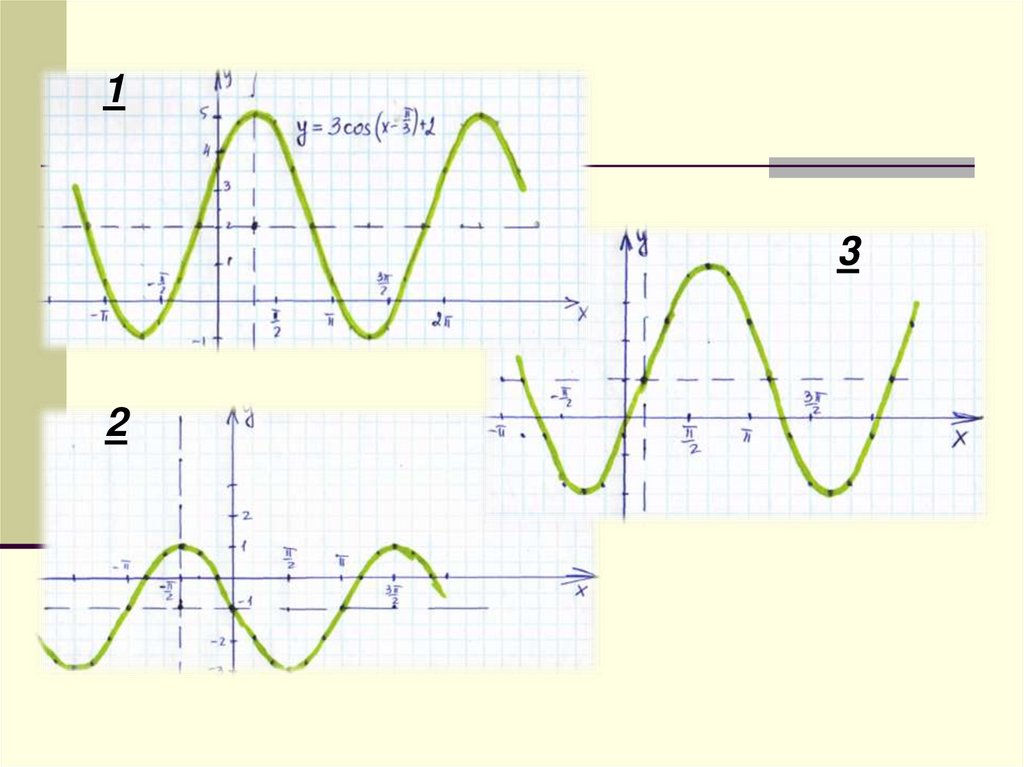
Постройте графикифункций
2
1
3
20.
13
2
21.
Алгоритм построения функцииy=|f(x)|
1) Строим график функции y=f(x)
2)Часть графика лежащую ниже оси Оx
отображаем зеркально вверх, при этом не
меняя часть графика выше оси Оx
22.
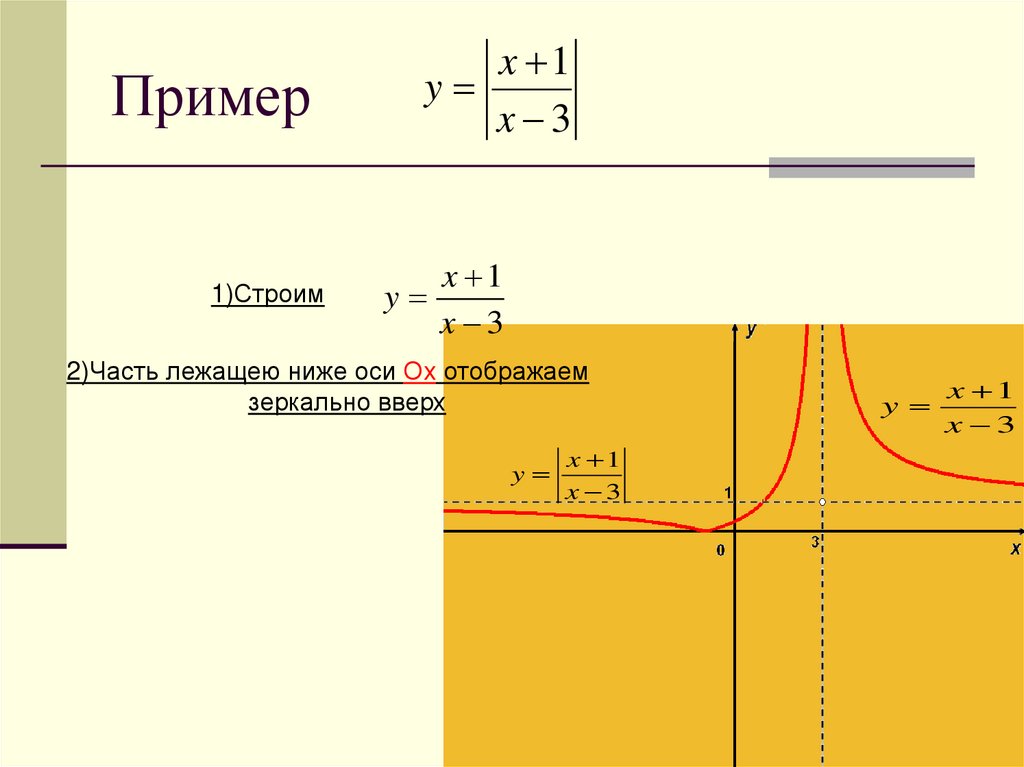
Пример1)Строим
x 1
y
x 3
x 1
y
x 3
2)Часть лежащею ниже оси Оx отображаем
зеркально вверх
y
x 1
x 3
y
x 1
x 3
23.
Алгоритм построения функцииy=f|x|
1)
Строим график функции y=f(x), где
x ≥0
2)
Эту часть графика отображаем
симметрично относительно Oy.
3)
Исходный график: y=f(x), где
и его отображение.
x ≥0
24.
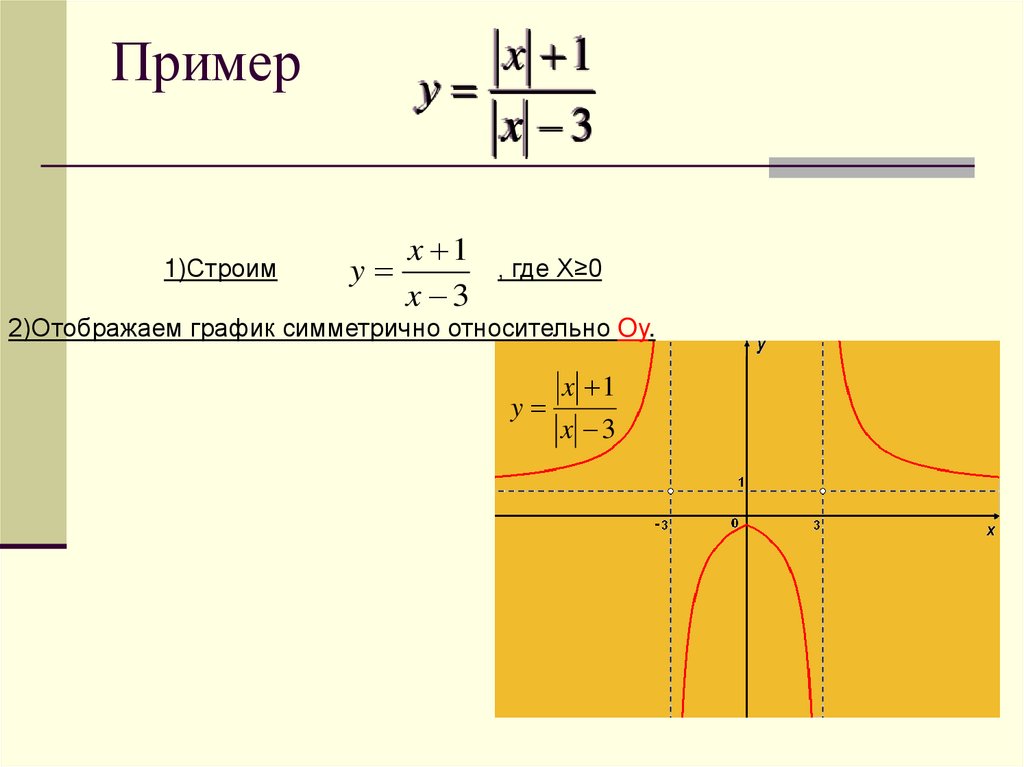
Пример1)Строим
y
x 1
y
x 3
x 1
x 3
, где X≥0
2)Отображаем график симметрично относительно Oy.
y
x 1
x 3
y
x 1
x 3
25.
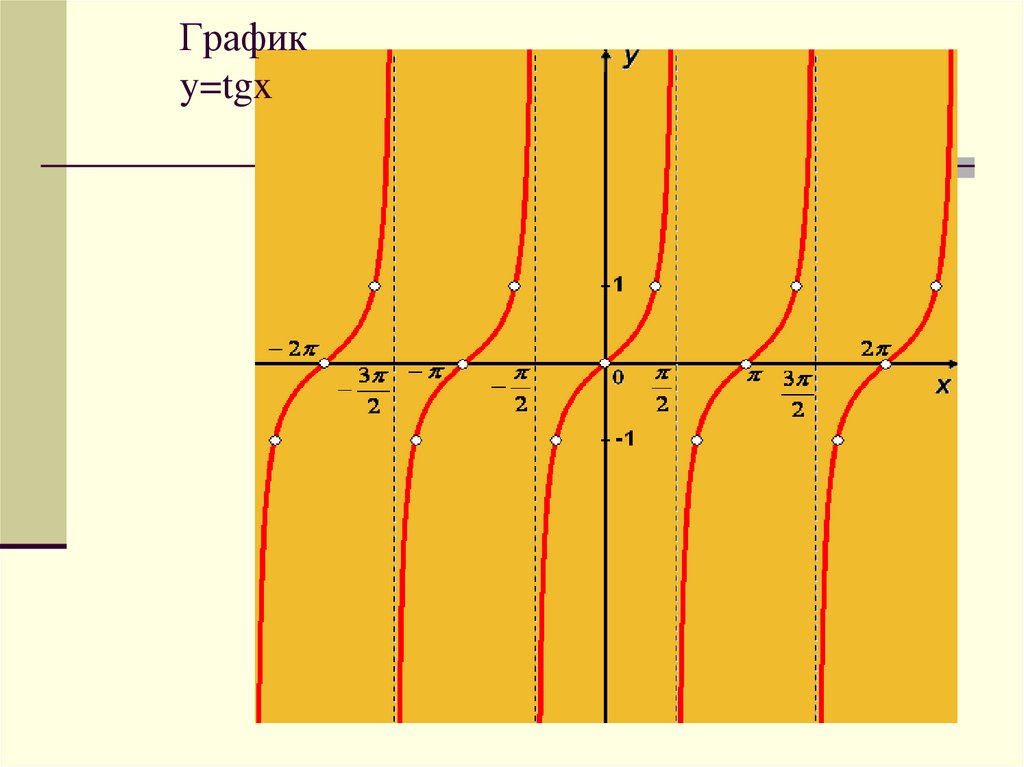
Графикy=tgx
26.
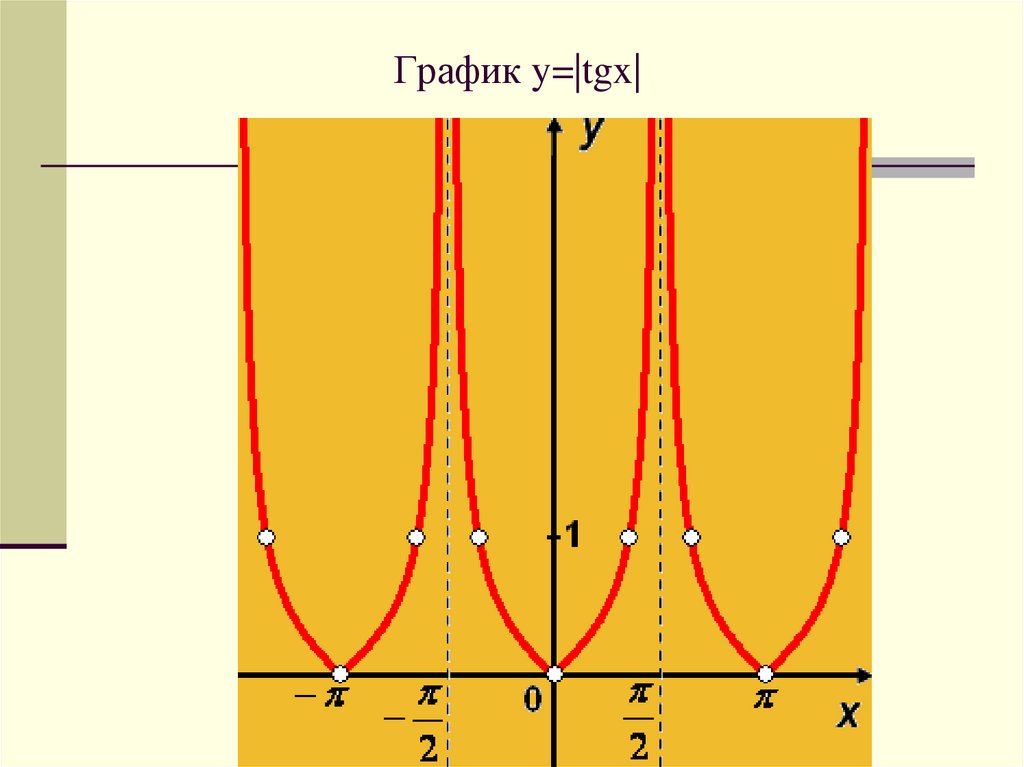
График y=|tgx|27.
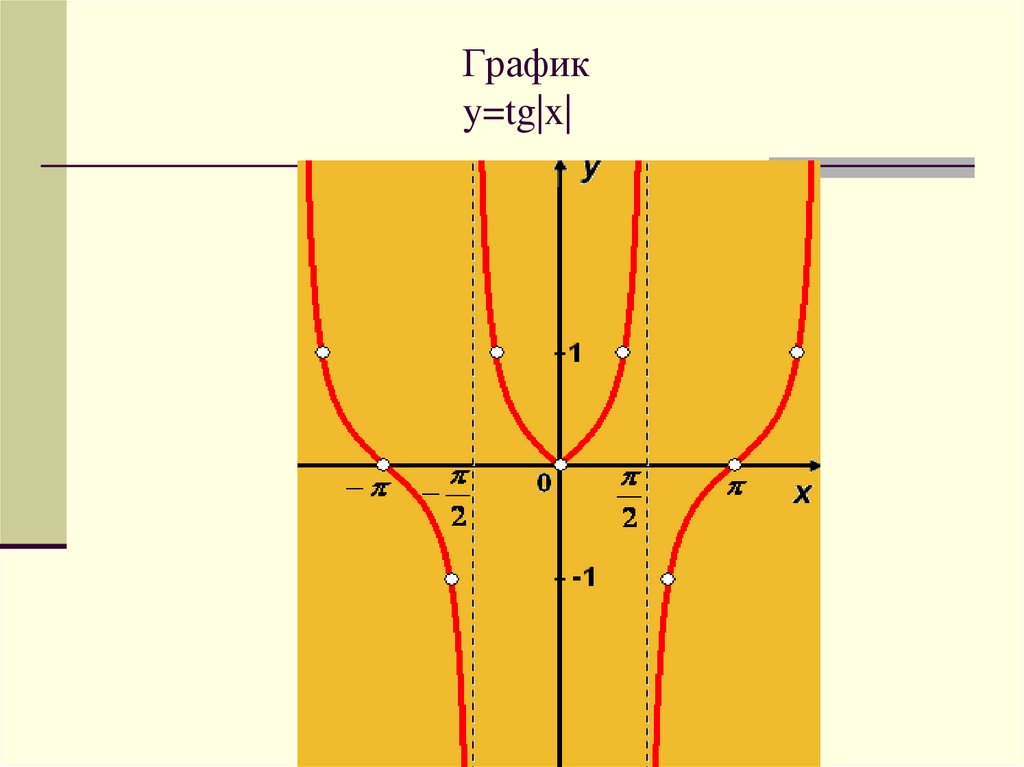
Графикy=tg|x|
28.
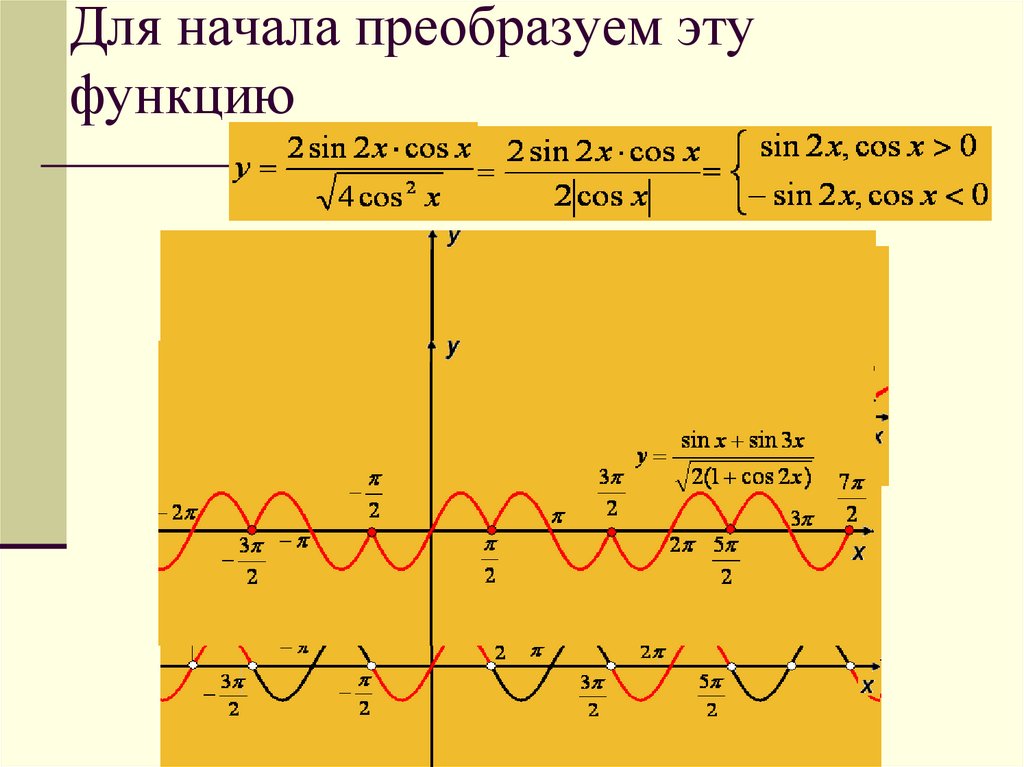
Примеры построения графиковсложных функций
Постройте график:
sin x sin 3 x
y
2(1 cos 2 x )
29.
Для начала преобразуем этуфункцию
30.
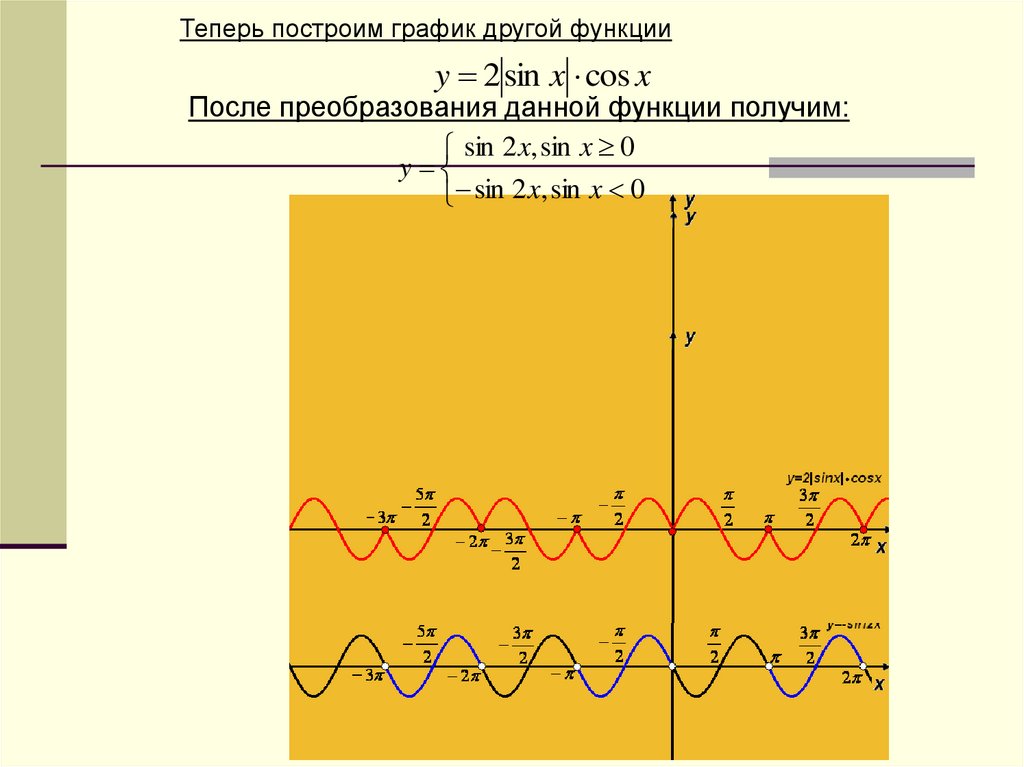
Теперь построим график другой функцииy 2 sin x cos x
После преобразования данной функции получим:
sin 2 x, sin x 0
y
sin 2 x, sin x 0
31.
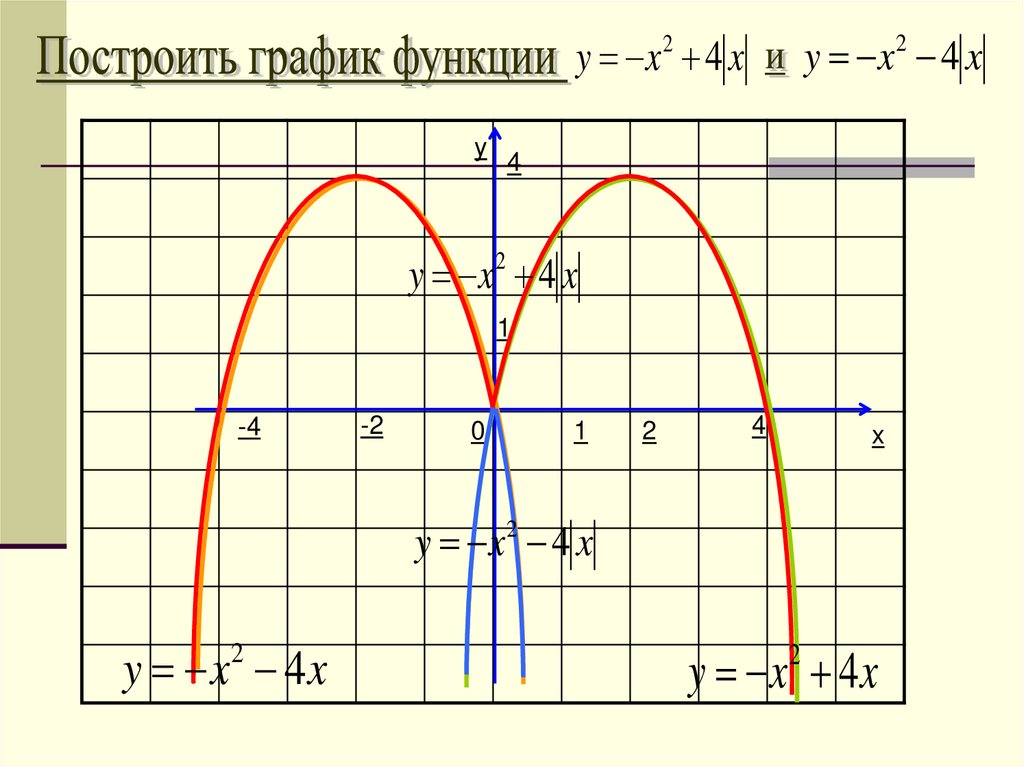
y x2 4 xy x2 4 x
y
4
y x2 4 x
1
-4
-2
0
1
2
4
x
y x2 4 x
y x 4x
2
y x 4x
2
32.
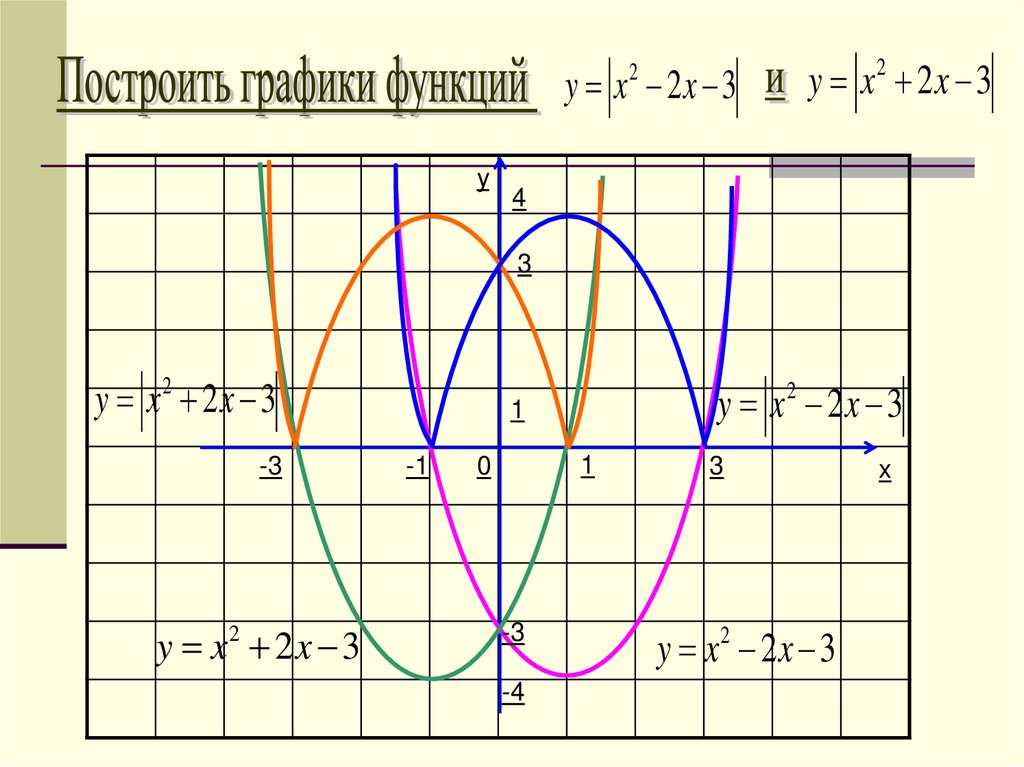
y x 2x 32
y
y x2 2x 3
4
3
y x2 2x 3
-3
y x2 2x 3
y x2 2x 3
1
-1
1
0
-3
-4
3
y x 2x 3
2
x
33.
y x 2 x 32
y
4
3
y x 2 x 3
2
1
-3
-1
1
0
3
y x 2 x 3
2
-3
-4
y x2 2x 3
x
34.
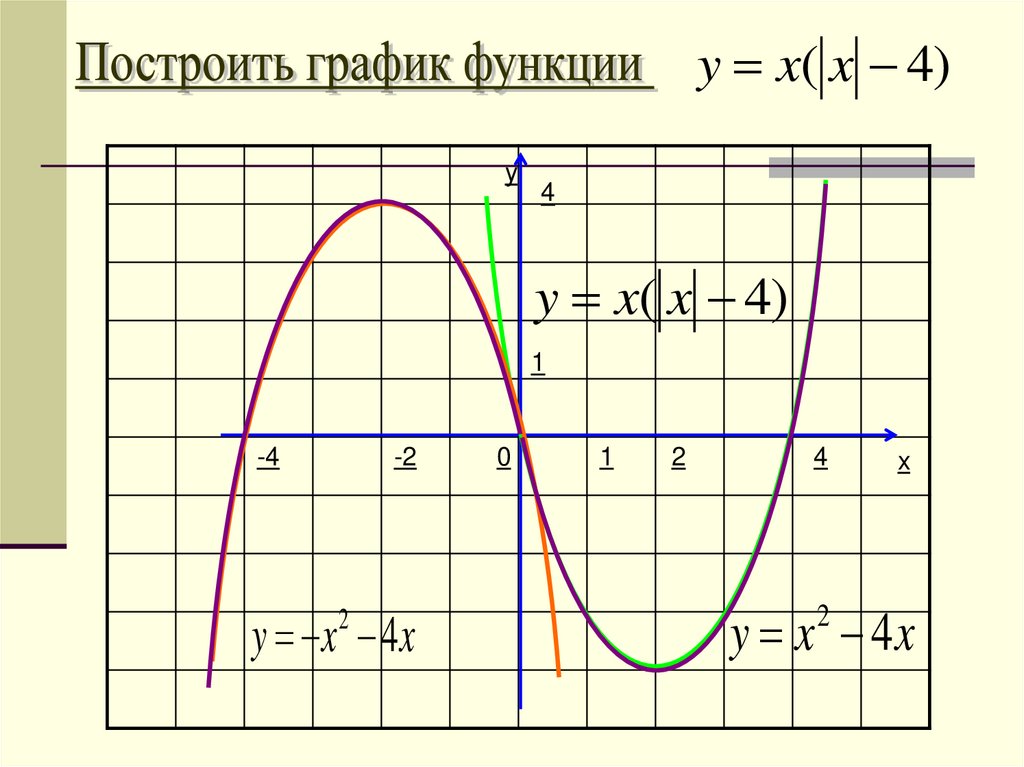
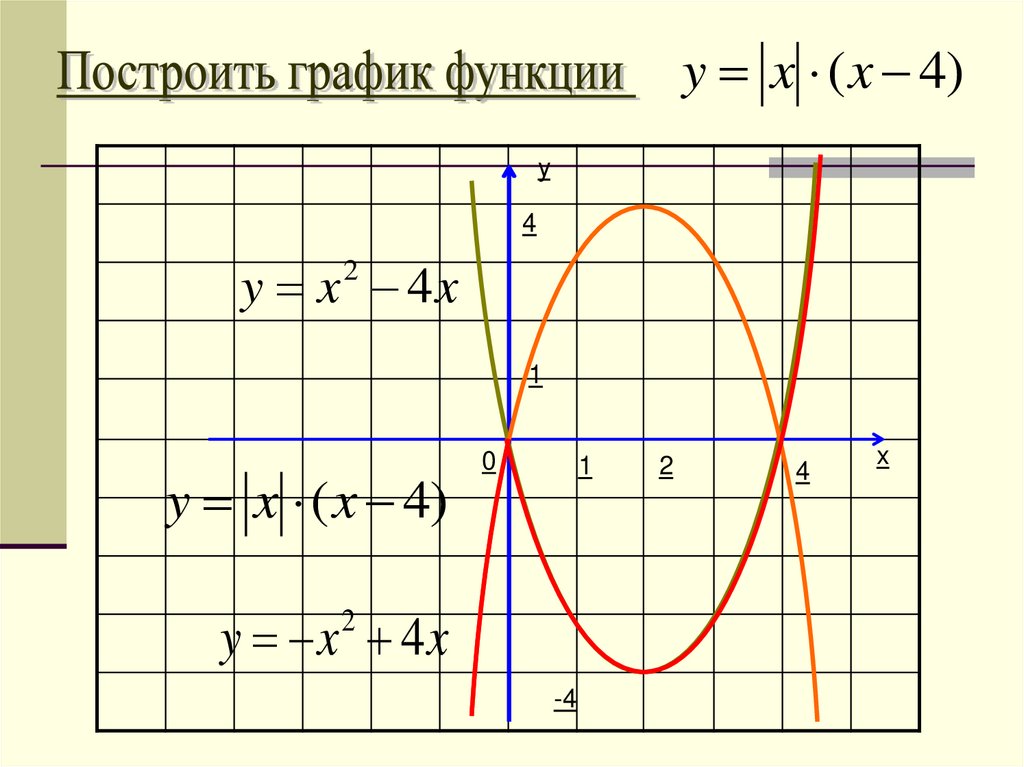
y x( x 4)y
4
y x( x 4)
1
-4
-2
y x 4x
2
0
1
2
4
x
y x 4x
2
35.
y x ( x 4)y
4
y x 4x
2
1
y x ( x 4)
0
1
y x 4x
2
-4
2
4
x
36.
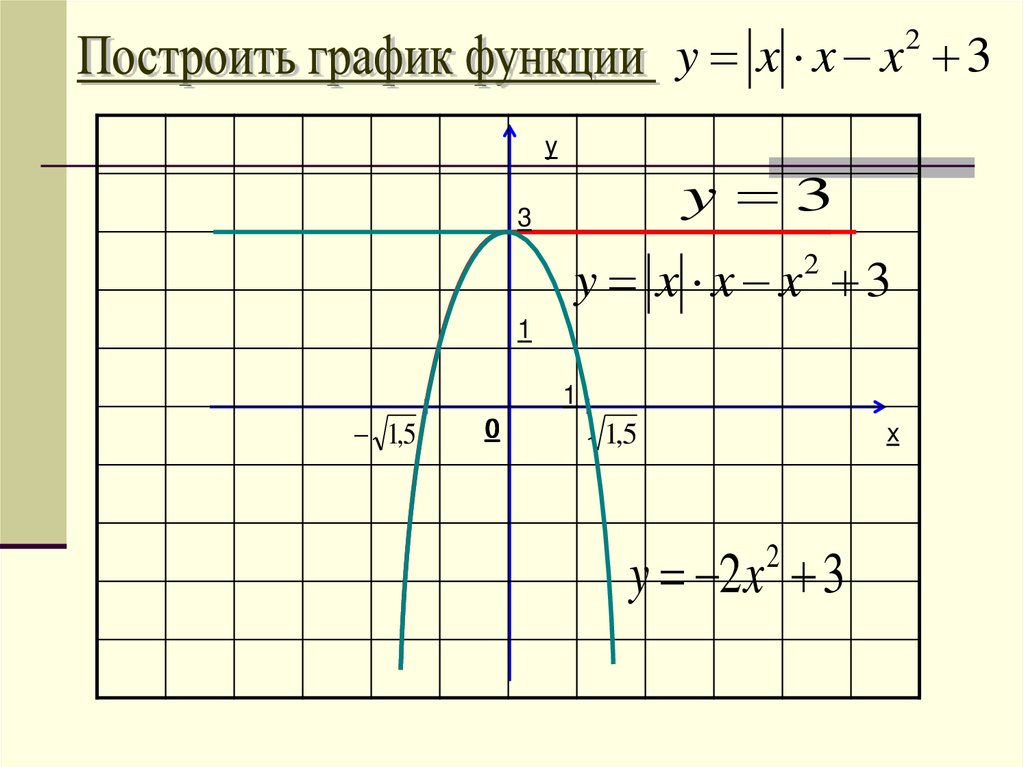
y x x x 32
y
y 3
3
y x x x 3
2
1
1
1,5
0
x
1,5
y 2 x 3
2
37.
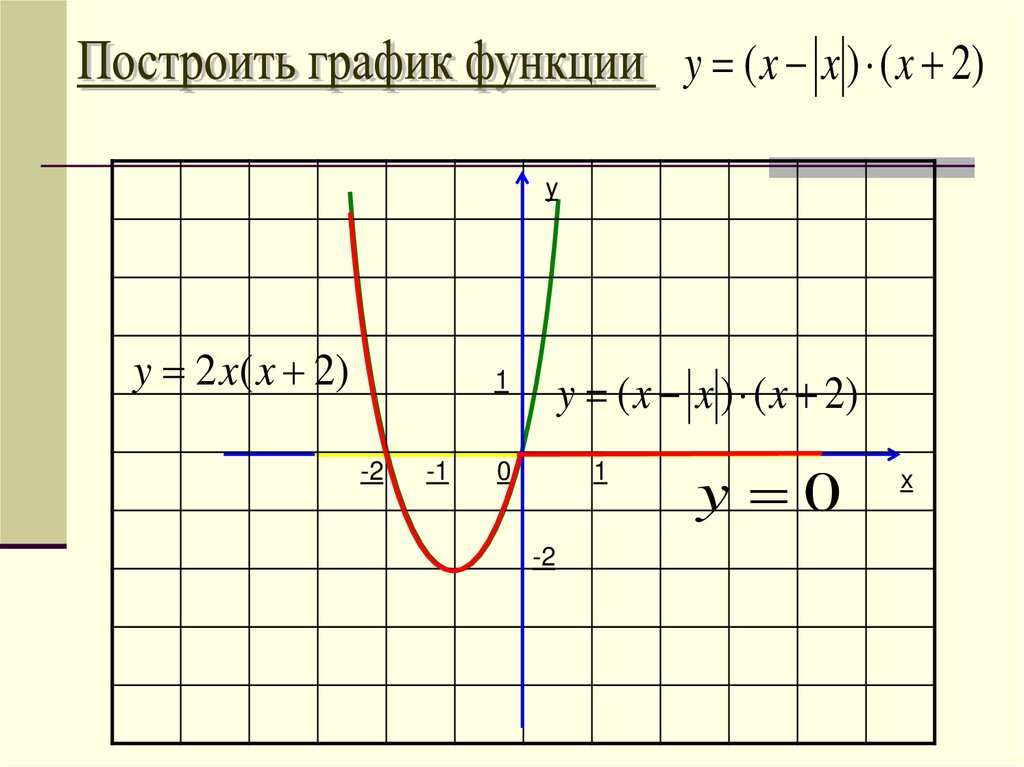
y ( x x ) ( x 2)y
y 2 x( x 2)
y ( x x ) ( x 2)
1
-2
-1
0
1
-2
y 0
x
38.
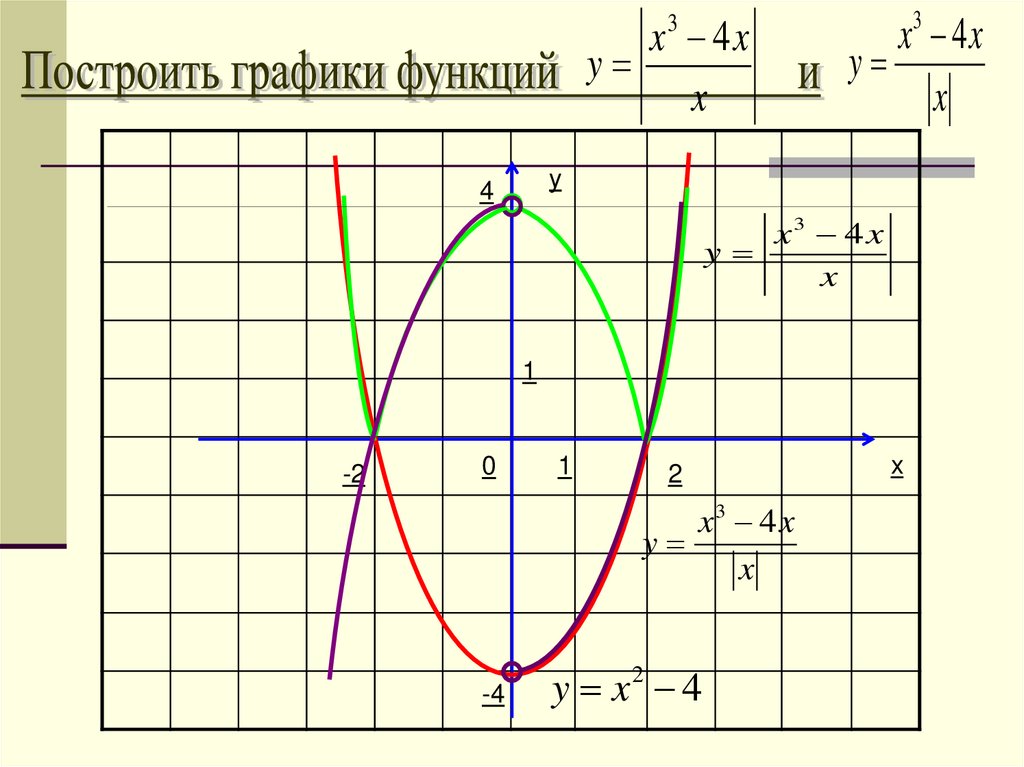
x 4xy
x
3
x3 4 x
y
x
y
4
x3 4x
y
x
1
-2
0
1
2
x3 4 x
y
x
-4
y x2 4
x
39.
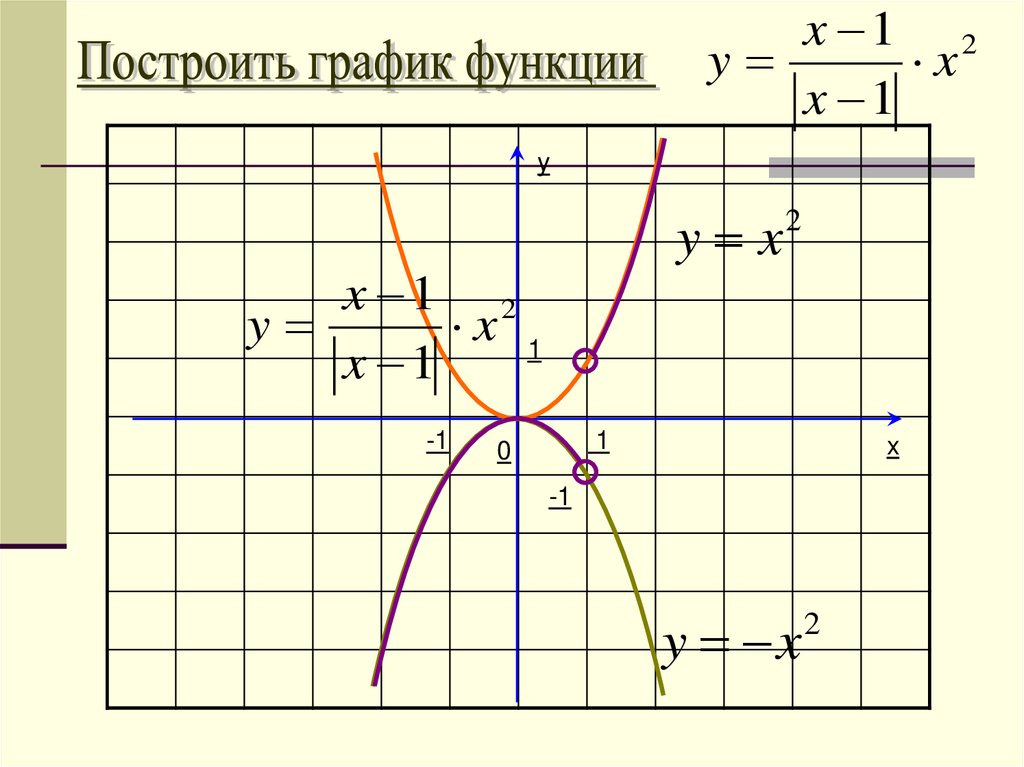
x 1 2y
x
x 1
y
y x
x 1 2
y
x 1
x 1
-1
2
1
0
x
-1
y x
2
40.
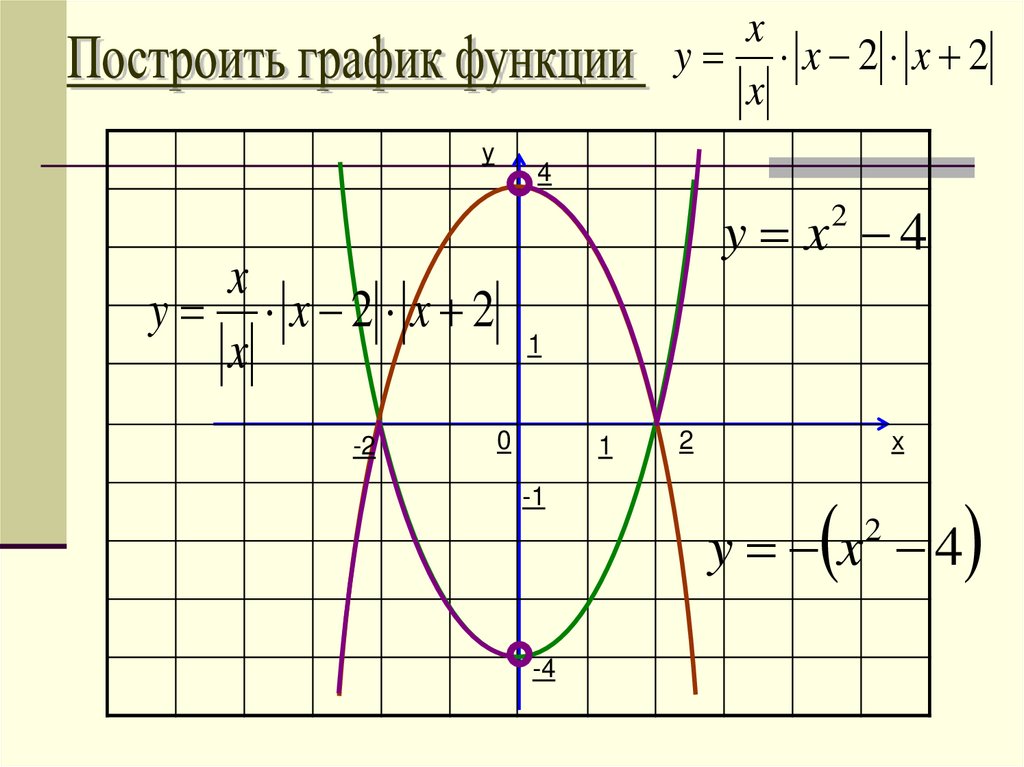
xy x 2 x 2
x
y
4
y x 4
2
x
y x 2 x 2
1
x
-2
0
1
-1
-4
2
x
y x 4
2
41.
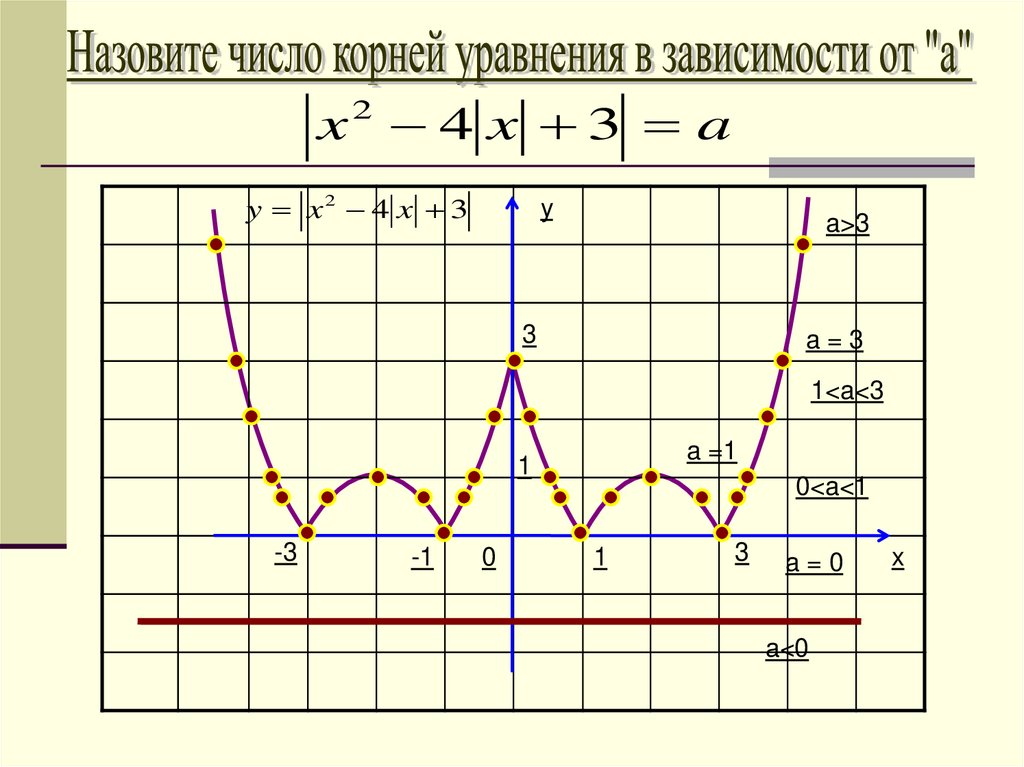
x2 4 x 3 ay x2 4 x 3
y
a>3
3
a=3
1<a<3
a =1
1
-3
-1
0
0<a<1
1
3
a=0
a<0
x
42.
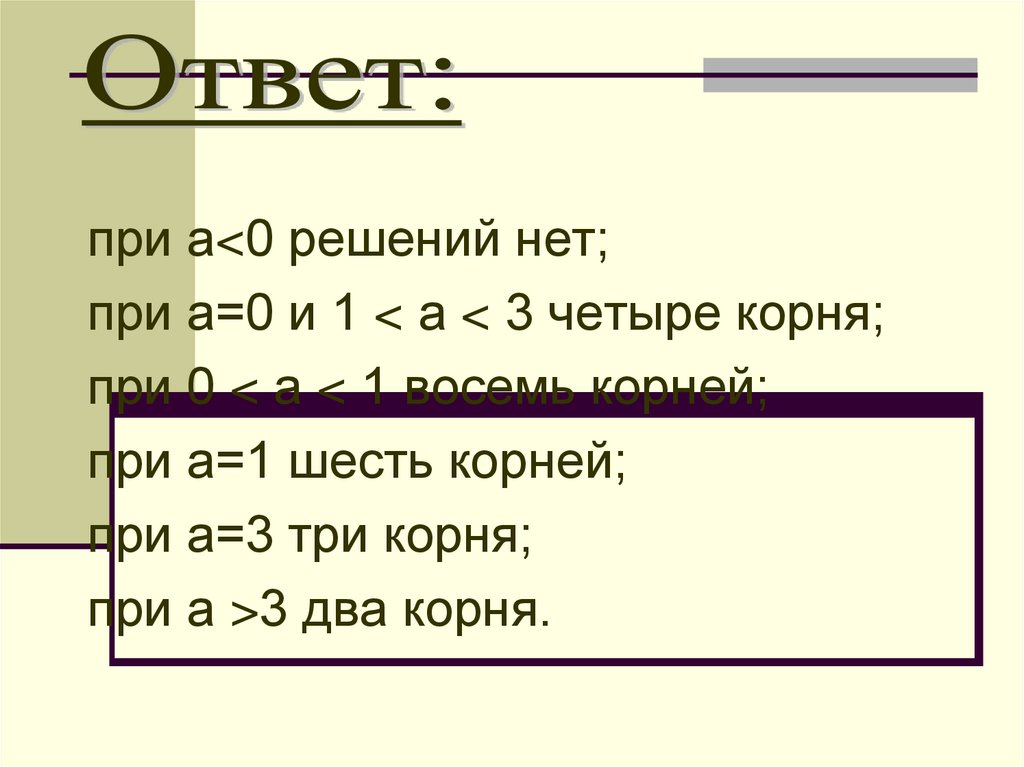
при а<0 решений нет;при а=0 и 1 < а < 3 четыре корня;
при 0 < а < 1 восемь корней;
при а=1 шесть корней;
при а=3 три корня;
при а >3 два корня.











 Математика
Математика








