Кристаллы. Дефекты в кристаллах. Симметрия и способы её описания. Лекция 3

1.

Лекция 3. Кристаллы. Дефекты в кристаллах. Симметрия и способы её описания.

2.

М. Эшер. Три мира

3.

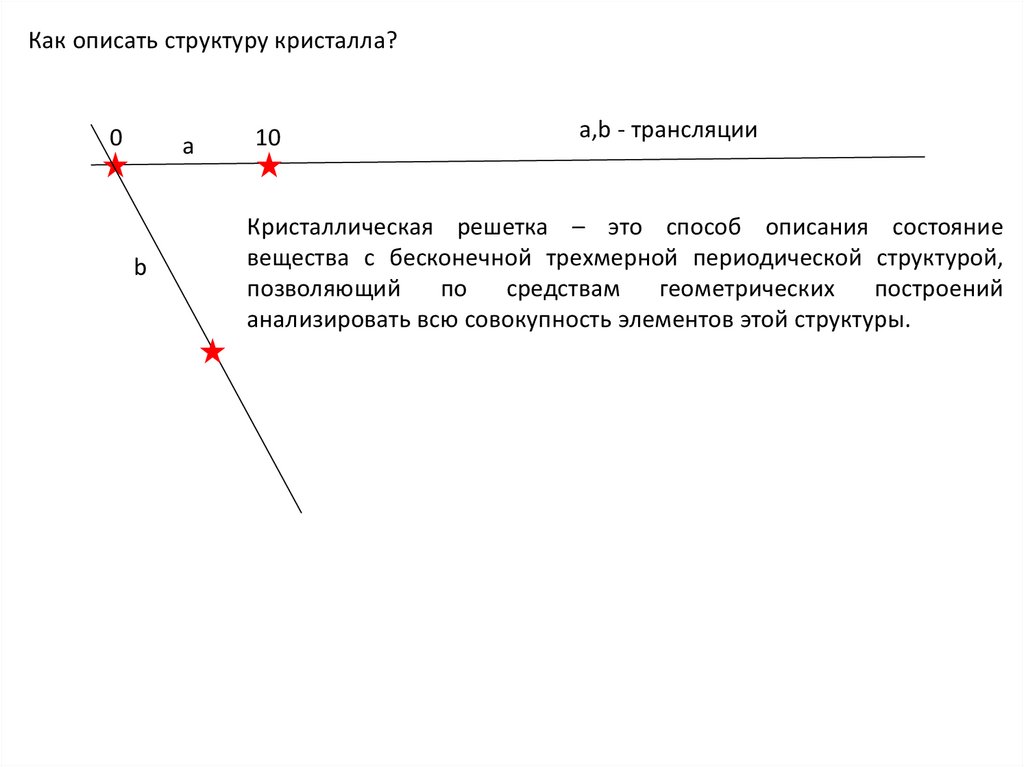
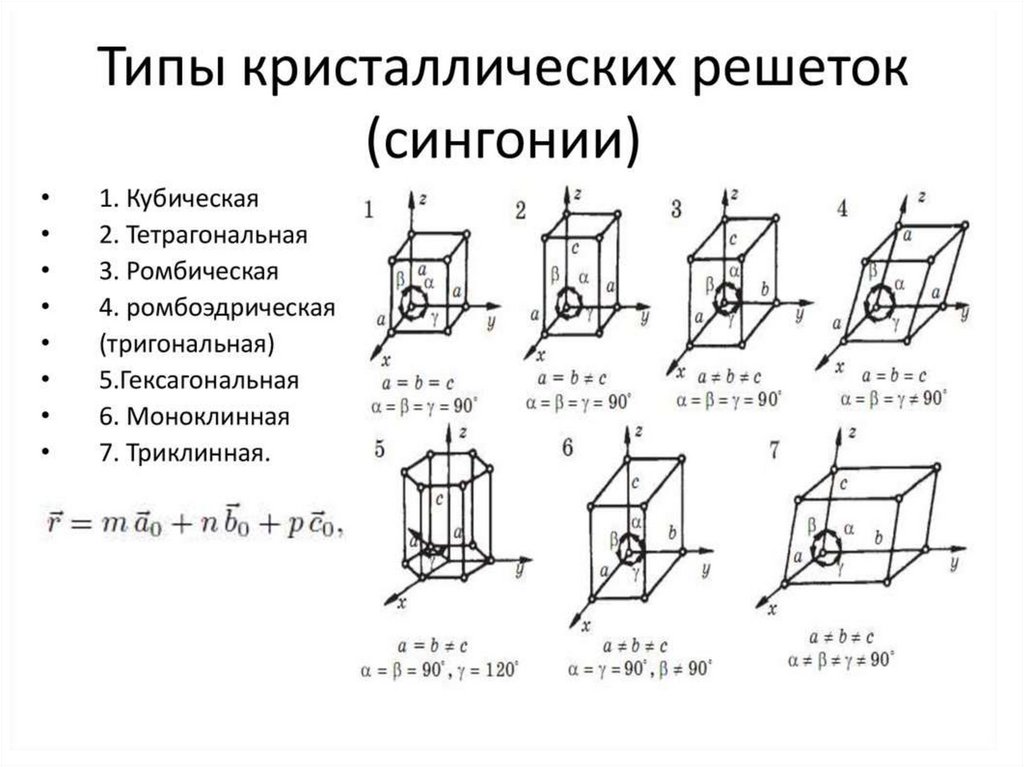
Как описать структуру кристалла?
0
а
b
10
а,b - трансляции
Кристаллическая решетка – это способ описания состояние
вещества с бесконечной трехмерной периодической структурой,
позволяющий
по
средствам
геометрических
построений
анализировать всю совокупность элементов этой структуры.

4.

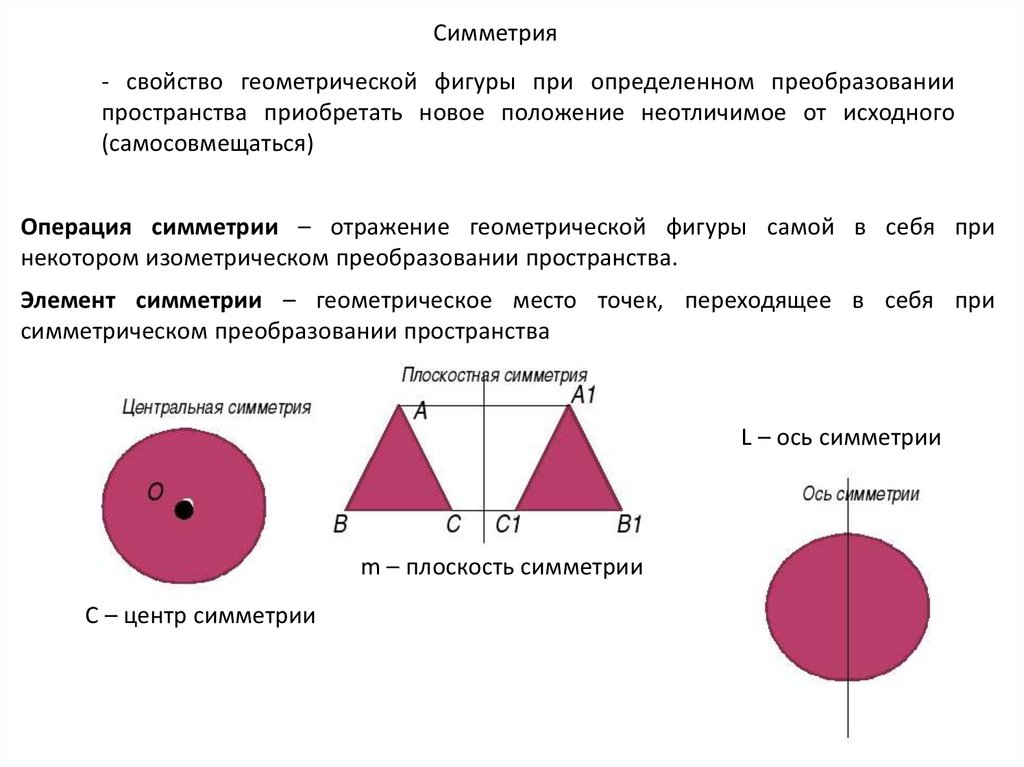
Симметрия
- свойство геометрической фигуры при определенном преобразовании
пространства приобретать новое положение неотличимое от исходного
(самосовмещаться)
Операция симметрии – отражение геометрической фигуры самой в себя при
некотором изометрическом преобразовании пространства.
Элемент симметрии – геометрическое место точек, переходящее в себя при
симметрическом преобразовании пространства
L – ось симметрии
m – плоскость симметрии
С – центр симметрии

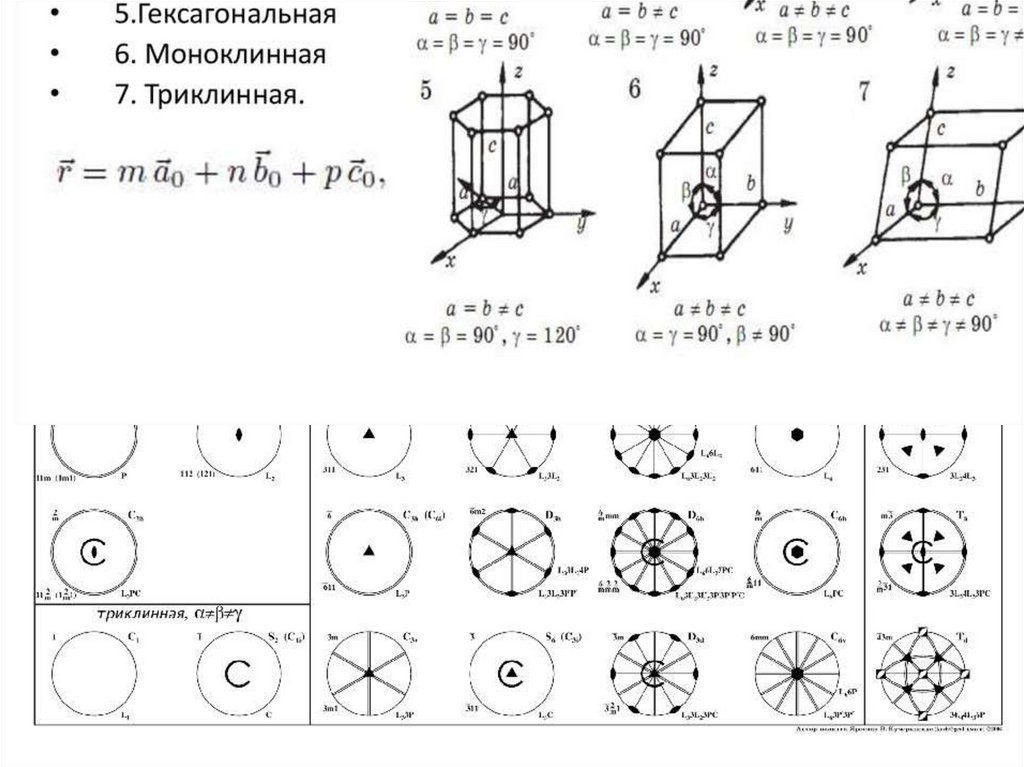
5.

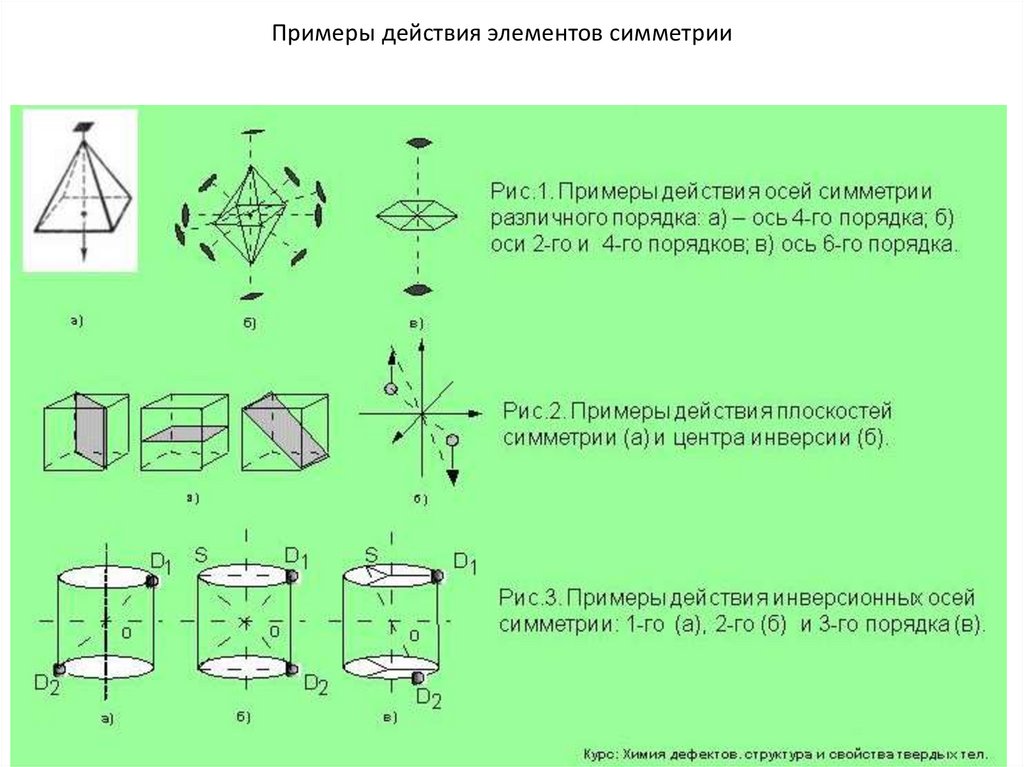
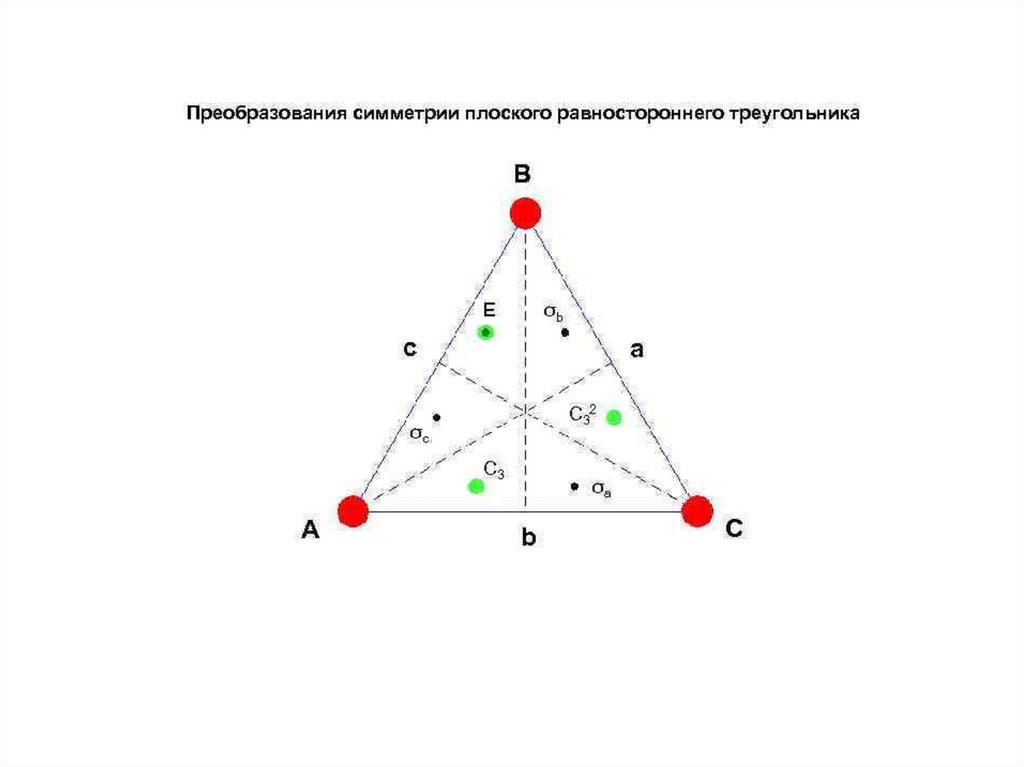
Примеры действия элементов симметрии

6.

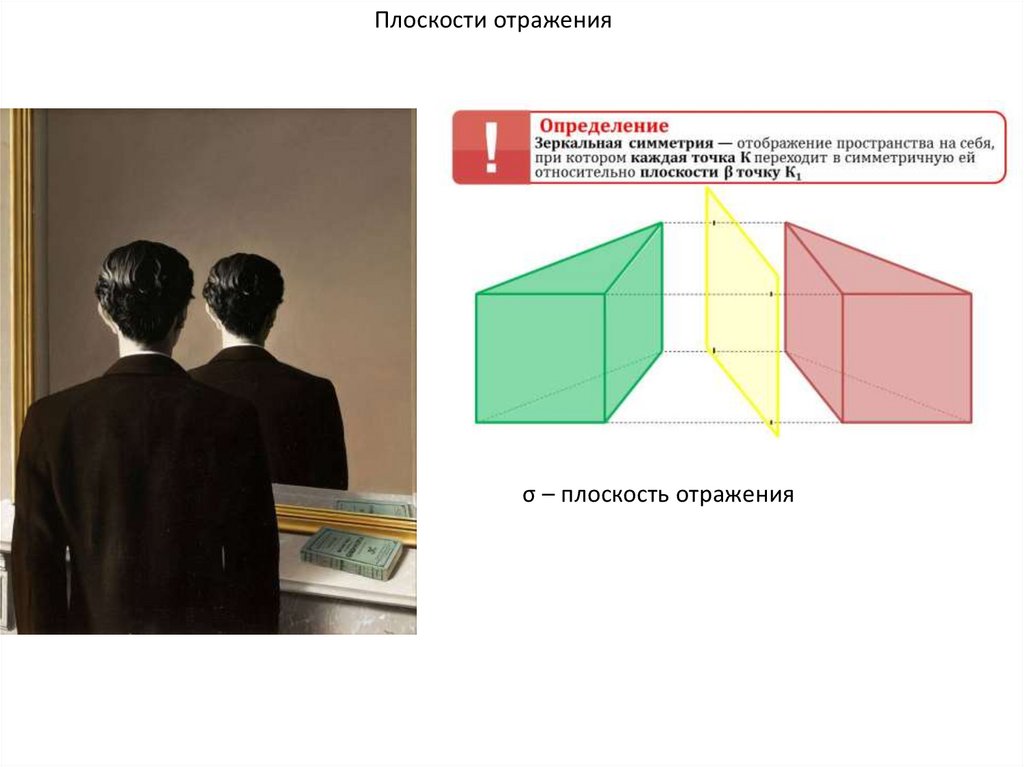
Плоскости отражения
σ – плоскость отражения

7.

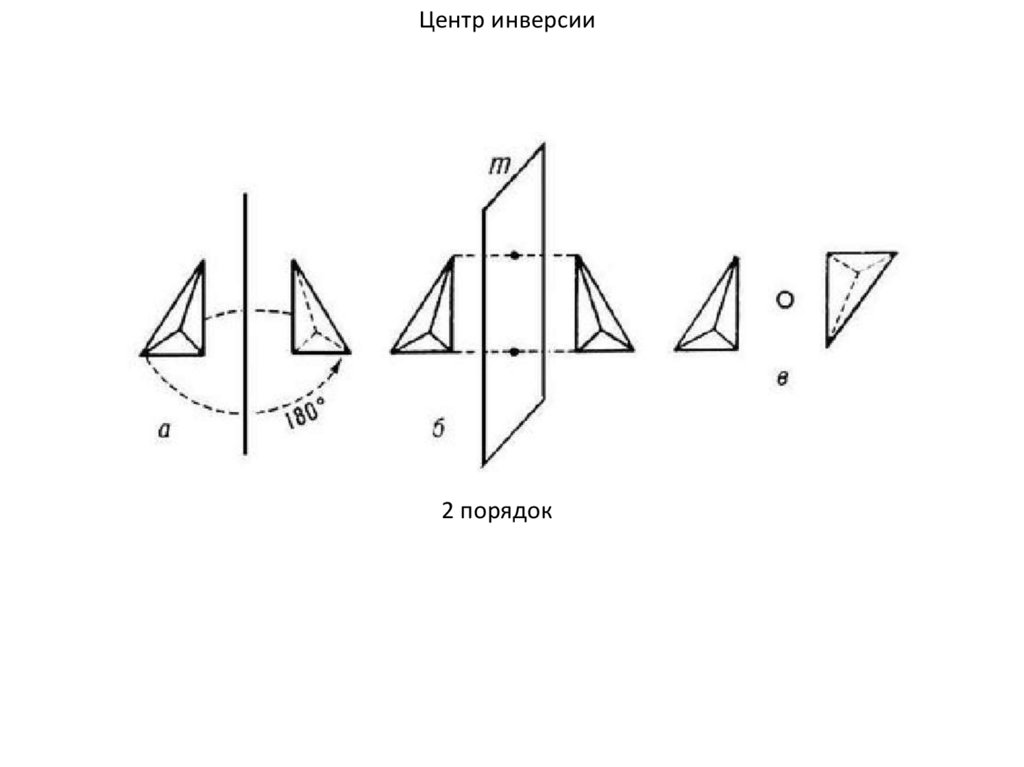
Центр инверсии
2 порядок

8.

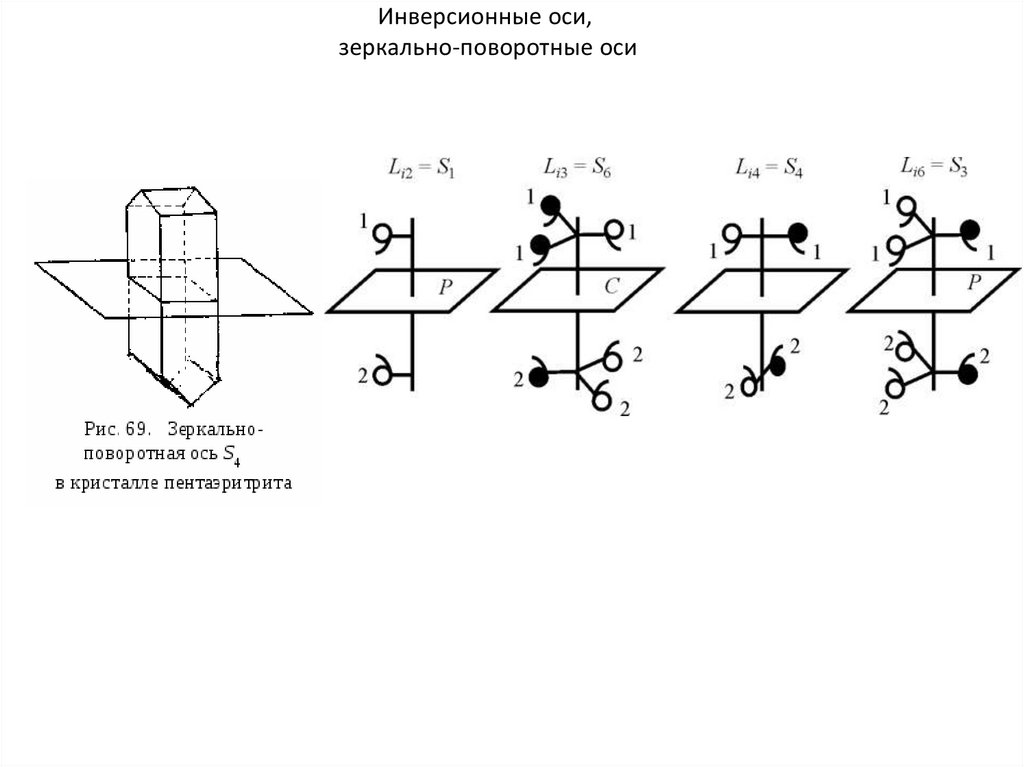
Инверсионные оси,
зеркально-поворотные оси

9.

10.

11.

12.

Квазикристаллы, есть порядок, но нет повторений…

13.

14.

15.

16.

17.

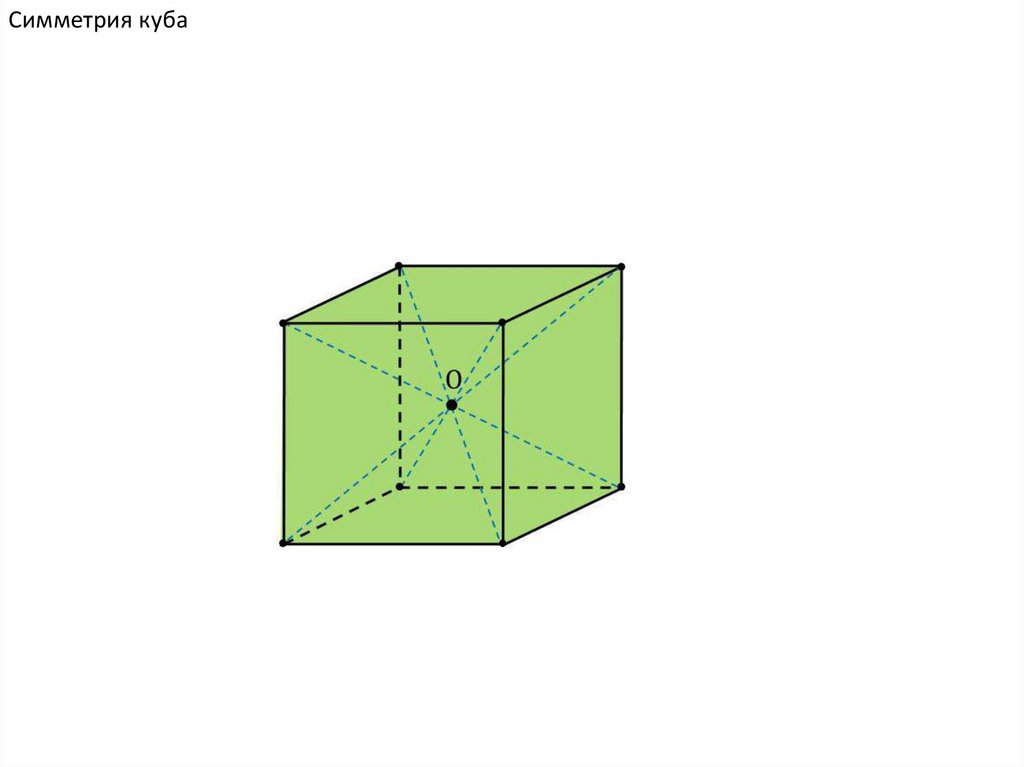
Симметрия куба

18.

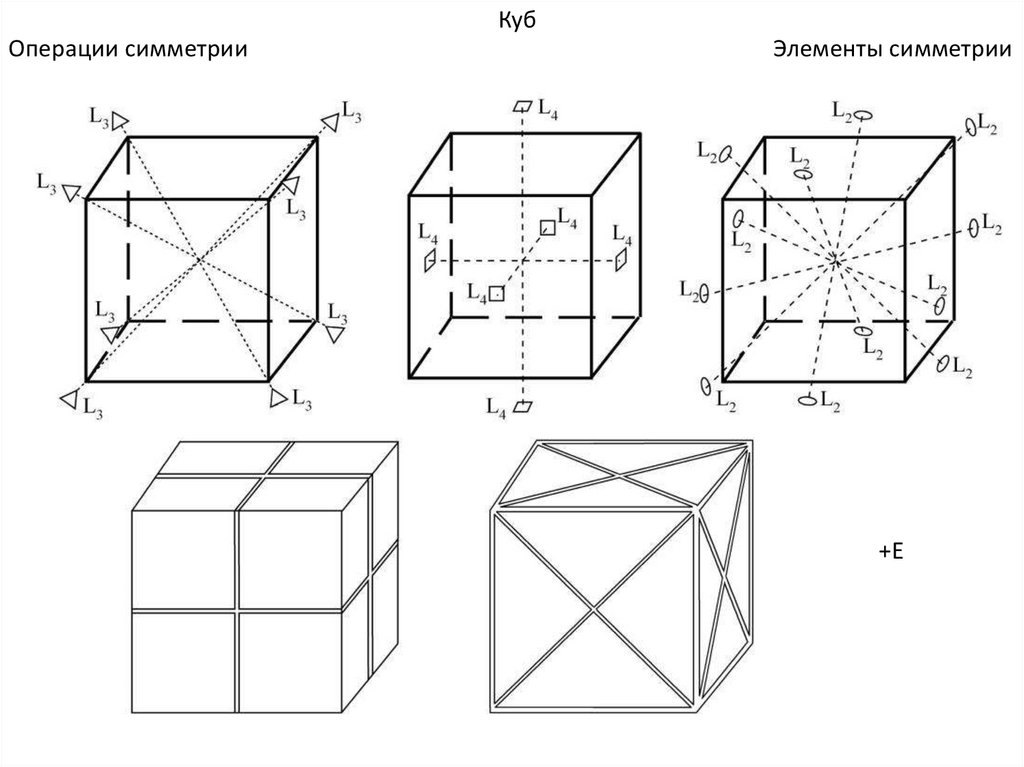
Куб
Операции симметрии
Элементы симметрии
+Е

19.

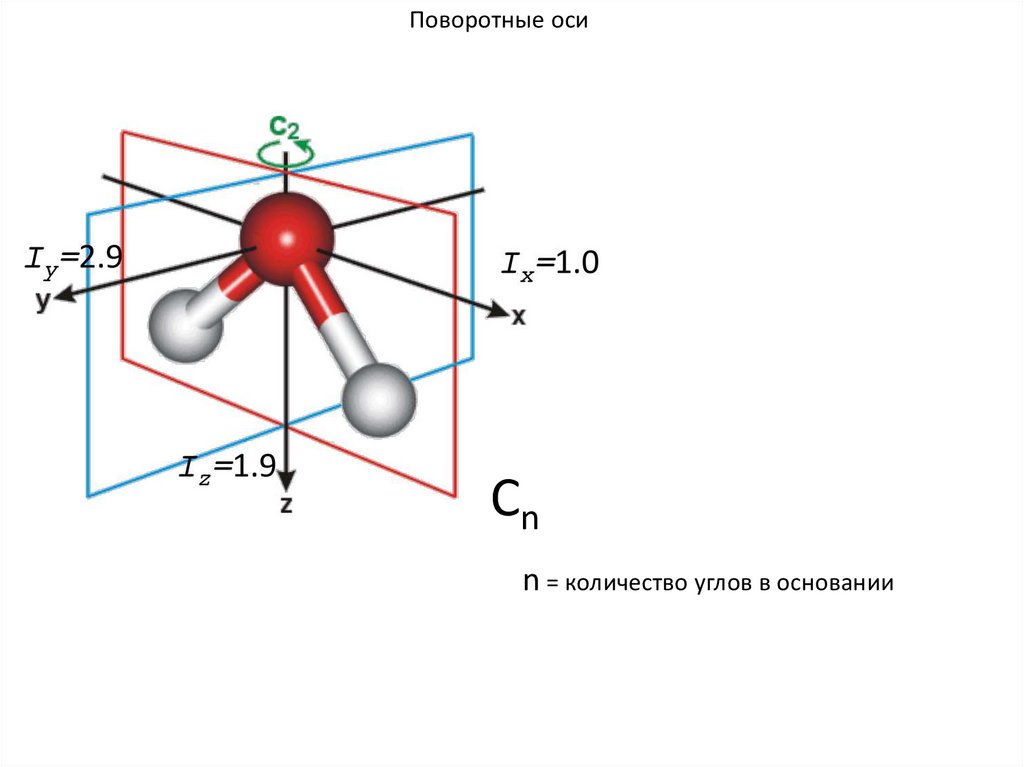
Поворотные оси
Сn
n = количество углов в основании

20.

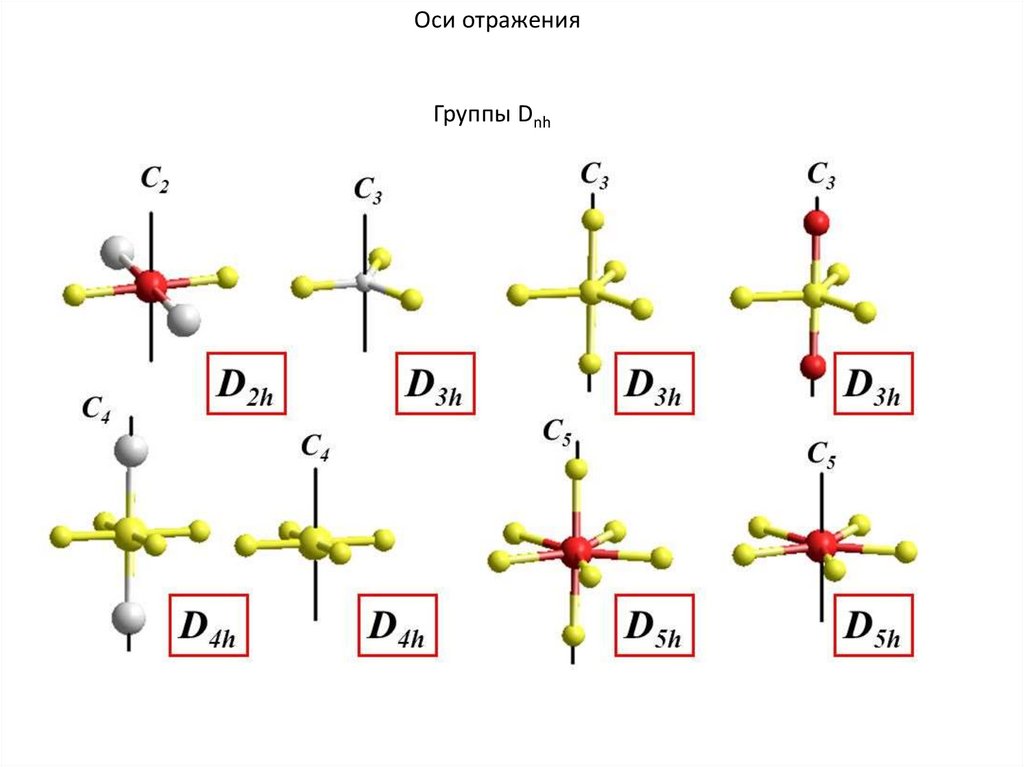
Оси отражения
Группы Dnh

21.

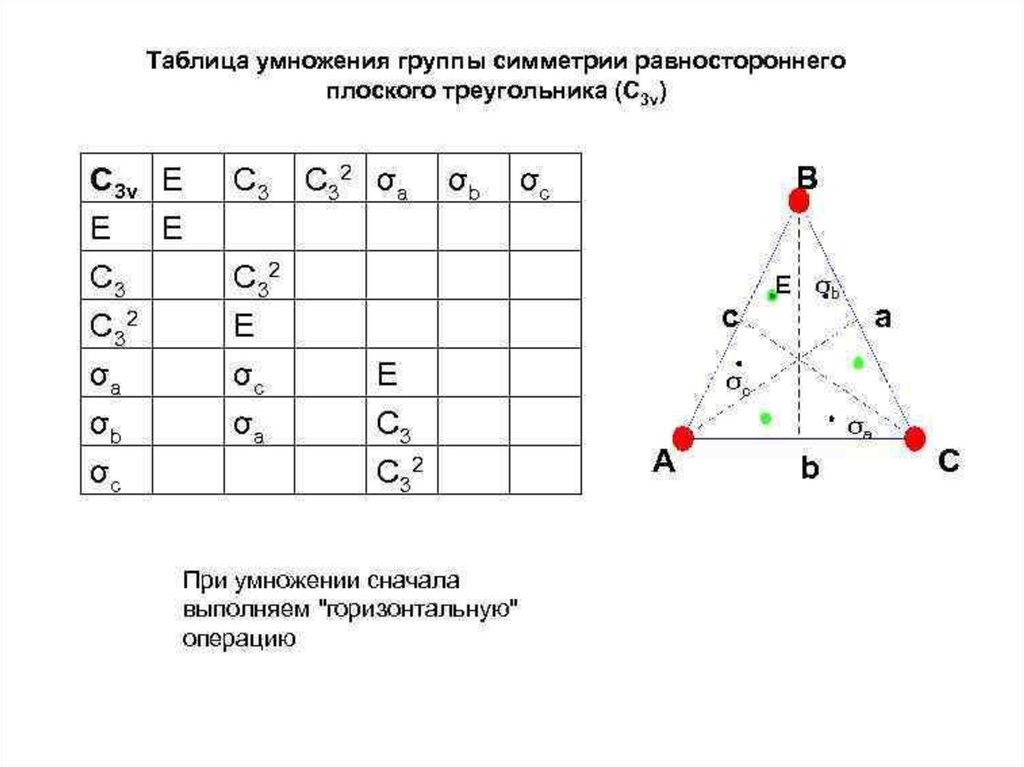
Символы Шенфлиса
Сn k
Sn k
- Поворот на 360/порядок оси
(центр инверсии -?)
- Поворот на 360/порядок оси + перпендикулярная плоскость отражения σ
σ – горизонтальная (h), вертикальная (v) или диагональная по отношению к оси
наибольшего порядка
Семейство Сn
Семейство Sn
Сn
n - четное
+горизонтальная плоскость Сnh
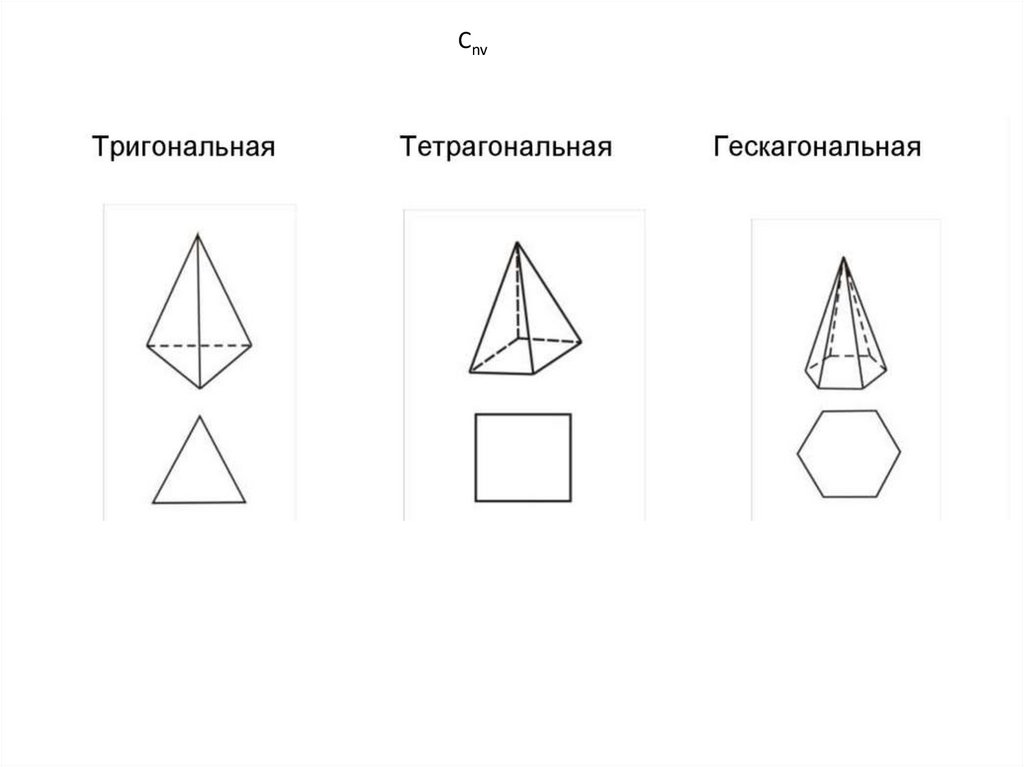
+вертикальная плоскость Сnv (пирамида)
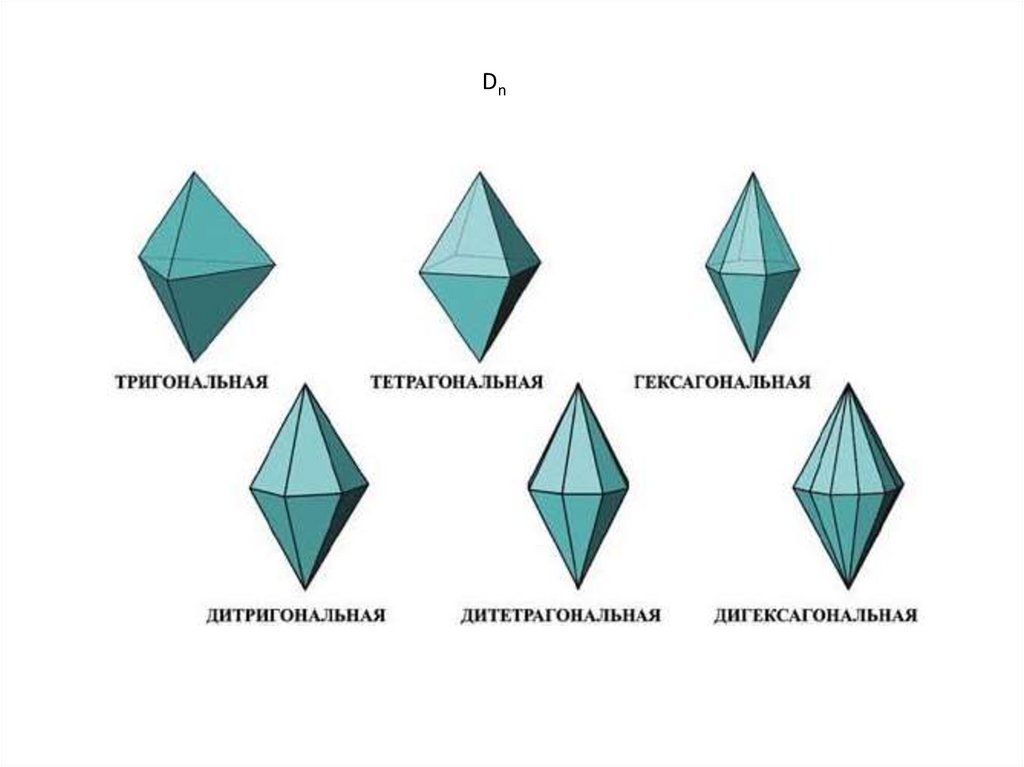
+перпендикулярные оси Dn (бипирамида)
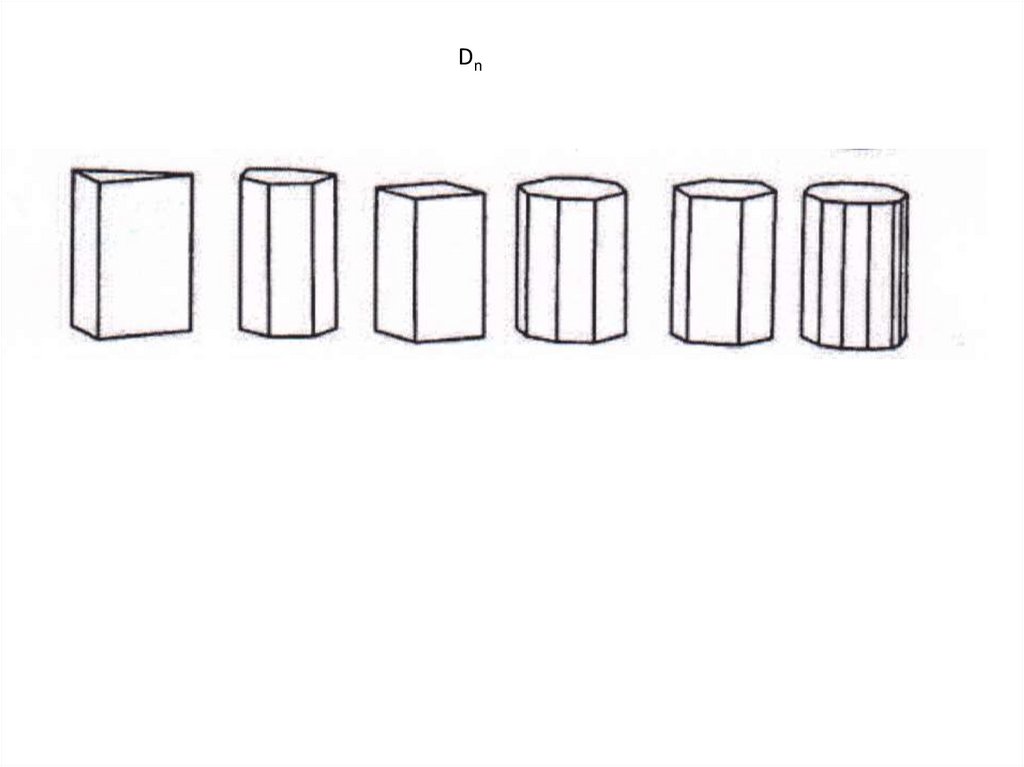
+горизонтальная плоскость и перпендикулярная ось Dnh (призма)
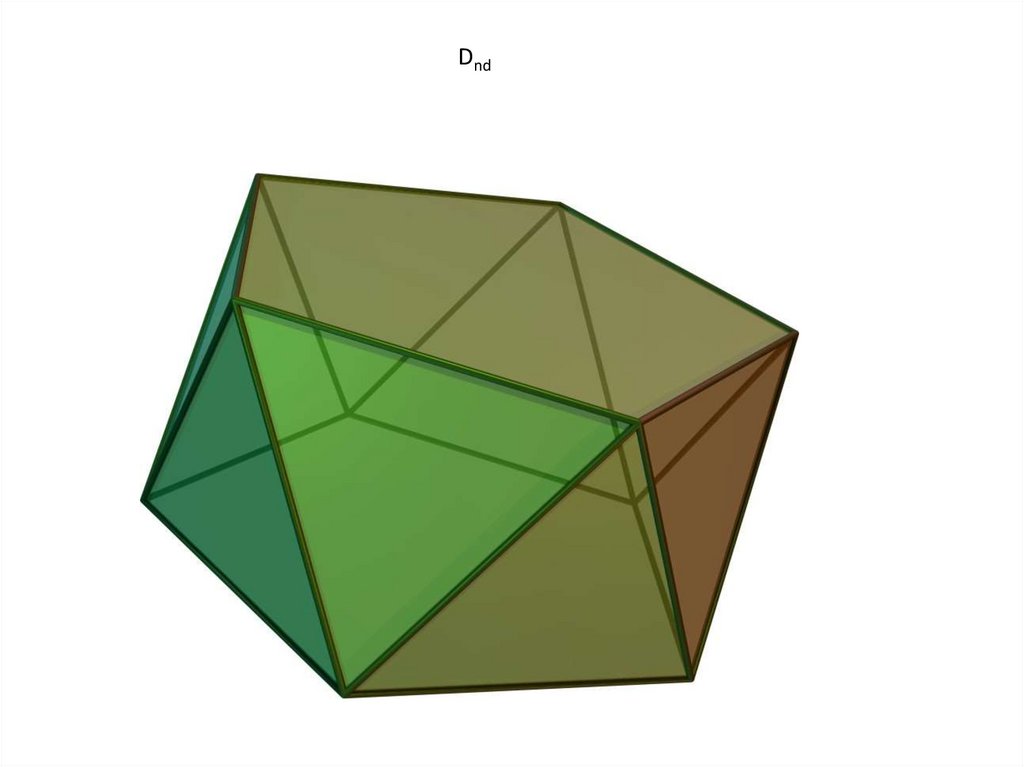
+перпендикулярная ось и горизонтальные оси Dnd (антипризма)

22.

Cnv

23.

Dn

24.

Dn

25.

Dnd

26.

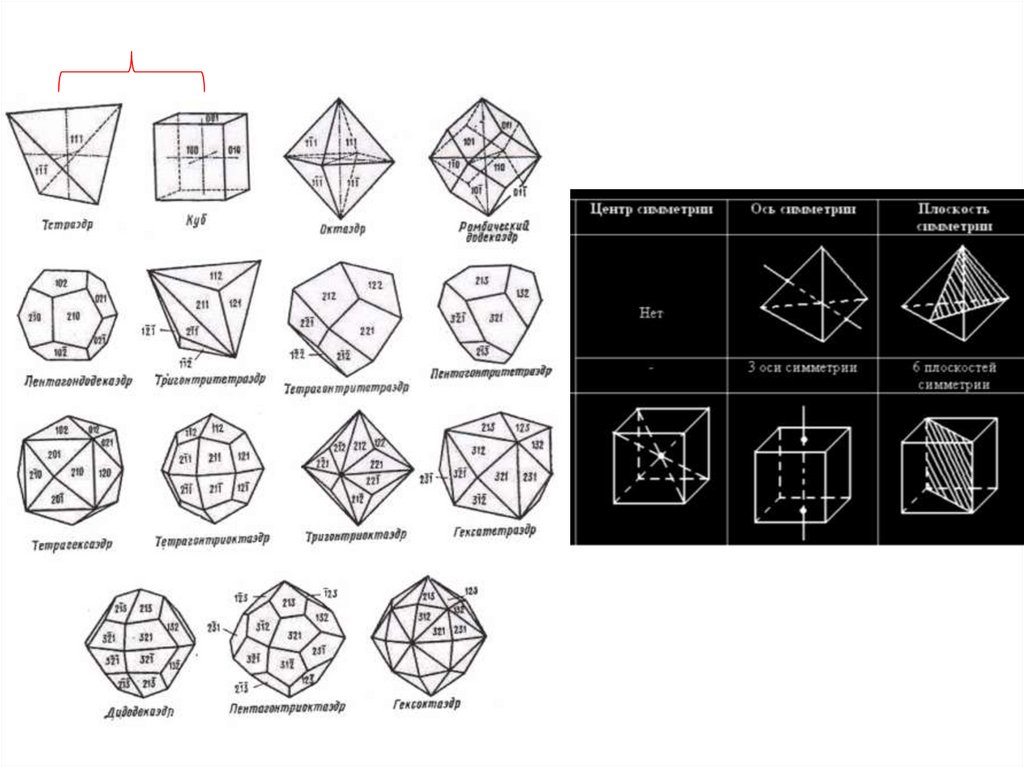
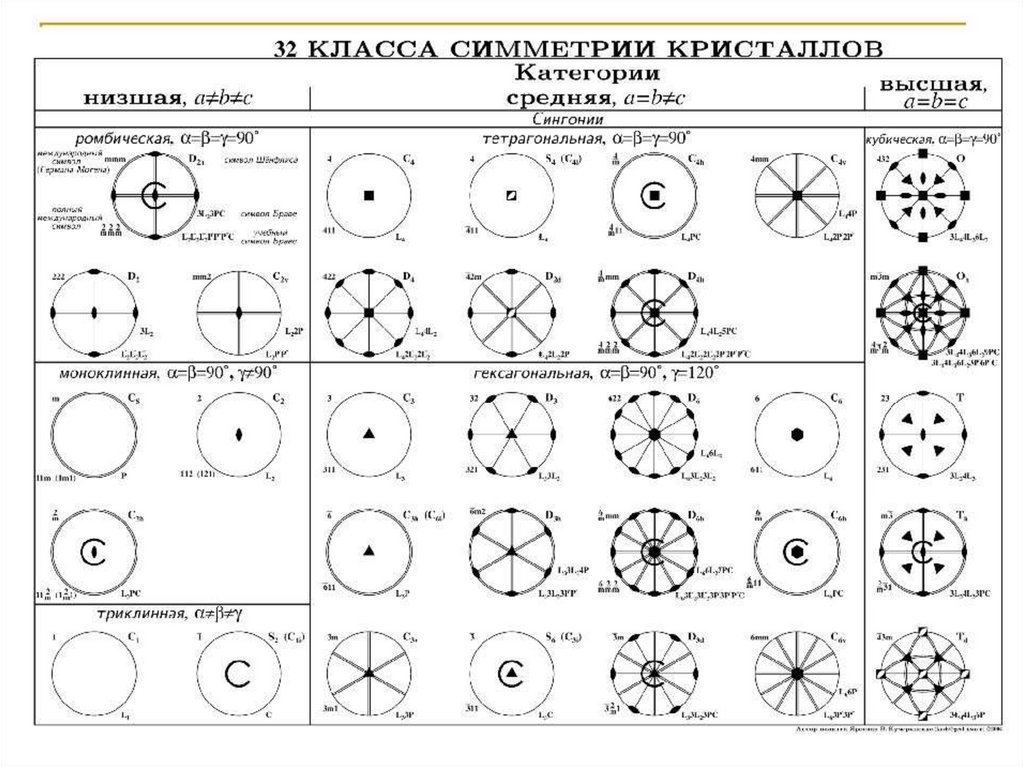
Категории полиэдров
1. Низшая категория (Порядок оси не выше 2)
Семь групп: C1, C2, S2, C2h, C2v, D2, D2h
2. Средняя категория (Одна ось порядка выше 2)
Семь семейств: Сn, Sn, Cnh, Cnv, Dn, Dnh, Dnd
3. Высшая категория (Больше 1 оси более высокого порядка, чем 2)
Семь групп: T, Th, Td, O, Oh, I, Ih

27.

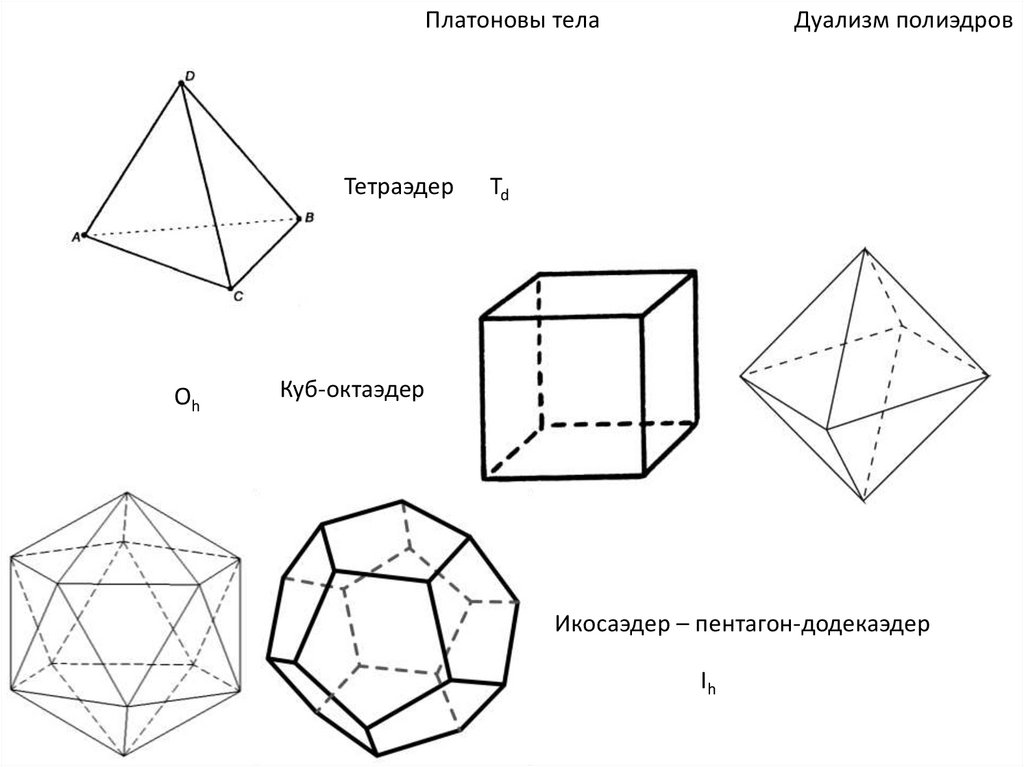
Платоновы тела
Тетраэдер
Oh
Дуализм полиэдров
Td
Куб-октаэдер
Икосаэдер – пентагон-додекаэдер
Ih

28.

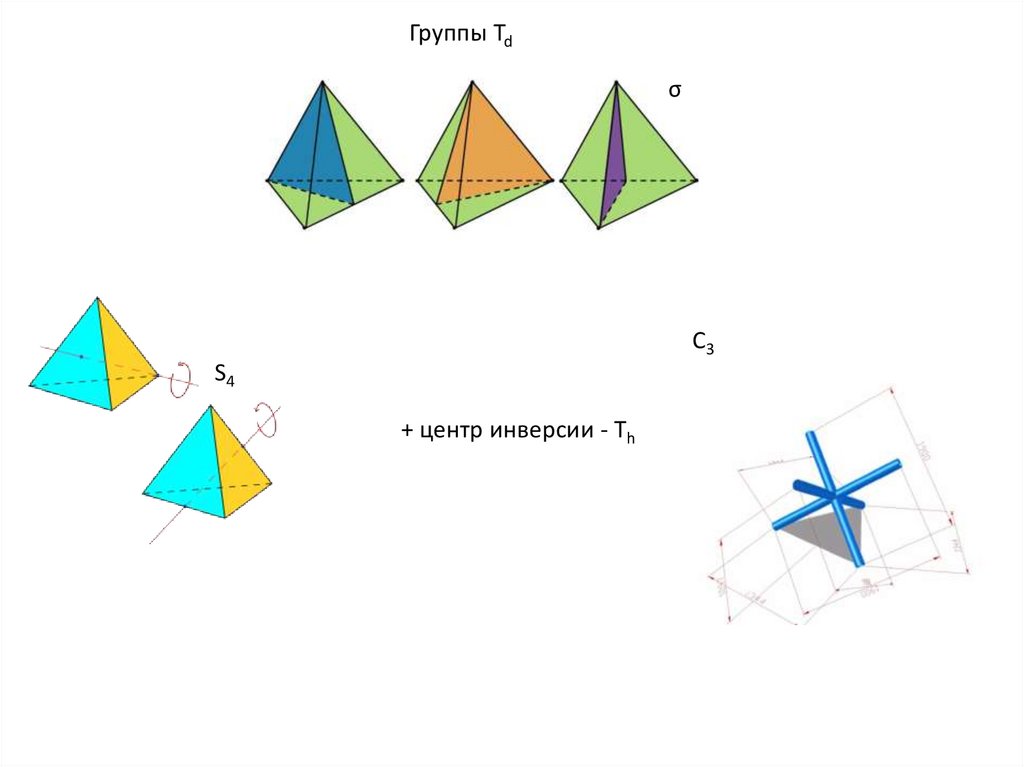
Группы Td
σ
С3
S4
+ центр инверсии - Тh

29.

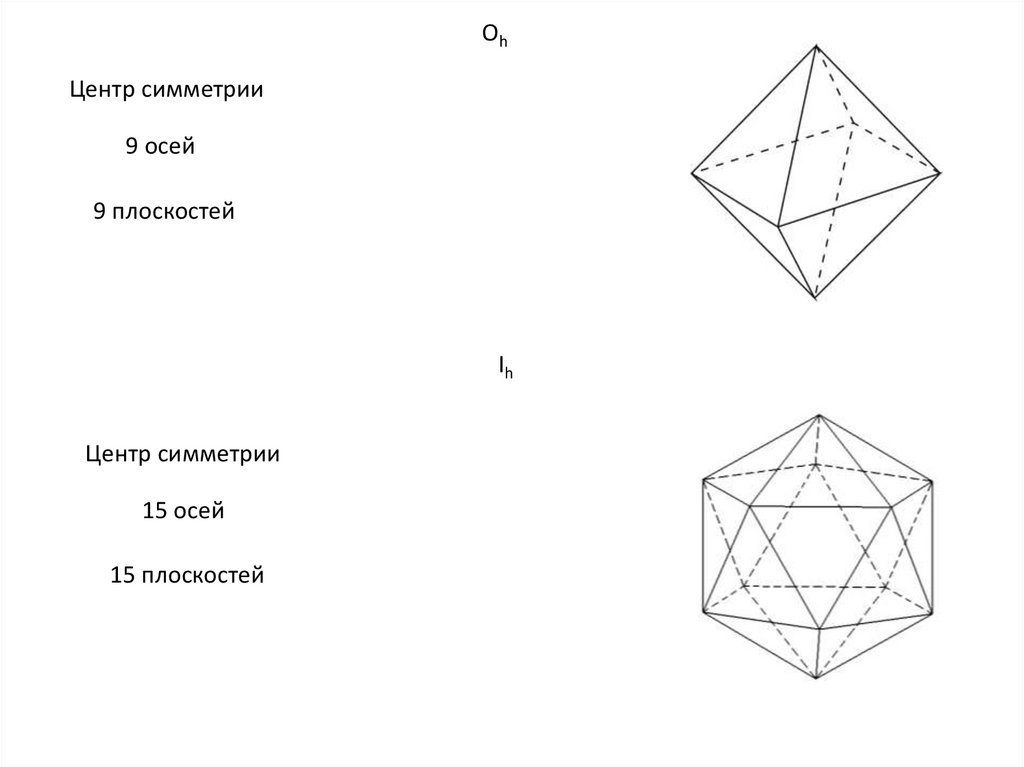
Oh
Центр симметрии
9 осей
9 плоскостей
Ih
Центр симметрии
15 осей
15 плоскостей

30.

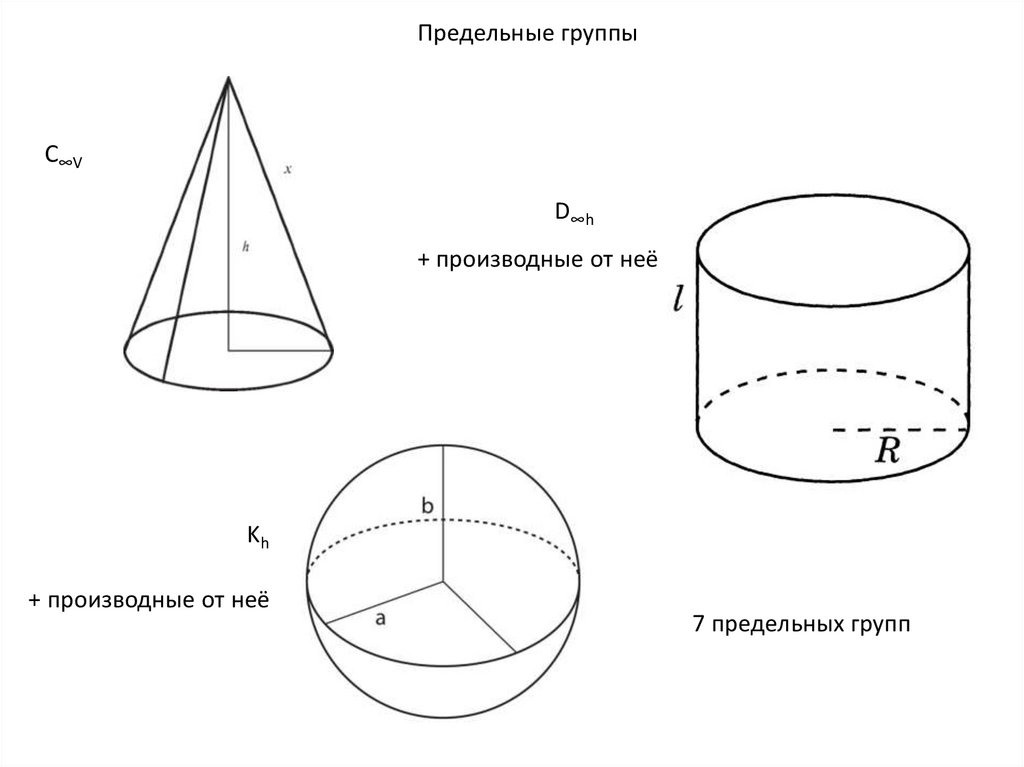
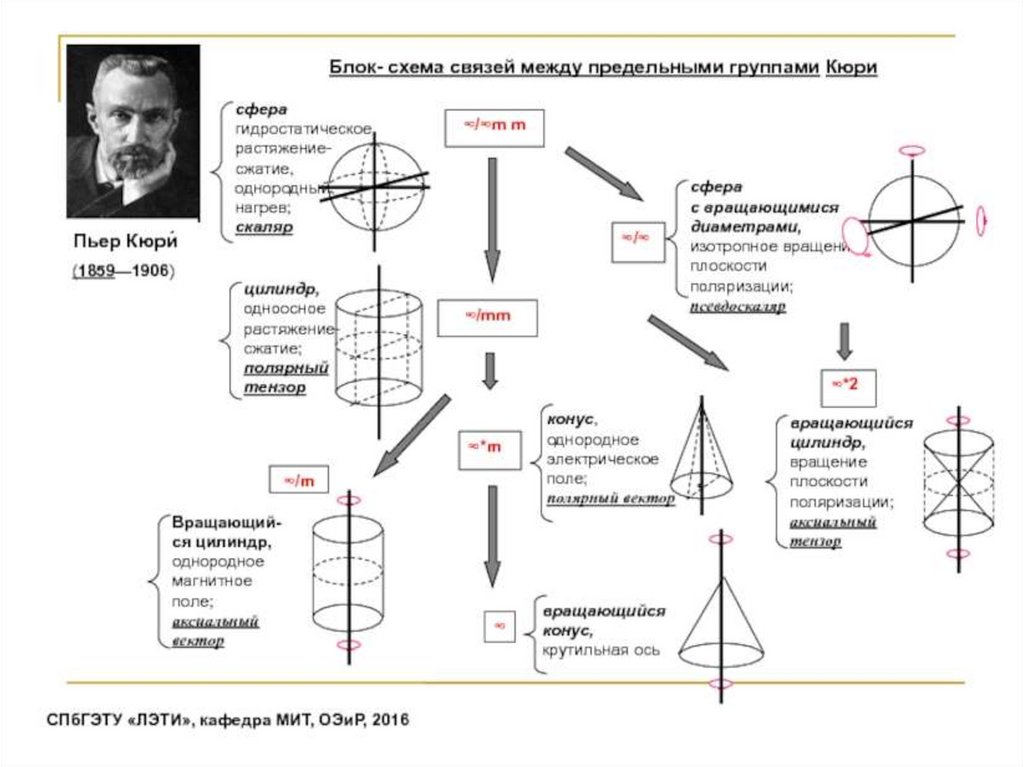
Предельные группы
С∞V
D∞h
+ производные от неё
Kh
+ производные от неё
7 предельных групп