Похожие презентации:
Основы математической обработки информации
1.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
Основы математической
обработки информации
Семестр: 3
Лекции: 6
Практические занятия: 10
Контрольная работа: 1
Зачёт
2.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
Лекция 2.
Дискретные и непрерывные модели
Аппроксимация
§1. Задача о размножении кроликов
Последовательности
§2. Задача о ступеньках из домино
Ряды
§3. Задача о площади сектора
Функции
§4. Задача об эксплуатации автомобиля
Аппроксимация
§5. Математическое моделирование
Лекция 2. Дискретные и непрерывные модели
2
3.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§1. Задача о размножении кроликов
Леона́ рдо Пиза́ нский
1170-1250
Лекция 2. Дискретные и непрерывные модели
3
4.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§1. Задача о размножении кроликов
В своей книге «Liber Abaci» (1202) Леонардо Пизанский,
известный как Фибоначчи, рассматривает развитие
идеализированной
(биологически
нереальной)
популяции кроликов, предполагая, что:
• изначально есть новорожденная пара кроликов
(самец и самка);
• со второго месяца после своего рождения кролики
начинают спариваться,
• и каждый месяц производить новую пару
кроликов;
• кролики никогда не умирают.
Сколько пар кроликов будет через n месяцев?
Лекция 2. Дискретные и непрерывные модели
4
5.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§1. Задача о размножении кроликов
Лекция 2. Дискретные и непрерывные модели
5
6.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§1. Задача о размножении кроликов
Обозначим через A пару зрелых кроликов, а через B –
пару новорожденных кроликов. Тогда процесс
«размножения» может быть описан с помощью двух
«переходов»:
A – AB моделирует ежемесячное превращение каждой
зрелой пары кроликов А в две пары, а именно в ту же
самую пару зрелых кроликов А и новорожденную пару
кроликов В;
B – A моделирует процесс «созревания» кроликов,
когда новорожденная пара кроликов В через месяц
превращается в зрелую пару А.
Лекция 2. Дискретные и непрерывные модели
6
7.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
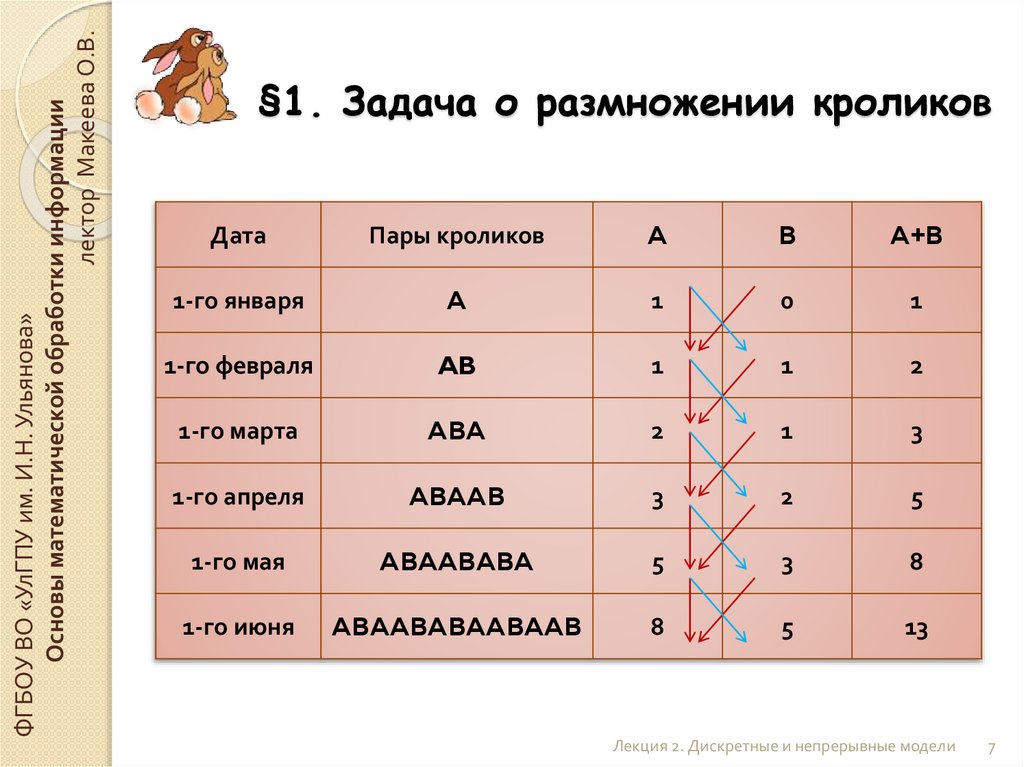
§1. Задача о размножении кроликов
Дата
Пары кроликов
A
B
A+B
1-го января
A
1
0
1
1-го февраля
AB
1
1
2
1-го марта
ABA
2
1
3
1-го апреля
ABAAB
3
2
5
1-го мая
ABAABABA
5
3
8
1-го июня
ABAABABAABAAB
8
5
13
Лекция 2. Дискретные и непрерывные модели
7
8.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
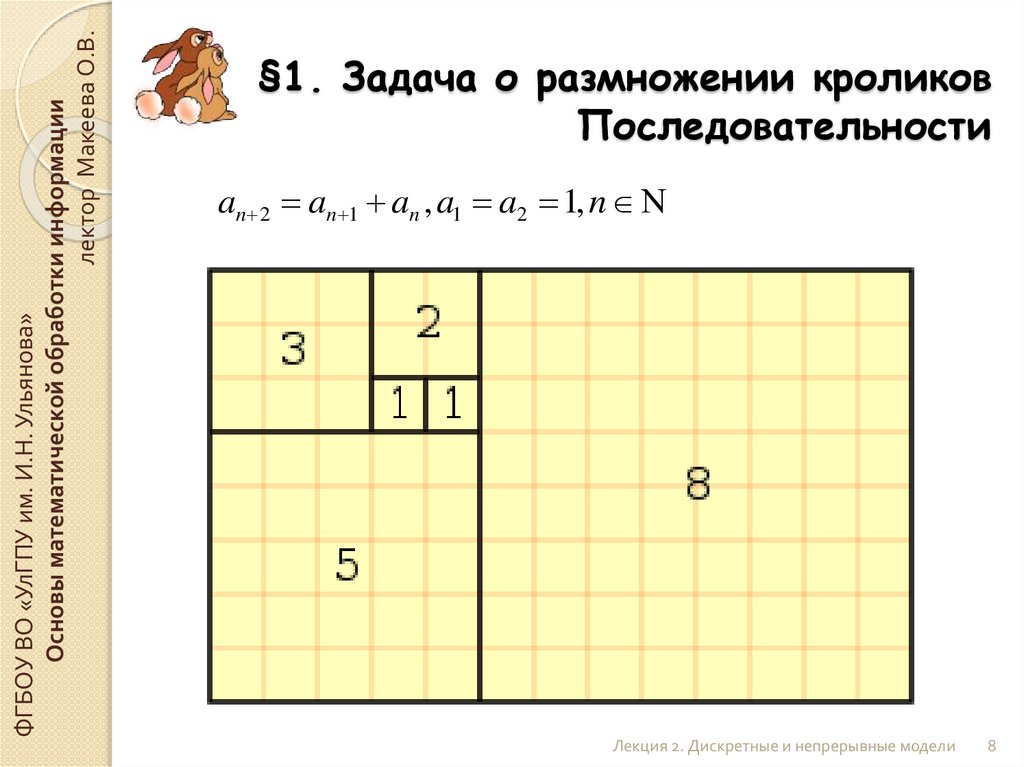
§1. Задача о размножении кроликов
Последовательности
an 2 an 1 an , a1 a2 1, n
Лекция 2. Дискретные и непрерывные модели
8
9.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§1. Задача о размножении кроликов
Последовательности
Последовательность
–
натурального аргумента.
числовая
функция
a a f n , n
n
n
Способы задания последовательности
• описание;
• перечисление элементов;
• формула общего члена;
1 1 1 1 1
, , , , ,
• рекуррентная формула;
1 2 3 4 5
• графический.
Лекция 2. Дискретные и непрерывные модели
9
10.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§1. Задача о размножении кроликов
Последовательности
Свойства последовательностей
• стационарность;
• цикличность;
• монотонность;
• ограниченность.
1 2 3 4 5
, , , , ,
3 5 7 9 11
Операции над последовательностями
• сложение;
• вычитание;
• умножение;
• деление;
• умножение на число.
Лекция 2. Дискретные и непрерывные модели
10
11.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§1. Задача о размножении кроликов
Последовательности
Частные случаи последовательностей
• арифметическая прогрессия: an 1 an d
an k an k
an
2
• геометрическая прогрессия: bn 1 bn q, q 0
bn bn k bn k
Предел последовательности
def
lim an a : 0, N , n N an a
n
2 3 4 5 6
, , , , , 1
1 2 3 4 5
Лекция 2. Дискретные и непрерывные модели
11
12.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Задача о ступеньках из домино
Лекция 2. Дискретные и непрерывные модели
12
13.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Задача о ступеньках из домино
Лекция 2. Дискретные и непрерывные модели
13
14.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Задача о ступеньках из домино
Пантаев
Михаил Юрьевич
Лекция 2. Дискретные и непрерывные модели
14
15.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Задача о ступеньках из домино
Лекция 2. Дискретные и непрерывные модели
15
16.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Задача о ступеньках из домино
Ряды
Лекция 2. Дискретные и непрерывные модели
16
17.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Задача о ступеньках из домино
Ряды
Ряд – это бесконечная сумма.
a1 a2 a3 an an
n 1
Виды рядов
1 1 1 1 1
1
• числовые ряды;
• положительные;
1 2 3 4 5
n 1 n
• знакопеременные;
• знакочередующиеся;
2
3
4
n
x
x
x
x
x
• функциональные; e x 1
1! 2! 3! 4!
n 0 n!
• степенные;
• тригонометрические;
Лекция 2. Дискретные и непрерывные модели
17
•…
18.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Задача о ступеньках из домино
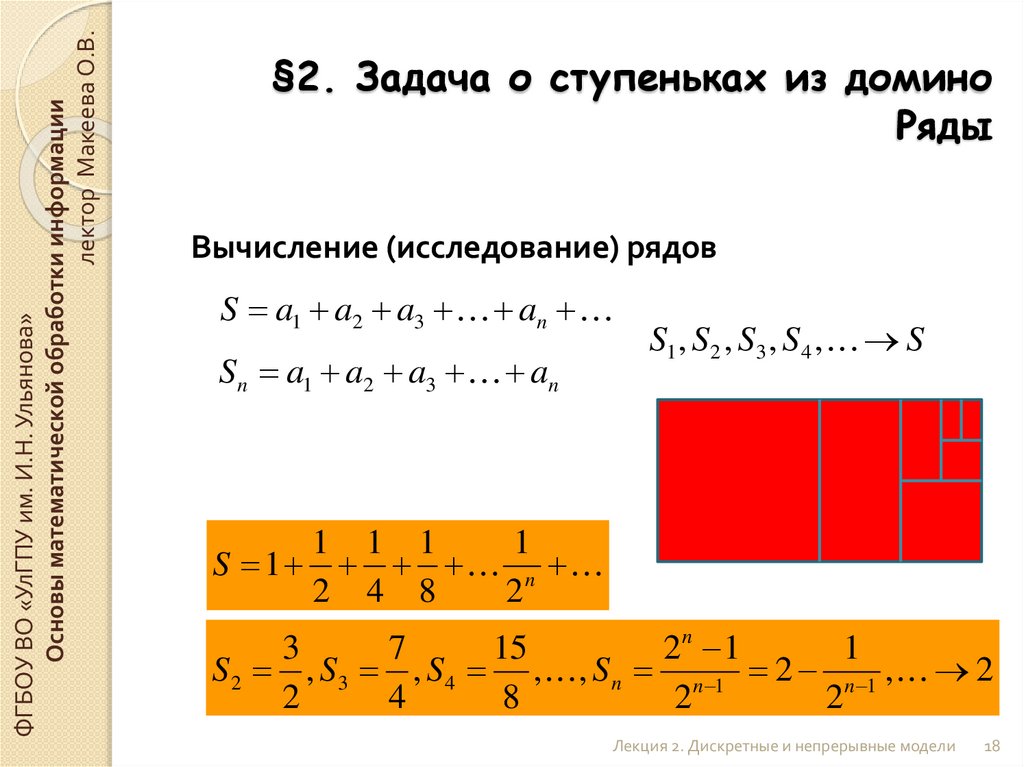
Ряды
Вычисление (исследование) рядов
S a1 a2 a3 an
S n a1 a2 a3 an
S 1
S1 , S2 , S3 , S4 , S
1 1 1
1
n
2 4 8
2
3
7
15
2n 1
1
S 2 , S3 , S 4 , , S n n 1 2 n 1 , 2
2
4
8
2
2
Лекция 2. Дискретные и непрерывные модели
18
19.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§3. Задача о площади сектора
Функции
Мордкович
Александр Григорьевич
Лекция 2. Дискретные и непрерывные модели
19
20.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§3. Задача о площади сектора
Функции
Лекция 2. Дискретные и непрерывные модели
20
21.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§3. Задача о площади сектора
Функции
Числовой функцией с областью определения D
называется зависимость, при которой каждому
числу из множества D ставится в соответствие
единственное число y, обычно обозначаемое у=f(x).1
Способы задания функций
• описание;
• табличный;
• графический;
• аналитический.
__________
1 Сравните с определением Лекции 1 (слайд 31).
Лекция 2. Дискретные и непрерывные модели
21
22.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§3. Задача о площади сектора
Функции
Свойства функций
• монотонность;
• ограниченность;
• чётность/нечётность;
• периодичность.
Операции над функциями
• сложение;
• вычитание;
• умножение;
• деление;
• умножение на число;
• суперпозиция.
Лекция 2. Дискретные и непрерывные модели
22
23.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§3. Задача о площади сектора
Функции
Основные элементарные функции
• линейная;
• квадратичная;
• степенная;
• показательная;
• логарифмическая;
• тригонометрические;
• обратные тригонометрические.
Лекция 2. Дискретные и непрерывные модели
23
24.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§3. Задача о площади сектора
Функции
Предел функции
def
lim f x A :
x
0, M 0, x M f x A
def
lim f x A :
x x0
0, 0, x : 0 x x0 f x A
Лекция 2. Дискретные и непрерывные модели
24
25.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§4. Задача об эксплуатации автомобиля
Аппроксимация
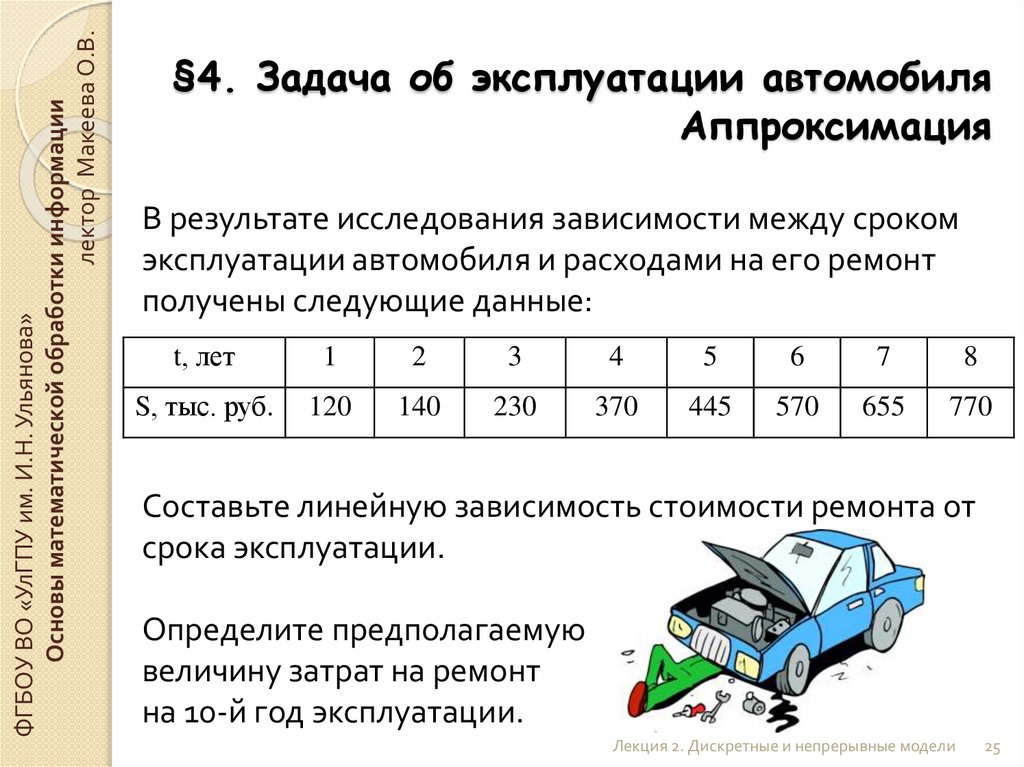
В результате исследования зависимости между сроком
эксплуатации автомобиля и расходами на его ремонт
получены следующие данные:
t, лет
1
2
3
4
5
6
7
8
S, тыс. руб.
120
140
230
370
445
570
655
770
Составьте линейную зависимость стоимости ремонта от
срока эксплуатации.
Определите предполагаемую
величину затрат на ремонт
на 10-й год эксплуатации.
Лекция 2. Дискретные и непрерывные модели
25
26.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§4. Задача об эксплуатации автомобиля
Аппроксимация
Аппроксима́ция (от лат. proxima – ближайшая) или
приближе́ние — научный метод, состоящий в
замене одних объектов другими, в каком-то смысле
близкими к исходным, но более простыми.
Аппроксимация позволяет исследовать числовые
характеристики и качественные свойства объекта,
сводя задачу к изучению более простых или более
удобных объектов.
Лекция 2. Дискретные и непрерывные модели
26
27.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§4. Задача об эксплуатации автомобиля
Аппроксимация
Интерполя́ция
интерполи́рование
—
в
вычислительной математике способ нахождения
промежуточных значений величины по имеющемуся
дискретному набору известных значений.
Экстраполя́ция, экстраполи́рование — особый тип
аппроксимации,
при
котором
функция
аппроксимируется вне заданного интервала, а не
между заданными значениями.
Лекция 2. Дискретные и непрерывные модели
27
28.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§4. Задача об эксплуатации автомобиля
Аппроксимация
Метод наименьших квадратов
Лекция 2. Дискретные и непрерывные модели
28
29.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§4. Задача об эксплуатации автомобиля
Аппроксимация
Метод наименьших квадратов
t, лет
1
2
3
4
5
6
7
8
S, тыс. руб.
120
140
230
370
445
570
655
770
S a t b
t
1
2
3
4
5
6
7
8
36
S
120
140
230
370
445
570
655
770
3300
t^2
1
4
9
16
25
36
49
64
204
t*S
120
280
690
1480
2225
3420
4585
6160
18960
n
n
n 2
a t i b t i t i S i ,
i 1
i 1
i 1
n
n
a t nb S .
i
i
i 1
i 1
a 204 b 36 18960,
a 36 8 b 3300
Лекция 2. Дискретные и непрерывные модели
30.
900Затраты на ремонт, S
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
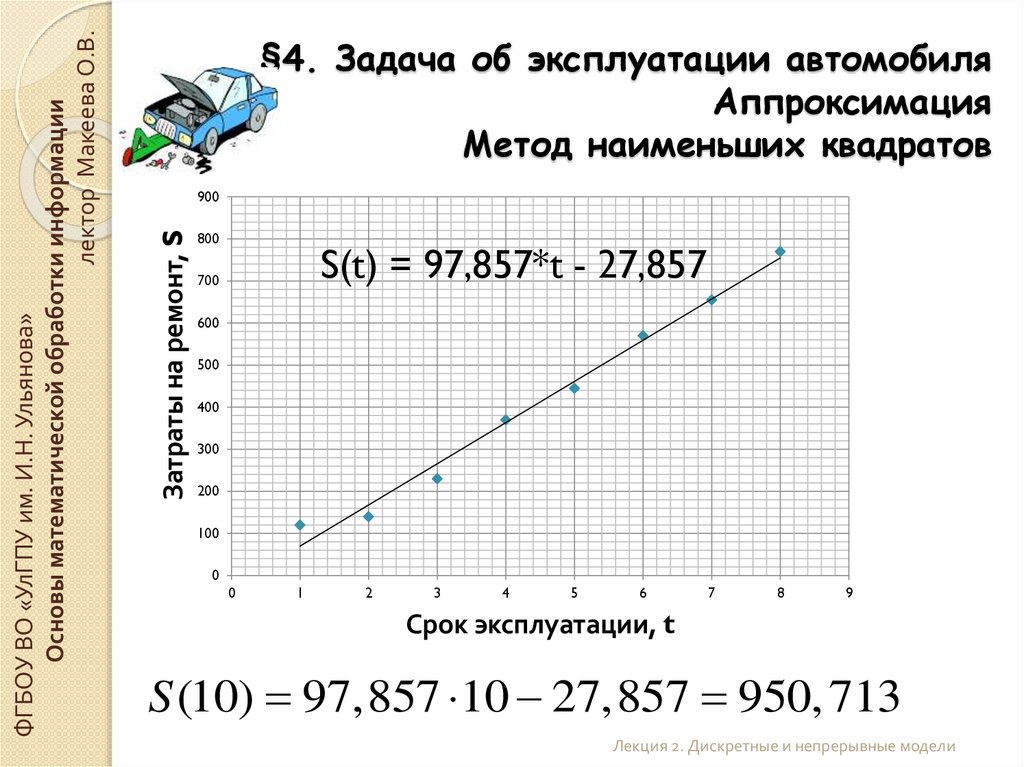
§4. Задача об эксплуатации автомобиля
Аппроксимация
Метод наименьших квадратов
800
S(t) = 97,857*t - 27,857
700
600
500
400
300
200
100
0
0
1
2
3
4
5
6
7
8
9
Срок эксплуатации, t
S (10) 97,857 10 27,857 950, 713
Лекция 2. Дискретные и непрерывные модели
31.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
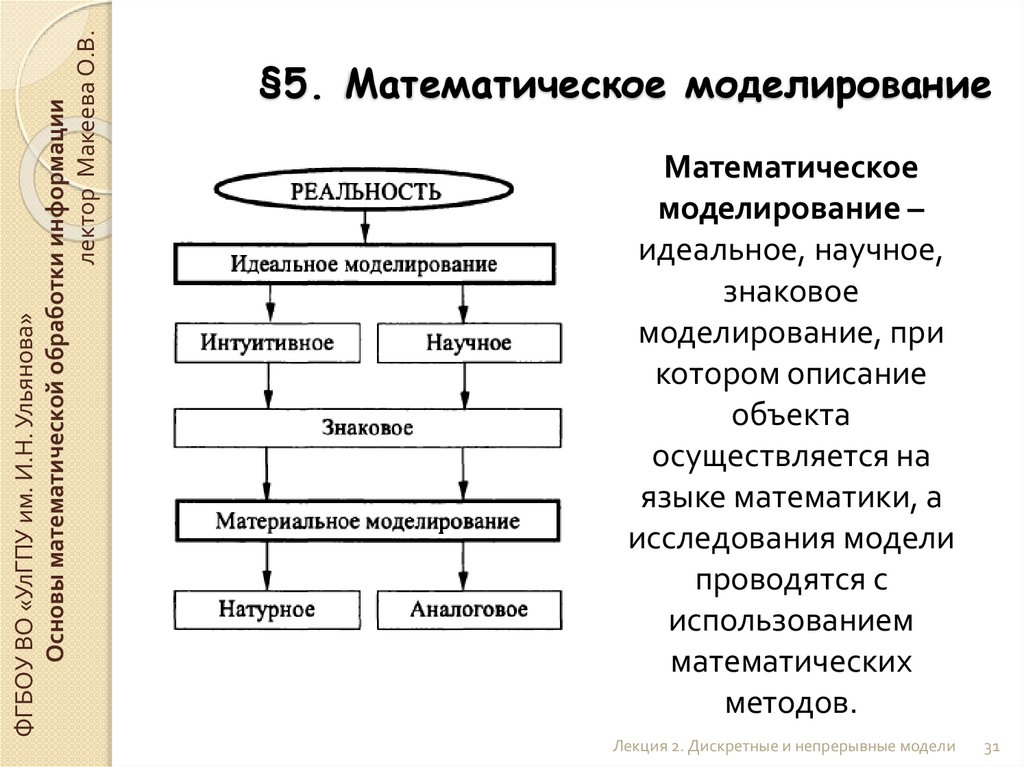
§5. Математическое моделирование
Математическое
моделирование –
идеальное, научное,
знаковое
моделирование, при
котором описание
объекта
осуществляется на
языке математики, а
исследования модели
проводятся с
использованием
математических
методов.
Лекция 2. Дискретные и непрерывные модели
31
32.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§5. Математическое моделирование
Классификация математических моделей
в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Лекция 2. Дискретные и непрерывные модели
32
33.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
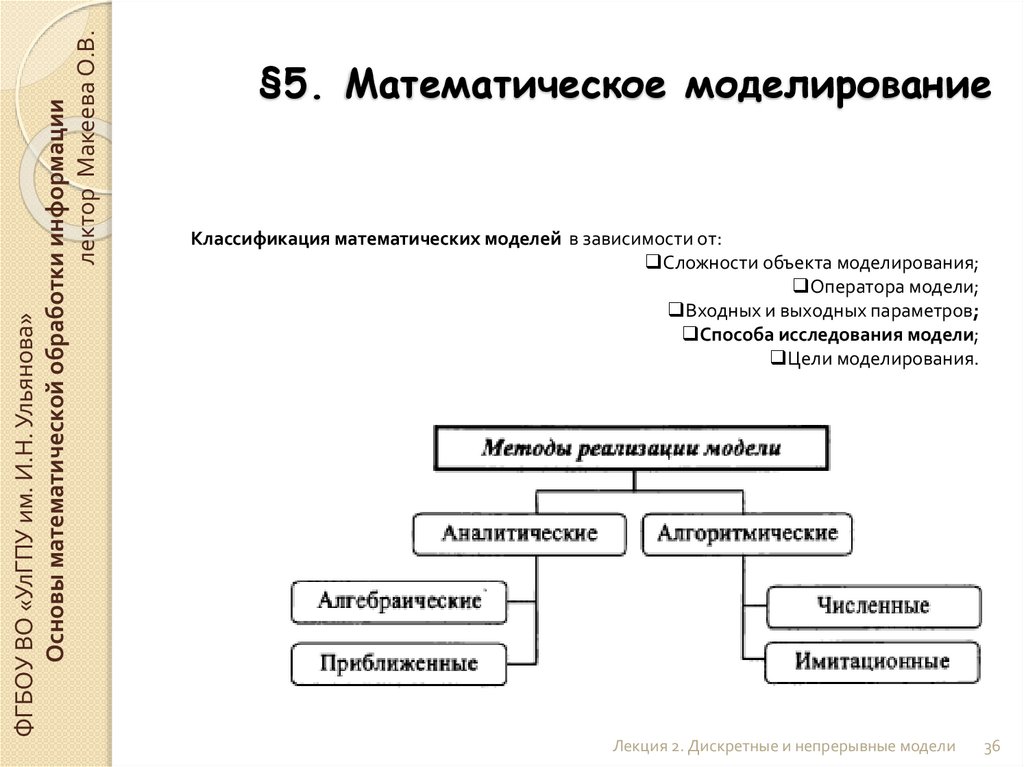
§5. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Лекция 2. Дискретные и непрерывные модели
33
34.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
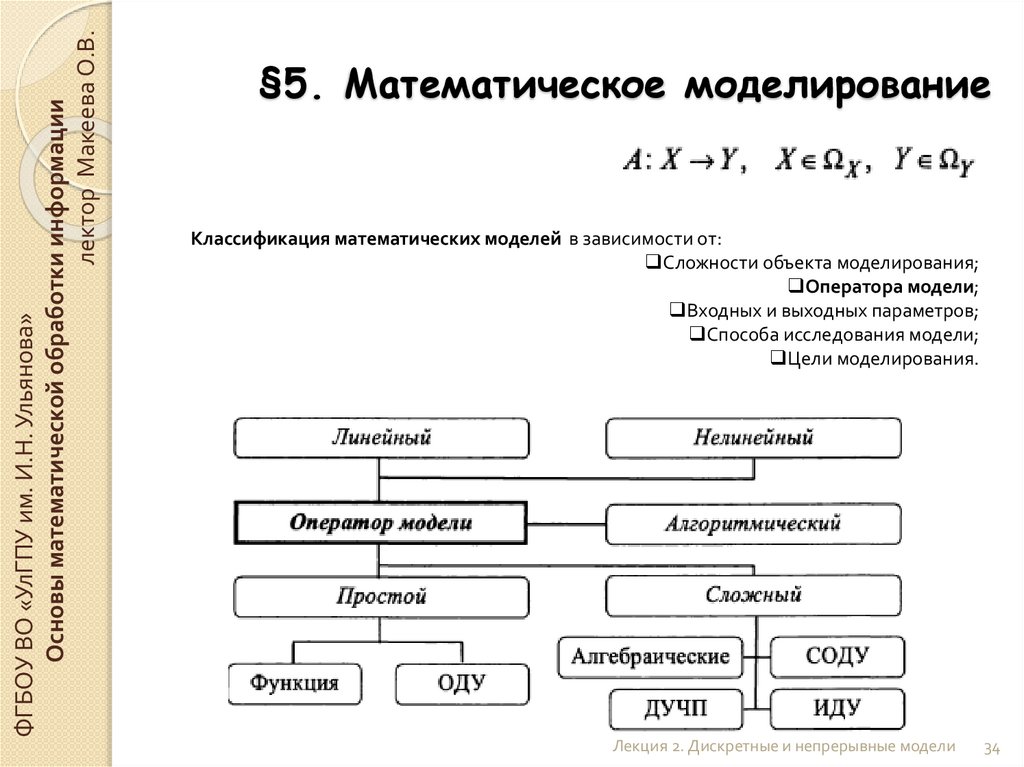
§5. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Лекция 2. Дискретные и непрерывные модели
34
35.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
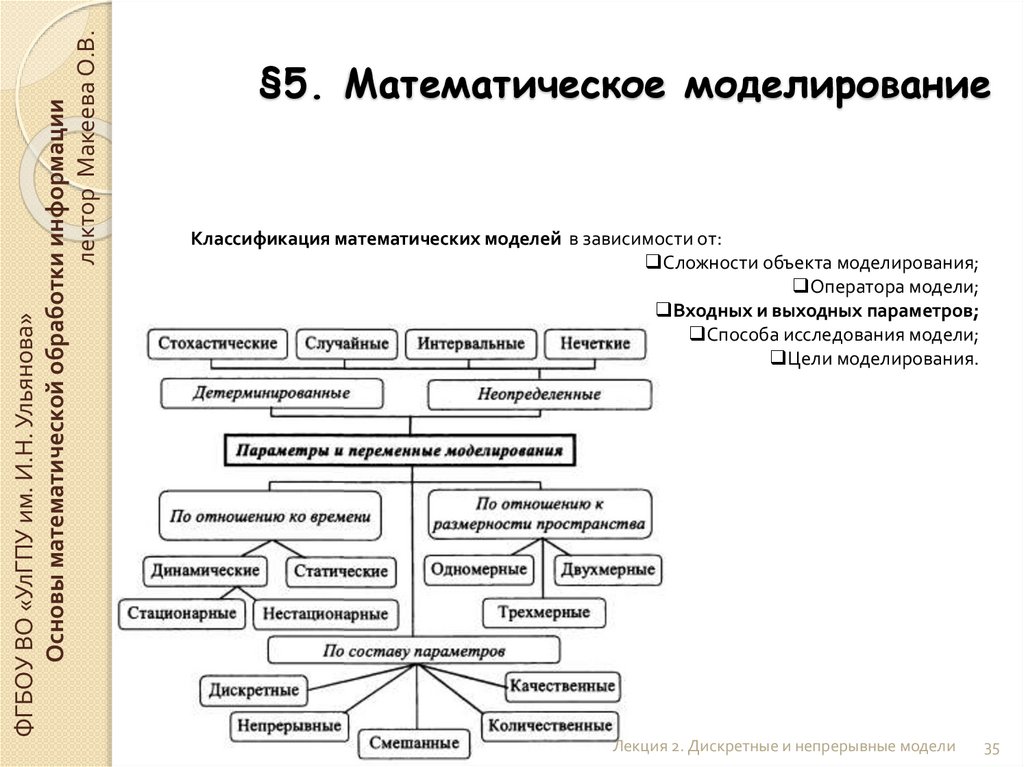
§5. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Лекция 2. Дискретные и непрерывные модели
35
36.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§5. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Лекция 2. Дискретные и непрерывные модели
36
37.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§5. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Лекция 2. Дискретные и непрерывные модели
37
38.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
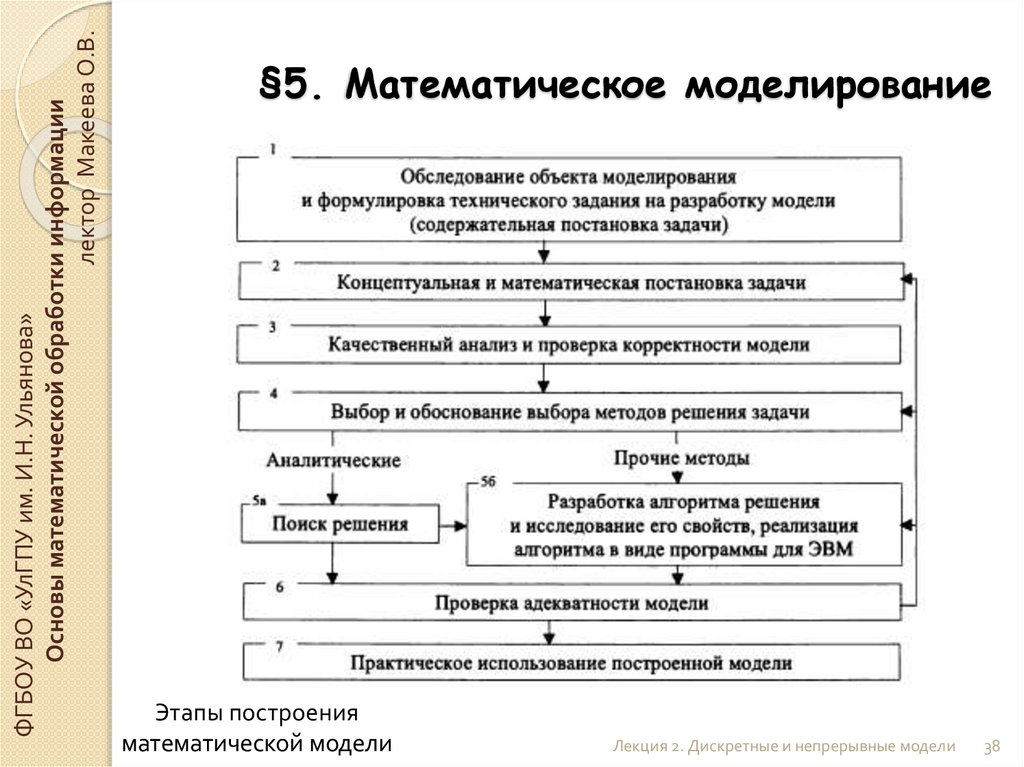
§5. Математическое моделирование
Этапы построения
математической модели
Лекция 2. Дискретные и непрерывные модели
38
39.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§5. Математическое моделирование
Абатурова Вера Сергеевна
к.п.н.; зав. отделом образовательных и
информационных технологий Южного
математического института
Владикавказского научного центра РАН;
директор ВЦНМО
Лекция 2. Дискретные и непрерывные модели
39
40.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§5. Математическое моделирование
а - количество единиц травы, которое
было на лугу первоначально;
b - количество единиц травы, которое
ежедневно вырастает на лугу;
с - количество единиц травы, которое
ежедневно съедает одна корова.
Ответ: 20 коров.
1. Выбор переменных.
2. Запись ограничений на
переменные.
3. Формулировка
требований задачи на
языке математики (с
помощью переменных).
4. Решение
математической задачи.
5. Интерпретация
результатов. Запись
ответа.
Лекция 2. Дискретные и непрерывные модели
40
41.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
Основы математической
обработки информации
Продолжение следует…































 Информатика
Информатика








