Дискретные и непрерывные модели

1. Основы математической обработки информации

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
Основы математической
обработки информации
Семестр: 1
Лекции: 6
Практические занятия: 10
Контрольная работа: 1
Зачёт

2.

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
Лекция 2.
Дискретные и непрерывные модели
Аппроксимация
§0. Фракталы. Поиски новых размерностей
§1. Задача о размножении кроликов
Последовательности
§2. Задача о ступеньках из домино
Ряды
§3. Задача о площади сектора
Функции
§4. Задача об эксплуатации автомобиля
Аппроксимация
Лекция 2. Дискретные и непрерывные модели
2

3.

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
Фракталы.
Поиски новых размерностей.
Лекция 2. Дискретные и непрерывные модели
3

4. §1. Задача о размножении кроликов

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Задача о размножении кроликов
Леона́ рдо Пиза́ нский
1170-1250
Лекция 2. Дискретные и непрерывные модели
4

5. §1. Задача о размножении кроликов

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Задача о размножении кроликов
В своей книге «Liber Abaci» (1202) Леонардо Пизанский,
известный как Фибоначчи, рассматривает развитие
идеализированной
(биологически
нереальной)
популяции кроликов, предполагая, что:
• изначально есть новорожденная пара кроликов
(самец и самка);
• со второго месяца после своего рождения кролики
начинают спариваться,
• и каждый месяц производить новую пару
кроликов;
• кролики никогда не умирают.
Сколько пар кроликов будет через n месяцев?
Лекция 2. Дискретные и непрерывные модели
5

6. §1. Задача о размножении кроликов

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Задача о размножении кроликов
Лекция 2. Дискретные и непрерывные модели
6

7. §1. Задача о размножении кроликов

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Задача о размножении кроликов
Обозначим через A пару зрелых кроликов, а через B –
пару новорожденных кроликов. Тогда процесс
«размножения» может быть описан с помощью двух
«переходов»:
A – AB моделирует ежемесячное превращение каждой
зрелой пары кроликов А в две пары, а именно в ту же
самую пару зрелых кроликов А и новорожденную пару
кроликов В;
B – A моделирует процесс «созревания» кроликов,
когда новорожденная пара кроликов В через месяц
превращается в зрелую пару А.
Лекция 2. Дискретные и непрерывные модели
7

8. §1. Задача о размножении кроликов

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Задача о размножении кроликов
Дата
Пары кроликов
A
B
A+B
1-го января
A
1
0
1
1-го февраля
AB
1
1
2
1-го марта
ABA
2
1
3
1-го апреля
ABAAB
3
2
5
1-го мая
ABAABABA
5
3
8
1-го июня
ABAABABAABAAB
8
5
1
Лекция 2. Дискретные и непрерывные модели
8

9. §1. Задача о размножении кроликов Последовательности

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
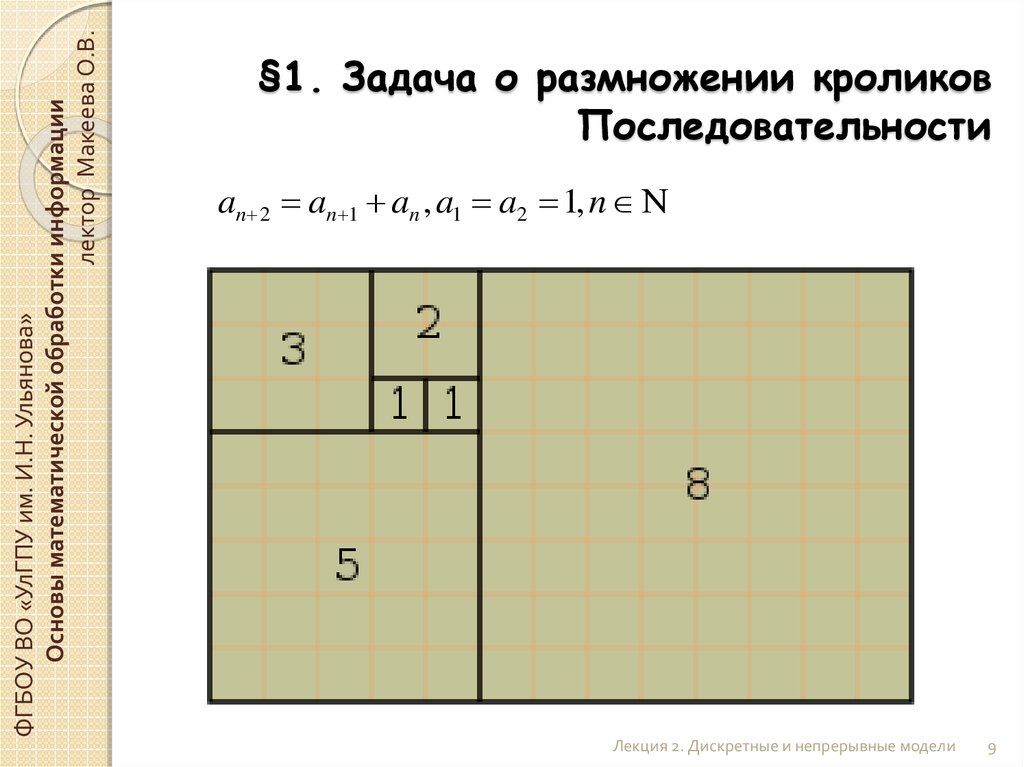
§1. Задача о размножении кроликов
Последовательности
an 2 an 1 an , a1 a2 1, n
Лекция 2. Дискретные и непрерывные модели
9

10. §1. Задача о размножении кроликов Последовательности

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Задача о размножении кроликов
Последовательности
Последовательность
–
натурального аргумента.
a
n
числовая
функция
an f n , n
Способы задания последовательности
• описание;
• перечисление элементов;
• формула общего члена;
1 1 1 1 1
, , , , ,
• рекуррентная формула;
1 2 3 4 5
• графически.
Лекция 2. Дискретные и непрерывные модели
10

11. §1. Задача о размножении кроликов Последовательности

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Задача о размножении кроликов
Последовательности
Свойства последовательностей
• стационарность;
• цикличность;
• монотонность;
• ограниченность.
1 2 3 4 5
, , , , ,
3 5 7 9 11
Операции над последовательностями
• сложение;
• вычитание;
• умножение;
• деление;
• умножение на число.
Лекция 2. Дискретные и непрерывные модели
11

12. §1. Задача о размножении кроликов Последовательности

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Задача о размножении кроликов
Последовательности
Частные случаи последовательностей
• арифметическая прогрессия: an 1 an d
an k an k
an
2
• геометрическая прогрессия: bn 1 bn q, q 0
bn bn k bn k
Предел последовательности
lim an a 0, N : n N an a
n
2 3 4 5 6
, , , , , 1
1 2 3 4 5
Лекция 2. Дискретные и непрерывные модели
12

13. §2. Задача о ступеньках из домино

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Задача о ступеньках из домино
Лекция 2. Дискретные и непрерывные модели
13

14. §2. Задача о ступеньках из домино

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Задача о ступеньках из домино
Лекция 2. Дискретные и непрерывные модели
14

15. §2. Задача о ступеньках из домино

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Задача о ступеньках из домино
Лекция 2. Дискретные и непрерывные модели
15

16. §2. Задача о ступеньках из домино Ряды

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Задача о ступеньках из домино
Ряды
Лекция 2. Дискретные и непрерывные модели
16

17. §2. Задача о ступеньках из домино Ряды

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Задача о ступеньках из домино
Ряды
Ряд – это бесконечная сумма.
a1 a2 a3 an an
n 1
Виды рядов
1 1 1 1 1
1
• числовые ряды;
• положительные;
1 2 3 4 5
n 1 n
• знакопеременные;
• знакочередующиеся;
2
3
4
n
x
x
x
x
x
• функциональные; e x 1
1! 2! 3! 4!
n 0 n!
• степенные;
• тригонометрические;
Лекция 2. Дискретные и непрерывные модели
17
•…

18. §2. Задача о ступеньках из домино Ряды

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Задача о ступеньках из домино
Ряды
Вычисление (исследование) рядов
S a1 a2 a3 an
S n a1 a2 a3 an
S1 , S2 , S3 , S4 , S
1 1 1
1
S 1 n
2 4 8
2
3
7
15
2n 1
1
S 2 , S3 , S 4 , , S n n 1 2 n 1 , 2
2
4
8
2
2
Лекция 2. Дискретные и непрерывные модели
18

19. §3. Задача о площади сектора

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§3. Задача о площади сектора
Мордкович
Александр Григорьевич
Лекция 2. Дискретные и непрерывные модели
19

20. §3. Задача о площади сектора

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§3. Задача о площади сектора
Лекция 2. Дискретные и непрерывные модели
20

21. §3. Задача о площади сектора Функции

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§3. Задача о площади сектора
Функции
Числовой функцией с областью определения D
называется зависимость, при которой каждому
числу из множества D ставится в соответствие
единственное число y, обычно обозначаемое у=f(x).
Способы задания функций
• описание;
• табличный;
• графический;
• аналитический.
Лекция 2. Дискретные и непрерывные модели
21

22. §3. Задача о площади сектора Функции

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§3. Задача о площади сектора
Функции
Свойства функций
• монотонность;
• ограниченность;
• чётность/нечётность;
• периодичность.
Операции над функциями
• сложение;
• вычитание;
• умножение;
• деление;
• умножение на число;
• суперпозиция.
Лекция 2. Дискретные и непрерывные модели
22

23. §3. Задача о площади сектора Функции

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§3. Задача о площади сектора
Функции
Основные элементарные функции
• линейная;
• квадратичная;
• степенная;
• показательная;
• логарифмическая;
• тригонометрические;
• обратные тригонометрические.
Лекция 2. Дискретные и непрерывные модели
23

24. §3. Задача о площади сектора Функции

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§3. Задача о площади сектора
Функции
Предел функции
lim f x A
x
0, M 0 : x M f x A
lim f x A
x x0
0, 0 : x, 0 x x0 f x A
Лекция 2. Дискретные и непрерывные модели
24

25. §4. Задача об эксплуатации автомобиля

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§4. Задача об эксплуатации автомобиля
В результате исследования зависимости между сроком
эксплуатации автомобиля и расходами на его ремонт
получены следующие данные:
t, лет
1
2
3
4
5
6
7
8
S, тыс. руб.
120
140
230
370
445
570
655
770
Составьте линейную зависимость стоимости ремонта от
срока эксплуатации.
Определите предполагаемую величину затрат на
ремонт на 10-й год эксплуатации.
Лекция 2. Дискретные и непрерывные модели
25

26. §4. Задача об эксплуатации автомобиля Аппроксимация

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§4. Задача об эксплуатации автомобиля
Аппроксимация
Аппроксима́ция (от лат. proxima – ближайшая) или
приближе́ние — научный метод, состоящий в
замене одних объектов другими, в каком-то смысле
близкими к исходным, но более простыми.
Аппроксимация позволяет исследовать числовые
характеристики и качественные свойства объекта,
сводя задачу к изучению более простых или более
удобных объектов.
Лекция 2. Дискретные и непрерывные модели
26

27. §4. Задача об эксплуатации автомобиля Аппроксимация

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§4. Задача об эксплуатации автомобиля
Аппроксимация
Интерполя́ция
интерполи́рование
—
в
вычислительной математике способ нахождения
промежуточных значений величины по имеющемуся
дискретному набору известных значений.
Экстраполя́ция, экстраполи́рование — особый тип
аппроксимации,
при
котором
функция
аппроксимируется вне заданного интервала, а не
между заданными значениями.
Лекция 2. Дискретные и непрерывные модели
27

28. §4. Задача об эксплуатации автомобиля Аппроксимация Метод наименьших квадратов

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§4. Задача об эксплуатации автомобиля
Аппроксимация
Метод наименьших квадратов
Лекция 2. Дискретные и непрерывные модели
28

29. §4. Задача об эксплуатации автомобиля Аппроксимация Метод наименьших квадратов

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§4. Задача об эксплуатации автомобиля
Аппроксимация
Метод наименьших квадратов
Лекция 2. Дискретные и непрерывные модели
29

30. §4. Задача об эксплуатации автомобиля Аппроксимация Метод наименьших квадратов

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§4. Задача об эксплуатации автомобиля
Аппроксимация
Метод наименьших квадратов
t, лет
1
2
3
4
5
6
7
8
S, тыс. руб.
120
140
230
370
445
570
655
770
S a t b
t
1
2
3
4
5
6
7
8
36
S
120
140
230
370
445
570
655
770
3300
t^2
1
4
9
16
25
36
49
64
204
t*S
120
280
690
1480
2225
3420
4585
6160
18960
n
n
n 2
a t i b t i t i S i ,
i 1
i 1
i 1
n
n
a t nb S .
i
i
i 1
i 1
a 204 b 36 18960,
a 36 8 b 3300
Лекция 2. Дискретные и непрерывные модели

31. §4. Задача об эксплуатации автомобиля Аппроксимация Метод наименьших квадратов

900
Затраты на ремонт, S
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
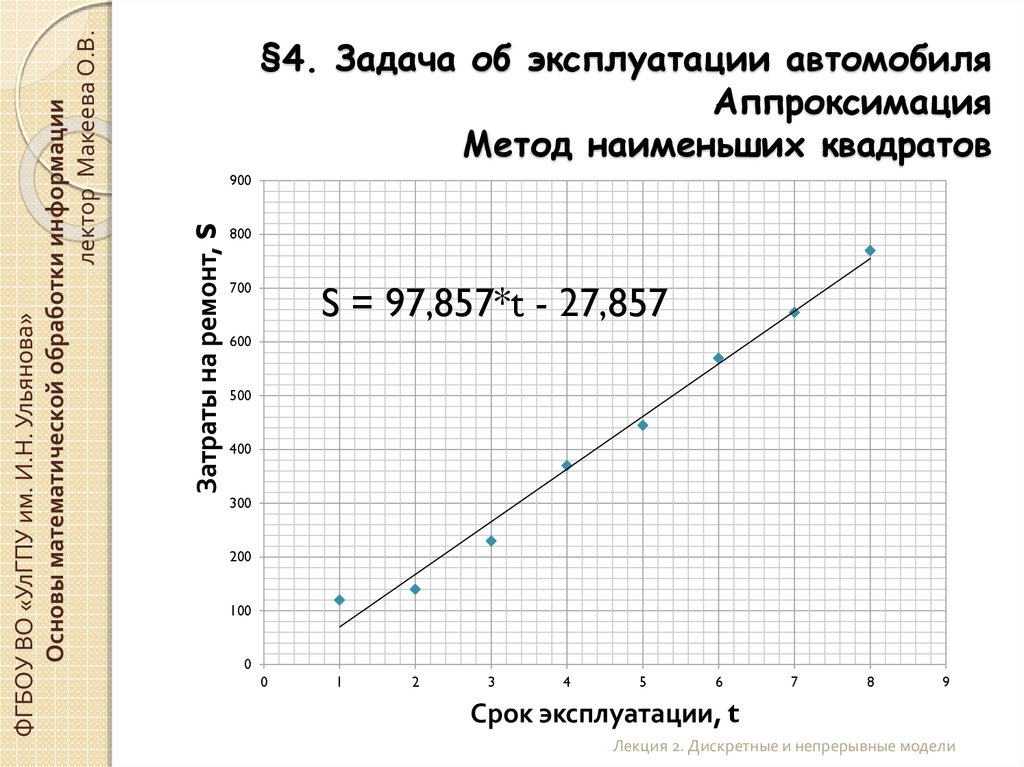
§4. Задача об эксплуатации автомобиля
Аппроксимация
Метод наименьших квадратов
800
S = 97,857*t - 27,857
700
600
500
400
300
200
100
0
0
1
2
3
4
5
6
7
8
9
Срок эксплуатации, t
Лекция 2. Дискретные и непрерывные модели

32. Продолжение следует…

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
Основы математической
обработки информации
Продолжение следует…