Похожие презентации:
Основы математической обработки информации
1.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
Основы математической
обработки информации
Семестр: 3
Лекции: 6
Практические занятия: 10
Контрольная работа: 1
Зачёт
2.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
Лекция 4.
Обработка статистических данных
§1. Математическая статистика
§2. Выборочный метод
§3. Визуализация статистических данных
§4. Меры усреднения статистических данных
§5. Меры разброса статистических данных
§6. Статистическое оценивание
Лекция 4. Обработка статистических данных
2
3.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§1. Математическая статистика
Математическая статистика – раздел математики, изучающий
методы сбора, систематизации, обработки и интерпретации результатов
наблюдений с целью выявления статистических закономерностей.
Лекция 4. Обработка статистических данных
3
4.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§1. Математическая статистика
Математическая статистика опирается на теорию вероятностей, но в
отличие от неё изучает не закономерности случайных явлений на основе
абстрактного описания действительности, а оперирует непосредственно
к результатам наблюдений над случайными явлениями; используя
результаты теории вероятностей математическая статистика позволяет
оценить значения искомых характеристик и указать степень точности
выводов, получаемых при обработке данных .
Вероятность
выпадения 6 очков
Вероятность
рождения мальчика
Лекция 4. Обработка статистических данных
4
5.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§1. Математическая статистика
Теория вероятностей
Математическая статистика
По результатам опроса 1500
респондентов рейтинг депутата
составил 30%. Найдите границы в
которых с надёжностью 0,95
Среднее изменение
курсарейтинг
акции компании
заключён
депутата. Сколько
Найдите
вероятность
того,
что
в серии
из 3%.чтобы с
в течение
одних
биржевых
торгов
составляет
респондентов
надо
опросить,
10-тивероятность
бросков решка
выпадет
2ближайших
раза.
Оцените
того,
что на99%
надёжностью
гарантировать
торгах курс изменится
более
чем на
3%.
предельную
ошибку
обследования
не
более 1%?
Лекция 4. Обработка статистических данных
5
6.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§1. Математическая статистика
STADIA – универсальный
статистический пакет
Excel – программа для работы
с электронными таблицами
Математические программные пакеты
Лекция 4. Обработка статистических данных
6
7.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Выборочный метод
В практике статистических наблюдений различают сплошное и
выборочное наблюдение.
Вся подлежащая изучению совокупность объектов (наблюдений)
называется генеральной совокупностью. Та часть объектов, которая
отобрана из генеральной совокупности непосредственно для изучения,
называется выборочной совокупностью (выборкой).
Понятие генеральной совокупности в некотором смысле аналогично
понятию случайной величины, а выборку можно рассматривать, как некий
эмпирический аналог генеральной совокупности.
Число объектов (наблюдений) совокупности называют её объёмом.
Генеральная совокупность может иметь как конечный, так и бесконечный
объём.
Лекция 4. Обработка статистических данных
7
8.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Выборочный метод
Сущность выборочного метода состоит в том, чтобы по некоторой
части генеральной совокупности (по выборке) выносить суждение о
свойствах совокупности в целом.
Кого нужно опрашивать, чтобы
получить достоверную информации
о мнении страны в целом?
Выборка называется репрезентативной (представительной), если
она хорошо воспроизводит генеральную совокупность.
Репрезентативность
выборки
обеспечивается
случайным
характером отбора при котором все элементы генеральной совокупности
имеют равные возможности быть отобранными в выборку.
Задача выборочного метода – оценить параметры (характеристики)
генеральной совокупности по данным выборки.
Лекция 4. Обработка статистических данных
8
9.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Выборочный метод
Задача
Сравнить уровень знаний по математике
первокурсников ФФиТО в текущем и
предыдущем году.
Лекция 4. Обработка статистических данных
9
10.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Выборочный метод
Предложите способ получения
репрезентативной выборки студентов
первого курса факультета ФМиТО.
N=132 - объём генеральной
совокупности
n =32 - объём выборочной
совокупности
Лекция 4. Обработка статистических данных
10
11.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Выборочный метод
№ п/п
Оценка по математике
Балл ЕГЭ по математике
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Сбор данных
28
29
30
31
32
Лекция 4. Обработка статистических данных
11
12.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Выборочный метод
№ п/п
Оценка по математике
Балл ЕГЭ по математике
1
3
5
5
3
4
5
3
3
4
4
4
5
4
4
3
4
4
4
5
4
3
3
5
4
4
4
5
3
4
4
3
3
27
78
68
27
50
72
33
27
56
56
62
88
50
56
45
56
56
50
90
62
39
45
68
50
56
62
74
45
56
56
27
33
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Сбор данных
28
29
30
31
32
Лекция 4. Обработка статистических данных
12
13.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Выборочный метод
№ п/п
Оценка по математике
Балл ЕГЭ по математике
1
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
5
5
5
5
5
5
5
27
27
27
27
33
33
39
45
45
45
50
50
50
50
56
56
56
56
56
56
56
56
62
62
62
68
68
72
74
78
88
90
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Ранжирование
данных
28
29
30
31
32
Лекция 4. Обработка статистических данных
13
14.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Выборочный метод
Номер варианты
i
1
2
3
Варианта
xi
3
4
5
Частота варианты
ni
Относительная
частота варианты
wi
n n
i
w 1
i
Группировка
данных
Лекция 4. Обработка статистических данных
14
15.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Выборочный метод
Номер варианты
i
1
2
3
Варианта
xi
Частота варианты
ni
3
10
4
15
5
7
Относительная
частота варианты
wi
0,31
0,47
0,22
n 32
i
w 1
i
Группировка
данных
Лекция 4. Обработка статистических данных
15
16.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Выборочный метод
m 1 3,322lg n количество частичных интервалов
Номер
интервала
i
1
2
…
m
Интервал
вариант
[xi; xi+1)
n n
i
Группировка
данных
Частота
ni
Относительная
частота
wi
w 1
i
xmax xmin
1 3,322 lg n
длина частичного интервала
h xi 1 xi
Лекция 4. Обработка статистических данных
16
17.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Выборочный метод
m 1 3,322 lg 32 6
Номер
интервала
i
1
2
3
4
5
6
Интервал
вариант
[xi; xi+1)
[26; 37)
[37; 48)
[48; 59)
[59; 70)
[70; 81)
[81; 92)
n 32
i
Группировка
данных
Частота
ni
6
4
12
5
3
2
w 1
Относительная
частота
wi
0,19
0,12
0,38
0,16
0,09
0,06
i
90 27 63
h
10,5 11
6
6
Лекция 4. Обработка статистических данных
17
18.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Выборочный метод
Вариационным рядом называется ранжированный в порядке
возрастания (или убывания) ряд вариант с соответствующими им весами
(частотами или частостями).
Вариационный ряд называется
дискретным, если
частоты
соответствуют конкретным значениям признака, и – интервальным
(непрерывным), если частоты соответствуют интервалам значений
признака.
Номер варианты
i
1
2
3
Варианта
Частота варианты
xi
ni
3
10
4
15
5
7
Относительная
частота варианты
wi
0,31
0,47
0,22
Дискретный вариационный ряд
Лекция 4. Обработка статистических данных
18
19.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§2. Выборочный метод
Вариационным рядом называется ранжированный в порядке
возрастания (или убывания) ряд вариант с соответствующими им весами
(частотами или частостями).
Вариационный ряд называется
дискретным, если
частоты
соответствуют конкретным значениям признака, и – интервальным
(непрерывным), если частоты соответствуют интервалам значений
признака.
Номер интервала
Интервал вариант
Частота
Относительная частота
i
[xi; xi+1)
ni
wi
1
[26; 37)
[37; 48)
[48; 59)
[59; 70)
[70; 81)
[81; 92)
6
4
12
5
3
2
0,19
0,12
0,38
0,16
0,09
0,06
2
3
4
5
6
Интервальный вариационный ряд
Лекция 4. Обработка статистических данных
19
20.
1614
12
Номер варианты
i
Варианта
xi
Частота варианты
ni
Относительная
частота варианты
wi
Чимсло студентов
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§3. Визуализация статистических
данных
1
2
3
3
4
5
10
15
7
0,31
0,47
0,22
10
8
6
4
Полигон частот
2
0
0
1
2
3
4
5
6
Оценка
Лекция 4. Обработка статистических данных
20
21.
0,50,45
0,4
Номер варианты
i
Варианта
xi
Частота варианты
ni
Относительная
частота варианты
wi
Доля студентов
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§3. Визуализация статистических
данных
0,35
0,3
0,25
0,2
0,15
1
2
3
3
4
5
10
15
7
0,31
0,47
0,22
0,1
Полигон относительных
частот
0,05
0
0
1
2
3
4
Оценка
5
6
Лекция 4. Обработка статистических данных
21
22.
14Номер 12
интервала
10
i
1
8
2
6
3
4
4
5
2
6
Число студентов
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§3. Визуализация статистических
данных
Интервал
вариантов
[xi; xi+1)
[26; 37)
[37; 48)
[48; 59)
[59; 70)
[70; 81)
[81; 92)
Частота
Частость
ni
wi
6
4
12
5
3
2
0,19
0,12
0,38
0,16
0,09
0,06
0
[26;37) [37;48) [48;59) [59;70) [70;81) [81;92)
Балл ЕГЭ
Гистограмма частот
Лекция 4. Обработка статистических данных
22
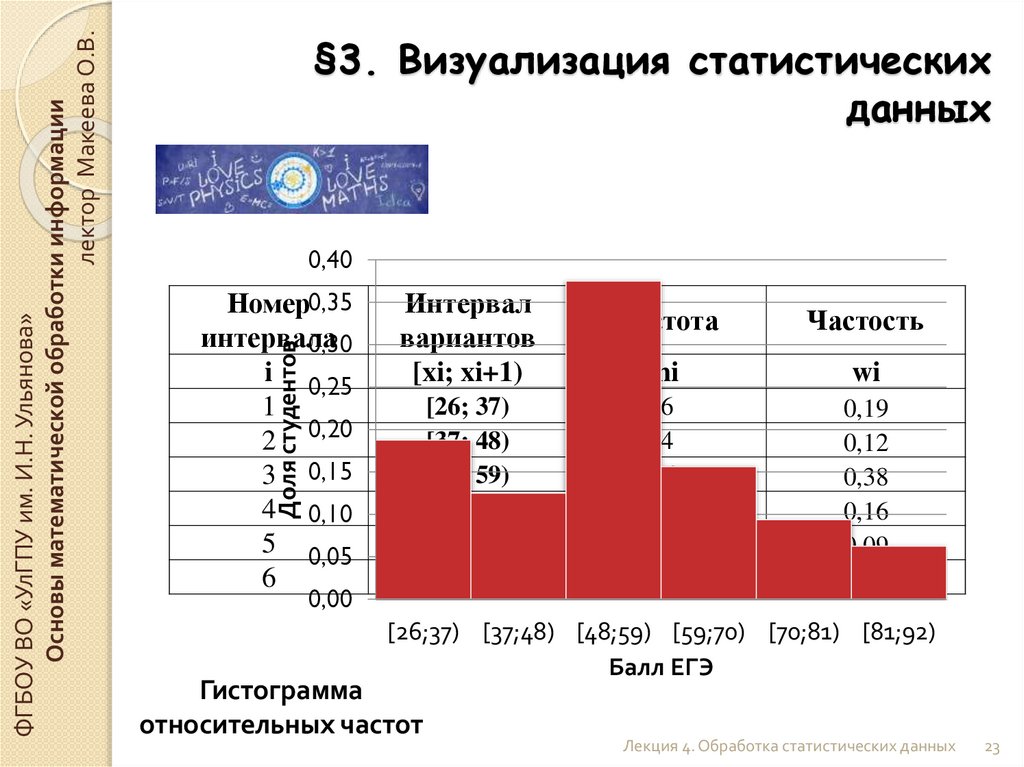
23.
0,40Номер0,35
интервала
0,30
i 0,25
1
2 0,20
3 0,15
4 0,10
5 0,05
6
Доля студентов
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§3. Визуализация статистических
данных
Интервал
вариантов
[xi; xi+1)
[26; 37)
[37; 48)
[48; 59)
[59; 70)
[70; 81)
[81; 92)
0,00
Частота
Частость
ni
wi
6
4
12
5
3
2
0,19
0,12
0,38
0,16
0,09
0,06
[26;37) [37;48) [48;59) [59;70) [70;81) [81;92)
Балл ЕГЭ
Гистограмма
относительных частот
Лекция 4. Обработка статистических данных
23
24.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§3. Визуализация статистических
данных
[26; 37)
0,4
0,3
[81; 92)
0,2
[37; 48)
0,1
0
[70; 81)
[48; 59)
[59; 70)
Лепестковая диаграмма
Лекция 4. Обработка статистических данных
24
25.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§3. Визуализация статистических
данных
[70; 81)
9%
[81; 92)
6%
[26; 37)
19%
[59; 70)
16%
[37; 48)
12%
[48; 59)
38%
Круговая диаграмма
Лекция 4. Обработка статистических данных
25
26.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§3. Визуализация статистических
данных
Номер
интервала
i
1
2
3
4
5
6
Интервал
Середина
интервала
вариант
[xi;xi*
xi+1)
[26;
3137)
[37;
4248)
[48;
5359)
[59;
6470)
[70;
7581)
[81;
8692)
Частота
ni
6
4
12
5
3
2
Относительная
частота
wi
0,19
0,12
0,38
0,16
0,09
0,06
Лекция 4. Обработка статистических данных
26
27.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§3. Визуализация статистических
данных
14
14
12
12
10
10
8
8
6
6
4
4
2
2
0
0
[26;37) [37;48) [48;59) [59;70) [70;81) [81;92)
0
20
40
60
80
100
Лекция 4. Обработка статистических данных
27
28.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§4. Меры усреднения статистических
данных
Номер варианты
i
1
2
3
Варианта
xi
3
4
5
Частота варианты
ni
10
15
7
Относительная
частота варианты
wi
0,31
0,47
0,22
Мода – варианта с наибольшей частотой.
Mo 4
Лекция 4. Обработка статистических данных
28
29.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§4. Меры усреднения статистических
данных
xn xn
Me
2
2
1
2
Номер варианты
i
1
2
3
Варианта
xi
3
4
5
Частота варианты
ni
10
15
7
Относительная
частота варианты
wi
0,31
0,47
0,22
Медиана – варианта , которая делит ранжированный ряд данных
на две равные по объёму части.
Если ряд содержит чётное количество вариант, то медиана равна
среднему арифметическому двух вариант, стоящих в середине.
x16 x17 4 4
n 32 Me
4
2
2 Лекция 4. Обработка статистических данных
29
30.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§4. Меры усреднения статистических
данных
n
x n
x B i 1
i
i
n
Номер варианты
i
1
2
3
Варианта
xi
3
4
5
Частота варианты
ni
10
15
7
Относительная
частота варианты
wi
0,31
0,47
0,22
Выборочная средняя – среднее арифметическое всех вариант.
3 10 4 15 5 7 30 60 35 125
xB
3,9
32
32
32
Лекция 4. Обработка статистических данных
30
31.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§4. Меры усреднения статистических
данных
Номер
интервала
i
1
2
3
4
5
6
Интервал
Середина
интервала
вариант
[xi;xi*
xi+1)
[26;
3137)
[37;
4248)
[48;
5359)
[59;
6470)
[70;
7581)
[81;
8692)
Частота
ni
6
4
12
5
3
2
Относительная
частота
wi
0,19
0,12
0,38
0,16
0,09
0,06
Mo 53 Mе 53
31 6 42 4 53 12 64 5 75 3 86 2
xB
53,3
32 Лекция 4. Обработка статистических данных 31
32.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§5. Меры разброса статистических
данных
R xmax xmin
Номер варианта
i
1
2
3
Вариант
xi
3
4
5
Частота варианта
ni
10
15
7
Частость варианта
wi
0,31
0,47
0,22
Размах варьирования
наименьшей вариантами.
–
разница
между
наибольшей
и
R 5 3 2
Лекция 4. Обработка статистических данных
32
33.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§5. Меры разброса статистических
данных
n
x x n
d B i 1
B
i
i
n
Номер варианта
i
1
2
3
Вариант
xi
3
4
5
Частота варианта
ni
10
15
7
Частость варианта
wi
0,31
0,47
0,22
Выборочная дисперсия – среднее арифметическое квадратов
отклонений вариант от их выборочной средней.
3 3,9 10 4 3,9 15 5 3,9 7
d
0,52
2
B
2
2
32
Лекция 4. Обработка статистических данных
33
34.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§5. Меры разброса статистических
данных
n
s
dB
n 1
2
Номер варианта
i
1
2
3
Вариант
xi
3
4
5
Частота варианта
ni
10
15
7
Частость варианта
wi
0,31
0,47
0,22
«Исправленная» выборочная дисперсия
32
s 0,52 0,53
31
2
Лекция 4. Обработка статистических данных
34
35.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§5. Меры разброса статистических
данных
s s2
Номер варианта
i
1
2
3
Вариант
xi
3
4
5
Частота варианта
ni
10
15
7
Частость варианта
wi
0,31
0,47
0,22
«Исправленное» выборочный стандарт
s 0,53 0,73
Лекция 4. Обработка статистических данных
35
36.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§5. Меры разброса статистических
данных
Номер
интервала
i
1
2
3
4
5
6
Интервал
Середина
интервала
вариант
[xi;xi*
xi+1)
[26;
3137)
[37;
4248)
[48;
5359)
[59;
6470)
[70;
7581)
[81;
8692)
Частота
ni
6
4
12
5
3
2
Относительная
частота
wi
0,19
0,12
0,38
0,16
0,09
0,06
R 86 31 55
2
2
2
2
2
2
31 53,3 6 42 53,3 4 53 53,3 12 64 53,3 5 75 53,3 3 86 53,3 2
d
238
B
s2
32
n
32
d B 238 246
n 1
31
s 246 16
Лекция 4. Обработка статистических данных
36
37.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§6. Статистическое оценивание
При изучении генеральной совокупности с помощью выборки
параметры совокупности заменяются их приближениями – оценками,
полученными на основе выборочных данных.
Оценки, которые выражаются одним числом, называют точечными.
Так для оценки генеральной средней можно использовать выборочную
среднюю, для оценки генеральной дисперсии – исправленную
выборочную дисперсию, для оценки генеральной доли – выборочную
долю.
Лекция 4. Обработка статистических данных
37
38.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§6. Статистическое оценивание
Более качественную информацию о параметре генеральной
совокупности дают интервальные оценки – интервалы (доверительные
интервалы), которые с заданной вероятностью (доверительной
вероятностью, надежностью оценки) накрывают изучаемый параметр
совокупности.
Интервальные оценки удобно строить, выбрав в качестве середины
интервала значение точечной оценки. Наибольшее отклонение Δ
выборочного значения оценки θn от истинного значения параметра θ
называется предельной ошибкой выборки (точностью оценки) при
заданном объеме выборки n и заданной доверительной вероятности γ.
Лекция 4. Обработка статистических данных
38
39.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§6. Статистическое оценивание
Пусть N и n – объёмы генеральной и выборочной совокупностей
соответственно;
S 2 – исправленная выборочная дисперсия;
– надёжность оценки;
t – аргумент функции Лапласа Ф(t) и Ф(t) = ;
– случайная величина, имеющая распределение Стьюдента с n-1
степенями свободы и P tn 1 .
Доверительные интервалы для генеральной средней a можно построить
используя данные таблицы, причём для выборок небольшого объёма это можно
сделать лишь для нормальной генеральной совокупности.
Лекция 4. Обработка статистических данных
39
40.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§6. Статистическое оценивание
При решении статистических задач часто требуется определить
необходимый объем выборки для достижения заданной надежности
доверительного интервала оценки некоторого параметра. Объем выборки n
определяется доверительной вероятностью и предельной ошибкой Δ.
Например, для построения оценки математического ожидания а
соответствующие формулы для объёма выборки приведены в таблице.
Лекция 4. Обработка статистических данных
40
41.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§6. Статистическое оценивание
Лекция 4. Обработка статистических данных
41
42.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
§6. Статистическое оценивание
Лекция 4. Обработка статистических данных
42
43.
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»Основы математической обработки информации
лектор Макеева О.В.
Основы математической
обработки информации
Продолжение следует…










































 Информатика
Информатика








