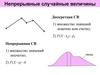
Непрерывные случайные величины (НСВ)

1.

НСВ – это СВ, возможные значения которых непрерывно заполняют
некоторый промежуток
Плотность
распределения (f(x)),
закон распределения
Функция
распределения (F(x))
Пример:
расстояние, которое пролетит снаряд при
выстреле из оружия;
скорость самолета при выходе на заданную
высоту;
изменение
температуры
жидкости
при
нагревании или охлаждении
И т.п.
Числовые
характеристики
Связь между f(x) и F(x)
f(x) = F’(x)
Вероятность попадания в
заданный интервал:
P( x ) f ( x)dx

2.

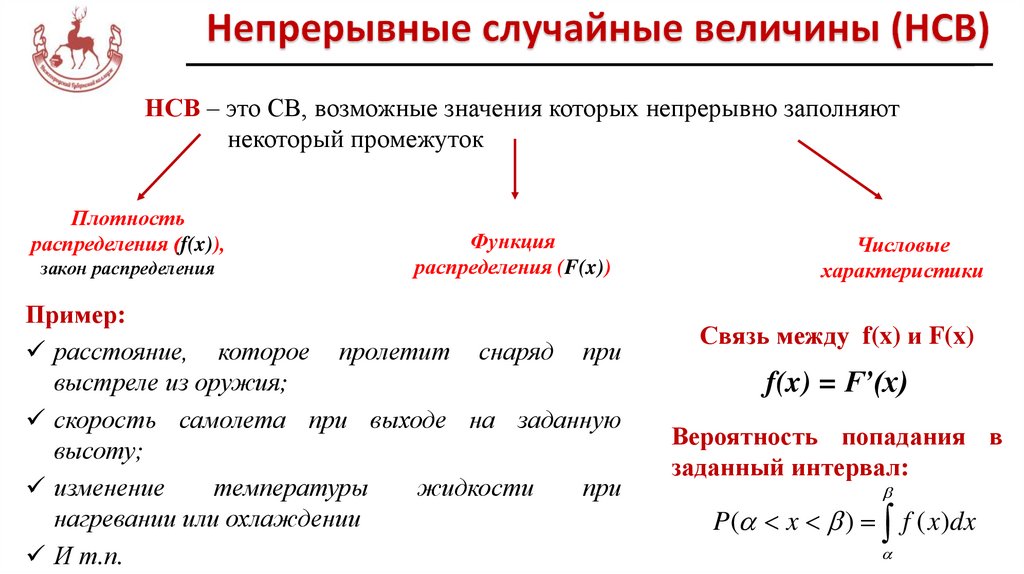
Плотность распределения вероятностей НСВ Х в точке х – это предел
отношения вероятности попадания значения этой величины в интервале
(x; x+ x) к длине x отрезка [x; x+ x] при x 0:
P( x x x x)
f ( x) lim
x x
x
Свойства плотности распределения:
1. Плотность распределения неотрицательна:
f(x)≥0
2. Плотность распределения нормирована на
единицу:
f ( x) 1

3.

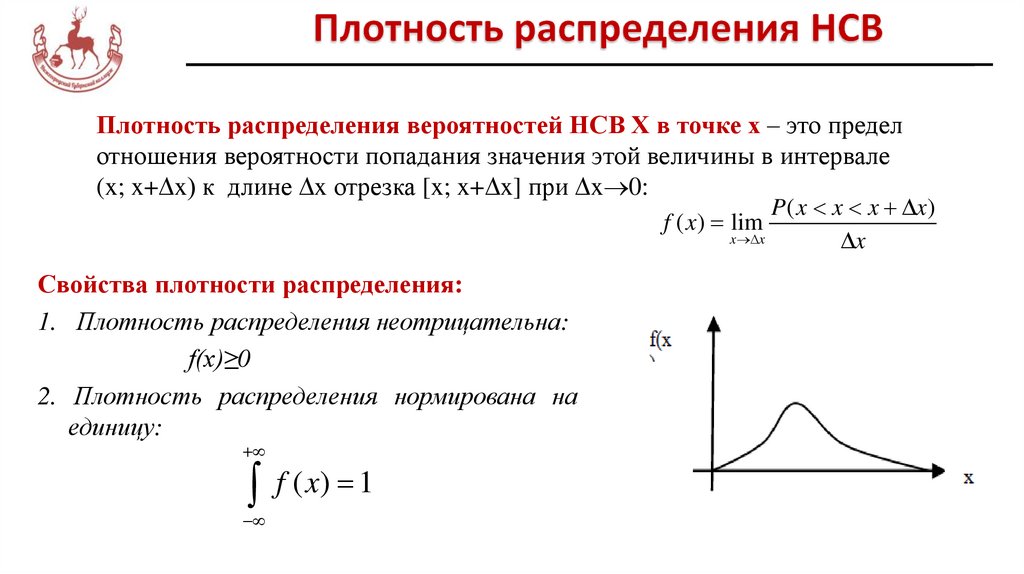
НСВ имеет непрерывную функцию распределения, график которой имеет
форму плавной кривой
F(x)
x1
…
x
xn
x
F(x)=F(X<x)=F( X x) f ( x)dx

4.

Мода (Mo) – значение НСВ при котором плотность вероятности
максимальная;
Медиана (Ме) – значение НСВ, для которого вероятность попасть справа и слева от
нее одинакова Ме
f ( x)dx f ( x)dx
Математическое ожидание М(х)
Ме
М ( х) x f ( x)dx
Дисперсия D(х)
D( х) [ x M ( x)]2 f ( x)dx
Среднее квадратическое отклонение (x)
( х) D( x)

5.

НСВ X задана плотностью распределения:
Найти:
1.
2.
3.
4.
5.
6.
7.
0, при х 0;
f(x)= Cx, при 0<x 2 ;
0, при x>2
постоянный параметр С,
функцию распределения F(x),
построить графики f(x) и F(x),
вероятность попадания X в (0;0,5),
математическое ожидание M(X),
дисперсию D(X)
среднее квадратическое отклонение (X)

6.

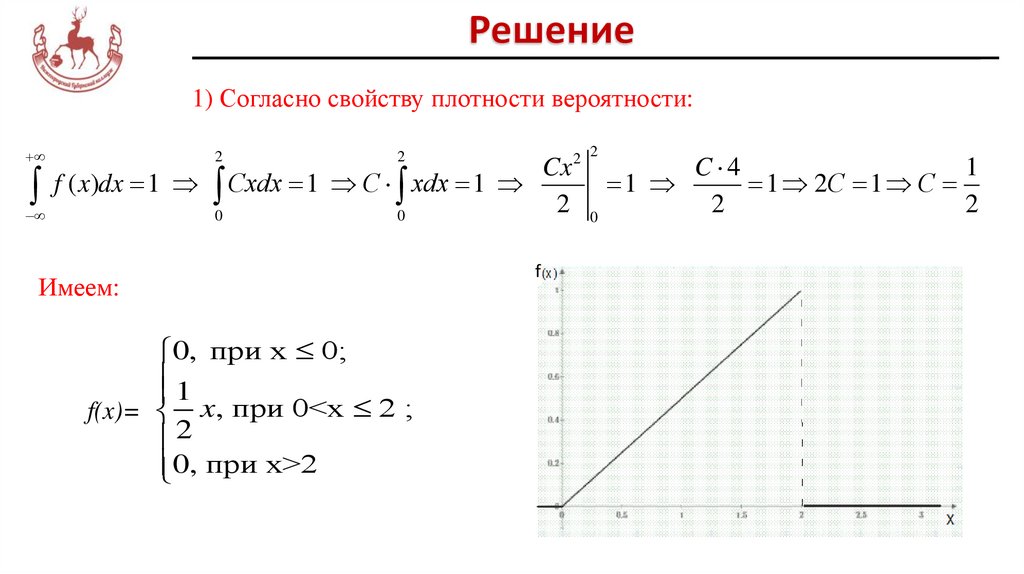
1) Согласно свойству плотности вероятности:
2 2
Cx
C 4
1
f ( x)dx 1 0 Схdx 1 C 0 xdx 1 2 1 2 1 2C 1 C 2
0
2
2
Имеем:
0, при х 0;
1
f(x)= x, при 0<x 2 ;
2
0, при x>2
f

7.

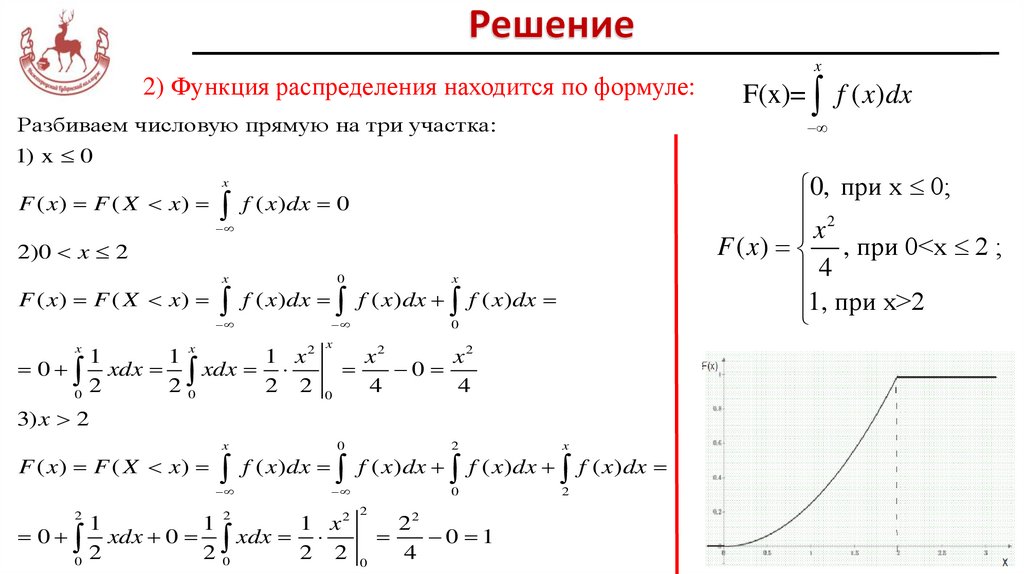
2) Функция распределения находится по формуле:
Разбиваем числовую прямую на три участка:
1) x 0
0, при х 0;
2
x
F ( x) , при 0<x 2 ;
4
1, при x>2
F ( x) F ( X x) f ( x)dx 0
2)0 x 2
0
x
0
F ( x) F ( X x) f ( x)dx f ( x )dx f ( x )dx
x
2 x
x
1
1
1 x
x2
x2
0 xdx xdx
0
2
20
2 2 0
4
4
0
3) x 2
x
0
2
x
0
2
F ( x) F ( X x) f ( x)dx f ( x )dx f ( x)dx f ( x)dx
2
2
2 2
1
1
1 x
22
0 xdx 0 xdx
0 1
2
20
2 2 0
4
0
F(x)= f ( x)dx
x
x
x

8.

4) Вероятность попадания НСВ в интервал (0;0,5): P( x ) f ( x)dx
Интервал (0;0,5) принадлежит второй строке плотности распределения,
поэтому используем значение функции в этой строке.
Имеем:
0,5
0.5
0.5
2 0,5
1
1
1 x
0, 52
0, 25
P (0 x 0, 5) f ( x)dx xdx xdx
0
0.0625
2
2 0
2 2 0
4
4
0
0
5) Математическое ожидание НСВ:
0
2
0
2
М ( х) x f ( x)dx x f ( x)dx x f ( x)dx x f ( x)dx
2
2
3
2
1
1 2
1 x
1 8
4
x xdx x dx
- 0
2
20
2 3 0 2 3
3
0

9.

6) Дисперсия НСВ:
D( х) [ x M ( x)]2 f ( x)dx
D( х) x 2 f ( x)dx [ M ( x)]2
2
1
1 3
16 1 x
4
D( х) x f ( x)dx x xdx x dx
2
20
9 2 4
3
0
2
2
2
4
2
2
1 16
16
16 2
- 0 2
2 4
9
9 9
6) Среднее квадратическое отклонение НСВ:
( х)
2
2
9
3
0
16
9