Кривые второго порядка

1. Кривые второго порядка

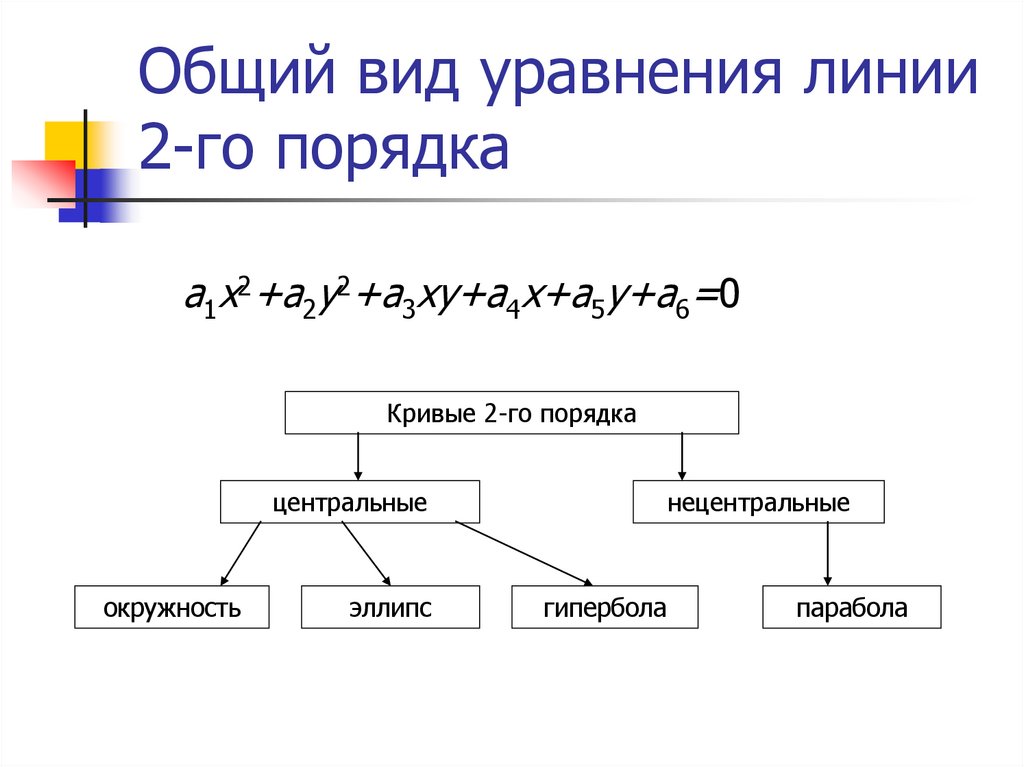
2. Общий вид уравнения линии 2-го порядка

a1x2+a2y2+a3xy+a4x+a5y+a6=0
Кривые 2-го порядка
центральные
окружность
эллипс
нецентральные
гипербола
парабола

3. Центральные кривые

- это кривые, имеющие собственный центр
симметрии
A(x-x0)2+C(y-y0)2=D,
A C
x=x0, y=y0 – оси симметрии кривой
точка (x0, y0) – центр симметрии

4. Центральные кривые эллиптического типа

Пусть x0=0 и y0=0
Кривая 2-го порядка принадлежит
эллиптическому типу, если коэффициенты A и C
имеют одинаковые знаки, т.е. AC>0

5. Центральные кривые эллиптического типа: эллипс

Пусть A>0 и C>0, тогда если:
● D>0 – действительный эллипс
x2/a2+y2/b2=1 – каноническое уравнение эллипса
● D=0 – вырожденный
● D<0 – мнимый эллипс

6. Центральные кривые эллиптического типа: окружность

действительная кривая 2-го порядка является
окружностью тогда и только тогда, когда:
• коэффициенты при квадратах текущих координат
равны между собой – A=C
• отсутствует член, содержащий произведение
текущих координат.
нормальное уравнение окружности:
(x-x0)2+(y-y0)2=r2,
C(x0, y0) – центр окружности
каноническое уравнение окружности:
x2+y2=r2,
C(0, 0) – центр окружности

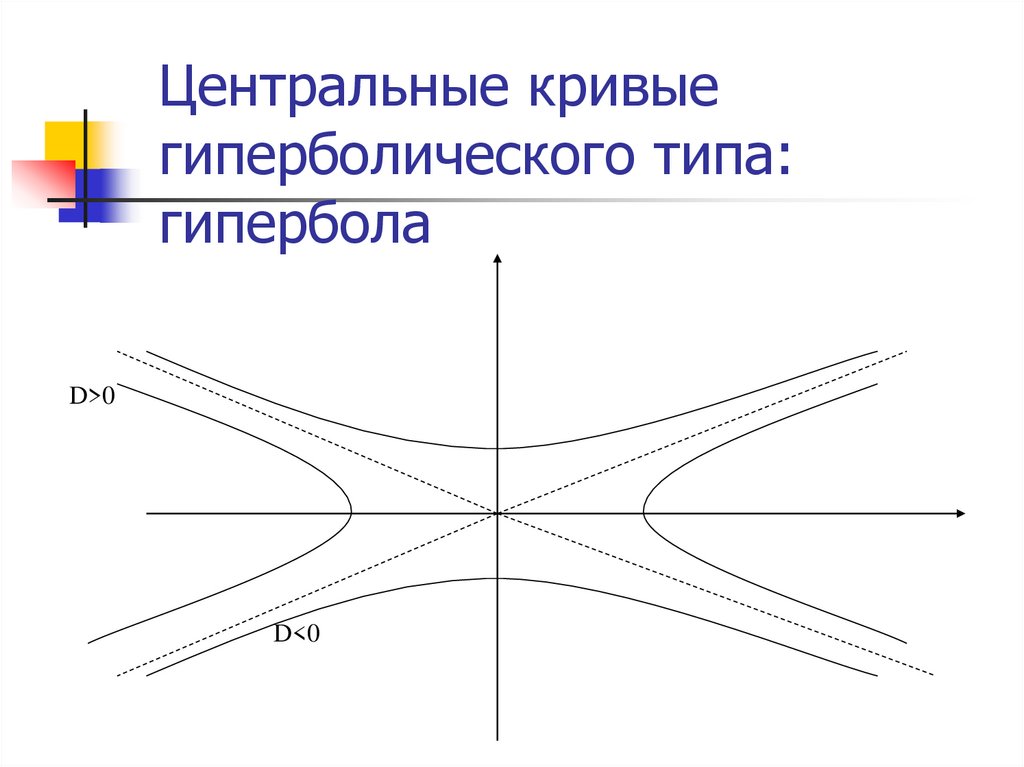
7. Центральные кривые гиперболического типа

Кривая 2-го порядка является кривой
гиперболического типа, если коэффициенты A и C
имеют противоположные знаки, т.е. AC<0
Пусть A>0, тогда C<0:
● D>0 – гипербола,
x2/a2-y2/b2=1 – каноническое уравнение гиперболы
● D=0 – вырожденная гипербола
● D<0 – сопряженная гипербола

8. Центральные кривые гиперболического типа: гипербола

D>0
D<0

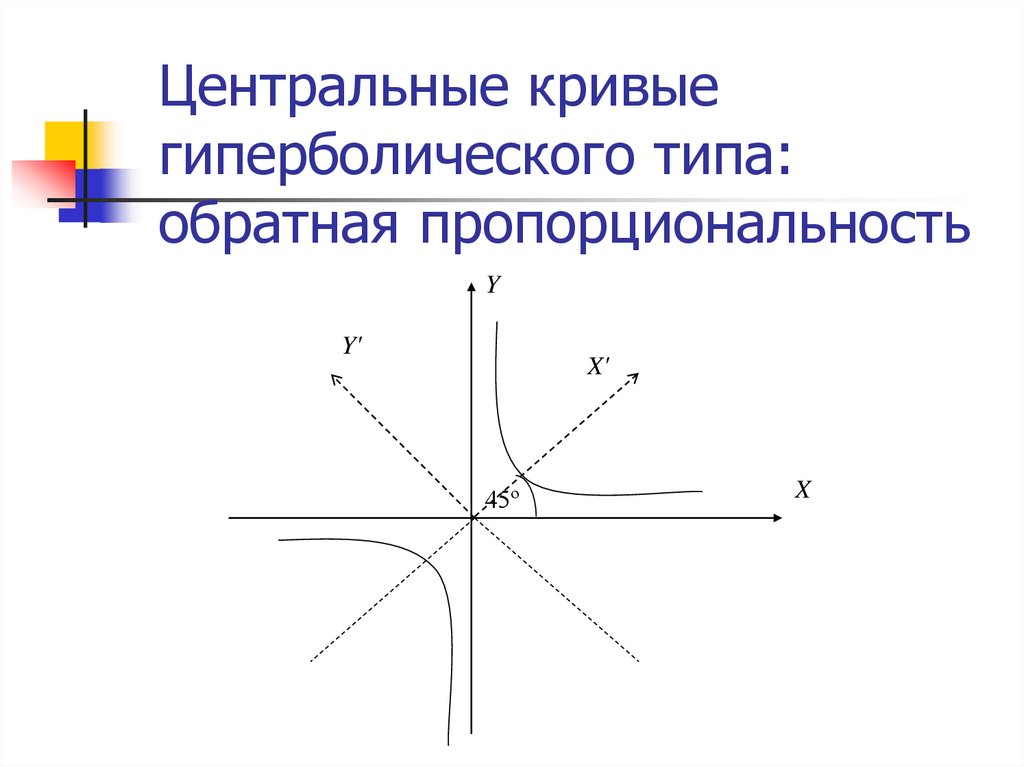
9. Центральные кривые гиперболического типа: обратная пропорциональность

Y
Y'
X'
45º
X

10. Нецентральные кривые: парабола

Не имеют центра симметрии или имеют бесконечное
множество центров, могут иметь ось симметрии
(y-y0)2=2p(x-x0) – парабола,
O(x0, y0) – вершина параболы,
P – параметр параболы
O(0, 0) и p>0:
y2=2px – каноническое уравнение параболы