Похожие презентации:
Описание ЛДС в Z - области. Передаточные функции (лекция 7)
1.
Дисциплина «Цифровая обработка сигналов»Тема: Описание ЛДС в Z-области. Передаточные
функции
Лекция 7
1
2.
Цель лекции: Изучить описание линейной дискретнойсистемы в Z-области
План лекции:
1.
2.
Передаточная функция и разностное
уравнение
Нули и полюса передаточной функции
2
3.
Описание ЛДС в Z - областиОсновной характеристикой ЛДС во временной области является импульсная характеристика. Основные
уравнения характеризующие вход-выход
интеграл свертки
разностные уравнения
y[n] = h[n − m] x[m],
m =0
y[n] = x[n − m] h[m],
m =0
4.
и разностные уравненияM
N
m =0
k =1
y[n] = bm x[n − m] − ak y[n − k ]
Основной характеристикой ЛДС в Z-области является передаточная функция:
5.
Передаточной функцией называется отношение Z –преобразования выходного сигнала y[n] к Z –преобразованию входного сигнала x[n], при нулевых начальных условиях.
z{ y[n]} Y ( z )
H ( z) =
=
.
z{x[n]} X ( z )
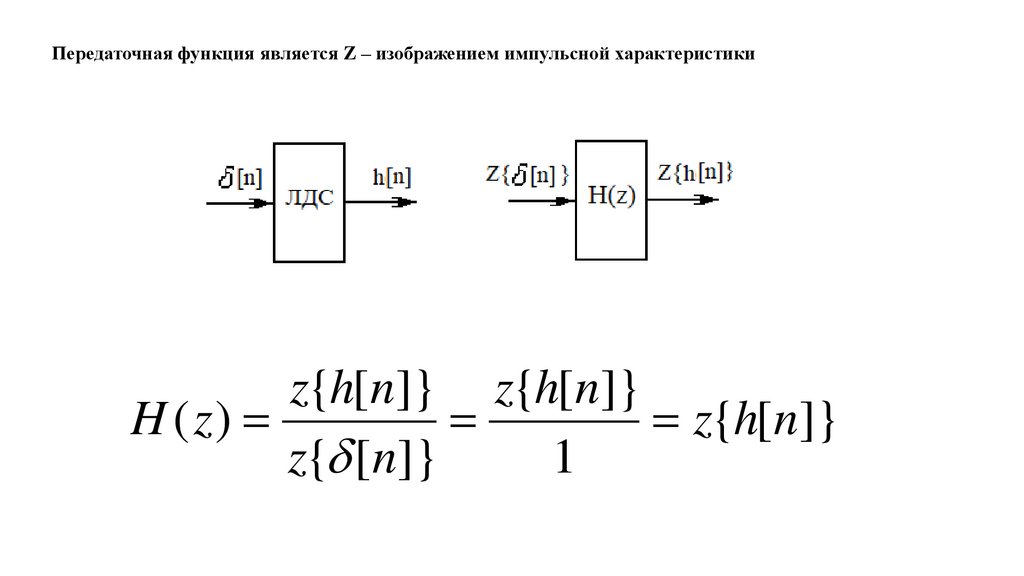
Передаточная функция является Z – изображением импульсной характеристики
6.
Передаточная функция является Z – изображением импульсной характеристикиz{h[n]} z{h[n]}
H ( z) =
=
= z{h[n]}
z{ [n]}
1
7.
H ( z ) = z{h[n]} = h[n] z−n
n =0
Если известно Z-изображение H(z), то импульсная характеристика h[n] определяется как обратное
Z- преобразование
−1
h[n] = z {H ( z )}
8.
Рассмотрим как отображаются вZ
- область формула свертки
h(n − m) x(m)
m = 0
y[n] =
x(n − m) h(m)
m = 0
Формула свертки в Z- области
Y ( z) = H ( z) X ( z)
9.
Зная передаточную функцию H(z), можно рассчитать Y(z) при любом входном воздействииX ( z ) = z{x[n]},
Y ( z ) = H ( z ) X ( z ),
−1
y[n] = Z {Y ( z )}.
10.
Разностные уравнения в Z – областиM
N
Z{ y[n]} = Z bi x[n − i] − a k y[n − k ]
k =1
i =0
11.
x[n] → X ( z ),−m
x[n − m] → X ( z ) z ,
−m
bm x[n − m] → bm X ( z ) z ,
y[n] → Y ( z ),
−k
y[n − k ] → Y ( z ) z .
12.
В результате преобразований получается следующее уравнение в Z- областиN
M
Y [ z ] = bi X ( z ) z − a k Y ( z ) z
−i
i =0
−k
k =1
M
N
k =1
i =0
Y ( z ) + Y ( z ) a k z −k = X ( z ) bi z −i .
N
Y ( z) =
b z
i =0
M
−i
i
1 + ak z
k =1
X ( z ).
−k
13.
Обе поделим на X(z) и получается передаточная функция H(z)N
Y ( z)
H ( z) =
=
X ( z)
b z
i =0
M
−i
i
1 + ak z
−k
−1
−2
k =1
N
Y ( z)
H ( z) =
=
X ( z)
b z
i =0
M
−i
i
1 + ak z
k =1
−N
b0 + b1 z + b2 z + ... + bN z
P( z )
=
=
−1
−2
−M
1 + a1 z + a2 z + ... + am z
Q( z )
−k
14.
Передаточная функция общего вида представляет собой дробно-рациональную функциючислитель и знаменатель
которой многочлены от
z
−1 ,
bi , a k
до порядка N и M с вещественными коэффициентами
Передаточная функция зависит исключительно от внутренних параметров ЛДС и не зависит ни от
воздействия ни от реакции. Порядком ПФ называют наибольшее из чисел N,M причем порядок многочлена
числителя не превосходит порядок многочлена знаменателя.
15.
Любая дробно-рациональная функция характеризуется своими особыми точками (полюсами и нулями).Нулями ПФ называют значения
Z при которых H (z)
Полюсами ПФ называются значения
оказывается равной нулю.
H ( z) = 0
Z , при которых H (z) оказывается равной бескрнечности
H ( z) → .
Чтобы найти нули передаточной функции нужно числитель передаточной функции приравнять к нулю,
чтобы найти полюса передаточной функции нужно знаменатель приравнять к нулю.
16.
Устойчивость ЛДСДля того чтобы ЛДС была устойчива, необходимо и достаточно, чтобы все полюса ПФ
располагались внутри (окружности) круга единичного радиуса на комплексной плоскости Z.
17.
Для определения особых точек и нулей ПФ предварительно записывают как отношение двух полиномовположительных степеней, для этого и числитель и знаменатель ПФ умножают на Z степени M.
После чего нули и полюса находятся как корни числителя и знаменателя.
Полюсы ПФ устойчивой системы должны находиться внутри единичной
окружности на комплексной плоскости Z.
Положение нулей ПФ не влияет на устойчивость ЛДС.
Нерекурсивные системы всегда устойчивые.
Рекурсивные системы устойчивы, если устойчивы соответствующие базовые системы.
18.
Разностное уравнение рекурсивного фильтра первого порядкаy[n] = b0 x[n] + b1 x[n − 1] − a1 y[n − 1]
−1
Y ( z ) = b0 X ( z ) + b1 X ( z ) z − a1Y ( z ) z
−1
−1
Y ( z )(1 − z ) = X ( z )(b0 + b1 z )
−1
Передаточная функция цепи первого порядка:
b0 + b1 z
H ( z) =
−1
1 + a1 z
−1
19.
Для нахождения нулей и полюсов числитель и знаменатель следует умножить нанаходятся как корни числителя и знаменателя.
b0 z + b1
H ( z) =
z + a1
после чего нули и полюса
20.
Числитель приравниваем нулю:b0 z + b1 = 0;
b1
z=− .
b0
Полюса функции передачи. Знаменатель приравниваем нулю:
z + а1 = 0;
z = −a1.
Полюс вещественный.
21.
Если дана передаточная функция общего вида, то можно записать соответствующее ей разностноеуравнение.
Например для звена первого порядка:
−1
b0 + b1 z
Y ( z)
H ( z) =
=
−1
1 + a1 z
X ( z)
X ( z )[b0 + b1 z −1 ] = Y ( z )[1 + a1 z −1 ],
Разностное звена первого порядка
b0 X ( z ) + b1 X ( z ) z −1 = Y ( z ) + a1Y ( z ) z −1 ,
X ( z ) = Z {x[n]}
b1 X ( z ) z −1 = b1 x[n − 1],
b0 x[n] + b1 x[n − 1] = y[n] + a1 y[n − 1].
y[n] = b0 x[n] + b1 x[n − 1] − a1 y[n − 1]
22.
Разностное уравнение рекурсивной фильтр второго порядка:y[n] = b0 x[n] + b1 x[n − 1] + b2 x[n − 2] − a1 y[n − 1] − a2 y[n − 2]
Передаточная функция фильтра второго порядка:
−1
−2
−1
Y ( z ) = b0 X ( z ) + b1 X ( z ) z + b2 X ( z ) z − a1Y ( z ) z − a2Y ( z ) z
−1
−2
X ( z ) b0 + b1 z + b2 z
H ( z) =
=
−1
−2
Y ( z ) 1 + a1 z + a2 z
−2
23.
Записать разностное уравнение для звена второго порядка, если передаточнаяфункция второго порядка от степени z −1 второго порядка
−1
−2
b0 + b1 z + b2 z
H ( z) =
−1
−2
1 + a1 z + a 2 z
Для нахождения нулей ПФ числитель приравнивают к нулю.
Для нахождения полюсов знаменатель приравнивают к нулю.
−1
−2
b0 + b1 z + b2 z
Y ( z)
H ( z) =
=
,
−1
−2
1 + a1 z + a2 z
X ( z)
−1
−2
−1
−2
X ( z )(b0 + b1 z + b2 z ) = Y ( z )(1 + a1 z + a2 z )
24.
Разностные уравнениеy[n] = b0 x[n] + b1 x[n − 1] + b2 x[n − 2] − a1 y[n − 1] − a 2 y[n − 2].
Пример 1. Передаточная функция имеет вид
1
z
H ( z) =
=
.
−1
1 + 0,5 z
z + 0,5
Нули функции:
z0 = 0.
25.
Полюса функции:z* = −0,5.
Система устойчивая, полюс лежит внутри окружности R = 1.
26.
Пример 2. Передаточная функция имеет вид−1
1 − 0,5 z
z − 0,5
H ( z) =
=
.
−1
1 + 0,5 z
z + 0,5
Нули функции:
z0 = 0,5
Полюс функции:
z* = −0,5
27.
Пример 3. Передаточная функция имеет вид2
1
z
H ( z) =
=
.
−1
−2
2
1 + 0,7 z + 0,49 z
z + 0,7 z + 0,49
Нули ПФ:
z0 = 0.
Полюса ПФ:
z + 0,7 z + 0,49 = 0
2
28.
z + 0,7 z + 0,49 = 0,2
z1, 2 = −0,35 0,1225 − 0,49 = −0,35 j 0,606
z1, 2 = −0,35 j 0,606
Cистема устойчивая, полюс лежит внутри окружности R =1.
29.
Пример 4. Передаточная функция имеет вид−1
1+ z
z +z
H ( z) =
=
.
−1
−2
2
1 − 0,7 z + 0,49 z
z − 0,7 z + 0,49
Нули функции:
z + z = 0,
z ( z + 1) = 0,
z0 = 0,
2
z0 = −1.
2
30.
Полюс функции:z − 0,7 z + 0,49 = 0
z1, 2 = 0,35 j 0,662
2
Полюса изображаются на комплексной плоскости Z.
Изображение нулей и полюсов на комплексной плоскости называют
называют картой нулей и полюсов.
31.
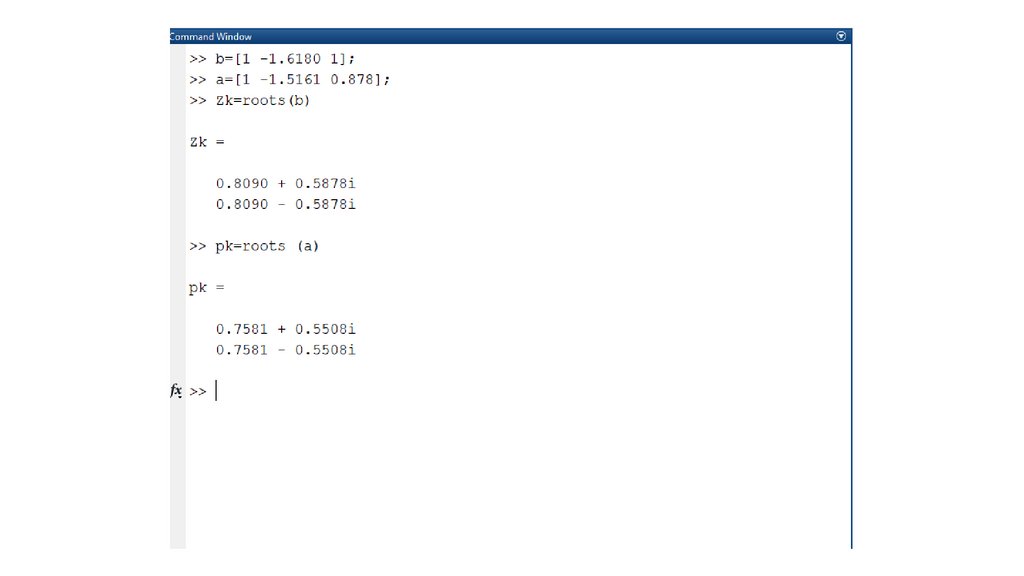
Пример 5. Передаточная функция имеет вид−1
−2
1 − 1,6180 z + z
H ( z) =
.
−1
−2
1 − 1,5161z + 0,878 z
Определить нули и полюса ПФ с помощью команды roots Мatlab
32.
33.
Передаточные функции рекурсивных фильтров 1 –го и 2-го порядка1. Базовый рекурсивный фильтр 1-го порядка.
Базовым рекурсивным фильтром первого порядка называют фильтр,
описываемый уравнением
y[n] = x[n] − y[n − 1]
Применив к этому уравнению Z-преобразование получим ПФ
−1
Y ( z) = X ( z) − Y ( z) z ,
−1
Y ( z )[1 + z ] = X ( z ).
34.
ПФ базового фильтра первого порядка1
H ( z) =
−1
1+ z
2. Рекурсивный фильтр первого порядка
Рекурсивный фильтр первого порядка описывается разностным уравнением
первого порядка
y[n] = b0 x[n] + b1 x[n − 1] − a1 y[n − 1]
35.
Применив к обеим частям уравнения Z –преобразование, ПФ рекурсивногофильтра первого порядка имеет вид:
−1
b0 + b1 z
H ( z) =
−1
1 + a1 z
3. Базовый рекурсивный фильтр второго порядка
Описывается разностным уравнением второго порядка
y[n] = x[n] − a1 y[n − 1] − a2 y[n − 2]
36.
ПФ базового рекурсивного фильтра второго порядка1
H ( z) =
−1
−2
1 + a1 z + a2 z
4. Рекурсивный фильтр второго порядка
y[n] = b0 x[n] + b1 x[n − 1] + b 2 x[n − 2] − a1 y[n − 1] − a2 y[n − 2]
37.
К обеим частям уравнения применяем Z-преобразование. ПФ рекурсивногофильтра второго порядка имеет вид:
−1
−2
b0 + b1 z + b2 z
H ( z) =
−1
−2
1 + a1 z + a2 z
5. Нерекурсивный фильтр второго порядка
Разностное уравнение нерекурсивного фильтра второго порядка имеет вид
y[n] = b0 x[n] + b1 x[n − 1] + b 2 x[n − 2]
38.
ПФ нерекурсивного фильтра второго порядка−1
H ( z ) = b0 + b1 z + b2 z
−2
Правило определения ПФ по разностному уравнению и наоборот:
1. коэффициенты разностного уравнения являются коэффициентами
передаточной функции;
2. коэффициенты разностного уравнения bm при x[n − m] равны коэффициентам
числителя передаточной функции;
3. коэффициенты разностного уравнения ak при y[n − m] равны коэффициентам
Знаменателя передаточной функции с обратным знаком.
39.
Пример. Известна передаточная функция−2
0,3 − 0,5 z
H ( z) =
−2
−1
1 − 0,8 z + 0,64 z
Написать разностное уравнение.
y[n] = 0,3x[n] − 0,5 x[n − 2] + 0,8y[n − 1] − 0,64 y[n − 2]
40.
1. В общем случае ПФ дискретного фильтра может быть получена путемприменения Z- преобразования к разностным уравнениям.
2. ПФ рекурсивного фильтра представляет собой дробно-рациональную
−1
функцию функцию по степеням z .
3.ПФ нерекурсивного фильтра представляет собой полином по степеням z
4. Коэффициенты ПФ являются коэффициентами разностного уравнения.
−1
41.
Контрольные вопросы:1.
2.
3.
4.
5.
6.
Передаточная функция ЛДС.
Нули передаточной функции,
Полюса передаточной функции.
Как определить полюса и нули передаточной функции?
Передаточная функция цифрового фильтра рекурсивного первого порядка.
Передаточная функция нерекурсивного фильтра пеpвого порядка.





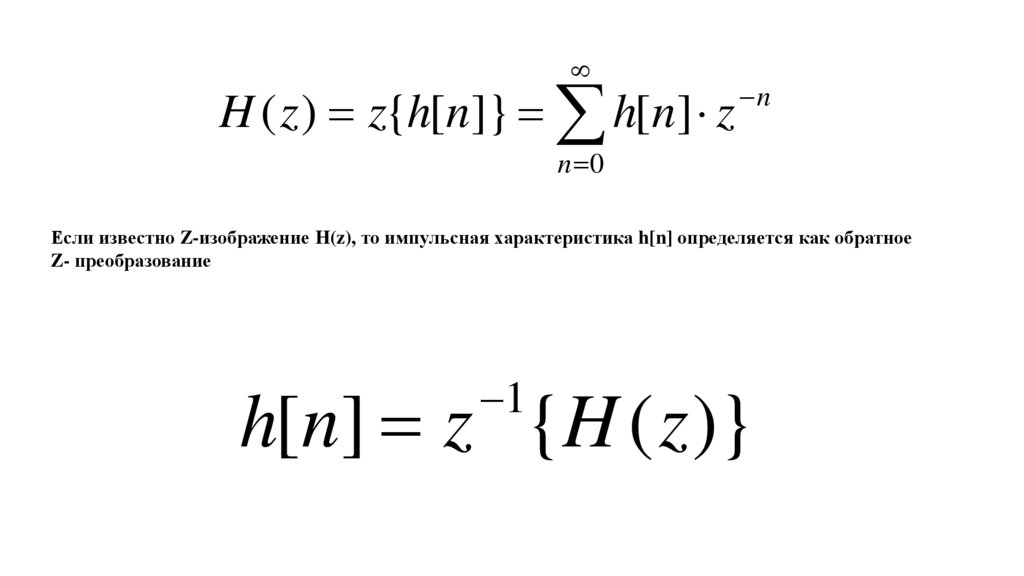
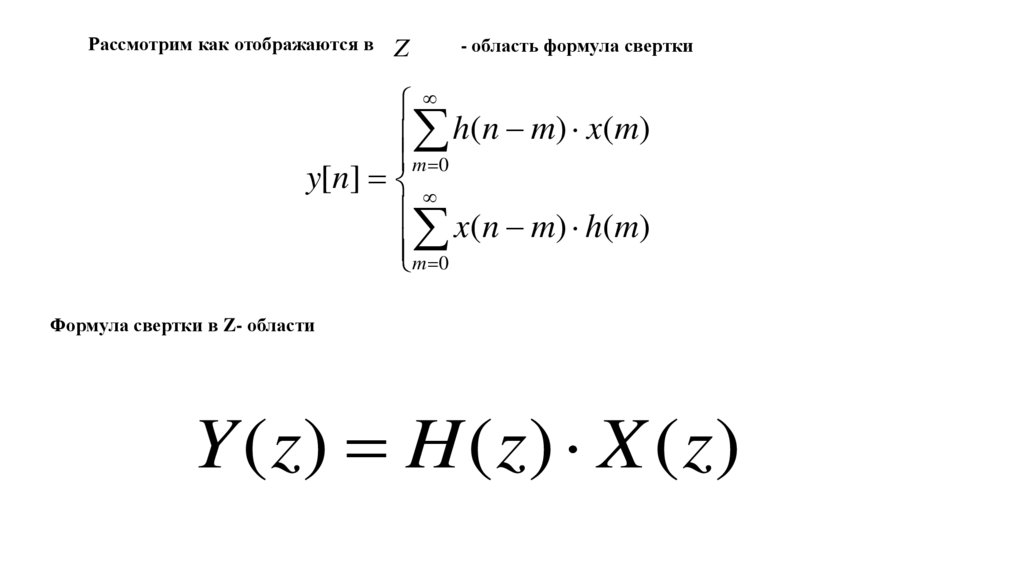

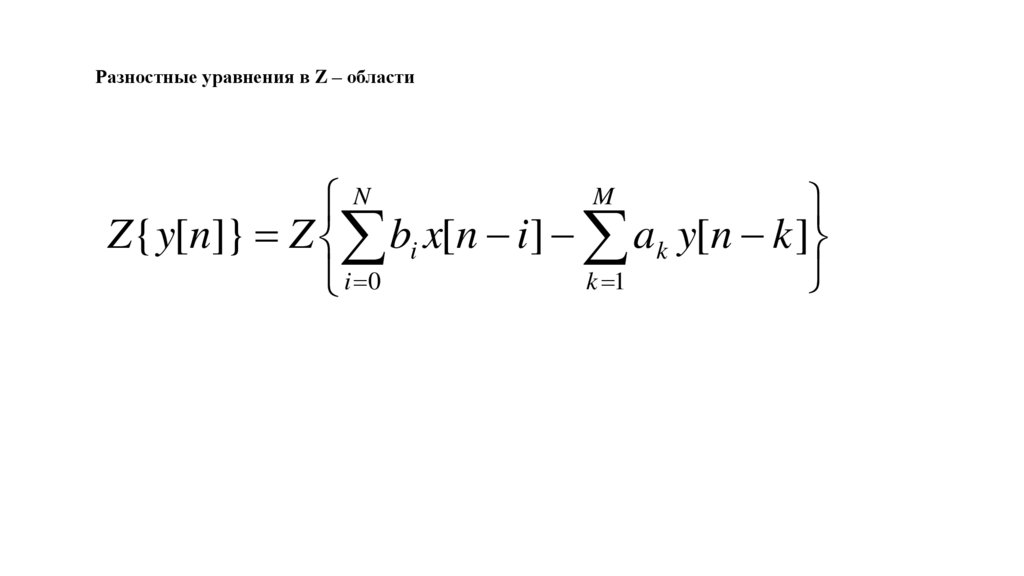
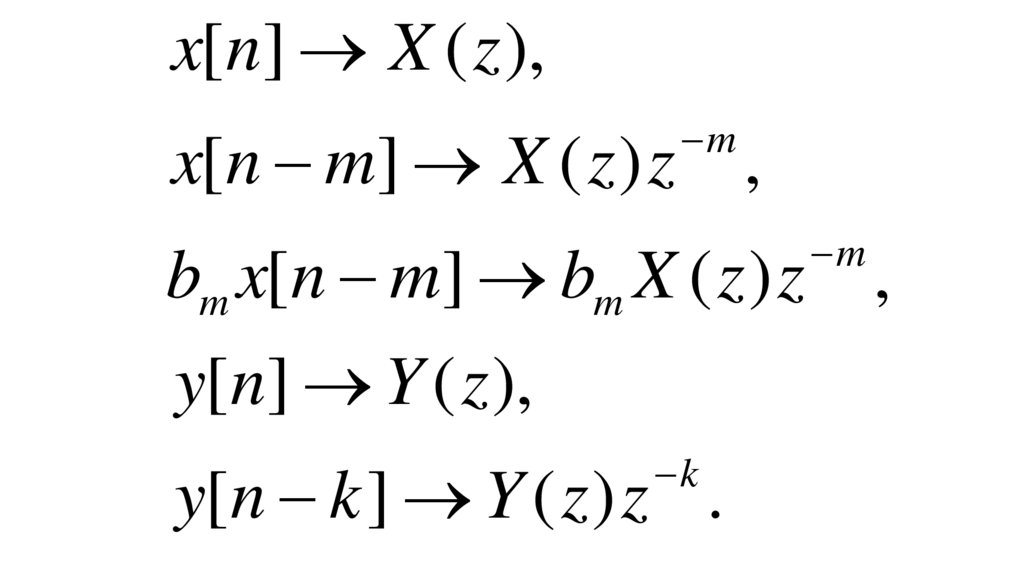
















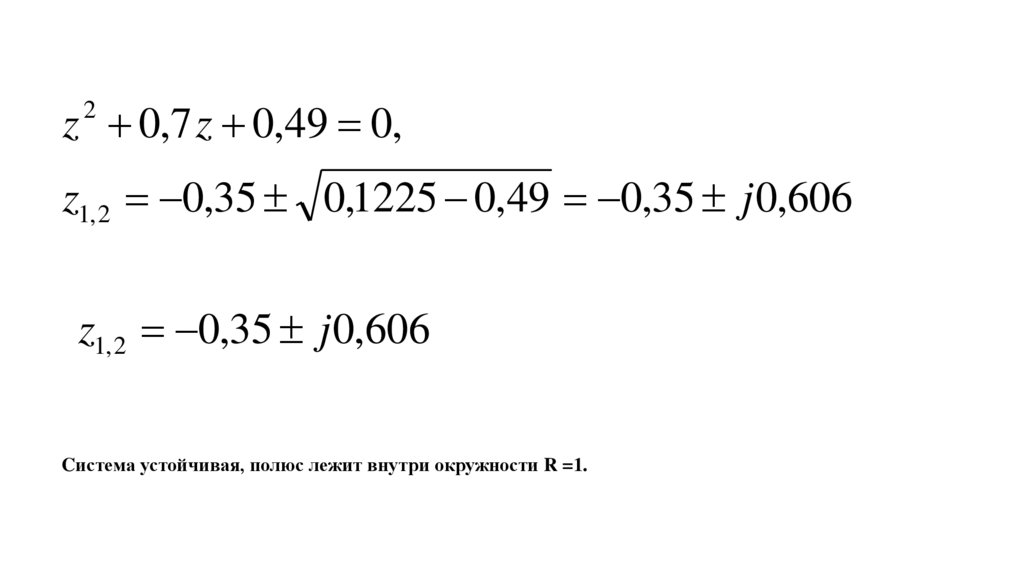












 Математика
Математика








