Алгебра передаточных функций

1.

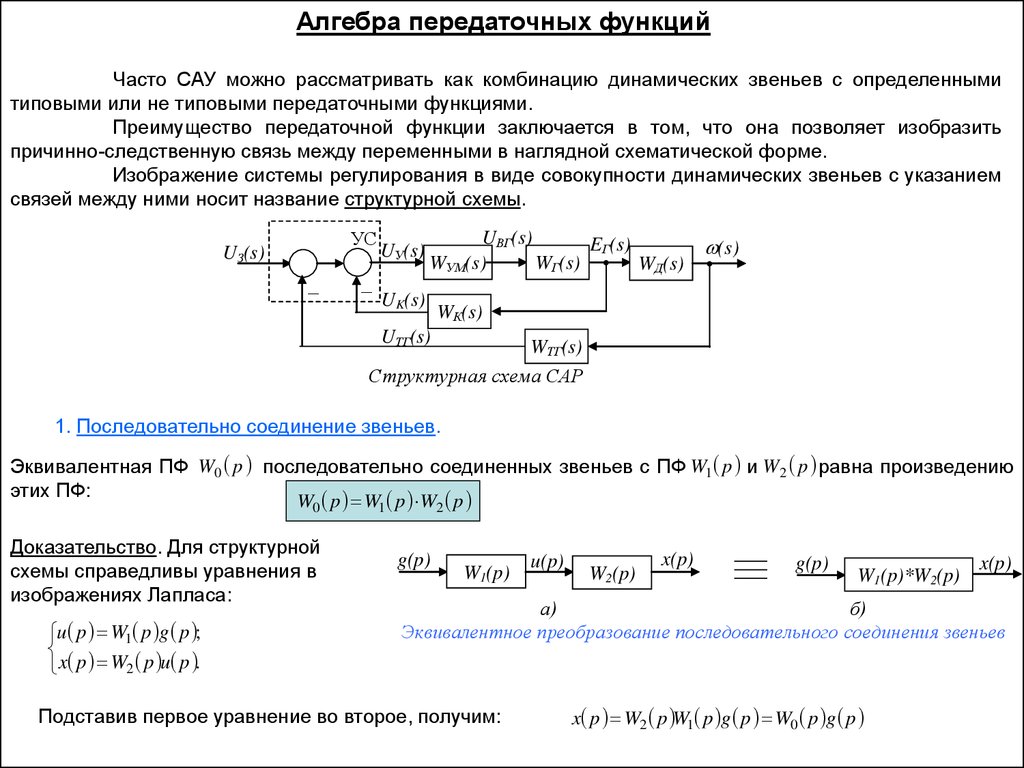
Алгебра передаточных функций
Часто САУ можно рассматривать как комбинацию динамических звеньев с определенными
типовыми или не типовыми передаточными функциями.
Преимущество передаточной функции заключается в том, что она позволяет изобразить
причинно-следственную связь между переменными в наглядной схематической форме.
Изображение системы регулирования в виде совокупности динамических звеньев с указанием
связей между ними носит название структурной схемы.
УС
UЗ(s)
–
UУ(s)
UВГ(s)
EГ(s)
WУМ(s)
WГ(s)
WД(s)
– U (s)
K
(s)
WК(s)
UTГ(s)
WТГ(s)
Структурная схема САР
1. Последовательно соединение звеньев.
Эквивалентная ПФ W0 p последовательно соединенных звеньев с ПФ W1 p и W2 p равна произведению
этих ПФ:
W0 p W1 p W2 p
Доказательство. Для структурной
схемы справедливы уравнения в
изображениях Лапласа:
u p W1 p g p ;
x p W2 p u p .
g(p)
W1(p)
u(p)
W2(p)
x(p)
g(p)
W1(p)*W2(p)
x(p)
а)
б)
Эквивалентное преобразование последовательного соединения звеньев
Подставив первое уравнение во второе, получим:
x p W2 p W1 p g p W0 p g p

2.

Алгебра передаточных функций
2. Параллельное соединение звеньев.
Эквивалентная ПФ W0 p параллельно соединенных звеньев с ПФ W1 p и W2 p равна сумме этих ПФ:
W0 p W1 p W2 p
g(p)
Доказательство.
Для
структурной
схемы
справедливы
уравнения
в
изображениях
Лапласа:
x1 p W1 p g p ;
x2 p W2 p g p ;
x p x p x p .
1
2
W1(p)
W2(p)
x1(p)
+
x(p)
+
g(p)
W1(p)+W2(p)
x(p)
x2(p)
а)
б)
Эквивалентное преобразование параллельного соединения
звеньев
Подставив первые два уравнения в третье, получим:
x p W1 p g p W2 p g p W1 p W2 p g p W0 p g p

3.

Алгебра передаточных функций
3. Передаточная функция цепи, охваченной обратной связью.
Эквивалентная ПФ W0 p цепи (прямой части САР) с ПФ Wпр p , охваченной обратной связью с ПФ Wобр p
(положительной или отрицательной) равна:
W0 p
Wпр p
g(p)
1 Wпр p Wобр p
u(p)
Wпр(p)
x(p)
g(p)
z(p)
Wпр p
1 Wпр p Wобр p
x(s)
Wобр(p)
а)
б)
Эквивалентное преобразование цепи, охваченной обратной
связью
Доказательство. Система уравнений для структурной схемы имеет вид:
u p g p z p ;
x p Wпр p u p ;
z p Wобр p x p .
Из второго уравнения выразим:
u p
1
Wпр p
x p
Теперь это выражение и третье уравнение системы подставим в первое уравнение:
1
Wпр p
x p g p Wобр p x p
Последовательно преобразуем это уравнение:
1
W
p
x p g p
обр
W
p
пр
1 Wпр p Wобр p x p Wпр p g p
Wпр p
x p
W0 p
g p 1 Wпр p Wобр p

4.

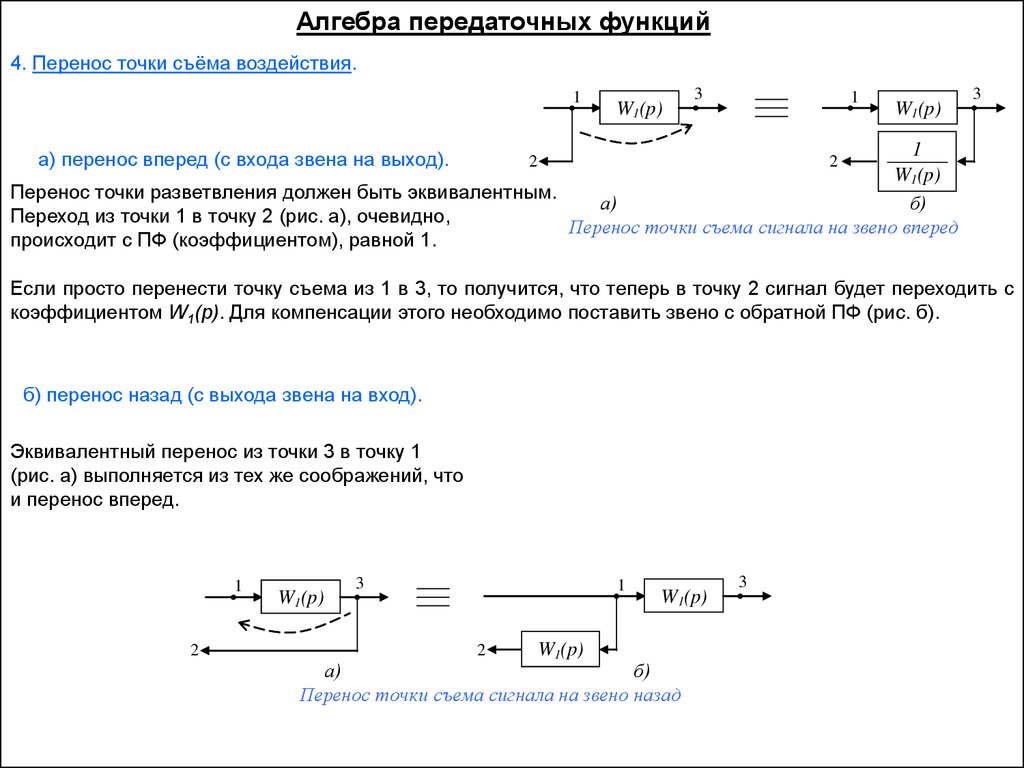
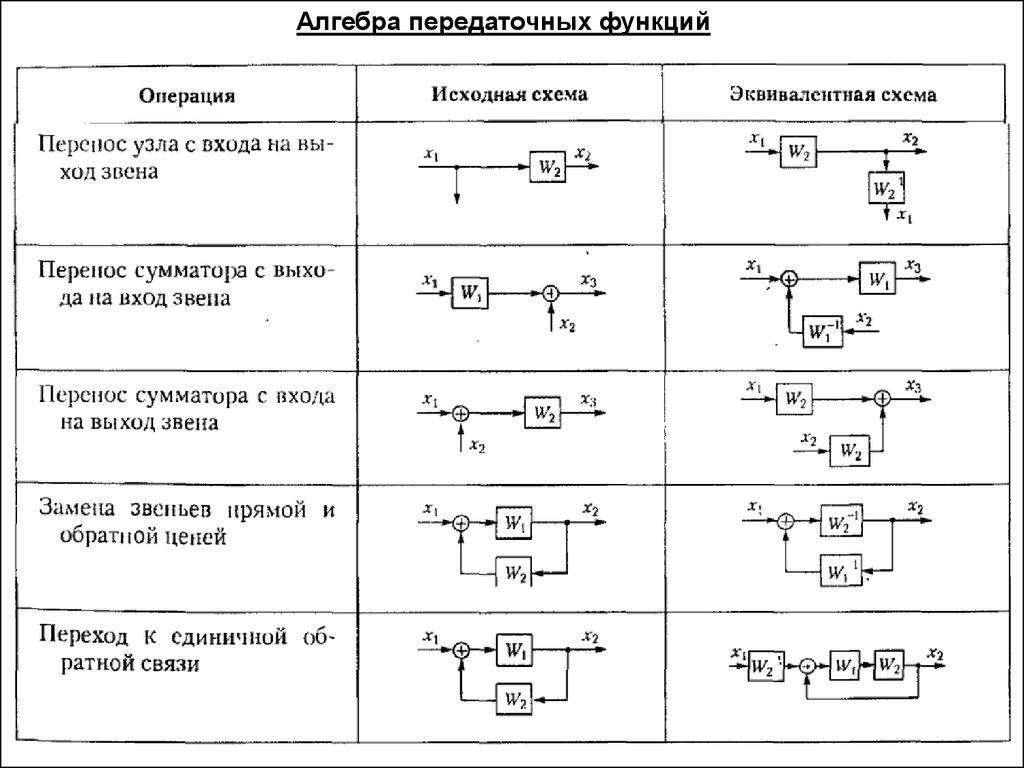
Алгебра передаточных функций
4. Перенос точки съёма воздействия.
1
W1(p)
3
1
W1(p)
3
1
W1(p)
Перенос точки разветвления должен быть эквивалентным.
а)
б)
Переход из точки 1 в точку 2 (рис. а), очевидно,
Перенос точки съема сигнала на звено вперед
происходит с ПФ (коэффициентом), равной 1.
а) перенос вперед (с входа звена на выход).
2
2
Если просто перенести точку съема из 1 в 3, то получится, что теперь в точку 2 сигнал будет переходить с
коэффициентом W1(p). Для компенсации этого необходимо поставить звено с обратной ПФ (рис. б).
б) перенос назад (с выхода звена на вход).
Эквивалентный перенос из точки 3 в точку 1
(рис. а) выполняется из тех же соображений, что
и перенос вперед.
1
2
W1(p)
3
1
2
W1(p)
W1(p)
а)
б)
Перенос точки съема сигнала на звено назад
3

5.

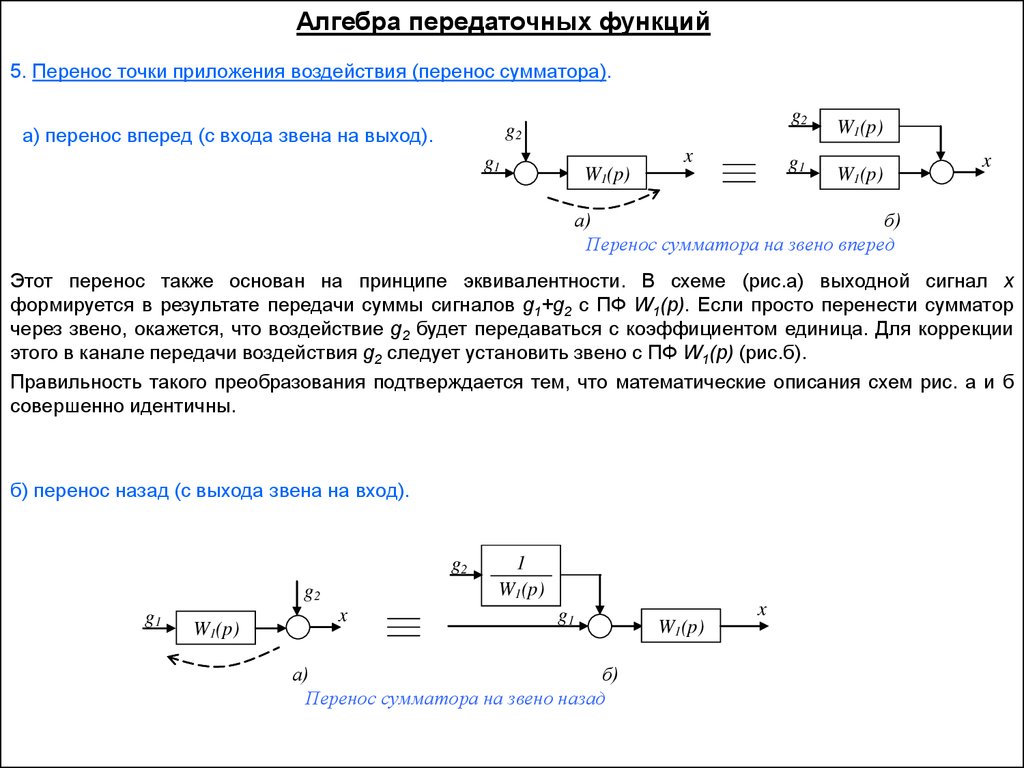
Алгебра передаточных функций
5. Перенос точки приложения воздействия (перенос сумматора).
g2
g2
а) перенос вперед (с входа звена на выход).
x
g1
g1
W1(p)
W1(p)
W1(p)
x
а)
б)
Перенос сумматора на звено вперед
Этот перенос также основан на принципе эквивалентности. В схеме (рис.а) выходной сигнал x
формируется в результате передачи суммы сигналов g1+g2 с ПФ W1(p). Если просто перенести сумматор
через звено, окажется, что воздействие g2 будет передаваться с коэффициентом единица. Для коррекции
этого в канале передачи воздействия g2 следует установить звено с ПФ W1(p) (рис.б).
Правильность такого преобразования подтверждается тем, что математические описания схем рис. а и б
совершенно идентичны.
б) перенос назад (с выхода звена на вход).
g2
g2
g1
W1(p)
x
1
W1(p)
g1
а)
б)
Перенос сумматора на звено назад
x
W1(p)

6.

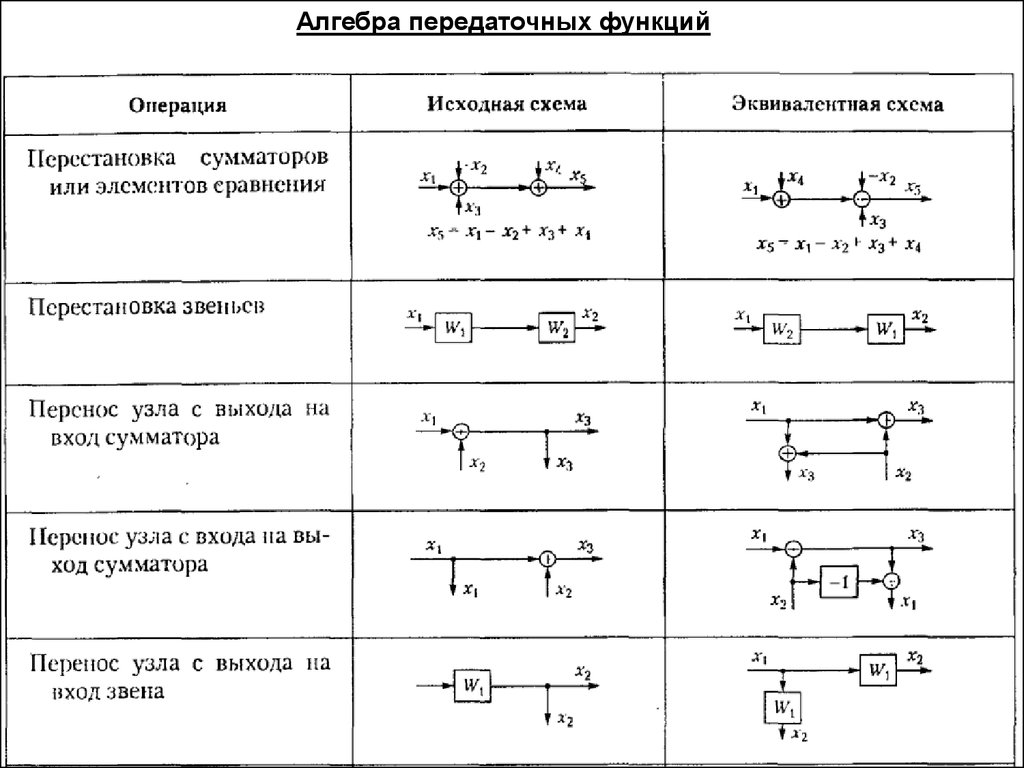
Алгебра передаточных функций

7.

Алгебра передаточных функций

8.

Алгебра передаточных функций
W4(p)
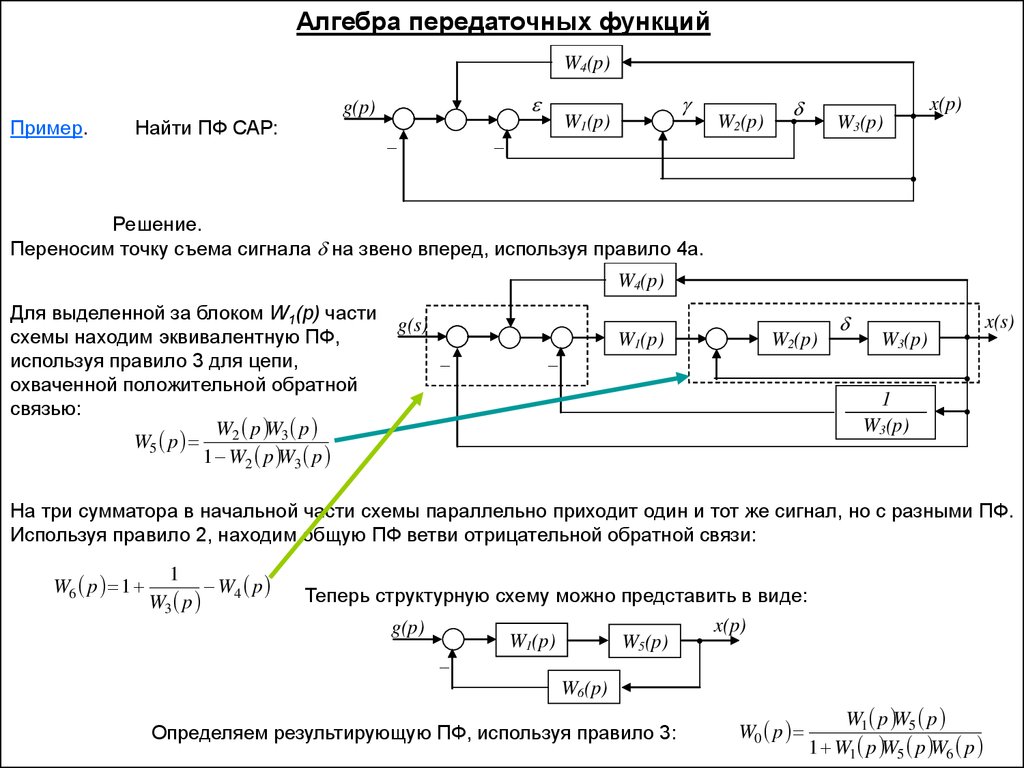
Пример.
Найти ПФ САР:
g(p)
–
W1(p)
W2(p)
x(p)
W3(p)
–
Решение.
Переносим точку съема сигнала на звено вперед, используя правило 4а.
W4(p)
Для выделенной за блоком W1(p) части
схемы находим эквивалентную ПФ,
используя правило 3 для цепи,
охваченной положительной обратной
связью:
W2 p W3 p
W5 p
1 W2 p W3 p
g(s)
W1(p)
–
W2(p)
x(s)
W3(p)
–
1
W3(p)
На три сумматора в начальной части схемы параллельно приходит один и тот же сигнал, но с разными ПФ.
Используя правило 2, находим общую ПФ ветви отрицательной обратной связи:
W6 p 1
1
W3 p
W4 p
Теперь структурную схему можно представить в виде:
x(p)
g(p)
W1(p)
W5(p)
–
W6(p)
Определяем результирующую ПФ, используя правило 3:
W0 p
W1 p W5 p
1 W1 p W5 p W6 p

9.

Алгебра передаточных функций
Передаточные функции разомкнутых и замкнутых САР
Современные регулируемые ЭП, обладающие высококачественными динамическими и статическими
характеристиками, строятся с использованием отрицательной обратной связи (ОС), т.е. работают по
замкнутому циклу.
Рассмотрим обобщенную схему такой САР, состоящую из прямой ветви, охваченной отрицательной ОС.
(p)
g(p)
–
z(p)
Wпр(p)
x(p)
Wобр(p)
g(p) – входное воздействие;
x(p) – выходная переменная;
z(p) – сигнал ОС;
(p) – ошибка.
САР с отрицательной ОС.
Передаточная функция замкнутой САР определяется по правилу 3 преобразования структурных схем:
WЗСАР p K 0 p
Wпр p
1 Wпр p Wос p
Wпр p
– ПФ прямой части САР, связывающая вход с интересующим нас выходом;
Wос p
– ПФ цепи ОС.
При обозначении ПФ замкнутых систем
вместо символа W используется символ
K.
Смысл ПФ замкнутой САР в том, что она показывает, как входной сигнал g(p) преобразуется в выходной
x(p):
x p K 0 p g p

10.

Алгебра передаточных функций
Передаточные функции разомкнутых и замкнутых САР
Передаточная функция разомкнутой САР получается после размыкания замкнутой САР в произвольном
месте, и рассмотрения образовавшегося разомкнутого контура как последовательного соединения
звеньев, не учитывая знак сумматора. Таким образом, используя правило 1, ПФ разомкнутой САР запишем
в виде:
WРСАР p W0 p Wпр p Wос p
(p)
g(p)
–
z(p)
Wпр(p)
Wобр(p)
x(p)
g(p) – входное воздействие;
x(p) – выходная переменная;
z(p) – сигнал ОС;
(p) – ошибка.
САР с отрицательной ОС.
Смысл ПФ разомкнутой САР в том, что она показывает, как сигнал ошибки (p) преобразуется в сигнал
обратной связи z(p).
1. ПФ разомкнутой САР W p не зависит от места размыкания САР.
2. Неправильно считать, что ПФ разомкнутой САР равна ПФ САР, полученной после отбрасывания цепи ОС.
3. ПФ разомкнутой САР совпадает с ПФ прямой части САР только в одном случае, когда Wос p 1 .
Связь между ПФ разомкнутой и замкнутой САР выражается следующей формулой:
K0 p
Wпр p
1 W0 p
то есть, ПФ цепи, замкнутой отрицательной ОС, равна ПФ прямой части, разделенной на ПФ
разомкнутой САР, увеличенную на единицу.
В редких случаях, когда ОС положительная, в знаменателе ПФ замкнутой САР символ "+" меняется на "–".

11.

Алгебра передаточных функций
W4
g
1
Понятие о графе САР.
W1
W2
W3
x
–1
–1
Граф САР, изображенной ранее.
Правило Мейсона (Мезона)
Это правило позволяет определить ПФ сколь угодно сложной замкнутой САР, не прибегая к
преобразованию ее структурной схемы. Для его формулирования введем следующие определения:
Путем между двумя координатами (простым или прямым путем) называется
последовательность линий и звеньев между этими двумя координатами такая, что каждое звено и каждая
промежуточная координата встречаются только один раз. Передаточная функция пути равна
произведению ПФ звеньев, встречающихся на этом пути.
Контур – это замкнутый путь. Другими словами – это такой путь, когда входная и выходная
координаты совпадают. Передаточная функция замкнутого контура равна произведению ПФ звеньев,
входящих в него, с учетом знаков сумматоров (если сигнал поступает на вход "+", ПФ сумматора равна
единице, если на "–" – то –1.
g(p) (p)
W1(p)
z(p)
W2(p)
x(p)
g(p) (p)
W1(s)
z(p)
W2(s)
x(p)
–
а)
–1
б)
g p x p – с ПФ WП p W1 p W2 p ,
В схеме присутствует один прямой путь –
и также один замкнутый контур – p p – с ПФ WK p W1 p,
где наличие знака "минус" понятно из эквивалентной схемы.

12.

Алгебра передаточных функций
Правило Мейсона гласит:
Передаточная функция САР относительно каких либо входа g и выхода x может быть определена по
формуле:
m
W Пi – ПФ i-го прямого пути;
WПi i
x p i 1
K g x p
g p
m – число прямых путей;
- главный определитель, вычисляемый по правилу:
1 WKj WKjWKk
j
WKj
j, k
WKjWKkWKl
j , k ,l
– сумма ПФ всех замкнутых контуров структурной схемы;
j
WKjWKk
j, k
– сумма произведений всех пар контуров, которые не касаются друг друга (не имеют общих
звеньев);
WKjWKkWKl
– сумма произведений всех троек контуров, которые не касаются друг друга;
j , k ,l
i – определитель i-го прямого пути (определитель подграфа i-го прямого пути), который
вычисляется по тому же правилу, что и главных определитель ,
но с учетом того, что учитываемые контуры, пары контуров, тройки контуров и т.д. не должны
касаться i-го прямого пути. В частном случае, когда все контуры касаются i-го пути, i 1

13.

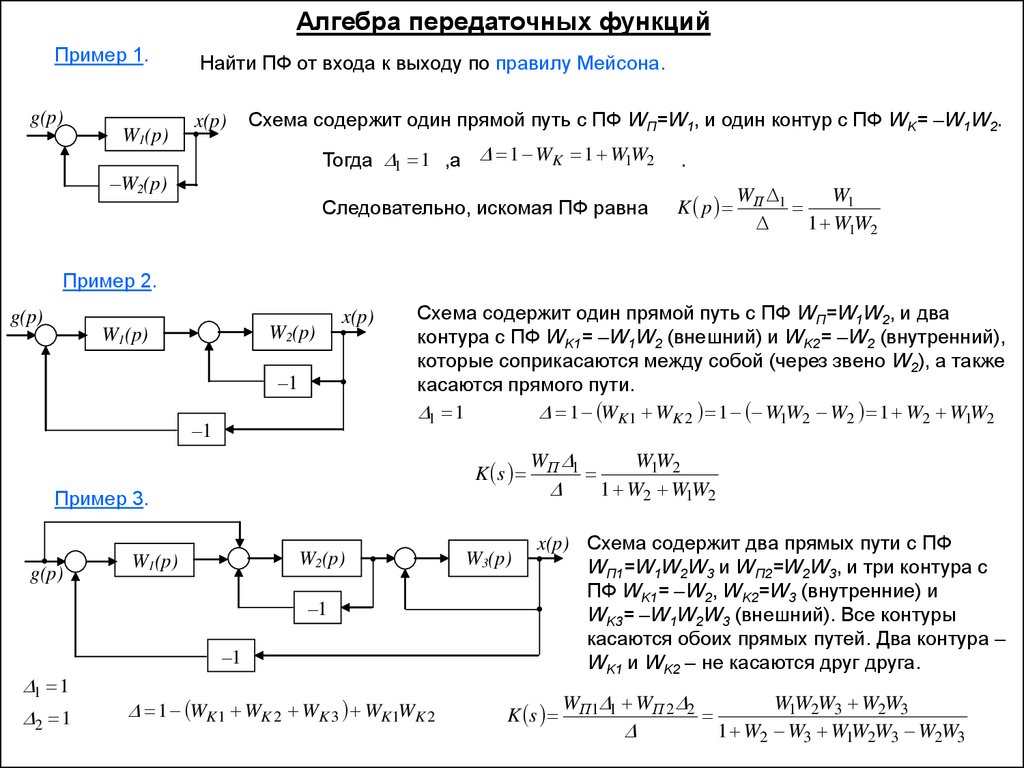
Алгебра передаточных функций
Пример 1.
g(p)
W1(p)
Найти ПФ от входа к выходу по правилу Мейсона.
x(p)
Схема содержит один прямой путь с ПФ WП=W1, и один контур с ПФ WK= –W1W2.
–W2(p)
Тогда 1 1 ,а 1 WK 1 W1W2
.
Следовательно, искомая ПФ равна
K p
WП 1
W1
1 W1W2
Пример 2.
g(p)
W2(p)
W1(p)
x(p)
–1
–1
Схема содержит один прямой путь с ПФ WП=W1W2, и два
контура с ПФ WK1= –W1W2 (внешний) и WK2= –W2 (внутренний),
которые соприкасаются между собой (через звено W2), а также
касаются прямого пути.
1 WK1 WK 2 1 W1W2 W2 1 W2 W1W2
1 1
K s
Пример 3.
g(p)
W2(p)
W1(p)
–1
–1
1 1
2 1
1 WK1 WK 2 WK 3 WK1WK 2
W3(p)
WП 1
W1W2
1 W2 W1W2
x(p) Схема содержит два прямых пути с ПФ
WП1=W1W2W3 и WП2=W2W3, и три контура с
ПФ WK1= –W2, WK2=W3 (внутренние) и
WK3= –W1W2W3 (внешний). Все контуры
касаются обоих прямых путей. Два контура –
WK1 и WK2 – не касаются друг друга.
K s
WП1 1 WП 2 2
W1W2W3 W2W3
1 W2 W3 W1W2W3 W2W3