Магнетизм. Магнитное поле

1.

Магнетизм

2.

I
Магнитное поле создаётся вокруг любых движущихся
зарядов, в том числе и вокруг проводников с током.
Магнитное поле действует только на движущиеся в
этом поле электрические заряды.
Магнитное поле может быть обнаружено по его
ориентирующему действию на магнитные стрелки и на
контуры с током.
Любая бесконечно малая магнитная стрелка имеет два
полюса – северный и южный. Следовательно, свободных
магнитных зарядов в природе не существует.

3.

Силовой характеристикой магнитного поля является
вектор магнитной индукции В.
Вектор магнитной индукции В в каждой точке поля
направлен так, как направлена сила, действующая на
северный полюс бесконечно малой магнитной стрелки,
помещенной в эту точку поля.
Силовыми линиями магнитного поля называют линии,
касательные к которым в каждой точке совпадают
с направлением вектора индукции В в этой точке.
Силовые линии магнитного поля замкнуты,
следовательно, магнитное поле - вихревое.
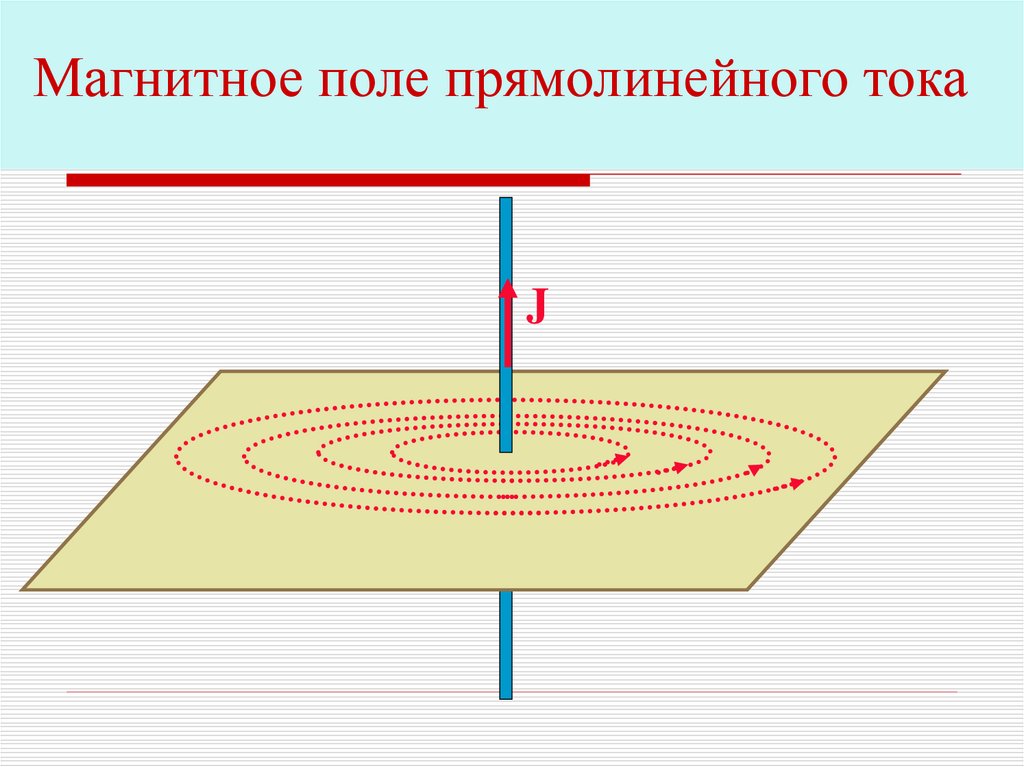
Силовые линии магнитного поля тока располагаются
в плоскостях перпендикулярных току. Их направление
определяется по правилу правого винта.

4.

Магнитное поле прямолинейного тока
J

5.

Магнитное поле кругового тока
J

6.

Магнитное поле полосового магнита
и соленоида (1)
S
N

7.

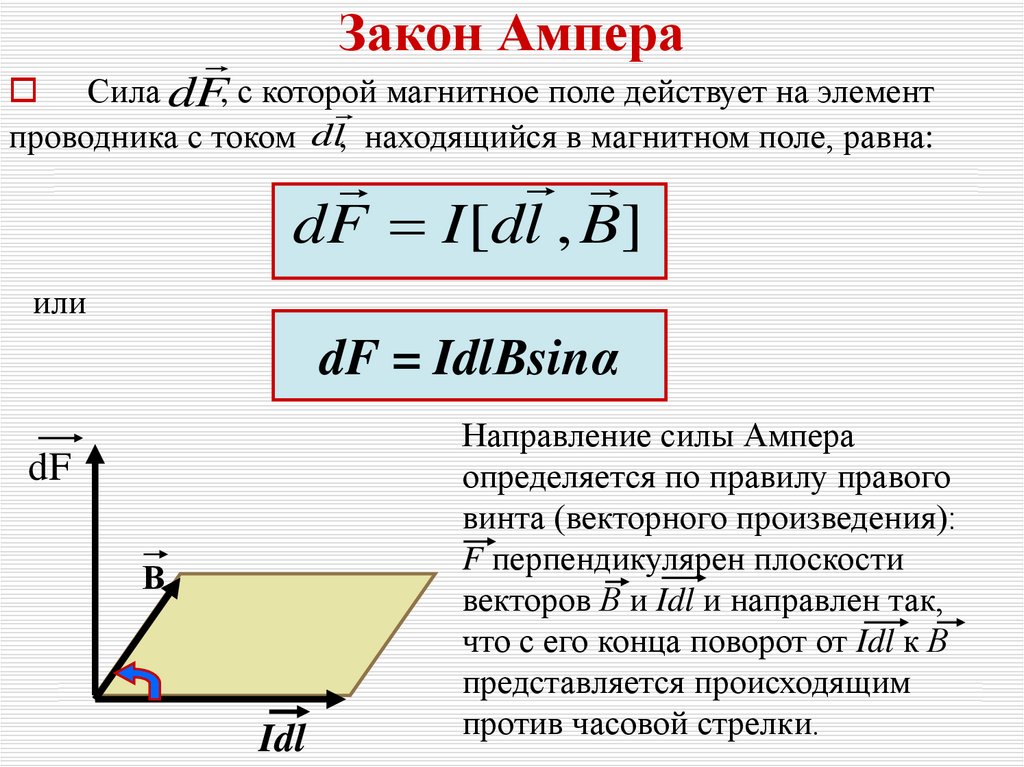
Закон Ампера
Сила dF, с которой
магнитное поле действует на элемент
проводника с током dl, находящийся в магнитном поле, равна:
dF I [dl , B]
или
dF = IdlΒsinα
dF
В
Idl
Направление силы Ампера
определяется по правилу правого
винта (векторного произведения):
F перпендикулярен плоскости
векторов В и Idl и направлен так,
что с его конца поворот от Idl к В
представляется происходящим
против часовой стрелки.

8.

Из закона Ампера следует:
dF
В
Idl sin
Индукция магнитного поля – физическая
величина, численно равная силе, действующей
на единицу длины перпендикулярного полю
проводника с током 1А.
Единица магнитной индукции в СИ - Тесла:
Тл = Н / (А.м)

9.

Сила Лоренца
На заряженную частицу, движущуюся со скоростью
в магнитном поле с индукцией В, действует сила Лоренца:
F л q [ B]
Модуль силы Лоренца :
Fл= |q|υBsina.
Направление силы Лоренца определяется по правилу векторного
произведения и зависит от знака заряда
В
Fл q>0
Fл [ υ, Β ]
q
υ
q<0
В
q +
υ
Fл
Fл
[ Β, υ ]

10.

Сила Лоренца (продолжение
1)
F л q [ B]
1) υ
Β В = const, Fл = (Fл)max= |q|υΒ
частица равномерно движется по окружности радиуса R.
В этом случае сила Лоренца является центростремительной
силой и справедливо
υ q>0
|q|υB = mυ2/R, отсюда:
m
R
|q|B
Fл
Период вращения частицы
2 m
Т
qB
В

11.

Сила Лоренца (продолжение
2)
F л q [ B]
2) α = 0, т. е.
Fл = 0
υ В
заряд движется прямолинейно вдоль
υ
силовой линии.
В
3) 0 <α < 900
заряд движется по винтовой линии
υ
α
В

12.

Fл= |q|υBsina
Из формулы силы Лоренца:
Fл
В
q sin
Индукция магнитного поля – физическая
величина, численно равная силе, действующей
на единичный заряд, движущийся с единичной
скоростью перпендикулярно магнитному полю.

13.

Закон Био-Савара-Лапласа
Определяет индукцию поля dB , созданного проводником dl с
током I в некоторой точке пространства А:
I [dl , r ]
,
dB 0
4
r3
где μ0 - магнитная постоянная
μ0 = 4 .10-7Гн/м или Вб/(A. м)
μ - относительная магнитная
проницаемость среды ( безразмерная
величина), показывающая во сколько раз
индукция магнитного поля в вакууме В0
отличается от индукции магнитного поля
В в среде.
dℓ
Ј

14.

Продолжение закона Б – С - Л
Модуль вектора dB:
0 Idl sin
dB
4
r2
Индукция поля, создаваемого всем проводником:
В dB
Напряжённость поля Н - силовая характеристика, не зависящая
от свойств среды:
B 0 H
1 Idl sin
dН
4
r2
Н dH

15.

B 0 H
Вектор магнитной индукции Bхарактеризует
результирующее магнитное поле, создаваемое
всеми макро- и микротоками.
Вектор напряженности H характеризует магнитное
поле создаваемое только макротоками.
Единица вектора напряжённости в СИ –
Ампер/метр:
[Н] = A/м

16.

1) Магнитное поле прямого бесконечно длинного
тока:
0 I
B
2 R
Н
I
2 R
2) Магнитное поле кругового тока в центре витка:
0 I
B
2 R
I
Н
2R
3) Магнитное поле внутри соленоида:
В = μ0 μ n I = μ0 μ I Ν / ℓ
Н = nI = IΝ / ℓ

17.

Закон полного тока для магнитного поля в вакууме
(теорема о циркуляции вектора В)
Циркуляция вектора B0 по произвольному замкнутому
контуру в вакууме равна произведению магнитной
постоянной 0 на алгебраическую сумму токов,
охватываемых
n
этим контуром:
( B dl ) B dlcos B dl I
0
L
0
L
0l
L
0
k 1
k
n — число проводников с токами, охватываемых контуром L
произвольной формы.
Каждый ток учитывается столько раз, сколько раз он
охватывается контуром.
Положительным считается ток, направление которого образует с
направлением обхода по контуру правовинтовую систему; ток
противоположного направления считается отрицательным.
Циркуляция вектора B магнитного поля по замкнутому
контуру не равна нулю. Такое поле называется вихревым.

18.

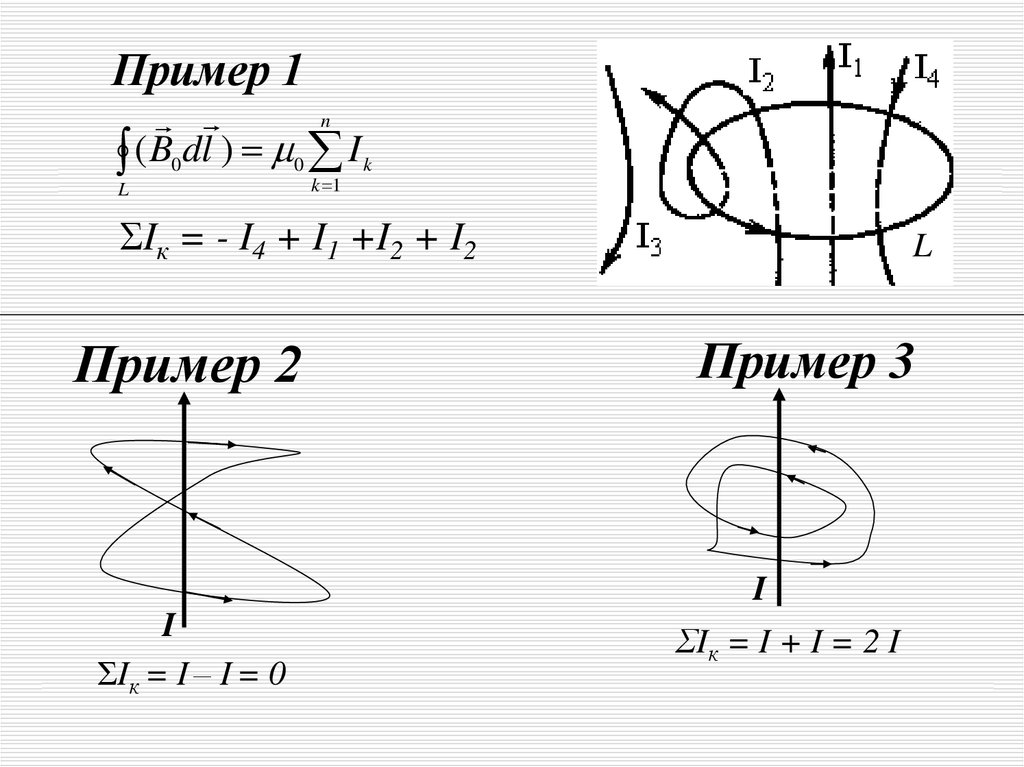
Пример 1
n
( B0dl ) 0 I k
L
k 1
ΣIк = - I4 + I1 +I2 + I2
Пример 2
L
Пример 3
I
I
ΣIк = I – I = 0
ΣIк = I + I = 2 I

19.

Поток вектора магнитной индукции
B через
Потоком вектора магнитной индукции
площадку dS называется скалярная физическая величина
dФ В dS BdS cos Вп dS
Поток через площадь S в произвольном магнитном поле:
Φ=∫ (В,dS)= ∫BdScosα
n
dS
α
B В СИ единицей магнитного
потока является вебер - Вб.
1Вб = 1Тл .1м2.
Если магнитный поток пронизывает несколько контуров,
то полный поток, называемый потокосцеплением Ψ,
равен сумме магнитных потоков через все контуры:
Ψ = Σ Φί
Для N одинаковых контуров:
Ψ=NΦ

20.

Теорема Гаусса для магнитного
поля
Поток вектора магнитной индукции через
любую замкнутую поверхность равен
нулю:
( B, dS ) B n dS 0
S

21.

Работа в магнитном поле
Проводник длиной ℓ с током I помещен в однородное внешнее
магнитное поле, перпендикулярное плоскости контура.
На проводник с током действует сила Ампера. Работа,
совершаемая магнитным полем при перемещении проводника на
отрезок dx из положения 1
в положение 2 равна:
δA = Fdx =ІdlBdx =ІBdS
δA= ІdΦ
А= I ΔΦ
ΔΦ – магнитный поток,
пересекаемый проводником.
1
І
dx
F
2
B

22.

Пусть замкнутый контур с током находится в
магнитном поле, причём В ≠ const.
×
×
×
×
I Ф
F×
×1
×
×
×
×
×
×
×
×
×
× ×
× ×
× F×
× ×
× ×
× × × × × × ×В
× × ×××× ×
Ф2
× × × ××××
× × × ×× × ×
× × × ×× × ×
Х
А = I ( Ф2 – Ф1 ) = I ΔФ *
ΔФ – изменение магнитного потока, пронизывающего
контур.
Формула * справедлива для любого контура и
произвольного магнитного поля

23.

Явление электромагнитной
индукции

24.

Опыты Фарадея
В 1831 г. Фарадей показал, что
меняющееся во времени (переменное)
магнитное поле вызывает появление
переменного электрического поля.
Это явление названо
электромагнитной индукцией.
Ток, возникающий в контуре, который пронизывается переменным
магнитным потоком, назван индукционным током.
Возникающая при этом электродвижущая сила названа
электродвижущей силой индукции.
Э.Д.С. индукции в замкнутом контуре равна по величине и
противоположна по знаку скорости изменения магнитного
потока сквозь поверхность, ограниченную этим контуром:
d
d - основной закон
инд ( BdS )
электромагнитной индукции
dt
dt

25.

Правило Ленца
Индукционный ток в контуре всегда имеет такое
направление, что создаваемое им магнитное поле
препятствует изменению магнитного потока,
вызвавшего этот индукционный ток.
В
0
t
В
Iин
В
0
t
В
Iин
д
д
Ві
Ві

26.

К закону Фарадея
В l sin ,
1) инд
где l – длина проводника АС.
Если l то:
инд В l
2)Если ЭДС индукции создается в
замкнутом
проводящем контуре с
сопротивлением R, то в нем возникает сила тока, имеющая
мгновенное значение i = / R , и полный заряд, протекающий
по контуру за время изменения магнитного потока, равен:
1
1
q idt
dt
(Ф Ф )
dФ
t
t
0
0
Ф
R
R Ф0
1
q (Ф0 Ф)
R
R
0

27.

Вращение рамки в магнитном поле
Если рамка площадью S равномерно вращается в однородном
магнитном поле (В = const) с угловой скоростью = const, то
магнитный поток, сцепленный с рамкой, в любой момент
времени t, равен
Ф BS cos BS cos t ,
где t – угол поворота рамки в момент времени t (начало
отсчета выбрано так, что при t =0, 0 ).
При вращении рамки в ней будет возникать
переменная ЭДС индукции:
dФ
i BS sin t
dt
Если число витков в рамке равно N, то
d
i NBS sin t
dt
Максимальная ЭДС:
εi = NBSω
В

28.

Индуктивность
Магнитный поток через контур прямо
пропорционален силе тока в контуре
Ф = LI
где L –индуктивность контура.
За единицу индуктивности в СИ принимается Генри (Гн):
1Гн 1Вб / А 1В с / A
Индуктивность зависит от размеров, формы проводника
и от магнитных свойств среды, в которой находится
проводник.

29.

Индуктивность бесконечно длинного соленоида
Магнитный поток сквозь один виток соленоида площадью S
Ф1 BS
Полный магнитный поток, сцепленный со всеми витками
соленоида (потокосцепление)
N2
Ф1 N NBS
IS
0 l
или
где n = N / l
Ψ=µ0 µ n2 І V ,
Т.к. для катушки Ψ = LI, получаем для L:
N2
L
S
0 l
или:
L = µ0 µ n2 V

30.

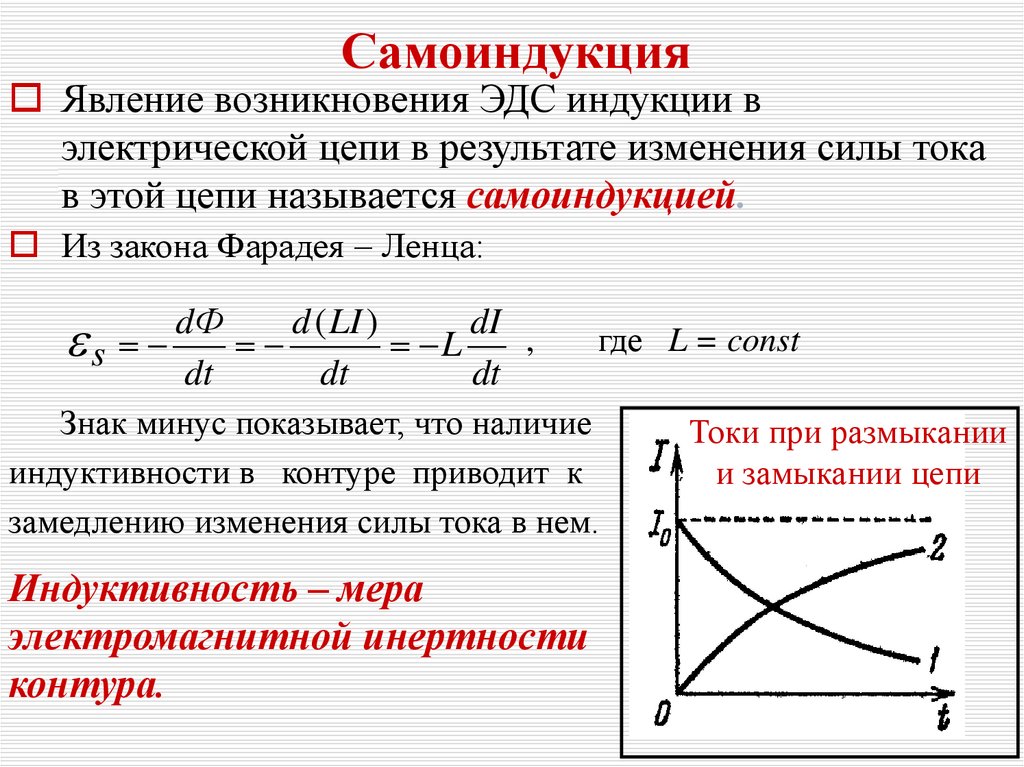
Самоиндукция
Явление возникновения ЭДС индукции в
электрической цепи в результате изменения силы тока
в этой цепи называется самоиндукцией.
Из закона Фарадея – Ленца:
dФ
d ( LI )
dI ,
s
L
dt
dt
dt
где L = const
Знак минус показывает, что наличие
индуктивности в контуре приводит к
замедлению изменения силы тока в нем.
Индуктивность – мера
электромагнитной инертности
контура.
Токи при размыкании
и замыкании цепи

31.

Энергия магнитного поля
Рассмотрим контур индуктивностью L, по которому
течет ток I.
Для изменения магнитного потока на dФ
необходимо совершить работу A IdФ LIdI
Полная работа
I
A LIdI LI / 2
2
0
Совершенная работа идет на создание энергии
магнитного поля
LI 2
Wм
2

32.

Объемная плотность энергии
магнитного поля
Энергия магнитного поля соленоида
LI 2 I
,
Wм
2
2
Ψ=µ0 µІn2 V,
0 I n V 0 H
Wм
V,
2
2
2 2
2
B
2
BH
Wм
V
V
2 0
2
Объемная плотность энергии магнитного поля
W
B
0 H
BH
w
V 2 0
2
2
2
2

33.

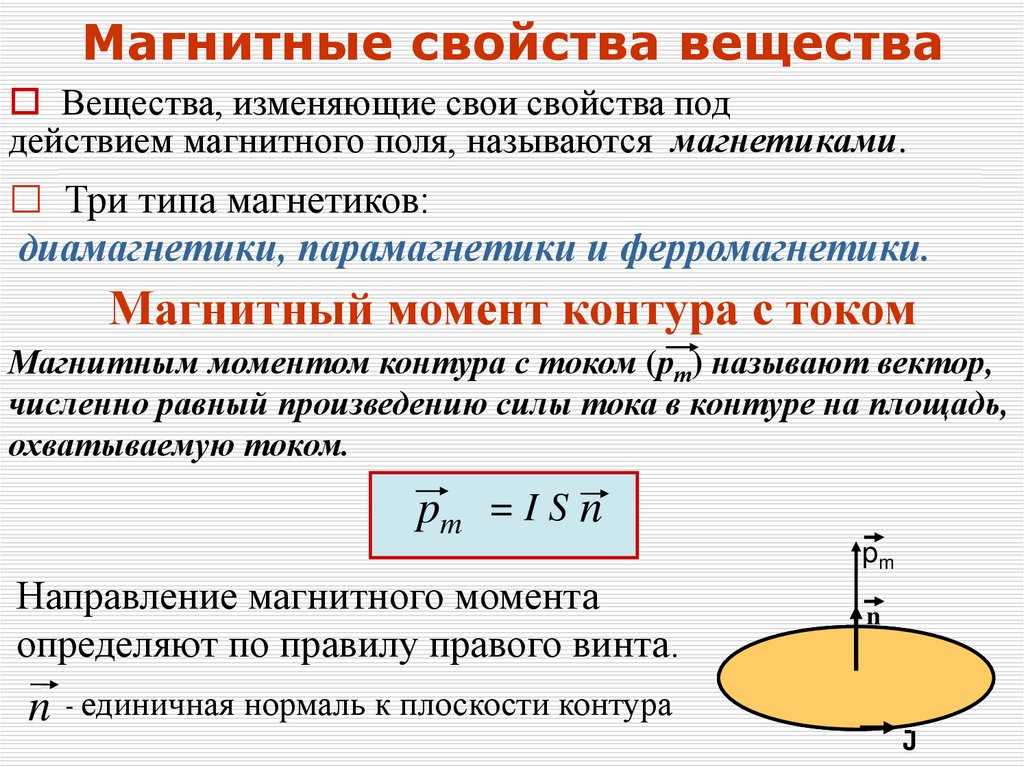
Магнитные свойства вещества
Вещества, изменяющие свои свойства под
действием магнитного поля, называются магнетиками.
□ Три типа магнетиков:
диамагнетики, парамагнетики и ферромагнетики.
Магнитный момент контура с током
Магнитным моментом контура с током (рт) называют вектор,
численно равный произведению силы тока в контуре на площадь,
охватываемую током.
pm = I S n
Направление магнитного момента
определяют по правилу правого винта.
pm
n
n - единичная нормаль к плоскости контура
J

34.

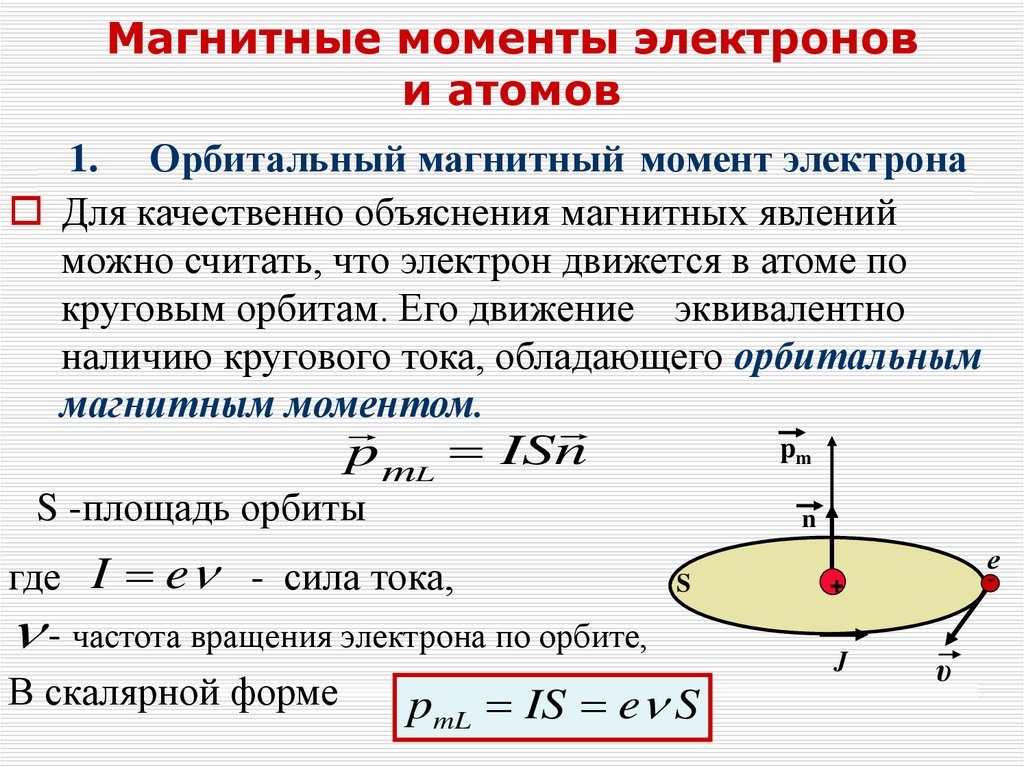
Магнитные моменты электронов
и атомов
1. Орбитальный магнитный момент электрона
Для качественно объяснения магнитных явлений
можно считать, что электрон движется в атоме по
круговым орбитам. Его движение эквивалентно
наличию кругового тока, обладающего орбитальным
магнитным моментом.
p mL ISn
S -площадь орбиты
pm
n
где I e - сила тока,
S
- частота вращения электрона по орбите,
В скалярной форме
p IS e S
mL
е
-
+
J
υ

35.

2. Механический (орбитальный) момент импульса
электрона
Движущийся по орбите электрон обладает
механическим
моментом импульса
Le Le m r m 2 r 2m S
2
где Le - орбитальный механический момент
электрона, 2 r ,
Из сравнения:
pmL e S
имеем:
и
S r 2.
pm
Le 2m S
n
S
e
Le g L Le
p mL
2m
+
е
r
J
Le
e
называется гиромагнитным отношением
gL
2m - орбитальных моментов или орбитальным
гиромагнитным отношением
υ

36.

3. Спиновые моменты электрона
Кроме орбитального электрон обладает собственным
механическим моментом
импульса , называемым спином.
Спину электрона L eS соответствует собственный
(спиновый) магнитный момент ртS .
p ms g s Les
Величина g s e
m
называется гиромагнитным
отношением спиновых моментов (спиновым гиромагнитным
отношением)

37.

Магнитный момент атома
Если атом состоит из Z электронов, то его орбитальный
магнитный момент равен:
Z
РmL pmLi
i 1
Спиновый магнитный момент атома равен:
Z
Pms pmsi
i 1
Магнитный момент атома состоит из векторной суммы его
орбитальных и векторной суммы его спиновых магнитных
моментов:
Pm PmL Pms

38.

Атом в магнитном поле
а) В0= 0
Fo цс= m ωo2 r
б) В0 ≠ 0,
В0
S,
Fцс= F0цс +Fл
Fл = eυ0 B0= eω0 r B0
mω2r = mω02r + eω0 r B0
S
В0
m(ω2-ω02) = eω0B0,
ω=ω0+Δω,
+
F0цс r е
Fл
υ
mΔω·2ω0 = eω0B0,
Δω = ωL,
eB0
L
2m
– частота Лармора
ωL не зависит от скорости электрона и от радиуса
его орбиты

39.

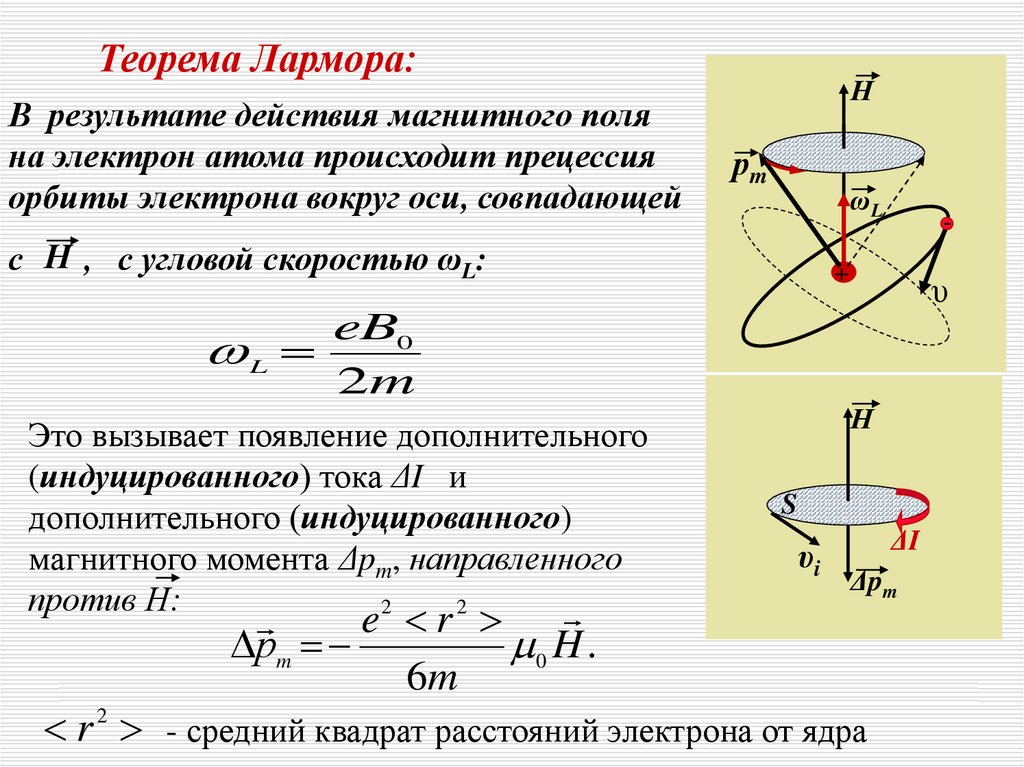
Теорема Лармора:
В результате действия магнитного поля
на электрон атома происходит прецессия
орбиты электрона вокруг оси, совпадающей
Н
рm
ωL
с Н , с угловой скоростью ωL:
-
+
υ
eB0
L
2m
Это вызывает появление дополнительного
(индуцированного) тока ΔI и
дополнительного (индуцированного)
магнитного момента Δpm, направленного
против Н:
2
2
e r
рm
0 H .
6m
Н
S
υi
ΔI
Δpm
r - средний квадрат расстояний электрона от ядра
2

40.

В общем случае у атома Z электронов и индуцированный
магнитный момент атома будет:
2
2
Ze a
Pm
B0
6m
a 2 - средний квадрат расстояний электронов от ядра
Полный магнитный момент
поле:
атома
в магнитном
Pm PmL PmS Pm
Намагниченность
Магнитный момент единицы объёма магнетика называется его
намагниченностью или вектором интенсивности намагничения:
N Pm
J
,
V
где Рm - магнитный момент атома, N – число атомов в однородном
магнетике, V – объём магнетика.
Намагниченность пропорциональна
напряжённости
внешнего магнитного поля:
J H,
т
χ т– магнитная восприимчивость вещества, безразмерная величина.

41.

Магнитное поле в магнетике
Вектор магнитной индукции результирующего магнитного поля
в магнетике равен векторной сумме магнитных индукций
внешнего поля (создаваемого намагничивающим током в
вакууме) и поля микротоков (создаваемого движением
электронов в атомах):
B B0 B '
Можно показать, что
B' 0 J , тогда:
B 0 H 0 J 0 ( H J )
J т H , то
B 0( 1 т )H . (*)
Известно, что B H . Сравним с формулой (*), получим:
0
Так как
1 + χт = μ.

42.

Закон полного тока для поля в
веществе
Закон полного тока для магнитного поля в
веществе (теорема о циркуляции вектора B )
имеет вид:
( Bdl ) Bl dl 0 ( I i I k ' )
i
k
где ∑І и ∑І ' – соответственно сумма макротоков и
сумма микротоков, охватываемых контуром.

43.

Диамагнетики
Диамагнетиками называются вещества, у атомов которых при
отсутствии внешнего магнитного поля магнитные моменты
равны нулю.
При внесении во внешнее магнитное поле диамагнетики
намагничиваются в направлении, противоположном этому
полю.
Причиной диамагнитного намагничивания является
возникновение индуцированных магнитных моментов,
ориентированных против внешнего магнитного поля.
Диамагнетики: инертные газы, цинк, золото, серебро, медь,
вода, ртуть, стекло, смолы, мрамор и др.
J
Для диамагнетиков:
В = В0 - В΄,
В΄<< В0 ,
В< В0.
H
|χт| ~ 10 -5 ÷ 10 -6; т.е. | χт |<<1; χт < 0, μ = (1 + χm ) < 1

44.

Парамагнетики
Магнитные моменты атомов парамагнетиков при отсутствии
внешнего магнитного поля не равны нулю. Они ориентированы
хаотично, поэтому в сумме намагниченность парамагнетика
равна 0.
При внесении парамагнетика в магнитное поле устанавливается
преимущественная ориентация магнитных моментов атомов по
полю (парамагнетик намагничивается по полю). При
уменьшении внешнего магнитного поля до нуля ориентация
магнитных моментов атомов вследствие теплового движения
нарушается и парамагнетик размагничивается.
Парамагнетики: кислород, окись азота, алюминий, платина,
редкоземельные, щелочные и щелочно-земельные металлы и др.
J
Для парамагнетиков:
В = В0 + В΄, В΄< В0 ,
JS
В > В0
|χт| ~ 10 -3 ÷ 10 -5; χт > 0, μ = (1 + χm ) > 1
НS
Н

45.

Ферромагнетики
Вещества, способные сильно намагничиваться в магнитном
поле, называются ферромагнетиками.
К ферромагнетикам относятся четыре химических элемента:
железо, никель, кобальт, гадолиний. Из них наибольшей
магнитной проницаемостью обладает железо. Поэтому вся эта
группа получила название ферромагнетиков.
Широкое применение в технике получили керамические
ферромагнитные материалы – ферриты.
Для ферромагнетиков:
В = В0 + В΄,
|χт| ~ 10 2 ÷ 10 5
В΄>>В0 ,
χт > 0,
В >> В0
μ = (1 + χm ) >> 1
Например, у стали μ ≈ 8000, у сплава железа с никелем магнитная
проницаемость достигает значений 250000, в сплаве супермаллой
(79%Ni+5%Mo+16%Fe) - 800 000.

46.

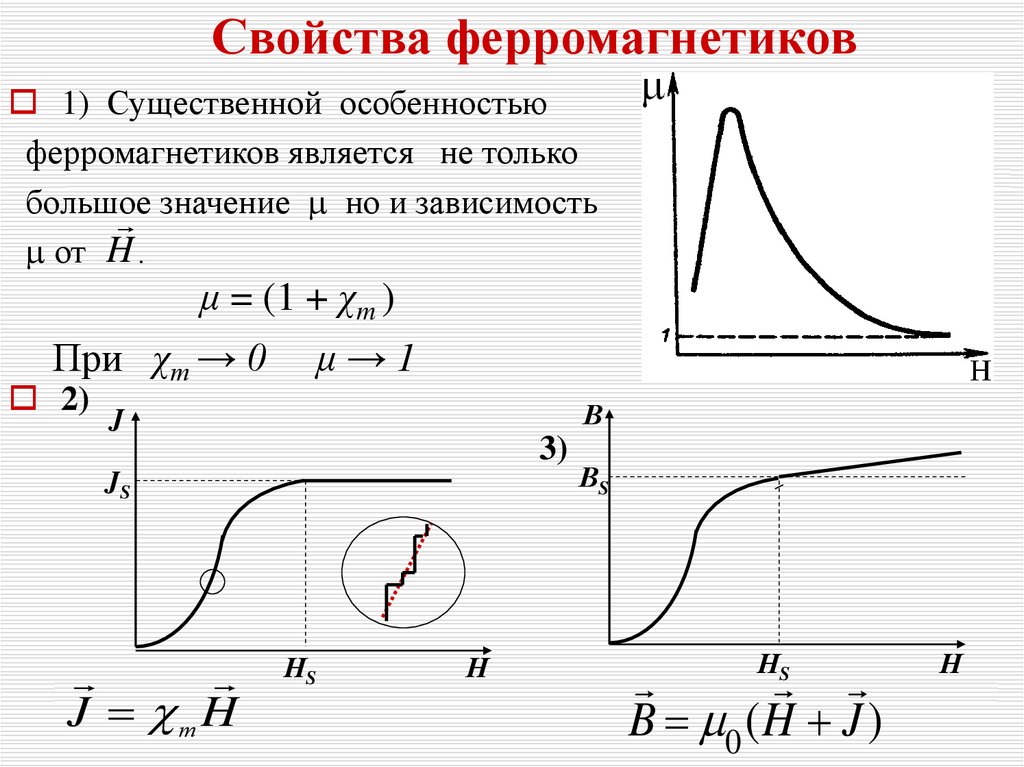
Свойства ферромагнетиков
1) Существенной особенностью
ферромагнетиков является не только
большое
значение но и зависимость
от H .
μ = (1 + χm )
При χт → 0
2)
μ→1
В
J
3)
JS
J т H
НS
Н
ВS
Н
B 0 ( H J )
S
Н

47.

4) Магнитный гистерезис
Характерной
особенностью процесса
намагничивания
ферромагнетиков
является наличие
магнитного
гистерезиса, то есть
зависимости
намагничивания от
предыстории образца.
Кривая намагничивания
ферромагнитного образца
представляет собой
петлю сложной формы,
которая называется
петлей гистерезиса.
Вос
-НS
-Нк
Нк
НS
Н
-Вос
Нк – коэрцитивная сила,
Вос – остаточная
намагниченность.

48.

Точка Кюри
Для каждого ферромагнетика имеется определенная
температура, называемая точкой Кюри, при нагревании выше
которой он теряет свои свойства и становится парамагнетиком.
Переход вещества из ферромагнитного состояния в
парамагнитное,
происходящий
в
точке
Кюри,
не
сопровождается поглощением или выделением теплоты, т.е. в
точке Кюри происходит фазовый переход второго рода.
Природа ферромагнетизма
Ферромагнетики обладают спонтанной намагниченностью, т.е.
они намагничены даже при отсутствии внешнего поля.
Французский физик Вейсс ввел гипотезу, согласно которой
ферромагнетик при температуре ниже точки Кюри состоит из
большого числа макроскопических областей - доменов,
самопроизвольно намагниченных до насыщения. Размер
доменов от 10-6 до 10-8 см3.

49.

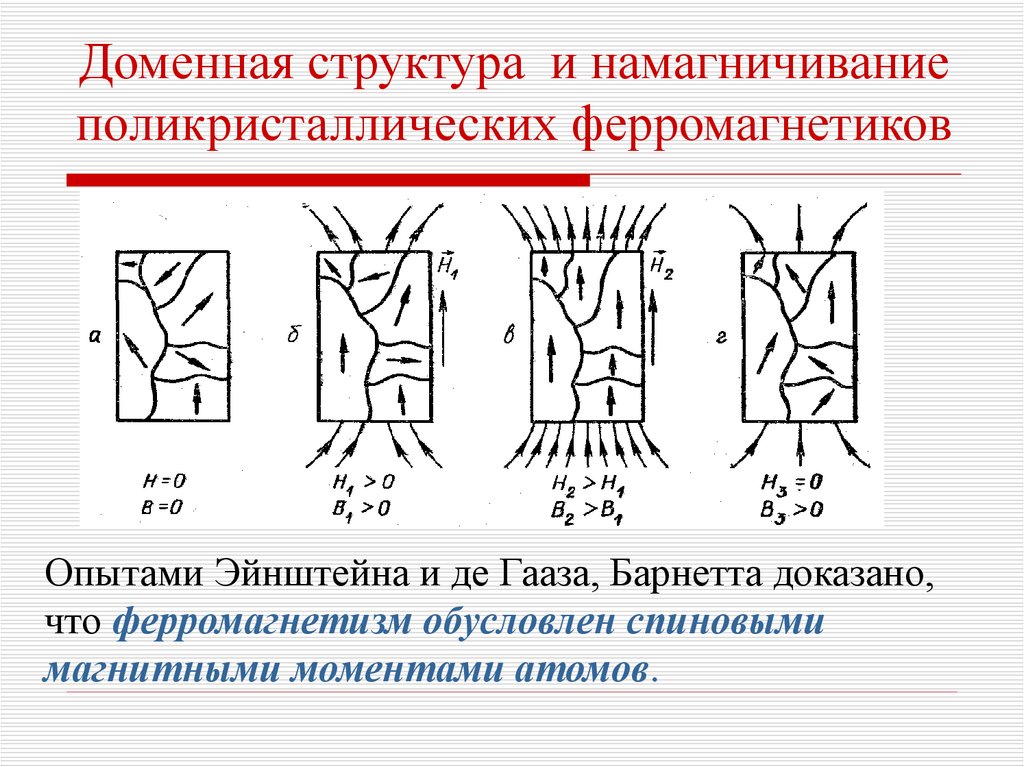
Доменная структура и намагничивание
поликристаллических ферромагнетиков
Опытами Эйнштейна и де Гааза, Барнетта доказано,
что ферромагнетизм обусловлен спиновыми
магнитными моментами атомов.

50.

Уравнения Максвелла
1) Ι уравнение Максвелла – обобщение закона
электромагнитной индукции Фарадея-Ленца):
Фт
( Е , dl ) t
Циркуляция вектора напряжённости электрического поля по
произвольному замкнутому контуру равна по величине и
противоположна по знаку скорости изменения магнитного
потока сквозь поверхность, ограниченную этим контуром.
Переменное магнитное поле в любой точке
пространства создаёт вихревое электрическое поле.

51.

2) II уравнение Максвелла - обобщение
закона полного тока.
Закон полного тока :
n
( Н , dl ) I k
k 1
n
I - алгебраическая сумма макротоков, охватываемых
k
контуром.
Максвелл предположил:
k 1
магнитное поле создаётся не только движущимися
зарядами, но и переменным электрическим полем
Докажем это.

52.

По теореме Остроградского-Гаусса:
Фе = Dn dS q
S
dq d e d
Dn dS
dt
dt
dt S
dq
Dn
Dn dS
dS
dt t S
S t
D
jсм ещ
t
dq
I jn dS
dt
e
Dn
I см ещ
t
S t
С учётом тока смещения закон полного тока:
n
( Н , dl ) I k I см ещ
k 1
е
( Н , dl ) t
- II уравнение Максвелла: переменное
электрическое поле в каждой точке
пространства создаёт вихревое
магнитное поле

53.

Система уравнений Максвелла
Фт
( Е , dl ) t
е
( Н , dl ) t
D dS q
n
свобод
S
В dS 0
j E
n
S
D = εοε E
В = μ0 μ Н