Магнитное поле в веществе

1.

МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ

2.

1. Магнитные моменты электронов и атомов
3
2. Атом в магнитном поле
7
3. Намагниченность вещества. Циркуляция вектора намагниченности
9
4. Напряженность магнитного поля. Циркуляция вектора напряженности
10
5. Магнитная восприимчивость. Магнитная проницаемость
13
6. Диамагнетики и парамагнетики в магнитном поле
15
7. Поле намагниченного стержня
20
8. Ферромагнетики
23
.
9. Условия на границе раздела двух магнетиков
30
10. Магнитное поле в зазоре электромагнита
34
11. Опыт Эйнштейна и де Гааза
35
12. Опыт Штерна и Герлаха
36 2

3.

1.Магнитные моменты
электронов и атомов
Все тела при внесении их во внешнее магнитное поле
намагничиваются в той или иной степени, т.е. создают собственное
магнитное поле, которое накладывается на внешнее магнитное поле.
Магнитные свойства вещества определяются строением
(электронным) их атомов.
Магнетики состоят из атомов, которые, в свою очередь, состоят из
положительных ядер и, условно говоря, вращающихся вокруг них электронов.
Электрон, движущийся по орбите в атоме эквивалентен
замкнутому контуру с орбитальным током:
где
1
T 2 r
I e e
- частота вращения

4.

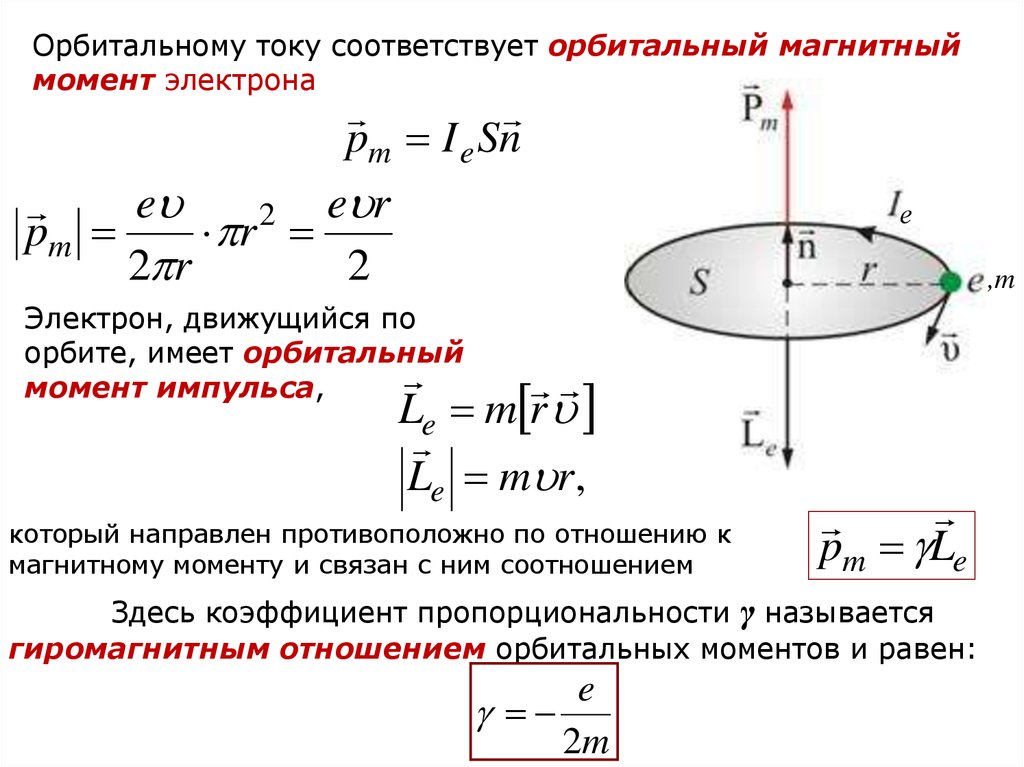
Орбитальному току соответствует орбитальный магнитный
момент электрона
pm I e Sn
e
e r
2
pm
r
2 r
2
е
,m
Электрон, движущийся по
орбите, имеет орбитальный
момент импульса,
Le m r
Le m r,
который направлен противоположно по отношению к
магнитному моменту и связан с ним соотношением
pm Le
Здесь коэффициент пропорциональности γ называется
гиромагнитным отношением орбитальных моментов и равен:
e
2m

5.

Кроме того, электрон обладает собственным моментом
импульса, который называется спином электрона L
s
Ls
h 2 1,05 10 34 Дж с.
2,
Спину электрона соответствует
спиновый магнитный момент
электрона (по аналогии с орбит.
магнитным моментом ),
направленный в противоположную
сторону и связанный с ним :
e
pms Ls
m
Б
e
pms Ls ;
m
e
pms
;
m2
– магнетон Бора.
Б 0,927 10 23 Дж Тл;
e
Б ;
2m

6.

pms s Ls
Итак
Величину s называют гиромагнитным отношением спиновых
моментов
e
s
m
Величина s может быть измерена в опыте Эйнштейна и де Гааза.
(см. далее)
Магнитным моментом атома называется векторная
сумма орбитальных и спиновых магнитных моментов всех
электронов атома
Z
Z
pma pmi pmsi
i 1
i 1
где Z – число всех электронов в атоме
(порядковый номер элемента в
периодической системе Менделеева)

7.

pm
2.
B
L
е
d
L
L
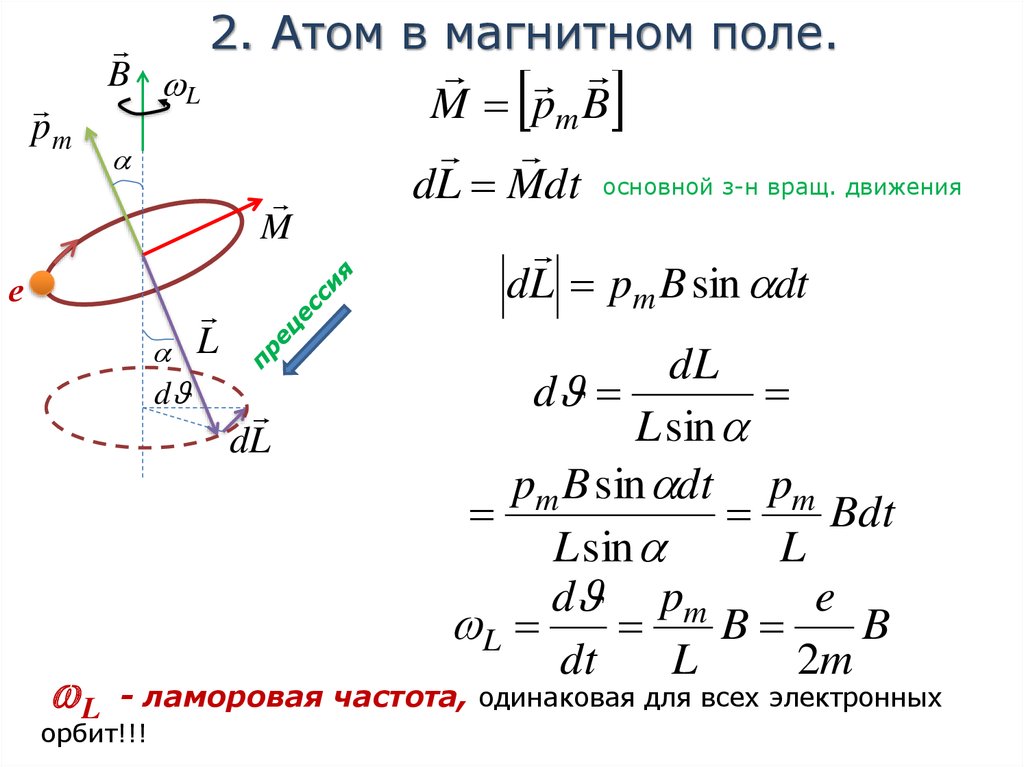
Атом в магнитном поле.
M pm B
dL Mdt основной з-н вращ. движения
M
dL pm B sin dt
dL
dL
d
L sin
pm B sin dt pm
Bdt
L sin
L
d pm
e
L
B
B
dt
L
2m
- ламоровая частота, одинаковая для всех электронных
орбит!!!

8.

pm
B L
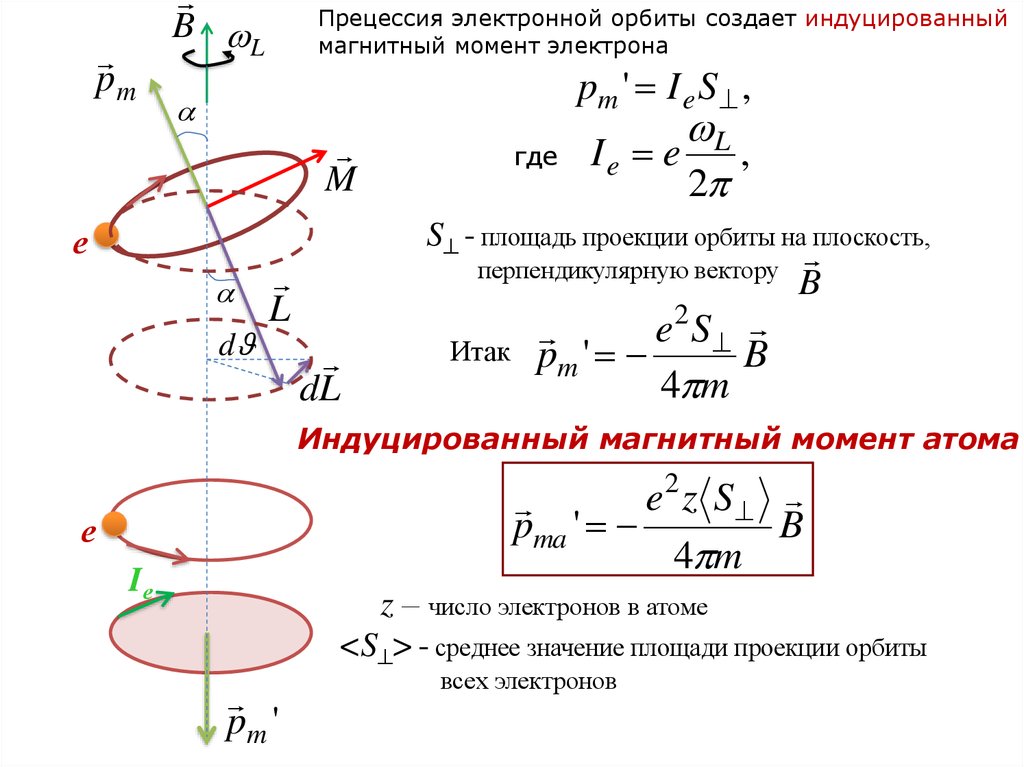
Прецессия электронной орбиты создает индуцированный
магнитный момент электрона
pm ' I e S ,
M
е
d
где
L
Ie e ,
2
S - площадь проекции орбиты на плоскость,
перпендикулярную вектору
L
dL
Итак
e2 S
pm '
B
4 m
B
Индуцированный магнитный момент атома
2
e
z S
pma '
B
4 m
е
Iе
z – число электронов в атоме
<S > - среднее значение площади проекции орбиты
pm '
всех электронов

9.

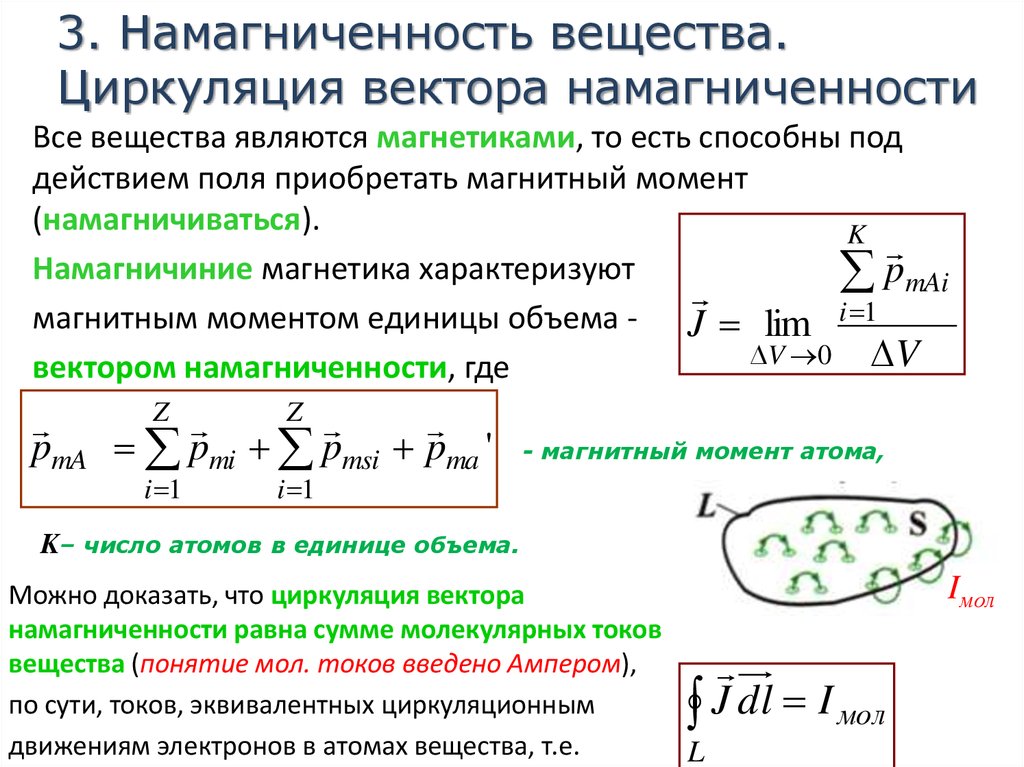
3. Намагниченность вещества.
Циркуляция вектора намагниченности
Все вещества являются магнетиками, то есть способны под
действием поля приобретать магнитный момент
(намагничиваться).
K
Намагничиние магнетика характеризуют
pmAi
магнитным моментом единицы объема - J lim i 1
V 0 V
вектором намагниченности, где
Z
Z
pmA pmi pmsi pma '
i 1
- магнитный момент атома,
i 1
K– число атомов в единице объема.
Можно доказать, что циркуляция вектора
намагниченности равна сумме молекулярных токов
вещества (понятие мол. токов введено Ампером),
по сути, токов, эквивалентных циркуляционным
J dl
движениям электронов в атомах вещества, т.е.
L
Iмол
I мол

10.

4. Напряженность магнитного поля.
Циркуляция вектора напряженности
Намагниченное вещество создает магнитное поле B' которое
накладывается на внешнее
поле B0 . Оба поля вместе дают
результирующее поле B .
Циркуляция результирующего поля определяется суммой
токов проводимости и молекулярных токов
Bdl 0 I I мол 0 I I мол
проблема
L
B
J dl I
Поскольку, I мол J dl то
L
L 0
B
Назовем
Тогда
J H вектором напряженности.
0
H dl I j dS
L
S

11.

B
0
J H
1)
H dl I j dS
L
2)
S
Итак:
- согласно 1)
H -искусственно введенный для описания
магнитного поля в веществе вектор;
- 2) - теорема о циркуляции вектора H : циркуляция вектора
напряженности магнитного поля по некоторому контуру равна
алгебраической сумме макроскопических токов (токов
проводимости), охватываемых этим контуром;
Вывод (теория): введение этого вектора снимает проблему
необходимости знания распределения молекулярных токов в
веществе для описания результирующего поля!!!
Вывод (практика): если необходимо рассчитать поле в веществе
(например, в сердечнике электромагнита) – используем т. о
циркуляции вектора напряженности магнитного поля!!!!
А
H J 1 .
м

12.

1 эрстед = 1000/(4π) A/м ≈
≈ 79,5774715 А/м.

13. 5. Магнитная восприимчивость. Магнитная проницаемость

H
B
0
J;
H
J H
B
0
H
Безразмерная величина
называется магнитной восприимчивостью вещества.
H H
B
0
H 1
B
0
B
H
.
0 1
Безразмерная величина
1+
называется относительной магнитной проницаемостью, или просто
магнитной проницаемостью вещества.
Таким образом, характеристики поля и вещества
связаны между собой соотношением
H
B
0
;или B 0 H . В вакууме = 0, = 1
B 0 H

14.

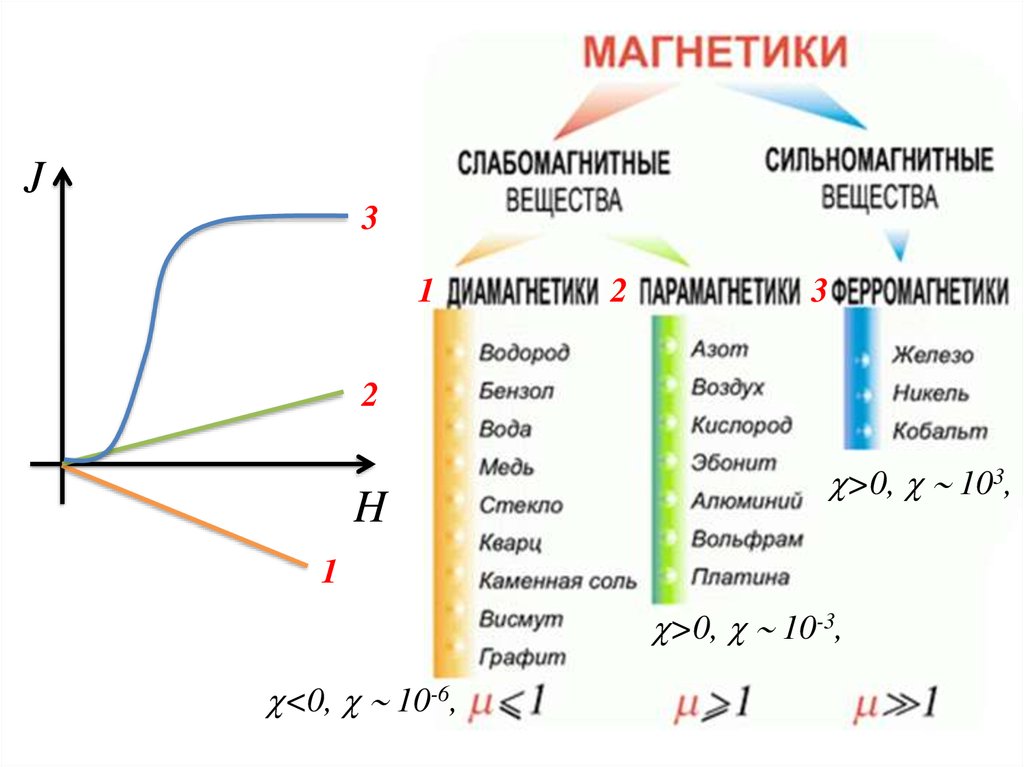
J
3
1
2
3
2
H
>0, 103,
1
>0, 10-3,
<0, 10-6,

15.

6. Диамагнетики и парамагнетики в
магнитном поле.
Из п.1 и 2 следует, что в общем случае магнитный момент атома
представляет собой векторную сумму орбитальных, спиновых и
индуцированных магнитных моментов всех электронов атома
Z
Z
pmA pmi pmsi pma '
i 1
i 1
или
pma 0
pmA pma '
pmA pma pma '
pma pma '
Диамагнетики
Z
pmA pma pmi
i 1
Парамагнетики

16.

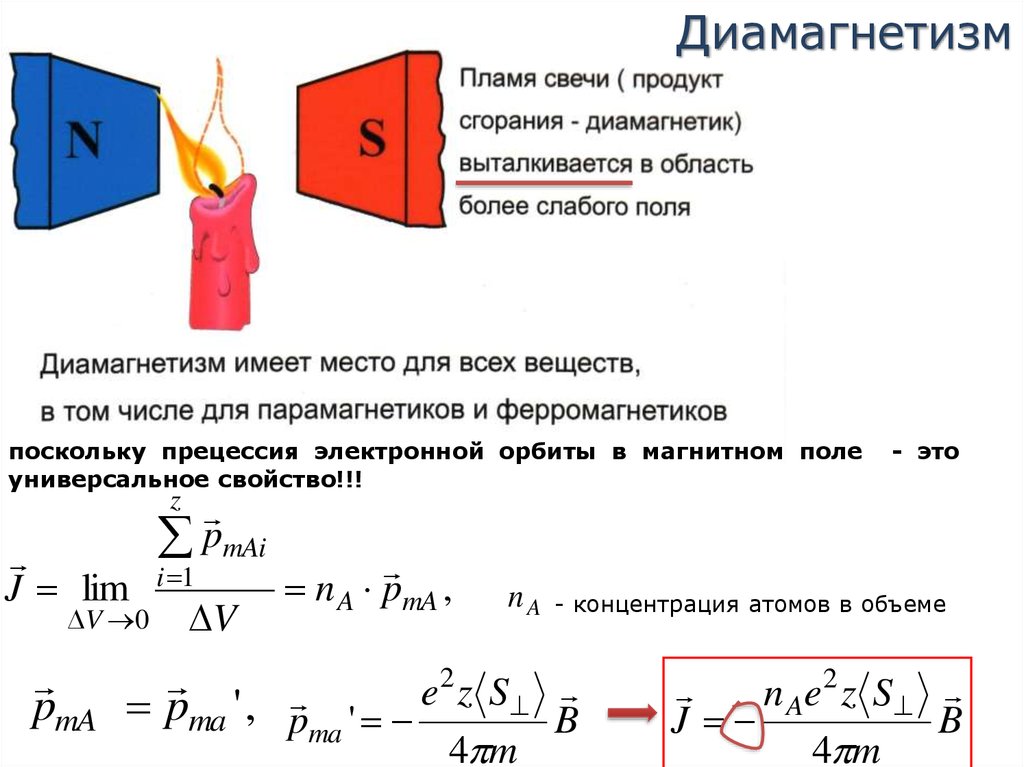
Диамагнетизм
поскольку прецессия электронной орбиты в магнитном поле
универсальное свойство!!!
- это
z
J lim
V 0
pmAi
i 1
V
n A pmA ,
nA
- концентрация атомов в объеме
2
e
z
S
pmA pma ' , p '
B
ma
4 m
n Ae 2 z S
J
B
4 m

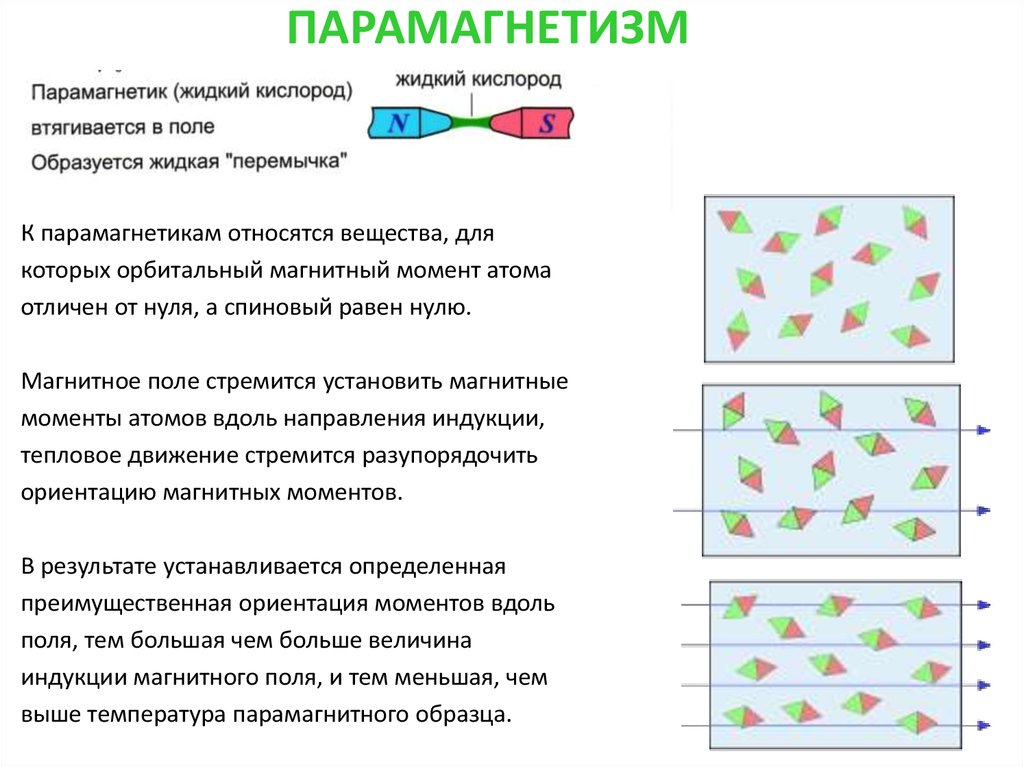
17. ПАРАМАГНЕТИЗМ

К парамагнетикам относятся вещества, для
которых орбитальный магнитный момент атома
отличен от нуля, а спиновый равен нулю.
Магнитное поле стремится установить магнитные
моменты атомов вдоль направления индукции,
тепловое движение стремится разупорядочить
ориентацию магнитных моментов.
В результате устанавливается определенная
преимущественная ориентация моментов вдоль
поля, тем большая чем больше величина
индукции магнитного поля, и тем меньшая, чем
выше температура парамагнитного образца.

18.

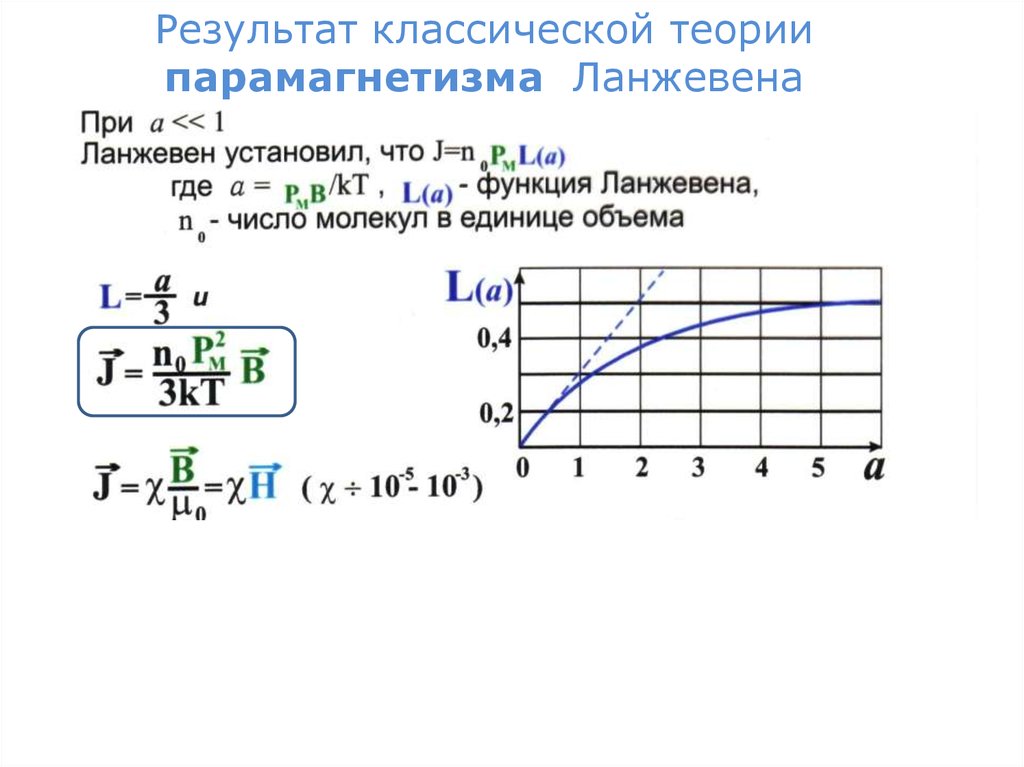
Результат классической теории
парамагнетизма Ланжевена

19. ЗАКОН КЮРИ ДЛЯ ПАРАМАГНЕТИКОВ

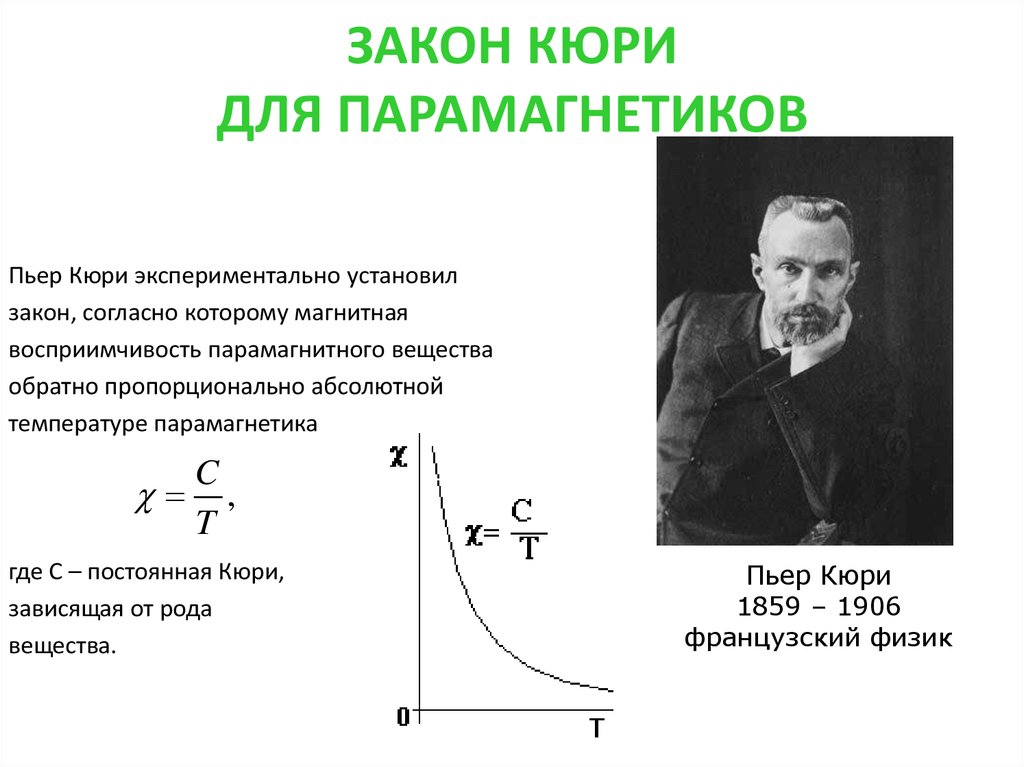
Пьер Кюри экспериментально установил
закон, согласно которому магнитная
восприимчивость парамагнитного вещества
обратно пропорционально абсолютной
температуре парамагнетика
C
,
T
где С – постоянная Кюри,
зависящая от рода
вещества.
Пьер Кюри
1859 – 1906
французский физик

20. 7. ПОЛЕ НАМАГНИЧЕННОГО СТЕРЖНЯ

J
Рассмотрим поле, создаваемое бесконечно
длинным круглым намагниченным стержнем.
Намагниченность
будем считать всюду
одинаковой и направленной по оси стержня.
Разобьем мысленно стержень на перпендикулярные к оси слои
Каждый слой разобьем на малые цилиндрические элементы.
Каждый такой элемент обладает магнитным моментом dpm
J
dpm JdldS ;
JdSdl.
dpm dI dS dI Jdl.
Поле каждого элемента эквивалентно полю, которое бы создавал ток
величиной dI Jdl , обтекающий элемент по боковой поверхности.
Воображаемые токи, текущие по общему для двух соседних элементов
участку, одинаковы по величине и противоположны по направлению,
поэтому их сумма равна нулю.
Таким образом, некомпенсированными оказываются лишь токи,
текущие по боковой поверхности слоя.

21. ПОЛЕ НАМАГНИЧЕННОГО СТЕРЖНЯ

Слой стержня толщиной dl создает поле,
которое создавал бы ток величиной
dI Jdl , обтекающий слой по боковой
поверхности. Линейная плотность этого
тока равна
dI
j лин
dl
J.
Весь бесконечно длинный стержень
создает поле, эквивалентное полю
цилиндра, обтекаемому током с
линейной плотностью j лин J .
Вне такого цилиндра поле равно нулю,
а внутри цилиндра поле однородно и равно
0 jлин .
Таким образом, вне стержня поле равно нулю.
Внутри стержня поле однородно и равно
B 0 J .

22. ПОЛЕ НАМАГНИЧЕННОГО СТЕРЖНЯ

Пусть имеется однородное поле B0 , создаваемое макротоками в
вакууме. Напряженность этого поля равна H B ( 1).
0
0
0
Внесем в это внешнее поле бесконечно длинный круглый стержень из
однородного и изотропного магнетика, расположив его ось вдоль B .
0
Из соображений симметрии следует, что возникающая
намагниченность
совпадает по направлению с B .
0
Намагниченный стержень создает внутри себя поле
В результате поле внутри стержня станет равным B J .
J
0
0 J
B B0 B B0 0 J ; H J
J H0.
0
0 0
B
B0
Напряженность поля в стержне такая же как во внешнем поле.
B 0 H ; H H 0 B0 0 B 0 B0 0 B0 .
Индукция в стержне в раз превышает индукцию внешнего
магнитного поля. Т.О. магнитная проницаемость показывает, во
сколько раз усиливается индукция магнитного поля в магнетике.

23. 8. ФЕРРОМАГНЕТИЗМ

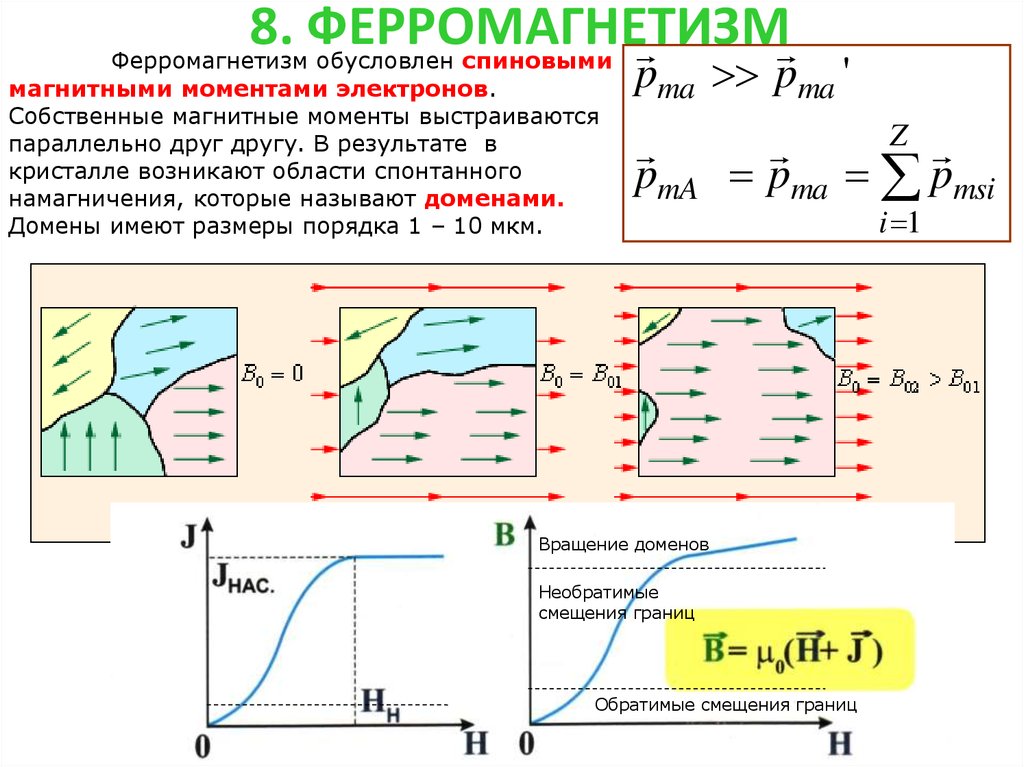
Ферромагнетизм обусловлен спиновыми
магнитными моментами электронов.
Собственные магнитные моменты выстраиваются
параллельно друг другу. В результате в
кристалле возникают области спонтанного
намагничения, которые называют доменами.
Домены имеют размеры порядка 1 – 10 мкм.
pma pma '
Z
pmA pma pmsi
Вращение доменов
Необратимые
смещения границ
Обратимые смещения границ
i 1

24.

Ферромагнетики – это вещества,
обладающие намагниченностью
при отсутствии внешнего поля.
Ферромагнетики являются сильномагнитными веществами
Намагниченность ферромагнетика
нелинейно зависит от напряженности.
Намагниченность быстро достигает
насыщения
После насыщения основная кривая
намагничения изменяется линейно.

25. МАГНИТНЫЙ ГИСТЕРЕЗИС

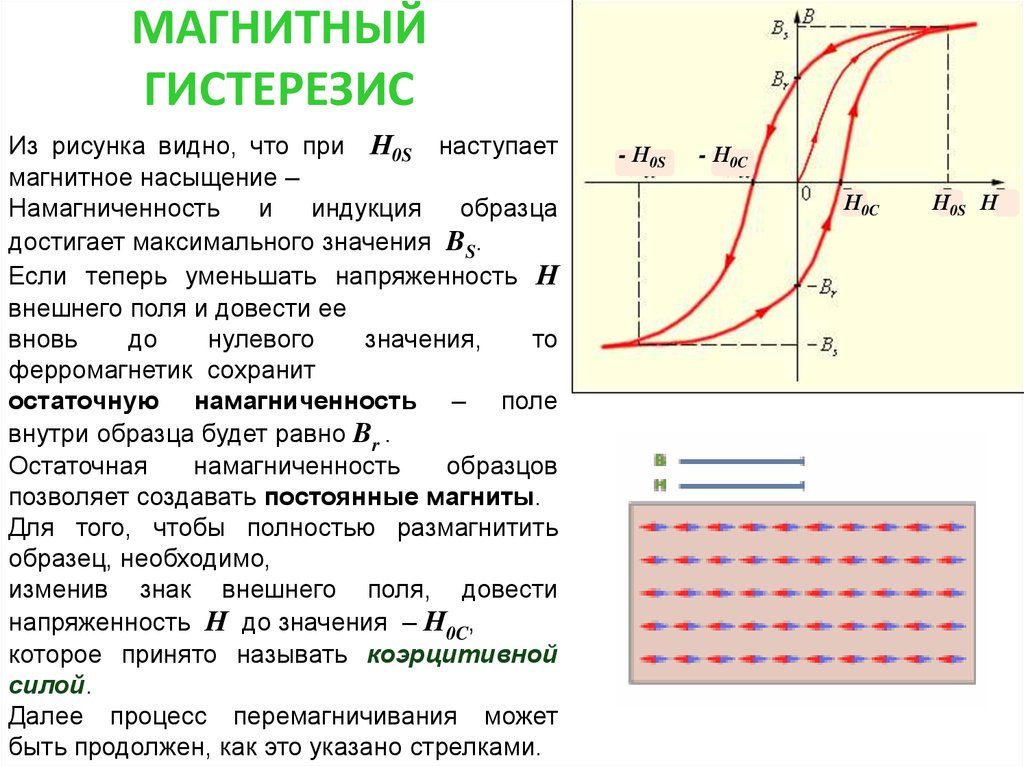
Из рисунка видно, что при Н0S наступает
магнитное насыщение –
Намагниченность
и индукция образца
достигает максимального значения BS.
Если теперь уменьшать напряженность Н
внешнего поля и довести ее
вновь
до
нулевого
значения,
то
ферромагнетик сохранит
остаточную намагниченность – поле
внутри образца будет равно Br .
Остаточная
намагниченность
образцов
позволяет создавать постоянные магниты.
Для того, чтобы полностью размагнитить
образец, необходимо,
изменив знак внешнего поля, довести
напряженность Н до значения – Н0C,
которое принято называть коэрцитивной
силой.
Далее процесс перемагничивания может
быть продолжен, как это указано стрелками.
- Н0S
- Н0C
Н0C
Н0S Н

26.

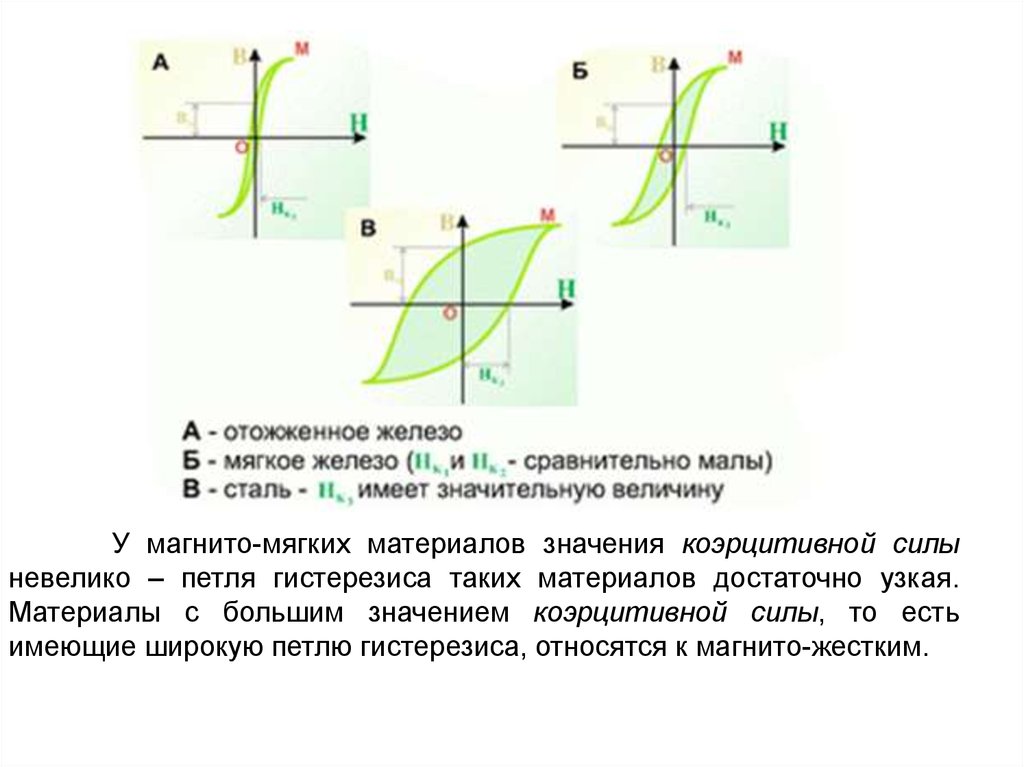
У магнито-мягких материалов значения коэрцитивной силы
невелико – петля гистерезиса таких материалов достаточно узкая.
Материалы с большим значением коэрцитивной силы, то есть
имеющие широкую петлю гистерезиса, относятся к магнито-жестким.

27.

11. МАГНИТНАЯ
ПРОНИЦАЕМОСТЬ
ФЕРРОМАГНЕТИКА
B
В связи с неоднозначностью
зависимости B от H понятие магнитной
проницаемости применяется лишь к
основной кривой намагничения.
B
tg
0 H
B 0 ( H J )
α
1 J H
H
1
H

28. ЗАКОН КЮРИ-ВЕЙССА

Для каждого ферромагнетика имеется
определенная температура Tc, при
которой области спонтанного намагничения
распадаются и вещество утрачивает ферромагнитные
свойства. Эта температура называется точкой Кюри.
При температуре выше точки Кюри ферромагнетик
становится обычным парамагнетиком, магнитная
восприимчивость которого подчиняется закону Кюри-Вейсса.

29.

В некоторых случаях обменные силы приводят к возникновению так
называемых антиферромагнетиков (хром, марганец). В
антиферромагнетиках собственные магнитные моменты электронов
ориентированы антипарралельно друг другу. Такая ориентация
охватывает попарно соседние атомы. В результате антиферромагнетики
обладают крайне малой магнитно восприимчивостью и ведут себя как
очень слабые парамагнетики.

30. 8. УСЛОВИЯ НА ГРАНИЦЕ ДВУХ МАГНЕТИКОВ

- используем т. Гаусса

31.

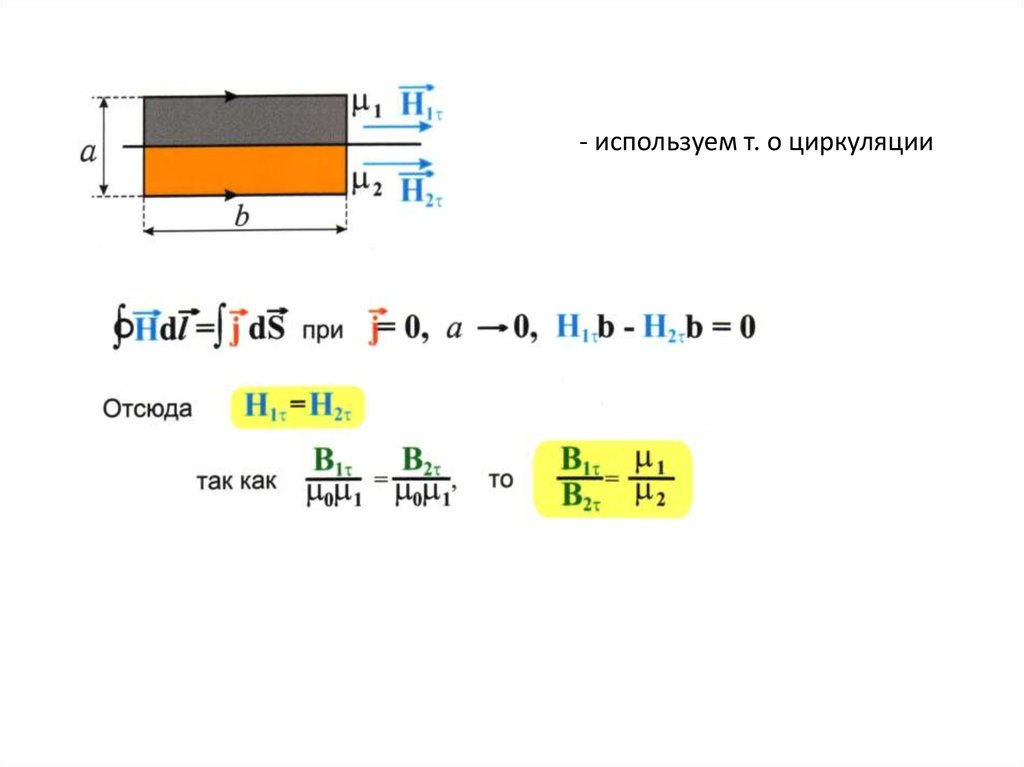
- используем т. о циркуляции

32.

1
B1
1
B1n
B1
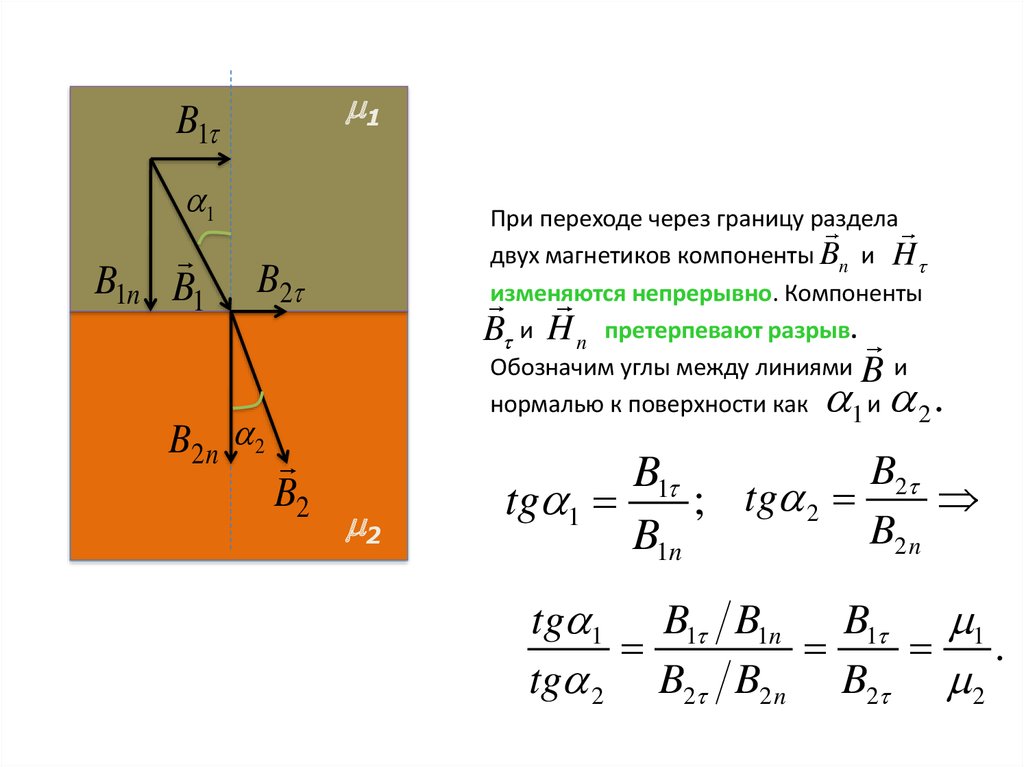
При переходе через границу раздела
двух магнетиков компоненты Bn и H
изменяются непрерывно. Компоненты
B и H n претерпевают разрыв.
Обозначим углы между линиями B и
нормалью к поверхности как
1и 2
B2
B2 n 2
B2
.
2
B2
B1
tg 1
; tg 2
B2n
B1n
tg 1 B1 B1n B1 1
.
tg 2 B2 B2 n B2 2

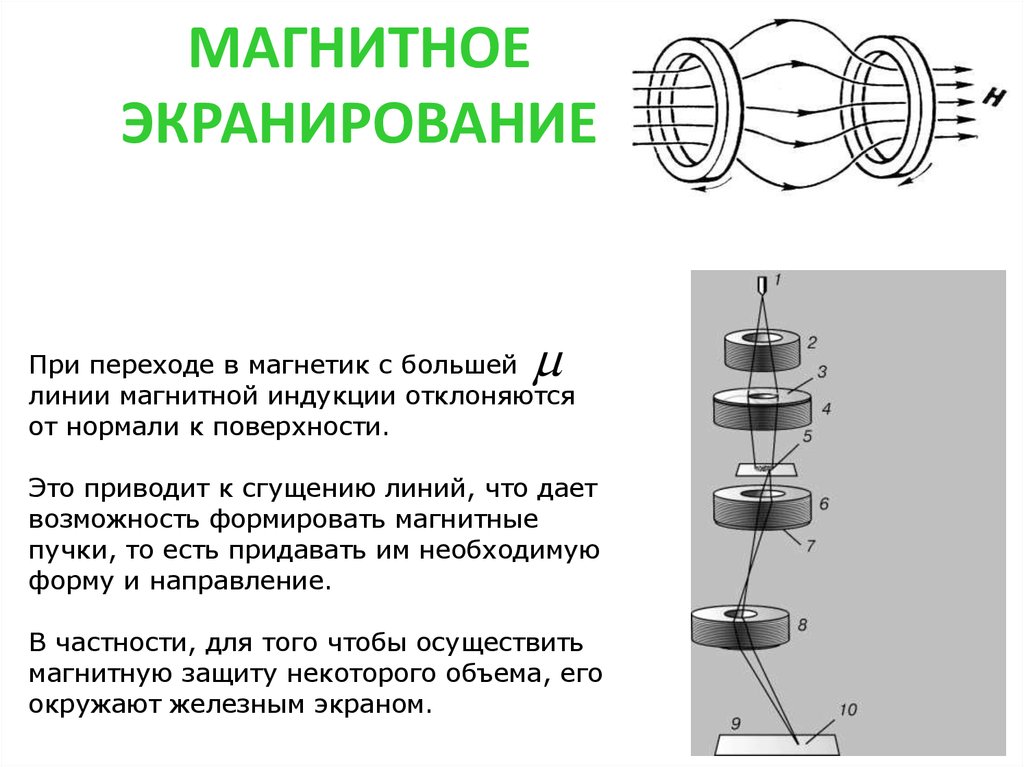
33. МАГНИТНОЕ ЭКРАНИРОВАНИЕ

При переходе в магнетик с большей
линии магнитной индукции отклоняются
от нормали к поверхности.
Это приводит к сгущению линий, что дает
возможность формировать магнитные
пучки, то есть придавать им необходимую
форму и направление.
В частности, для того чтобы осуществить
магнитную защиту некоторого объема, его
окружают железным экраном.

34. 9. МАГНИТНОЕ ПОЛЕ В ЗАЗОРЕ ЭЛЕКТРОМАГНИТА

Используем т. о циркуляции Н (см. вывод на слайде 11 и
граничные условия для Вn)
H жlж H вlв NI ;
lв - ширина воздушного зазора
Hж
l ж - длина сердечника
Bж
0 ж
Hв
Bв
0 в
;
Bж Bв B
Blж
0 ж
N – число витков в электрообмотке,
c силой тока I
B
;
0 NI
Blв
0 в
NI
0 NI
;
lв в lж ж lв lж ж
lж
N
lв >>
B 0 I .
ж
lв

35.

36.

37.

38.

39.

40.

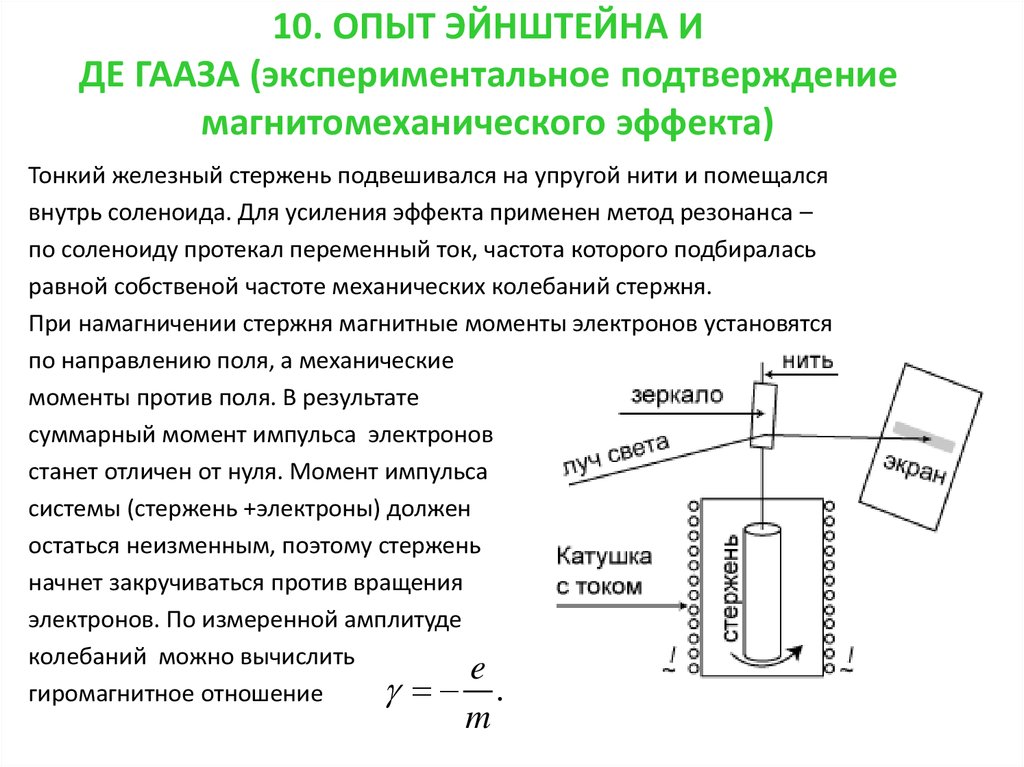
41. 10. ОПЫТ ЭЙНШТЕЙНА И ДЕ ГААЗА (экспериментальное подтверждение магнитомеханического эффекта)

Тонкий железный стержень подвешивался на упругой нити и помещался
внутрь соленоида. Для усиления эффекта применен метод резонанса –
по соленоиду протекал переменный ток, частота которого подбиралась
равной собственой частоте механических колебаний стержня.
При намагничении стержня магнитные моменты электронов установятся
по направлению поля, а механические
моменты против поля. В результате
суммарный момент импульса электронов
станет отличен от нуля. Момент импульса
системы (стержень +электроны) должен
остаться неизменным, поэтому стержень
начнет закручиваться против вращения
электронов. По измеренной амплитуде
колебаний можно вычислить
e
.
гиромагнитное отношение
m

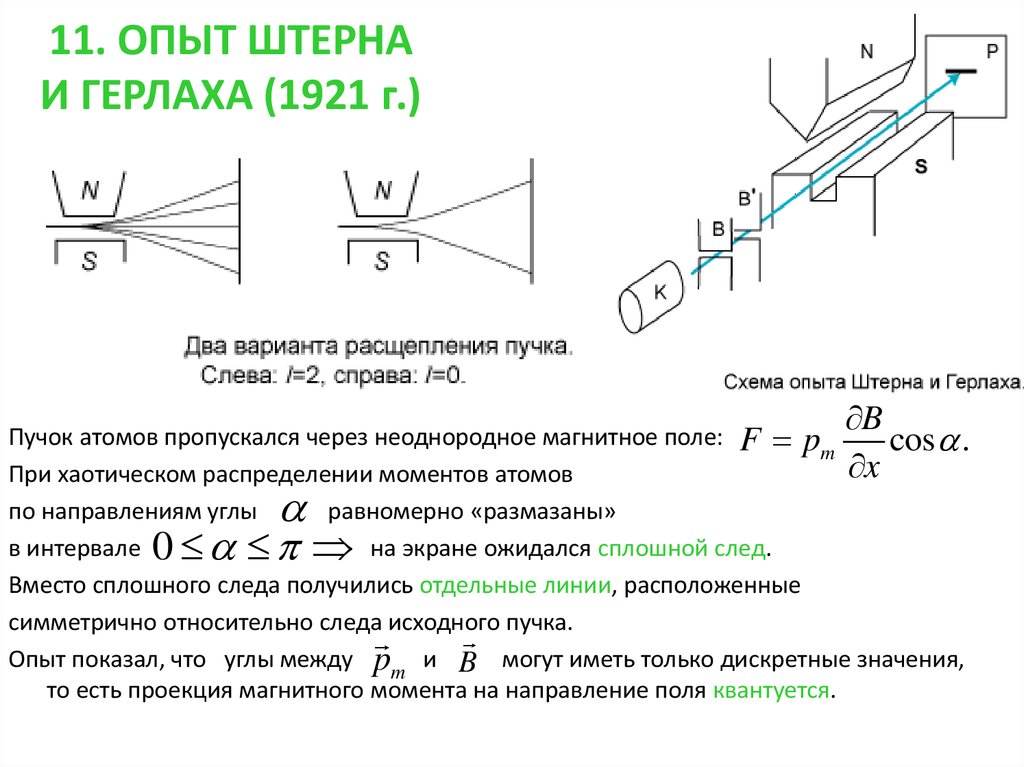
42. 11. ОПЫТ ШТЕРНА И ГЕРЛАХА (1921 г.)

B
Пучок атомов пропускался через неоднородное магнитное поле: F p
cos .
m
x
При хаотическом распределении моментов атомов
по направлениям углы
равномерно «размазаны»
в интервале 0
на экране ожидался сплошной след.
Вместо сплошного следа получились отдельные линии, расположенные
симметрично относительно следа исходного пучка.
Опыт показал, что углы между pm и B могут иметь только дискретные значения,
то есть проекция магнитного момента на направление поля квантуется.

43. КЛАССИКИ

Вандер де Гааз
1878 – 1960
нидерландский
физик
Отто Штерн
1888 – 1969
немецкий
физик
Вальтер Герлах
1889 – 1979
немецкий
физик