Передаточные функции и структурные схемы бокового движения самолета (лекция 9)

1. РАЗДЕЛ 1. ВОЗДУШНОЕ СУДНО КАК ОБЪЕКТ УПРАВЛЕНИЯ

Тема 2 Математические модели продольного и
бокового движения самолета
ЛЕКЦИЯ № 9. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И СТРУКТУРНЫЕ
СХЕМЫ БОК0ВОГО ДВИЖЕНИЯ САМОЛЕТА
Учебные вопросы:
• 1. Линейная модель бокового движения в векторно-матричной форме.
• 2. Передаточные функции и структурные схемы бокового движения
самолета.
Задание на самостоятельную работу:
[1] Вавилов Ю.А., Системы автоматического управления летательных аппаратов. ВВИА им. проф.
Н.Е. Жуковского, 2009. с.70…76.
[2] Мигунов А.И., Иванов Р.В., Серов А.Н. Системы автоматического управления полетом.
Электронный учебник. ВУНЦ ВВС «ВВА», 2018. Л-9, тематический план, учебная программа
[3] Красовский А.А., Вавилов Ю.А., Сучков А.И. Системы автоматического управления
летательных аппаратов. ВВИА им. проф. Н.Е. Жуковского, 1986. с. 75…84.
[7] Кичигин Е.К., Демчук В.А., Лущик А. В., Агеев А.М. Системы автоматического управления
полетом. Ч. 1: Учебное пособие. − Воронеж: ВАИУ, 2011. с. 25…27.

2.

Вопрос №1.
Линейная модель бокового движения в
векторно-матричной форме.

3.

К изолированному боковому движению относится движение центра масс
вдоль траекторной оси OZк, лежащей в горизонтальной плоскости, и вращения
относительно связанных осей ОХ и ОY (угловые скорости ωx и ωy).
При выделении бокового движения предполагается, что при боковом
маневрировании продольная балансировка сохраняется ( Fхк = Fук =0) и угловая
скорость ωz = 0 . Тогда из уравнений
mW Fxк
mW Fy
к
cos Fz
mW
к
J x x J y J z y z M x
J y y J z J x z x M y
J z z J x J y x y M z
вытекает, что уравнения динамики бокового движения имеют следующий вид:

4.

.
mW cos Fz к
Уравнения динамики бокового движения:
J x x M x
J y y M y
x sin
Кинематические уравнения:
y cos cos sin
z g V0 cos sin Ψ
а z a z 0
Окончательный вид системы amxx amxy amx
amxэ э аmxн н
уравнений
изолированного
у
х
э
н
a
a
a
a
а
бокового движения :
mу
mу
mу
mу
н
mу э
Ψ в
z V0 Ψ

5.

Физический смысл коэффициентов, входящих в уравнение
бокового движения
а
Полученные коэффициенты указывают не только место в уравнениях
y
у
х
э
н
э
x
н
mx
mу
mу mу mу
mx
z mx
mx mx mу
z
a a
a
a
a а
a
a
a а
a
бокового движения, но и имеют глубокий физический смысл.
При наличии угла за счет скольжения возникает боковая сила
приложенная в центре давления (положительный вызывает отрицательную
силу
)
Z
Z
а
z характеризует приращение боковой силы Z при
Коэффициент
единичном приращении угла
Z
Т.к. ЦД расположен за ЦМ, ближе к хвостовой части ВС, то сила
вызывает
появление момента путевой устойчивости M y ( ), стремящегося развернуть
ВС относительно оси ОY, устраняя
a
Коэффициент
mу характеризует путевую устойчивость

6.

При наличии угла :
1) изменяется стреловидность правого и левого крыла по отношению к
набегающему потоку, следовательно у полукрыла с меньшей
стреловидностью величина подъемной силы больше чем у крыла с
большей стреловидность, следовательно появится момент относительно
оси ОХ.
2) Кроме того ЦД находится выше ЦМ, что также приводит к появлению
момента относительно оси ОХ.
В итоге сумма моментов 1 и 2 приводит к появлению момента поперечной
устойчивости M ( ) , стремящегося накренить ВС в сторону
x
противоположную скольжению.
Коэффициент
a
характеризует поперечную устойчивость
mx

7.

При вращении ВС относительно оси ОХ с угловой скоростью
на
х
опускающемся полукрыле местные углы атаки увеличиваются, а на
поднимающемся уменьшаются, следовательно на опускающемся крыле
возникает положительное приращение Y , а на поднимающемся
отрицательное приращение Y . В результате возникает
демпфирующий момент крена M x ( x ) , препятствующий исходному
вращению.
Коэффициент
x
amx характеризует демпфирующий момент крена
При вращении ВС относительно оси ОХ с угловой скоростью
изменение
х
местных углов атаки приводит к изменению сил лобового сопротивления: на
опускающемся – увеличение, на поднимающемся – уменьшение. В
результате возникает спиральный момент рыскания M y ( x )
разворачивающий самолет в сторону развивающегося крена.
Коэффициент
х
amу характеризует спиральный момент рыскания

8.

При вращении ВС относительно оси OY с угловой скоростью
y у
полукрыла идущего вперед скорость увеличивается, а у другого
уменьшается. Следовательно у крыла с большей скостью увеличивается
сила лобового сопротивления, а у другого уменьшается.
В результате возникает демпфирующий момент рыскания M y ( y ),
препятствующий исходному вращению.
Коэффициент
рыскания
у
amу характеризует демпфирующий момент
При увеличении скорости крыла идущего вперед увеличивается и
подъемная сила, а у другого уменьшается. В результате появляется
спиральный момент крена M х ( y ), кренящий ВС в сторону отстающего
крыла.
Коэффициент
y
amx характеризует спиральный момент крена

9.

При положительном крене ВС создается составляющая силы тяжести,
направленная вдоль оси OZ, и возникает положительное скольжение (ВС
скользит на правое крыло), т.е. возникает боковая сила Z.
a
Коэффициент
z характеризует возникновение боковой силы при
крене ВС.
При единичном отклонении рулевых поверхностей э и н возникают
управляющие моменты M х ( э ) и M y ( н ) .
э
н
Коэффициенты
характеризуют эффективность
mx amу
рулевых поверхностей
a
При отклонении э на опускающемся крыле увеличивается сила лобового
сопротивления, а на поднимающемся – уменьшается, следовательно
возникнет момент M у ( э ) .
При отклонении н на опережающем крыле увеличивается подъемная сила,
а на отстающем – уменьшается, следовательно возникает момент M х ( н ) .
э
Коэффициенты аmу и аmxн характеризуют перекрестное влияние
отклонения элеронов и руля направления
"0"

10.

Статическая устойчивость бокового движения
Статическая устойчивость БД характеризуется:
- Боковой балансировкой
- Путевой устойчивостью
- Поперечной устойчивостью
J y y M y
J x x M x
Боковая балансировка
Для обеспечения прямолинейного полета с постоянной скоростью
необходимо, чтобы все силы и моменты были уравновешены, это значит:
Fzк 0, M y 0, M x 0
Для выполнения условия Fz
к
0 необходимо:
Z mg sin 0
Однако, для прямолинейного полета (без потери высоты):
Y
Y mg cos mg
cos

11.

Y
Z
sin 0
cos
cz
V
2
2
S cy
V
sin
S
0
2
cos
2
cz cy tg 0
(1)
Физический смысл: компенсировать боковую силу возникшую в
результате появления угла скольжения можно отклонением ВС по крену в
сторону скольжения

12.

Для выполнения условия M y 0,
x
y
x
y
M x 0 y 0, x 0
mx mx x mx y mx mx э э m x н н
э
н
my my x my y my my э m y н
(2)
Уравнения 1 и 2 представляют собой условия боковой балансировки
Путевая устойчивость
Под путевой (флюгерной) устойчивостью понимается
самостоятельно стабилизировать заданный угол скольжения.
свойство
ВС
Условием обеспечения путевой устойчивости является заднее расположение ЦД (за
ЦМ). Помимо этого на заднем вертикальном оперение, из-за изменения условий
обтекания набегающим воздушным потоком, возникает аэродинамическая сила и
момент, разворачивающие ВС на ветер (флюгер).
В этом случае возникающий момент M y ( )
устойчивого ВС коэффициент a
0
mу
стремится устранить скольжение. У

13.

Поперечная устойчивость
Под поперечной устойчивостью понимается свойство ВС самостоятельно
стабилизировать угол крена.
При крене под действием силы тяжести на ось OZ происходит искривление
траектории в сторону опущенного крыла. Следовательно возникает скольжение в эту
сторону и боковая сила Z ( ) , приложенная в ЦД.
Если ЦД располагается выше ЦМ и стреловидность опущенного крыла меньше
стреловидности поднятого (подъемная сила опущенного крыла больше поднятого) то
возникает восстанавливающий момент крена M ( ) , действующий в сторону
x
противоположную крену.
У устойчивого ВС коэффициент a
0
mx
Динамическая устойчивость бокового движения
Под динамической устойчивостью ВС понимается устойчивость движения при
однократном приложении управляющего или возмущающего воздействия.

14.

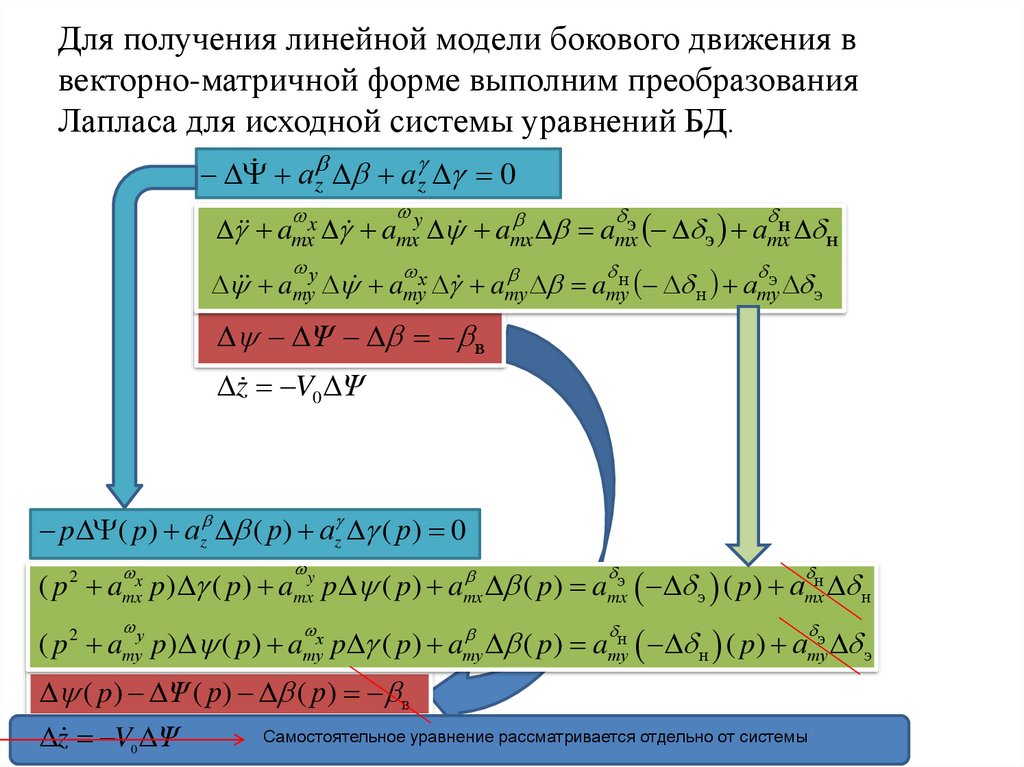
Для получения линейной модели бокового движения в
векторно-матричной форме выполним преобразования
Лапласа для исходной системы уравнений БД.
а z a z 0
amxx amxy amx
amxэ э аmxн н
amуу amух amу
amун н аmуэ э
Ψ в
z V0 Ψ
p ( p) аz ( p) az ( p) 0
x
y
( p amx p) ( p) amx p ( p) amx
( p) amxэ э ( p) аmxн н
2
( p 2 amуу p) ( p) amух p ( p) amу
( p) amун н ( p) аmуэ э
( p) Ψ ( p) ( p) в
z V0 Ψ
Самостоятельное уравнение рассматривается отдельно от системы

15.

p ( p) аz ( p) az ( p ) 0
x
y
у
х
( p amx p) ( p ) amx p ( p ) amx
( p ) amxэ э ( p )
2
( p amу p) ( p) amу p ( p ) amу ( p ) amу н ( p )
2
н
( p) Ψ ( p) ( p) 0
Перейдем к матричной форме записи (ветер не учитывали) с
учетом у :
р
0
az
az
0
x
amx
p 2 amx p
x
0
amy
amy p
1
1
0
0
( p)
amx
э
a
( p)
mx
y
p amy ( p)
0
1
( p)
0
р
y
0
0
н
amу
0
э ( p)
н ( p)

16.

Определитель этой системы имеет следующую структуру:
р
az
az
0
x
0
р 0
a mx
a my
p a mx p
a m xy p
1
1
0
2
y
a mx
y
p amy
1
р
Характеристический
полином
системы
формируется
раскрытием определителя и имеет следующий вид:
р р а3 р а2 р а1 р а0 р
4
3
2

17.

j
j
2
0,8
-0,01
0,6
4
0,4
0
1
0,2
1
0
1,6 1,2 0,8
0,4
-0,2
-0,4
-0,6
3
y
x
, град
1
y
0,5
0
2
-2
-1
-4
-6
-2
х , у , град с 1
4
-0,8
-1,0
0
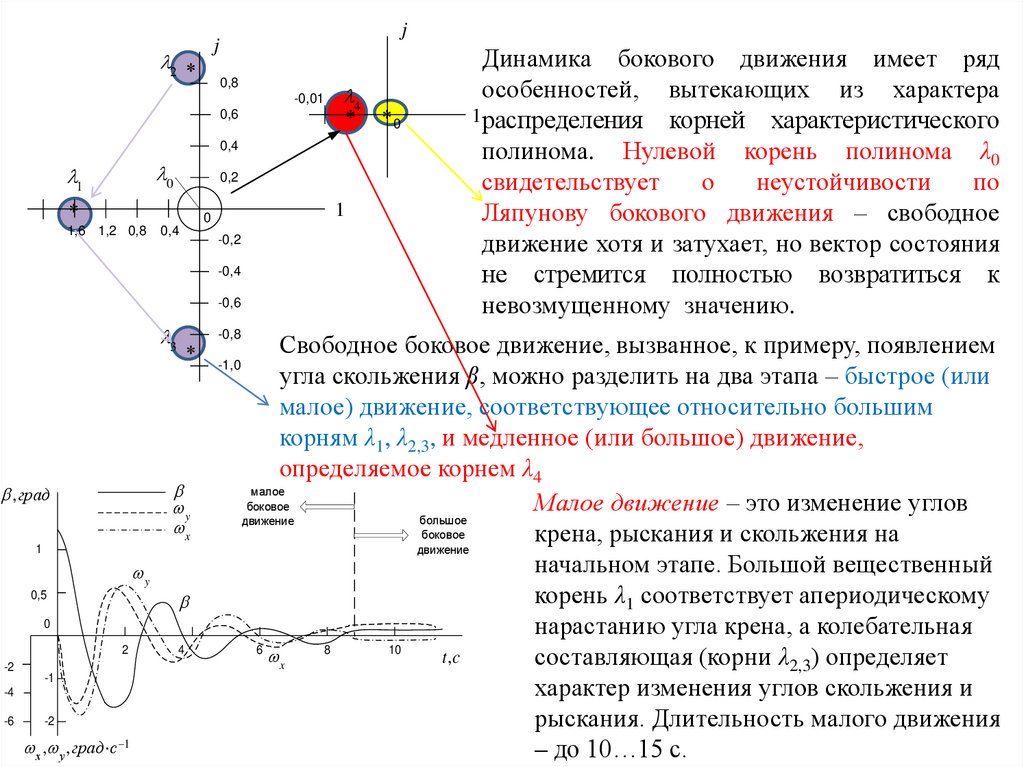
Динамика бокового движения имеет ряд
особенностей, вытекающих из характера
1 распределения корней характеристического
полинома. Нулевой корень полинома λ0
свидетельствует
о
неустойчивости
по
Ляпунову бокового движения – свободное
движение хотя и затухает, но вектор состояния
не стремится полностью возвратиться к
невозмущенному значению.
Свободное боковое движение, вызванное, к примеру, появлением
угла скольжения β, можно разделить на два этапа – быстрое (или
малое) движение, соответствующее относительно большим
корням λ1, λ2,3, и медленное (или большое) движение,
определяемое корнем λ4
малое
боковое
Малое движение – это изменение углов
большое
движение
боковое
крена, рыскания и скольжения на
движение
начальном этапе. Большой вещественный
корень λ1 соответствует апериодическому
нарастанию угла крена, а колебательная
6
8
10
x
t, c
составляющая (корни λ2,3) определяет
характер изменения углов скольжения и
рыскания. Длительность малого движения
– до 10…15 с.

18.

К концу малого движения накапливается некоторый угол крена и
сохраняется относительно малое значение угла скольжения. Траектория
движения под действием боковой силы Z(β) и проекции подъемной силы
Y(γ) продолжает искривляться. Дальнейшее движение (большое движение)
зависит от малого вещественного корня λ4. Если он находится в левой
полуплоскости, то остаточные значения β и γ апериодически исчезают и
траектория движения становится прямолинейной. Длительность затухания
движения составляет десятки секунд. При положительном корне λ4
движение будет апериодически расходящимся, углы крена и скольжения
будут медленно и апериодически нарастать, а центр масс самолета будет
двигаться по спирали.

19.

2. Передаточные функции и структурные
схемы бокового движения

20.

Математическую модель бокового движения можно представить в форме
структурной схемы, если провести простые преобразования системы уравнений
бокового движения. Для этого уравнения угловых боковых движений запишем в
несколько ином виде:
x
y
amx amx amx
amxэ э аmxн н
amуу amух amу
amун н аmуэ э
Применяя к последним уравнениям преобразование Лапласа при нулевых
начальных условиях:
T p 1 T a a a э а
T p 1 T a a a а
y
э
н
mx
mx
mx
mx
н
T
х
mу
mу
н
mу
э
mу
э
T
н
1
amxx
1
y
amy
Если полученную систему уравнений, описывающую (в новой форме) динамику
угловых движений, дополнить уравнением движения центра масс и кинематическим
уравнением связи углов:
a z a z 0 в U z U z
в
W0
V0
Получим новую форму системы уравнений бокового движения, на основе которой
можно построить структурную схему бокового движения, объединяющую движения
крена и рыскания.

21.

az az 0 ( р)
1
az ( р) az ( р)
р
T p 1 T amxy amx amx э э аmx н н
х
T
amx y у amx amx э э аmx н н
T p 1
T p 1 T a a a а
х
mу
mу
н
mу
н
э
mу
э
T
у
amу х х amу amу н н аmу э э
T p 1
в

22.

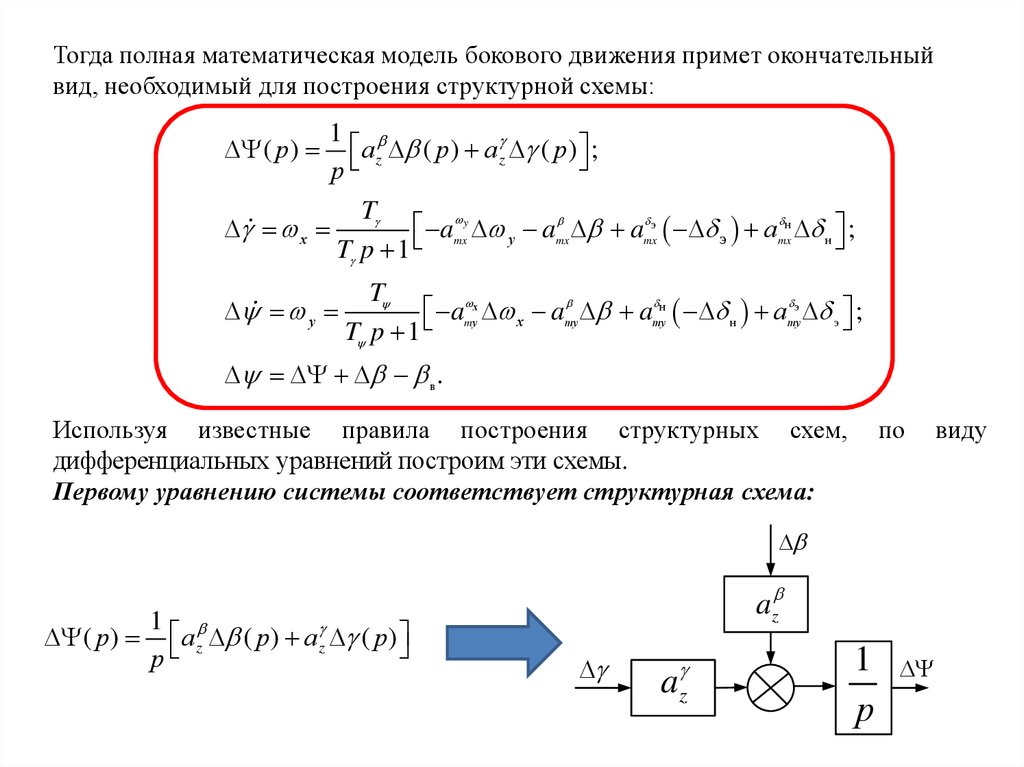
Тогда полная математическая модель бокового движения примет окончательный
вид, необходимый для построения структурной схемы:
1
az ( р) az ( р) ;
р
T
amx y у amx amx э э аmx н н ;
х
T p 1
( р)
у
T
amу х х amу amу н н аmу э э ;
T p 1
в .
Используя известные правила построения структурных схем,
дифференциальных уравнений построим эти схемы.
Первому уравнению системы соответствует структурная схема:
по
( р)
1
az ( р) az ( р)
р
az
az
1
р
виду

23.

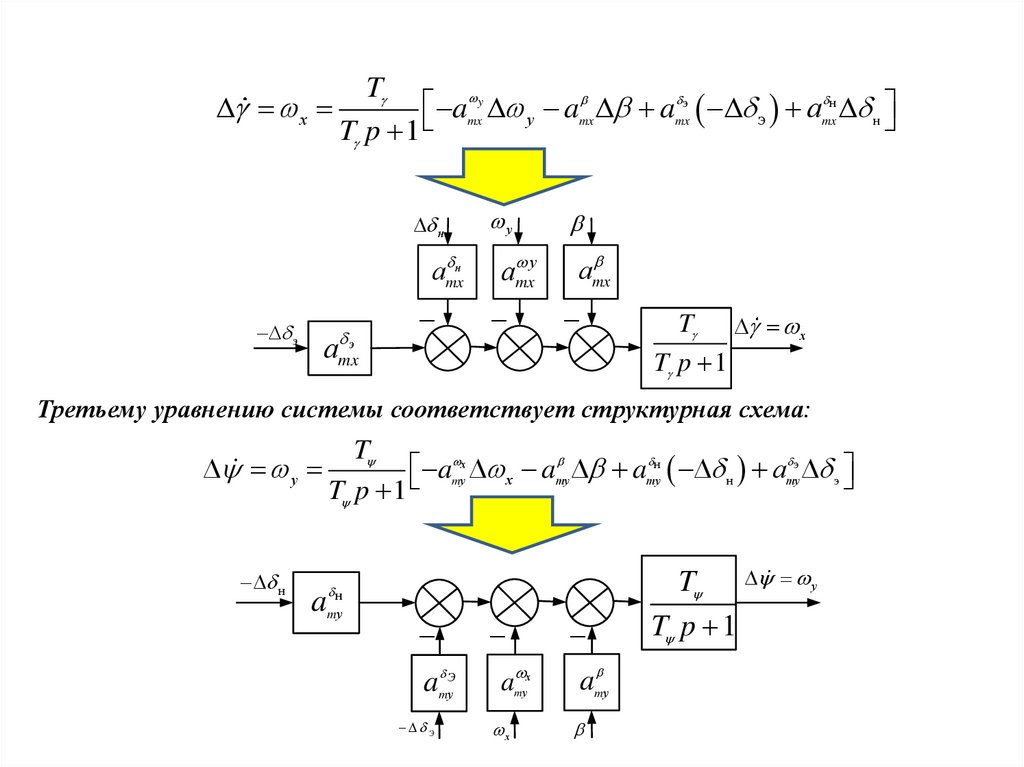
Второму уравнению системы соответствует структурная схема:
х
T
amx y у amx amx э э аmx н н
T p 1
н
н
аmx
э
э
аmx
у
у
аmx
аmx
T х
T p 1
Третьему уравнению системы соответствует структурная схема:
у
н
T
amу х х amу amу н н аmу э э
T p 1
н
amу
amу Э
amу х
amу
х
Э
T у
T p 1

24.

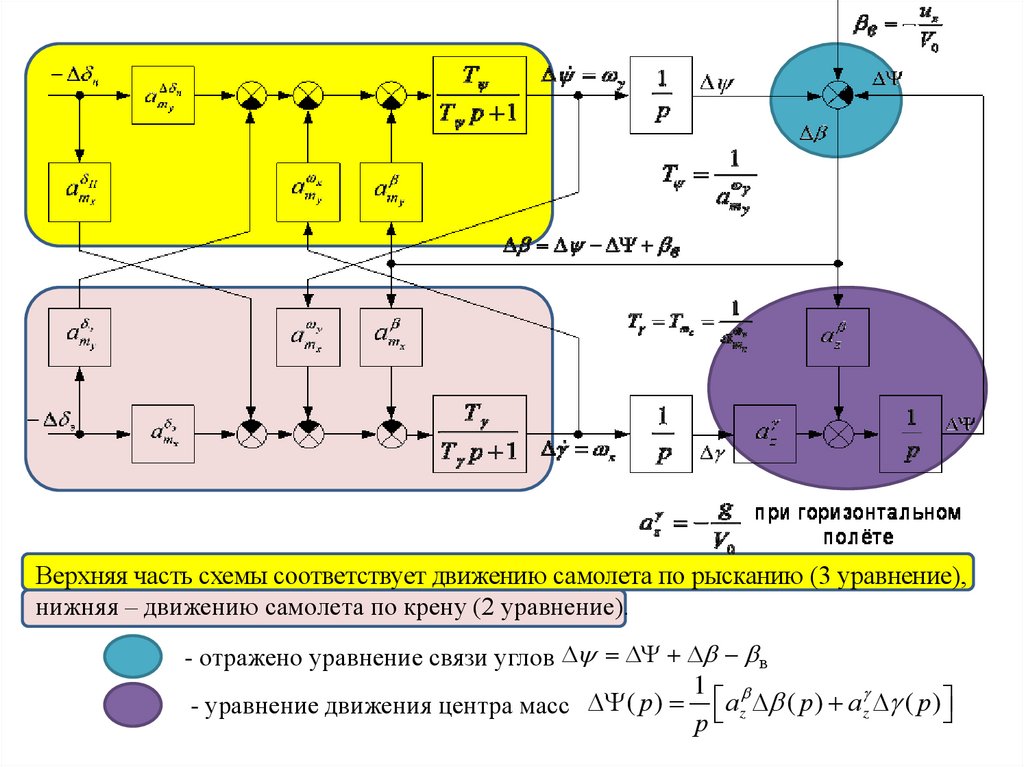
Верхняя часть схемы соответствует движению самолета по рысканию (3 уравнение),
нижняя – движению самолета по крену (2 уравнение).
- отражено уравнение связи углов в
1
az ( р) az ( р)
(
р
)
- уравнение движения центра масс
р

25.

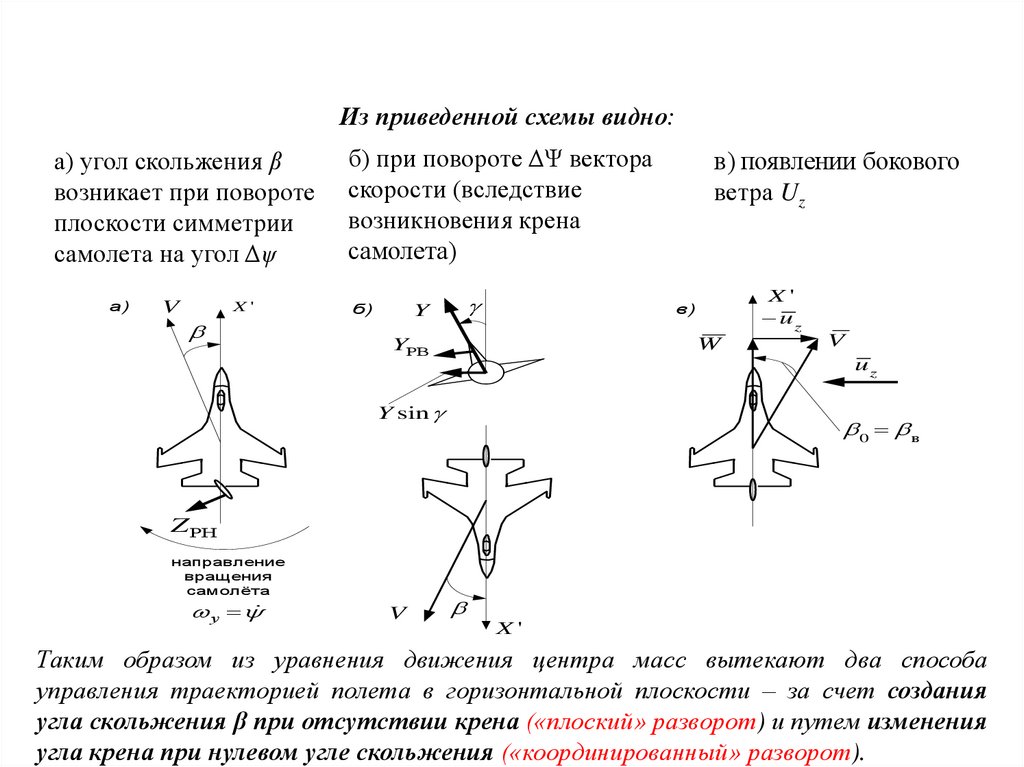
Целесообразность и условия разделения бокового движения на
изолированные
Из приведенной схемы видно:
а) угол скольжения β
возникает при повороте
плоскости симметрии
самолета на угол Δψ
а)
V
X'
б) при повороте ΔΨ вектора
скорости (вследствие
возникновения крена
самолета)
б)
Y
в) появлении бокового
ветра Uz
X'
uz
в)
W
YРВ
V
uz
Y sin
0 в
Z РН
направление
вращения
самолёта
у
V
X'
Таким образом из уравнения движения центра масс вытекают два способа
управления траекторией полета в горизонтальной плоскости – за счет создания
угла скольжения β при отсутствии крена («плоский» разворот) и путем изменения
угла крена при нулевом угле скольжения («координированный» разворот).