Динамика бокового возмущенного движения

1.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Приближенный анализ быстрого бокового движения
Б2
a1
0 и
a3
hб 0
y
всегда, когда M y 0

2.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Приближенный анализ быстрого бокового движения
(17.20)
2

3.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Приближенный анализ быстрого бокового движения
движение носит колебательный характер.
3

4.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Приближенный анализ быстрого бокового движения
АААААА
4

5.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Изолированное движение рыскания
В первом уравнении системы (17.20), слайд 34, отсутсвует x :
*
Cz qS
Cz н qS
н ,
y
mV0
mV0
M M у M н .
y
y
у
y
н
y
Структура уравнений такая же, как и в продольном
короткопериодическом движении. В частности, угол скольжения
соответствует углу атаки, угловая скорость рыскания соответствует угловой
скорости тангажа, а руль направления соответствует рулю высоты. Как и в
случае
продольного
коротко-периодического
движения
силой,
возникающей при отклонении органа управления пренебрегаем, т.е.
считаем (dCz/dδн)→0 и получаем:
C
qS
y z
.
mV0
(1)
Продифференцировав это выражение по времени, получаем
z
y
(2)
0
C qS
.
mV
5

6.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Изолированное движение рыскания
Подставляем во второе уравнение системы (*) выражение для производной
угловой скорости рыскания (2) и, учитывая (1), получаем:
Cz qS
C
y
z qS
My My
M y н н
mV0
mV0
Cz qS
C
y
н
y
z qS
M y
M
M
M
y
y
y н
mV0
mV0
Очевидно, что уравнение является уравнением колебательного звена:
x 2 б x x u
2
б
y
б M y M y
cz qS
,
mV0
С
y
z qS
б
( M y
)
2 0
mV0
1
6

7.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
В первом приближении, пренебрегая
б
my SL
2 I yy
My y
( H ) V0 .
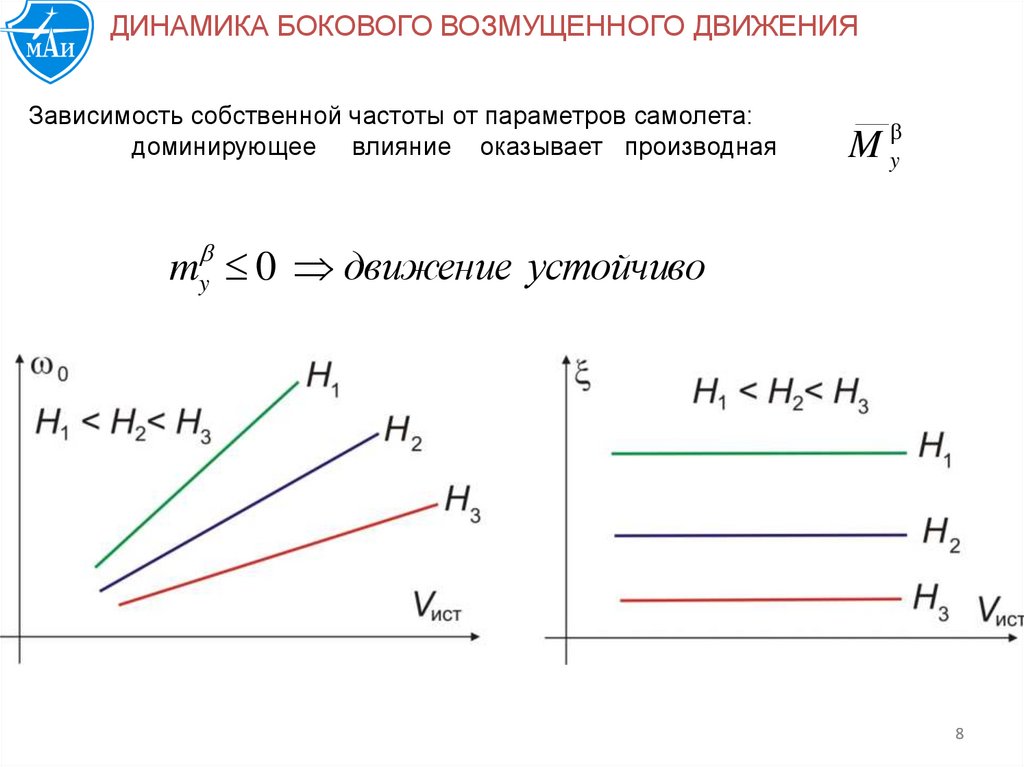
Собственная частота прямо пропорциональна квадратному корню из плотности воздуха и
прямо пропорциональна скорости полета, качественно зависимость параметров от
высоты и скорости полета такая же, как для продольного короткопериодического
движения. Демпфирование (декремент затухания) прямо пропорциональна квадратному
корню из плотности воздуха
2
C
V0
1 V0 Sl 2
y
z I yy
б
( my
)~
~ ( H ),
2
4 0 I yy
mL
V0
демпфирование не зависит от скорости и сильно падает с высотой
7

8.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Зависимость собственной частоты от параметров самолета:
доминирующее влияние оказывает производная
M y
m y 0 движение устойчиво
8

9.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
m y 0 движение устойчиво ?
Всегда ли это справедливо ?
только при 0.
А
Боковая утойчивость обратная связь на .
Но устранения скольжения можно добиться :
и при вращении отн но оси OY ,
и при вращении отн но оси OХ !!
9

10.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Угловые скорости крена и рыскания, а также угол крена связаны с wx, wy
и γ следующим образом
y cos 0 x sin 0 , x cos 0 y sin 0 , a cos 0
Проводя преобразования системы уравнений
g
Z ( т ) x sin 0 y cos 0 cos 0 Z
V
x M x ( т ) M x x M x y M x
x
y
y
y M y ( т ) M y x M y y M y
x
x y tg 0
получим для случая исходного
горизонтального полета при т=0
следующую систему уравнений:
g
Z a Z ,
V
M M M ,
M M M ,
a ,
10

11.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
g
Z
a Z ,
V
(15.6)
M M M ,
M M M ,
a ,
В системе
M y cos 0 M x sin 0 , M x cos 0 M y sin 0 ,
M M y cos 0 M x sin 0 , M M x cos 0 M y sin 0 ,
M , M , M , M - демпфирующие моменты в
полусвязанной системе координат .
x
M M y y cos2 0 ( M y x M x y ) sin 0 cos 0 M x x sin 2 0 ,
x
y
y
M M y cos 0 ( M x M y ) sin 0 cos 0 M x sin 2 0 ,
2
M M x y cos2 0 ( M x x M y y ) sin 0 cos 0 M y x sin 2 0 ,
M M x x cos2 0 ( M x y M y x ) sin 0 cos 0 M y y sin 2 0.
11

12.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Выполняя преобразование Лапласа уравнений
g
Z
a Z ,
V
M M M ,
M M M ,
a ,
при нулевых начальных условиях, получим:
p
Z
0
1
0
p M
M
0
M
p M
1
g
( p) Z н
0
V
( p) M н M э ( p)
н
0
.
э
н
( p ) M M э ( p )
0
( p) 0
0
p
12

13.

13

14.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Физическая
сущность
В системе
M y cos 0 M x sin 0 ,
g
Z
1
Э
Н
(
Z
Z
Э ),
y
Н
V0
mV0
mV0
M M x M y M Н M Э ,
y
y
y
y
y
x
y
Н
Э
y
x
y
Н
Э
x M x M x x M x y M x Н M x Э
tg ( cos sin ) ,
x
y
z
x
ф
14

15.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Но это и значит
M y cos 0 M x sin 0 0
15

16.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Физическая сущность
Рассмотрим систему уравнений в полусвязанной СК. С учетом демпфирования.
Если демпфирование колебаний невелико, приближенно выполняется
соотношение:
k
Тогда, пренебрегая влиянием гравитационных сил, получим из первого и второго
уравнений системы в ПСвСК приближенное уравнение для движения самолета
по углу скольжения:
M k M 0.
Отсюда следует, что для колебательной устойчивости колебательного бокового
движения необходимо выполнение (условия Гурвица) неравенств:
M
k M 0
0
16

17.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Физическая сущность
Jy
qSl
qSl
mx sin 0
0.
my cos 0
Jy
Jx
Jy
Т.к.
M k M
0,
частота колебательного движения по углу скольжения
определяется величиной
Она зависит от соотношения моментов инерции Jx и Jy и
запасов путевой и поперечной статической устойчивости.
- коэффициент динамической устойчивости самолета по рысканию
17

18.

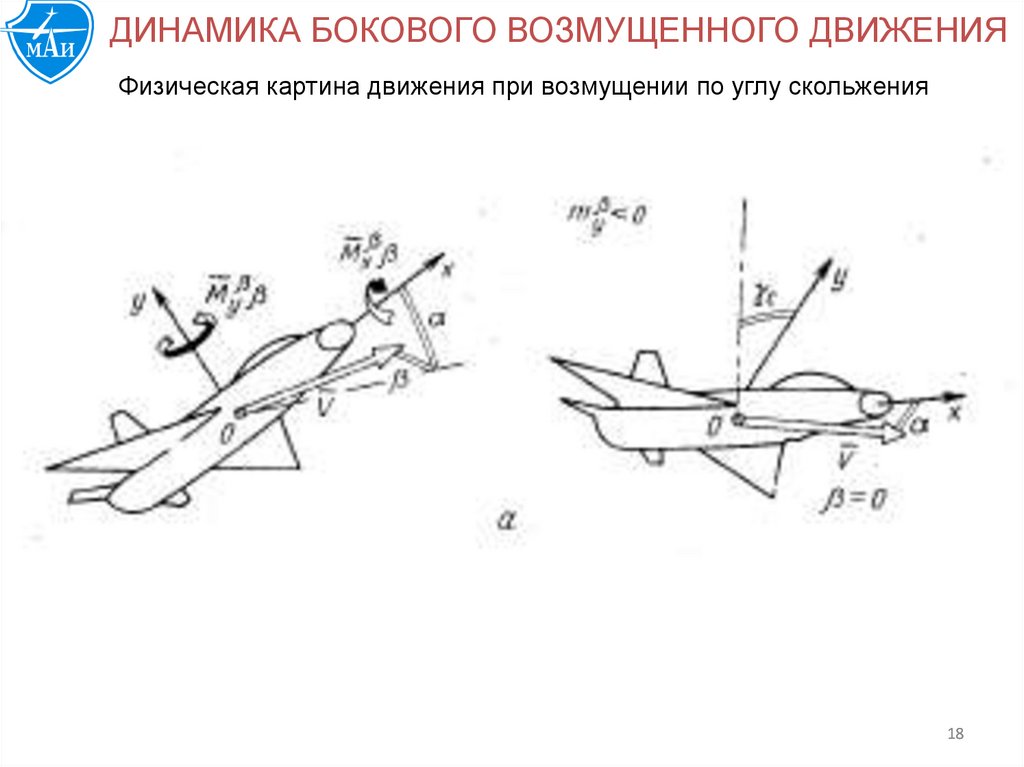
ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Физическая картина движения при возмущении по углу скольжения
18

19.

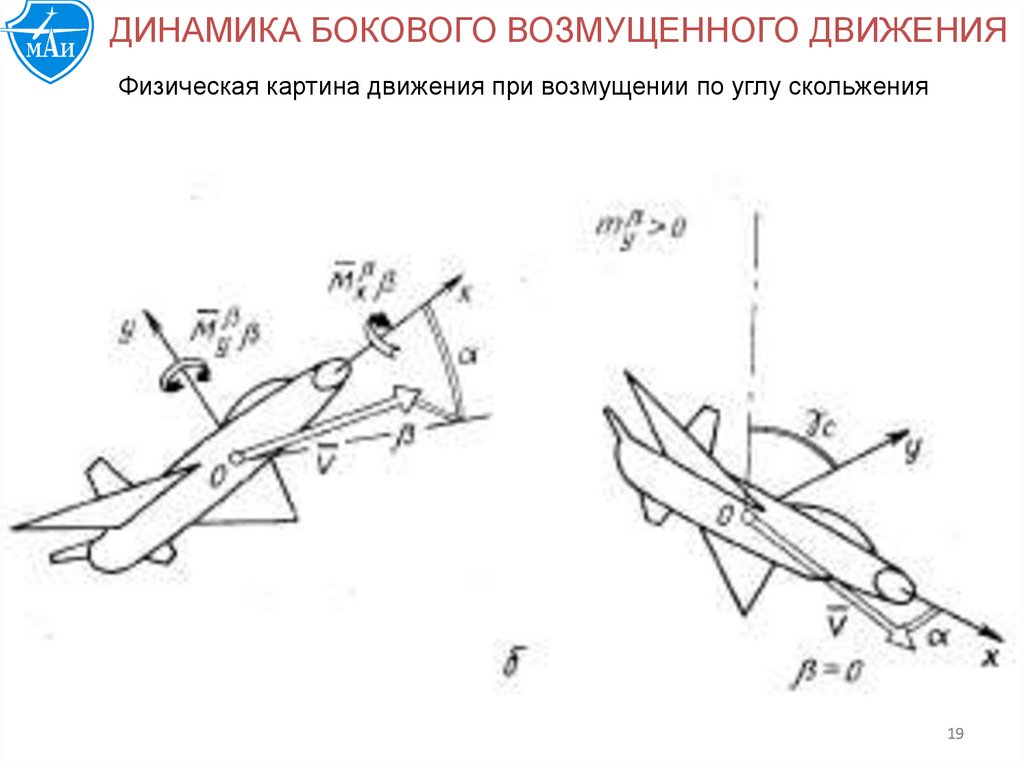
ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Физическая картина движения при возмущении по углу скольжения
19

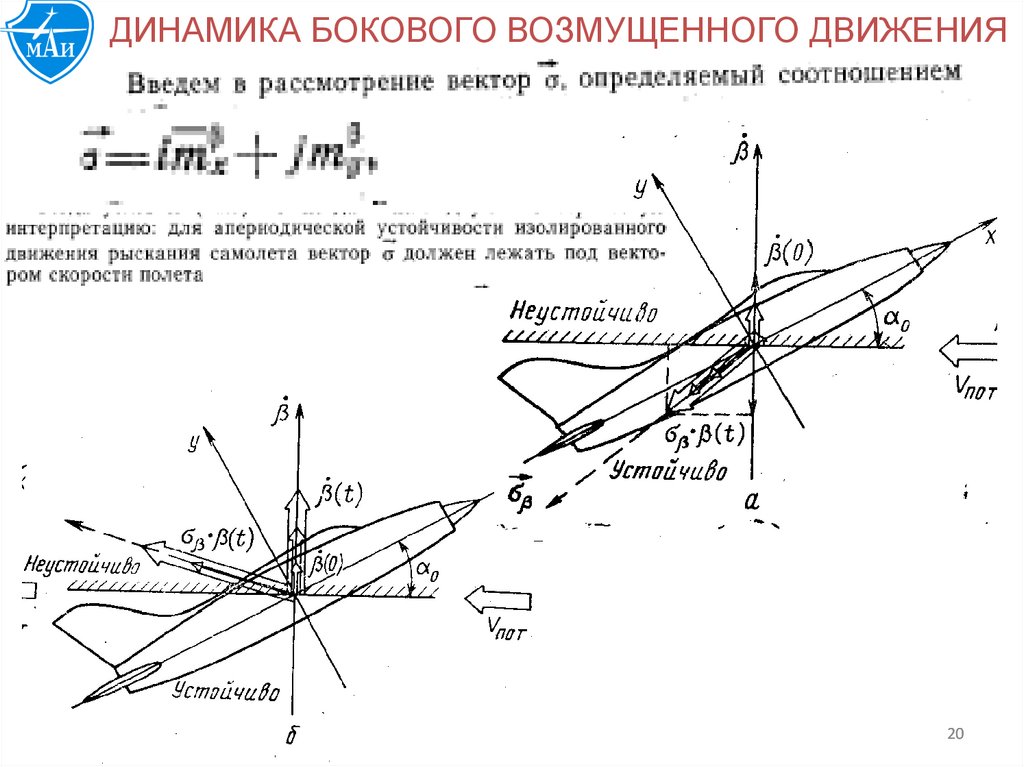
20.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
ф
20

21.

ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
21

22.

ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
Изо всех
22

23.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
23

24.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
24

25.

ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
25

26.

ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
26

27.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
27

28.

ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
28

29.

ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
29

30.

ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
30

31.

ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
31

32.

ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
1
32

33.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
33

34.

ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
34

35.

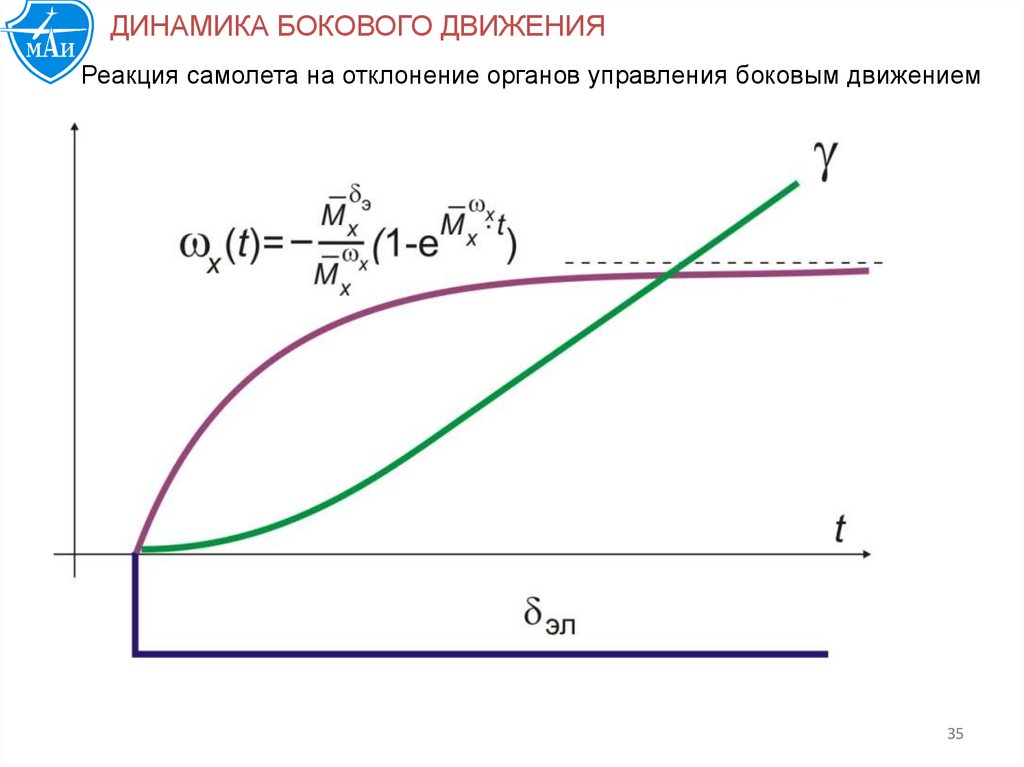
ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
35

36.

ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
Определим как меняется постоянная времени крена и установившееся
значение угловой скорости от высоты и скорости полета.
2
m
q
S
L
m
q
S
L
1 / Tкр кр M x x
x
~ V0 .
I xx
2V0 I xx
x
x
x
36

37.

ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
Для горизонтального полета
mg C yа гп q S
скоростной напор оптимального режима горизонтального полета:
qS mg / C ya Кmax
2 I xx
Tкр x
C ya Kmax V0
2
mx mg L
При H V Tкр
37

38.

ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
38

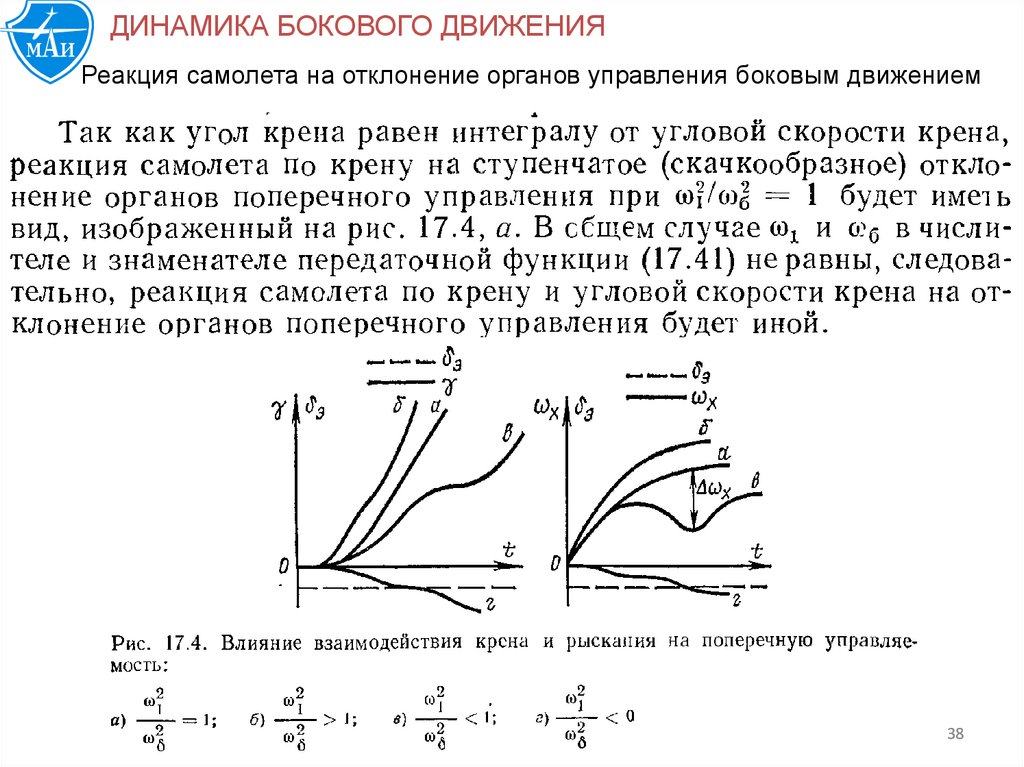
39.

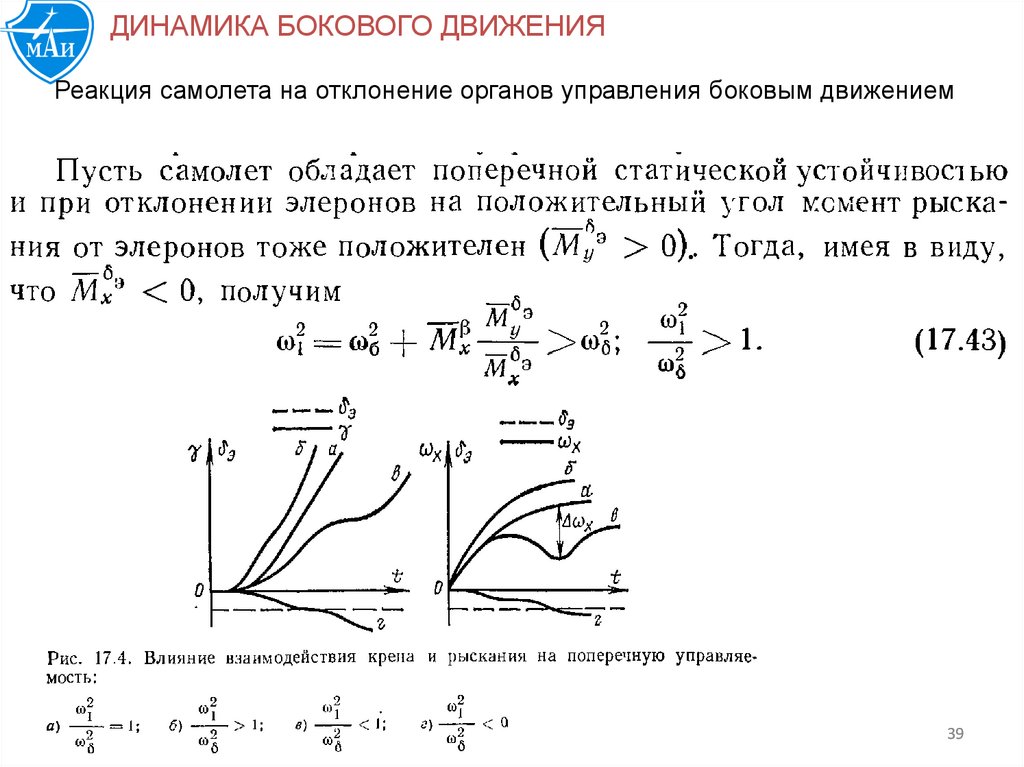
ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
39

40.

ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
40

41.

ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
41

42.

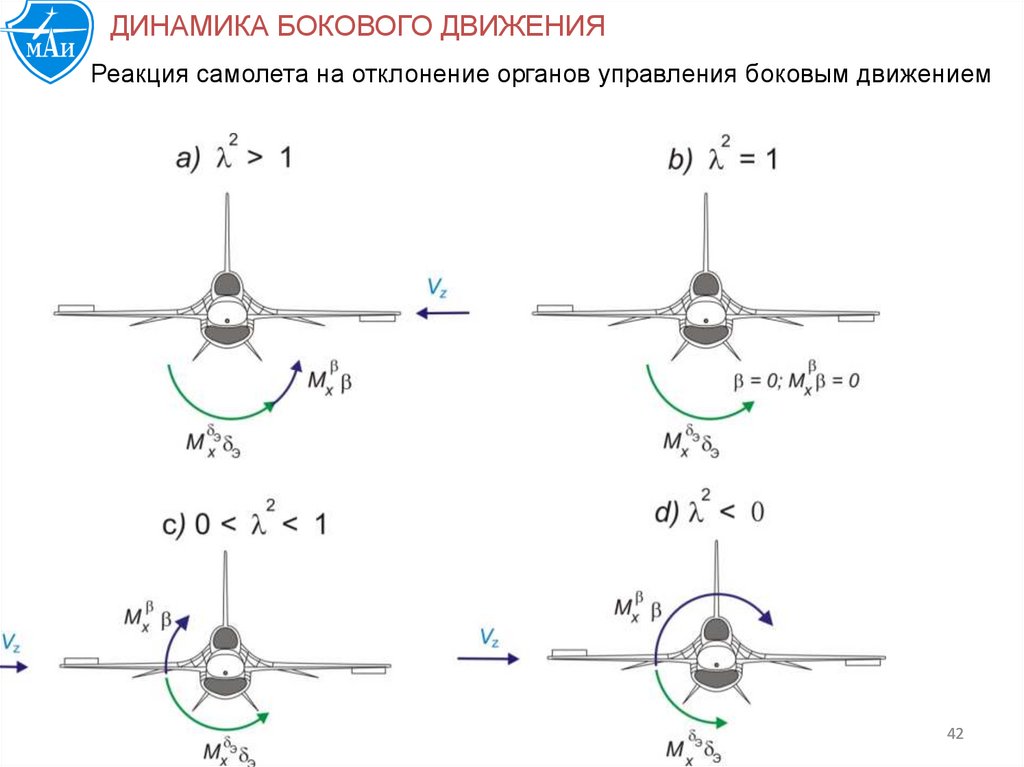
ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
42

43.

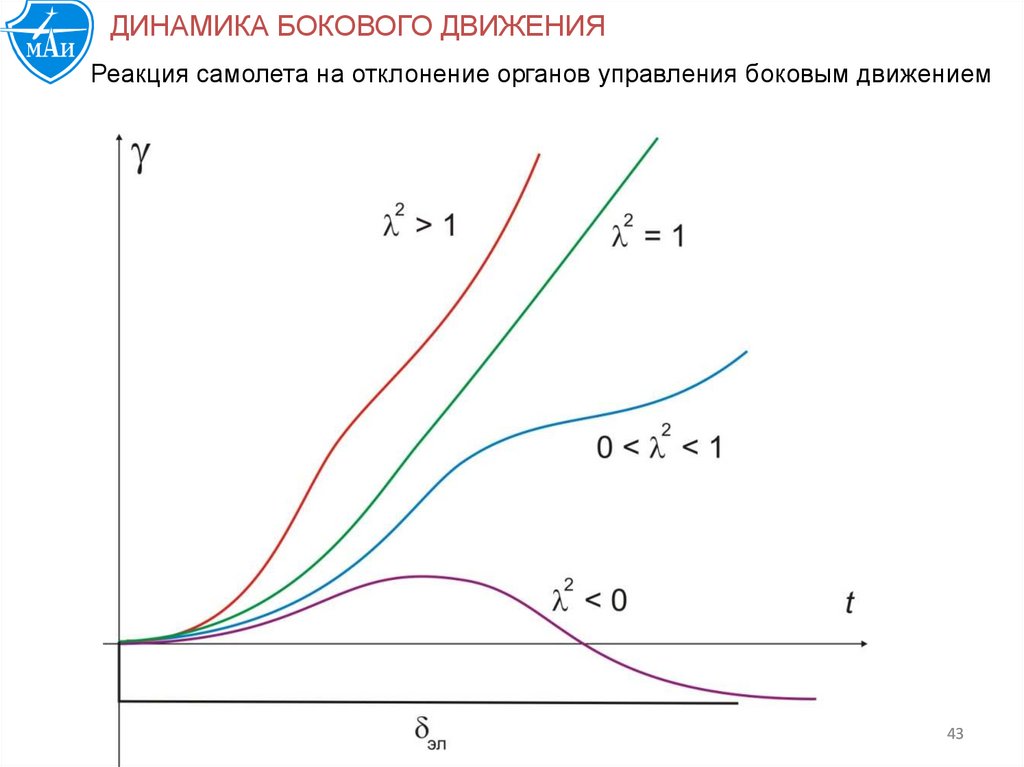
ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
43

44.

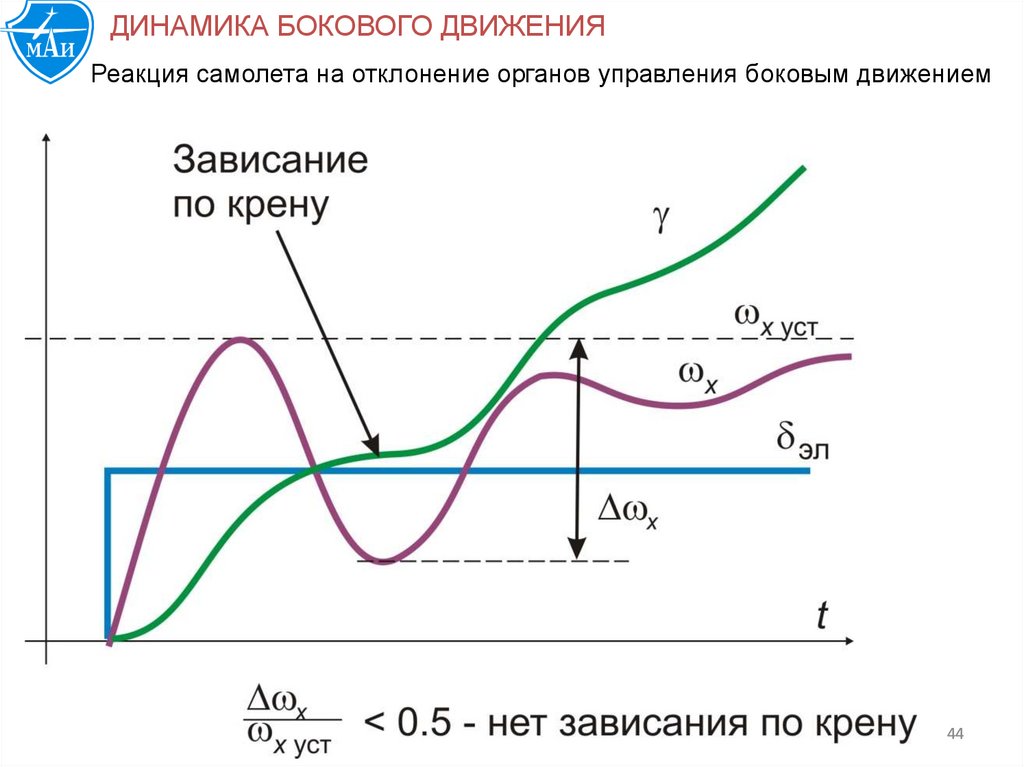
ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
44

45.

ДИНАМИКА БОКОВОГО ДВИЖЕНИЯ
Реакция самолета на отклонение органов управления боковым движением
45

46.

ДИНАМИКА БОКОВОГО ВОЗМУЩЕННОГО ДВИЖЕНИЯ
46