Похожие презентации:
Уравнения бокового движения самолета (лекция № 8)
1. РАЗДЕЛ 1. ВОЗДУШНОЕ СУДНО КАК ОБЪЕКТ УПРАВЛЕНИЯ.
Тема 2 Математические модели продольного ибокового движения самолета
ЛЕКЦИЯ № 8. УРАВНЕНИЯ БОКОВОГО ДВИЖЕНИЯ
САМОЛЕТА
Учебные вопросы:
1 Математические модели изолированного бокового движения
самолета.
2 Линеаризация уравнений бокового движения
Задание на самостоятельную работу:
[1] Вавилов Ю.А., Системы автоматического управления летательных аппаратов. ВВИА им.
проф. Н.Е. Жуковского, 2009. с.65…70.
[2] Мигунов А.И., Иванов Р.В., Серов А.Н. Системы автоматического управления полетом.
Электронный учебник. ВУНЦ ВВС «ВВА», 2016. Л-8, тематический план, учебная программа
[3] Красовский А.А., Вавилов Ю.А., Сучков А.И. Системы автоматического управления
летательных аппаратов. ВВИА
им. проф. Н.Е. Жуковского, 1986. с. 32…38.
[7] Кичигин Е.К., Демчук В.А., Лущик А. В., Агеев А.М. Системы автоматического управления
полетом. Ч. 1: Учебное пособие. -Воронеж: ВАИУ, 2011. с. 23…25.
2.
Вопрос №1 Математические моделиизолированного бокового движения
самолета
3.
mW FxkmW Fyк
mW cos Fzк
J z z J x J y x y M z
J y y J z J x z x M y
J x x J y J z y z M x
z cos cos sin
y cos cos sin
x sin
xg W cos cos
y g W sin
z g W cos sin
.
Уловия
изолированного
бокового движения
mW cos Fzк
J x x M x
J y y M y
Fхк 0
x sin
Fук 0
y cos cos sin
М zк 0 z 0
z g V0 cos sin Ψ
в
(1)
4.
Вопрос №2Линеаризация уравнений
бокового движения
5.
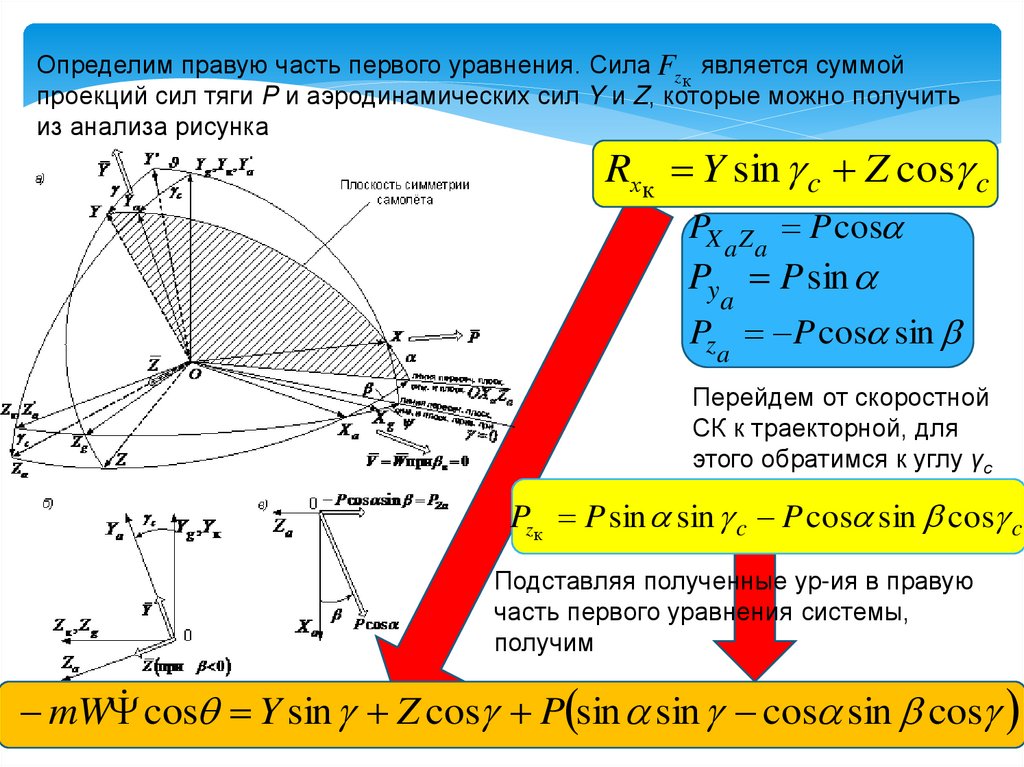
Определим правую часть первого уравнения. Сила Fz является суммойк
проекций сил тяги P и аэродинамических сил Y и Z, которые можно получить
из анализа рисунка
Rхк Y sin c Z cos c
PX Z P cos
a a
Py P sin
a
Pz P cos sin
a
Перейдем от скоростной
СК к траекторной, для
этого обратимся к углу γс
Pzк P sin sin c P cos sin cos c
Подставляя полученные ур-ия в правую
часть первого уравнения системы,
получим
cos Y sin Z cos P sin sin cos sin cos
mW
6.
Условия линеаризации уравнений бокового движения:прямолинейный горизонтальный полет в спокойной атмосфере без крена и
скольжения (ψ=0, γ0 = 0, β0 = 0, θ0 = 0 , Uz = 0).
Уравнение движения центра масс в приращениях имеет такой вид:
mV0 Y0 Z P sin 0 sin 0 cos 0 sin 0 cos 0
P0 (sin sin cos sin cos ).
P0 (sin 0 cos 0 cos 0 cos 0 cos 0
«0»
(2)
cos 0 sin 0 sin 0 ) P0 sin 0 P0 cos 0
Подставив в исходное уравнение получим:
Y0 P0 sin 0 P0 cos 0 Z 0
mV0
az
P0 cos 0 Z
mV0
P sin 0 Y0
a z 0
mV0
(3)
a z a z 0
7.
a z a z 0Размерность уравнения c-1, и оно описывает процесс изменения скорости
поворота траектории в плоскости горизонта при нарушении боковой
балансировки.
- первая составляющая создается в результате появления угла скольжения и
зависит от силы тяги и боковой аэродинамической силы,
- вторая – в результате появления крена самолета и возникновения боковой
силы, обусловленной действием подъемной силы и силы тяги.
При линеаризации уравнений моментов системы уравнений
основные факторы, определяющие Mx и My .
M x M x V , H , , x , y , э , н
M y M y V , H , , x , y , э , н
Приращения Мi имеют вид:
(4)
x
y
э
н
x
y
э
н
M x M x M x x M x y M x э M x н
M y M y M y x M y y M y э M y н
(5)
8.
Осуществим линеаризацию кинематических уравненийх sin 0 0 cos 0
y 0 cos 0 0 cos 0 sin 0 sin 0 0 cos 0
z Т W cos 0 sin 0 W0 sin 0 sin 0 W0 cos 0 cos 0
(6)
в
Если учесть малость угла 0 и отсутствие в невозмущенном движении Ψ0,
γ0, θ0, ψ0, 0 и ветра ΔW = ΔV и W0 = V0, то
x ; y ; z V0 Ψ ;
Ψ в ; в
Uz
V0
(7)
J x M x M x x M x y M x э э М х н н
x
э
н
y
J у M у M у M у M у э М х н
9.
Разделим правую и левую части на соответствующие моменты инерции:M x
M x x
Mx y
M x э
М х н
э
н
Jx
Jx
Jx
Jx
Jx
amxx
amxy
amxэ
M у
M у x
Mуy
M у э
Jу
amу
amx
Jу
Jу
х
amуу
amу
amxн
(8)
М х н
э
н
Jу
Jу
amун
amуэ
amxэ , amун - коэффициенты, характеризующие эффективность отклонения
рулевых органов самолета
2
Оба уравнения имеют размерность c и описывают процессы развития
угловых ускорений по крену и рысканию при нарушении боковой
балансировки.
10.
Система линеаризованных уравненийизолированного бокового движения
а a 0;
z
z
amx amx amx amx э аmx н ;
x
y
у
э
н
amу amух amу
amун н аmуэ э ;
Ψ в ;
z V0 Ψ .
(9)









 Физика
Физика








