Похожие презентации:
Минимальные дизъюнктивные нормальные формы
1. 5. Минимальные дизъюнктивные нормальные формы
Минимизация ДНФ.2. Определение
ДНФ называется минимальной, если онасодержит по сравнению с другими
эквивалентными ей формами
минимальное количество букв (при
подсчете учитывается каждое вхождение
буквы в формулу).
01.11.2022
2
3. Сокращенная ДНФ
kСокращенная ДНФ
Сокращенной ДНФ данной булевой функции
называется ее ДНФ, составленная только из простых
импликант.
Элементарная конъюнкция k называется
импликантой булевой функции f, если не
существует такого двоичного набора переменных,
k принимает значение 1,
при котором функция
а функция f – значение 0, то есть k f f .
Элементарная конъюнкция, входящая в ДНФ
булевой функции, называется ее простой
импликантой, если никакая ее часть не является
импликантой этой функции.
4. Проверка импликанты
Для того чтобы проверить является ли заданнаяэлементарная конъюнкция импликантой функции f,
следует всем переменным, которые входят в эту
конъюнкцию без знака отрицания, придать
значение 1, а тем переменным, которые входят с
отрицанием – значение 0. Тогда элементарная
конъюнкция будет иметь истинностное значение 1.
После этого следует, проверить, принимает ли
функция f значение 1 при любых значениях
остальных переменных.
5. Пример
f x y z x yz x yz x yz xyzk xz
x 1, z 1
f 0 0 y y 1
k yz
y 1 y 0, z 1
f 0 x 0 x 0 1
6. Метод Квайна
Записать СДНФ.
Произвести все возможные полные и неполные
склеивания и поглощения. Получим
сокращенную ДНФ.
Строится матрица Квайна: строки матрицы –
простые импликанты сокращенной ДНФ,
столбцы – конъюнкты СДНФ. На пересечении
соответствующей строки и столбца ставится
метка (*), если простая импликанта входит в
соответствующий конъюнкт.
Их простых импликант составить МДНФ по
следующему правилу.
7. Метод Квайна
1. Найти ядро - импликанты, для каждой изкоторых имеется хотя бы один столбец,
перекрываемый только данной
импликантой.
2. Выбрать из импликант, не входящих в
ядро, такое минимальное их число с
минимальным количеством букв в
каждой из этих импликант, которое
обеспечит перекрытие всех столбцов, не
перекрытых членами ядра.
8. Пример
Найти МДНФ для функции , заданнойвектором значений (11001011).
Решение.
1. Строим таблицу истинности
и записываем СДНФ.
2. Произведем в ней все
Возможные склейки и
поглощения.
9.
x y z x yz x yz x yz xyzx y xz yz yz xz x y z
3. Строим матрицу Квайна
4. Находим ядро.
xy z
Ядро содержит * во всех столбцах,
значит является МДНФ.
10. Геометрический метод
Любой грани, ребру или вершине можнопоставить в соответствие простую импликанту
по правилу – в нее войдут переменные,
значение которых сохраняется на данном
подмножестве куба, причем, если
переменная равна 1, то она входит без
отрицания, если 0, то с отрицанием.
11. Геометрический метод
12. Геометрический метод
1. Задать булеву функцию единичным n-мернымкубом.
2. Составить все интервалы куба: грани, ребра,
вершины покрытые * (записывать именно в такой
последовательности).
3. Выписать тупиковые интервалы – интервалы,
содержащие вершины (вершину), входящие
только в данный интервал.
4. Записать из полученных тупиковых интервалов
ядро.
5. Если в ядро входят не все вершины, отмеченные
*, то добавляя к нему по одному, по два и т.д.
неядровые интервалы найти все МДНФ.
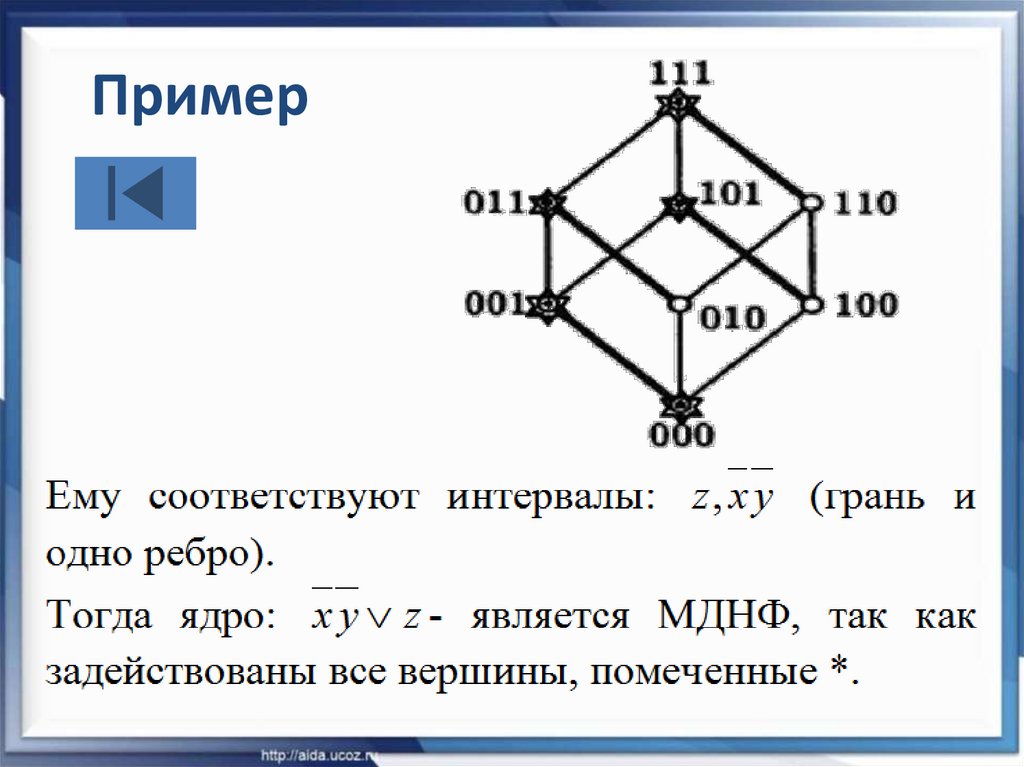
13. Пример
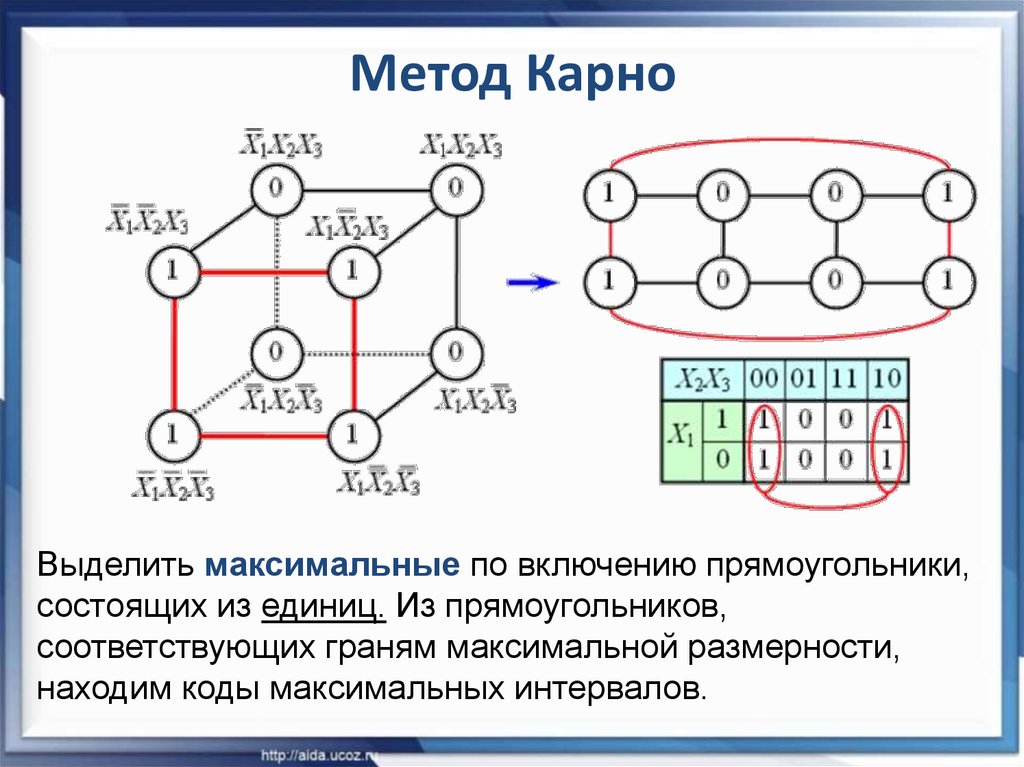
14. Метод Карно
Выделить максимальные по включению прямоугольники,состоящих из единиц. Из прямоугольников,
соответствующих граням максимальной размерности,
находим коды максимальных интервалов.
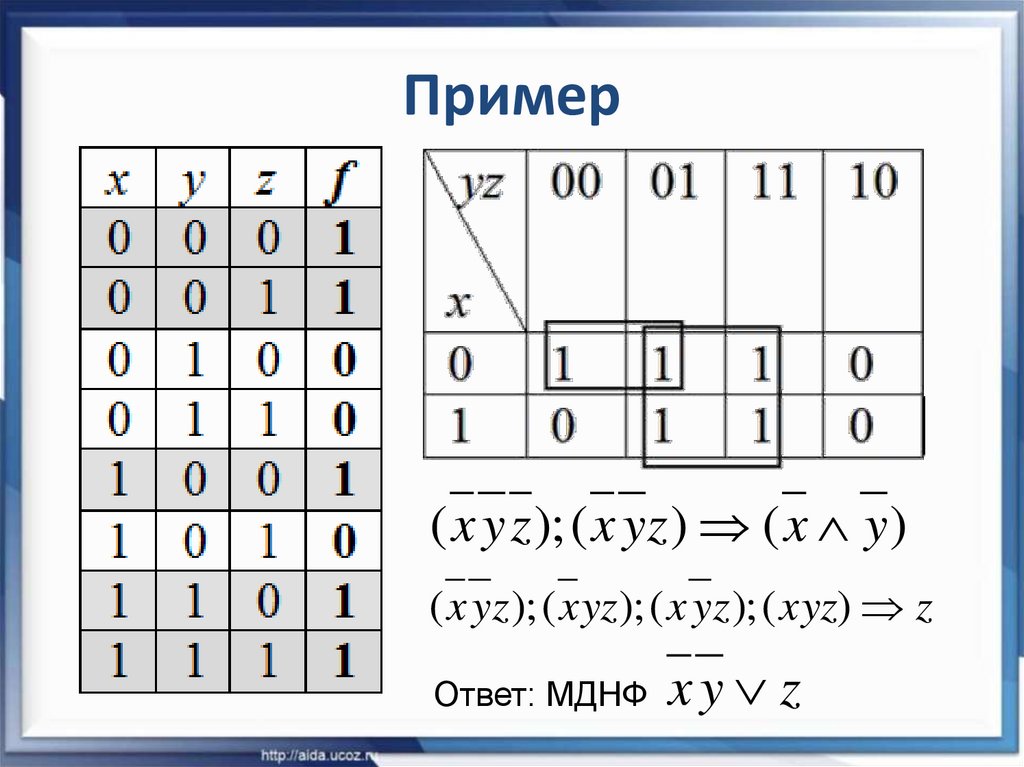
15. Пример
( x y z ); ( x yz ) ( x y )( x yz ); ( x yz ); ( x yz ); ( xyz) z
Ответ: МДНФ x y z
16. Решить самостоятельно
1. 110010112. 10001101
Ответы:
1.
x y xy y z , x y xy x z
2.
x yz













 Математика
Математика








