Похожие презентации:
Булева функция. Дизъюнктивные и конъюнктивные нормальные формы
1. 3. Булева функция. Дизъюнктивные и конъюнктивные нормальные формы.
Понятие булевой функции.Способы задания.
Дизъюнктивная нормальная
форма (ДНФ), конъюнктивная
нормальная форма (КНФ).
2. Булева функция
Функция f, зависящая от n переменныхназывается булевой (или
переключательной), если функция f и
любой из ее аргументов принимают
значения только из множества {0,1}.
Аргументы булевой функции также
называются булевыми.
3. Джордж Буль (1815 – 1864)
Английский математик и логик.Автор произведения «Математический анализ
логики» (1847).
Основной труд «Исследование законов
мышления», в которой представлен раздел
логики – алгебра высказываний.
1844 г – золотая королевская медаль за
работу по математическому анализу.
Логические исчисления, построенные в
соответствии с идеями Буля, находят сейчас
широкое применение в приложениях
математической логики к технике, в частности
к теории релейно-контактных схем.
Сегодня идеи Буля используются во всех
современных цифровых устройствах.
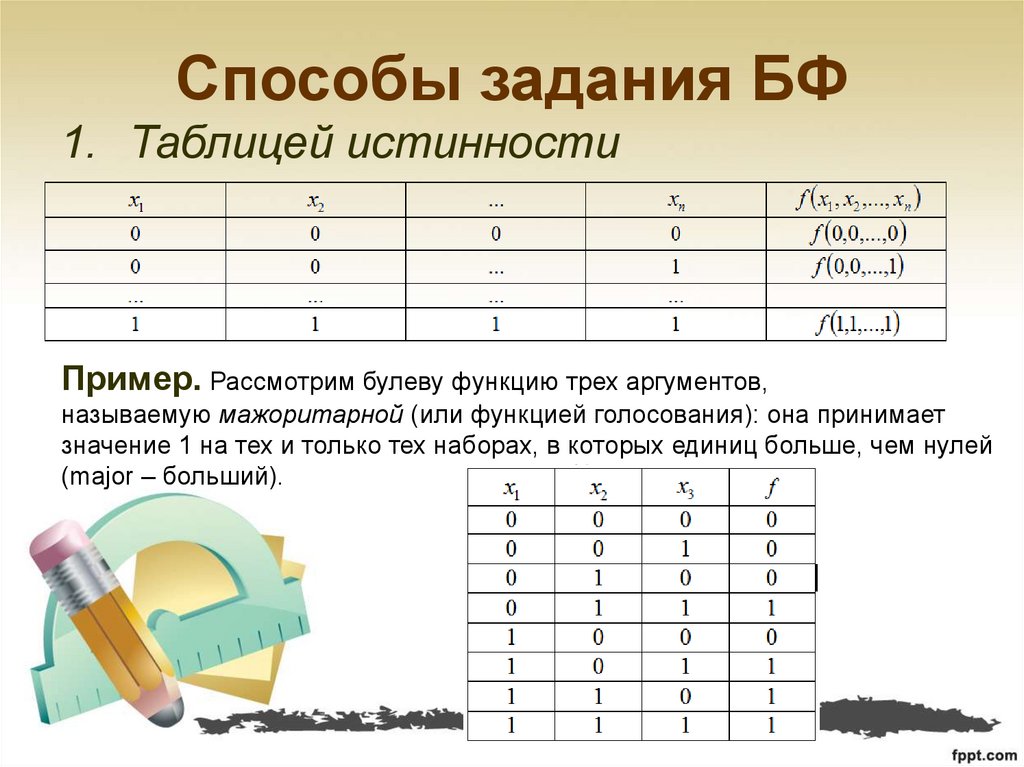
4. Способы задания БФ
1. Таблицей истинностиПример. Рассмотрим булеву функцию трех аргументов,
называемую мажоритарной (или функцией голосования): она принимает
значение 1 на тех и только тех наборах, в которых единиц больше, чем нулей
(major – больший).
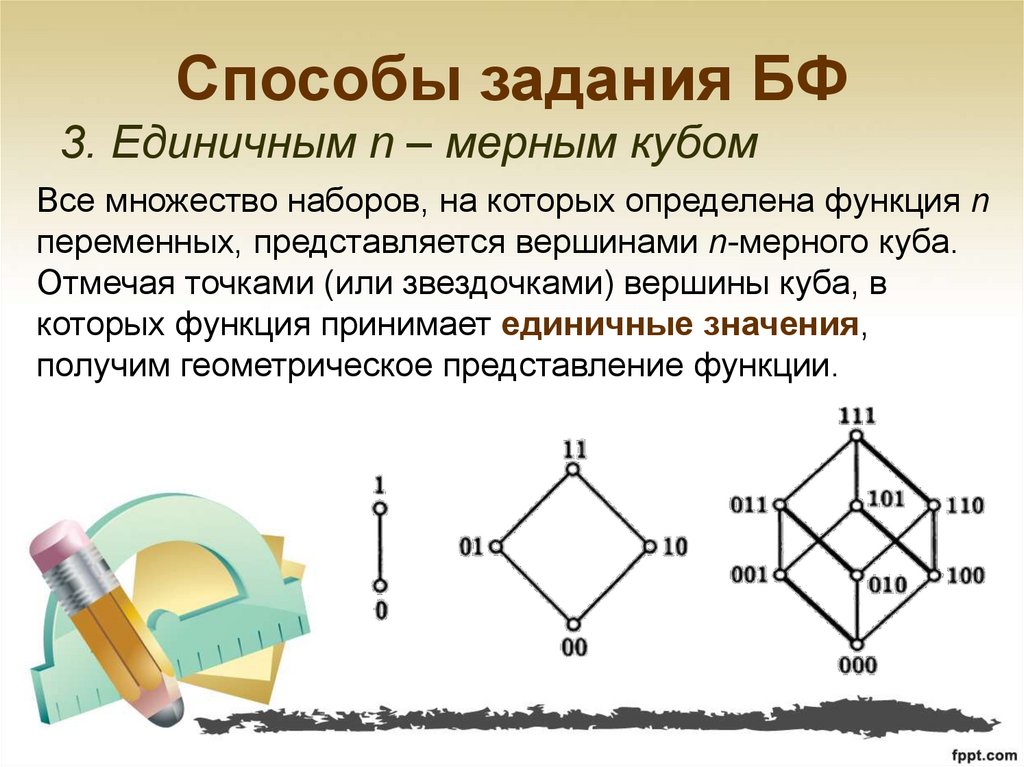
5. Способы задания БФ
2. Характеристическими множествами.6. Способы задания БФ
3. Единичным n – мерным кубомВсе множество наборов, на которых определена функция n
переменных, представляется вершинами n-мерного куба.
Отмечая точками (или звездочками) вершины куба, в
которых функция принимает единичные значения,
получим геометрическое представление функции.
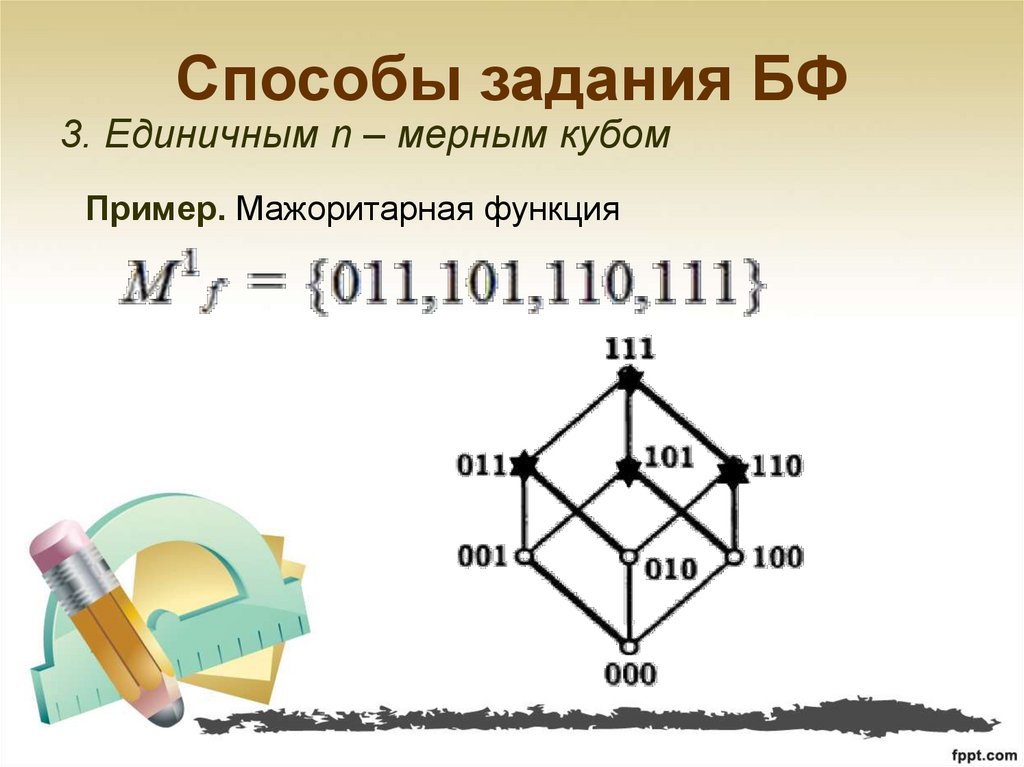
7. Способы задания БФ
3. Единичным n – мерным кубомПример. Мажоритарная функция
8. Способы задания БФ
3. Формулой алгебры логикиБулева функция может быть задана формулой
алгебры логики.
Если булева функция f и формула φ имеют одну и
ту же таблицу истинности, то говорят,
что формула φ представляет функцию f.
Такое представление не является
единственным.
9. Конъюнктивные и дизъюнктивные нормальные формы
Простой (элементарной) конъюнкцией иликонъюнктом называется конъюнкция некоторого
конечного набора переменных или их отрицаний,
причём каждая переменная встречается не более
одного раза.
Простой (элементарной) дизъюнкцией или
дизъюнктом называется дизъюнкция некоторого
конечного набора переменных или их отрицаний,
причём каждая переменная встречается не более
одного раза.
10. Примеры
11. Конъюнктивные и дизъюнктивные нормальные формы
• Конъюнктивной нормальной формой илиКНФ называется конъюнкция простых
дизъюнкций.
• Дизъюнктивной нормальной формой или
ДНФ называется дизъюнкция простых
конъюнкций.
12. Примеры
1.x y z2. x z x z x y
3. z x y
5. y x z
1. ДНФ
6.x y
6. ДНФ и
КНФ
7.x yz
7. ДНФ и
КНФ
4. x y z
2. ДНФ
3. ДНФ
4. ДНФ
5. КНФ
13. Конъюнктивные и дизъюнктивные нормальные формы
Утверждение: Любую булеву функцию,заданную формулой алгебры логики с
помощью элементарных
преобразований можно привести к ДНФ
и КНФ.
Это представление не
является единственным.
14. Алгоритм приведения формулы к ДНФ (КНФ)
1. Выражают все логические операции в формулечерез дизъюнкцию, конъюнкцию и отрицание.
2. Используя законы Де-Моргана, переносят все
отрицания к переменным и сокращают двойные
отрицания.
3. Используют закон дистрибутивности конъюнкции
относительно дизъюнкции, преобразуют формулу
так, чтобы все конъюнкции встречались раньше
дизъюнкции.
Алгоритм приведения к КНФ аналогичен, только на
шаге 3 делают так, чтобы все дизъюнкции
встречались раньше конъюнкции.
15. Пример
Данную формулу с помощьюравносильных преобразований
привести к ДНФ и КНФ. Считая, что
формула задает булеву функцию,
задать ее с помощью таблицы
истинности, вектора значений,
характеристических множеств и
единичного куба.
x y z xy
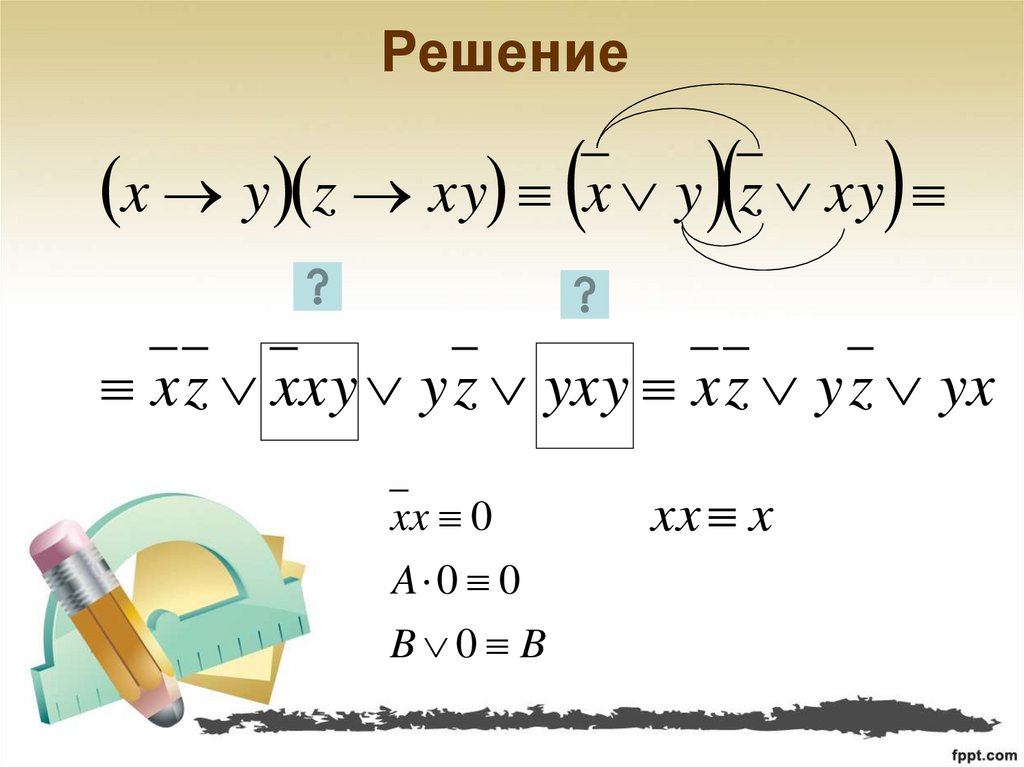
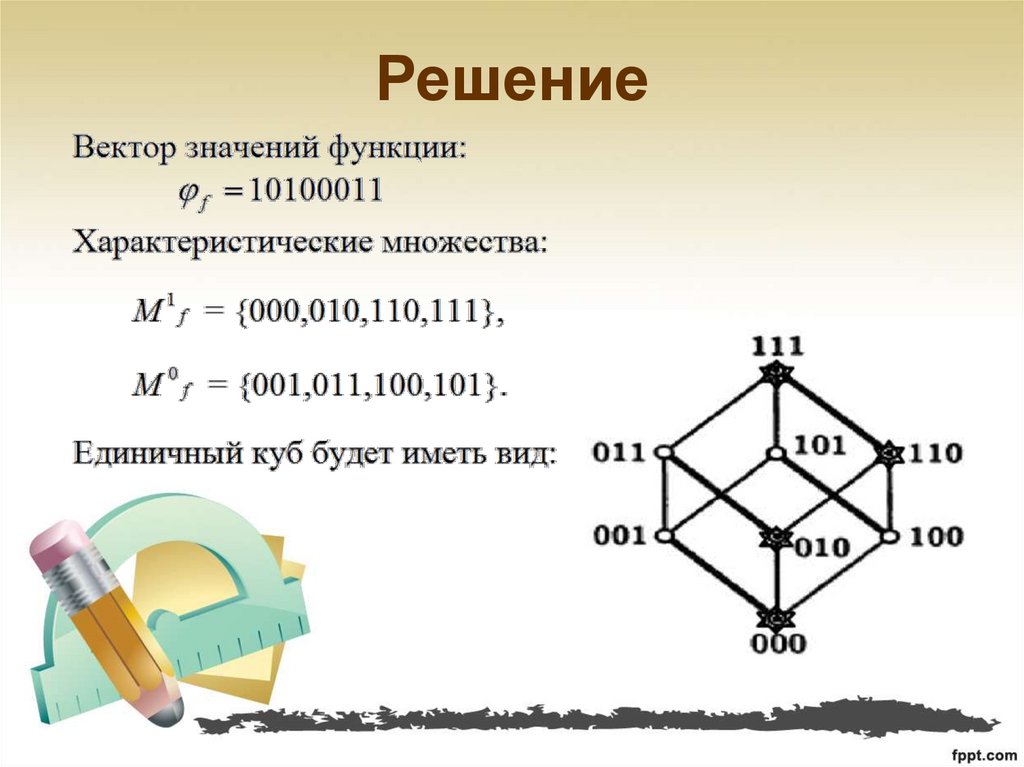
16. Решение
x y z xy x y z xyx z xxy y z yxy x z y z yx
xx 0
A 0 0
B 0 B
xx x
17. Решение
x y z xy x y z xyx y z x z y
Таблица истинности
18. Решение
19. Пример №2
x y zРешение
x y z x y z z y
x y z yz
ДНФ
x y z x y z z y
x y z x y z
КНФ
20. Решить самостоятельно
3. x z y z4.x y z
6. z y x x
7. y z x z
5. x y z y
21. Ответы:
ДНФКНФ
3
y z
y z
4
x yz x y z
x y z y z
5
x y yz
y x z
6
x yz
x z x y
7
x z
x z
















 Математика
Математика








