Проводники в электростатическом поле

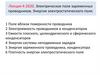
1. Проводники в электростатическом поле

Вещества, у которых под действием электрического поля
преобладающим является процесс неограниченного движения
зарядов, называются проводниками.
Заряды в проводниках называются свободными, в результате их
движения возникает электрический ток.
При внесении проводника в
электростатическое
поле
носители заряда приходят в
движение:
- в направлении
вектора E ,
- в обратную
сторону.
У концов проводника собираются
заряды противоположного знака
Это индуцированные заряды. Процесс их возникновения называется
электростатической индукцией.
- линии напряженности внешнего поля без проводника
- линии напряженности внешнего поля с проводником
1

2.

Заряды располагаются в поверхностном тонком слое проводника и
характеризуются поверхностной плотностью
Во всех точках проводника, включая его поверхность, значение потенциала
одинаково. Проводник эквипотенциален
2

3.

Распределение электрических зарядов на проводнике
При внесении металлического проводника во внешнее
электрическое
поле
электроны
проводимости
перераспределяются до тех пор, пока всюду внутри
проводника электрическое поле электронов проводимости и
положительных
ионов
не
скомпенсирует
внешнее
электрическое поле.
В установившемся состоянии:
- внутри проводника E = 0, во всех
точках поверхности E = En (E = 0);
- весь объём проводника –
эквипотенциален
(включая поверхность);
- не скомпенсированные заряды
располагаются только на поверхности
проводника.
E0
E'
E=0
3

4.

Напряжённость поля вблизи поверхности
заряженного проводника
D E
dS'
n
dl
S
E=0
D=0
dS
dS' = dS = dS''
На поверхности проводника вектора E и
D перпендикулярны поверхности S.
Поток вектора через боковую
поверхность цилиндра ФD = 0.
dS''
Поток вектора D через площадку dS'' тоже равен нулю, так как dS''
лежит внутри проводника, где E = 0 D = 0.
dФD Dn dS
По теореме Остроградского-Гаусса:
dФD dq dS Dn dS dS
Dn =
– поверхностная плотность зарядов на площадке dS
4

5.

En
0 0
Dn
Напряжённость поля вблизи
поверхности заряженного проводника
прямо пропорциональна
поверхностной плотности зарядов.
5

6.

ш.
пр.
4
3
2
1
3
Если заряженный металлический шарик
привести в соприкосновение с
поверхностью проводника, то заряд
шарика частично передаётся проводнику.
Шарик разряжается до тех пор, пока их
1 потенциалы не станут равными. Если
шарик привести в соприкосновение с
внутренней поверхностью полого
проводника, то весь заряд с шарика
стечёт на проводник и распределится на
внешней поверхности проводника.
В точке 1 потенциал шарика меньше
потенциала проводника, ш пр но
при перемещении мы совершаем работу
по преодолению сил отталкивания и тем
самым, увеличиваем потенциальную
энергию, т.е. увеличиваем потенциал
шарика
Генератор Ван-дер-Граафа
1929 (потенциал ~ 1МВ)
6

7.

Свойства замкнутой проводящей оболочки
Если в полости нет электрических зарядов, электрическое поле
в ней равно нулю. Внешние заряды на наружной поверхности
проводника, не создают в полости внутри проводника
никакого электрического поля.
Именно на этом основана электростатическая защита –
экранирование тел, например измерительных приборов, от
влияния внешних электростатических полей.
7

8.

Электроемкость уединенного проводника
Различные по величине заряды распределяются на уединённом
проводнике подобным образом (отношение плотностей заряда в двух
произвольных точках поверхности проводника при любом заряде будет
одним и тем же).
Коэффициент пропорциональности между
потенциалом и зарядом называется электроёмкостью
C
q
q C
Ёмкость численно равна заряду, сообщение которого
проводнику вызывает повышение его потенциала на
единицу.
Единица электроемкости – фарад.
1Кл
1Ф
1В
Электроемкость заряженного шара радиуса R
q
CШ 4 0 R
C
4 0 R
q
Ёмкостью 1 Ф обладал бы уединенный шар радиуса 9 109 м (для
сравнения радиус Земли равен 6,378 106 м)
8

9.

Конденсаторы
Конденсаторы – это два проводника, расположенных близко друг к
другу. Проводники называют обкладками и располагают так, чтобы
их поле было сосредоточено внутри конденсатора
Например, две пластинки, два коаксиальных цилиндра или две
концентрические сферы, расположенные близко друг к другу.
q
q
C
1 2 U
U – напряжение между обкладками
Найдём формулу для ёмкости плоского конденсатора.
S
d
q
E
0 0 S
S – площадь обкладки,
q – заряд конденсатора
q d
U E d
0 S
q 0 S
C
U
d
9

10.

Конденсаторы
Воздушный
Электролитический
10

11.

Соединение конденсаторов
При параллельном соединении общим (одинаковым) является
напряжение U.
q1 C1 U , q2 C2 U
C1
C2
U
q q1 q2 U C1 C2
q
C C1 C2
U
N
C Ci
i 1
11

12.

При последовательном соединении - крайние обкладки конденсаторов
зарядятся разноимёнными зарядами q. Вследствие электростатической
индукции на всех промежуточных пластинах наведутся заряды, также
численно равные q. Следовательно, одинаковым для конденсатора
является заряд q.
U
U1
U2
q
q
C1
C2
1
1
1
C C1 C2
q
q
U1
, U2
C1
C2
N
N
1
U Ui q
i 1
i 1 Ci
N
1
1
C i 1 Ci
12

13.

Энергия заряженного конденсатора
Если замкнуть обкладки заряженного конденсатора накоротко тонкой
проволокой, то по ней потечёт ток, и она может нагреться и даже
расплавиться. Следовательно, конденсатор запасает энергию. При замыкании
конденсатор разряжается.
U' – мгновенное значение напряжения на обкладках конденсатора
Если при этом значении напряжения между обкладками
проходит заряд dq, то совершается следующая работа.
dA U dq
q = C U
dA C U ' dU '
U
1
2
A W C U ' dU ' C U
2
0
C U
W
2
2
2
1
q
1
2
W C U
q U
2
2C 2
13

14.

ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
Если в проводнике создать электрическое поле, то свободные заряды
придут в упорядоченное движение.
Упорядоченное движение зарядов называется электрическим
током.
Сила тока есть величина, равная заряду, переносимому через
поперечное сечение проводника в единицу времени.
dq
I
dt
Для протекания электрического тока необходимы два условия.
1. Наличие частиц, которые могут свободно перемещаться в пределах
проводящей среды (носителей заряда).
2. Электрическое поле внутри среды.
14

15.

Более детально ток характеризуется вектором плотности тока j
Плотность тока в некоторой точке численно равна току через
единичную площадку, расположенную в данной точке
перпендикулярно к направлению движения носителей заряда.
Зная плотность тока можно найти ток.
dI
j
I j dS , или
dS
S
E
v dt
dS
j
I jn dS
S
Через сечение dS за время dt пройдут
только те электроны, которые находятся в
объёме dV = dS v dt.
Тогда за dt через dS пройдёт заряд.
dq = en v dS dt.
n – концентрация
электронов.
dq
dI
en
I
en dS j
dS
dt
j en
15

16.

Уравнение непрерывности
Пусть в некоторой области V проводящей среды имеется
избыточный заряд dq
V
dq
0
dt
S
j
dq
S j dS dt
(*)
Слева – заряд, выходящий в единицу времени из объёма V,
а справа – скорость убывания заряда.
Представим:
q dV
Тогда:
V
- объёмная плотность заряда
dq
dV
dt
t
V
16

17.

По формуле Остроградского-Гаусса
j dS div j dV
S
V
Подставим в (*)
V div j dV V t dV
div j
t
j
t
divj
t
или
Эти уравнения называют уравнением непрерывности. Оно
выражает закон сохранения заряда и показывает, что в точках,
которые являются источниками тока, происходит убывание заряда.
17

18.

В случае стационарного тока = const
j 0
Таким образом, в случае постоянного тока вектор j не имеет
источников. Это означает, что линии тока нигде не начинаются и
не заканчиваются. Следовательно, линии тока всегда замкнуты.
dq
0
dt
j
j dS 0
S
Это условие стационарности тока в интегральной форме. Ток,
протекающий через замкнутую поверхность, будет постоянным,
если входящий внутрь поверхности поток вектора j равен
выходящему.
18

19.

Электродвижущая сила (ЭДС)
Электростатическое поле не может поддержать в проводнике
постоянный электрический ток.
Для кругооборота зарядов должна быть совершена работа против
сил электрического поля.
Такая работа может совершаться только за счет сил, имеющих не
электростатическую природу.
Силы, поддерживающие постоянный электрический ток,
называются сторонними электродвижущими силами (ЭДС)
Электродвижущая сила (ЭДС) измеряется работой, совершаемой
сторонними силами источника по перемещению единичного
положительного заряда внутри источника от отрицательного
полюса к положительному.
2
2
2
A12
A12 Fст dl q E * dl , 12
E * dl
q
1
1
1
*
E – напряжённость поля сторонних сил.
19

20.

Обобщённый закон Ома
для неоднородного участка цепи
Участок цепи, содержащий ЭДС, называется неоднородным.
1
R
2
На участке 1-2 контура на заряд q действует поле, суммарная
напряженность которого равна
E Ee E *
*
E – напряжённость поля сторонних сил.
Величина, численно равная работе по переносу единичного
положительного заряда суммарным полем кулоновских и
сторонних сил на участке цепи (1–2), называется напряжением
на этом участке цепи (U12).
20

21.

2
2
1
1
U12 Ee dl E * dl
Ee dl d
Так как напряжённость связана
с потенциалом, то можно
записать
2
E dl
e
1
1
2
2
E * dl
12
1
U12 1 2 12
Известно, что U12 = I R12
I R12 1 2 12
Это выражение представляет собой обобщённый закон Ома.
21

22.

В замкнутой цепи 1 = 2 и = I R
I
R
R =R + r, где r – сопротивление источника ЭДС
l
Для однородного проводника R
S
– удельное сопротивление, измеряемое в Ом м. l и S – длина и
площадь поперечного сечения проводника.
E
j
Найдём связь между
вектором плотности
тока j и вектором
напряжённости
электрического поля E I
.
2
1
U
I
R
E dl E dS
dl
dS
22

23.

dI
1
j
E
dS
= 1/ – удельная электрическая
проводимость или электропроводность,
которая измеряется (Ом м)-1 = Сим (сименс).
Закон Ома в дифференциальной форме:
j E
23

24.

Мощность тока. Закон Джоуля-Ленца
За время dt через каждое сечение проводника проходит заряд dq = I dt.
При этом силы электростатического поля и сторонние силы на
этом участке совершают работу
dA U dq U I dt
Разделим работу на время и получим выражение для мощности.
dA
P
U I
dt
Мощность может расходоваться на совершение работы над
внешними телами, на нагрев участка проводника и т.д.
t
Q R I dt
2
t
Q U I t A
0
24

25.

Получим закон Джоуля-Ленца в дифференциальной форме:
dl
2
2
dQ R I dt
j dS dt j dl dS dt
dS
2
j dV dt
2
dV = dl dS – элементарный объём.
Тогда количество теплоты, выделяющейся в единице объёма в
единицу времени будет равно.
Qуд j
2
Удельная тепловая мощность тока пропорциональна
квадрату плотности электрического тока и удельному
сопротивлению среды в данной точке.
25

26.

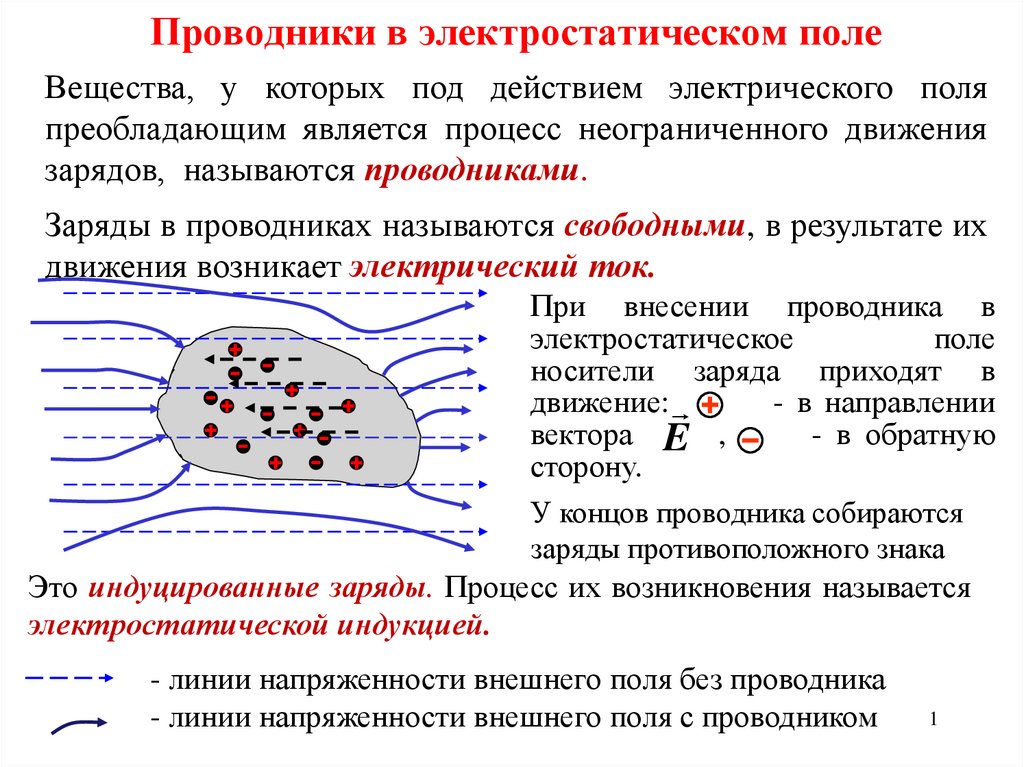
Разветвлённые цепи. Правила Кирхгофа
Первое правило Кирхгофа
Относится к узлам цепи, т.е. точкам разветвления цепи.
Алгебраическая сумма токов, сходящихся в узле, равна нулю.
I 0
i
I2
Для изображенной на рисунке цепи
первое правило Кирхгофа запишется в
виде
I1
I3
I1 I2 I3 0
26

27.

Второе правило Кирхгофа
Относится к любому выделенному в разветвлённой цепи
замкнутому контуру.
Алгебраическая сумма произведения сил токов в отдельных
участках произвольного замкнутого контура на их
сопротивления равна сумме ЭДС, действующих в этом
контуре.
N
N
3
2 I 1
2
R2
3
1
R3
R1
I1
I3
2
I R
k 1
k
k 1
k
k
N – число рассматриваемых участков
выбранного контура
ЭДС положительна, если при обходе
контура она создает ток сонаправленный с
направлением обхода контура.
I1 R1 I 2 R2 I 3 R3 1 2 3 .
27