Похожие презентации:
Применение дифференциальных уравнений для решения прикладных задач механики. Зависимость угловой скорости от времени
1.
Применение дифференциальныхуравнений для решения
прикладных задач механики
Зависимость угловой скорости от времени
Подготовил
Самсонов В.Ю. гр. МТЭП-17-1/9
2.
Цель проекта1. Научиться применять дифференциал при
решении прикладных задач механики
2. Научиться составлять математическую
модель прикладной задачи
3.
Задача:• Замедляющее действие трения на диск, вращающийся
в жидкости, пропорционально угловой скорости
вращения. Найти зависимость угловой скорости от
времени, если известно что диск, начав вращаться со
скоростью 200 об/мин, по истечении 1 мин вращается
со скоростью 120 об/мин.
4.
Угловая скорость — величина, характеризующаяскорость вращения материальной точки вокруг центра
вращения. Для вращения в двухмерном пространстве угловая
скорость выражается числом, в трёхмерном пространстве
представляется псевдовектором.
5.
Диск – это предмет в виде плоского круга.Деталь машины или какого
либо устройства в виде такого предмета.
6.
Вернемся к задаче!Решение:
Пусть - угловая скорость вращения диска,
об/мин; k – коэффициент
пропорциональности;
- изменение
угловой скорости вращения диска в
жидкости.
Силовому воздействию вращения оказывают
сопротивление переменной от изменения
скорости вращения.
7.
Таким образом, из уравнения действующих силили
8.
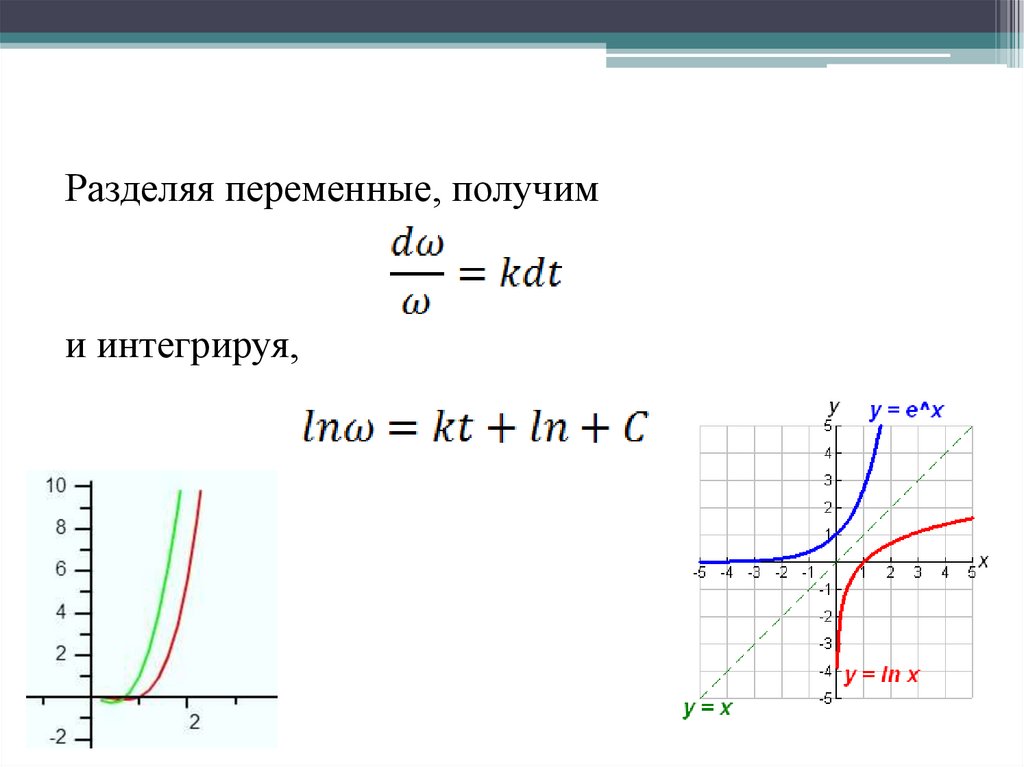
Разделяя переменные, получими интегрируя,
9.
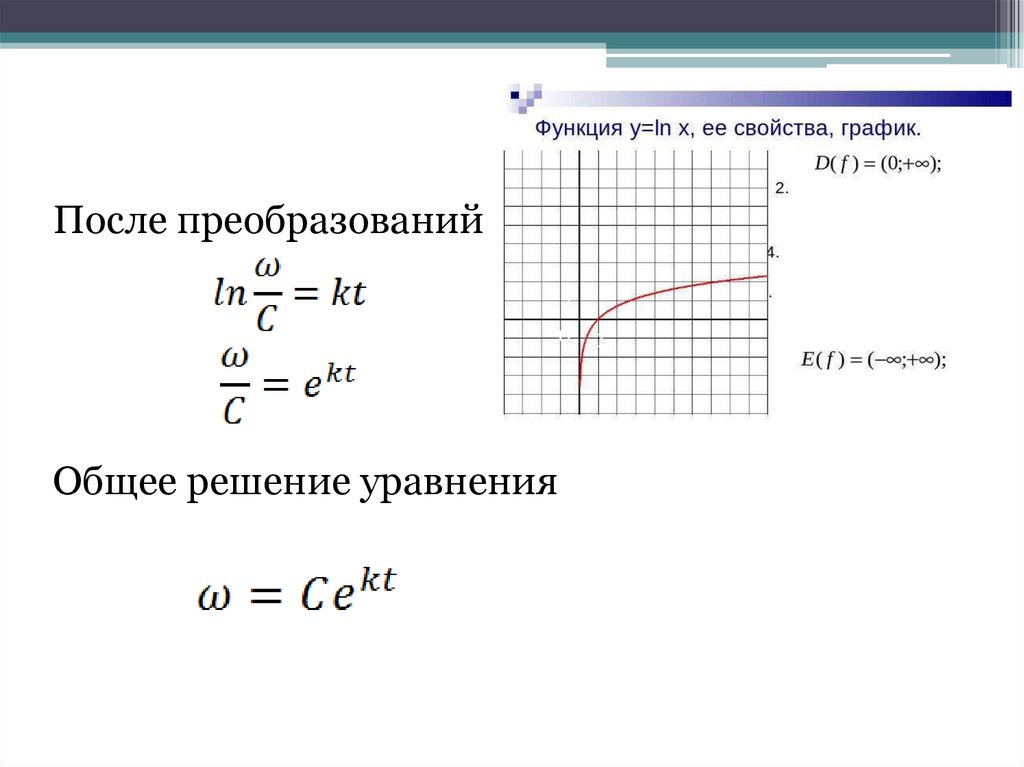
После преобразованийОбщее решение уравнения
10.
Продолжаем решать задачу:Необходимо определить значения С и
коэффициента пропорциональности k.
Из начальных условий
,
,
Тогда
и
11.
Далее, имеемИз этого равенства определим величину k:
Откуда
12.
Подводим итогИскомая зависимость угловой скорости от времени











 Механика
Механика








