Исследование рычажных механизмов (лекция № 2)

1.

Компьютерные технологии
ЦКТ ВЕКТОР
МГУ им. адм. Г. И. Невельского
Кузлякина Валентина Васильевна
д.т.н., проф., зав. кафедрой «Механика машин и САПР»,
Ст. преподаватель Власов Игорь Борисович
Адрес: 690059, Владивосток,
ул. Верхнепортовая, 50А
Тел.: (4232) 49-77-45, 49-77-46
№2
E-mail: [email protected]
1

2.

Курс лекций по дисциплине
Механика.Теории механизмов и машин,
детали машин и основы конструирования.
Версия 1.0., 2005
Авторское право принадлежит
, проф. Кузлякиной В. В.
программа защищена от копирования
2

3. ЛЕКЦИЯ № 2.

Исследование рычажных механизмов.
План лекции:
2. 1. Исследование кинематики.
Графический метод.
2. 2. Исследование кинетостатики
механизма.
2. 3. Элементы динамики машин.
3

4.

2. 1. Исследование кинематики.
Целью
кинематического
исследования
механизмов
является
изучение
движения
отдельных его звеньев и точек без учета сил,
обусловливающих их движения, т.е. движение
механизмов рассматривается с чисто геометрической стороны, с учетом только фактора
времени.
Задача
кинематического
исследования
механизмов: определение положений звеньев и
точек в зависимости от положения начального
(входного) звена, а также определение скоростей и
ускорений всех точек и звеньев механизма.
4

5.

Положение звеньев механизма и траекторий их точек необходимо знать при проектировании
механизмов
для
конструирования
корпусных деталей, определения хода звеньев,
выяснения свободного перемещения звеньев.
Скорости необходимо знать для определения
условий работы. Например, стойкость большинства видов режущего инструмента зависит от
скорости резания, и следовательно, скорости
движения рабочего звена.
Ускорения необходимо знать для определения сил инерции, которые зависят от массы и
ускорения центра масс и влияют на величину
усилий в соединениях.
5

6.

В результате кинематического исследования
механизмов устанавливают соответствие кинематических
параметров
заданным
условиям,
определяют размеры пространства, необходимого
для размещения механизмов, а также получают
исходные данные для выполнения динамических
расчетов.
Существует несколько методов
кинематического исследования механизмов:
экспериментальный;
графический;
аналитический.
6

7.

Вопросами кинематического исследования
занимались многие зарубежные и русские ученые.
Разработано несколько методов и способов
решения этих задач, как графических так и
аналитических.
Графические методы:
а) метод кинематических диаграмм;
б) метод планов скоростей и ускорений.
Наибольший вклад в разработку графических
методов кинематического исследования внесли: Н.
И. Мерцалов, Г. Г. Баранов, В. В. Егоров.
7

8.

Геометрические аналоги
кинематических величин
Механизм – это связанная система тел. Положение каждого тела (звена) в ней определяется
положением входных (начальных) звеньев, число
которых чаще всего равно числу степеней подвижности.
Положение входных звеньев определяется
обобщенными координатами:
qi = qi(t), i = 1, 2, …,W.
8

9.

Для любого звена кинематические параметры:
k (t ) k [q1 (t ), q2 (t ),..., qw (t )],
(2.1)
dq j
d
(
t
)
qj
k
k
k (t )
k q j , (2.2)
dt
dt
j 1 q j
w
q
q
w
w
w
w qi,q j
q
d
j
j
2
j
(t) ( k q j ) k q j k q j 2 k q i q j . (2.3)
k
dt j 1
j 1
j 1
j 1
9

10.

Для любой точки звена:
rM (t ) rM [q1 (t ), q2 (t ),..., qw (t )],
(2.4)
w
dq j
d
r
(
t
)
r
qj
M
M
rM (t )
vM q j , (2.5)
dt
dt
j 1 q j
w qj
w
w qi q j
r a (q )2 vM q 2 a
q q . (2.6)
M
M
M
j
j
i j
j 1
j 1
j 1
10

11.

Эти же зависимости можно представить
в другом виде:
w
vM v
j 1
w
aM a
j 1
w
w
qj
M
qj
M
k
q j ;
j 1
w
j ) v
(q
2
j 1
w
qj
M
qj
k
w
j 2 a
q
j 1
w
qi q j
M
k (q j ) q j 2 a
j 1
qj
k
2
j 1
qj
k
j 1
q j .
i q
j,
q
qi q j
M
q i q j
11

12.

На
начальном
этапе
проектирования
механизмов в качестве кинематических параметров удобно пользоваться геометрическими аналогами скоростей и ускорений, так как это позволяет
исключить
влияние
силового
фактора
и
кинематику рассмотреть с точки зрения структуры
и геометрии механизма. В этом случае для
механизмов, у которых степень подвижности равна
единице (одно входное звено), аналоги угловых
скоростей и ускорений любого звена при угловой
обобщённой координате будут:
12

13.

d i
i
d 1
d 2 i d i
i
2
d 1
d 1
(2. 7)
аналоги линейных скоростей и ускорений
любой точки по угловой обобщённой координате :
V K
d rK
d 1
d 2 r K dV K
a K 2
d 1
d 1
(2. 8)
13

14.

Связь кинематических параметров и их
аналогов для плоского механизма при j = 1
qi q1 1
qi S B
2 2 (S B ) ,
2 2 ( 1 ) ,
2 2 1 2 1 , 2 vB ,
1
1
1
2 2 2 1 ,
2
1
2 2S vB2 2S aB ,
B
1
vA v
1
aA a
vB vB 1,
1
aB aB vB 1,
2
1
2
2
i21 .
1
SB
2
1
1
vB
B
vB ,
SB
A
vB
A
v v
2
B
SB
A
vB
1
aB ,
.
14

15.

2. 3. Виды движений звеньев механизма.
Движения, совершаемые звеньями механизмов различного рода, несмотря на свое
многообразие, непроизвольны, а встречаются в
вполне установившихся геометрических формах.
Звенья плоских механизмов совершают
плоское движение.
Плоским движением называется такое
движение, когда все точки движущегося
твердого тела перемещаются в плоскостях,
параллельных данной неподвижной плоскости.
15

16.

Вращательное движение, или плоское движение
с неподвижной осью вращения. Различают два
основных вида такого движения:
• вращательное круговое движение (когда
звенья совершают полные обороты);
• неполное вращательное движение (когда
звенья совершают только часть оборота).
Первый тип движения совершают различного
рода кривошипы, рукоятки, зубчатые колеса,
шкивы, маховики, валы и т.д.
Второй - поводки, педали, балансиры.
16

17.

Вращательным называют такое движение
твердого тела, при котором остаются
неподвижными все его точки, лежащие на
некоторой прямой, называемой осью вращения.
Каждая точка тела, не лежащая на оси
вращения, описывает окружность, плоскость
которой перпендикулярна к оси вращения, а
центр вращения лежит на этой оси.
Рис. 2.1. Вращательное движение: а)равномерное;
б) ускоренное; в) замедленное.
17

18.

Твердое тело вращается вокруг неподвижной
оси
А , которая перпендикулярна плоскости
вращения тела ( рис. 2. 1 ). При движении тела
угол поворота φ будет непрерывно меняться с
течением времени.
Зависимость угла поворота от времени
описывается уравнением (t) ,
(2. 9.)
которое
выражает
закон
вращательного
движения.
Характеристикой быстроты изменения
угла поворота, является угловая скорость
вращения, равная первой производной от угла
d , рад / с.
поворота по времени.
18
dt

19.

В
общем
вращении
случае
угловая
течением времени, т. е.
при
скорость
t
неравномерном
изменяется
с
Характеристикой
быстроты
изменения
угловой скорости является угловое ускорение
вращения, равное первой производной от угловой
2.
d
,
рад
/
с
скорости по времени.
dt
Если знаки ω и ε одинаковы, то имеет
место ускоренное вращение, если различны замедленное вращение.
19

20.

Если угол поворота твердого тела изменяется
пропорционально времени, то угловая скорость
остается постоянной, т. е. const , рад / с2.
t называется
Такое вращение твердого тела
равномерным вращением.
Уравнение: t выражает закон
равномерного вращения.
Иногда удобно угловую скорость равномерного вращения выражать через n
оборотов, совершаемых в одну минуту.
Число оборотов в минуту называют
частотой вращения.
20

21.

За один оборот тело поворачивается на угол
равный 2π радиан, а за n оборотов в течении
одной минуты ( 60 с) на угол :
2 n
радиан, поэтому
2 n n
t
60
30
( 2. 10)
При вращении тела все его точки движутся
по окружностям, центры которых лежат на оси
вращения. Их скорости и ускорения являются
величинами
векторными
и
называются
линейными.
21

22.

Между угловыми характеристиками вращательного движения тела и линейными
характеристиками движения его точек
существует определенная зависимость.
Величина линейной скорости точки В
определяется (см. рис. 2. 2):
dsB d r Δ
d
VB
r r ω
dt
dt
dt
где dsB r Δ , м - расстояние, которое
проходит точка В при повороте твердого тела
на угол φ , по дуге ВВ1 окружности радиуса
r.
22

23.

Рис. 2. 2. Вращательное движение
Модуль вектора линейной скорости точки
вращающегося тела равен произведению угловой
скорости тела на радиус окружности,
описываемой точкой.
V r ;
( 2.11 )
23

24.

Вектор линейной скорости точки вращающегося твердого тела направлен по касательной
к траектории движения в данной точке в сторону
вращения твердого тела. Эта скорость точки,
называется также окружной скоростью.
Согласно формуле (2.11) окружная скорость
точки
тела
пропорциональна
радиусу
окружности описываемой точкой, поэтому при
увеличении радиуса - скорость возрастает и,
наоборот.
Векторная величина, характеризующая
быстроту изменения модуля и направления
линейной скорости, называют линейным
24
ускорением точки.

25.

Линейное ускорение точки вращающегося
твердого тела в каждый момент времени равно
геометрической
сумме
касательного
(вращательного) и нормального (центростремительного) ускорений.
,
a B a B n a B
,
(2.12.)
d V B d rB
dω
aB
rB
r B ε
dt
dt
dt
τ
dω
где ,
,
dt
рад / с2 - угловое ускорение
вращения твердого тела.
25

26.

Модуль вектора касательного ускорения
точки вращающегося твердого тела равен
произведению углового ускорения тела на радиус
окружности, описываемой точкой
a r .
(2. 13)
Вектор касательного ускорения точки вращающегося твердого тела направлен по касательной в данной точке к траектории ее движения и, в
зависимости от направления углового ускорения,
либо совпадает с направлением линейной скорости
этой точки (ускоренное движение) рис.2.1б, либо
направлен в противоположную сторону (замедленное движение).
26

27.

Нормальная составляющая ускорения точки
характеризует изменение направления ее скорости.
Величина нормального ускорения точки равна
отношению квадрата ее скорости к радиусу
кривизны траектории:
n
a
B
VB rB
rB ω2.
rB
rB
2
2
(2.14.)
Модуль вектора нормального ускорения
точки вращающегося твердого тела равен
произведению квадрата угловой скорости тела
на радиус окружности, описываемой точкой.
a r
n
2
27

28.

Вектор нормального ускорения точки вращающегося твердого тела направлен по нормали
(радиусу) окружности, описываемой точкой в
направлении центра вращения тела.
Модуль полного линейного ускорения точки
твердого тела определяется:
a
a a r r r
2
n 2
2
2
2
2
Модули касательных, нормальных и полных ускорений точек вращающегося твердого
тела пропорциональны радиусу окружности,
описываемой точкой.
28
4

29.

При равномерном вращении тела const ,
следовательно линейная скорость точки тела
V const, а касательное ускорение:
a
B
dvB
0.
dt
В этом случае полное ускорение точки :
n 2
V
(2.15)
a 0 a
a
r
При равномерном вращении твердого
тела любая его точка имеет только
нормальное линейное ускорение, направленное к центру вращения тела.
29
2
n

30.

Полное линейное ускорение точки вращающегося тела определяется как диагональ
прямоугольника, построенного на составляющих
n ( см. рис. 2.1, б) или по правилу
и
a
a
треугольника.
Направление вектора полного ускорения
точки можно определить по углу α , образованному этим вектором с радиусом окружности,
описываемой точкой тела:
a
r
tg n
2
2
a
r
(2.16)
30

31.

На рис. 2.1 показаны направления полного,
нормального и касательного ускорений в случаях
равномерного (рис. 2.1, а), и ускоренного ( рис.
2.1, б) вращения тела.
Сложное движение звеньев механизмов.
Простейшие виды движения твердого тела
были рассмотрены относительно системы
отсчета, связанной с Землей (неподвижной
системы
координат).
Иногда
приходится
рассматривать движение тела относительно
системы отсчета, связанной с каким-нибудь
подвижным телом. В этом случае движение тела
удобно представить себе как сложное движение,
состоящее из двух ( или более ) независимых
31
движений.

32.

Различают движения тела:
- относительно неподвижной системы отсчета
абсолютное.
- относительно подвижной системы отсчета
относительное.
- вместе с подвижной системой отсчета
относительно неподвижной системы отсчета
переносное.
Абсолютное движение тела - совокупность
двух движений: относительного и переносного.
32

33.

Соответственно, различают
относительные и переносные
ускорения точек твердого тела.
абсолютные,
скорости и
Теорема о сложном движении твердого тела:
Абсолютные скорости и ускорения
любой точки твердого тела, совершающего
сложное движение, в каждый момент
времени определятся как геометрическая
сумма относительных и переносных скоростей или ускорений.
33

34.

Vавс Vпер Vотн
(2. 17)
аавс апер аотн
(2. 18)
Графически абсолютные скорость или
ускорение точки твердого тела могут быть
определены по правилу параллелограмма или
треугольника.
Обычно составляющие части сложного
движения это простейшие виды движения тела :
поступательное и вращательное.
В технике широко встречается один из
случаев сложного движения тела плоскопараллельное движение.
34

35.

Например, движение шатуна в кривошипно ползунном механизме.
При плоскопараллельном движении твердого тела, каждая его точка движется в
плоскости, и, следовательно, траектория данной точки расположена в этой плоскости и
является замкнутой кривой.
Положение плоской фигуры S ( рис. 2. 3 )
в плоскости XOY определяется положением
какого - либо отрезка АВ , принадлежащего
фигуре, которое задается координатами какойлибо его точки, например точки А и углом φ ,
образованным отрезком с положительным
направлением оси X ( углом поворота фигуры ).
35

36.

Точка А называется в этом случае полюсом.
Всякое произвольное перемещение плоской
фигуры, а следовательно, и движение всего тела,
определится тремя уравнениями плоскопараллельного движения:
X A X A t YA YA t t
Первые два уравнения характеризуют
поступательное движение твердого тела, третье вращательное движение.
Если при движении будет оставаться
постоянным угол φ, то тело движется только
поступательно. Если при движении не будут
изменяться координаты полюса точки А - тело
36
совершает вращательное движение.

37.

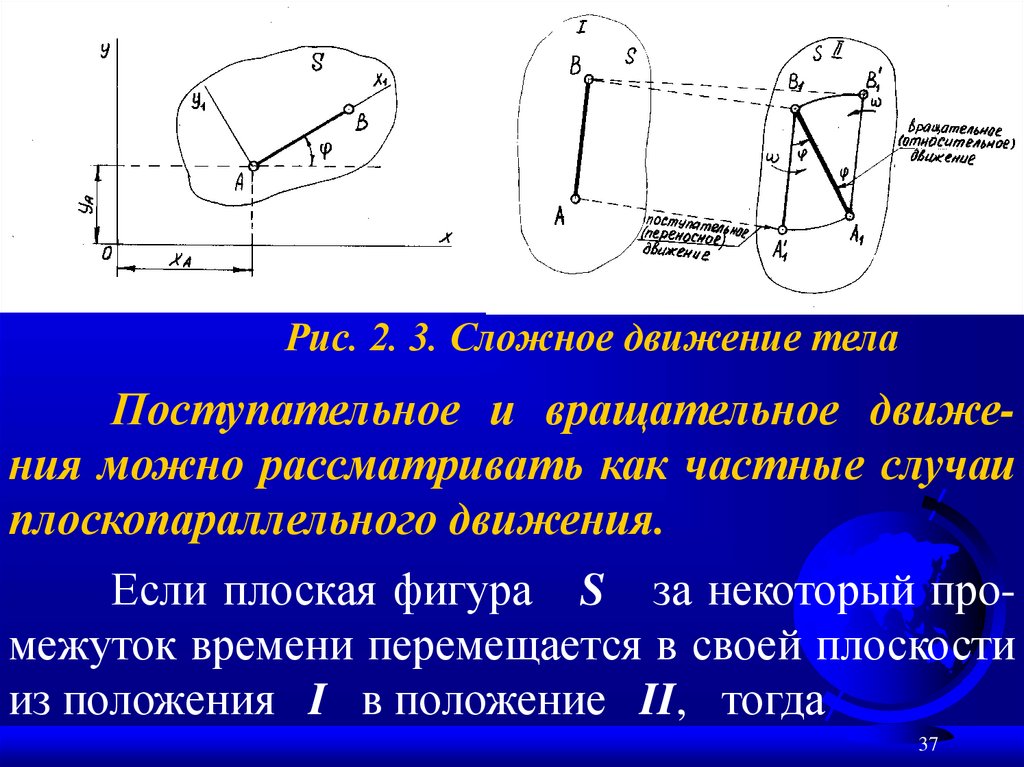
Рис. 2. 3. Сложное движение тела
Поступательное и вращательное движения можно рассматривать как частные случаи
плоскопараллельного движения.
Если плоская фигура S за некоторый промежуток времени перемещается в своей плоскости
из положения I в положение II, тогда
37

38.

отрезок, соединяющий точки А и В этой
фигуры можно переместить в положение
А1В1
следующим образом:
• перенести его параллельно самому себе в
положение А1В1’ (при этом фигура совершит
поступательное
перемещение),
а
затем
повернуть отрезок вокруг точки А1 против
часовой стрелки на угол φ (фигура при этом
совершит вращательное движение и займет
положение II )
• сначала сообщить фигуре поступательное
перемещение в положение отрезка В1А1' , а
затем повернуть вокруг точки
В1
против
38
часовой стрелки на угол φ.

39.

Точку, вокруг которой фигура совершает
поворот, называют полюсом.
В первом случае полюсом была точка А1 , во
втором - В1 . Очевидно, что за полюс может быть
принята произвольная точка фигуры. Измене-ние
положения
полюса
отразится
только
на
поступательной части движения - характеристики
поступательной части плоского движения (перемещение, скорость и ускорение полюса) будут
зависеть от того, какая точка выбрана за полюс.
Характеристики вращательной части плоского движения (угол поворота, угловая скорость и
угловое ускорение) не зависит от выбора полюса, т.
к. угол φ и направление вращения при этом не
39
меняются.

40.

Свойство плоскопараллельного движения:
Угол поворота не зависит от выбора полюса.
При изменении полюса изменяется поступательное
движение, а вращательное остается неизменным.
Плоскопараллельное движение твердого
тела можно разложить на два простых :
переносное - поступательное движение вместе с
точкой, выбранной за полюс и со скоростью
полюса, и относительное - вращательное вокруг
оси, проходящей через полюс перпендикулярно
плоскости движения.
Эти два простых движения совершаются
одновременно.
40

41.

Разложение плоскопараллельного движения
на простейшие виды движения используется для
определения скоростей и ускорений точек твердого
тела.
Например, абсолютную скорость любой
точки В (рис. 2. 4а) твердого тела VВ абс = VВ
можно найти , приняв за полюс точку А.
Она будет равна геометрической сумме двух
скоростей: переносной скорости поступательного
движения, равной скорости полюса VВ пер = VА , и
относительной скорости вращательного движения
вокруг этого полюса VВ отн = VВА : VB VA VBA
41

42.

а)
б)
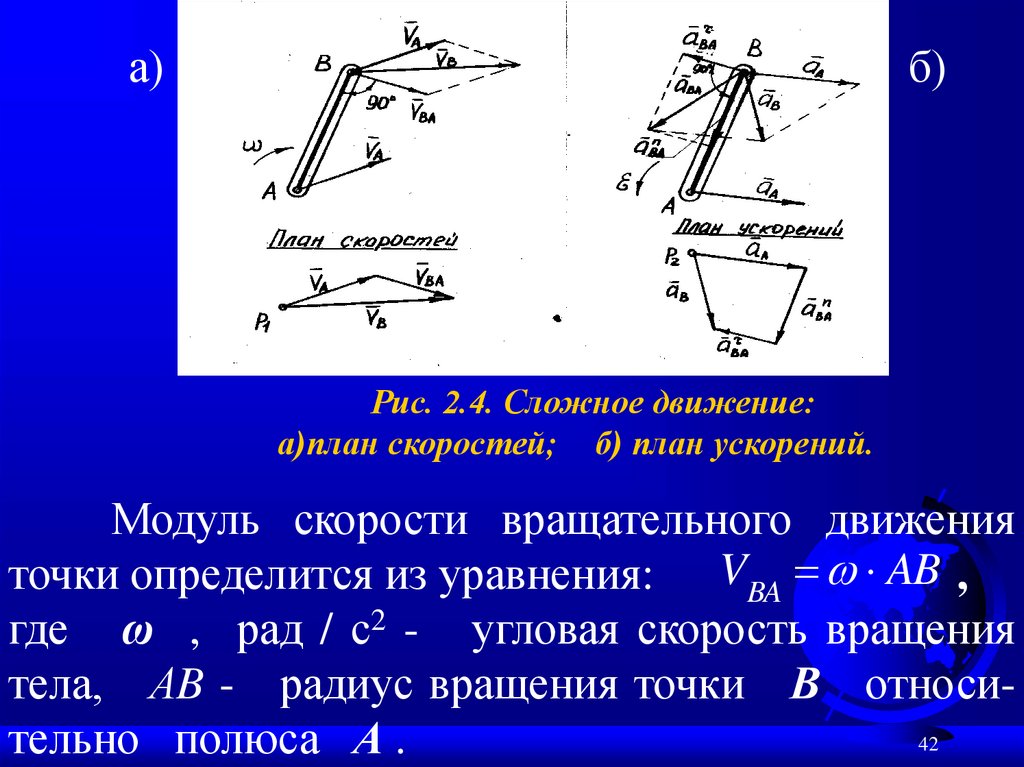
Рис. 2.4. Сложное движение:
а)план скоростей; б) план ускорений.
Модуль скорости вращательного движения
точки определится из уравнения: VBA AB ,
где ω , рад / с2 - угловая скорость вращения
тела, АB - радиус вращения точки В относи42
тельно полюса А .

43.

Вектор скорости VВА перпендикулярен радиусу
вращения и направлен в сторону вращения тела.
Аналогично можно найти абсолютное
ускорение любой точки В твердого тела (рис.
2.3.б) aB абс aB , приняв за полюс точку А.
Оно будет равно геометрической сумме двух
ускорений: переносного ускорения поступательного движения, равного ускорению полюса
aB пер aA и относительного ускорения
вращательного движения вокруг этого полюса.
aB отн aBA ; аB а A аBA ;
Относительное ускорение раскладывается на
две составляющие:
n
аBA аBA аBA
43

44.

Модуль нормального ускорения вращательного движения точки определится из
2
V
уравнения:
Вектор нормального
n AB
aBA
AB
n
ускорения
aBA направлен по радиусу
вращения точки и направлен в сторону полюса А.
Вектор касательного ускорения aBA
направлен перпендикулярно радиусу вращения
точки в сторону направления углового ускорения
вращательного движения тела.
2.4. Графический метод исследования.
Для изучения кинематики механизма
необходимо знать:
44

45.

• сочетание кинематических пар;
• геометрические размеры;
• взаимное расположение звеньев и
кинематических пар.
Это определяется кинематической схемой
механизма. Кинематические схемы изображаются
с помощью условных изображений, при этом
звенья считаются жесткими, неизменяемыми.
Кинематическая схема механизма - это его
изображение с применением условных обозначений звеньев и кинематических пар, построенное
на основании точных размеров звеньев,
45

46.

позволяющее определить характер движения ведомых звеньев по заданному движению ведущих.
План механизма - это кинематическая схема
механизма, выполненная с учетом определенного
масштабного коэффициента длин.
Масштабный коэффициент – это отношение истинной величины, измеренной в присущих
ей единицах, к длине отрезка, изображающего эту
величину на чертеже (в миллиметрах).
Масштабные коэффициенты обозначаются
буквой
с индексом, указывающим к какой
величине они относятся.
46

47.

Например:
масштабный коэффициент длин -
l м
l ,
;
l мм
V
м
V
,
;
Масштабн. коэффициент скорости V c мм
a м
a
,
; ,
Масш. коэф. аналога ускорения a мм
где: l, V, aφ - истинные величины, соответственно, длины звена, скорости точки звена, ускорения точки звена;
l , V , a - длины отрезков, изображающих на
чертеже истинную величину, соответственно,
длины звена, скорости точки звена, аналога
47
ускорения точки звена в миллиметрах.

48.

Обычно при выборе масштабных коэффициентов выбирают изображение (длину отрезка), а
масштабный коэффициент вычисляют. Выбор
масштабных коэффициентов обусловливается
размерами величин исследуемого механизма и
необходимостью соответствовать стандартным
масштабам.
Согласно ГОСТа принимаются следующие
масштабы:
Масштаб уменьшения:
1:2; 1:5; 1:10
допускаются, но не рекомендуются 1:2,5; 1:4
Масштаб увеличения:
2:1; 5:1; 10:1
допускаются, но не рекомендуются: 2,5:1,4:1
Возможно любое десятикратное увеличение
или уменьшение указанных значений масштабов.
48

49.

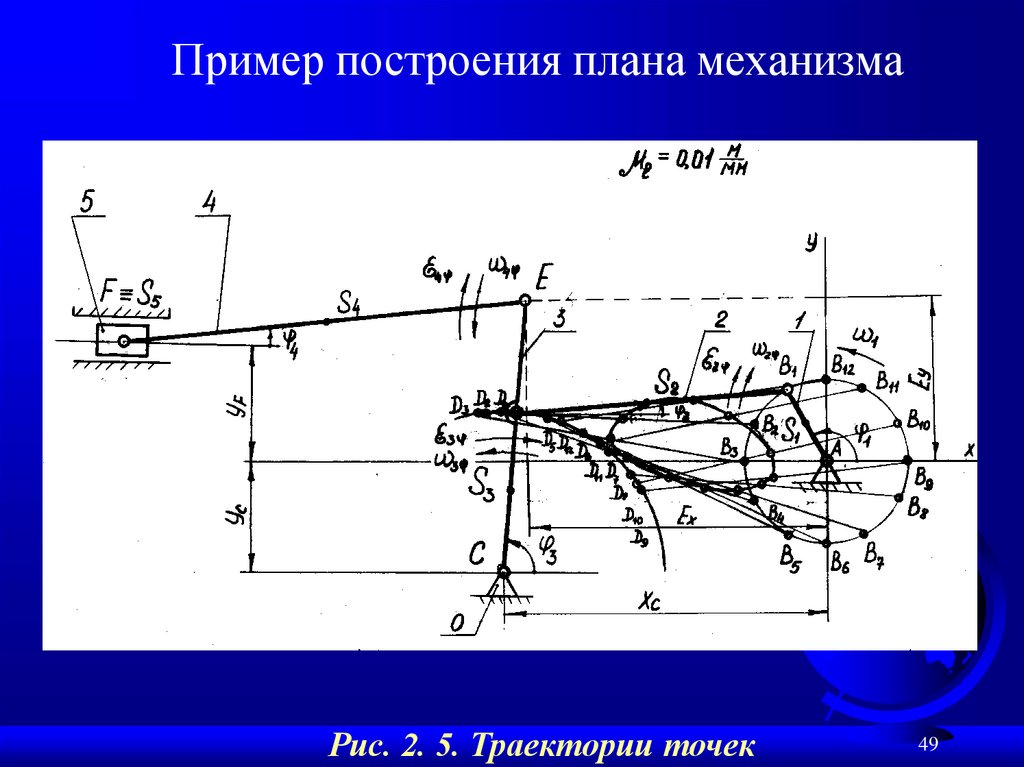
Пример построения плана механизма
Рис. 2. 5. Траектории точек
49

50.

Планы скоростей и ускорений
При решении задачи определения скоростей и
ускорений графическим методом, в теории
механизмов и машин часто пользуются методом
планов. Он осуществляется графическим построением планов скоростей и ускорений, которые
представляют собой изображения векторов
скоростей и ускорений точек движущегося
механизма в данный момент времени.
Этот метод основан на основных законах
исследования кинематики движущихся тел.
Метод отличается универсальностью,
наглядностью и простотой.
50

51.

Преимуществом его является то, что в
результате построения планов определяются не
только величины, но и направления скорос-тей и
ускорений точек механизма.
Построение планов скоростей и ускорений
выполняются с учетом масштабных коэффициентов μV и μа, которые подбирают так, чтобы
планы получились достаточно точными и
рационально использовалось поле чертежа. При
вычислении
масштабных
коэффициентов
рекомендуется
принимать
длины отрезков,
изображающие вектора скоростей и ускорений
точки ведущего (входного) звена, не менее 50 мм.
51

52.

На рис. 2. 6. рассмотрен пример построения
плана скоростей звена (шатуна) кривошипноползунного механизма. Задан закон движения
ведущего звена АВ : звено вращается с постоянной угловой скоростью ω . Требуется определить
линейные скорости и ускорения точек звена ВС
методом планов.
Звено 0 - стойка, звено, принятое за неподвижное. Движение точек звеньев относительно
стойки является абсолютным.
Звено 1 - кривошип, совершает полное
вращение. Все точки кривошипа при его вращении
описывают окружности различных радиусов,
соответственно этому различны их скорости и
52
ускорения.

53.

Звено 3 - ползун, совершает поступательное
движение. Все точки ползуна движутся по
одинаковым прямолинейным траекториям с
одинаковыми скоростями и ускорениями.
Звено 2 - шатун, совершает сложное плоское (плоскопараллельное) движение: левый его
конец, совпадающий с центром в шарнире B ,
описывает окружность, а правый конец (центр
шарнира A ) - прямую линию. Траектории всех
остальных его точек представляют собой разные
сложные кривые.
53

54.

Абсолютное (плоскопараллельное) движение
шатуна ВС , раскладывают на переносное
(поступательное) движение вместе с шарниром В
и относительное (вращательное) движение вокруг
центра шарнира В .
Точка механизма, движение которой рассматривается как переносное, называется полюсом.
Кинематические характеристики точки, принятой
за полюс, должны быть известны.
Построение плана скоростей (рис. 2. 6)
План скоростей дает возможность графическим путем определить скорости точек звеньев
54
механизма.

55.

План строится по векторным уравнениям,
которые составляются согласно теории о плоскопараллельном движении. За полюс принимаем
шарнир В . Абсолютная скорость точки С шатуна ВС определится как геометрическая сумма
скорости переносного (поступательного) движения
полюса В и скорости относительного (вращательного) движения точки С относительно точки В :
V V V ;
(2.
19.)
C
B
CB
Это уравнение можно решить графически,
если один вектор VB известен по величине и
направлению, а два других
VC , VCB только по
55
направлению.

56.

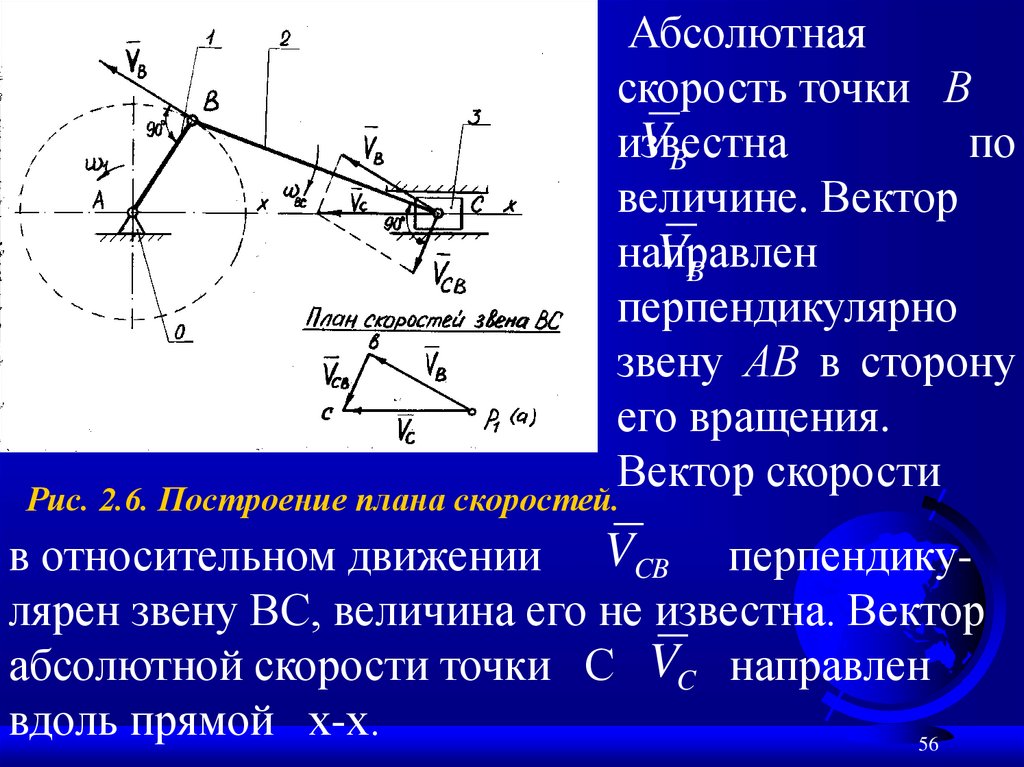
Абсолютная
скорость точки В
VB
известна
по
величине. Вектор
направлен
VB
перпендикулярно
звену АВ в сторону
его вращения.
Вектор скорости
Рис. 2.6. Построение плана скоростей.
в относительном движении VCB перпендикулярен звену ВС, величина его не известна. Вектор
абсолютной скорости точки С VC направлен
вдоль прямой х-х.
56

57.

Решением векторного уравнения будет
векторный треугольник, построенный по правилу
сложения векторов. Построение можно выполнить
на плане механизма ( см. рис. 2.6 ). Однако геометрическое сложение векторов скоростей для
многозвенных механизмов и ряда его положений
неудобно, так как векторные многоугольники
скоростей различных точек механизма будут
налагаться друг на друга, векторы будут пересекаться, возникнут затруднения при чтении, расшифровке таких векторных многоугольников и
определению по ним скоростей. Целесообразно
построение в плоскости чертежа планов скоростей
отдельно для каждого из последовательных
положений кривошипа.
57

58.

Для построения плана скоростей звена ВС
в плоскости чертежа нужно выбрать произвольную
точку p1 в качестве полюса (центра) плана
скоростей. Из полюса отложить отрезок p1 b (в
определенном масштабе) параллельно направлению скорости VB . Через точки p1 и b провести
прямые, параллельные скоростям VCB и VC .
Точка пересечения этих прямых определяет
фигуру p1 b с , которая является планом скоростей
звена ВС и решением векторного уравнения (2.
19.). Совокупность планов скорос-тей всех
звеньев механизма с одним общим полюсом и
одним
масштабом
называется
планом
58
скоростей механизма.

59.

План скоростей механизма имеет следующие
свойства:
1. Точкам плана скоростей (b, с) соответствуют
одноименные точки (В, С) на плане
механизма и наоборот.
2. Скорости точек, равные нулю ( А ), на плане
скоростей совпадают с полюсом p1 .
3. Любая фигура, построенная на плане скоростей
(отрезок, треугольник, многоугольник) и
обозначенная малыми буквами, подобна
соответствующей фигуре, обозначенной
большими буквами на плане механизма, и
повернута относительно нее на 90 в
59
направлении вращения.

60.

4. Отрезки, изображающие вектора абсолютных
скоростей точек звеньев механизма на плане
скоростей [p1 b], [p1c] выходят из полюса плана.
5. Отрезки, изображающие вектора относительных скоростей точек звеньев механизма на плане
скоростей [bc] соединяют концы векторов абсолютных скоростей и всегда перпендикулярны
одноименным отрезкам на схеме механизма ВС.
60

61.

Свойство подобия справедливо для любого
числа точек на звене механизма. Теорема подобия
для плана скоростей звена:
Отрезки прямых линий, соединяющих
точки одного и того же звена на плане механизма, и отрезки прямых линий, соединяющих
концы векторов скоростей этих точек на
плане скоростей, образуют подобные и
сходственные фигуры.
Теорема подобия позволяет определить
скорость любой точки звена, если известны
скорости двух других точек этого звена.
61

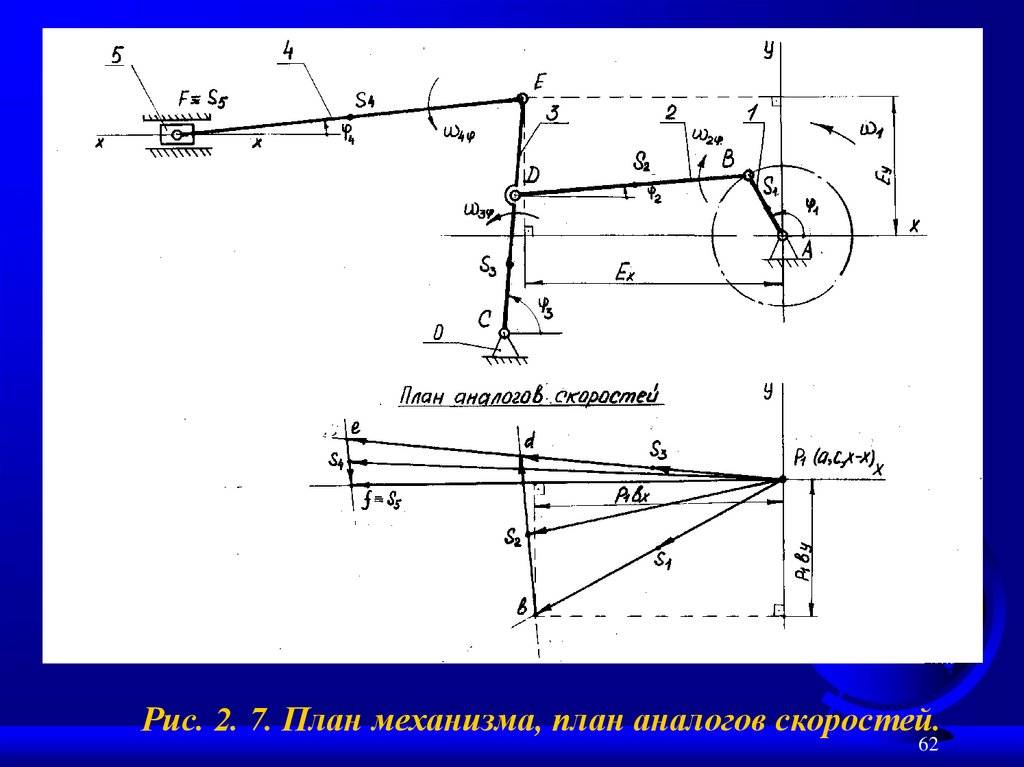
62.

Рис. 2. 7. План механизма, план аналогов скоростей.
62

63.

Построение плана ускорений
План ускорений (рис. 2. 8.) дает возможность
графическим путем определить ускорения точек
звеньев механизма. Прежде, чем строить план
ускорений должен быть построен план скоростей и
определены скорости характерных точек звеньев
механизма.
План ускорений строится по векторным
уравнениям, которые составляются согласно
теории о плоскопараллельном движении.
aC aB a
n
CB
aCB ;
(2. 20.)
63

64.

Так абсолютное ускорение точки С шатуна
ВС определится как геометрическая сумма ускорения переносного движения полюса В и относительного ускорения точки С во вращательном
движении вокруг точки В :
aC aB aCB ;
Полное ускорение точки В во вращательном
движении определяется как геометрическая сумма
n
нормального aB и тангенциального ускорений
:
a
n
B
aB aB aB ;
64

65.

Ускорение точки В состоит только из нормального ускорения, известного по величине и
направлению. Модуль ускорения aBn = 2 ·lAB , а
его вектор направлен параллельно звену AB к
центру (точке B). Вектор тангенциального
ускорения a перпендикулярен звену ВС,
а
B
величина его не известна.
Вектор абсолютного ускорения точки
направлен вдоль прямой х - х.
Согласно уравнению (2. 20) :
aC aB a
n
CB
С
aCB ;
65

66.

В этом уравнении два неизвестных по величине
ускорения: aС и aB , которые определяются в
процессе дальнейшего решения.
Решением векторного уравнения будет многоугольник, построенный по правилу сложения
векторов, который является планом ускорений
звена ВС .
Порядок построения плана ускорений звена ВС :
1. В плоскости чертежа выбрать произвольную
точку p2 в качестве полюса плана ускорений.
2. Из полюса отложить отрезок p2b (в определенном масштабе) параллельно направлению
n
66
a
ускорения
B .

67.

3. К концу отрезка p2 b прибавить вектор nCB,
для этого через точку b провести прямую,
n
параллельную ускорению aB и отложить на ней
отрезок, bn соответствующий в определенном масштабе
нормальному ускоn
рению aB .
4. К вектору nCB,
прибавить вектор aCB
Для этого из точки
n провести линию
параллельную
Рис. 2. 8. План механизма, план ускорений.
67

68.

направлению ускорения aCB до пересечения с
линией, параллельной направлению ускорения aС ,
проведенной из полюса плана ускорений. Точка
пересечения этих прямых определяет положение
точки C.
Совокупность планов ускорений всех звеньев
механизма с одним общим полюсом и одним масштабным коэффициентом называется планом
ускорений механизма. План ускорений имеет
свойства, аналогичные свойствам плана скоростей. Теорема подобия для плана ускорений звена:
68

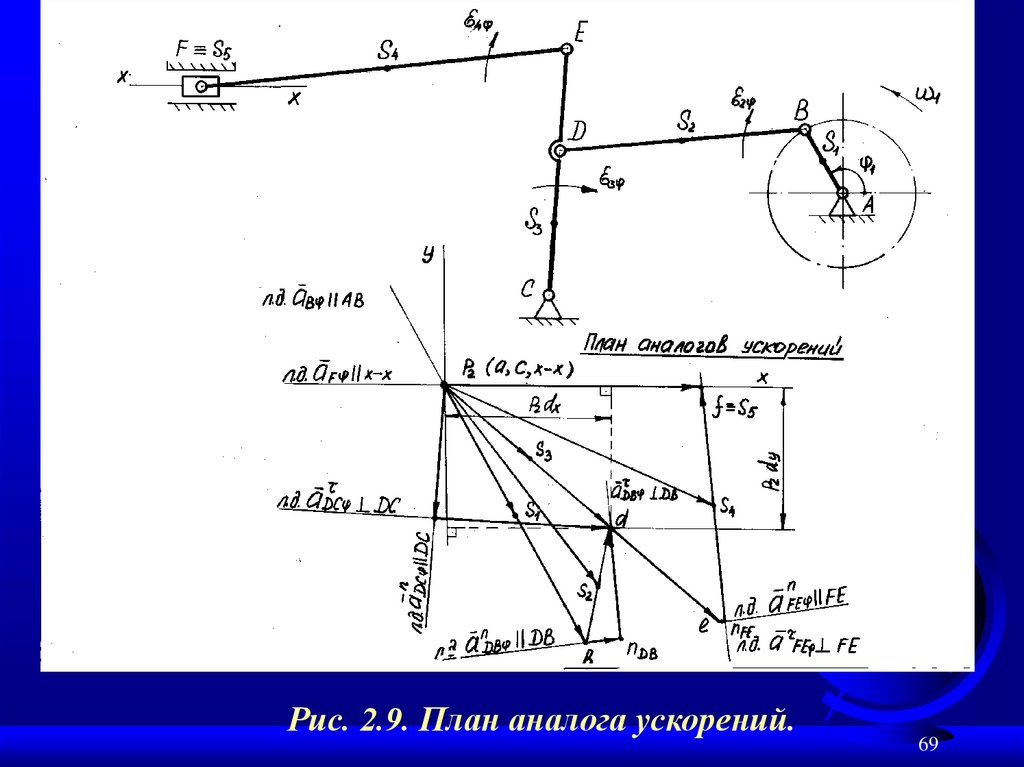
69.

Рис. 2.9. План аналога ускорений.
69

70.

Отрезки прямых линий, соединяющие
данные точки на плане звена, и отрезки прямых,
соединяющие концы векторов полных ускорений
этих точек на плане ускорений, образуют
подобные и сходственно расположенные фигуры.
Планы скоростей и ускорений позволяют
определить угловые скорости
ω
и угловые
ускорения ε звеньев механизма. Зная относительную скорость и радиус звена, определяем:
VCB
CB
lCB
Направление угловой скорости определяется
70
направлением скорости V CВ .

71.

τ и
Зная модуль относительного ускорения
a
CB
a CB
радиус звена lCB , определяем: CB
.
lCB
Направление углового ускорения определяет .
ся направлением ускорения
a
CB
Из сопоставления направления CB и aCBτ
видно, что в рассматриваемый момент времени
шатун движется замедленно.
При
выполнении
расчётно-графической
работы необходимо сделать все расчёты для одного
положения кривошипа заданной схемы механизма
графически - методом планов.
71

72.

2. 2. Исследование кинетостатики механизма.
Силы, действующие в машинах.
Первая задача динамического анализа
машин называется также кинетостатикой.
В простейшем случае машина или агрегат
состоит из двигателя и рабочей машины.
Fдв
Д
РМ
Fпс
Рис 2. 10. Схема агрегата.
72

73.

При исследовании кинетостатики агрегат
разделяют и исследование ведется отдельно для
двигателя и рабочей машины:
Fдв
РМ
Д
- заменяет отброшенный двигатель.
Fпс
- заменяет отброшенную машину.
73

74.

В теоретической механике дается общая
характеристика сил, деление их на внешние (или
задаваемые) и внутренние (или реакции связей).
Дадим более подробную характеристику сил,
действующих в машинах. К внешним силам
относятся:
Движущие силы.
Для выполнения требуемого движения к
звеньям механизма необходимо приложить силы.
Заданное
движение можно осуществить с
помощью двигателя, способного преодолевать все
остальные силы, приложенные к разным звеньям
исполнительного механизма.
74

75.

Силы, развиваемые двигателем и стремящиеся ускорить движение звеньев, называются
силами движущими. Эти силы направлены в
сторону движения их точек приложения, поэтому с
энергетической точки зрения эта группа сил
характеризуется положительной работой.
Сумму работ всех движущих сил будем
Fдв
V
обозначать Адв
Движущие силы, создаются двигателями,
которые осуществляют преобразование какоголибо вида энергии в механическую работу.
75

76.

в
паровых машинах, в паровых и газовых
турбинах , в двигателях внутреннего сгорания
в механическую работу превращается тепловая
энергия;
в электродвигателях – электрическая;
потенциальная энергия, накопленная водой,
преобразуется в механическую работу гидротурбинами;
натянутая пружина может произвести
механическую работу;
поднятая гиря также является источником
получения механической работы;
мускульная сила человека также источник
движущей силы.
76

77.

Силы полезных сопротивлений.
Во время движения звеньев рабочей машины
совершается полезная (производственная) работа,
при этом возникают силы сопротивления,
стремящиеся замедлить движение звеньев. Такие
силы называются силами полезного сопротивления. Это сила резания, вес поднимаемого груза,
сопротивление воды. Они приложены к выходным
(рабочим) звеньям, в сторону, противоположную
движению их точек приложения.
Fпс
V
77

78.

С энергетической точки зрения эти силы
характеризуются отрицательной работой.
Работу всех сил полезного сопротивления
будем обозначать - А пс
Сила тяжести звеньев.
Эти силы совершают положительную работу (когда центры тяжести звеньев опускаются),
отрицательную работу (когда центры тяжести
звеньев поднимаются) и нулевую работу (когда
центры
тяжести
неподвижны,
например,
маховик, или совершают горизонтально поступательное движение, например, поршень в
горизонтальных кривошипно - ползунных
механизмах). В общем случае работу сил тяжести
78
можно обозначить ± АFG.

79.

Большинство машин работают циклически и
время одного цикла соответствует времени одного
оборота входного звена. За это время центры
тяжести звеньев поднимутся и на столько же
опустятся, поэтому сумма их работ за цикл равна
нулю.
АFG = 0
Силы сопротивления среды.
Это может быть, например, сопротивление
воздуха при движении машин, самолётов, поездов;
воды – при движении теплоходов и так далее.
Необходимо стремиться к уменьшению этих сил за
счет более рациональных конструкций, лучшей
обработки поверхности и других способов. 79

80.

При исследовании большинства механизмов
силы сопротивления внешней среды не учитываются.
К внутренним силам относятся:
Силы реакций связи.
Это силы давления в кинематических парах,
возникающие в результате действия внешних сил,
а также в следствие движения звеньев с ускорением. Дополнительные давления в кинематических
парах за счет движения звеньев с ускорением,
определяются с учетом сил и моментов инерций.
Силы реакций не влияют на характер движения
80
звеньев .

81.

Силы трения.
Являются составляющей реакций связей и
зависят от величины давления в кинематических
парах. Силы трения, влияют на закон движения
звеньев, препятствуют их движению и относятся к
силам вредного сопротивления.
Кроме перечисленных сил в динамике машин
учитываются также силы упругой деформации.
Прикладываются также силы и моменты инерции.
Подробно их природа и характеристика изучались
ранее в курсе теоретической механике.
Некоторые частные случаи при определении
сил инерции в плоских механизмах.
81

82.

Силы и моменты инерции
Сила инерции прикладывается к звену в
центре масс и определяется по формуле:
Fu mas .
Момент инерции прикладывается к звену и
определяется по формуле:
Tui J s i i .
В общем случае к звену прикладываются и
сила инерции и момент инерции:
Fu mas .
Tui J si i .
82

83.

Частные случаи
поступательное движение звена:
Tux = 0; Tuy = 0; Tu = 0;
если
a s 0 , то и
Fu 0;
вращательное движение звена:
d 2 i
d2 i
Tu J s i J s ( i i ) J s ( 2
);
2
d
d
2
2
если центр масс совпадает с осью вращения:
R s 0; a s 0; Fu 0;
83

84.

если центр масс совпадает с осью
вращения, угловое ускорение звена j 0
Rs 0 ; as 0 ; Fu 0 ; j 0 ; Tu 0 ;
если центр масс не совпадает с осью
вращения, а угловое ускорение звена
j 0
j 0; Fu mRs .
2
84

85.

Механические характеристики
механизмов.
Теория
механизмов
не
занимается
изучением
энергетики
или
технологии
производства, поэтому внешние силы (силы
полезного сопротивления или силы движущие)
при расчете механизмов будут заданы.
Они могут быть постоянными (силы тяжести, сила сопротивления резанию металла при
постоянном сечении стружки), могут зависеть от
положения звена (сила давления газов на поршень
в двигателе внутреннего сгорания),
85

86.

от скорости звена (момент электродвигателя), от
времени, а также силы могут зависеть от
нескольких независимых параметров. Во многих
случаях закон изменения какой-то внешней силы
можно выразить аналитически. В ряде же случаев
эта зависимость описывается графически.
Функциональная зависимость сил и
моментов движущих сил сопротивления от
перемещения,
скорости
или
времени,
выраженная аналитически или графически
называется механической характеристикой.
86

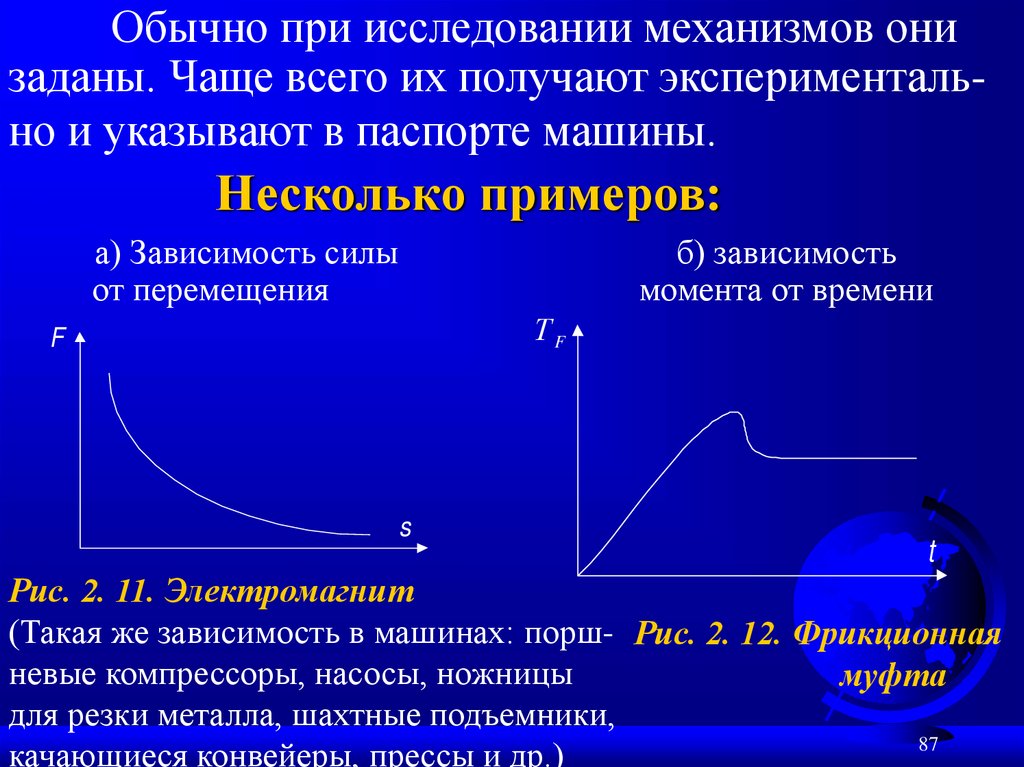
87.

Обычно при исследовании механизмов они
заданы. Чаще всего их получают экспериментально и указывают в паспорте машины.
Несколько примеров:
а) Зависимость силы
от перемещения
б) зависимость
момента от времени
ТF
F
s
t
Рис. 2. 11. Электромагнит
(Такая же зависимость в машинах: порш- Рис. 2. 12. Фрикционная
невые компрессоры, насосы, ножницы
муфта
для резки металла, шахтные подъемники,
87
качающиеся конвейеры, прессы и др.)

88. в) зависимость момента от перемещения.

Тg
Тg
2. 13. Пружинный двигатель
2. 14. Роторные машины
(момент не периодичен)
(электродвигатели,
электрогенераторы,
ветродвигатели,
вентиляторы, турбины,
88
центробежные насосы).

89.

г) зависимость момента от скорости
T
T
w
w
Рис. 2. 15. Электродвигатель
постоянного тока с параллельным возбуждением.
T
Рис. 2. 16. Электродвигатель
постоянного тока с последовательным возбуждением.
FС
v
w
2. 17. Асинхронный электродвигатель трехфазного тока.
2. 18. Воздушный демпфер
измерительного прибора.
89

90.

Механические характеристики необходимы для
определения сил, действующих на звенья.
В четырехтактном двигателе внутреннего
сгорания с помощью приборов можно снять
индикаторную диаграмму, изображающую закон
изменения давления газа в цилиндре. Она имеет
вид:
Р
i
3
Рi
1 ат
4
1
2
S
С
Н
Е
s
А
Рис. 2. 19. Индикаторная диаграмма 4-х тактного ДВС
90

91.

Полный цикл работы двигателя заканчивается за
H
s
два оборота кривошипа. По диаграмме: AC AE
s - расстояние от правой крайней точки.
При любом s можно по диаграмме определить
ординату, соответствующую индикаторному давлению. Сила, действующая в этот 2момент на пор d
шень, определяется:
p p
;
i
4
pi - избыточное давление (измеряется от линии атмосферного давления).
d 2
Так как
- величина постоянная, то эта же
4
диаграмма есть и диаграмма изменения силы F в
зависимости от перемещения.
91

92.

Можно развернуть эту диаграмму и условиться:
силы движущие изображать со знаком “+”, а силы
сопротивления со знаком “-”.
Получим диаграмму:
р а б о чи й
ход
P
s
H
H
H
вса сы ва ни е с ж а т и е
H
вы хло п
Рис. 2. 20. Диаграмма усилий для 4-х тактного ДВС. 92

93.

Зная диаграмму F-s можно определить работу, производимую расширяющимися газами, а
также ее изменение в зависимости от перемещения
A
поршня.
s
dA Fds ; A Fds ;
0
s
Рис. 2. 21. График работ.
За период работа сил движущих F будет положительной, хотя есть и участки отрицательной
работы (силы сопротивления). Имея график работ
можно определить и среднюю индикаторную
мощность, т.е. мощность, развиваемую силой,
93
действующей на поршень.

94.

Если n - число оборотов кривошипа,то время цикла
A
2 60
t
, а средняя индикаторная мощность Pi
t
n
Мощность, измеренная на валу двигателя
естественно меньше индикаторной, так как часть
ее тратится на преодоление сил трения. Эта
мощность показана на графике.
P
Pi - индикаторная мощность
Pэ - эффективная мощность
PF - мощность, затраченная
на сопротивление
0
N imax
N эmax
Ni
Nэ
NF
n
94
Рис. 2. 22. График мощностей.

95.

Связь мощности и момента: Pэ =Tэ w , т.е. с
изменением скорости вращения вала меняются и
момент, и мощность, поэтому чаще всего механическая характеристика - это зависимость
мощности и момента от скорости.
Если механическая характеристика задана в
виде зависимости от времени, то для получения
зависимости её от перемещения, необходимо иметь
еще зависимость перемещения от времени, а затем
методом исключения параметра t следует
определить
P - s или Т - , а затем
интегрированием определить функцию работы.95

96.

T
P
T
T
P
P
T
P
w
Рис. 2. 23. Электродвигатель
постоянного тока
T
P
w
Рис. 2. 24. Электродвигатель
переменного тока
T
P
T
P
P
T
w
Рис. 2. 25. Водяная турбина
w
Рис. 2. 26. Центробежный насос
96

97.

T
P
w
Рис. 2. 27. Прядильная машина
Движение звеньев
в исполнительных механизмах
механической
системы определяется
или (
выходными параметрами двигателя q, q
или ), которые в свою очередь зависят от
входного параметра двигателя u.
Для двигателей механическая характеристика
u, q , q , M g .
- это зависимость между
97

98.

В зависимости от решаемых задач динамики
используются
следующие
характеристики
двигателей:
Идеальная кинематическая характеристика.
q f ( u)
Эта характеристика соответствует отсутствию
нагрузки
и
ее
также
называют
характеристикой холостого хода.
98

99.

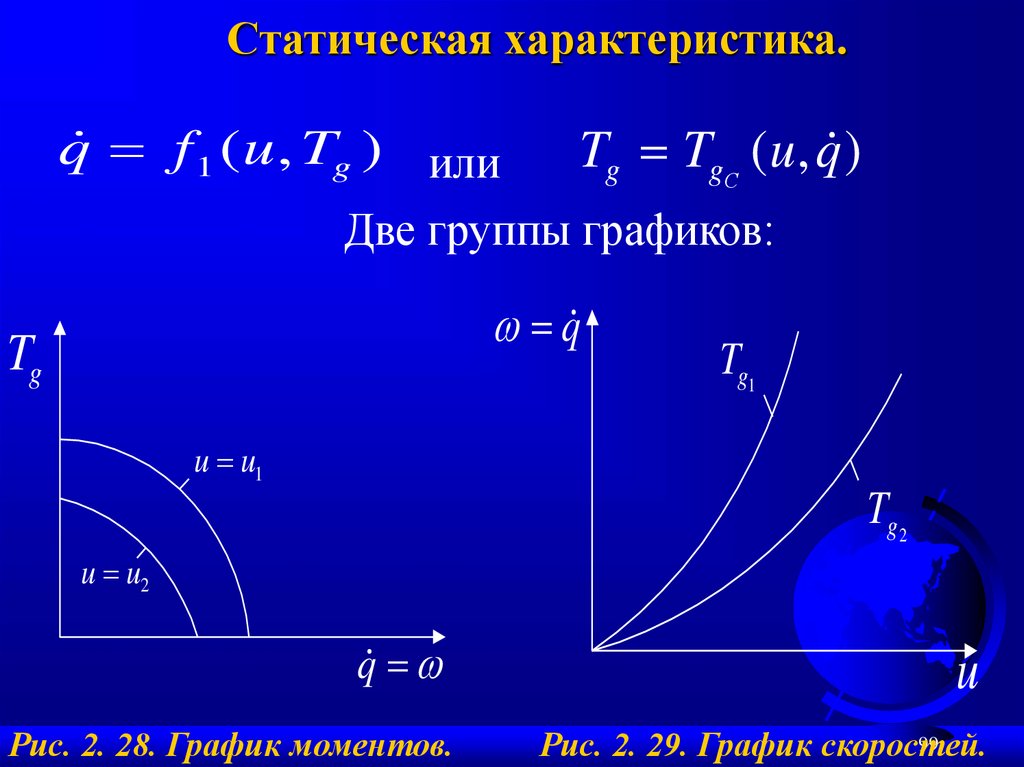
Статическая характеристика.
q f 1 ( u , Tg ) или
Tg TgС ( u , q )
Две группы графиков:
q
Tg
Tg1
u u1
Tg2
u u2
q
Рис. 2. 28. График моментов.
u
99
Рис. 2. 29. График скоростей.

100.

На рис. 2. 28 представлены рабочие характеристики (u = const).
На рис. 2. 29 представлены регулировочные
характеристики (Тд = const).
Статические характеристики двигателей
используются при исследовании режимов
установившегося движения.
В
переходных
режимах
(разгон,
торможение,
изменение
нагрузки)
использование статических характеристик
дают
неточные
результаты,
поэтому
учитывают динамические характеристики. 100

101.

Динамическая характеристика:
q f 2 (u, Tg , T g );
q f 2 (u, Tg T g );
Tg T g Tg„ (u, q );
- величина, имеющая размерность времени,
называется собственной постоянной времени
двигателя и отражает инерционность физических
процессов, протекающих в двигателе.
Характеристики некоторых механизмов
рассмотрим в пакете ДИНАМО. Для этого
выйдите на рабочий стол и нажмите ярлык
DINA.
101

102.

Определение сил давления
в кинематических парах.
Основная задача силового расчёта определение всех сил и моментов, действующих на
звенья механизма и в их соединениях.
Определение внешних сил изложено выше,
поэтому будем считать их заданными.
Рассмотрим определение реакций в соединениях звеньев.
Методы расчёта: аналитические и графиче-
ские.
102

103.

На начальном этапе
принимаются допущения:
расчёта
• все звенья абсолютно твёрдые;
• в соединениях звеньев зазоры отсутствуют;
• силы трения не учитываются.
С учетом принятых допущений сила реакции
во вращательной паре приложена в центре
шарнира и раскладывается: при графическом
решении по направлениям вдоль звена
и
перпендикулярно ему; при аналитическом
решении - по направлению осей ОХ и ОY; в
поступательной паре сила реакции направлена
103
перпендикулярно направляющей.

104.

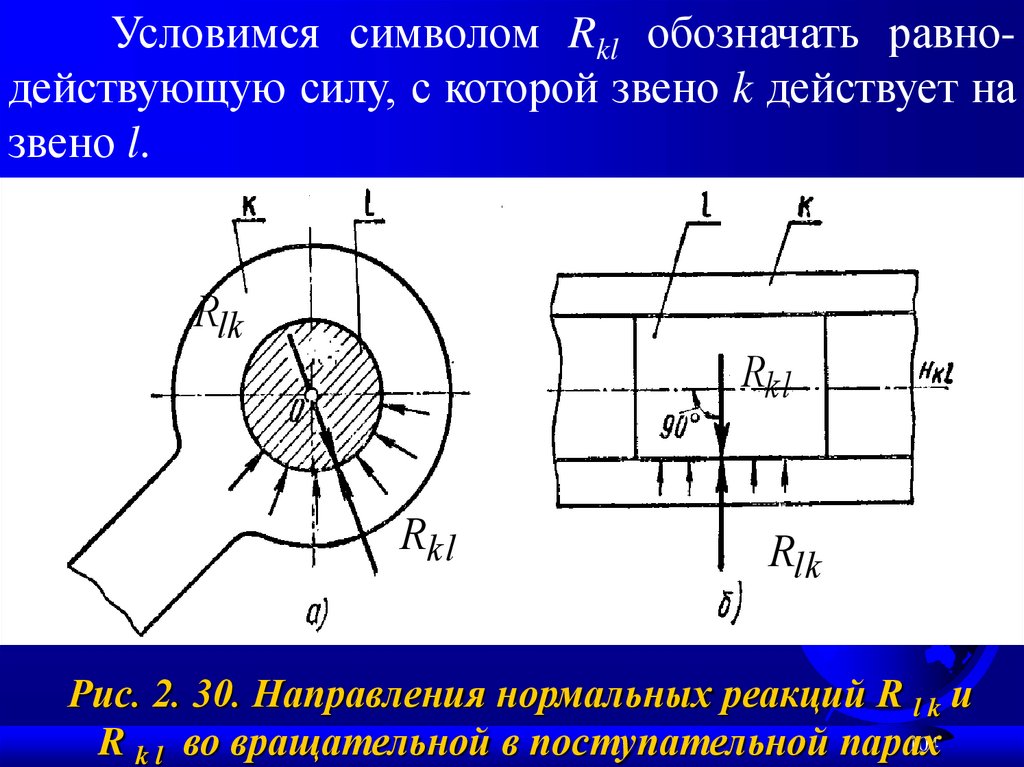
Условимся символом Rkl обозначать равнодействующую силу, с которой звено k действует на
звено l.
Rlk
Rkl
Rkl
Rlk
Рис. 2. 30. Направления нормальных реакций R l k и
104
R k l во вращательной в поступательной парах

105.

Тогда Rlk будет сила действия звена l на звено
k, причем по третьему закону Ньютона
R kl R lk .
Итак, если звенья k и l образуют
вращательную пару с центром в точке A, то сила
Rkl проходит через точку A, причем величина и
направление этой силы неизвестны. Если же
звенья k и l образуют поступательную пару, то сила
Rkl известна по направлению (перпендикулярно
направляющей), но неизвестны ее величина и
точка приложения. Таким образом, в обоих этих
случаях число неизвестных элементов равно двум.
105

106.

Расчёт группы Ассура II1
Рассмотрим
четырёхзвенника.
R32
F2
R43t
F2
шарнирного
R43
R12n
T3
Fур
R
примере
F3
T2
n
12
на
R
n
43
F3
R43n
R43t
Fур R12
R12t
R12t
Рис. 2. 31. Определение сил в кинематических парах
четырёхшарнирного механизма
106

107.

На каждое звено механизма, например на
звено 2, может действовать ряд сил и пар сил.
К силам и парам сил, действующим на звено
2, добавляем силу инерции Fин2 и пару сил
инерции. Сложив все силы, действующие на звено
2, получим результирующую силу F2.
Сложив моменты всех пар сил, действующих
на звено 2, получим момент T2.
Звено 3 нагружаем силой F3, которая является
результирующей всех сил, действующих на звено
3, и силы инерции Fин3, а также моментом T3 ,
представляющим собой сумму моментов всех пар
сил и пары сил инерции.
107

108.

На звено 2 действует, кроме того, сила в точке
А со стороны звена 1, которую обозначим R12, и
сила в точке В со стороны звена 3, которую будем
обозначать R32 . На звено 3 в точке В действуют
сила R23 со стороны звена 2 и в точке С — сила R43
со стороны звена 4.
Таким образом, в рассматриваемом примере
считаем заданными силы Fi и моменты Ti , а также
линию действия силы Fур. Искомыми являются
силы в кинематических парах R41 , R12 , R23 , R43
также величина и направление силы Fур (или Tур).
108

109.

Применяя способ, предложенный II. Г.
Бруевичем разложим силу R12 на две —
параллельно АВ и перпендикулярно АВ. Первую
составляющую будем называть нормальной
составляющей (R12)n; вторую — тангенциальной
(R12) .
Поставим на силе (R12) стрелку в произвольном направлении.
Затем составим уравнение моментов сил
звена 2 относительно точки В, считая, например,
моменты, действующие по часовой стрелке,
положительными. Из этого уравнения находим
109
(R12) .

110.

Знак минус показывает, что первоначально
направление силы выбрано неправильно и должно
быть заменено на противоположное. Плечи li
должны быть взяты в действительных мерах (в
метрах). Для этого следует отрезки, изображающие эти величины на чертеже (в миллиметрах),
умножить на масштабный коэффициент l.
Аналогично определяем силу (R43) .
Составляем далее уравнение суммы всех сил,
приложенных к звеньям 2 и 3. В этом уравнении не
указаны силы R32 и R23, так как звенья 2 и 3
рассматриваются совместно и эти силы будут
внутренними силами.
110

111.

Силы, известные и по величине и по
направлению,
подчеркиваются
дважды,
а
известные только по направлению — один раз.
Уравнение решается построением плана сил.
Имея величины всех известных сил, выбираем масштабный коэффициент для сил F и вычисляем длины отрезков, изображающих эти силы.
Начиная от произвольной точки Н откладывают последовательно все известные силы.
Проведя через начальную и конечную точки
линии, параллельные силам (R41)n и (R43)n, находим
в пересечении этих линий точку е.
111

112.

Замкнув план сил, получаем нормальные
составляющие (R41)n и (R43)n. Сложив силы (R41)n и
(R41) , т. е. соединив точки с и е, получаем полную
силу R41 . Аналогично,
соединив точку а с
точкой е, получим полR32
ную силу R43 . Затем
R12
составляем уравнение
сил звена 2 и строим для
F2
него план сил, определяем силу R32. После
этого выполняется расРис. 2. 32. План сил звена 2.
чёт первого звена.
112

113.

Уравновешивающую
силу Fур считаем приложенной
к звену 1. Линию действия
силы Fур полагаем известной.
Для упрощения задачи будем
считать, что других сил (в том
числе и сил инерции) к звену 1
не приложено. На звено 1,
однако, действует в точке А
сила R12 со стороны звена 2 и
в точке О — сила R01 со
стороны звена 0.
Fур
R21
R01
Рис. 2. 33. План сил звена 1.
113

114.

В точке А на звено 1 действует сила R21 = - R12 .
Определяется сила Fур из уравнения моментов
сил, действующих на звено 1, относительно точки
О. Далее составляем уравнение суммы сил,
приложенных к звену 1. Построив план сил,
находим силу R01 в виде замыкающей.
Расчёт группы Ассура II2
Рассмотрим определение реакций в группе
Ассура второго класса второго вида.
В этом случае в поступательной паре известно направление реакции R01 - перпендикулярно
направляющей, неизвестна точка приложения её,
114
т. е. плечо H03

115.

F2
F
S 3
R12
S2
А
T3
R03
R32
F2
3
В
T2
R12n
F3
H03
R03
С
R12
R12
R12n
Рис. 2. 33. Определение реакций в группе Ассура
второго класса второго вида.
Порядок расчёта: 1. Составляется сумма моментов всех сил, приложенных к звену 2, относительно точки B - определяется R .
12
2. Строится план сил для звеньев 2 и 3 - опреде115
ляется R03 .

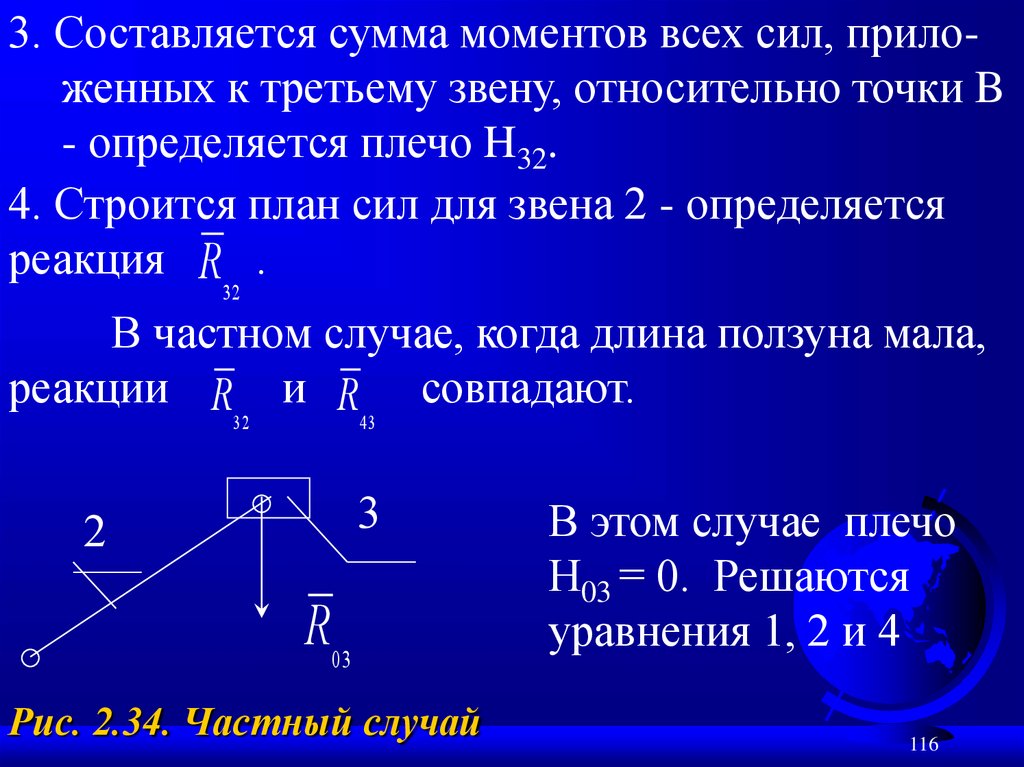
116.

3. Составляется сумма моментов всех сил, приложенных к третьему звену, относительно точки B
- определяется плечо H32.
4. Строится план сил для звена 2 - определяется
реакция R .
32
В частном случае, когда длина ползуна мала,
реакции R и R совпадают.
32
43
3
2
R03
Рис. 2.34. Частный случай
В этом случае плечо
Н03 = 0. Решаются
уравнения 1, 2 и 4
116

117.

ПОРЯДОК СИЛОВОГО РАСЧЁТА
1. Определяются все внешние силы
(силы тяжести FGi , силы инерции Fиi , сила
полезного сопротивления Fпс , моменты пар
сил инерции Tиi) и прикладываются к звеньям
на кинематической схеме механизма.
2. Расчёт начинается с самой удалённой от
входного звена группы Ассура. Связи
заменяются реакциями, которые раскладываются на две составляющие (рис. 2. 31).
3. Составляются уравнения моментов для
отделённой группы.
117

118.

4. Выполняется графическое решение
векторного
уравнения
суммы
всех
сил,
действующих на оба звена рассматриваемой
группы (строится план сил). Для его построения
задаются масштабным коэффициентом. В этом
случае определяются реакции в крайних (во
внешних) кинематических парах.
5. Реакция во внутренней кинематической
паре определяется построением плана сил для
одного (любого) из звеньев рассчитываемой
группы Ассура.
6. Уравновешивающий момент определяется
после расчёта всех групп Ассура.
118

119.

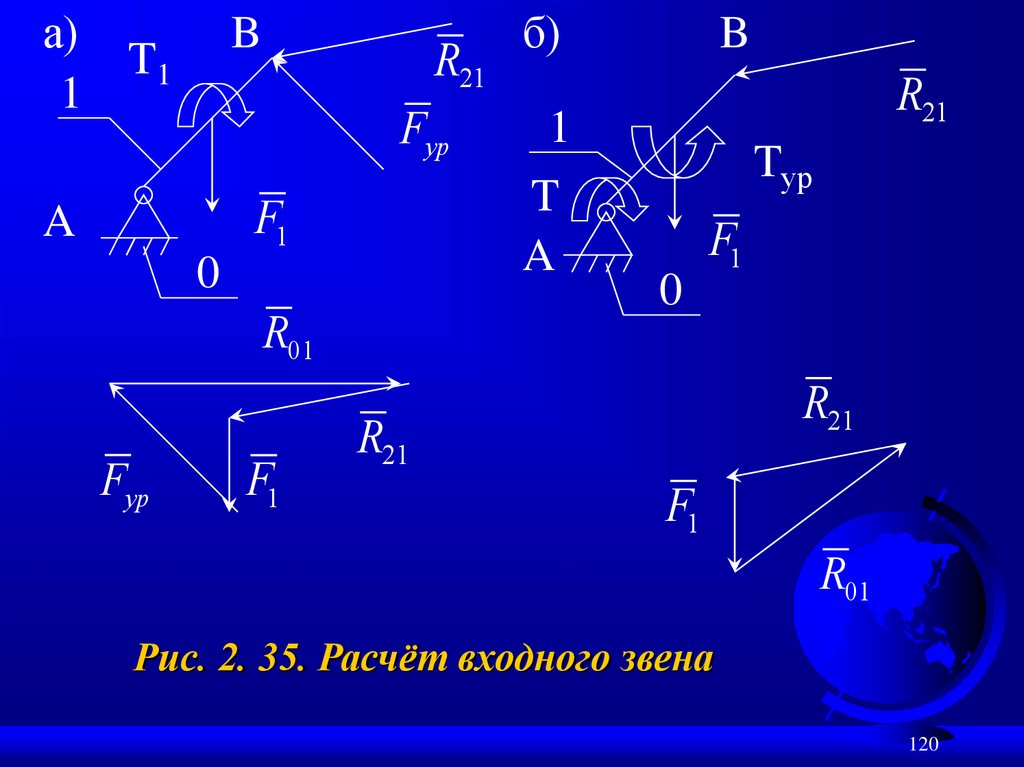
Для этого составляется уравнение равновесия
для входного звена. Реакция в соединении
входного звена со стойкой
определяется
построением плана сил для него.
На рис.2. 35. показано два варианта:
а) к входному звену приложена уравновешивающая сила Fур .
б) к входному звену приложен уравновешивающий момент Tур .
Реакция R01 отличается и по величине и по направлению. Это зависит от способа соединения
валов двигателя и исполнительного механизма
119

120.

а)
T1
1
B
R21
Fур
F1
A
0
R01
Fур
F1
б)
1
T
A
B
R21
Tур
0
F1
R21
R21
F1
R01
Рис. 2. 35. Расчёт входного звена
120

121.

После определения Fур можно определить
уравновешивающий момент.
7. По уравновешивающему моменту определяется мгновенная мощность двигателя:
Pмгн = Tу • 1, где
Pмгн - мгновенная мощность, вт ;
Tу - уравновешивающий момент, Нм;
1 - угловая скорость входного звена с-1;
С помощью системы ДИНАМО можно
определить средний уравновешивающий момент.
121

122.

Мощность двигателя необходимого для данного
механизма можно примерно определить:
P = Tу • 1/ , где
- коэффициент полезного действия
механизма ( 0,75).
Расчёт других групп Ассура рассмотрите
самостоятельно.
Для изучения используйте рекомендованную
литературу и методические указания:
Зиборов С. А., Кузлякина В.В, Кинетостатика
рычажных механизмов, МГУ, Владивосток, 2006 г.
122

123.

2. 3. Элементы динамики машин.
Задачи динамического анализа механизмов :
Кинематическое исследование механизмов
выполняется при условии, что движение входных
звеньев заданы. Движение выходных звеньев
определяется без учета сил, действующих между
звеньями механизма, а также внешних сил.
Геометрические аналоги кинематических
величин зависят от структуры механизмов и геометрических соотношений в размерах звеньев.
123

124.

1. Изучение сил, действующих на звенья механизмов и сил, возникающих при их движении.
2. Изучение энергетического баланса машины,
т. е. соотношения между работами, производимыми силами, действующими в механизме,
а также сравнение машин с помощью КПД.
3. Изучение истинного движения звеньев механизмов под действием заданных сил (прямая
задача динамики). В большинстве случаев эта
задача решается приближенно, широко используются экспериментальные методы исследования.
124

125.

Задачи динамического синтеза машин:
1. Определение условий, обеспечивающих
требуемые практикой режимы движения звеньев
машины и режимы работы машины (обратная
задача динамики). Эта задача, называемая также
теорией регулирования, одна из труднейших в
теории механизмов.
2. Определение условий, уменьшающих динамические нагрузки в подвижных кинематических
парах механизмов и в опорах. Этот раздел
называется теорией уравновешивания масс.
3. Обеспечение требуемой точности движения
входных звеньев на различных режимах работы
машины и уменьшения колебательных процессов
125
в машинах (виброзащита машин).

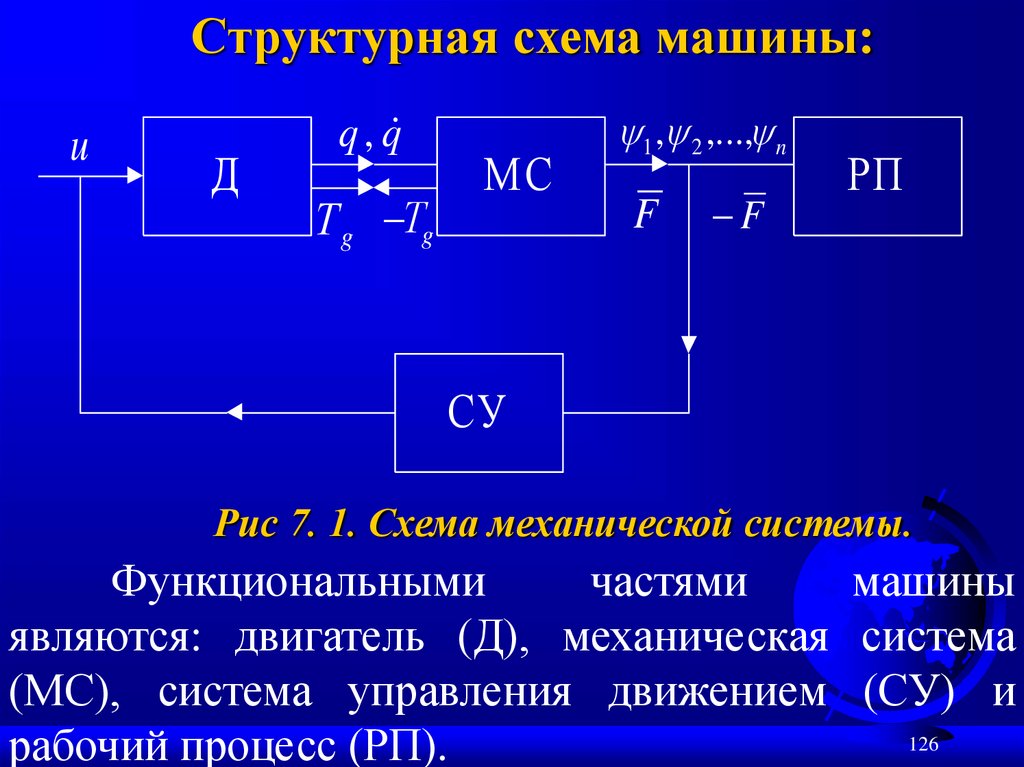
126.

Структурная схема машины:
u
Д
q , q
Т g Тg
МС
1 , 2 ,..., n
F
F
РП
СУ
Рис 7. 1. Схема механической системы.
Функциональными
частями
машины
являются: двигатель (Д), механическая система
(МС), система управления движением (СУ) и
126
рабочий процесс (РП).

127.

Для двигателя входным параметром является
параметр u, управляющий преобразованием
энергии. Это, например, напряжение в обмотке
якоря в электродвигателях, в ДВС – это
перемещение заслонки, подающей топливо, в
пневматических машинах – это перемещение
дросселя, в гидравлических двигателях – перемещение золотника. Выходной параметр двигателя q
- скорость.
- перемещение звена или q
Число степеней подвижности механической
системы определяется числом двигателей m.
Выходными параметрами механической
системы являются: координаты рабочих звеньев.
127

128.

s =Пs (q1 , q2 , …, qm ) .
(7. 1.)
В общем случае в машине или агрегате может
быть m двигателей и n механизмов. Это могут
быть механизмы передаточные, исполнительные и
управляющие.
Важным элементом любой машины является
система управления – совокупность устройств,
обеспечивающих нормальное протекание рабочего процесса. Разнообразные функции систем
управления в большинстве случаев исполняется
человеком - оператором. Сейчас в большинстве
случаев процедура управления автоматизирована.
128

129.

На современном этапе развития науки и техники автоматизация производства решается на
уровне роботизированных комплексов. Промышленный робот – машина для комплексного
осуществления функций управления, обеспечиающий замену человека при управлении машинами.
129

130.

3. 4. Динамическая модель машины.
Теоретическое исследование любого физи-
ческого процесса начинается с составления физической модели, в которой стремятся отобразить на-
иболее существенные факторы рассматриваемой
задачи. При динамическом исследовании такая
модель называется динамической. Это есть идеализированное отображение рассматриваемой сис-
темы, используемое при ее теоретическом исследовании и инженерных расчетах.
130

131.

Простейшая динамическая модель представлена на
рис.10.2. В этой модели все звенья приняты неупругими и
модель практически кинетостатическая. Её можно
представить в виде:
б)
а)
в)
m
сопр
F пр
пр
дв
F пр
T
дв
m
сопр сопр
T
F пр
пр
пр
T дв
пр
I пр
Рис. 10. 2. Динамические модели
а). поступательно движущаяся масса;
б). сосредоточенная масса, движущаяся
вращательно;
в). распределённая масса, движущаяся
вращательно.
Эта модель, как правило, используется для
предварительных расчетов.
131

132.

Основными параметрами динамической
модели являются приведённые силы и массы.
Приведение масс и моментов инерции
базируется на известных положениях механики
и в частности на равенстве кинетической
энергии масс приводимых и приведенной.
динамической модели.
Приведение масс и сил - это прием,
позволяющий упростить расчетную схему и
привести ее к какой-то динамической модели.
Приведённая масса определяется из условия
равенства кинетической энергии приведённой
массы и кинетической энергии всех звеньев
машин.
132

133.

Епр = Еi
mi Si2
i2
Епр
I Si
;
(10. 5)
2
2
В основе приведения сил и моментов сил
лежит известное в механике положение о равенстве элементарных работ на возможных перемещениях для приводимых сил и моментов и приведенных.
Апр = Аi
S
Aпр F j dS j Т k d k
S0
(10. 6)
0
133
Для нашего примера без учета упругости звеньев:

134.

Кинетическая энергия выходной части механизма
(приводимых масс):
1
2
2
2
2
Епр I 21 2 I 22 2 I 23 3 m4 4
2
z
3
2
Причем:
;
r2 ;
2 z3
2
I2 = I21 + I22 + I23(z 2 )2 + mr22,
т.е. в этом примере
В общем случае:
z3
I2 = const
2
;
2
I пр mi Si I Si i
134

135.

Приводить можно к любому звену и соответственно этому звену будут аналоги скоростей.
На начальной стадии проектирования
мы вы-бираем динамическую модель I класса I
модифика-ции по условной формуле О - П - О и
именно мо-дель с распределенной массой. Для
этой модели
I
пр
М
Т
пр
Aпр Tпр d
0
135

136.

2
2
Si
i
I Si
;
I пр mi
пр
пр
т.к. звеном приведения чаще является входное
звено, то
S S
S ;
пр 1
i
i
i
Тогда
2
i
i ;
пр
2
I пр mi Si I Si i ;
S
T d F d S T d
пр
0
i
S0
i
1
0
k
136

137.

Поделив на dt обе части, придем к мгновенной
мощности
Tпр пр F i i T k k ;
Tпр F i i T k k .
Для определения параметров динамической
модели Iпр и Tпр необходимо использовать систему
ДИНАМО. Сначала необходимо выполнить
структурирование и определение кинематических
характеристик
исследуемого
механизма
с
помощью подсистемы КИНМЕХ.
137

138.

Выполнив приведение сил и масс, любой
механизм с одной степенью свободы (рычажный,
зубчатый, кулачковый и др.), сколь сложным бы он
ни был, можно заменить его динамической
моделью. Эта модель в общем случае имеет
переменный приведенный момент инерции Jпр, и к
ней приложен суммарный приведенный момент
Tпр. Закон движения модели такой же, как и закон
движения начального звена механизма. Каждой
физической
модели
соответствует
своя
математическая модель, то есть система
138

139.

дифференциальных, интегральных или интегрально - дифференциальных уравнений с
помощью которых описывается исследуемое
явление. При составлении математической модели
часто приходится принимать некоторые гипотезы и
допущения либо из-за неполной информации об
исследуемом объекте, либо с целью упрощения
исследования.
Основой
для
составления
уравнения
движения механизма с одной степенью свободы
служит теорема об изменении кинетической
энергии:
E - Eнач = А.
139

140.

Работу совершают все активные силы и
моменты, силы трения во всех кинематических
парах механизма.
Епр I пр
1
2
2
;
k
Sj
(11. 1)
A F j dS j Т k d k
S jна ч
kна ч
Здесь переменная интегрирования - координата
начального звена.
140

141.

Для упрощения записи здесь и в дальнейшем
опускаем значок “пр” при приведенных моментах
и приведенных моментах инерции, а также номер 1
начального звена в обозначении его координаты ,
угловой скорости и углового ускорения . В
общем случае верхний предел интегрирования в
уравнении (11. 1) считается переменным.
Уравнение движения в энерТ
гетической форме для этой
динамической модели:
2
I
ω
Iω
нач
нач
ΣA (11.2)
2
2
141
Рис. 11. 1. Динамическая модель
2

142.

По этому уравнению можно определить
зависимость скорости начального звена от его угла
поворота, т. е. ( ). Подобная задача является
распространённой. Например, механизмы дизелькомпрессоров, буровых станков и подъёмных
кранов с приводом от двигателей внутреннего
сгорания, различных устройств с пневмоприводом,
приборов с пружинным двигателем. Для решения
поставленной задачи нужно взять уравнение
движения в энергетической форме (11. 2):
I нач нач
2 A
I
I
2
(11.10)
142

143.

3. 5. Регулирование движения в машинах
Процесс движения машинного агрегата в
общем случае состоит из трех фаз (рис. 12. 1.).
• разбега;
• установившегося режима;
• выбега.
Разбег и выбег относятся к неустановившимся
режимам, которые характеризуются непериодическими, т. е. неповторяющимися, изменениями
скорости главного вала агрегата (начального
звена).
143

144.

При установившемся режиме скорость главного вала изменяется периодически. В частном
случае скорость может быть постоянной.
Рис 12. 1. Этапы движения в машинах
Часто установившееся движение чередуется с
разгонами (при повышениях скоростного режима)
и торможениями (при понижениях скоростного
144
режима).

145.

Так работает, например, автомобильный
двигатель. Многие механизмы в установившемся
режиме вообще не работают. Это особенно
характерно для целого ряда приборов (реле,
контакторы и т. п.). Их механизм во время
срабатывания переходит из одного положения в
другое, не совершая замкнутого повторяющегося
кинематического цикла.
Установившимся движением называется
такое, при котором скорость начального звена
(обобщенная скорость) является периодической
функцией времени. График (t) при установившемся движении (тахограмма) представлен на рис.
145
12. 2.

146.

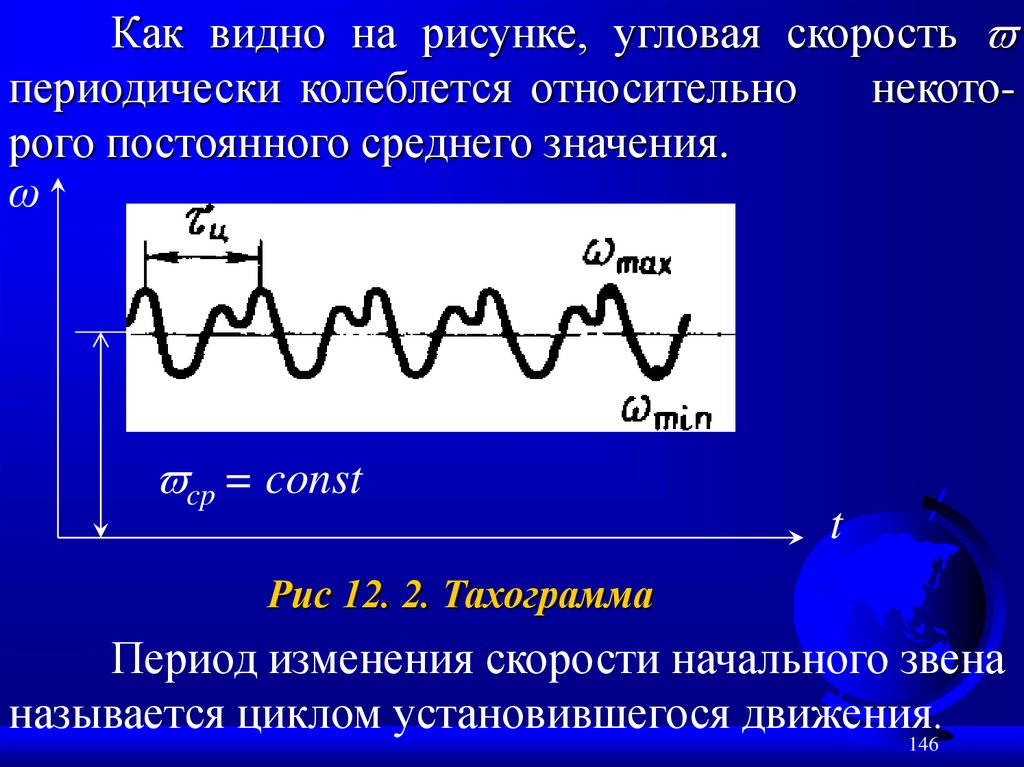
Как видно на рисунке, угловая скорость
периодически колеблется относительно
некоторого постоянного среднего значения.
ω
cp = const
t
Рис 12. 2. Тахограмма
Период изменения скорости начального звена
называется циклом установившегося движения.
146

147.

Время ц равно или кратно периоду действия
сил. При установившемся режиме сумма работ
всех сил за цикл равна нулю:
Ац = 0
(12. 1.)
Так как работа сил тяжести за цикл равна
нулю, то равенство 12. 1. Будет выполняться, если
работа движущих сил за цикл равна работе всех
сил сопротивления за цикл (по модулю):
ц
ц
Aд Ac .
(12. 2.)
Из уравнения 12. 2. Следует, что приращения кинетической энергии механизма за цикл не
147
происходит.

148.

Tкон = Тнач
Следовательно, угловая скорость начального
звена в начале и в конце цикла одинакова, но
внутри цикла она изменяется, проходя через max
и min значения.
При установившемся режиме скорость
начального звена остается в среднем постоянной.
Неравномерность вращения оценивается коэффициентом неравномерности:
( max min )
.
(12. 3.)
cp
148

149.

Из уравнения (12. 3) видно, что —
характеризует размах колебаний скорости по
отношению к ее среднему значению. Чем меньше
, тем относительно меньше размах колебаний,
тем спокойнее вращается начальное звено.
Величина ср (рад/с) подсчитывается по
формуле ср = 2 n, в которой п — частота
вращения начального звена, с-1.
Для каждого вида машин имеется своя допус
тимая величина коэффициента неравномерности
[б], выработанная практикой.
Для металлорежущих станков это 1/25 - 1/50,
для прядильных машин 1/50 - 1/100, для дизельного
149
привода электрогенераторов 1/100 - 1/200.

150.

Коэффициент неравномерности - величина
весьма малая, что позволяет принять среднюю
величину угловой скорости равной среднему
арифметическому из ее максимального и
минимального значений:
( max min )
(12. 4.)
cp
.
2
Совместное решение уравнений (12.3) и (12.4) дает
величины максимальной и минимальной скорости:
max cp (1 / 2),
min cp (1 / 2). (12. 5.)
Как видно из уравнений (12.5), отличие max и
min от cp , отнесенное к cp , составляет ± /2, т.
150
е. обычно не более ± 2%.

151.

В установившемся режиме работают очень
многие машины (станки, прессы, прокатные станы,
лесопильные
рамы,
текстильные
машины,
генераторы электрической энергии, компрессоры,
насосы и т.д.). Наилучшее условие для работы всех
этих машин — абсолютно равномерное вращение
их главного вала (принимаемого обычно в качестве
начального звена).
Колебания скорости главного вала вызывают
дополнительные
динамические
нагрузки,
вследствие чего снижается долговечность и
надежность машин.
Колебания скорости ухудшают рабочий
151
процесс машины.

152.

Поскольку колебания скорости полностью
устранить нельзя, то необходимо по возможности
сократить их размах.
Иными словами, величину коэффициента
неравномерности надо сделать допустимо
малой. Рассмотрим, каким образом можно
решить эту задачу.
Все звенья механизма обладают инертностью.
Как известно из физики, это свойство состоит в
том, что чем инертнее материальное тело, тем
медленнее происходят изменения его скорости,
вызываемые действием приложенных сил.
152

153.

Чтобы получить вращение главного вала
машины с циклической неравномерностью, не
превышающей требуемой величины, инертность
этого вала со всеми жестко связанными с ним
деталями надо сделать достаточно большой. Для
этого на главном валу машины надо закрепить
добавочную массу, выполненную в виде колеса с
развитым ободом и называемую маховиком.
Это хорошо видно из уравнения (12. 6).
1 dI 2
T ( )
1
2 d
1
.
(12. 6.)
I ( ) I М
153

154.

Подбирая его момент инерции, можно
обеспечить вращение главного вала машины с
заданным коэффициентом неравномерности [ ].
Основное назначение маховика состоит в
ограничении колебаний угловой скорости в
пределах, устанавливаемых величиной коэффициента неравномерности [ ].
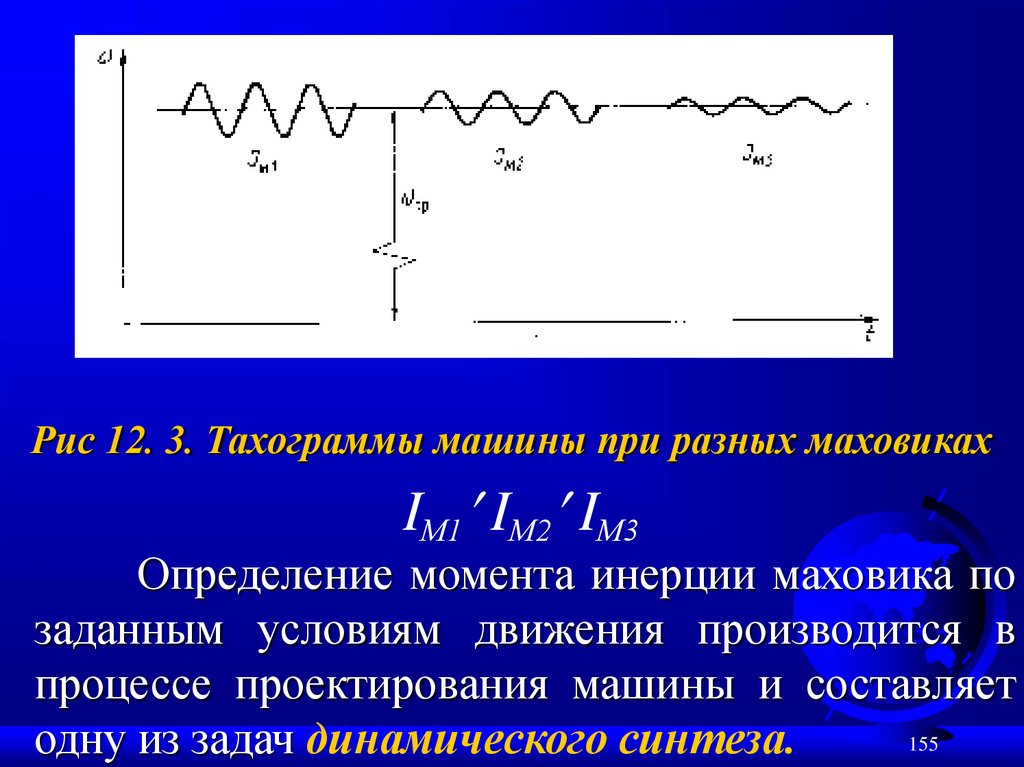
На рис. 12. 3 показано влияние момента
инерции маховика на уровень колебаний
скорости.
Чем меньше заданное значение коэффициента
неравномерности , тем больше должен быть
момент инерции маховика, тем массивнее он будет.
154

155.

Рис 12. 3. Тахограммы машины при разных маховиках
IМ1 IМ2 IМ3
Определение момента инерции маховика по
заданным условиям движения производится в
процессе проектирования машины и составляет
155
одну из задач динамического синтеза.

156.

3.6. Уравновешивание механизмов.
Из всех сил, приложенных к механизму
наиболее вредное действие оказывает на его
крепления и фундамент динамические давления.
Всякий механизм, у которого звенья движутся в
параллельных плоскостях, можно рассматривать
как систему материальных точек, центр масс
которых при движении механизма занимает в
общем случае последовательно изменяющиеся
положения относительно неподвижной системы
координат. Если привести силы инерции всех
mas
материальных точек механизма к их центруFu масс,
156
то получится главный вектор сил инерции

157.

где m - сумма масс всех его подвижных звеньев,
a s - ускорение центра масс и главный момент
сил инерции материальных точек.
Для равновесия механизма необходимо,
чтобы Pu 0 , что возможно при as 0 , то есть
центр масс должен находиться в покое, а главный
момент сил инерции равняться нулю.
157

158.

Используйте для выполнения курсового
проектирования рекомендованную литературу и
методические пособия:
Попов. С. А., Тимофеев Г. П., Курсовое
проектирование по ТММ, М., Высшая школа ,
1999 г.
Зиборов С. А.. Кузлякина В.В., Рослякова С.Р.
Кинематика рычажных механизмов, МГУ,
Владивосток, 2003 г.
Зиборов С. А., Кузлякина В.В, Кинетостатика
рычажных механизмов, МГУ, Владивосток,
2006 г.
158

159.

ЛЕКЦИЯ № 2
Исследование рычажных
механизмов.
Лекция окончена.
Спасибо за внимание!
159