Двумерные статистические совокупности. Корреляционный анализ

1. Двумерные статистические совокупности. Корреляционный анализ

2. Корреляционный анализ

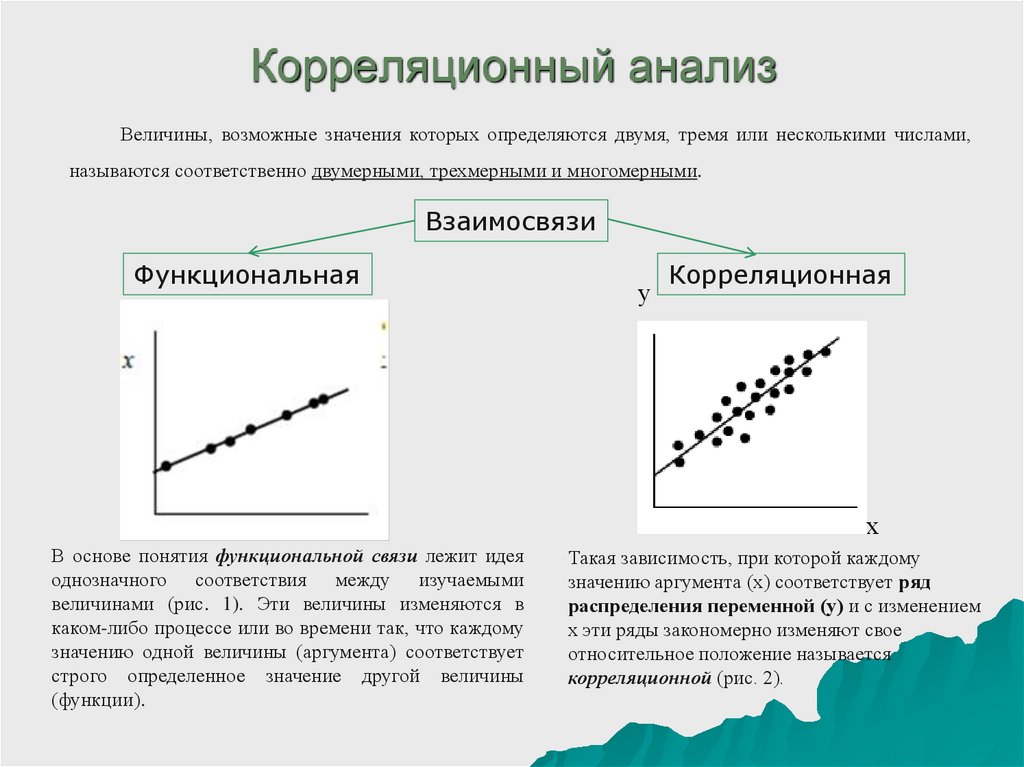
Величины, возможные значения которых определяются двумя, тремя или несколькими числами,
называются соответственно двумерными, трехмерными и многомерными.
Взаимосвязи
Функциональная
у
Корреляционная
х
В основе понятия функциональной связи лежит идея
однозначного соответствия между изучаемыми
величинами (рис. 1). Эти величины изменяются в
каком-либо процессе или во времени так, что каждому
значению одной величины (аргумента) соответствует
строго определенное значение другой величины
(функции).
Такая зависимость, при которой каждому
значению аргумента (x) соответствует ряд
распределения переменной (y) и с изменением
x эти ряды закономерно изменяют свое
относительное положение называется
корреляционной (рис. 2).

3. Корреляционный анализ

Известно, что промышленные скопления магнетитовых руд обычно обнаруживают там,
где фиксируются магнитные аномалии, т.е. между величиной запасов таких руд и
интенсивностью магнитного поля существует определенная зависимость, которая не является
функциональной. Так как, она осложняется магнитностью вмещающих пород, глубиной
залегания рудного тела и другими факторами.
Запасы
Fe, млн.
т.
Магн.
поле,
Тл
15
10
20
10
20
12
25
12
25
15
30
20
30
25

4. Корреляционный анализ

Математический анализ связей, существующих между случайными величинами
составляет содержание корреляционного анализа.
С помощью корреляционного анализа решаются две основные задачи:
1. Установление формы корреляционной связи, т.е. линии регрессии (линейная,
квадратичная, показательная и т.д.);
Корреляция называется линейной, когда направление связи между признаками x и
y графически или аналитически выражается прямой линией.
Когда корреляционная зависимость имеет другое направление, она называется
нелинейной.
2. Оценка силы корреляционной связи или степени сопряженности между
варьирующими признаками.

5. Корреляционный анализ

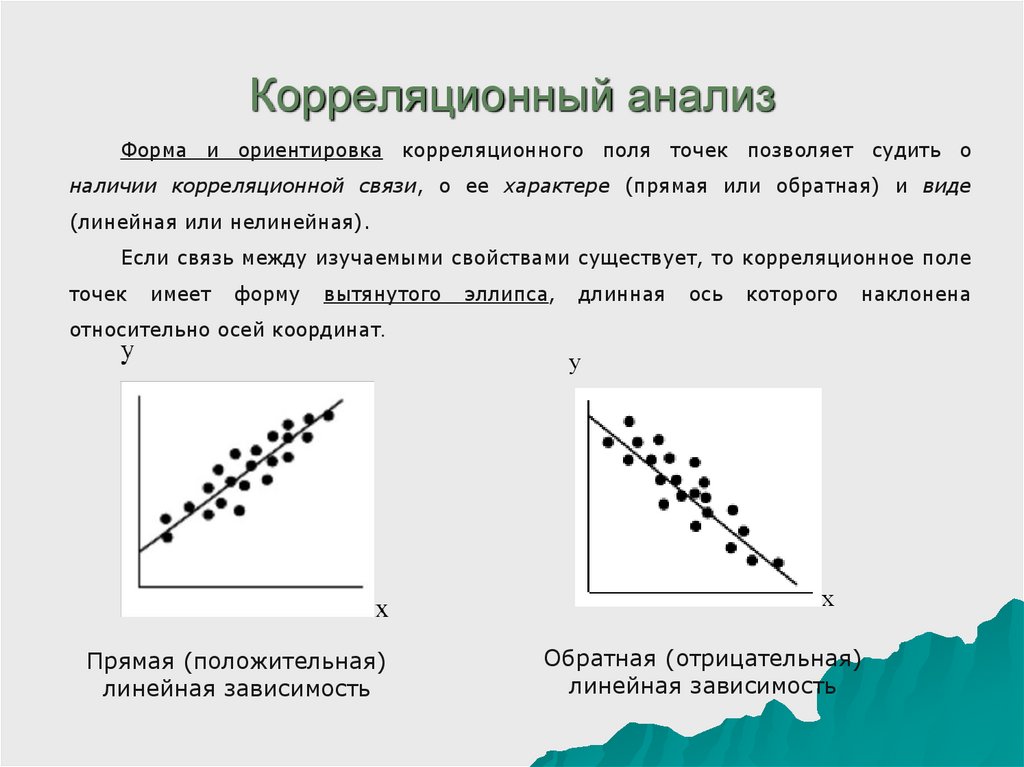
Форма и ориентировка корреляционного поля точек позволяет судить о
наличии корреляционной связи, о ее характере (прямая или обратная) и виде
(линейная или нелинейная).
Если связь между изучаемыми свойствами существует, то корреляционное поле
точек
имеет
форму
вытянутого
эллипса,
длинная
ось
которого
наклонена
относительно осей координат.
у
х
Прямая (положительная)
линейная зависимость
Обратная (отрицательная)
линейная зависимость

6. Корреляционный анализ

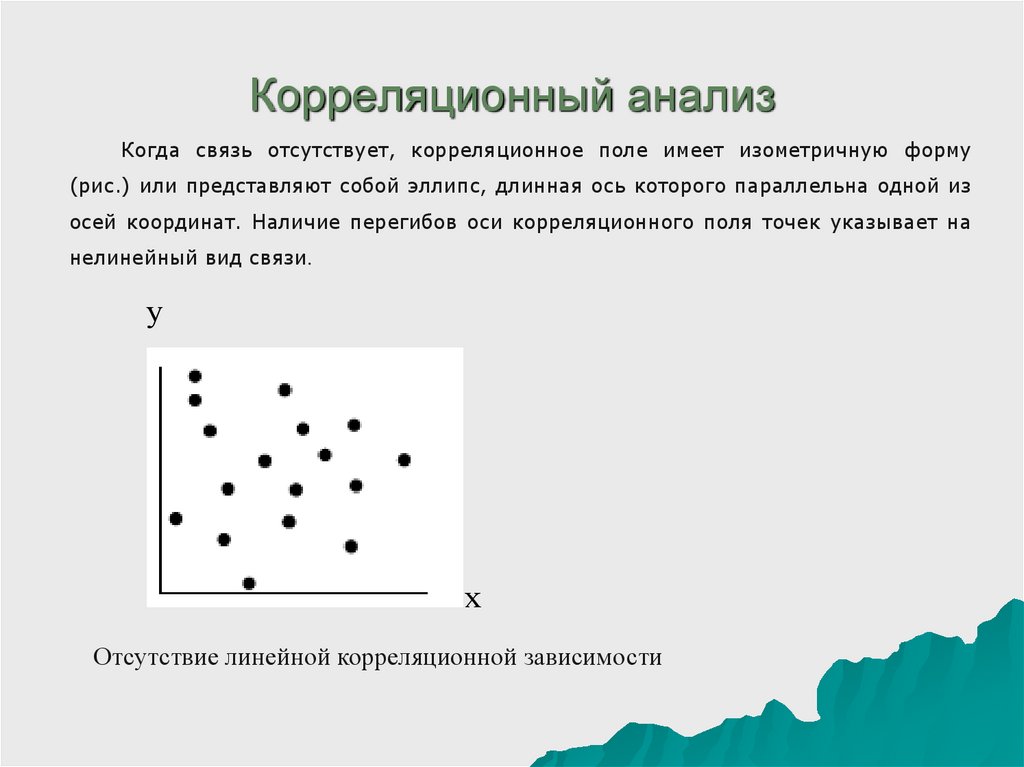
Когда связь отсутствует, корреляционное поле имеет изометричную форму
(рис.) или представляют собой эллипс, длинная ось которого параллельна одной из
осей координат. Наличие перегибов оси корреляционного поля точек указывает на
нелинейный вид связи.
у
х
Отсутствие линейной корреляционной зависимости

7. Регреcсионный анализ

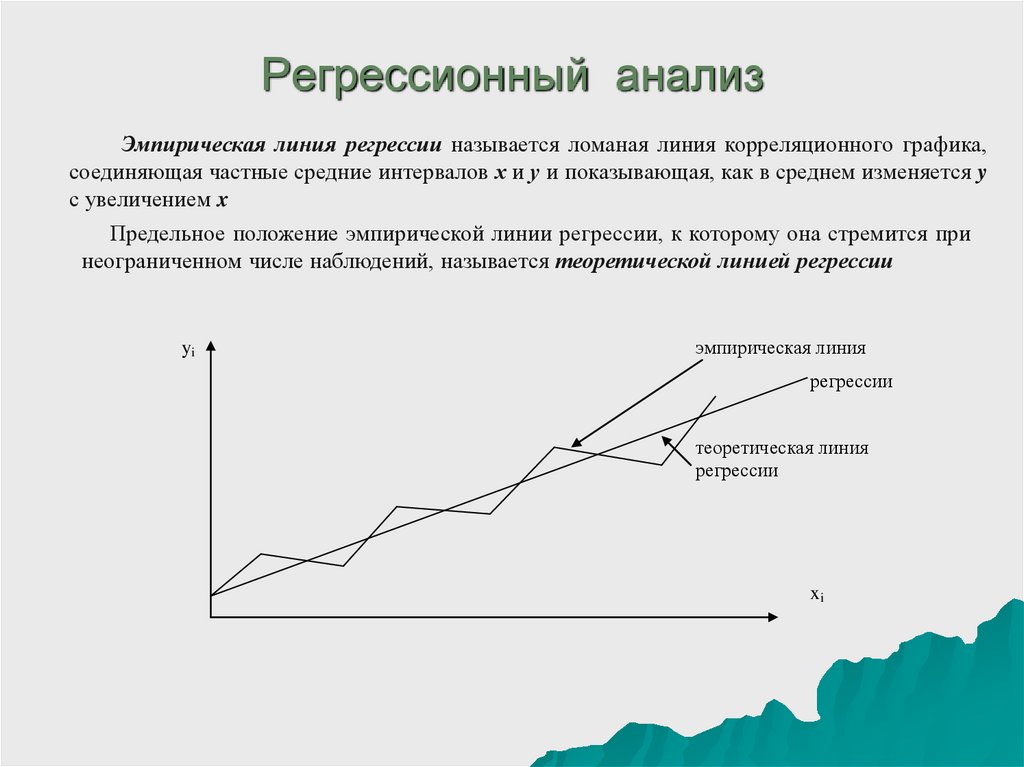
Эмпирическая линия регрессии называется ломаная линия корреляционного графика,
соединяющая частные средние интервалов х и у и показывающая, как в среднем изменяется y
с увеличением x
Предельное положение эмпирической линии регрессии, к которому она стремится при
неограниченном числе наблюдений, называется теоретической линией регрессии
yi
эмпирическая линия
регрессии
теоретическая линия
регрессии
xi

8. Количественные меры оценки корреляционной связи

1. Коэффициент корреляции
r
r = covху / SхSу
covху = (хi- х) (уi- у)/ n – ковариация х и y (совместная изменчивость).
Sх и Sу – стандарты признаков х и у.
Представляет собой правильную дробь, изменяющуюся от –1 до +1
При r>0 зависимость прямая,
при r<0 – обратная,
r=0 свидетельствует об отсутствии линейной связи, но не является
показателем независимости X и Y.
При r =1 между X и Y устанавливается функциональная зависимость
вида y = a+ bx.
По модулю r выделяют группы по силе связи:
0 < r 0,25 отсутствие связи;
0,25 < r 0,5 слабая связь;
0,5 < r 0,75 средняя связь;
0,75 < r 0,9 сильная связь;
0,9 < r 1,0 очень сильная связь, близкая к функциональной.
Проверка значимости коэффициента корреляции
Значимость коэффициента корреляции определяется по критическим значениям r (таблица критических значений).
rкрит. = 0,05 или 0,01;
f= N-c - число степеней свободы, N – количество проб,
с- количество наложенных связей (2).
Если r вычисленное меньше табличного, то значение r незначимое.

9. Статистические характеристики оценки корреляционной связи

2. Корреляционное отношение
Корреляционным отношением называется отношение меры рассеяния условных
средних зависимой переменной к мере рассеяния всех значений зависимой переменной, т.е.
=
( yi )
, где
( y)
y – значения, принимаемые зависимой переменной;
yi – условные средние, соответствующие значениям xi.
По выборочным данным вычисляют выборочное корреляционное отношение
=
S ( yi )
.
S ( y)
значение изменяется от 0 до 1.равенство =0 – необходимое и достаточное условие
отсутствия корреляционной зависимости. При =1 корреляционная связь переходит в
функциональную S( yi) = S(y).
Доказано, что всегда r .
Равенство = r .имеет место в тех случаях, когда зависимость между X и Y
линейная, т.е. это равенство может служить критерием линейности зависимости X и Y.

10. Статистические характеристики оценки корреляционной связи

3. Коэффициент детерминации
Коэффициент
детерминации
–
коэффициент
причинности
( uv2,
vu2).
Он
рассчитывается по формулам
S ф(v)
uv2 =
S (u )
2
2
;
vu2 =
S ф(u )
S (v)
2
2
;
Su2 – дисперсия признака u,
Sv2 - дисперсия признака v,
Sф – факторная дисперсия. Она характеризует изменчивость признака условной
функции под действием фактора условного аргумента.
Коэффициент детерминации оценивает долю изменчивости условной функции под
действием условного аргумента от общей дисперсии условной функции.
Если 2Au-Ag =81 %, то
Это значит, что на 81 % изменчивость содержаний Au в руде обусловлена
изменчивостью содержаний Ag и на 19 % какими-то неучтенными нами другими факторами.

11.

Использование корреляционной зависимости в геологии
1 - Для количественного прогнозирования значений одного признака по значению другого.
2 - Для реконструкции процессов рудообразования.
1. При первом рассчитываются корреляционные уравнения регрессии, оценивается точность в
прогнозировании по уравнению регрессии и в том случае, если точность удовлетворительная, то
определяют значения одного признака по значению уравнения, не производя никаких аналитических
определений.
Пример: в рудах Cd входит в состав сфалерита, Re в состав молибденита. По ограниченному
составу мономинеральных проб рассчитывают характеристики корреляционной зависимости между
содержаниями основного и попутного компонента, которые в дальнейшем используют для
определения средних содержаний попутного компонента в каждом подсчетном блоке.
2. При изучении месторождений отмечается зависимость между знаком коэффициента
корреляции и характером рудообразования.
Если два минерала-носителя двух коррелируемых компонентов образуются одновременно или
сингенетично, то коэффициент корреляции компонентов всегда имеет положительный знак.
Пример: Кусинское месторождение ильменита и магнетита.
rTiO2-Fe = +0,85
Если два минерала носителя двух коррелируемых компонентов метасоматически замещают друг
друга, то корреляция всегда отрицательная.
Пример: Месторождение магнетита г. Высокая.
rSiO2-Fe = -0,85

12. Многомерные методы анализа

1. Многомерный корреляционный анализ применяется для выявления
зависимостей между наблюденными значениями различных геологических
характеристик и разделения множества признаков по характеру их внутренних
связей
2. Модели множественной регрессии используются для предсказания значений
зависимой переменной (содержания ценного компонента, объемной массы руды,
глубины формирования минерала и т.д.) по набору независимых переменных
(содержаний петрогенных элементов, объемной массы тяжелых минералов в рудах,
содержаний элементов–индикаторов и т.д.).
3. Многие прогнозные и интерпретационные задачи решаются в практической
геологии путем сопоставления комплексов признаков изучаемого объекта с
комплексом тех же признаков эталонного объекта. Совокупность подобных методов
основанных на принципе аналогии получила название методов распознавания
образов
4. Дискриминантный анализ является статистическим средством разделения
(дискриминации) многомерных нормально распределенных совокупностей на
группы таким образом, чтобы была достигнута максимальная однородность внутри
групп и минимальная между ними

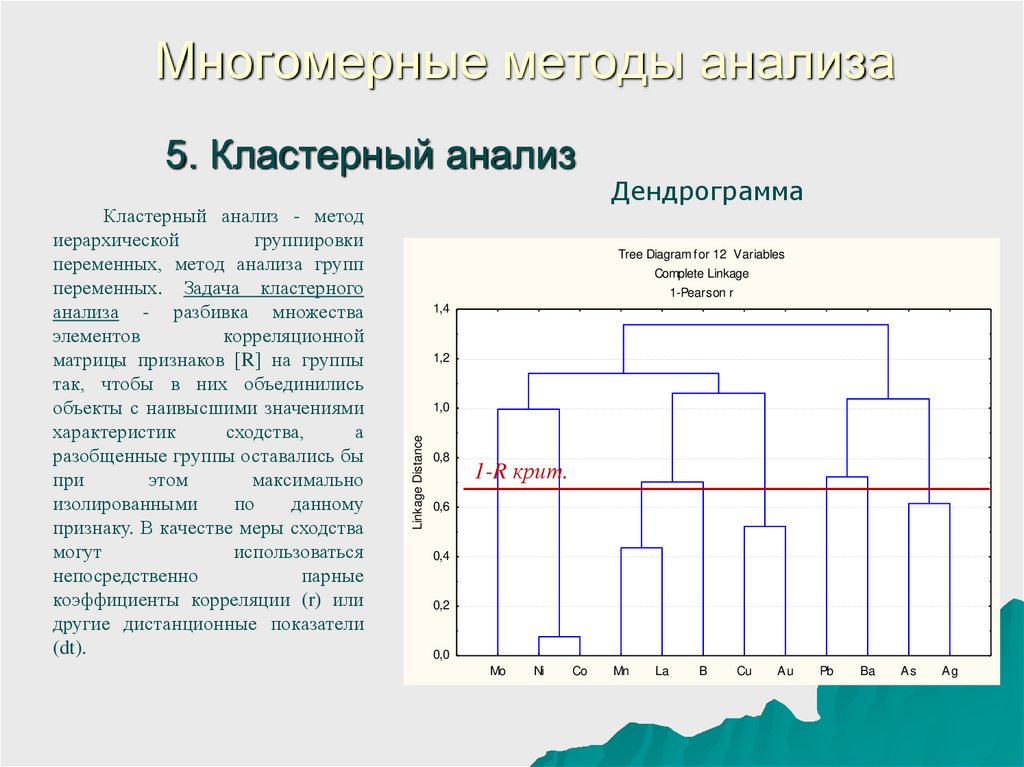
13. 5. Кластерный анализ

Многомерные методы анализа
5. Кластерный анализ
Tree Diagram for 12 Variables
Complete Linkage
1-Pearson r
1,4
1,2
1,0
Linkage Distance
Кластерный анализ - метод
иерархической
группировки
переменных, метод анализа групп
переменных. Задача кластерного
анализа - разбивка множества
элементов
корреляционной
матрицы признаков R на группы
так, чтобы в них объединились
объекты с наивысшими значениями
характеристик
сходства,
а
разобщенные группы оставались бы
при
этом
максимально
изолированными
по
данному
признаку. В качестве меры сходства
могут
использоваться
непосредственно
парные
коэффициенты корреляции (r) или
другие дистанционные показатели
(dt).
Дендрограмма
0,8
1-R крит.
0,6
0,4
0,2
0,0
Mo
Ni
Co
Mn
La
B
Cu
Au
Pb
Ba
As
Ag

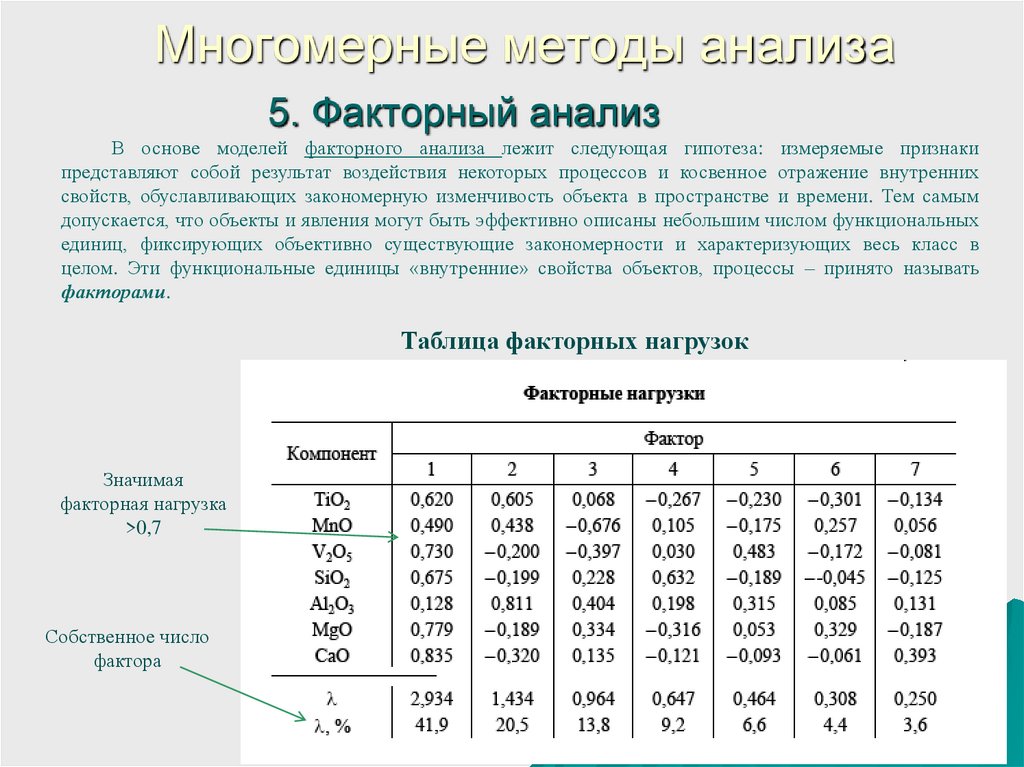
14. 5. Факторный анализ

Многомерные методы анализа
5. Факторный анализ
В основе моделей факторного анализа лежит следующая гипотеза: измеряемые признаки
представляют собой результат воздействия некоторых процессов и косвенное отражение внутренних
свойств, обуславливающих закономерную изменчивость объекта в пространстве и времени. Тем самым
допускается, что объекты и явления могут быть эффективно описаны небольшим числом функциональных
единиц, фиксирующих объективно существующие закономерности и характеризующих весь класс в
целом. Эти функциональные единицы «внутренние» свойства объектов, процессы – принято называть
факторами.
Таблица факторных нагрузок
Значимая
факторная нагрузка
>0,7
Собственное число
фактора