Лекция 7. Корреляционный анализ

1. ЛЕКЦИЯ 7

ТЕМА: «КОРРЕЛЯЦИОННЫЙ
АНАЛИЗ».

2. ПЛАН ЛЕКЦИИ:

Функциональные
и статистические связи.
Корреляция и причинность.
Корреляционная зависимость: отрицательная и
положительная.
Параметрические
показатели
связи. Коэффициент корреляции. Диаграмма
рассеяния. Значение коэффициента корреляции.
Ковариация.
Дисперсия
объединенной
совокупности.
Интерпретация
коэффициента
корреляции.
Непараметрические меры связи: ранговый
коэффициент
корреляции
Спирмена.
Бисериальный
коэффициент
корреляции.
Множественная корреляция. Частная корреляция.

3.

Случаи, когда определенному значению
одной переменной X, называемой
аргументом, соответствует
определенное значение другой
переменной Y, называемой функцией.

4.

Однозначная зависимость между
переменными величинами X и Y, называется
функциональной
Y = f (X)

5.

Зависимость меду переменными
величинами называется корреляционной
или корреляцией от лат correlation –
соотношение или связь.

6.

Впервые термин был применен Ж. Кювье в
труде «Лекции по сравнительной
анатомии».
Развитие теории корреляции связано с
Ф. Гальтоном и К. Пирсеном.
В биометрию ввел понятие Ф. Гальтон
(1888г).

7.

коэффициент корреляции
-показатель степени прямолинейной
связи между признаками

8.

cov { x, y}

9.

Оценка среднего значения
парных произведений
центральных отклонений
называется ковариацией.
cov { x, y}
Может рассматриваться как
мера совместной вариации
величин, как
«совместная дисперсия x и y»

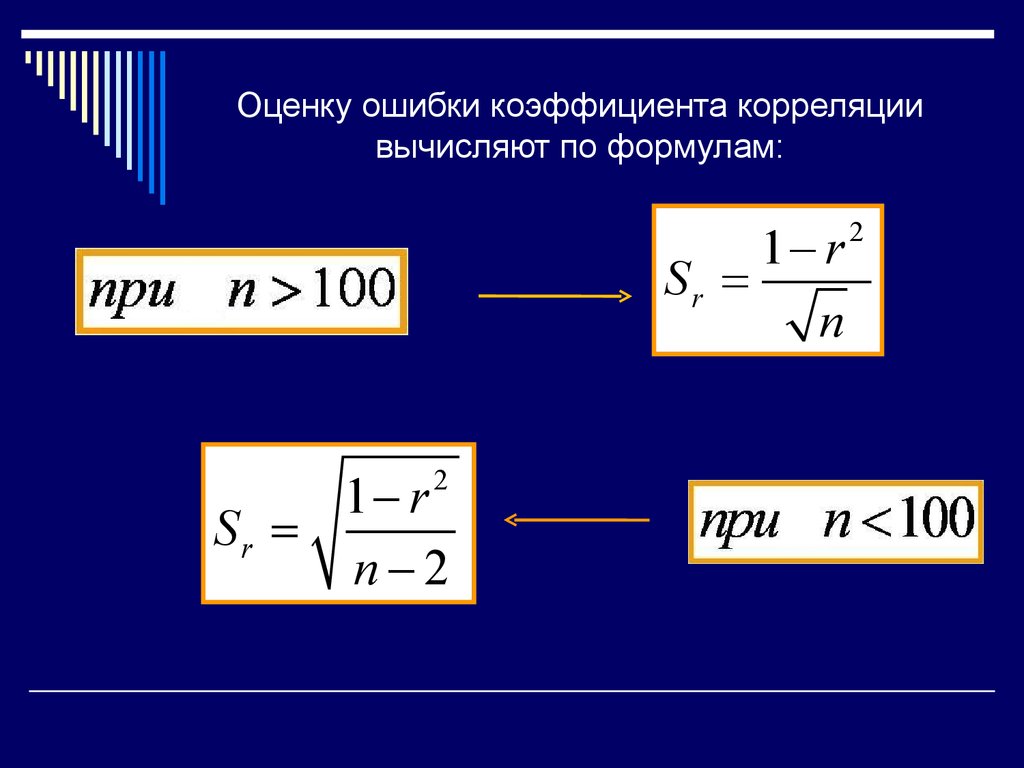
10. Оценку ошибки коэффициента корреляции вычисляют по формулам:

1- r
Sr =
n
1- r
Sr =
n-2
2
2

11.

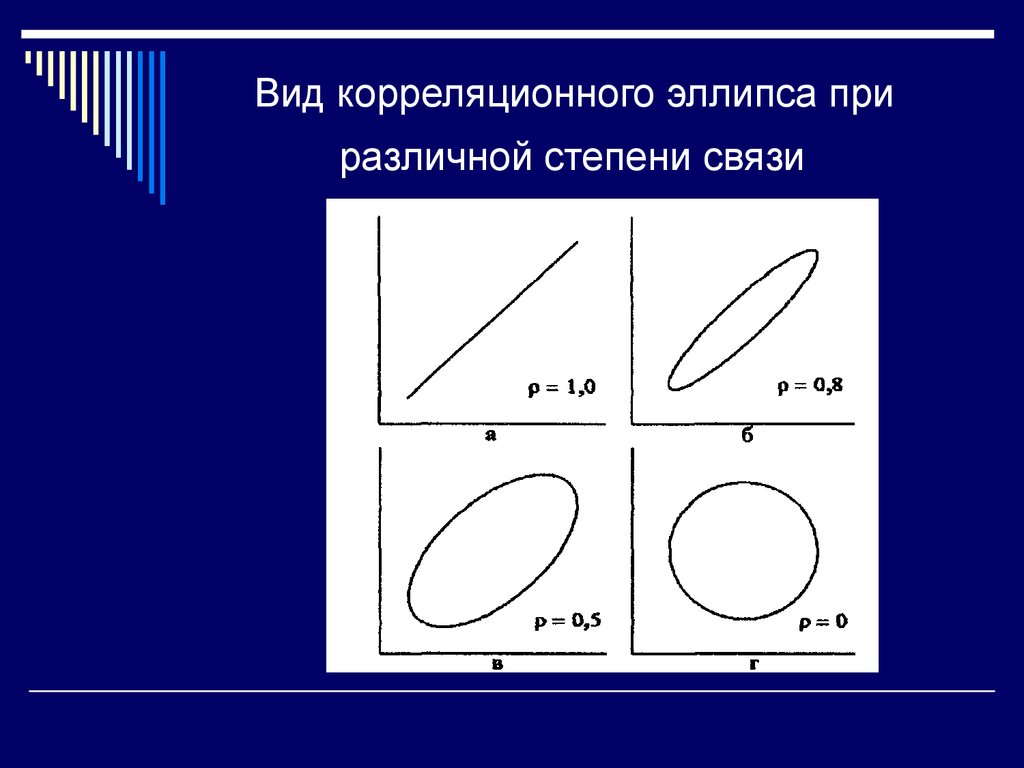
12. Вид корреляционного эллипса при различной степени связи

13.

14. Величина и смысл коэффициента корреляции

при r > 0,85 (при этом варьирование признаков
взаимосвязано приблизительно на 75% и
более) - весьма тесная связь,
при 0,85 > r > 0,7 (при этом взаимосвязанная
вариация признаков лежит в пределах 7550%) - тесная связь,
если r≤ 0,7 (при этом варьирование одного
признака менее чем на 50% связано с
варьированием другого признака) - связь
можно считать слабой.

15. Коэффициент детерминации (R²) -величина квадрата коэффициента корреляции.

Величина R² показывает долю (%)
части варьирования одного из
признаков, связанную с
варьированием другого.
Может иметь самостоятельный интерес, поэтому ее
иногда выделяют в качестве особого параметра.

16.

Минимальная повторность, которая
может обеспечить значимость
коэффициента корреляции при г =
0,70, есть n0,05=9, что следует иметь в
виду, если опыт планируется
повторить.

17. Минимальное число наблюдений для планируемой точности

2
t
n = 2 +3
z
Где:
n- искомый объем выборки;
t - величина, заданная по принятому уровню
значимости;
z - преобразованная (по Фишеру) величина
эмпирического коэффициента корреляции.

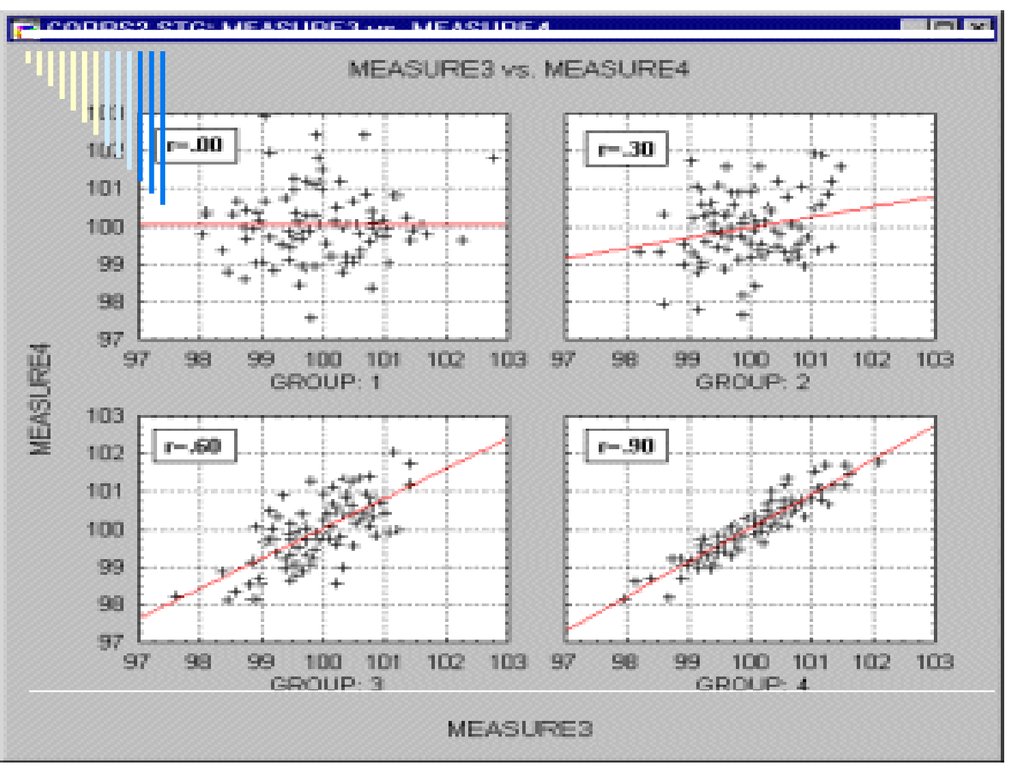
18. Вычисление коэффициента корреляции

19. Вычисление коэффициента корреляции

Корреляционная решетка
Способ условных средних

20. ОЦЕНКИ И ЗНАЧИМОСТЬ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ

Для проверки нулевой гипотезы
Н0: р = 0
против альтернативы
H0: p≠0
прибегают к вычислению статистики
t - Стьюдента
И если t ≥ta (ta берется при n< 100 для k=n- 1, при n > 100 для k=∞), то Но
отвергается c соответствующим уровнем значимости делается утверждение
о наличии линейной связи (р ≠0).

21.

Многомерный анализ
корреляционных
связей

22. Множественная корреляция

Используется когда корреляция
измеряется одновременно
между несколькими
варьирующими признаками
R=
0 £ R £1
r 2 xz + r 2 yz - 2rxy rxz ryz
1 - r 2 xy

23. Частный коэффициент корреляции

В случае, когда между любой парой
признаков из X, У и Z связь не очень
сильно
отличается
от
прямолинейной и степень связи
оценивается
парными
коэффициентами корреляции rxy, rxz
и ryz, то частный коэффициент
корреляции rxy(z) между признаками
X и У при исключенном влиянии Z
может быть вычислен по формуле:
rxy ( z ) =
Частный коэффициент корреляции
имеет тот же смысл, что и
обыкновенный парный коэффициент
корреляции
rxy - rxz ryz
(1 - r
2
xz
)(1 - r
2
yz
)

24. Коэффициент корреляции Спирмена

rs = 1 -
åd
2
n(n - 1)
2
Используют в тех случаях, когда о законе
распределений ничего не известно, а
тем более, когда есть серьезные
основания думать, что одна обе
случайные величины имеют
распределения заметно отличные от
нормального или "засоренные" сильно
отклоняющимися от основной массы
значениями.

25. Бисеральный коэффициент корреляции

x1 - x2
rbs =
Sx
n1n2
N ( N - 1)
Применяется при измерении
тесноты связи между
качественными признаками,
группируемыми в
альтернативные группы (+ и -)
и непрерывно варьирующими
количественными признаками

26. Тест по теме:

«Корреляционный
анализ»

27. Эмперический коэффициент (r), характеризующий степень связи между признаками в генеральных совокупностях

а) коэффициент пропорциональности
б) коэффициент водопрочности
в) коэффициент вариации
г) коэффициент корреляции

28. Значение коэффициента корреляции лежит в пределах

а) от 1 до ∞
б) от -1 до +1
в) от 1 до 10
г) от – 10 до +10

29. Что показывает коэффициент детерминации?

Что
показывает
коэффициент
а) долю (%) части варьирования одного из
признаков, связанную с варьированием
другого
б)
отклонение
арифметической
вариант
от
средней
в)
разницу
между
максимальным
минимальным значением
г) среди предложенных
правильного ответа
вариантов
и
нет
детерминации?

30. Какие задачи можно решать с помощью коэффициента Спирмена? Выберите неправильный вариант ответа

а)
оценка
закономерности
изменения
переменной в пространстве и во времени
б) оценка степени связи, когда один или оба
признака имеют нормальное распределение
в) оценка степени связи когда один или оба
признака измерены на порядковой шкале
г) оценка степени связи, когда один или оба
признака имеют распределение заметно
отличное от нормального

31. Укажите константу, не являющуюся характеристикой среднего уровня случайной величины

а) мода
б) медиана
в) дисперсия
г) коэффициент корреляции

32. С каким знаком может быть коэффициент корреляции между переменными X и Y?

а) только «+»
б) только «-»
в) «+» или «-»
г) среди вариантов нет правильного

33. Формула описывающая коэффициент корреляции в генеральных совокупностях X и Y

а)
r =
б)
в)
å( x
r =
i
)
- x ( yi - y )
( n - 1) S x S y
cov { x, y}
s xs
y
-¥ £ r £ +¥
г) другой вариант ответа

34. Формула для расчета оценки непараметрического коэффициента корреляции Спирмена

а)
rs = 1 б)
в)
r =
6å d i 2
N ( N 2 - 1)
Cxy
C 2 x C2 y
другой вариант ответа
г)
tô
= r
N -2
1- r2

35. Как оценивается статистическая значимость коэффициента корреляции?

Как
оценивается
статистическая
коэффициента корреляции?
а)
H0 : r £ 0
б)
в)
г)
H0 : r ¹ 0
H0 : r = 0
H0 : r ³ 0
значимость

36.

Спасибо за внимание!