Окружность

1.

МБОУ «Средняя общеобразовательная школа №77 г. Пензы»
Презентация
на тему «Окружность»
Подготовил
ученик 9Г класса
Герасимов Глеб

2.

Содержание
Определение окружности
Элементы окружности
Число π
Касательные и секущие
Вписанная и описанная окружность
Углы в окружности
Уравнение окружности

3.

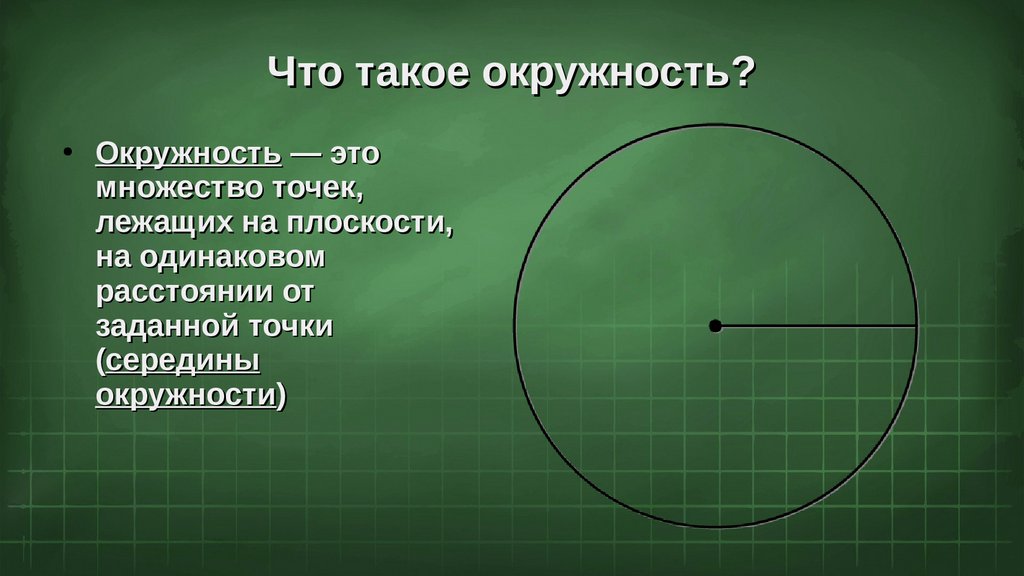
Что такое окружность?
Окружность — это
множество точек,
лежащих на плоскости,
на одинаковом
расстоянии от
заданной точки
(середины
окружности)

4.

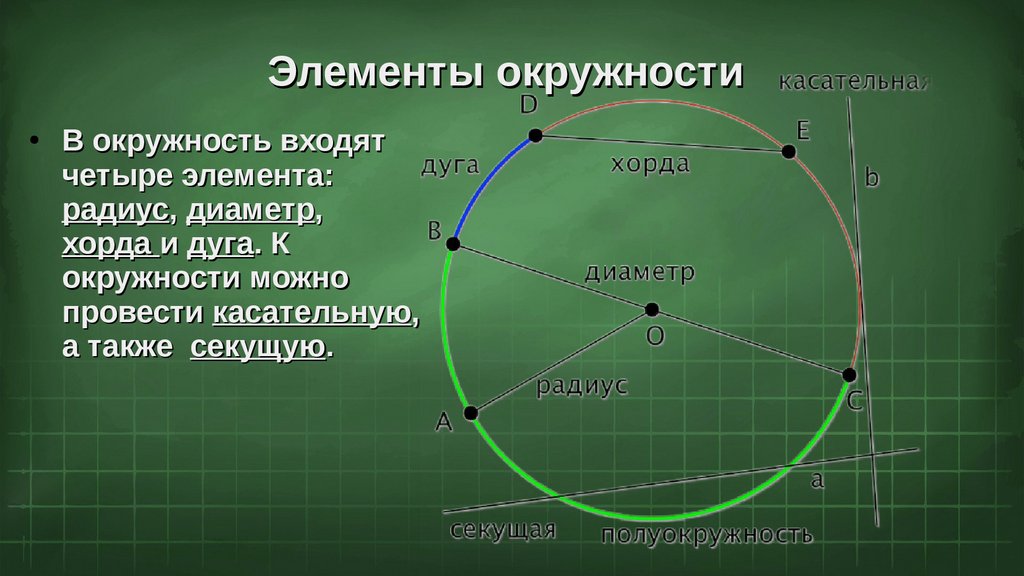
Элементы окружности
В окружность входят
четыре элемента:
радиус, диаметр,
хорда и дуга. К
окружности можно
провести касательную,
а также секущую.

5.

Свойства хорды и диаметра
Радиус равен половине
диаметра
Равные хорды лежат на
равных дугах
Окружность составляет
360° и делится хордой на
половины по 180°
Хорда перпендикулярная
диаметру (радиусу)
делится пополам
Хорды равноудалённые от
центра равны
Из двух хорд большая та
что меньше удалена от
центра

6.

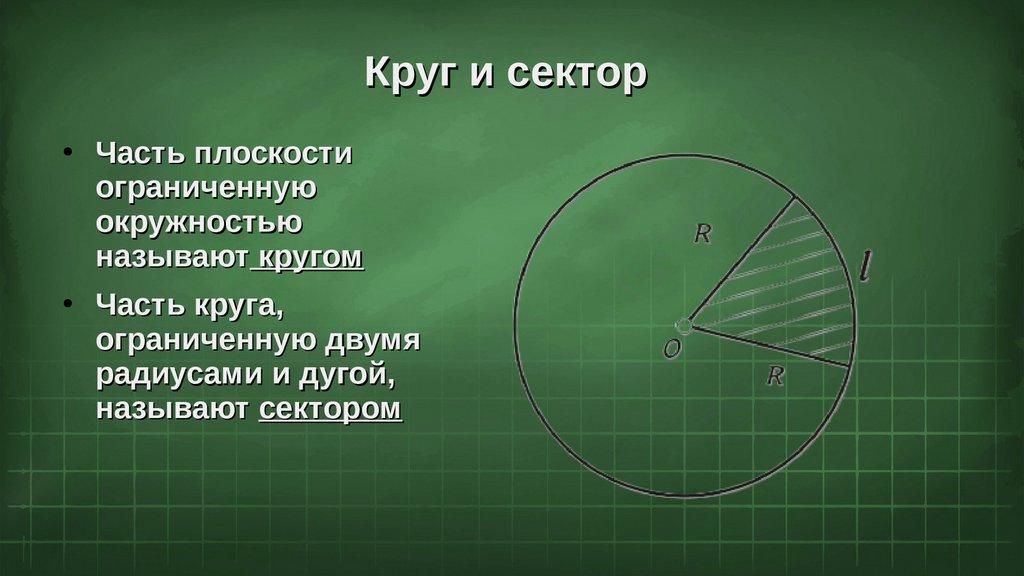
Круг и сектор
Часть плоскости
ограниченную
окружностью
называют кругом
Часть круга,
ограниченную двумя
радиусами и дугой,
называют сектором

7.

Число π и формулы окружности
Число π (пи) — математическая
постоянная, равная отношению длины
окружности к её диаметру
π = 3,14
Периметр (длина) окружности: P = 2πR
Площадь окружности: S = πR2

8.

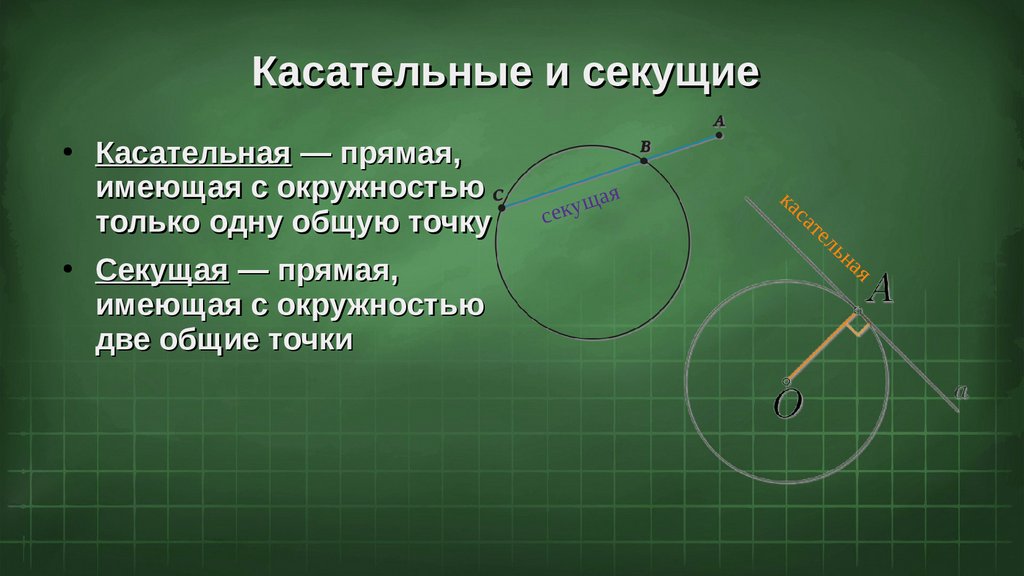
Касательные и секущие
Касательная — прямая,
имеющая с окружностью
только одну общую точку
Секущая — прямая,
имеющая с окружностью
две общие точки
ая
щ
у
с ек
ка
са
те
ль
на
я

9.

Свойства секущей и касательной
Касательная
перпендикулярна радиусу
проведённому в точку
касания
Отрезки касательных
проведённых к окружности
из одной точки равны и
образуют равные углы с
прямой, проходящей через
середину окружности и эту
точку
Если касательная и секущая
проведены из одной точки, то
квадрат расстояния от этой
точки до точки касания равен
произведению длины секущей
на её внешнюю часть
Если из одной точки к
окружности проведены две
секущие, то произведение
секущей на её внешнюю часть
равно произведению другой
секущей на её внешнюю часть

10.

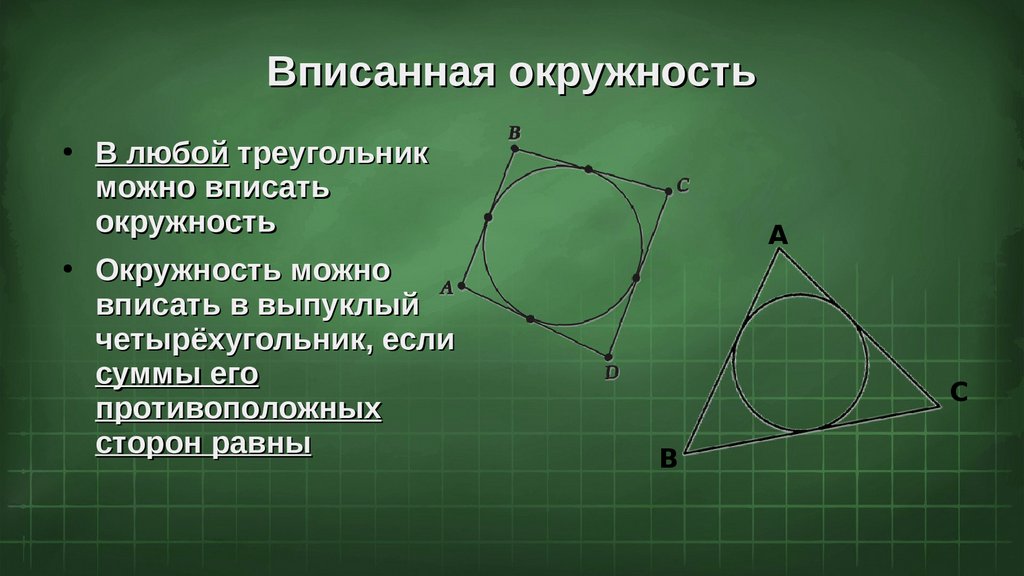
Вписанная окружность
В любой треугольник
можно вписать
окружность
Окружность можно
вписать в выпуклый
четырёхугольник, если
суммы его
противоположных
сторон равны
A
C
B

11.

Свойства вписанной окружности
S (треугольника) = RP/2
Центром вписанной
окружности является
точка пересечения
биссектрис внутренних
углов треугольника
В равнобедренном
треугольнике окружность
точкой касания делит
основание пополам
В равностороннем
треугольнике: R = h/3
В прямоугольном
треугольнике: R = (a+bc)/2
S (многоугольника) = RP/2

12.

Описанная окружность
Около любого
треугольника можно
описать окружность
(причём только одну)
В любом описанном
четырёхугольнике
сумма
противоположных
сторон будет равна 180°
В описанном
многоугольнике
серединные
перпендикуляры
пересекаются в одной
A
точке
B
C

13.

Свойства описанной окружности
В равностороннем
треугольнике: R = 2h/3
В прямоугольном
треугольнике центр
описанной окружности
лежит на середине
гипотенузы и R = c/2
В треугольнике: R =
a/2sina
Центром описанной
окружности является
точка пересечения
серединных
перпендикуляров
треугольника
В треугольнике: R =
abc/4S

14.

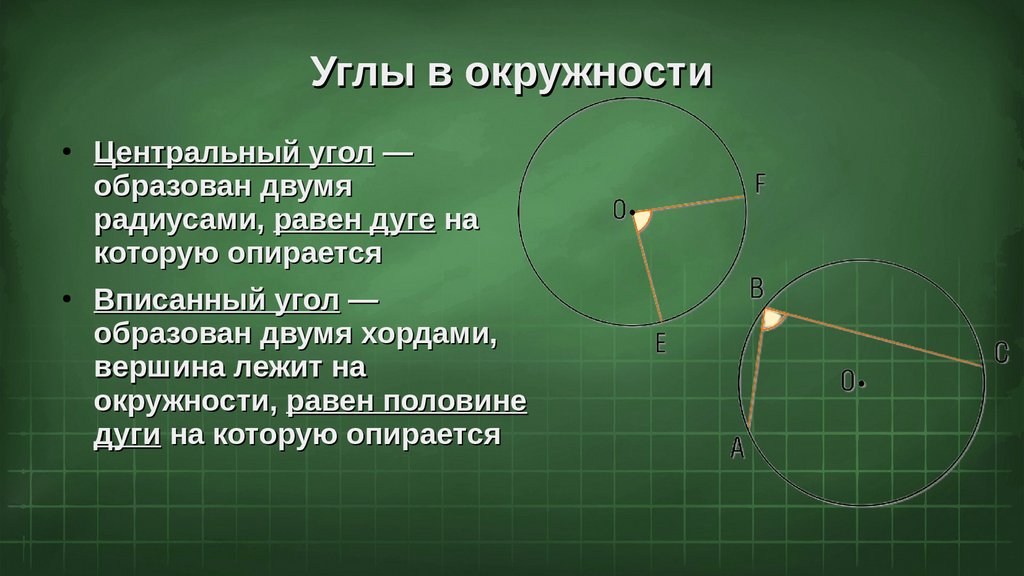
Углы в окружности
Центральный угол —
образован двумя
радиусами, равен дуге на
которую опирается
Вписанный угол —
образован двумя хордами,
вершина лежит на
окружности, равен половине
дуги на которую опирается

15.

Уравнение окружности
Все точки окружности находятся на определённом
расстоянии (радиус) от центра, следовательно, зная
формулу расстояния между двумя точками можем
вывести уравнение окружности:
R2 = (x - x0)2 + (y - y0)2

16.

Спасибо за внимание!
2022