Электромагнетизм. Лекция 6. Намагничивание вещества. Модель молекулярных токов. Вектор намагничивания

1.

Электромагнетизм
Лекция 6
Намагничивание вещества. Модель молекулярных токов. Вектор намагничивания.
Общий вид теоремы о циркуляции для постоянного магнитного поля при наличии
вещества. Магнитная проницаемость и восприимчивость веществ. Классификация
магнитных материалов. Магнитное поле Земли.

2.

Намагничивание вещества
Пусть в вакууме создается магнитное поле B0. Опыт показывает,
что если в это поле B0 поместить какое-либо вещество, то в нем
появляются собственные магнитные поля. Этим свойством
обладает всякое вещество, и в этом смысле все вещества
являются магнетиками. При помещении магнетика во внешнее
магнитное поле в нем возникает магнитный момент.
Этот процесс называется намагничиванием. Намагниченным
веществом создается дополнительное магнитное поле Bвещ. Таким
образом, поле в веществе является суперпозицией внешнего B0 и
внутреннего Bвещ магнитных полей:
B = B0 + Bвещ.

3.

Намагничивание вещества
В 1820 г. для объяснения намагничивания вещества в
магнитном поле Ампер предположил, что в веществе
существуют микроскопические замкнутые токи
(молекулярные токи). Каждый такой ток имеет магнитный
момент pm (pm = IS) и создает вокруг себя магнитное поле.
В большинстве материалов в отсутствие
внешнего магнитного поля
микроскопические токи (а следовательно и
их магнитные моменты) ориентированы
хаотичным образом (см. рис.). Поэтому
суммарный магнитный момент всех
микроскопических токов равен нулю и их
результирующее поле тоже равно нулю.

4.

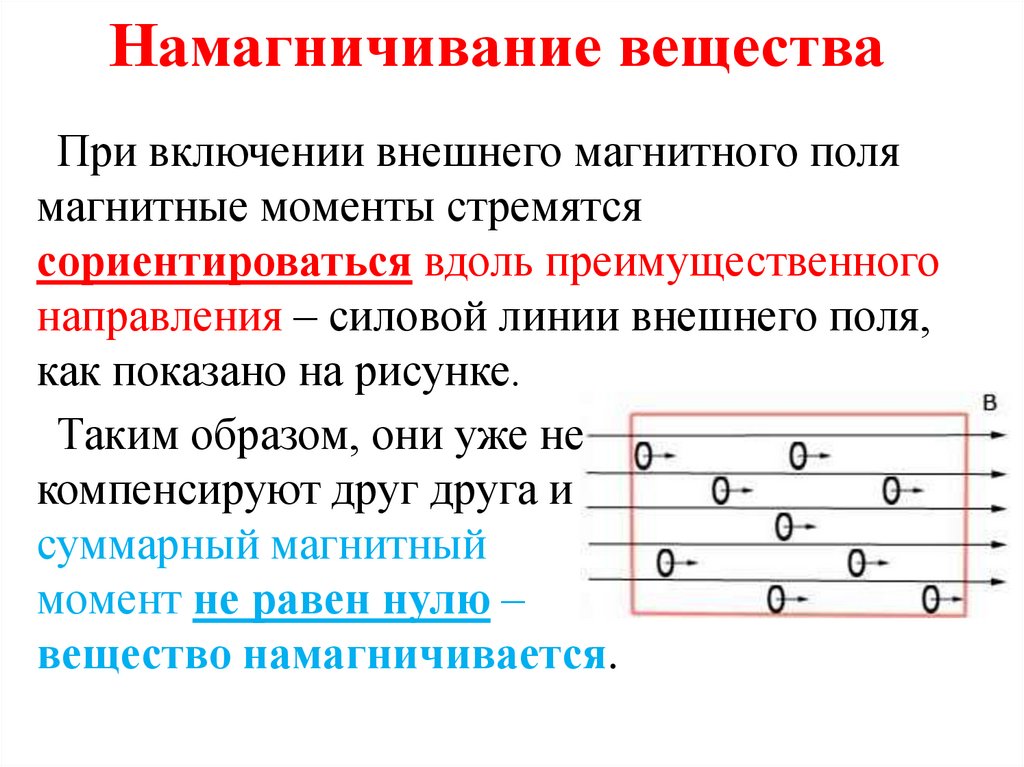
Намагничивание вещества
При включении внешнего магнитного поля
магнитные моменты стремятся
сориентироваться вдоль преимущественного
направления – силовой линии внешнего поля,
как показано на рисунке.
Таким образом, они уже не
компенсируют друг друга и
суммарный магнитный
момент не равен нулю –
вещество намагничивается.

5.

Модель молекулярных токов
Таким образом, результирующее поле Bвещ всех
микроскопических контуров с током не равно нулю.
Описанная модель, созданная Ампером, носит название модели
молекулярных токов. Отметим, что в настоящее время модель
Ампера о существовании молекулярных токов является чуть ли не
очевидной, но для своего времени его предположение являлось
очень смелым и конкурировало с гипотезой элементарных
магнитиков – магнитных диполей Вебера. Кроме того, в начале
XIX века еще не была создана электронная теория строения атома,
согласно которой вращающиеся вокруг ядра
электроны представляют микроскопические
замкнутые токи (в качестве примера на рисунке
представлен атом водорода).
Таким образом, гипотеза Ампера во многом
предвосхитила появление электронной
теории строения атома.

6.

Факультативно: Спин
Эксперименты показывают, что помимо орбитального магнитного
момента (связанного с движением по орбите), у электрона есть
собственный механический момент (момент импульса) – спин
(или собственный момент количества движения). Собственный
механический момент имеет квантовую природу, не связан с
движением частицы как целого, его проекция на заданное
направление может иметь два значения s = ±1/2 (в единицах ħ) , те
он может находиться в двух спиновых состояниях . Спин не может
быть описан в классической теории электричества и магнетизма.
Как показала квантовая механика, наличие собственного
механического момента приводит к возникновению спинового
(собственного) магнитного момента. Спиновый магнитный
момент электрона в магнитном поле может иметь только две
равные и противоположно направленные проекции на направление
поля H, которые равны по модулю магнетону Бора µВ= ħe/2mc.
Спиновые и орбитальные магнитные моменты электрона и
создают суммарные магнитный моменты атомов и молекул.

7.

Намагниченность
Для характеристики магнитного состояния
макроскопического тела используют величину, которая
называется намагниченностью. Намагниченность
определяется как магнитный момент единицы объема
вещества и обозначается как M или J. В настоящих лекциях
будем использовать обозначение M. В соответствии с
определением намагниченность равна:
1
M
pm
V V
где ΔV – малый объем в
окрестности рассматриваемой
точки. При этом каждая
молекула в этом объеме имеет
магнитный момент pm.

8.

Теорема Гаусса для магнетика
Итак, намагниченное вещество создает внутреннее магнитное поле
Bвещ, которое накладывается на внешнее поле B0. Эти поля в сумме
дают результирующее магнитное поле B = B0 + Bвещ, при этом поле
B это макроскопическое (т. е. усредненное по малому объему
вещества) поле. Так как силовые линии полей B0 и, Bвещ являются
замкнутыми, (напомним, что магнитное поле является вихревым и
его силовые линии всегда являются замкнутыми) поток
результирующего поля B через произвольную замкнутую
поверхность S равен нулю. Таким
образом, теорема Гаусса в случае
магнетика имеет такой же вид, как и
для вакуума:
Ф BdS 0
S

9.

Циркуляция магнитного поля в случае наличия
вещества
Рассмотрим теперь циркуляцию вектора B по
замкнутому контуру в случае наличия магнетика.
Согласно теореме о циркуляции:
B
d
l
I
0
Мы рассматриваем магнитное поле в веществе, поэтому
под I’ имеется в виду сумма макроскопических (I) и
молекулярных (Iмол) токов:
I’ = I + Iмол
Таким образом, выражение для циркуляции можно
переписать:
B
d
l
I
I
0
0
м ол
(*)

10.

Циркуляция магнитного поля в случае
наличия вещества
Сумма всех молекулярных токов, которые охватываются
контуром интегрирования:
1
1
I мол V pmdl V pm dl M dl
(**)
Где была произведена операция выноса интеграла из под знака
суммирования а затем замена с использованием определения
намагниченности. Подставляя выражение (**) в (*) получим
следующий вид теоремы о циркуляции:
B
0 M dl I
Величина, стоящая в круглых скобках называется
напряженностью магнитного поля и обозначается как H:
B
H
M
0

11.

Циркуляция магнитного поля в случае наличия
вещества, напряженность магнитного поля
С учетом этого, теорема о циркуляции для магнитного
поля при наличии вещества может быть записана
как:
Hd l I
Циркуляция вектора напряженности магнитного поля по
некоторому замкнутому контуру равна алгебраической
сумме макроскопических токов, охваченных этим
контуром. Единицей измерения H в СГС является Эрстед
(Э), в СИ – ампер на метр (А/м)

12.

Напряженность магнитного поля
Вектору напряженности магнитного поля H в электрическом поле
соответствует вектор электрической индукции D, а не вектор
напряженности электрического поля E. Такое различие в названиях
сложилось исторически.
Первоначально считалось, что в природе существуют «магнитные
заряды», и построение теории магнетизма проводилось так же как
это было сделано для электричества. В то время ввели понятия
«электрическая индукция» для D и «магнитная индукция» для B.
Уже после введения этих названий выяснилось, что в природе
«магнитных зарядов» нет, и на самом деле магнитная индукция
является аналогом не D, а напряженности электрического поля E;
напряженность магнитного поля H соответствует индукции
электрического поля D.
Магнитная индукция
B E Напряженность эл-го поля
Напряженность магн-го поля H D Электрическая индукция

13.

Магнитная восприимчивость
Итак, магнитная индукция связана с намагниченностью и
напряженностью внешнего магнитного поля
B 0 ( H M )
Величина намагниченности вещества изменяется
пропорционально изменению значений
напряженности магнитного поля:
M H
Коэффициент пропорциональности χ называется
магнитной восприимчивостью и характеризует
связь между намагниченностью вещества и
магнитным полем в этом веществе. Так как и
намагниченность, и напряженность измеряются
в А/м восприимчивость – величина безразмерная.

14.

Магнитная проницаемость
Таким образом, для индукции магнитного поля можем
записать:
B 0 ( H M ) 0 (1 ) H 0 H
В данной формуле выражение 1 + χ обозначено через величину μ.
Коэффициент μ называют относительной магнитной
проницаемостью – это физическая величина, которая
характеризует связь между магнитной индукцией и
напряженностью магнитного поля в этом веществе.
Относительная магнитная проницаемость является безразмерной
величиной и различна для разных магнетиков, может зависеть от
температуры, состава, состояния материала и других факторов.

15.

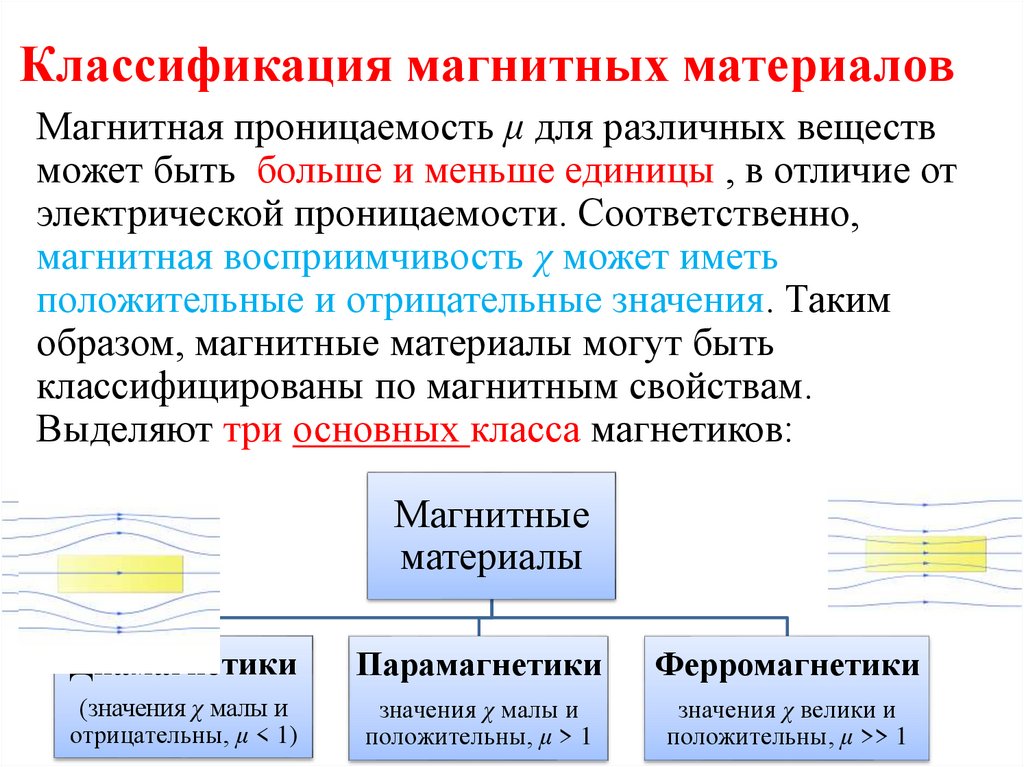
Классификация магнитных материалов
Магнитная проницаемость μ для различных веществ
может быть больше и меньше единицы , в отличие от
электрической проницаемости. Соответственно,
магнитная восприимчивость χ может иметь
положительные и отрицательные значения. Таким
образом, магнитные материалы могут быть
классифицированы по магнитным свойствам.
Выделяют три основных класса магнетиков:
Магнитные
материалы
Диамагнетики
Парамагнетики
Ферромагнетики
(значения χ малы и
отрицательны, μ < 1)
значения χ малы и
положительны, μ > 1
значения χ велики и
положительны, μ >> 1

16.

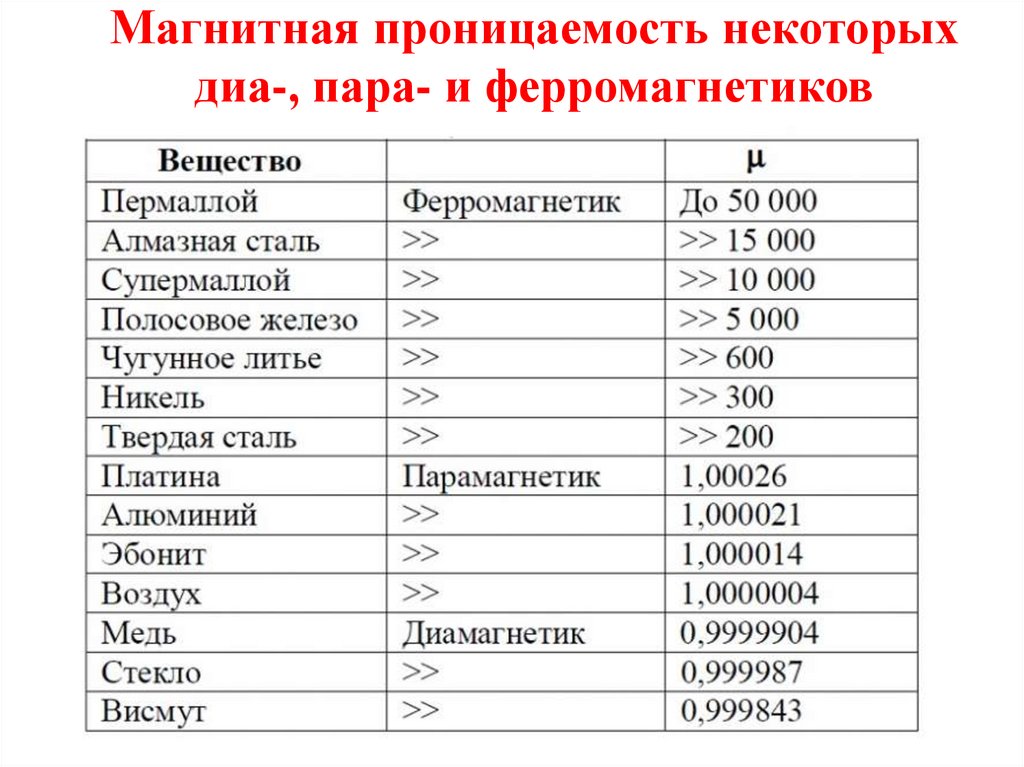
Магнитная проницаемость некоторых
диа-, пара- и ферромагнетиков

17.

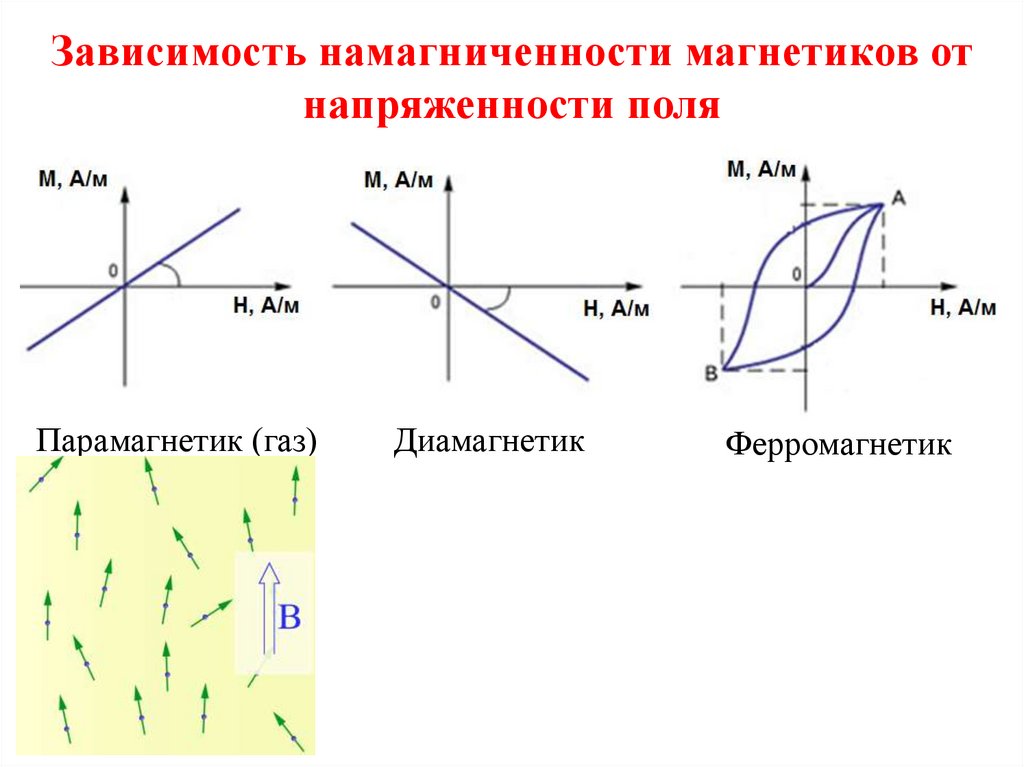
Зависимость намагниченности магнетиков от
напряженности поля
Парамагнетик (газ)
Диамагнетик
Ферромагнетик

18.

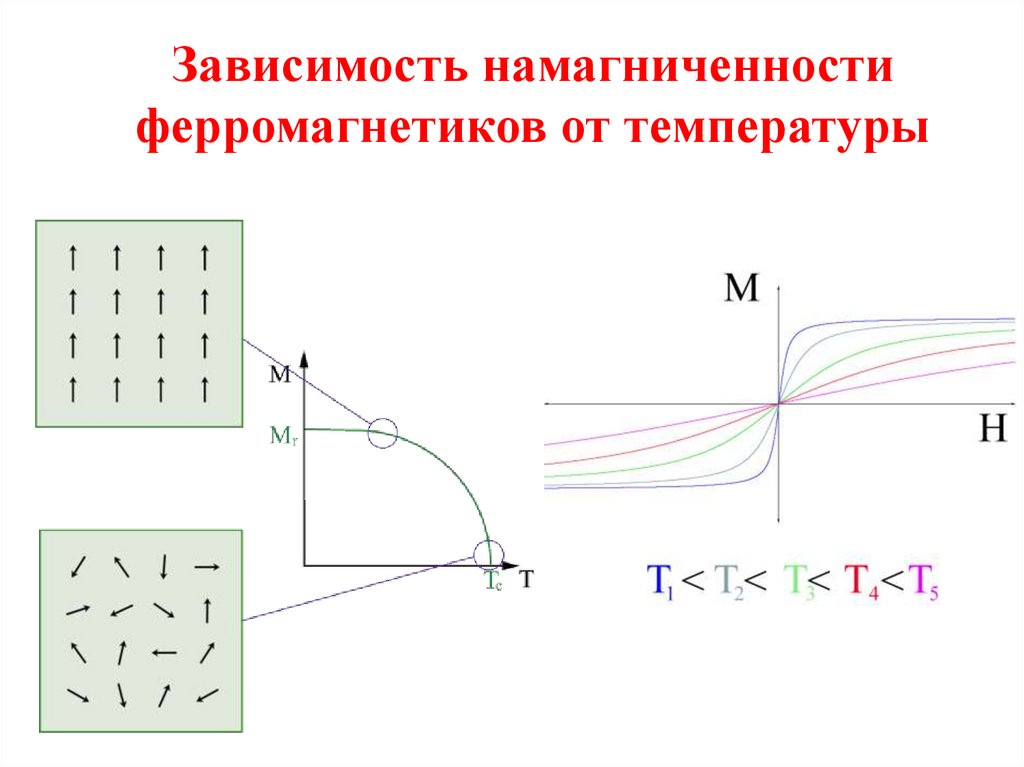
Зависимость намагниченности
ферромагнетиков от температуры

19.

Диамагнетики
К диамагнетикам можно отнести все материалы (все они состоят
из атомов) , а диамагнетизм связан с законом электромагнитной
индукции. В магнитном поле молекулярные токи в веществе
изменяются так, чтобы помешать возникновению внешнего
поля. Таким образом, направление магнитного момента
противоположно направлению внешнего поля. Это приводит
к уменьшению магнитного
поля, т.е. в диамагнетиках
величина меньше единицы.
По абсолютной величине
магнитная восприимчивость
диамагнетиков очень мала,
составляет 10 –4 – 10-5.
Диамагнетиками являются,
например, серебро (χ = - 2,6∙10-5),
вода (χ = - 9∙10-6),
висмут χ = - (1,7-2.84)∙10-4.

20.

Диамагнитная левитация
При достаточно сильных внешних полях поле может быть
полностью вытеснено из диамагнитного материала и может
наблюдаться левитация диамагнетика в поле, подобно левитации
сверхпроводника над магнитом, но без охлаждения.
Сотрудники лаборатории высоких магнитных полей
университета Nijmegen (Нидерланды) поместили живую лягушку
в сильное магнитное поле 20 Тл и она «левитировала».
За этот эксперимент
Андрею Гейму 2000 году
была вручена
Шнобелевская премия.
х

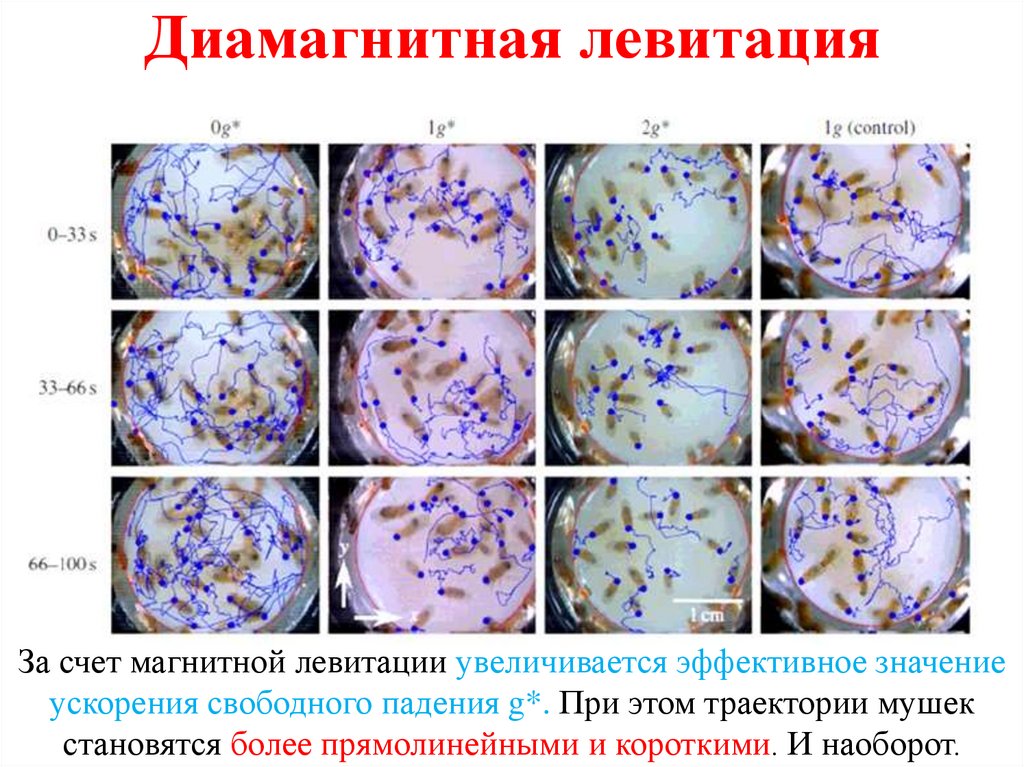
21.

Диамагнитная левитация
За счет магнитной левитации увеличивается эффективное значение
ускорения свободного падения g*. При этом траектории мушек
становятся более прямолинейными и короткими. И наоборот.

22.

Диамагнитная левитация
Графит является одним из самых сильных диамагнетиков (наряду
с упоминаемыми ранее висмутом и сверхпроводниками), причем
магнитная проницаемость у графита зависит от направления
(диамагнетизм максимально выражен в направлении,
перпендикулярном слоям), поэтому если тонкую пластинку
графита поместить над сильными магнитами NdFeB (снизу), она
будет левитировать на высоте в пару миллиметров

23.

Парамагнетики
Парамагнетиками являются вещества, у которых имеются
незаполненные электронные оболочки. Таким образом, атомы
парамагнетика имеют магнитные моменты в отсутствие
внешнего магнитного поля, но в этом случае все они направлены
беспорядочно (из-за теплового движения), поэтому суммарный
момент парамагнитного материала равен нулю при нулевом поле.
При включении внешнего поля эти моменты стремятся
выстроиться вдоль его силовых линий. В отличие от
диамагнетика в парамагнетике намагниченность направлена в
сторону внешнего поля и магнитная проницаемость > 1, а
восприимчивость χ > 0.
К парамагнетикам относятся
алюминий (χ = 2,1∙10-6),
платина (χ = 3∙10-4),
хлористое железо (χ =2,5∙10-3)

24.

Ферромагнетики
В ферромагнетиках между атомами имеется особый вид
взаимодействия – обменное. Наличие обменного
взаимодействия приводит к возникновению малых областей –
доменов – в которых все атомы направлены в одну сторону.
Таким образом, каждый из доменов намагничен, но при нулевом
внешнем магнитном поле все они намагничены в различных
направлениях, и суммарный магнитный момент
ферромагнетика равен нулю. При включении внешнего поля,
магнитные моменты доменов стремятся повернуться в сторону
направлении поля (вверх на рис) ) , и ферромагнетик
намагничивается.Поле, которое возникает в ферромагнетике как
правило намного превышает внешнее, поэтому значение μ >> 1.
Относятся железо, никель,
кобальт, некоторые
редкоземельные металлы
(например, гадолиний),
сплавы металлов

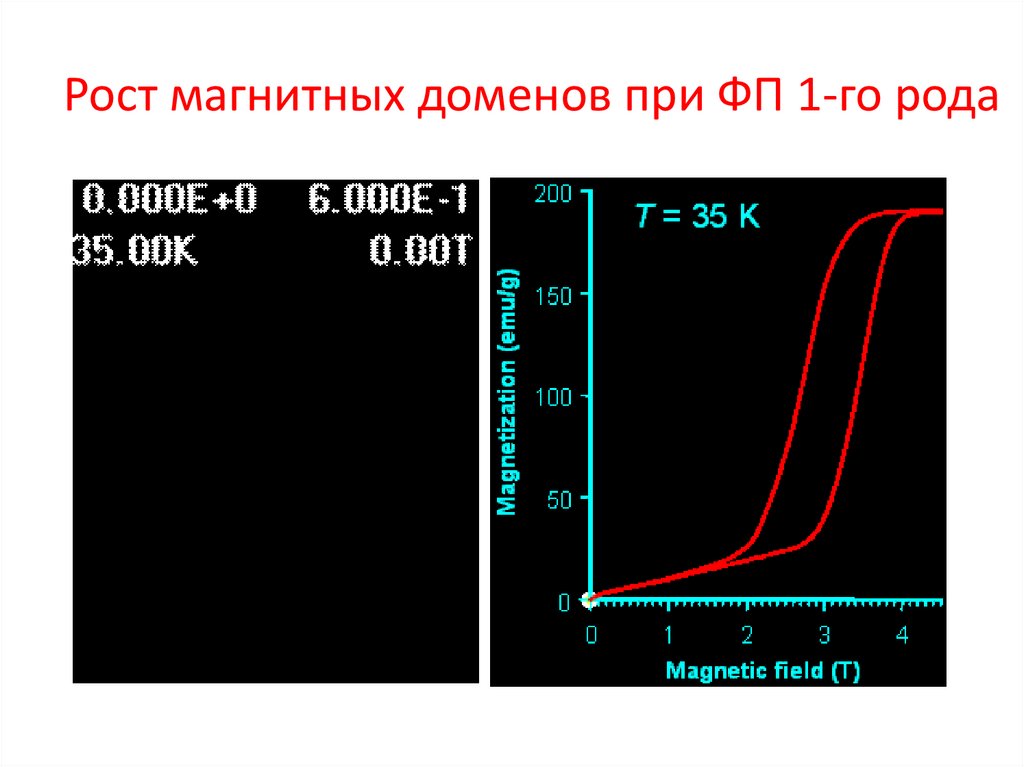
25.

Рост магнитных доменов при ФП 1-го рода

26.

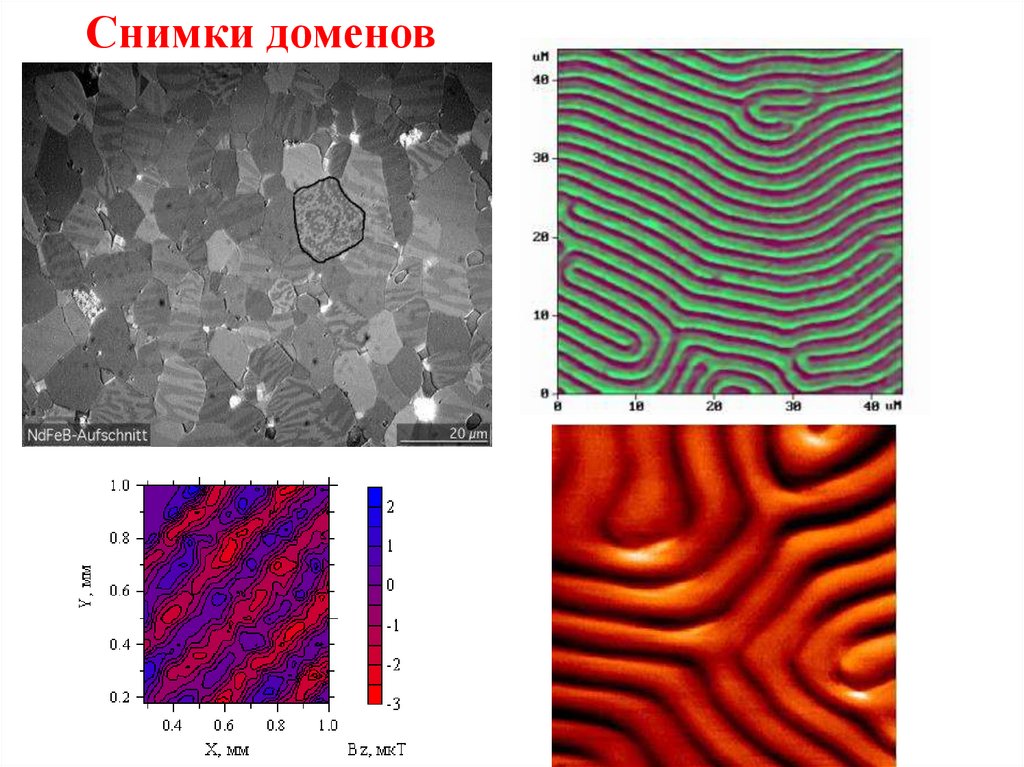
Снимки доменов

27.

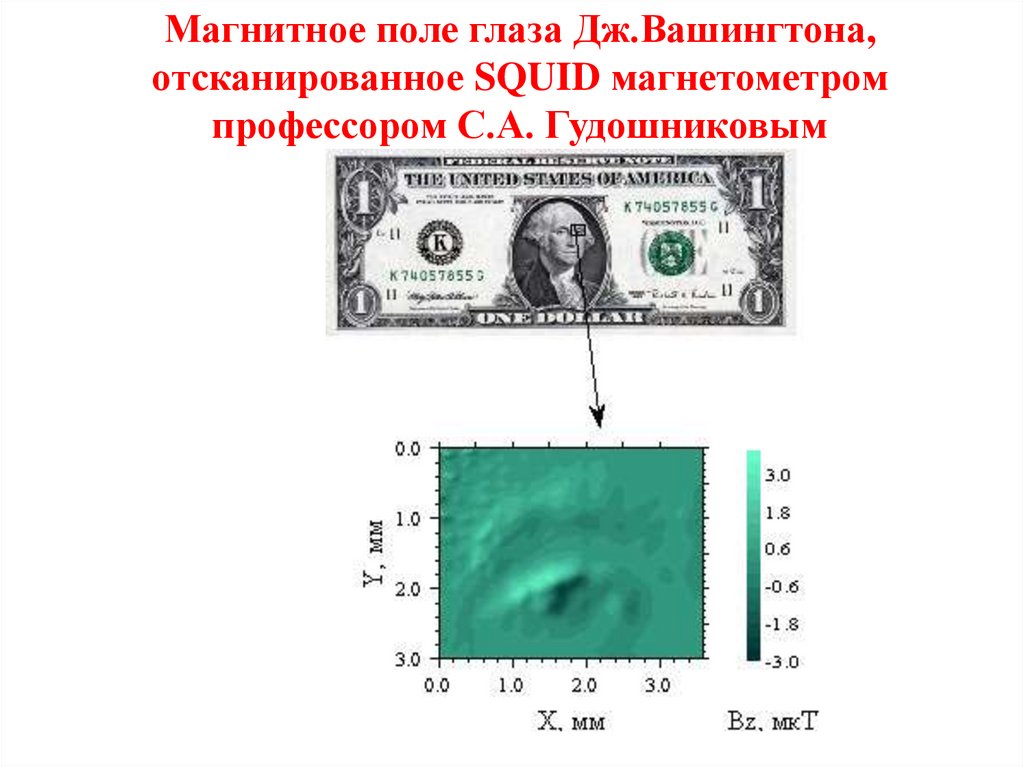
Магнитное поле глаза Дж.Вашингтона,
отсканированное SQUID магнетометром
профессором С.А. Гудошниковым

28.

Размагничивающий фактор
РАЗМАГНИЧИВАЮЩИЙ ФАКТОР -коэффициент
размагничивания N при намагничивании во внешнем поле
образца или постоянного магнита разомкнутой формы
(например, цилиндра). Размагничивающий фактор
применяется для того, чтобы вычислить внутреннее
размагничивающее поле, исходя из внешнего. А суммарное
поле внутри магнетика - это просто суперпозиция этих полей
Нвнут = Нвнеш — NM. В гауссовой системе единиц
максимальное значение равно 4 для плоскости (в СИ = 1),
а минимальное ноль для для бесконечно длинного стержня.
Это и приводит к тому, что магнитное поле, например, внутри
постоянного магнита может сильно отличаться от внешнего.
Для тел в форме эллипсоидов для вычисления N есть таблицы
Осборна. Они применяются для материалов, изготовленных из
однородного магнитного материала и находящиеся в
однородном магнитном поле .

29.

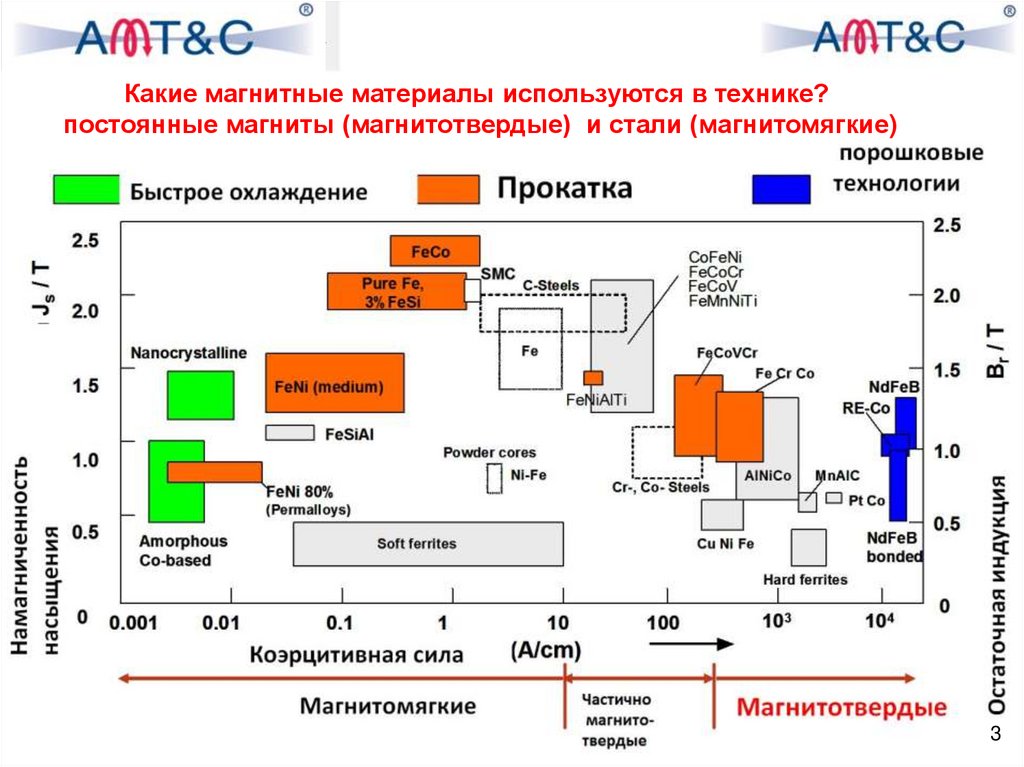
Какие магнитные материалы используются в технике?
постоянные магниты (магнитотвердые) и стали (магнитомягкие)
3

30.

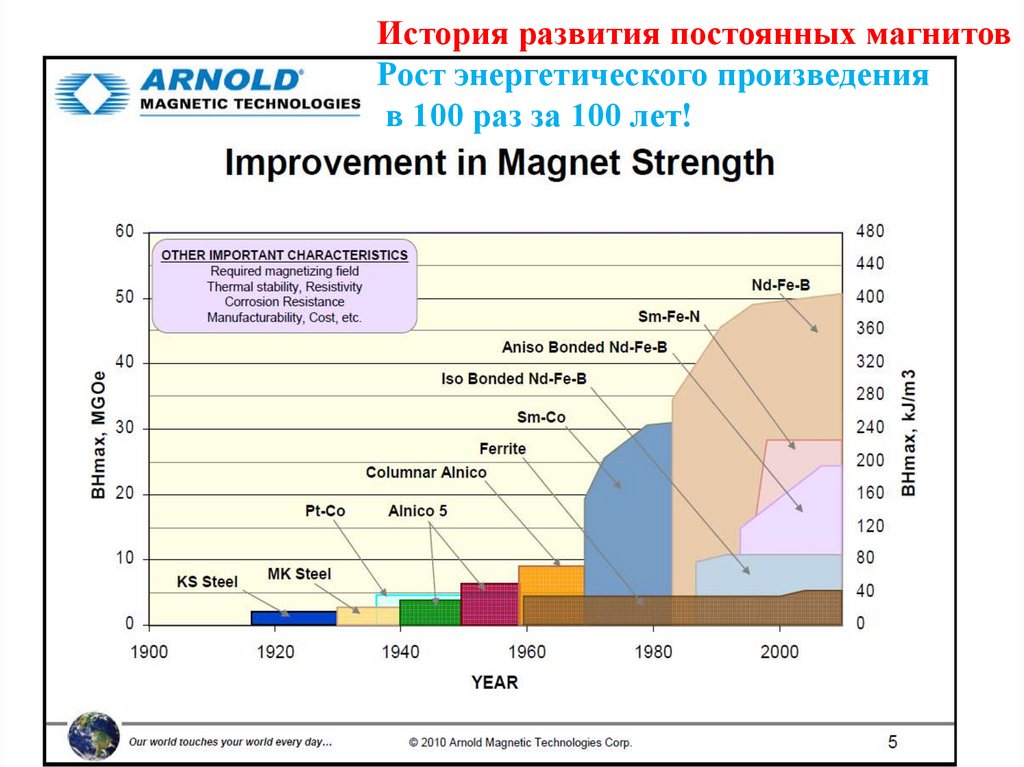
История развития постоянных магнитов
Рост энергетического произведения
в 100 раз за 100 лет!

31.

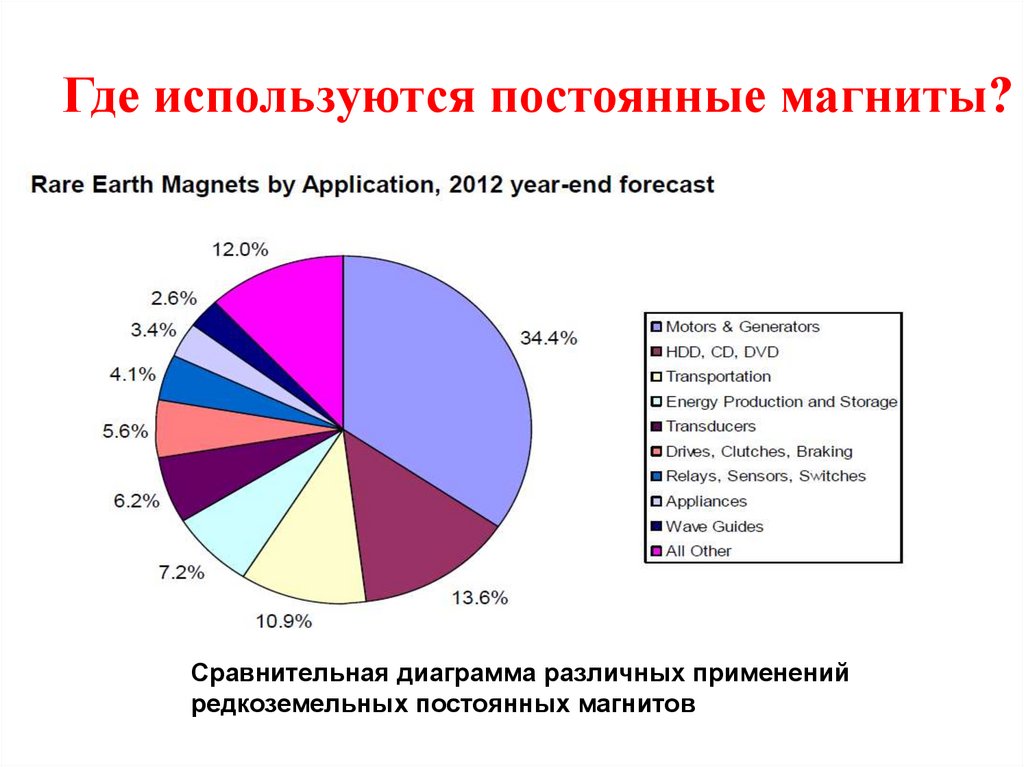
Где используются постоянные магниты?
Сравнительная диаграмма различных применений
редкоземельных постоянных магнитов

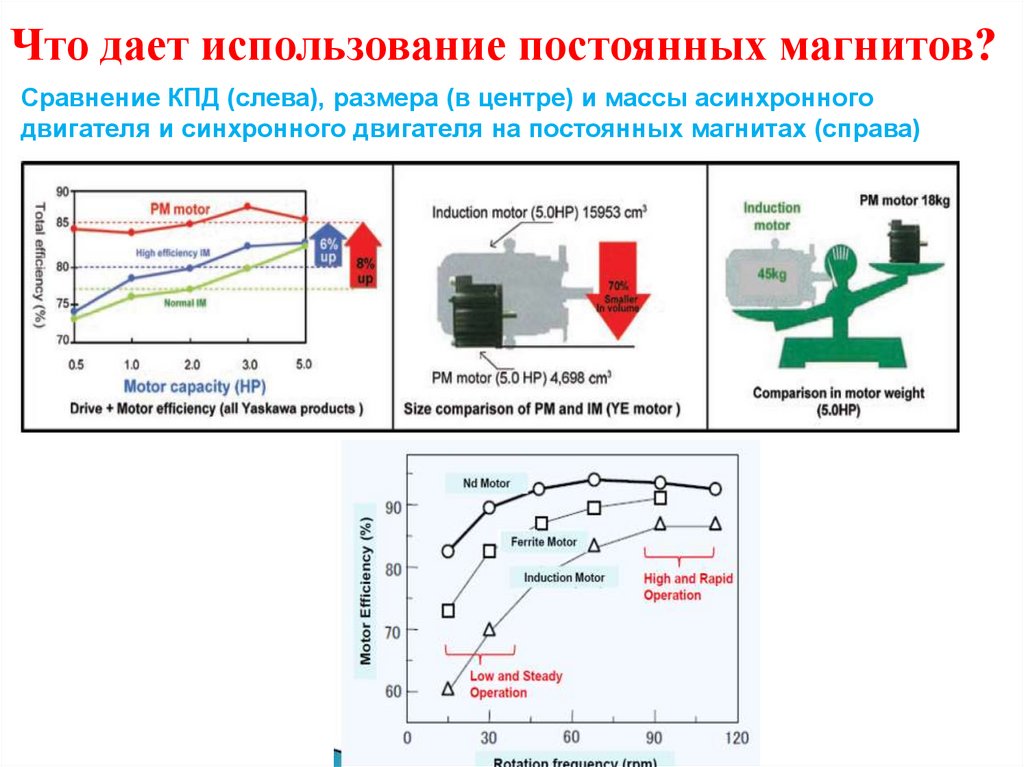
32.

Что дает использование постоянных магнитов?
Сравнение КПД (слева), размера (в центре) и массы асинхронного
двигателя и синхронного двигателя на постоянных магнитах (справа)

33.

"Полимагнит СПб" (группа компаний AMT&C) в качестве соисполнителя приняла
участие в проекте Петербургского государственного университета путей сообщения
Императора Александра I по разработке, изготовлению и проведению натурных
испытаний грузовой магнитолевитационной транспортной платформы. Испытания
успешно прошли 31 марта 2015 года на территорий Александровского завода в г.
Пушкин. В ходе испытание воздушный зазор между платформой с 40-ка футовым
контейнером и активной путевой структурой составил 26 мм при нагрузке 27 тонн.