Переменный электрический ток. Лекция 9

1.

Переменный
электрический ток
Лекция 9
Главы 13.1-13.5
1

2.

Список литературы
• Савельев И.В. Курс общей физики. В 5-и тт. Том 2.
Электричество и магнетизм. ISBN - 978-5-8114-1208-2.
Издательство «Лань». 2021 г.
• Савельев И.В. Курс общей физики. В 5-и тт. Том 4. Волны.
Оптика. ISBN - 978-5-8114-1210-5. Издательство «Лань».
2021 г.
• Трофимова Т. И. Руководство к решению задач по физике :
учебное пособие для прикладного бакалавриата: Учебное
пособие/Трофимова Т. И..-М:Издательство Юрайт,2019,
ISBN 978-5-9916-3429-8.-265. https://elis.psu.ru/node/557918
2

3.

Основные темы
• Квазистационарное поле
• Свободные колебания в контуре без активного сопротивления
• Свободные затухающие колебания
• Вынужденные электрические колебания
• Переменный ток
3

4.

Квазистационарное поле
• При рассмотрении электрических колебаний приходится иметь
дело с токами, изменяющимися со временем.
• Закон Ома и вытекающие из него правила Кирхгофа были
установлены для постоянного тока.
• Однако они остаются справедливыми и для мгновенных значений
изменяющихся тока и напряжения, если только их изменения
происходят не слишком быстро.
• Электромагнитные возмущения распространяются по цепи с
огромной скоростью, равной скорости света с.
4

5.

Квазистационарное поле
• Пусть длина цепи равна l. Если за время =l/c, необходимое для
передачи возмущения в самую отдаленную точку цепи, сила тока
изменяется незначительно, то мгновенные значения силы тока во
всех сечениях цепи будут практически одинаковыми.
• Токи, удовлетворяющие такому условию, называются
квазистационарными.
• Для периодически изменяющихся токов условие
квазистационарности имеет вид
l
=
c
T,
• где T – период изменений.
5

6.

Квазистационарное поле
• Для цепи длиной 3 м запаздывание =10-8 с.
• Таким образом, вплоть до T 10-6 c (что соответствует частоте 106
Гц) токи в такой цепи можно считать квазистационарными.
• Мгновенные значения квазистационарных токов подчиняются
закону Ома.
• Следовательно, для них справедливы и правила Кирхгофа.
• В дальнейшем при изучении электрических колебаний мы всегда
будем предполагать, что рассматриваемые нами токи
квазистационарны.
6

7.

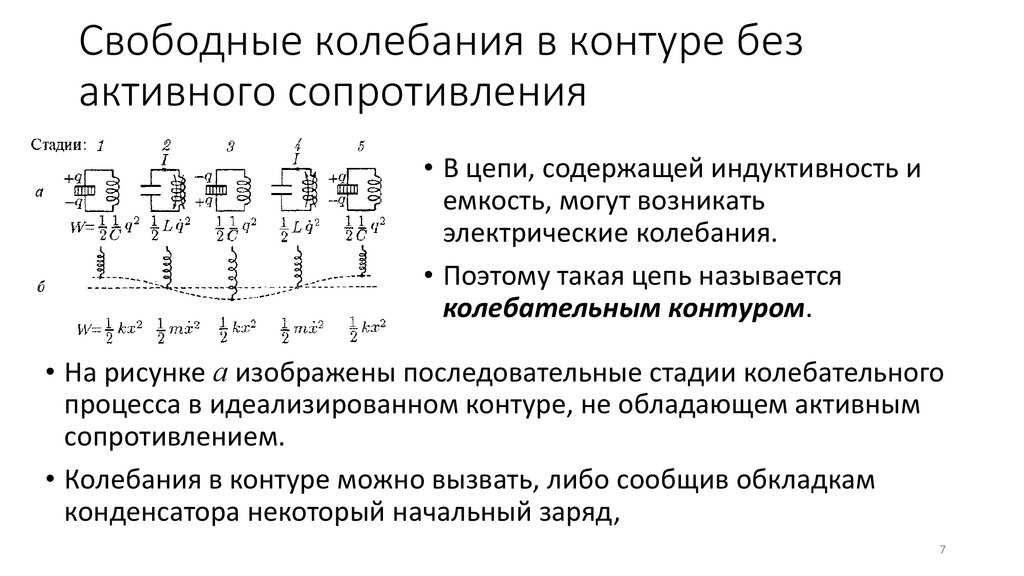
Свободные колебания в контуре без
активного сопротивления
• В цепи, содержащей индуктивность и
емкость, могут возникать
электрические колебания.
• Поэтому такая цепь называется
колебательным контуром.
• На рисунке а изображены последовательные стадии колебательного
процесса в идеализированном контуре, не обладающем активным
сопротивлением.
• Колебания в контуре можно вызвать, либо сообщив обкладкам
конденсатора некоторый начальный заряд,
7

8.

Свободные колебания в контуре без
активного сопротивления
• либо возбудив в индуктивности ток
(например, путем выключения
внешнего магнитного поля,
пронизывавшего витки катушки).
• Воспользуемся первым способом.
• Присоединим отключенный от
индуктивности конденсатор к
источнику напряжения.
• Это приведет к возникновению на обкладках конденсатора
разноименных зарядов +q и –q (стадия 1).
• Между обкладками возникнет электрическое поле, энергия
которого равна (1/2)(q2/C).
8

9.

Свободные колебания в контуре без
активного сопротивления
• Если затем отключить источник
напряжения и замкнуть конденсатор
на индуктивность, емкость начнет
разряжаться и в контуре потечет ток.
• В результате энергия электрического
поля будет уменьшаться, но зато
возникнет все возрастающая энергия
магнитного поля, обусловленного
током, текущим через индуктивность.
• Эта энергия равна (1/2)LI2.
9

10.

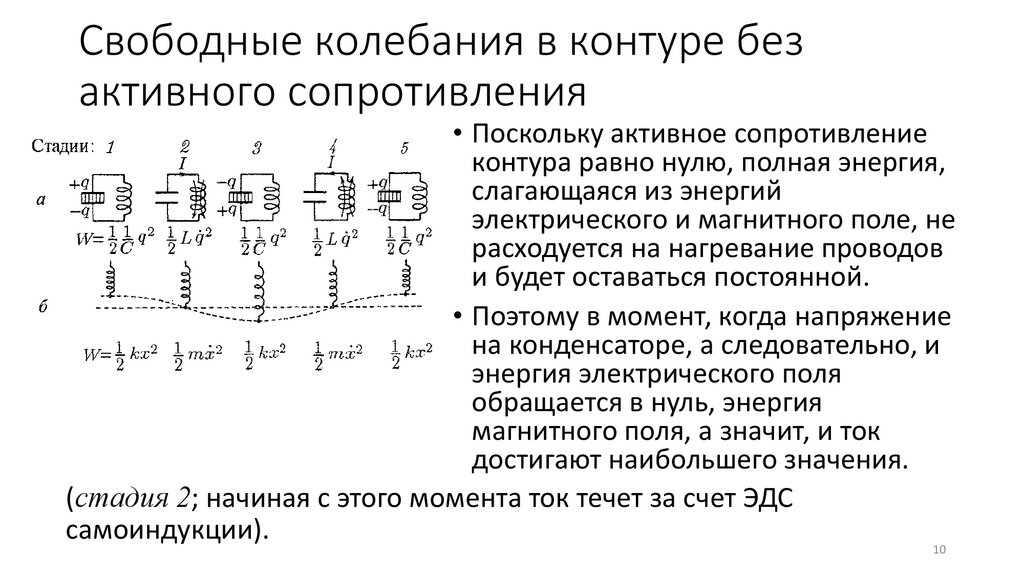
Свободные колебания в контуре без
активного сопротивления
• Поскольку активное сопротивление
контура равно нулю, полная энергия,
слагающаяся из энергий
электрического и магнитного поле, не
расходуется на нагревание проводов
и будет оставаться постоянной.
• Поэтому в момент, когда напряжение
на конденсаторе, а следовательно, и
энергия электрического поля
обращается в нуль, энергия
магнитного поля, а значит, и ток
достигают наибольшего значения.
(стадия 2; начиная с этого момента ток течет за счет ЭДС
самоиндукции).
10

11.

Свободные колебания в контуре без
активного сопротивления
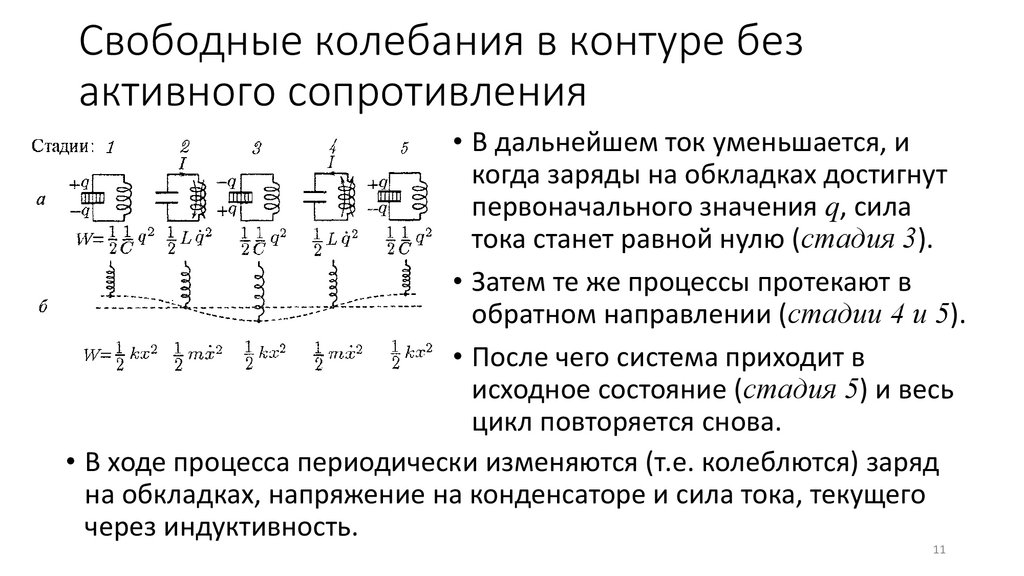
• В дальнейшем ток уменьшается, и
когда заряды на обкладках достигнут
первоначального значения q, сила
тока станет равной нулю (стадия 3).
• Затем те же процессы протекают в
обратном направлении (стадии 4 и 5).
• После чего система приходит в
исходное состояние (стадия 5) и весь
цикл повторяется снова.
• В ходе процесса периодически изменяются (т.е. колеблются) заряд
на обкладках, напряжение на конденсаторе и сила тока, текущего
через индуктивность.
11

12.

Свободные колебания в контуре без
активного сопротивления
• Колебания сопровождаются
взаимными превращениями
энергий электрического и
магнитного полей.
• На рисунке б колебаниям в контуре
сопоставлены колебания
пружинного маятника.
• Сообщению зарядов обкладкам конденсатора соответствует
выведение маятника внешней силой из положения равновесия и
сообщения ему первоначального отклонения x.
12

13.

Свободные колебания в контуре без
активного сопротивления
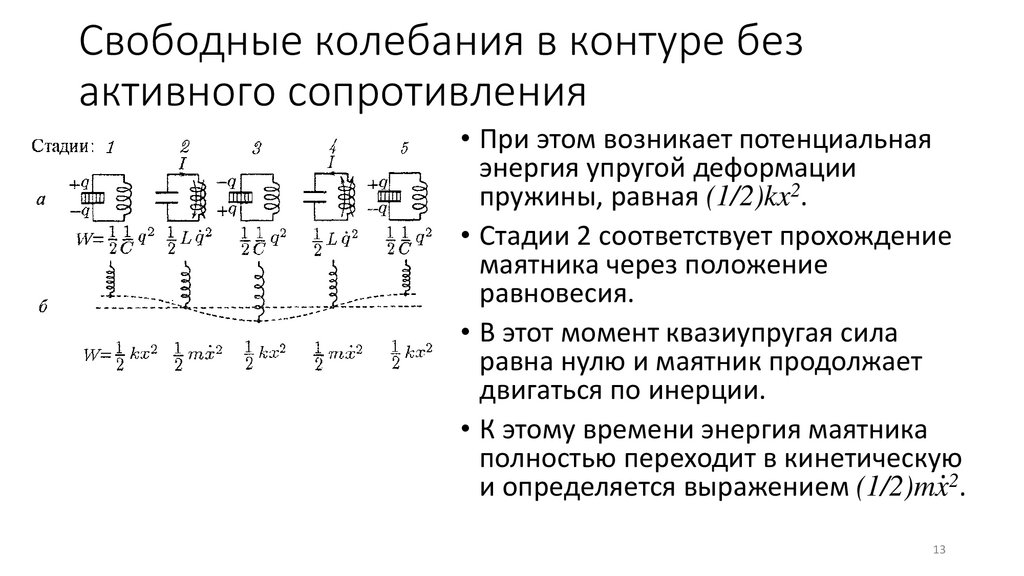
• При этом возникает потенциальная
энергия упругой деформации
пружины, равная (1/2)kx2.
• Стадии 2 соответствует прохождение
маятника через положение
равновесия.
• В этот момент квазиупругая сила
равна нулю и маятник продолжает
двигаться по инерции.
• К этому времени энергия маятника
полностью переходит в кинетическую
.2
и определяется выражением (1/2)mx .
13

14.

Свободные колебания в контуре без
активного сопротивления
• Из сопоставления электрических и механических колебаний
следует, что энергия электрического поля (1/2)х(q2/C) аналогична
потенциальной энергии упругой деформации, а энергия
магнитного поля (1/2)LI2 аналогична кинетической энергии.
• Индуктивность играет роль массы m, величина, обратная емкости
(1/С), - роль жесткости k.
• Наконец, заряду q соответствует смещение
. маятника. из
положения равновесия x, а силе тока I=q – скорость x.
• Оказывается, аналогия между электрическими и механическими
колебаниями распространяется и на описывающие их
математические уравнения.
14

15.

Свободные колебания в контуре без
активного сопротивления
• Найдем уравнение колебаний в контуре без
активного сопротивления.
• Условимся считать положительным ток, заряжающий
конденсатор. Тогда
dq
I=
dt
=q
(13.1)
• Напишем для цепи 1-3-2 выражение закона Ома
IR = 1 − 2 + E 12
• В нашем случае
(13.2)
q
dI
R = 0, 1- 2 = − , E12 = ES = − L
C
dt
15

16.

Свободные колебания в контуре без
активного сопротивления
• Подстановка этих значений в (13.2) дает
q
dI
0=− −L
C
dt
(13.3)
..
• Заменив dI/dt на q, получим уравнение
1
q+
q=0
LC
(13.4)
• Если ввести обозначение
0 =
1
,
LC
(13.5)
16

17.

Свободные колебания в контуре без
активного сопротивления
• Тогда уравнение (13.4) принимает вид, хорошо знакомый из
изучения механических колебаний:
q + q = 0,
2
0
(13.6)
• Решением этого уравнения является функция
q = qm cos ( 0t + )
(13.7)
• Таким образом, заряд на обкладках конденсатора изменяется по
гармоническому закону с частотой, определяемой выражением
(13.5).
• Эта частота называется собственной частотой контура.
17

18.

Свободные колебания в контуре без
активного сопротивления
• Для периода колебаний получается формула Томсона (Кельвина)
T = 2 LC
(13.8)
• Напряжение на конденсаторе отличается от заряда множителем
1/С:
qm
(13.9)
U=
cos ( 0t + ) = U m cos ( 0t + )
C
• Продифференцировав функцию (13.7) по времени, получим
выражение для силы тока
I = − 0 qm sin( 0t + ) = I m cos( 0t + + 2).
(13.10)
• Таким образом, сила тока опережает по фазе напряжение на
конденсаторе на /2.
18

19.

Свободные колебания в контуре без
активного сопротивления
• Сопоставление формул (13.7) и (13.9) с формулой (13.10)
показывает, что в момент, когда ток достигает наибольшего
значения, заряд и напряжение обращаются в нуль и наоборот.
• Это соотношение между зарядом и током мы уже установили
ранее, основываясь на энергетических соображениях.
• Из форму (13.9) и (13.10) следует, что
qm
Um =
, I m = 0 qm
C
• Взяв отношение этих амплитуд и заменив 0 по формуле (13.5),
получим
Um = Im L C
(13.11)
19

20.

Свободные колебания в контуре без
активного сопротивления
• Эту формулу можно получить также, исходя из того, что
наибольшее значение энергии электрического поля CU m2 2
должно быть равно наибольшему значению энергии магнитного
поля LI m2 2
CU m2 LI m2
L 2
2
2
2
=
CU m = LI m U m = I m U m = I m L C
2
2
C
20

21.

Свободные затухающие колебания
• Всякий реальный контур обладает активным
сопротивлением.
• Энергия, запасенная в контуре, постепенно
расходуется в этом сопротивлении на нагревание,
вследствие чего колебания затухают.
• Уравнение (13.2), написанное для цепи 1-3-2 на
рисунке имеет вид
q
dI
IR = − − L
C
dt
(13.12)
• Разделив это уравнение на L и заменив I на q, а dI/dt на q, получим
R
1
q+ q+
q=0
(13.13)
L
LC
21

22.

Свободные затухающие колебания
• Приняв во внимание, что величина, обратная LC, равна квадрату
собственной частоты контура 0, и введя обозначение
= R 2L
(13.14)
• Уравнению (13.13) можно придать вид
q + 2 q + 02 q = 0
(13.15)
• Уравнение (13.15) совпадает с дифференциальным уравнением
2
2
затухающих механических колебаний. При условии, что 0 ,
то есть при R 2 4 L2 1 ( LC ), решение (13.15) имеет вид
q = qm 0 exp ( − t ) cos( t + ),
• где = 02 − 2
(13.16)
22

23.

Свободные затухающие колебания
• Подставив значение (13.5) для 0 и (13.4) для , найдем, что
1
R2
(13.17)
=
− 2
LC 4 L
• Таким образом, частота затухающих колебаний меньше
собственной частоты 0.
• При R=0, выражение (13.17) переходит в (13.5).
• Разделив функцию (13.16) на емкость C, получим напряжение на
конденсаторе:
qm 0
U=
exp ( − t ) cos( t + ) = U m 0 exp ( − t ) cos( t + ). (13.18)
C
23

24.

Свободные затухающие колебания
• Чтобы найти силу тока, продифференцируем (13.16) по времени:
I = q = qm 0 exp(− t ) − cos( t + ) − sin( t + ) .
• Умножив правую часть этой формулы на равное единице
выражение 0 2 + 2 , получим
I = 0 qm 0 exp(− t ) −
cos( t + ) −
sin( t + ) .
2 + 2
2 + 2
• Введя угол , определяемый условиями
cos = −
= − , sin =
=
2
2
2
2
0
+
+
0
24

25.

Свободные затухающие колебания
• Можно написать I = 0 qm 0 exp ( − t ) cos ( t + + )
(13.19)
• Поскольку cos < 0, а sin > 0, значение заключено в пределах
от /2 до .
• Таким образом, при наличии в контуре активного сопротивления
сила тока опережает по фазе напряжение на конденсаторе более
чем на /2 (при R=0 опережение составляет /2).
• График функции (13.16) изображен на
рисунке.
• Графики для напряжения и силы тока
имеют аналогичный вид.
25

26.

Свободные затухающие колебания
• Затухание колебаний принято характеризовать
логарифмическим декрементом затухания
(t )
= ln
= T
(t + T )
(13.20)
• Здесь (t) – амплитуда соответствующей величины (q, U или I).
• Напомним, что логарифмический декремент затухания обратен
числу колебаний Ne, совершаемых за время, в течение которого
амплитуда уменьшится в e раз:
= 1 Ne .
• Подставив в (13.20) значение (13.14) для и заменив T на 2 / ,
получим следующее выражение:
26

27.

Свободные затухающие колебания
R 2 R
=
=
.
(13.21)
2 L L
• Частота , а следовательно, и определяются параметрами
контура L, C и R.
• Таким образом, логарифмический декремент затухания является
характеристикой контура.
• Если затухание невелико ( 2 02 ), можно положить в (13.21)
0 = 1 LC .
• Тогда
R LC
C
(13.22)
= R
.
L
L
27

28.

Свободные затухающие колебания
• Колебательный контур часто характеризуют его добротностью,
которая определяется как величина, обратно пропорциональная
логарифмическому декременту затухания:
Q = = Ne .
(13.23)
• Из (13.23) следует, что добротность контура тем выше, чем
большее число колебаний успевает совершиться прежде, чем
амплитуда уменьшится в e раз.
• В случае слабого затухания (см. (13.22))
1 L
Q=
.
R C
(13.24)
28

29.

Свободные затухающие колебания
• В лекции по механическим колебаниям было показано, что при
слабом затухании добротность механической колебательной
системы с точностью до множителя 2 равна отношению энергии,
запасенной в системе в данный момент, к убыли этой энергии за
один период колебаний.
• Покажем, что это справедливо и для электрических колебаний.
• Амплитуда силы тока в контуре убывает по закону exp(- t).
• Энергия W, запасенная в контуре, пропорциональна квадрату
амплитуды силы тока (или квадрату амплитуды напряжения на
конденсаторе).
• Следовательно, W убывает по закону exp(-2 t).
29

30.

Свободные затухающие колебания
• Относительное уменьшение энергии за период равно
W W (t ) − W (t + T )
−
=
=
W
W (t )
1 − exp(−2 T )
=
= 1 − exp(−2 ).
1
• При незначительном затухании ( т.е. при условии, что
можно exp(-2 ) приближенно положить равной 1 - 2 :
W
−
= 1 − (1 − 2 ) = 2 .
W
1)
30

31.

Свободные затухающие колебания
• Наконец, заменив в этом выражении на добротность контура Q
в соответствии с формулой (13.23) и решив полученное
уравнение относительно Q, получим
W
Q = −2
.
(13.25)
W
• В заключение отметим, что при R 2 4 L2 1 ( LC ) , т.е. при 2 02
вместо колебаний происходит апериодический разряд
конденсатора.
• Сопротивление контура, при котором колебательный процесс
переходит в апериодический, называется критическим.
• Значение критического сопротивления
L
(13.26)
RК = 2
.
C
31

32.

Вынужденные электрические колебания
• Чтобы вызвать вынужденные колебания, нужно
оказывать на систему внешнее периодически
изменяющееся воздействие.
• В случае электрических колебаний это можно
осуществить, если включить последовательно с
элементами контура переменную ЭДС или,
разорвав контур, подать на образовавшиеся
контакты переменное напряжение
(13.27)
U = U m cos t
• Это напряжение нужно добавить к ЭДС самоиндукции. В результате
формула (13.12) примет вид
q
dI
(13.28)
IR = − − L + U m cos t.
32
C
dt

33.

Вынужденные электрические колебания
• Произведя преобразование, получим уравнение
Um
2
q + 2 q + 0 q =
cos t.
L
(13.29)
2
• Здесь 0 и определяются формулами (13.5) и (13.14).
• Уравнение (13.29) совпадает с дифференциальным уравнение
вынужденных механических колебаний (см. формулу (8.112)).
• Частное решение этого уравнения имеет вид
(13.30)
q = qm cos( t − ),
• Где
2
qm =
, tg = 2
2
2
0 −
2
2
2 2
−
+
4
( 0 )
Um L
33

34.

Вынужденные электрические колебания
• Подстановка 02 и дает
qm =
Um
,
(13.31)
R
tg =
.
1 ( C ) − L
(13.32)
R + L − 1 ( C )
2
2
• Общее решение получится, если к частному решению (13.30)
прибавить общее решение соответствующего однородного
уравнения.
• Это решение было получено в предыдущей главе (см. (13.16)).
34

35.

Вынужденные электрические колебания
• Оно содержит экспоненциальный множитель exp(- t), поэтому по
прошествии достаточного времени становится очень малым и им
можно пренебречь.
• Следовательно, установившиеся вынужденные колебания
описываются функцией (13.30).
• Продифференцировав выражение (13.30) по t, найдем силу тока в
контуре при установившихся колебаниях:
I = − qm sin( t − ) = I m cos( t − + 2)
• Запишем это выражение в виде
I = I m cos( t − ),
(13.33)
• Где - сдвиг по фазе между током и приложенным напряжением.
35

36.

Вынужденные электрические колебания
• В соответствии с (13.32)
L − 1 ( C )
1
tg = tg − = −
=
.
(13.34)
2
tg
R
• Из этой формулы следует, что ток отстает по фазе от напряжения
( > 0) в том случае, когда L 1 ( C ) , и опережает напряжение
( < 0) при условии, что L 1 ( C ).
• Согласно (13.31)
I m = qm =
Um
R + L − 1 ( C )
2
2
.
(13.35)
36

37.

Вынужденные электрические колебания
• Представим соотношение (13.28) в виде
q
dI
IR + + L = U m cos( t ).
C
dt
(13.36)
• Произведение IR равно напряжению на активном
сопротивлении, q/C есть напряжение на конденсаторе UС,
выражение L(dI/dt) определяет напряжение на индуктивности UL.
• С учетом этого можно написать
U R + U C + U L = U m cos( t ).
(13.37)
• Таким образом, сумма напряжений на отдельных элементах
контура равна в каждый момент времени напряжению,
приложенному извне.
37

38.

Вынужденные электрические колебания
• В соответствии с (13.33)
U R = RI m cos( t − ).
(13.38)
• Разделив выражение (13.30) на емкость, получим напряжение на
конденсаторе
qm
UC =
cos( t − ) = U Cm cos( t − − ).
(13.39)
C
2
• Здесь
qm
Um
Im
U Cm =
=
=
(13.40)
C C R 2 + L − 1 ( C ) 2 C
• Умножив производную функцию (13.33) на L, получим
напряжение на индуктивности
38

39.

Вынужденные электрические колебания
dI
(13.41)
U L = L = − LI m sin( t − ) = U Lm cos( t − + )
dt
2
(13.42)
U Lm = LI m
• Здесь
• Сопоставление формул (13.33), (13.38), (13.39) и (13.41)
показывает, напряжение на емкости отстает по фазе от силы тока
на /2, а напряжение на индуктивности опережает ток на /2.
• Напряжение на активном сопротивлении изменяется в фазе с
током.
• Фазовые соотношения можно представить очень наглядно с
помощью векторной диаграммы (см. векторную диаграмму из
лекции по механическим колебаниям).
39

40.

Вынужденные электрические колебания
• Напомним, что гармоническое колебание (или гармоническую
функцию) можно задать с помощью вектора, длина которого
равна амплитуде колебания, а направление вектора образует с
некоторой осью угол, равный начальной фазе колебания.
• Возьмем в качестве прямой, от которой отсчитывается начальная
фаза, ось токов.
• Согласно (13.37) три функции UR, UC, и UL в сумме должны быть
равны приложенному напряжению U.
• В соответствии с этим напряжение U изображается на диаграмме
вектором, равным сумме векторов UR, UC, и UL.
40

41.

Вынужденные электрические колебания
• Тогда получается диаграмма,
изображенная на рисунке.
• Заметим, что из прямоугольного
треугольника, образованного на
диаграмме векторами U, UR и
разностью UL-UC, легко получить
формулу (13.35).
41

42.

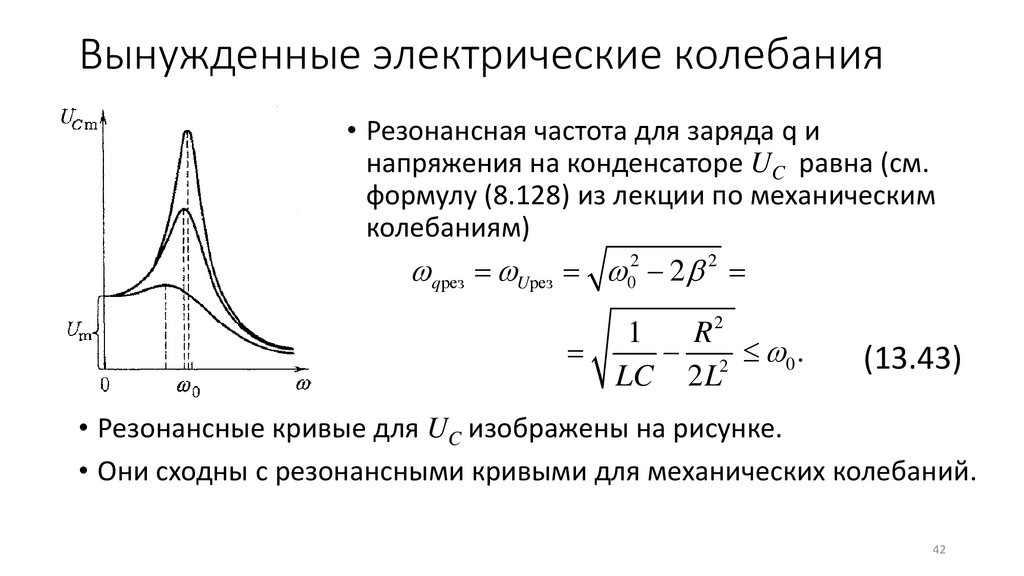
Вынужденные электрические колебания
• Резонансная частота для заряда q и
напряжения на конденсаторе UC равна (см.
формулу (8.128) из лекции по механическим
колебаниям)
qрез = Uрез = 02 − 2 2 =
=
2
1
R
− 2 0 .
LC 2 L
(13.43)
• Резонансные кривые для UC изображены на рисунке.
• Они сходны с резонансными кривыми для механических колебаний.
42

43.

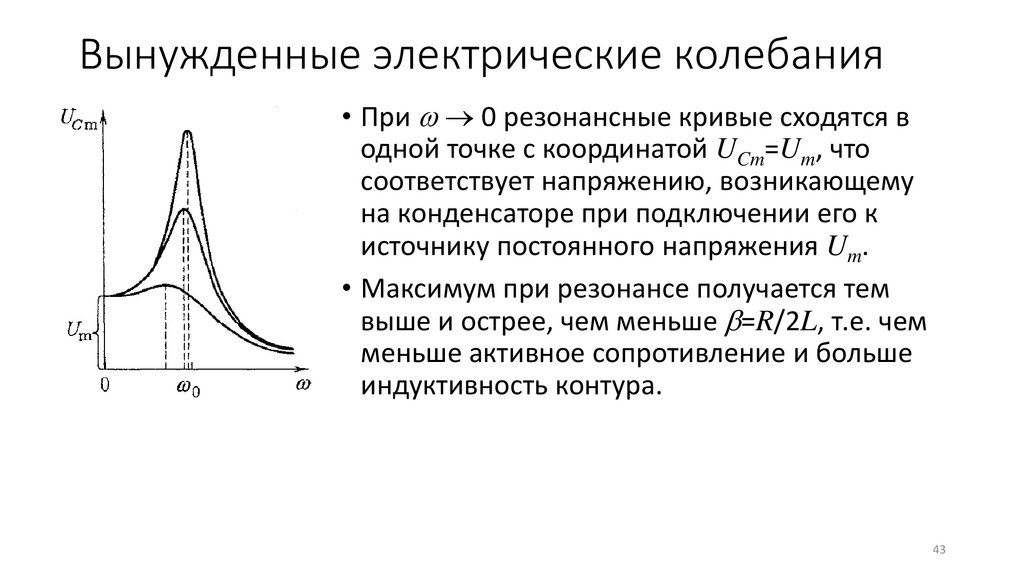
Вынужденные электрические колебания
• При → 0 резонансные кривые сходятся в
одной точке с координатой UCm=Um, что
соответствует напряжению, возникающему
на конденсаторе при подключении его к
источнику постоянного напряжения Um.
• Максимум при резонансе получается тем
выше и острее, чем меньше =R/2L, т.е. чем
меньше активное сопротивление и больше
индуктивность контура.
43

44.

Вынужденные электрические колебания
• На рисунке представлены резонансные кривые
для силы тока.
• Они соответствуют резонансным кривым для
скорости при механических колебаниях.
• Амплитуда силы тока имеет максимальное
значение при L − 1 ( C ) = 0.
• Следовательно, резонансная частота для силы
тока совпадает с собственной частотой контура 0:
1
Iрез = 0 =
.
(13.44)
LC
• Отрезок, отсекаемый резонансными кривыми на оси Im, равен нулю – при
постоянном напряжении установившийся ток в цепи с конденсатором течь не
44
может.

45.

Вынужденные электрические колебания
• При малом затухании (при 2 02 ) резонансную частоту для
напряжения можно положить равной 0.
• Соответственно можно считать, что рез L − 1 ( C ) 0.
• Согласно формуле (13.40) отношение амплитуды напряжения на
конденсаторе при резонансе UCmрез к амплитуде внешнего
напряжения Um будет в этом случае равно
U Cmрез
Um
1
LC 1 L
=
=
=
=Q
0CR CR
R C
(13.45)
• (мы положили в (13.40) = Uрез = 0 ).
• Здесь Q – добротность контура (см. (13.24)).
45

46.

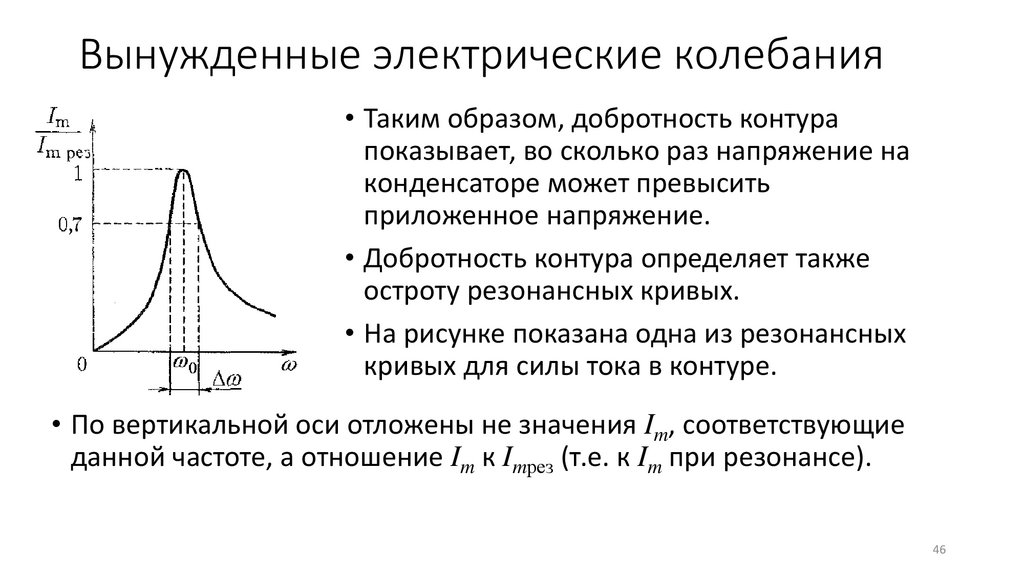
Вынужденные электрические колебания
• Таким образом, добротность контура
показывает, во сколько раз напряжение на
конденсаторе может превысить
приложенное напряжение.
• Добротность контура определяет также
остроту резонансных кривых.
• На рисунке показана одна из резонансных
кривых для силы тока в контуре.
• По вертикальной оси отложены не значения Im, соответствующие
данной частоте, а отношение Im к Imрез (т.е. к Im при резонансе).
46

47.

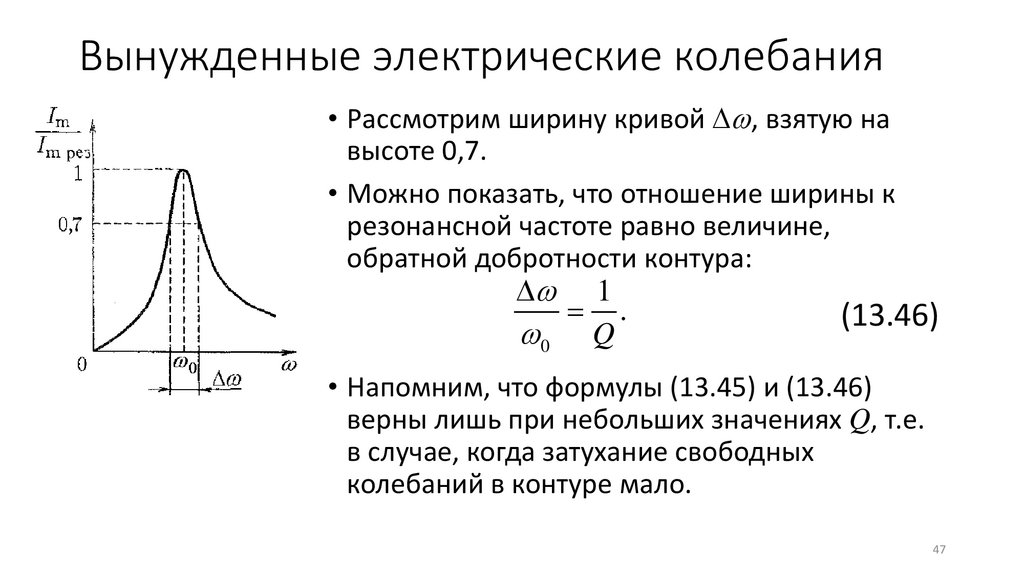
Вынужденные электрические колебания
• Рассмотрим ширину кривой , взятую на
высоте 0,7.
• Можно показать, что отношение ширины к
резонансной частоте равно величине,
обратной добротности контура:
1
= .
(13.46)
0 Q
• Напомним, что формулы (13.45) и (13.46)
верны лишь при небольших значениях Q, т.е.
в случае, когда затухание свободных
колебаний в контуре мало.
47

48.

Вынужденные электрические колебания
• Явление резонанса используется для выделения из сложного
напряжения нужной составляющей.
• Пусть напряжение, приложенное к контуру, равно
U = U m1 cos( 1t + 1 ) + U m 2 cos( 2t + 2 ) + ...
• Настроив контур на одну из частот 1, 2 и т.д. (т.е. подобрав
соответствующим образом его параметры L и С), можно получить
на конденсаторе напряжение, в Q раз превышающее значение
данной составляющей, в то время как напряжение, создаваемое
на конденсаторе другими составляющими, будет слабым.
• Такой процесс осуществляется при настройке радиоприемника
на нужную длину волны.
48

49.

Переменный ток
• Описанные в предыдущей главе установившиеся вынужденные
колебания можно рассматривать как протекание в цепи,
обладающей емкостью, индуктивностью и активным
сопротивлением, переменного тока, обусловленного
переменным напряжением
U = U m cos( t ).
(13.47)
• Согласно формулам (13.33) – (13.35) этот ток изменяется по
закону
I = I m cos( t − ).
(13.48)
• Амплитуда тока определяется амплитудой напряжения Um,
параметрами C, L, R и частотой :
Um
Im =
.
(13.49)
2
2
R + L − 1 ( C )
49

50.

Переменный ток
• Ток отстает от напряжения на угол , который зависит от
параметров цепи и частоты:
L − 1 ( C )
tg =
.
(13.50)
R
• В случае, когда < 0, ток фактически опережает напряжение.
• Стоящее в знаменателе формулы (13.49) выражение
Z = R + L − 1 ( C )
2
2
(13.51)
• Называется полным электрическим сопротивлением или
импедансом .
50

51.

Переменный ток
• Если цепь состоит из одного лишь активного сопротивления R,
уравнение закона Ома имеет вид
IR = U m cos( t ).
• Отсюда следует, что ток в этом случае изменяется в фазе с
напряжением, а амплитуда силы тока равна
Um
Im =
.
R
• Сравнение этого выражения с (13.49) показывает, что замена
конденсатора закороченным участком цепи означает переход не
к C=0, а к С= .
• Всякая реальная цепь обладает конечными R, L и С.
51

52.

Переменный ток
• В отдельных случаях некоторые из этих параметров бывают
таковы, что их влиянием можно пренебречь.
• Допустим, что R цепи можно положить равным нулю, а C –
равным бесконечности.
• Тогда из формул (13.49) и (13.50) следует, что
Um
Im =
,
(13.52)
L
• а tg = (соответственно = /2).
(13.53)
X L = L
• Величину
• Называют реактивным индуктивным сопротивлением цепи
или просто индуктивным сопротивлением цепи.
52

53.

Переменный ток
• Если L выразить в генри, а - в обратных секундах, то XL будет
выражено в омах.
• Из (13.53) следует, что индуктивное сопротивление растет с
частотой .
• Постоянному току при =0 индуктивность не оказывает
сопротивления.
• Ток в индуктивности отстает от напряжения на /2.
• Соответственно напряжение на индуктивности опережает ток на
/2.
• Теперь допустим, что можно положить равным нулю R и L.
53

54.

Переменный ток
• Тогда согласно формулам (13.49) и (13.50)
Um
Im =
,
1 ( C )
(13.54)
• tg =- (соответственно =- /2). Величину
1
XC =
(13.55)
C
• Называют реактивным емкостным сопротивлением или просто
емкостным сопротивлением. Если С выразить в фарадах, а - в
обратных секундах, то XС будет выражено в омах.
• Из (13.55) следует, что емкостное сопротивление убывает с
частотой.
54

55.

Переменный ток
• Для постоянного тока XC= , следовательно постоянный ток через
конденсатор течь не может.
• Поскольку =- /2, ток, текущий через конденсатор, опережает
напряжением на /2.
• Соответственно напряжение на конденсаторе отстает от тока на
/2.
• Наконец допустим, что можно положить R равным нулю.
• В этом случае формула (13.49) переходит в
Um
Im =
.
(13.56)
L − 1 ( C )
55

56.

Переменный ток
• Величина
1
X = L −
= X L − XC
(13.57)
C
• Называется реактивным сопротивлением или реактансом.
• Формулы (13.50) и (13.51) можно представить в виде
tg = X R, Z = R 2 + X 2 .
• Таким образом, если значение сопротивлений R и X отложить
вдоль катетов треугольника, то длина гипотенузы будет численно
равна Z.
• Найдем мощность, выделяемую в цепи переменного тока.
56

57.

Переменный ток
• Мгновенное значение мощности равно произведению
мгновенных значений напряжения и силы тока:
P(t ) = U (t ) I (t ) = U m cos t I m cos( t − ).
(13.58)
• Воспользовавшись формулой
1
1
cos cos = cos( − ) + cos( + )
2
2
• Выражению (13.58) можно придать вид
1
1
P ( t ) = U m I m cos + U m I m cos(2 t − ).
2
2
(13.59)
57

58.

Переменный ток
• Практический интерес представляет среднее
по времени значение P(t), которое мы
обозначим просто P.
• В связи с тем, что среднее значение cos(2 t ) равно нулю
Um Im
(13.60)
P=
cos .
2
• Из (13.59) следует, что мгновенная
мощность колеблется около среднего
значения с частотой в два раза
превышающей частоту тока.
58

59.

Переменный ток
• В соответствии с формулой (13.50) можем записать
R
R
cos =
= .
2
2
Z
R + L − 1 ( C )
(13.61)
• Подставив это значение в cos в формулу (13.60) и учтя, что
Um/Z=Im, получим
2
RI m
(13.62)
P=
2
• Такую же мощность развивает постоянный ток, сила которого
равна
Im
I=
.
(13.63)
2
• Эта величина I называется действующим (или эффективным)
значением силы тока.
59

60.

Переменный ток
• Аналогично величина
Um
U=
(13.64)
2
называется действующим значением напряжения.
• Выражение средней мощности через действующие значения
силы тока и напряжения имеет вид
P = UI cos .
(13.65)
• Входящий в это выражение множитель cos называют
коэффициентом мощности.
• В технике стремятся сделать cos как можно большим.
• При малом cos при той же мощности существенно возрастают
потери в проводящих проводах.
60