Похожие презентации:
Электрические колебания
1.
Сегодня: четверг, 27 февраля 2020 г.Тема 4. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
4.1.Переменный ток.
Колебательный контур
4.2. Свободные колебания в электрическом
контуре без активного сопротивления
4.3. Свободные затухающие электрические
колебания
4.4. Вынужденные электрические колебания
1
2.
4.1. Переменный токПри рассмотрении электрических колебаний приходится иметь дело с
токами, изменяющимися во времени – переменными токами:
I = I0 sin( t + )
Закон Ома и вытекающие из него правила Кирхгофа были установлены
для постоянного тока. Однако они остаются справедливыми и для
мгновенных значений изменяющегося тока.
3.
Переменный токЭлектромагнитные сигналы распространяются по цепи со
скоростью света с.
• Пусть l – длина электрической цепи.
• Время распространения сигнала в данной цепи
t l / c.
• Если t T
то такие токи называются
квазистационарными (Т – период колебаний тока).
• При этом условии мгновенное значение силы тока во всех
участках цепи будет постоянным.
f 105 Гц условие квазистационарности
• Для частоты
будет выполняться в нашей лаборатории «Электричество» при
1
1
длине цепи ~ 1 м.
9
5
3
10
10
Рассматривая в дальнейшем электрические колебания,
мы будем считать, что токи квазистационарны.
4.
1.Сопротивление в цепи переменного токаТок в цепи I = I0 sin t ;
По закону Ома:
U = IR = I0 R sin t - напряжение
изменяется синфазно с током;
U0 = I0 R - амплитуда напряжения.
С, L
пренебрежимо малы
Векторная диаграмма напряжения на сопротивлении:
5.
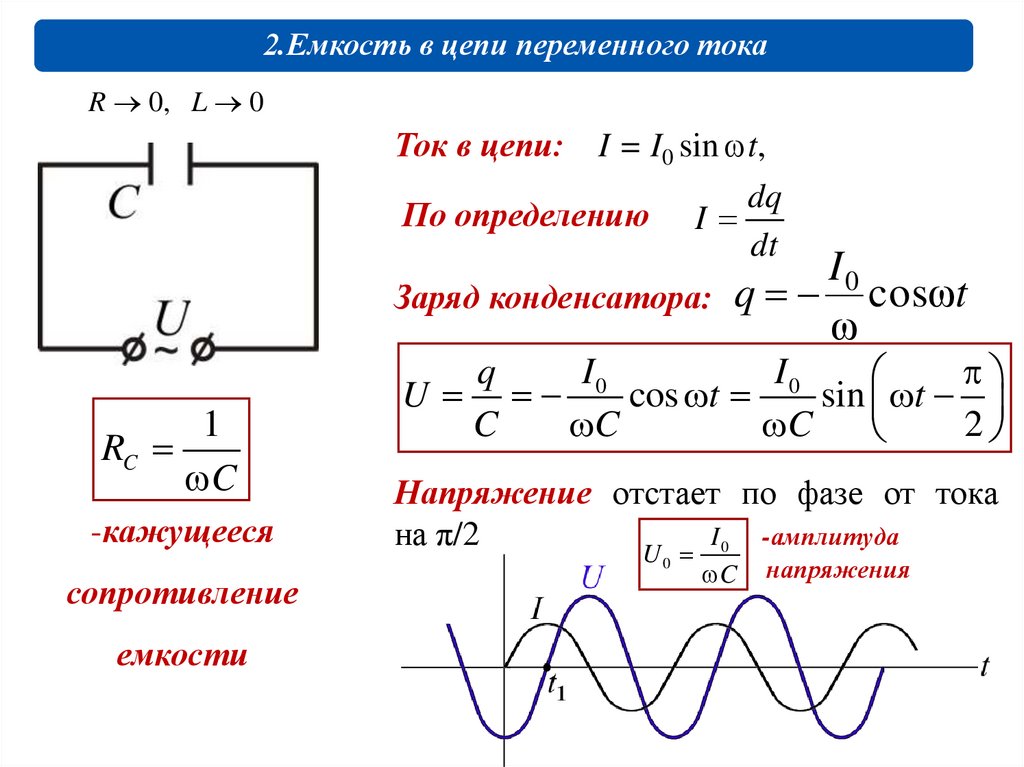
2.Емкость в цепи переменного токаR 0, L 0
I = I0 sin t,
dq
По определению I
dt
Ток в цепи:
Заряд конденсатора:
1
RC
C
-кажущееся
I0
I0
q
U
cos t
sin t
C
C
C
2
Напряжение отстает по фазе от тока
на π/2
-амплитуда
I
U 0
0
сопротивление
емкости
I0
q cosωt
ω
C
напряжения
6.
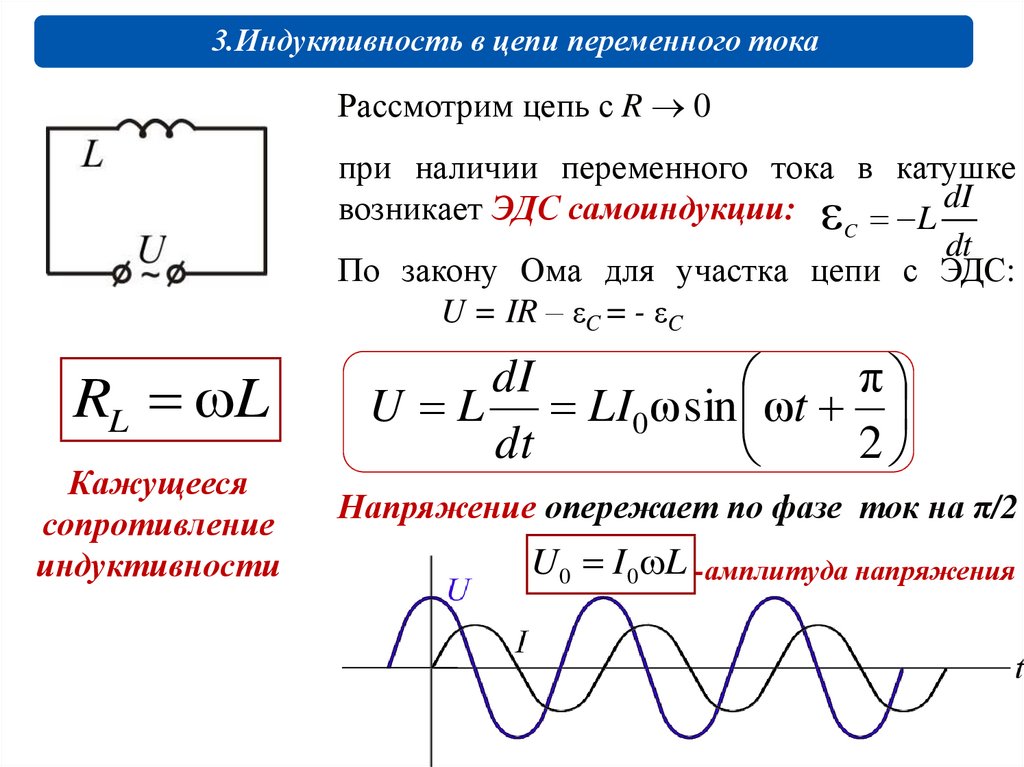
3.Индуктивность в цепи переменного токаРассмотрим цепь с R 0
при наличии переменного тока в катушке
возникает ЭДС самоиндукции: L dI
C
dt
По закону Ома для участка цепи с ЭДС:
U = IR – εC = - εC
RL L
Кажущееся
сопротивление
индуктивности
dI
π
U L LI0ω sin ωt
dt
2
Напряжение опережает по фазе ток на π/2
U 0 I 0 L -амплитуда напряжения
7.
4.1. Колебательный контурСреди различных колебательных систем особое место занимают
электромагнитные
(электрические)
системы,
при
которых
электрические величины (токи, заряды) периодически изменяются и
которые сопровождаются взаимными превращениями электрического
и магнитного полей.
Для возбуждения и поддержания электромагнитных колебаний
используется колебательный контур.
R
L
C
Колебательный контур – это электрическая
цепь, состоящая из последовательно
включенных резистора сопротивлением R .
катушки индуктивностью L , и конденсатора
емкостью C.
Для выяснения механизма возникновения электрических колебаний
рассмотрим идеализированный контур, сопротивление которого
пренебрежимо мало ( R 0 ).
8.
Колебательный контур.L
C
Для возбуждения в контуре колебаний
конденсатор предварительно заряжают,
сообщая его обкладкам заряды q .
В момент времени t 0 между обкладками
конденсатора возникает электрическое
поле,
2
энергия которого равна q 2C .
Вся энергия колебательного контура сосредоточена в конденсаторе.
Если теперь замкнуть конденсатор на катушку индуктивности, то в
контуре потечет возрастающий со временем ток I.
Электрическая энергия конденсатора начнет превращаться в
магнитную энергию катушки.
Этот процесс закончится, когда конденсатор полностью разрядится,
а ток в цепи достигнет максимума.
Вся энергия колебательного
контура сосредоточена в магнитном поле
2
катушки и равна LI 2 .
9.
Колебательный контур.С этого момента ток, не меняя
направления, начнет убывать.
Однако он прекратится не сразу – его будет
C
поддерживать ЭДС самоиндукции.
Ток будет перезаряжать конденсатор,
возникнет
электрическое
поле,
стремящееся ослабить ток.
Наконец, ток прекратится, а заряд на пластинах конденсатора
достигнет максимума.
С этого момента конденсатор начнет вновь разряжаться, ток потечет в
обратном направлении и процесс повторится.
Поскольку потерь энергии нет, в контуре будут совершаться
периодические незатухающие колебания: будут изменяться заряд и
напряжение на конденсаторе и ток, текущий через катушку.
Следовательно, в контуре возникнут колебания, сопровождаемые
превращениями энергии электрического и магнитного полей.
L
10.
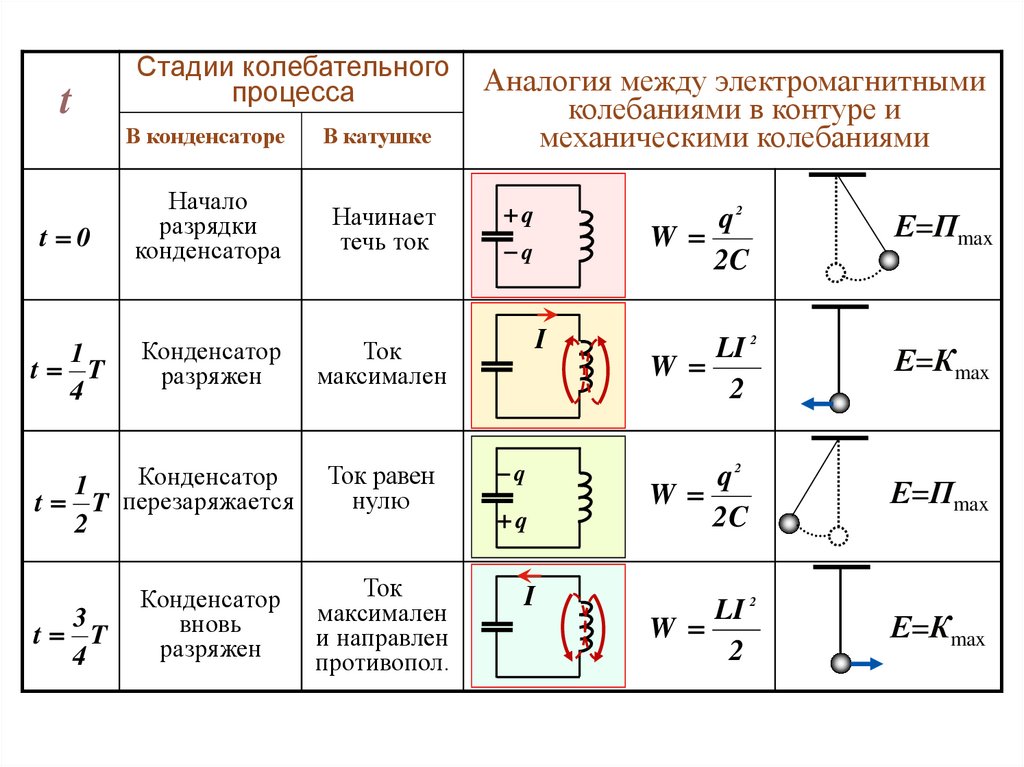
tСтадии колебательного
процесса
В конденсаторе
В катушке
t 0
Начало
разрядки
конденсатора
Начинает
течь ток
1
t T
4
Конденсатор
разряжен
Ток
максимален
Конденсатор
1
t T перезаряжается
2
3
t T
4
Конденсатор
вновь
разряжен
Ток равен
нулю
Ток
максимален
и направлен
противопол.
Аналогия между электромагнитными
колебаниями в контуре и
механическими колебаниями
q
q
I
q
q
I
q2
W
2C
Е=Пmax
LI 2
W
2
Е=Кmax
q2
W
2C
Е=Пmax
LI 2
W
2
Е=Кmax
11.
Колебаниямеханические
Дифференциальное уравнение
Масса
Коэффициент
жесткости
электромагнитные
R
1
r
k
q 0
x x x 0 Дифференциаль- q q
L
LC2
m
m2
ное уравнение
q 2 q 0 q 0
x 2 x 0 x 0
m
k
Индуктивность
катушки
L
Обратная
величина емкости
1
C
Заряд
q qm sin( t )
Смещение
x xm sin( t )
Скорость
υ dx / dt
Сила тока
I dq / dt
Потенциальная
энергия
kx 2
W
2
Энергия электрич.
поля
q 2 CU 2
W
2C
2
Кинетическая
энергия
m 2
K
2
Энергия
магнитного поля
LI 2
K
2
12.
Собств. частотапружинного
маятника
k
ω0
m
Собств. частота
колебательного
контура
Период колебаний
T 2π m / k
Период колеб.
Формула Томсона
Циклич. частота
затухающих
колебаний
k r
ω
m 2m
2
Циклич. частота
затухающих
колебаний
ω0
1
LC
T 2π LC
ω
1
R2
2
LC 4 L
Коэффициент
затухания
r
β
2m
Коэффициент
затухания
β
Логарифмич.
декремент
затухания
A(t )
χ ln
βT
A(t T )
Логарифмич.
декремент
затухания
T πR
Добротность
пружинного
маятника
π 1
Q
km
χ r
Добротность
колебательного
контура
Резонансная
частота
ω рез ω02 2β 2
Резонансная
частота
Q
R
2L
C
L
1 L
R C
ω рез ω02 2β 2
13.
4.2. Свободные колебания в электрическомконтуре без активного сопротивления
Найдем уравнение колебаний в контуре без активного сопротивления.
Будем искать закон изменения заряда на обкладках конденсатора.
Пусть положительным будет такое направление тока в контуре, когда
конденсатор заряжается.
Сила тока в цепи определяется I dq q
L
выражением
dt
3
I
2
q
C
1
q
Рассмотрим цепь 1 – 3 – 2 и запишем для нее
закон Ома в общем виде для неоднородного
участка цепи:
IR 1 2 E12
E12 - ЭДС, действующая на участке цепи 1 – 2.
ЭДС положительна, т.к. способствует движению положительно
заряженных носителей тока в выбранном направлении.
14.
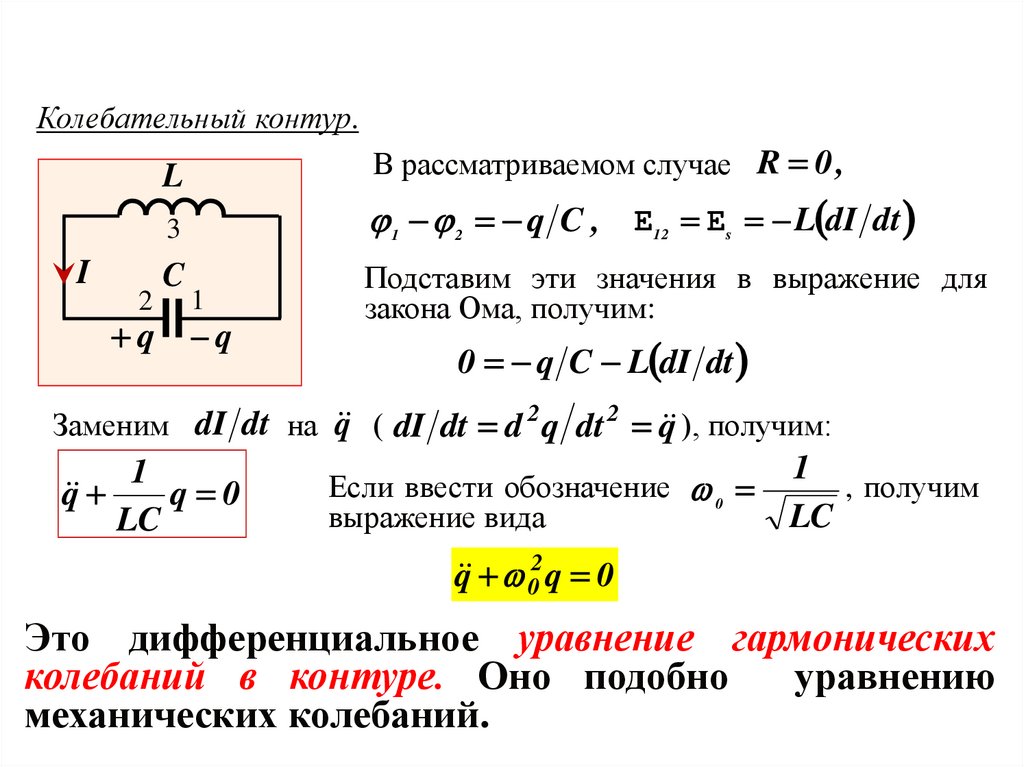
Колебательный контур.В рассматриваемом случае R 0 ,
L
1 2 q C , E12 Es L dI dt
3
I
2
q
C
1
q
Подставим эти значения в выражение для
закона Ома, получим:
0 q C L dI dt
Заменим dI dt на q ( dI dt d 2 q dt 2 q
), получим:
1
q
q 0
LC
Если ввести обозначение 0
выражение вида
1
, получим
LC
q 02 q 0
Это дифференциальное уравнение гармонических
колебаний в контуре. Оно подобно
уравнению
механических колебаний.
15.
Колебательный контур.L
Решением этого уравнения является выражение
q qmax cos 0 t
3
I
2
q
C
1
q
Таким образом, заряд на обкладках конденсатора
изменяется по гармоническому закону с частотой,
определяемой параметрами контура L и C .
Эта частота называется собственной частотой
контура и соответствует собственной частоте
гармонического осциллятора.
Выражение для периода колебаний называется
формулой Томсона:
T 2 LC
1
q
q 0
LC
Запишем формулу для напряжения на конденсаторе:
q q max
U
cos 0 t
C
C
16.
Колебательный контур.L
Продифференцировав соотношение для
заряда, получим выражение для тока в
контуре :
3
I
2
q
C
1
q
1
q 0
LC
q qmax cos 0 t
q
qmax
U
cos 0 t
C
dq
I
dt
I qmax 0 sin 0 t
I I max cos 0 t
2
Видно, что сила тока опережает по фазе
напряжение на конденсаторе на 2.
В момент, когда ток достигает наибольшего
значения, заряд и напряжение обращаются
в нуль и наоборот.
17.
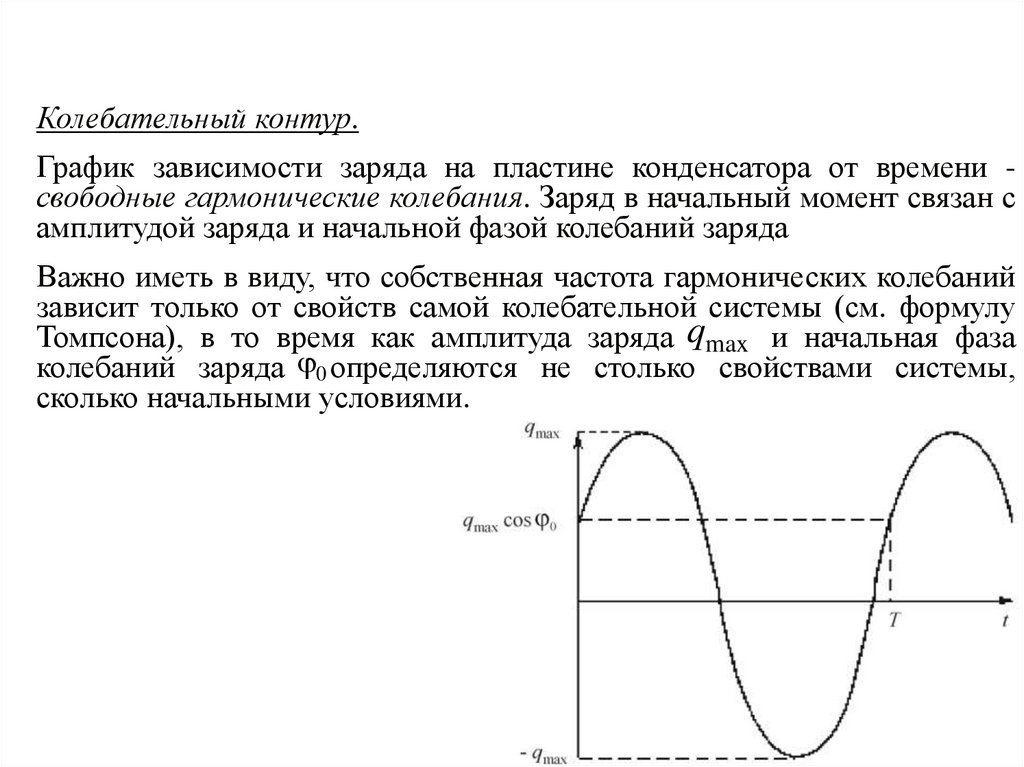
Колебательный контур.График зависимости заряда на пластине конденсатора от времени свободные гармонические колебания. Заряд в начальный момент связан с
амплитудой заряда и начальной фазой колебаний заряда
Важно иметь в виду, что собственная частота гармонических колебаний
зависит только от свойств самой колебательной системы (см. формулу
Томпсона), в то время как амплитуда заряда qmax и начальная фаза
колебаний заряда 0 определяются не столько свойствами системы,
сколько начальными условиями.
18.
4.3. Свободные затухающие колебания вконтуре
Реальный контур обладает активным сопротивлением.
Энергия, запасенная в контуре, постепенно расходуется на этом
сопротивлении на нагревание, вследствие чего свободные колебания
затухают.
Учтем фактор затухания в выражении для закона Ома:
IR q C L dI dt
Разделим это уравнение на L и заменим ток I на заряд q . В итоге
получим:
R
1
q q
q 0
L
LC
1
R
Введем обозначение
и, учитывая, что 0
, получим
2L
LC
окончательно:
q 2 q 02 q 0
19.
Свободные затухающие колебания в контуре.q 2 q 02 q 0
Это уравнение, как и ожидалось, совпадает с дифференциальным
уравнением затухающих механических колебаний.
2
R
1
При условии, что 2 0 , т.е. при
решение уравнения
2
4L
LC
затухающих колебаний имеет вид
2
q qmax 0 e t cos t
где 02 2 .
Если в это выражение подставить соответствующие выражения для
и 0 , получим следующее соотношение для частоты затухающих
колебаний:
2
При R 0 получится выражение для
1
R
собственной частоты незатухающих
2
свободных колебаний в контуре.
LC 4 L
20.
Свободные затухающие колебания в контуре.Из уравнения для затухающих колебаний легко получить формулу
для напряжения на конденсаторе, разделив уравнение на емкость С, и
выражение для тока в контуре. ( СМ. ИРОДОВ параграф 11.2)
Запишем один из выводов, которые можно сделать из анализа формул
для тока и падения напряжения на конденсаторе колебательного
контура: при наличии активного сопротивления в контуре сила тока
опережает по фазе напряжение на конденсаторе на угол больший,
чем 2 ( 2 ).
Изобразим график изменения заряда со временем.
21.
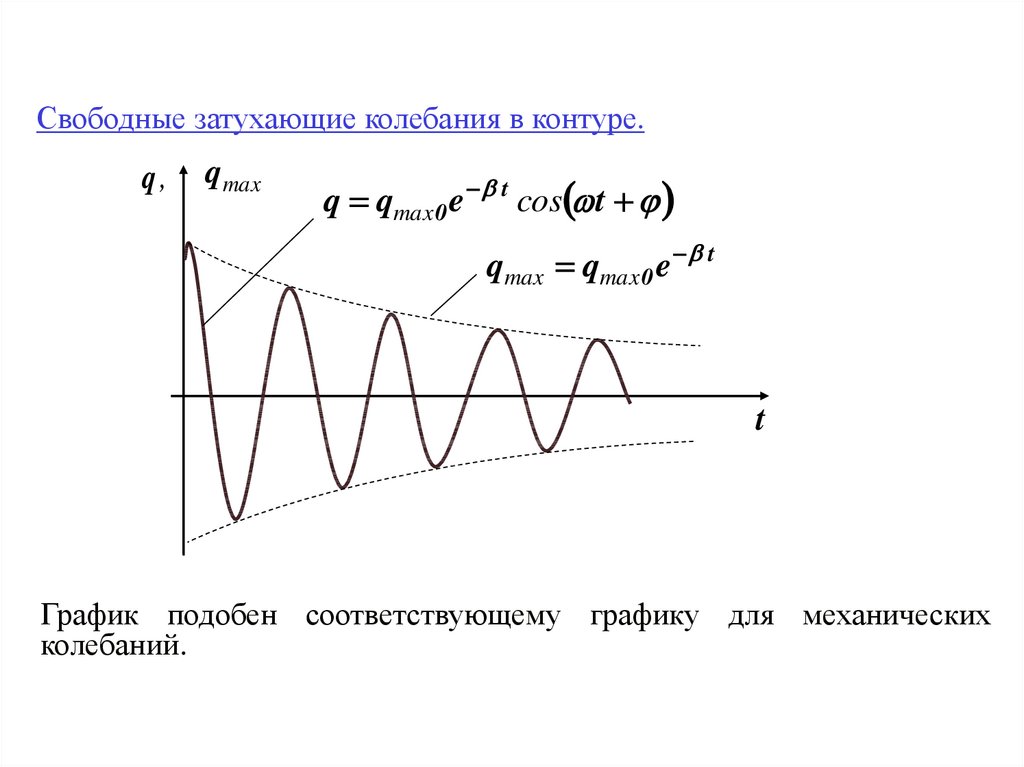
Свободные затухающие колебания в контуре.q,
qmax
q qmax 0 e t cos t
qmax qmax 0 e t
t
График подобен соответствующему графику для механических
колебаний.
22.
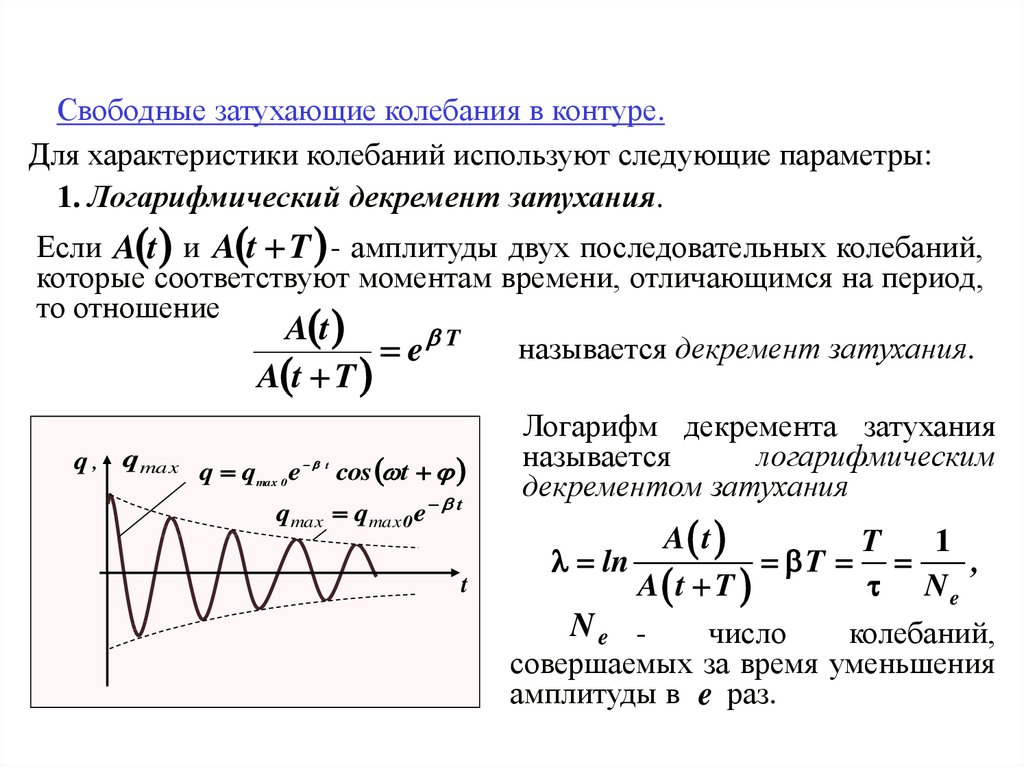
Свободные затухающие колебания в контуре.Для характеристики колебаний используют следующие параметры:
1. Логарифмический декремент затухания.
Если A t и A t T - амплитуды двух последовательных колебаний,
которые соответствуют моментам времени, отличающимся на период,
то отношение
A t
называется декремент затухания.
e T
A t T
q , qmax q q e t cos t
max 0
qmax qmax 0 e t
t
Логарифм декремента затухания
называется
логарифмическим
декрементом затухания
A t
T
1
ln
T
,
A t T
Ne
Ne число
колебаний,
совершаемых за время уменьшения
амплитуды в e раз.
23.
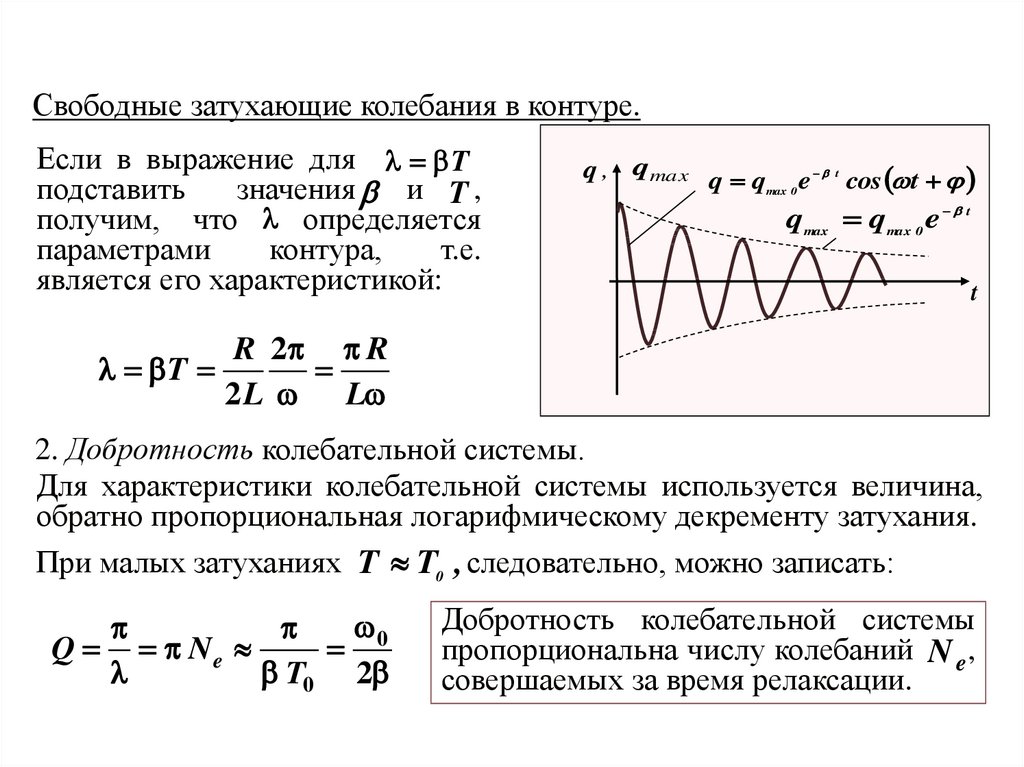
Свободные затухающие колебания в контуре.Если в выражение для T .
подставить
значения и T ,
получим, что определяется
параметрами
контура,
т.е.
является его характеристикой:
T
q , qmax q q e t cos t
max 0
qmax qmax 0 e t
t
R 2 R
2 L L
2. Добротность колебательной системы.
Для характеристики колебательной системы используется величина,
обратно пропорциональная логарифмическому декременту затухания.
При малых затуханиях T T0 , следовательно, можно записать:
0
Q Ne
T0 2
Добротность колебательной системы
пропорциональна числу колебаний N e ,
совершаемых за время релаксации.
24.
Добротность колебательного контураопределяется как величина обратно
пропорциональная
(Чем меньше
затухание, тем выше добротность)
1
Q
Время затухания – время за которое
амплитуда колебаний уменьшается в е раз
1
Ne
T T
W
Q 2π
ΔW
Число колебаний совершаемых
за время затухания
1
Nе
то
Q πN е
W – энергия контура в данный момент,
ΔW – убыль энергии за один период, следующий
за этим моментом
25.
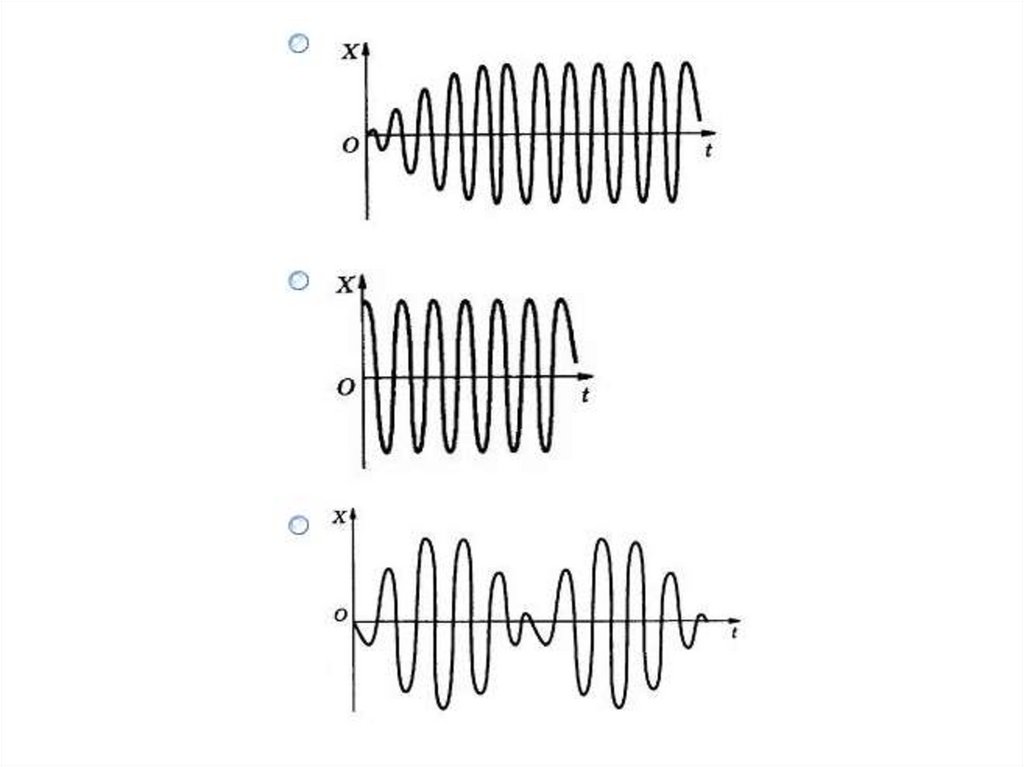
4.4. Вынужденные колебания в контуреДля компенсации потерь в колебательном контуре нужно оказывать
на контур периодически изменяющееся воздействие.
Это можно осуществить, например, включив последовательно с
элементами контура переменную ЭДС или, разорвав контур, подать на
образовавшиеся контакты переменное напряжение.
R
L
U
U U max cos t
C
Это напряжение нужно прибавить к ЭДС
самоиндукции в исходной формуле для
затухающих колебаний:
IR q C L dI dt U max cos t
После преобразований получим уравнение вынужденных колебаний:
U max
q 2 q 0 q
cos t
L
2
26.
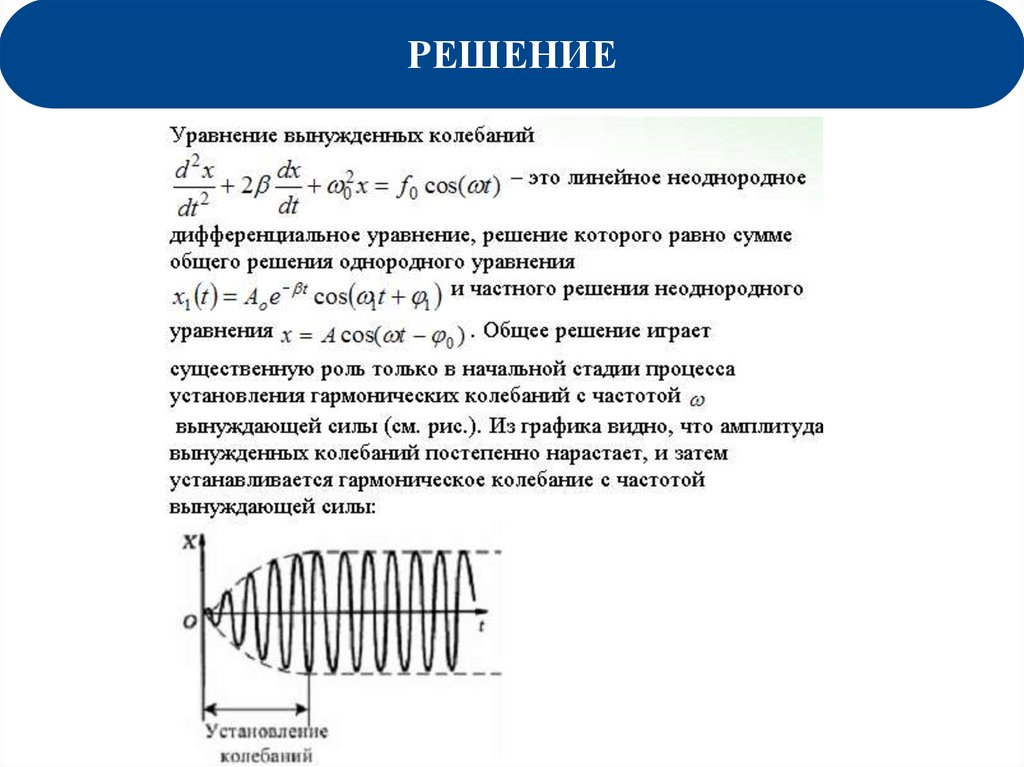
Вынужденные колебания в контуре.Получили
уже
известное
нам
линейное
неоднородное
дифференциальное уравнение вынужденных колебаний.
Решение неоднородного дифференциального уравнения представим в
виде его частного решения для установившихся колебаний. Это
решение, как и для механических колебаний, имеет вид:
q qmax cos t
где qmax - амплитуда заряда на конденсаторе; (пси) – разность фаз
между колебаниями заряда и внешней ЭДС.
R
L
U
C
Выражения для qmaxи , как и для
механических колебаний, запишем без вывода:
qmax
ω
U max L
2
0
ω
2
2
4β 2 ω 2
2
arctg 2
0 2
27.
Вынужденные колебания в контуре.С использованием соотношений для
R
L
C
постоянных величин qmax и можно
провести
анализ
параметров
вынужденных колебаний в контуре.
Как и в случае затухающих
U
свободных колебаний ограничимся
U max L
лишь общими выводами о сдвиге фаз
qmax
колебаний тока и напряжения на
2
2 2
2
2
ω0 ω 4β ω
элементах контура:
2
arctg 2
0 2
а) напряжение на R
фазе с током;
изменяется в
б) напряжение на индуктивности
опережает по фазе ток на угол 2 ;
в) напряжение на емкости отстает по фазе от тока на угол 2 .
РАССМ. РЕШЕНИЕ ЗАДАЧИ №4.142) ПОСТРОИТЬ ВЕКТОРНЫЕ
ДИАГРАММЫ!!! (разобрана в И.Е.ИРОДОВ № 11.10)
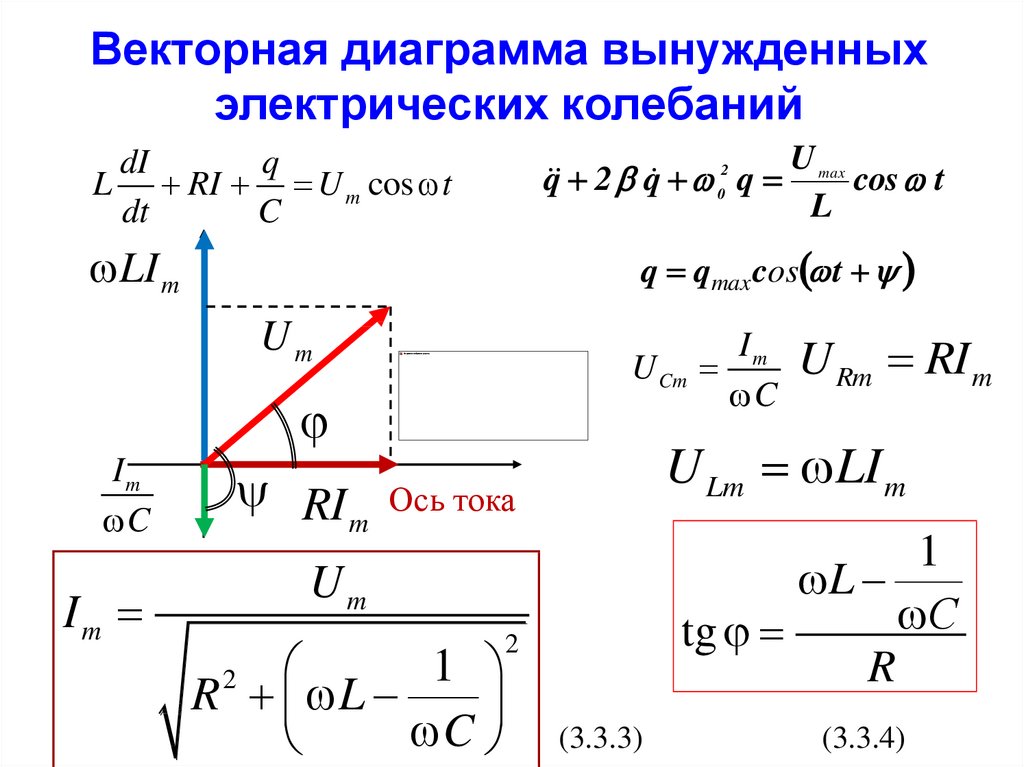
28. Векторная диаграмма вынужденных электрических колебаний
U maxq 2 q 0 q
cos t
L
dI
q
L RI U m cos t
dt
C
2
LI m
q qmax cos t
Um
U Cm
Im
C
RI
m
Im
Um
U Rm RI m
U Lm LI m
Ось тока
1
R L
C
Im
C
1
L
С
tg
R
2
2
(3.3.3)
(3.3.4)
29.
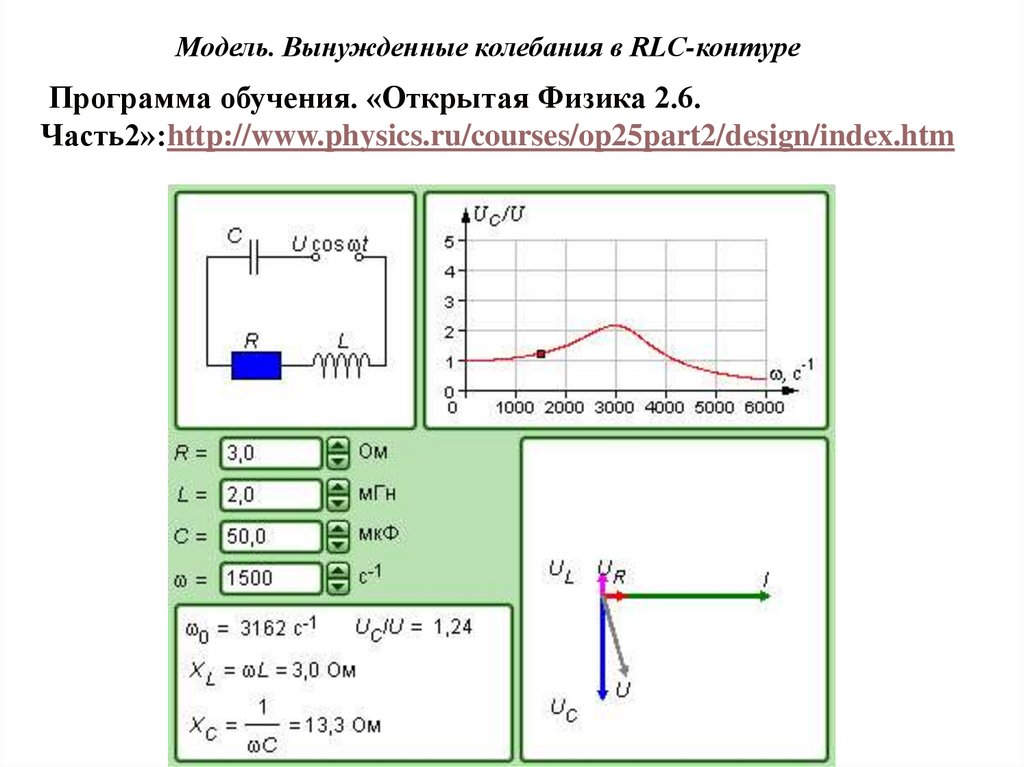
Модель. Вынужденные колебания в RLC-контуреПрограмма обучения. «Открытая Физика 2.6.
Часть2»:http://www.physics.ru/courses/op25part2/design/index.htm
30.
Пояснения к модели. Вынужденные колебания в RLC-контуреВынужденные колебания всегда происходят на частоте ω внешнего источника.
Если внешнее гармоническое напряжение включено в RLC-контур, то амплитуда
вынужденных колебаний тока или напряжения на элементах цепи сильно зависит от
соотношения между частотой ω генератора и собственной частотой ω0. При ω = ω0
наступает резонанс. При резонансе амплитуды напряжений на конденсаторе (UC) и катушке
индуктивности (UL) становятся максимальными. График зависимости отношения (UC / U)
или (UL / U) называется резонансной кривой.
«Острота» резонансной кривой сильно зависит от энергетических потерь в контуре. При
увеличении активного сопротивления контура резонансная кривая становится менее
«острой».
Между напряжением генератора и напряжением на конденсаторе имеется фазовый сдвиг,
зависящий от соотношения между ω и ω0. При резонансе фазовый сдвиг равен π / 2.
Соотношения между амплитудами напряжений и токов и их фазами при вынужденных
колебаниях удобно анализировать с помощью векторных диаграмм.
В компьютерной модели можно изменять параметры RLC-контура, а также частоту ω
внешнего источника. При изменении параметров на дисплее высвечивается новая
резонансная кривая, на которой точкой отмечается результат компьютерного эксперимента.
Одновременно высвечивается векторная диаграмма, на которой с помощью векторов
изображаются колебания тока и напряжений на элементах цепи.
31.
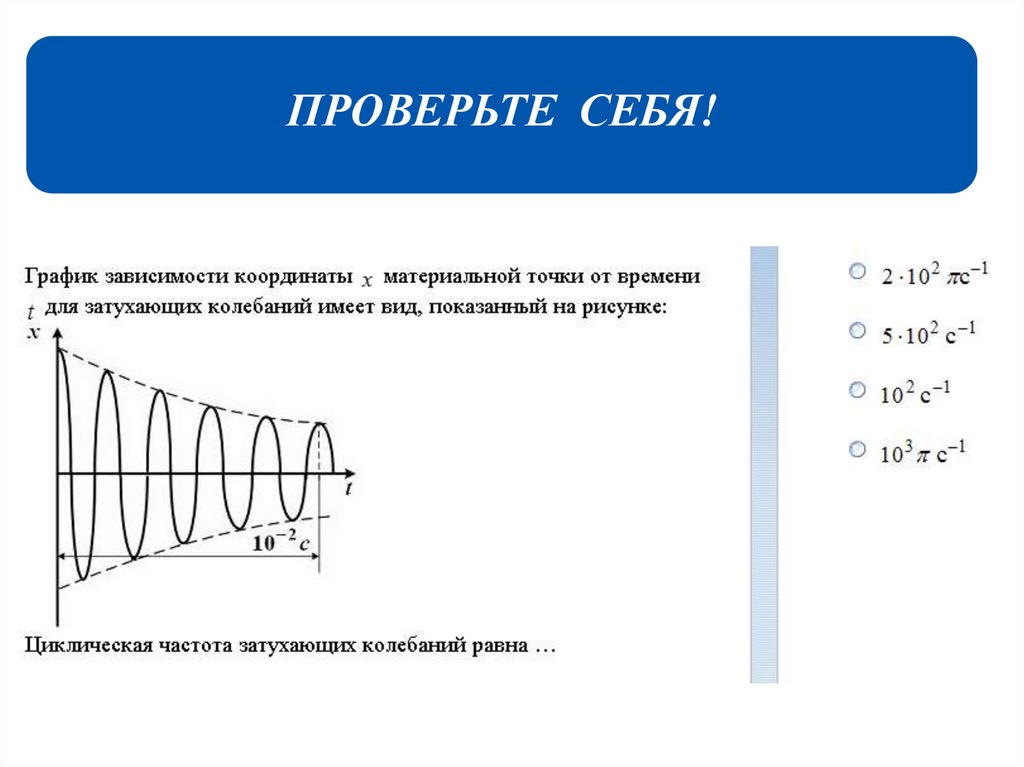
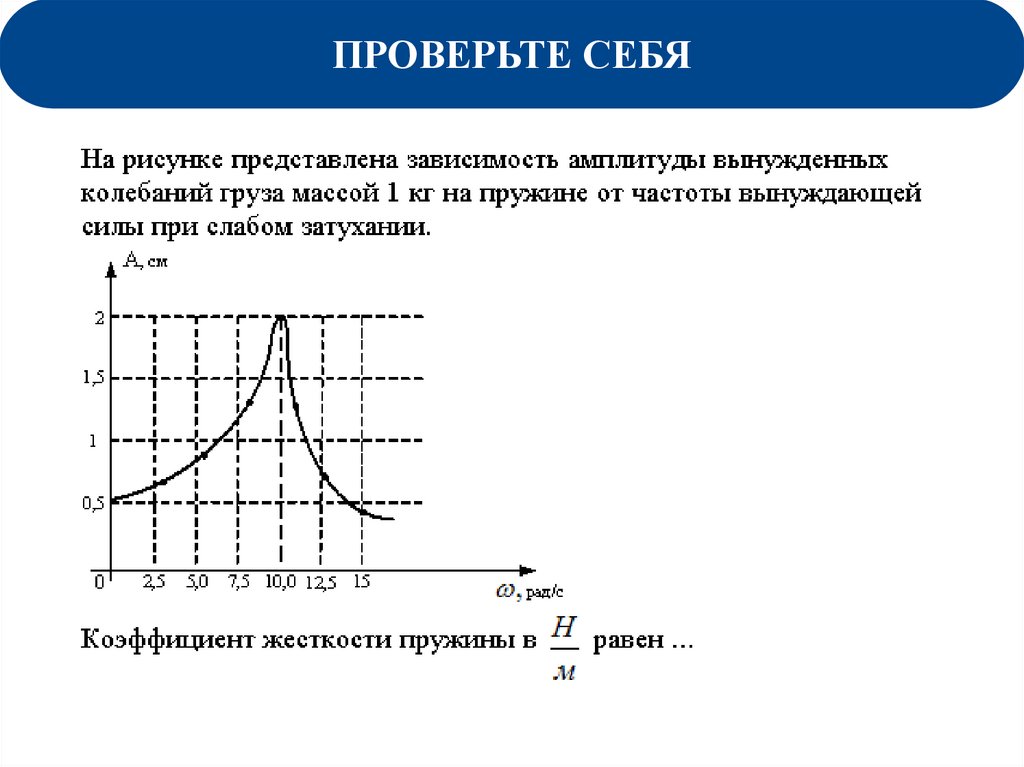
ПРОВЕРЬТЕ СЕБЯ!32.
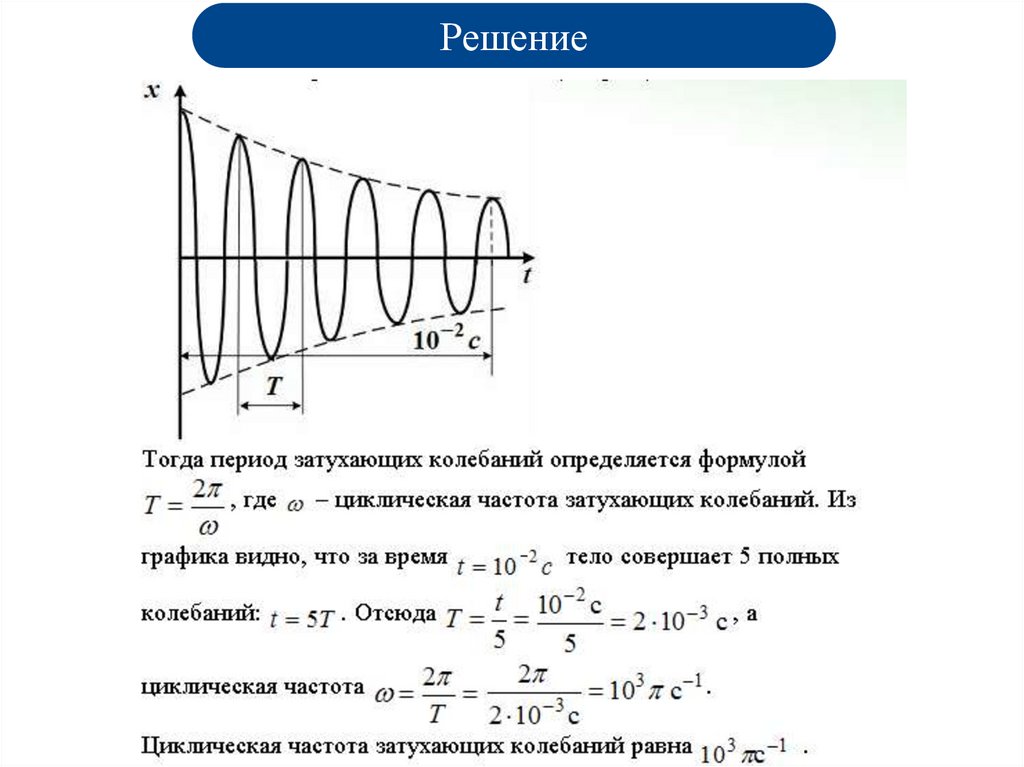
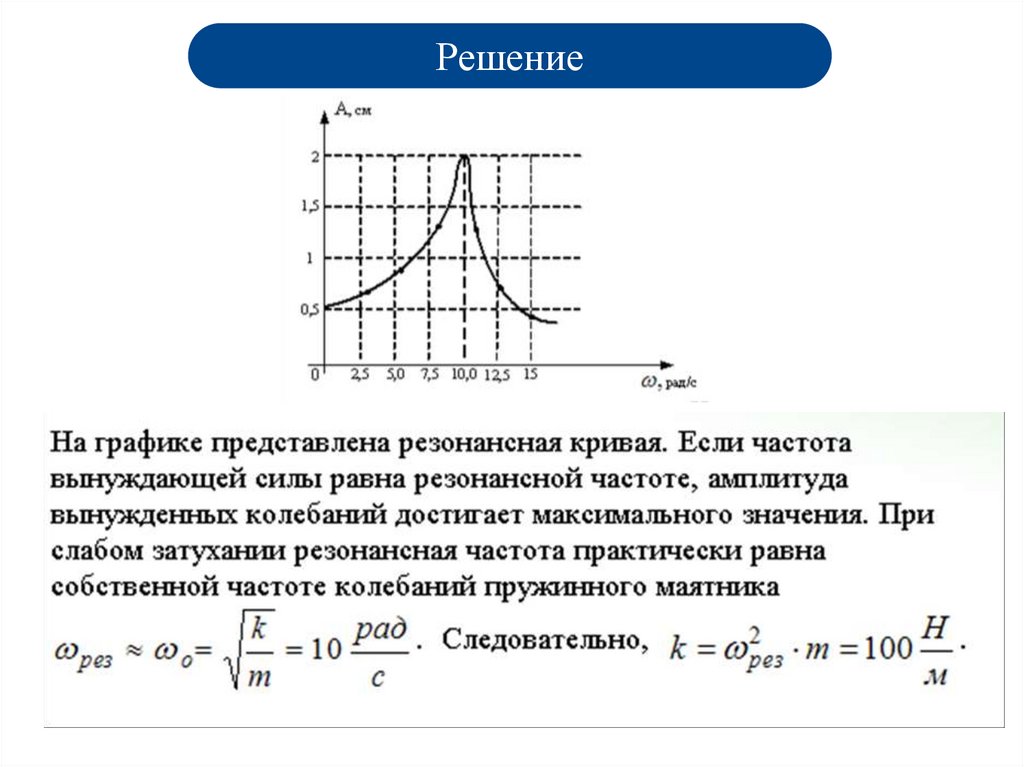
Решение33.
ПРОВЕРЬТЕ СЕБЯ!Задание из теста 27.11.2010
34.
Задание из теста 27.11.201035.
РЕШЕНИЕЗадание из теста 27.11.2010
36.
Задание из экзаменационного теста37.
РешениеВеличина U0 2 U R 1, 4 B. Полное сопротивление контура
38.
ПРОВЕРЬТЕ СЕБЯЗадание из теста 27.11.2010
39.
РешениеЗадание из теста 27.11.2010
40.
ПРОВЕРЬТЕ СЕБЯ!Задание из теста 27.11.2010
41.
РешениеЗадание из теста
27.11.2010
42.
Колебаниямеханические
Дифференциальное уравнение
Масса
Коэффициент
жесткости
Смещение
Скорость
электромагнитные
R
1
r
k
q 0
x x x 0 Дифференциаль- q q
L
LC2
m
m2
ное уравнение
q 2 q 0 q 0
x 2 x 0 x 0
m
k
x xm sin( t )
dx / dt
Индуктивность
катушки
L
Обратная
величина емкости
1
C
Заряд
q qm sin( t )
Сила тока
I dq / dt
q 2 CU 2
W
2C
2
Потенциальная
энергия
kx 2
W
2
Энергия электрич.
поля
Кинетическая
энергия
m 2
K
2
Энергия
магнитного поля
LI 2
K
2
43.
Собств. частотапружинного
маятника
k
0
m
Собств. частота
колебательного
контура
Период колебаний
T 2 m / k
Период колеб.
Формула Томсона
Циклич. частота
затухающих
колебаний
Коэффициент
затухания
k r
m 2m
2
r
2m
Циклич. частота
затухающих
колебаний
Коэффициент
затухания
Логарифмич.
декремент
затухания
A(t )
ln
T
A(t T )
Логарифмич.
декремент
затухания
Добротность
пружинного
маятника
1
Q
km
r
Добротность
колебательного
контура
Резонансная
частота
рез 02 2 2
Резонансная
частота
0
1
LC
T 2 LC
1
R2
2
LC 4 L
R
2L
C
T πR
L
Q
1 L
R C
рез 02 2 2



























 Физика
Физика








