Похожие презентации:
Электрические колебания. Переменный электрический ток. Тема 3
1.
Тема 3. Электрические колебания.Переменный электрический ток.
Основные вопросы темы:
3.1.1. Свободные незатухающие электрические колебания
3.1.2. Затухающие электрические колебания
3.1.3. Вынужденные электрические колебания. Резонанс
3.1.4. Переменный электрический ток.
2.
ПовторениеГармонические колебания
A sin t 0
А – амплитуда колебания; ω – круговая частота
(ωt+φ0)– фаза колебания;φ0 – начальная фаза колебания.
Дифференциальное уравнение свободных незатухающих
гармонических колебаний:
2 0
0
Уравнение плоской гармонической волны,
распространяющейся вдоль оси Х:
x, t A cos t kx
3.
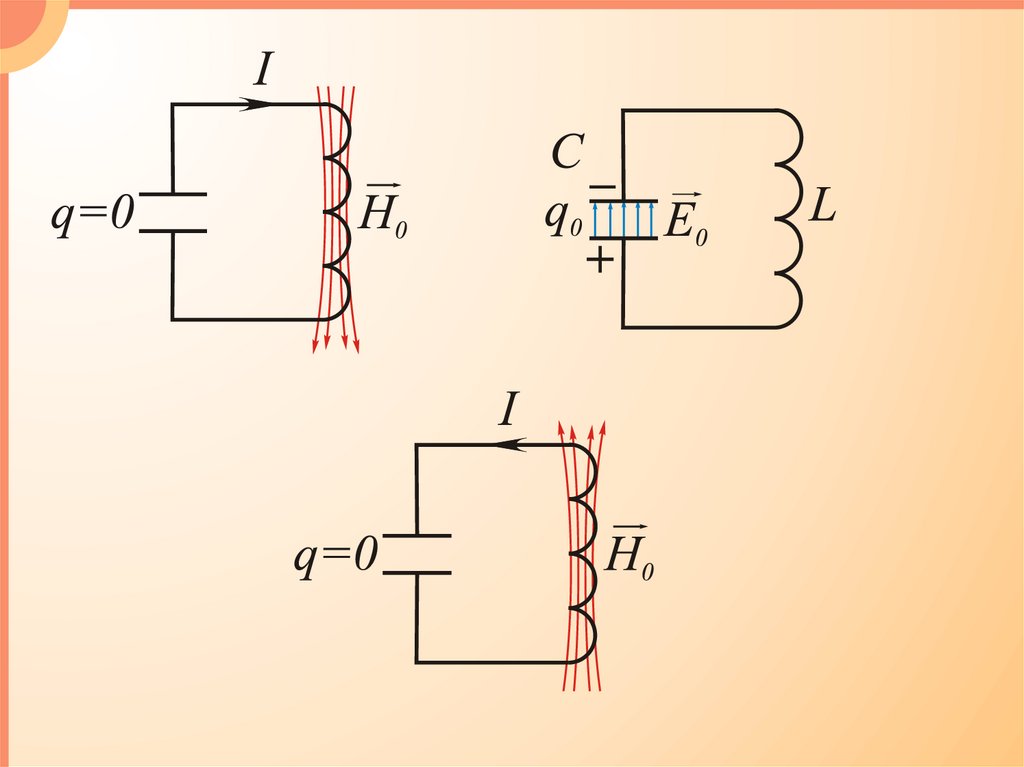
3.1. Свободные незатухающие электрические колебанияКолебательный контур – цепь,
состоящая из конденсатора и
катушки.
Е –напряженность электрического поля;
H – напряженность магнитного поля;
q – заряд; С –емкость конденсатора;
L – индуктивность катушки,
I – cила тока в контуре
4.
5.
Энергия заряженного конденсатора – энергияэлектрического поля:
We
Энергия магнитного поля:
В любой момент времени:
q2
2C
LI 2
Wm
2
W We Wm
6.
Для квазистационарных токов можно использовать законы Ома.с = 3·108 м/с
Условие квазистационарности:
l
c
l
T
c
50 Гц l 100 км
7.
Сила тока:Закон Ома:
dq
I
q
dt
I R 1 2 E12
q
dI
R 0, 1 2 , E12 EC L
C
dt
E C - Э.Д.С самоиндукции
q
dI
0 L
C
dt
8.
dI d qq
q 0 L q
dt
dt
C
Дифференциальное уравнение свободных незатухающих
электрических колебаний
1
q
q 0
LC
q qm cos 0t
(1)
(2)
9.
01
LC
- собственная круговая частота
колебаний
Формула Томсона:
T 2 LC
(3)
Т – период собственных колебаний в колебательном контуре
10.
Напряжение на конденсаторе:U m qm C
q
U U m cos 0t
C
Ток через контур:
dq
I
0 qm sin 0t
dt
11.
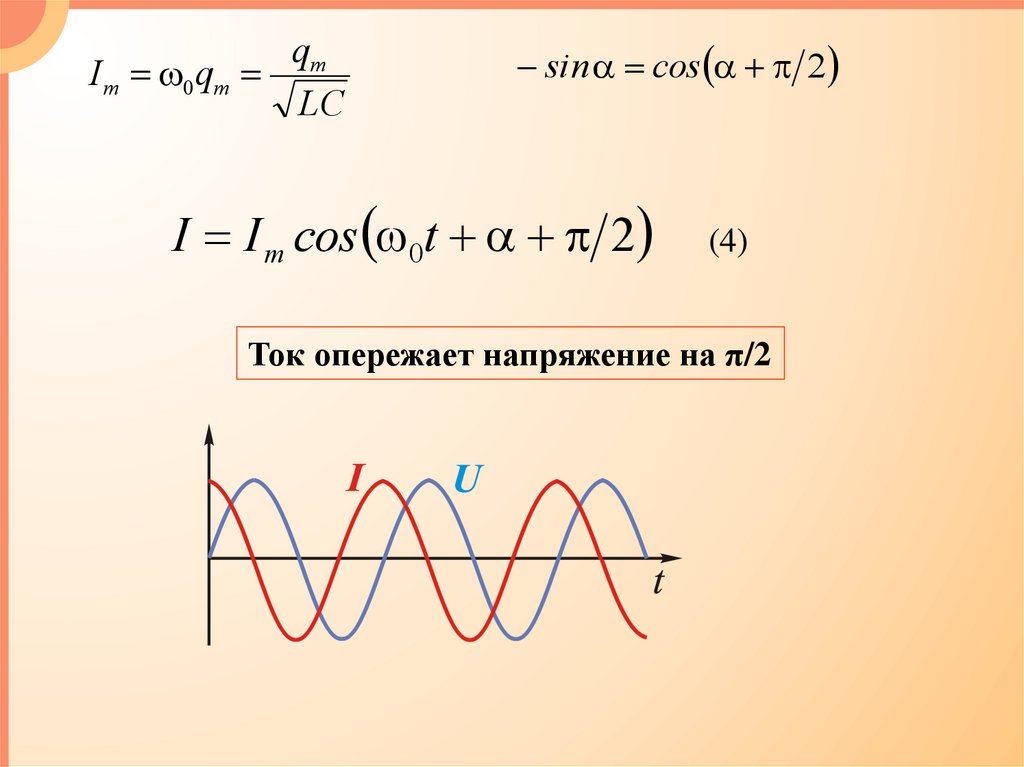
qmI m 0 qm
LC
sin cos 2
I I m cos 0t 2
(4)
Ток опережает напряжение на π/2
12.
Найдем соотношение между амплитудными значениямитока и напряжения:
qm
Im
LC
L
Um
Im
Im
C 0C
C
C
Из закона Ома: U=IR
L C
- волновое сопротивление.
13.
Энергия электрического поля (энергия заряженного конденсатора)в любой момент времени:
2
2
m
q
q
2
We
cos 0t
2C 2C
Энергия магнитного кого поля (энергия катушки индуктивности)
в любой момент времени:
LI 2 LI m2
Wm
sin 2 0t
2
2
14.
Максимальное (амплитудное) значение энергии магнитного поля:LI
L q
Lq
q - максимальное значение
2
2
2 LC 2C энергии электрического поля
2
m
2 2
0 m
2
m
2
m
Полная энергия колебательного контура в любой момент времени:
qm2
W We Wm
cos 2 0t sin 2 0t
2C
qm2 LI m2
2C
2
Полная энергия контура сохраняется постоянной
15.
Задача 3.1Колебательный контур состоит из конденсатора и катушки
индуктивности. Определить частоту колебаний, возникающих в
контуре, если максимальная сила тока в катушке индуктивности
1,2 А, максимальная разность потенциалов на обкладках
конденсатора 1200 В, полная энергия контура 1,1 мДж.
Дано:
Im = 1,2 A
UCm = 1200 В
W = 1,1 мДж = 1,1 · 10-3
Дж
ν-?
2
m
LI
W
2
q
CUCm CU
W
2C
2C
2
2
m
2
2
Cm
2W
L 2
Im
2W
C 2
U Cm
16.
2W 2W4W 2
LC 2 2 2 2
I m U Cm I mU Cm
I mU Cm
1,2 А 1200 В
-3
4 W
4 3,14 1,1 10 Дж
2 LC
1
Вт
5 1
1,04 10
1,04 10 1,04 105 Гц
Вт с
с
5
17.
ЗаданиеВ колебательном контуре емкость возросла в 8 раз,
а индуктивность уменьшилась в два раза.
Как изменится период собственных колебаний
контура?
а) уменьшится в 2 раза;
б) увеличится в 2 раза;
в) уменьшится в 4 раз;
г) увеличится в 4 раз.
18.
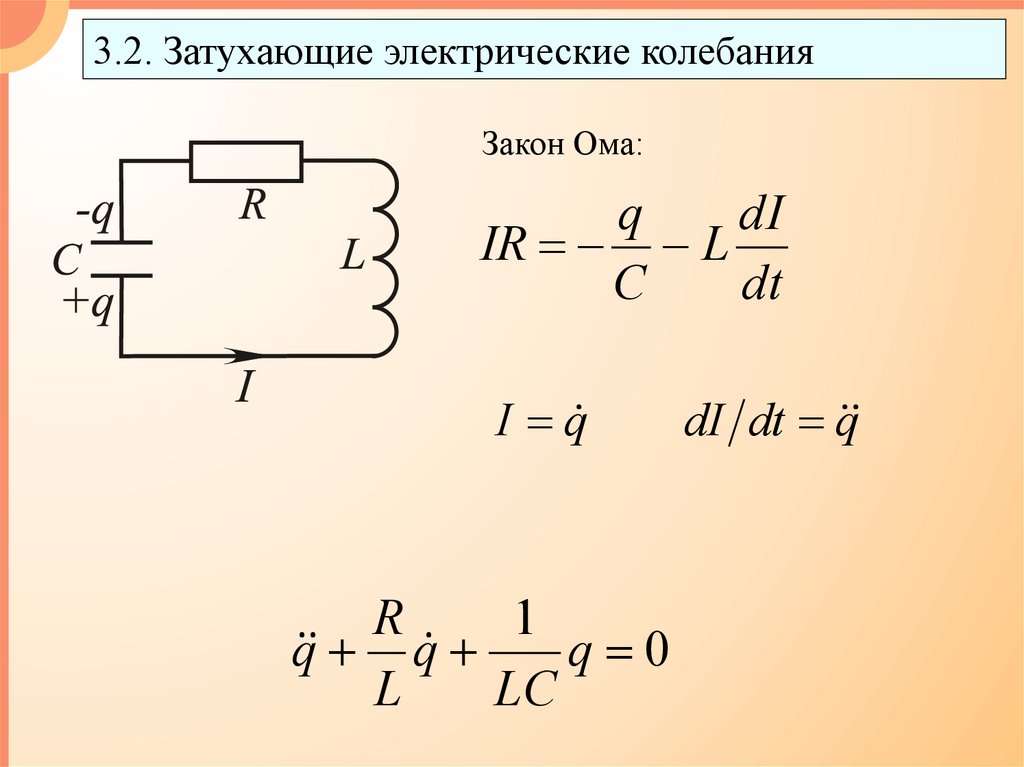
3.2. Затухающие электрические колебанияЗакон Ома:
q
dI
IR L
C
dt
I q
R
1
q q
q 0
L
LC
dI dt q
19.
102
LC
R
2L
- коэффициент затухания
q 2 q q 0
2
0
(5)
Слабое затухание:
,
2
2
0
т.е. R 4L 1 LC
2
2
Решение уравнения (5) :
q qm0e
t
cos t
(6)
20.
21
R
2
LC 4 L
2
0
2
(7)
21.
Напряжение на конденсаторе:q
t
U U m0e cos t
C
(8)
U m 0 qm 0 C
Ток через контур:
I dq dt
q qm0e t cos t
I qm 0e
t
cos t qm 0e
t
sin t
22.
0 cos0 sin
I 0 qm0e t cos cos t sin sin t
I I m0e
t
cos t
(9)
Ψ – сдвиг фаз между током и напряжением
sin 0, cos 0 2
23.
Логарифмический декремент затухания:A t
ln
T
A t T
2 02
0
Добротность:
Q
R 2 R
2 L L
R C L
(10)
1 L
Q
R C R
(11)
24.
3.3. Вынужденные электрические колебанияq
dI
IR L U m cos t
C
dt
I q
dI dt q
1
2
0
LC
R
2L
25.
Umq 2 q q
cos t
L
2
0
(12)
Решение (12) :
q qm cos t
qm
(13)
Um
R L 1 C
2
R
tg
1 C L
2
(14)
(15)
26.
dqI
qm sin t I m cos t
dt
2
2
- сдвиг фаз между током и напряжением
I I m cos t
(16)
27.
1 L 1 Ctg tg 2
tg
R
(17)
L 1 C 0, ток отстает от напряжения
L 1 C 0, ток опережает напряжение
28.
Найдем связь между амплитудными значениями тока и напряжения:I m qm
U R IR ,
Um
R L 1 C
2
2
UC q C ,
(18)
dI
UL L
dt
U R U C U L U m cos t
U R IR U Rm cos t
U Rm RI m
(19)
29.
q qmU C cos t U Cm cos t 2
C C
qm
Im
U Cm
C C
dI
U L L LIm sin t U Lm cos t 2
dt
U Lm LI m
30.
31.
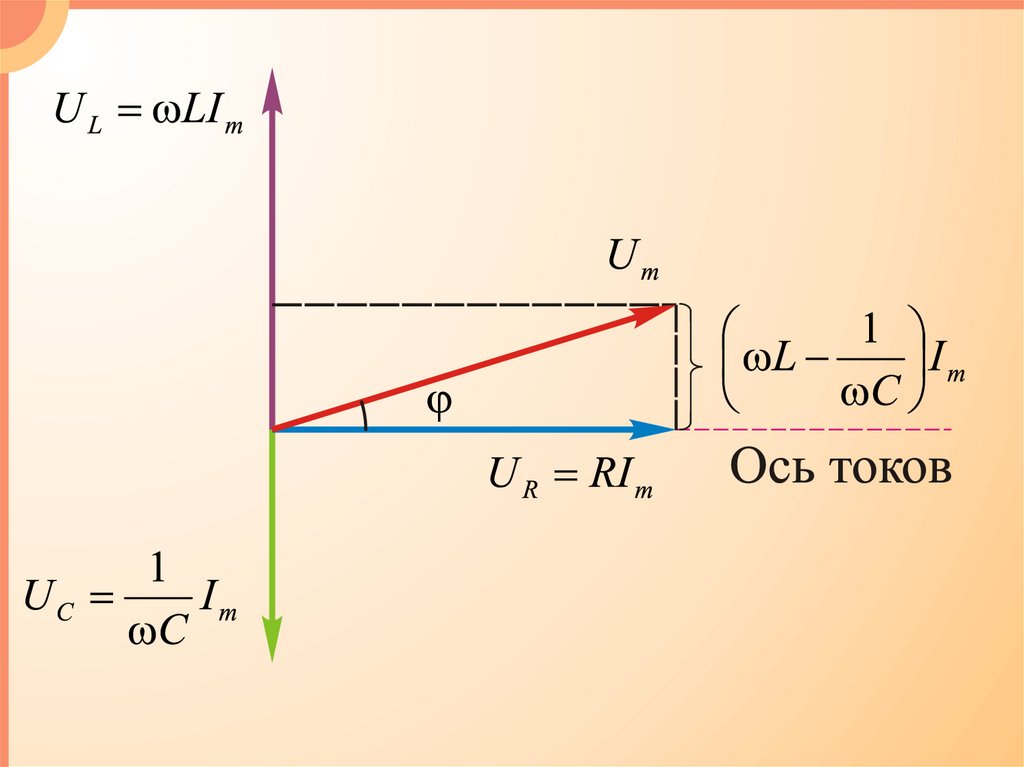
Резонанс напряжения на конденсаторе:2
1
R
рез 2
2
LC 2 L
2
0
2
(20)
Малое затухание (ωрез≈ω0):
U Cmрез
Um
1
LC 1 L
Q
0CR CR
R C
(21)
Резонанс силы тока в контуре:
L 1 C 0
Iрез 0 1
LC
(22)
32.
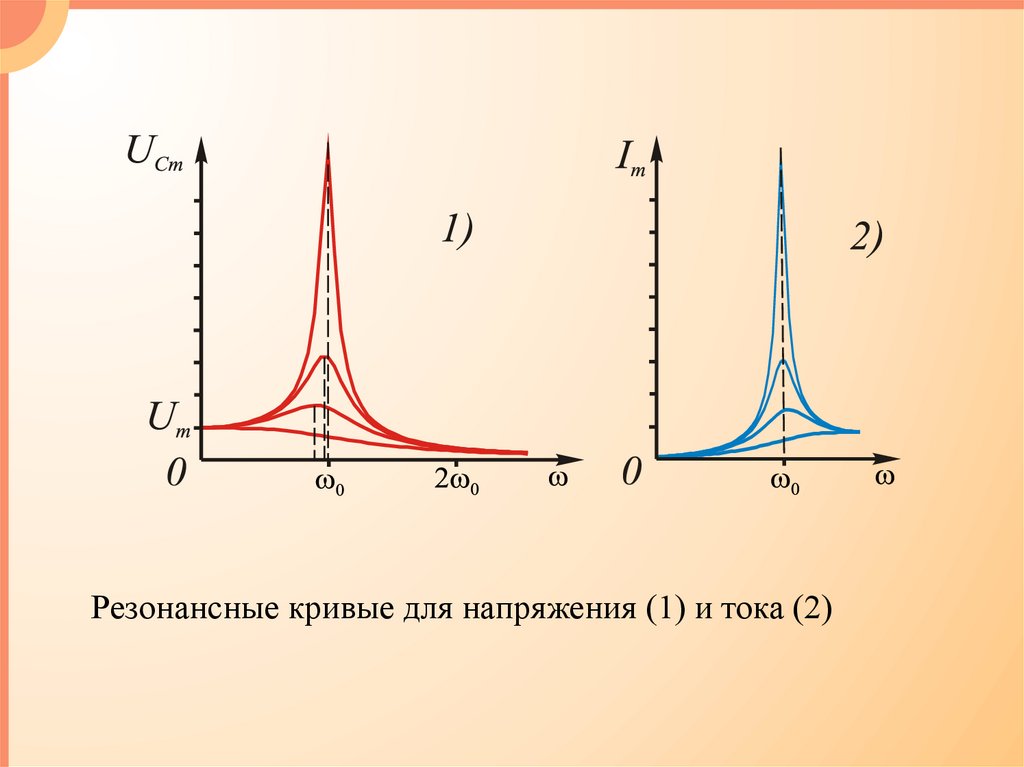
Резонансные кривые для напряжения (1) и тока (2)33.
Влияние на колеб. контур вынуждающих Э.Д.С., частоты которых отличныот ω0, будет тем слабее, чем «острее» резонансная кривая. «Острота»
резонансной кривой характеризуется относительной шириной этой кривой,
равной Δω/ω0 , где Δω – разность цикл. частот при I=Im/√2
0
Q
34.
Задача 3.2Колебательный контур состоит из резистора сопротивлением
100 Ом, конденсатора емкостью 0,55 мкФ и катушки индуктивностью 0,03 Гн. Определить сдвиг фаз между током через контур
и приложенным напряжением, если частота приложен-ного
напряжения 1000 Гц.
Дано:
R = 100 Ом
C = 0,55 мкФ = 5,5·10-7 Ф
L = 0,03 Гн
ν = 1000 Гц
φ-?
L 1 C
tg
R
L 2 L 2 103 0,03
188 Ом
35.
11
1
288 Ом
3
6
C 2 C 2 10 0,55 10
L 1 C 188 288
tg
1
R
100
45
Таким образом, колебания силы тока опережают по
фазе колебания приложенного напряжения на 45º.
36.
3.4. Переменный электрический ток.U U m cos t
(23)
I I m cos t
(24)
Im
Um
R L 1 C
2
L 1 C
tg
R
2
(25)
(26)
37.
Полным электрическим сопротивлением илиимпедансом называется величина
Z R L 1 C
2
2
(27)
X L L - индуктивное сопротивление
X C 1 C - емкостное сопротивление
X X L X C - реактивное сопротивление
X
tg
R
(28)
Z R X
2
2
(29)
38.
Мощность, выделяемая в цепи переменного тока:P t U t I t U m cos t I m cos t
1
1
cos cos cos cos
2
2
1
1
P t U m I m cos U m I m cos 2 t
2
2
Найдем среднее за период значение мощности:
1
P P t U m I m cos
2
39.
Rcos ,
Z
Um
Im
Z
1
R RIm2
P U mIm
2
Z
2
Такую мощность развивает постоянный ток, равный: I I m
2
называется действующим
I Д Im 2
UД Um 2
значением силы тока, а величина
Величина
дйствующим значением напряжения.
P U Д I Д cos
cos φ – называется коэффициентом мощности.
(30)
40.
Задача 3.3Катушка длиной 50 см и площадью поперечного сечения 10 см2
включена в цепь переменного тока с частотой 50 Гц. Число
витков катушки 3000. Найти активное сопротивление катушки,
если сдвиг фаз между током и напряжением 60º.
Дано:
l = 50 см = 0,5 м
S = 10 см2 = 10-3 м2
ν = 50 Гц
N = 3000
φ = 60º
R-?
X L X C L
tg
R
R
L 2 L
R
tg tg
41.
L 0 n V 0 N l Sl2
2
7
0 N S l 1 4 10 9 10 10
2
6
3
0,5
2
2,26 10 Гн
2 L 2 50 2 ,26 10
R
tg
3
2
4 ,1 Ом
42.
задание• От чего зависит полное сопротивление
(импеданс) в цепи переменного тока:
• 1) I, U;
• 2) R, L, I;
• 3) U, R, I;
• 4) R, L, C, ω.






















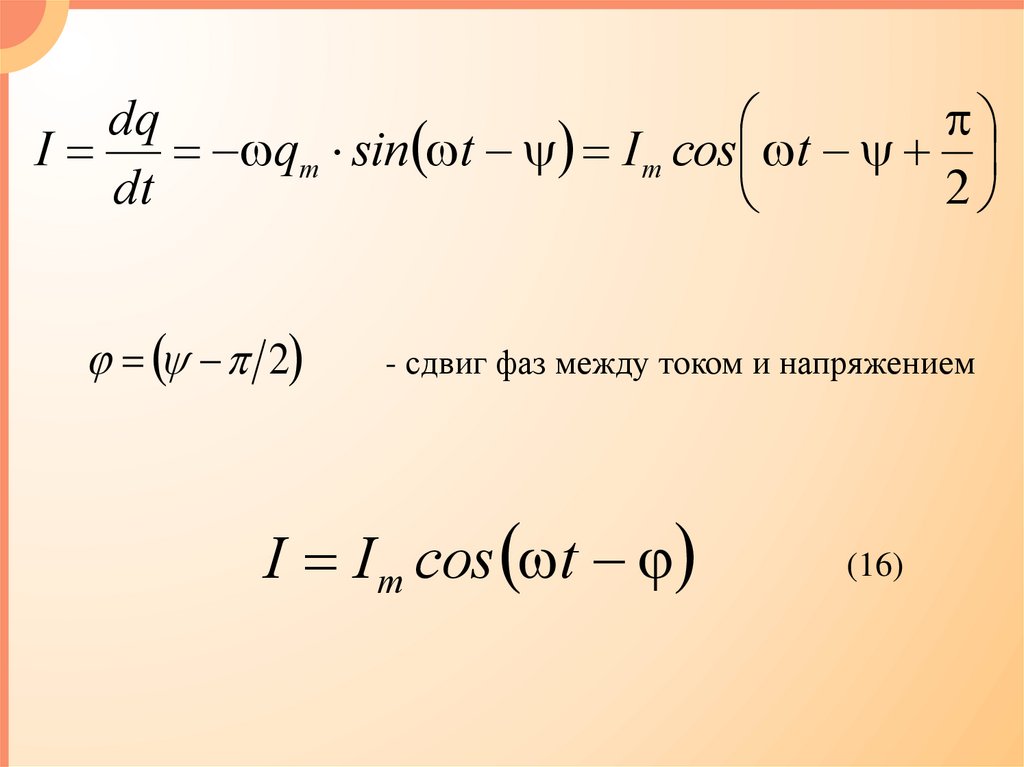














 Физика
Физика








