Линейное программирование

1.

1.
2.
3.
4.
5.
Линейное программирование
Общий вид ЗЛП
Целевая функция, ограничения, граничные условия
Основная задача линейного программирования
Построение математических моделей для задач
линейного программирования

2.

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
Что такое математическое программирование?
В чем состоит общая задача математического
программирования?
Что такое целевая функция в экстремальных задачах?
Что такое линейное программирование?
Каков общий вид задачи линейного программирования?
Что такое целевая функция в задачах линейного
программирования?
Что такое ограничения в задачах линейного
программирования?
Что представляют собой граничные условия в задачах
линейного программирования?
Что такое допустимые решения?
Что такое оптимальное решение?
Что можно сказать о размерности в задачах оптимизации?
Что такое основная задача линейного программирования?
Разработайте математические модели для ЗЛП 1-3.

3.

Математическое программирование – область
математики, объединяющая различные математические
методы и дисциплины: линейное программирование,
нелинейное программирование, динамическое
программирование и др.
Общая задача математического программирования
состоит в нахождении оптимального (максимального
или минимального) значения целевой функции, причем
значения переменных должны принадлежать некоторой
области допустимых значений и записывается так:
max G(x), где x = (x1, x2, …, xn) – совокупность
управляющих воздействий;
все x - из области допустимых значений переменных;
G – целевая функция.
Целевая функция (ЦФ) в экстремальных задачах –
функция, минимум или максимум которой нужно найти.

4.

Линейное программирование – область
математического программирования,
рассматривающая теорию и методы решения
экстремальных задач для линейно-зависимых
переменных.

5.

Задача линейного программирования
заключается в нахождении n переменных
x1, x2, … xn , минимизирующих (или
максимизирующих) линейную ЦФ f(x1, …, xn)
при определенных ограничениях и граничных
условиях на переменные .

6.

Целевая функция (ЦФ):
Z = f(x1, …, xn) ≡ min (max, const);
Ограничения на ЦФ (ОГР):
a1(x1, x2, … xn) = (<= или >=) b1;
a2(x1, x2, … xn) = b2;
…
am(x1, x2, … xn) = bm;
Граничные условия для переменных (ГРУ):
d1<=x1<=D1;
…
dm<=xn<=Dm

7.

ЦФ – целевая функция или критерий
оптимизации. Возможны три вида
назначения ЦФ: максимизация,
минимизация, назначение заданного
значения. Если ЦФ – линейная, то задачи
относятся к линейному программированию.
ОГР – ограничения - устанавливают
зависимости между переменными. Могут
быть односторонними (ai(xj) <=bi) и
двусторонними (ci<= ai(xj) <=bi). (Обычно
при решении задач в Excel двустороннее
ограничение записывается в виде двух
односторонних.)
ГРУ – граничные условия - показывают
пределы значений искомых переменных
при поиске оптимального решения.

8.

Решения задачи, удовлетворяющие всем
ограничениям и граничным условиям,
называются допустимыми решениями.
Допустимое решение, удовлетворяющее
целевой функции является оптимальным
решением.

9.

Возможно три соотношения:
n < m – решений нет, например,
х1 + 2 = 5
х1 - 8 = 15 (n=1, m=2)
n = m – Есть решение для линейно-независимых
уравнений, например,
х1 + х2 = 5
х1 - х2 = 1 (n=2, m=2)
n > m – бесчисленное множество решений (если
х1 и х2- любые, например,
х1 + х2 = 5 (n=2, m=1))
n > m – обязательное требование для задач
оптимизации

10.

Для ряда переменных x1, x2, … xn
требуется найти такие неотрицательные
значения этих переменных, которые
удовлетворяли бы системе линейных
уравнений:

11.

Основная задача линейного программирования
(продолжение)

12.

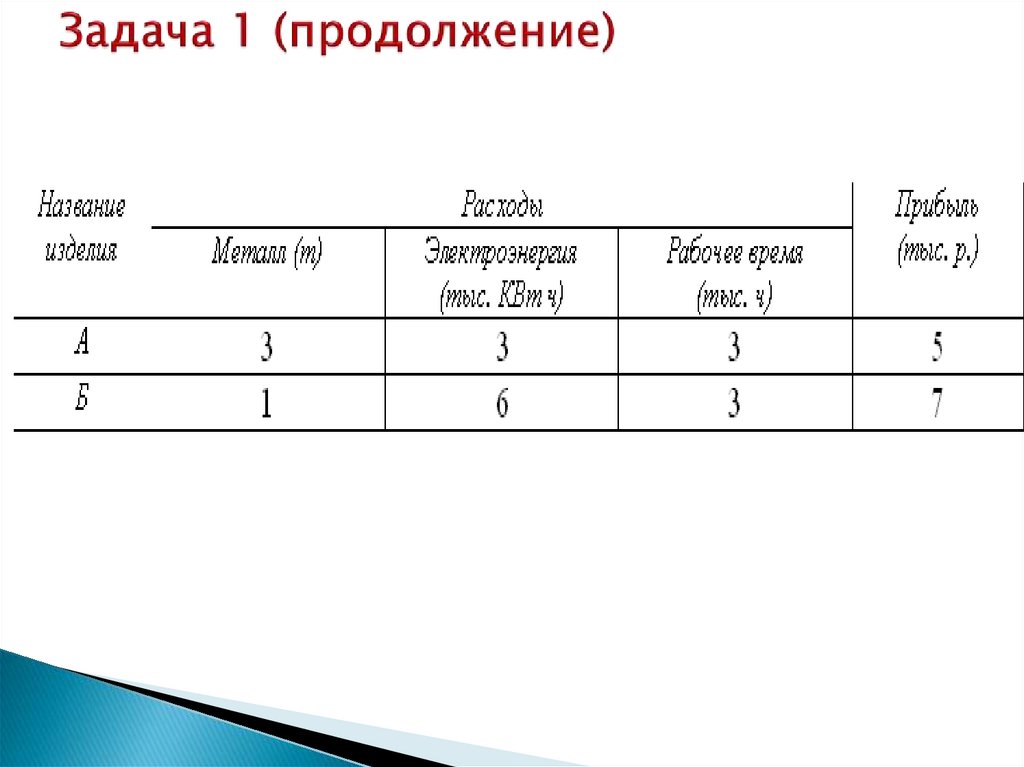
Задача 1.
На заводе организуется участок по выпуску изделий
А и Б. Необходимо спланировать производство
так, чтобы при минимальном объеме производства
каждого изделия прибыль была максимальной. На
участке работает 20 человек. Каждый в среднем за
год работает в течение 1800 часов. Выделенные
ресурсы: 32 т металла, 54 тыс. кВт ч
электроэнергии. План по реализации (на основе
изучения спроса) – не менее 2 тыс. изделий А и не
менее 3 тыс. изделий Б. Расходы и прибыль от
реализации на каждую 1 тыс. изделий
представлены далее в таблице:

13.

14.

15.

Фирма выпускает прогулочные и спортивные
велосипеды. За месяц можно собрать не более
600 штук прогулочных велосипедов и не более
300 – спортивных. Для обеспечения качества
продукции каждый прогулочный велосипед
тестируется в течение 0,3 часа на стенде А и 0,1
часа – на стенде Б, аналогично каждый
спортивный велосипед – 0,4 часа на стенде А и
0,3 часа – на стенде Б. По техническим причинам
стенд А может быть загружен в течение 240 часов
в месяц, а стенд Б – в течение 120 часов. Как
спланировать производство по выпуску
велосипедов того и другого типа для обеспечения
максимальной прибыли, если стоимость
прогулочного велосипеда составляет 2000 руб., а
спортивного велосипеда 3000 руб.

16.

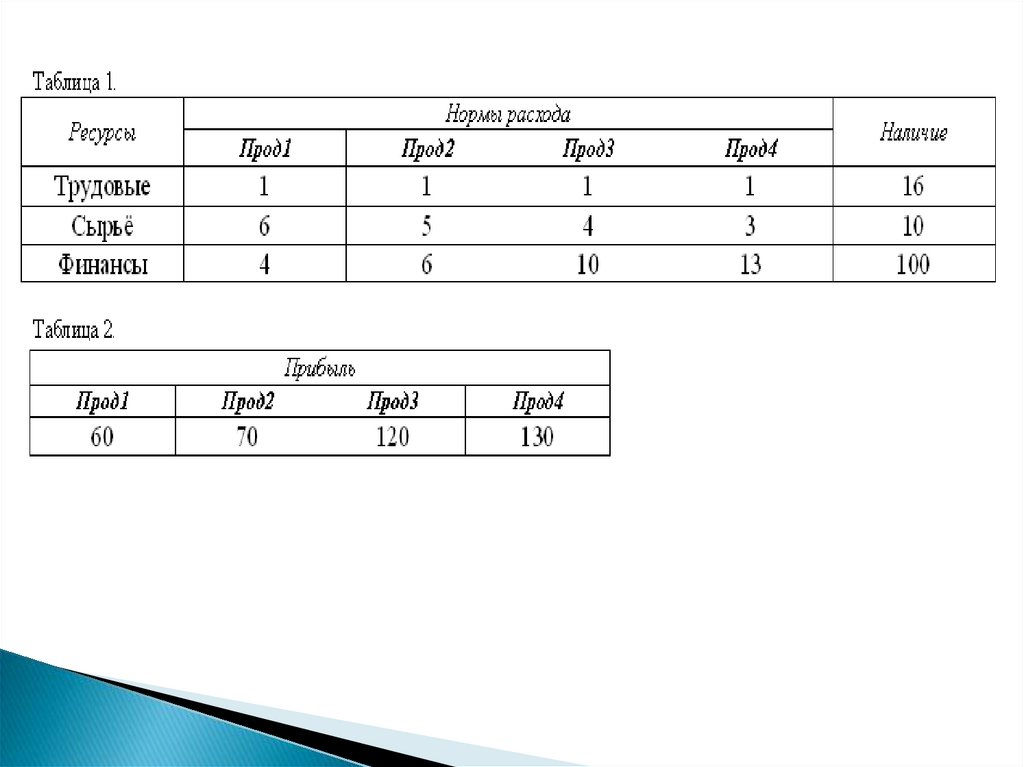
Требуется определить, в каком количестве надо
выпускать продукцию каждого из четырех
типов Прод1, Прод2, Прод3, Прод4 для
получения максимальной прибыли при
имеющихся ограничениях на ресурсы. Для
изготовления данных типов продукции
требуются ресурсы трех видов: трудовые,
сырье, финансы. Количество единиц ресурса,
необходимое для выпуска единицы
продукции данного типа, называется нормой
расхода. Нормы расхода, прибыль (в
некоторых единицах), получаемая от
реализации каждого типа продукции, и
количество единиц имеющихся в наличии
ресурсов приведены в таблицах 1 и 2.