Похожие презентации:
Дифракция. Лекция №8
1.
ДифракцияИллюстративный материал к
лекции №8
пятница, 11 ноября 2022 г.
2.
Эволюция представлений о природе светаПИФАГОР
Объяснял видимость предметов
тем, что из них вылетают
мельчайшие частички, которые
попадают в глаз наблюдателя
ДЕКАРТ
ГУК
Свет – это импульсы сжатия,
распространяющиеся с большой
скоростью в идеально упругой
среде - эфире
3.
4.
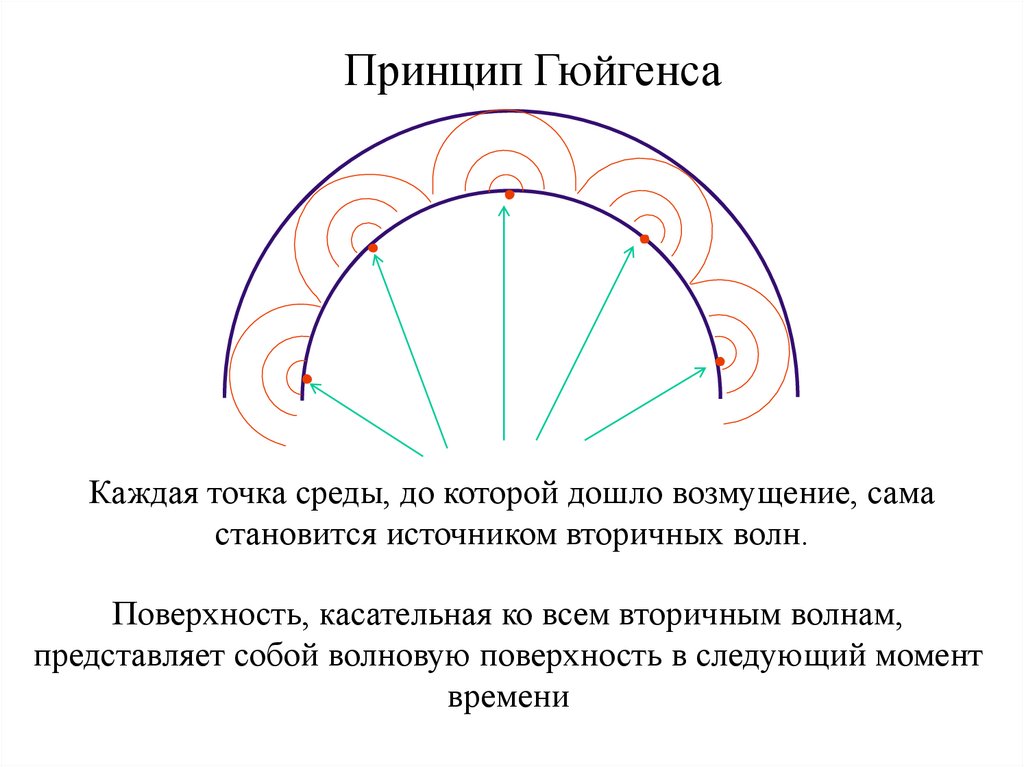
Принцип ГюйгенсаКаждая точка среды, до которой дошло возмущение, сама
становится источником вторичных волн.
Поверхность, касательная ко всем вторичным волнам,
представляет собой волновую поверхность в следующий момент
времени
5.
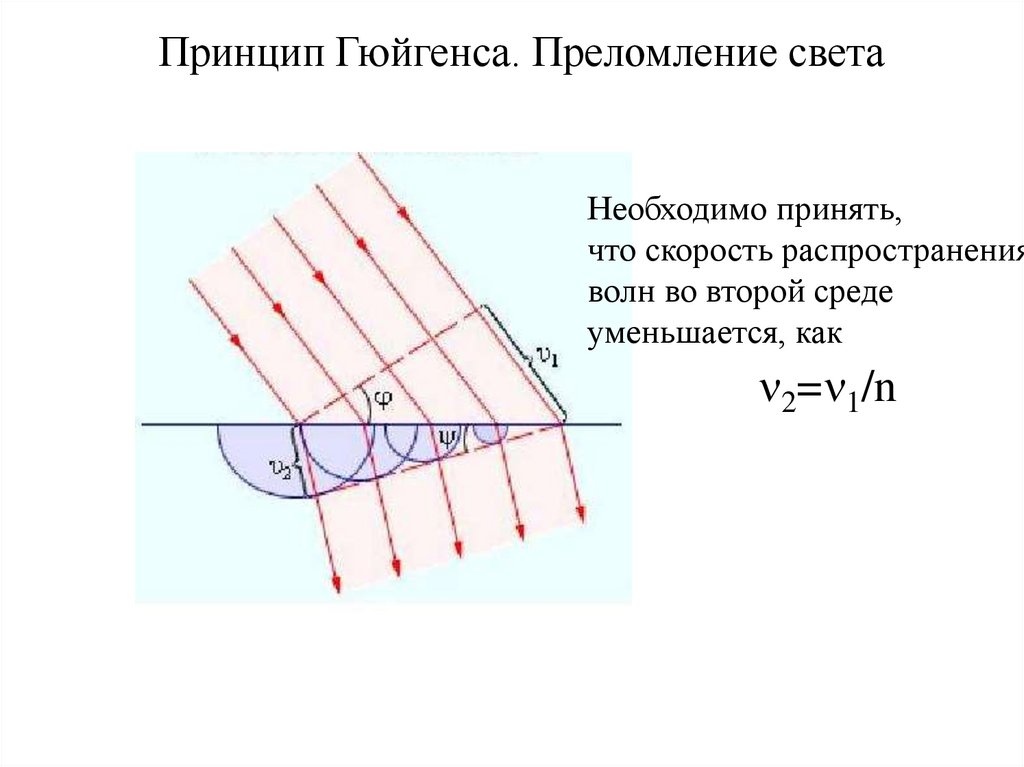
Принцип Гюйгенса. Преломление светаНеобходимо принять,
что скорость распространения
волн во второй среде
уменьшается, как
n2=n1/n
6.
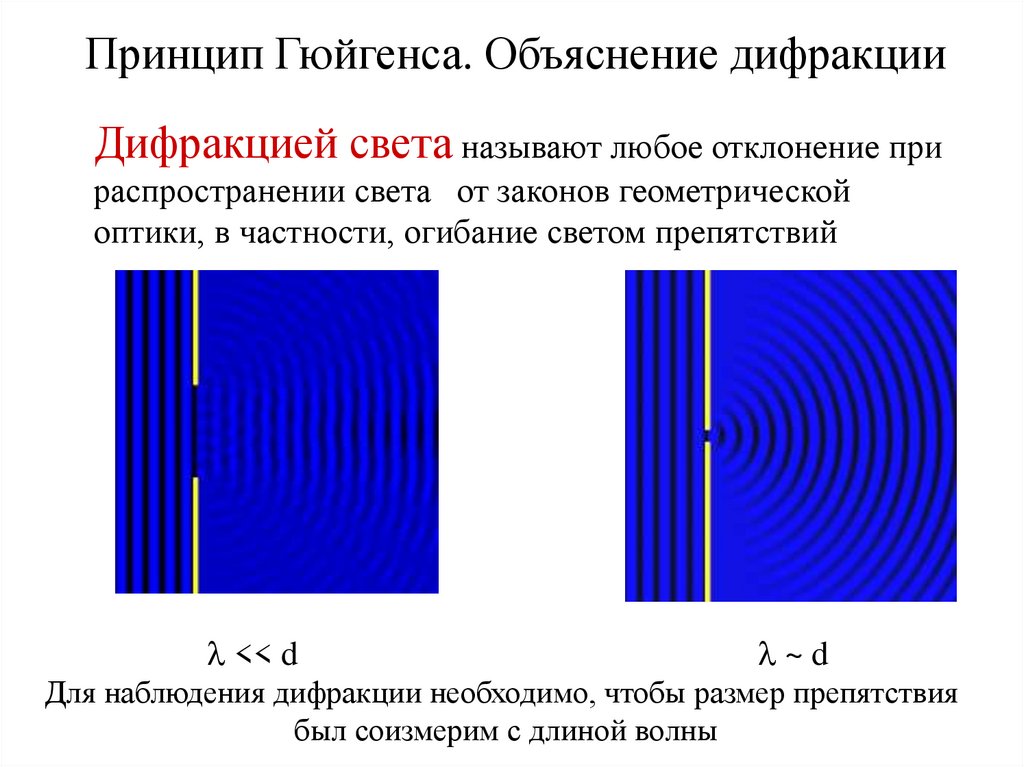
Принцип Гюйгенса. Объяснение дифракцииДифракцией света называют любое отклонение при
распространении света от законов геометрической
оптики, в частности, огибание светом препятствий
l << d
l~d
Для наблюдения дифракции необходимо, чтобы размер препятствия
был соизмерим с длиной волны
7.
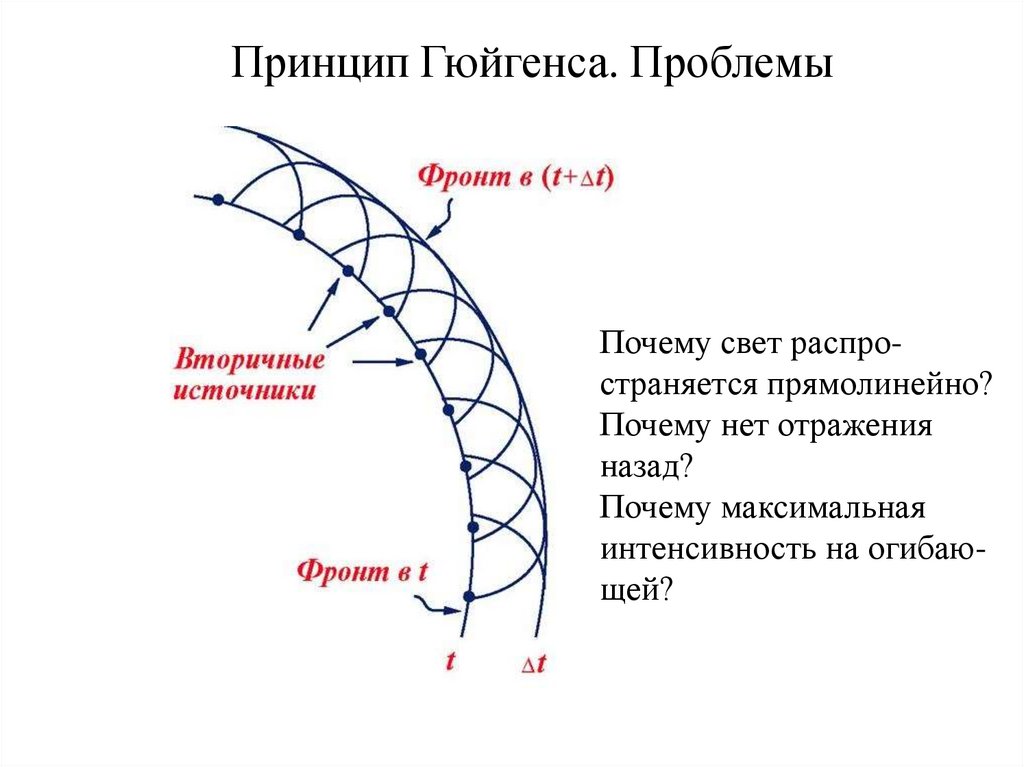
Принцип Гюйгенса. ПроблемыПочему свет распространяется прямолинейно?
Почему нет отражения
назад?
Почему максимальная
интенсивность на огибающей?
8.
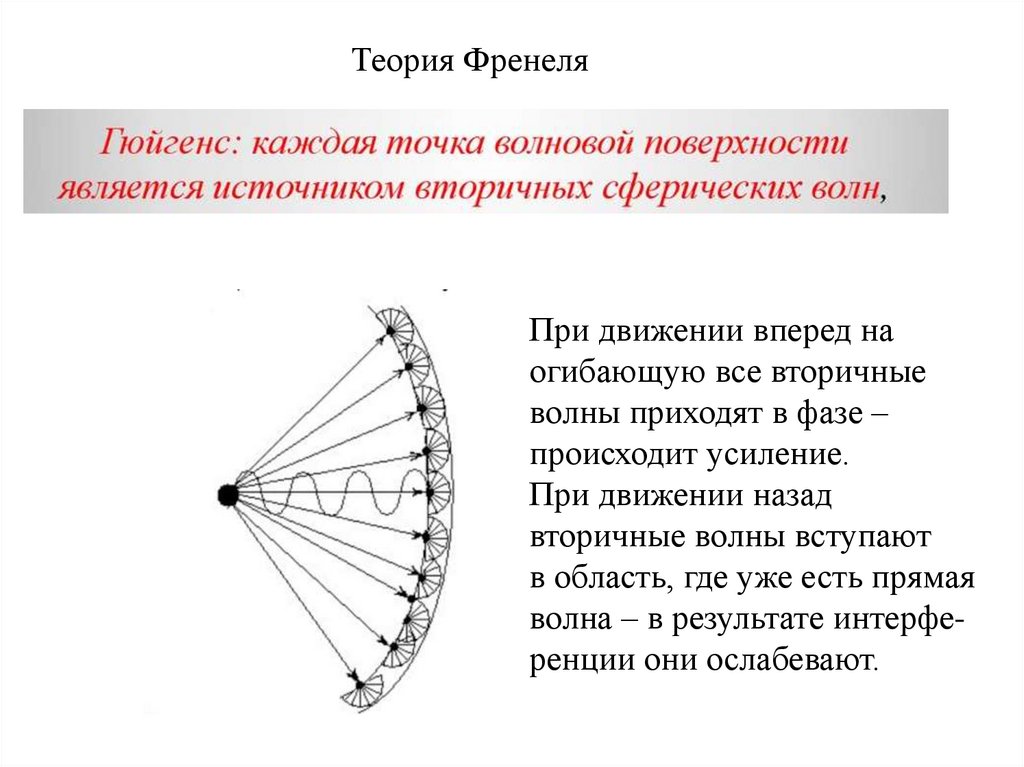
Теория ФренеляПри движении вперед на
огибающую все вторичные
волны приходят в фазе –
происходит усиление.
При движении назад
вторичные волны вступают
в область, где уже есть прямая
волна – в результате интерференции они ослабевают.
9.
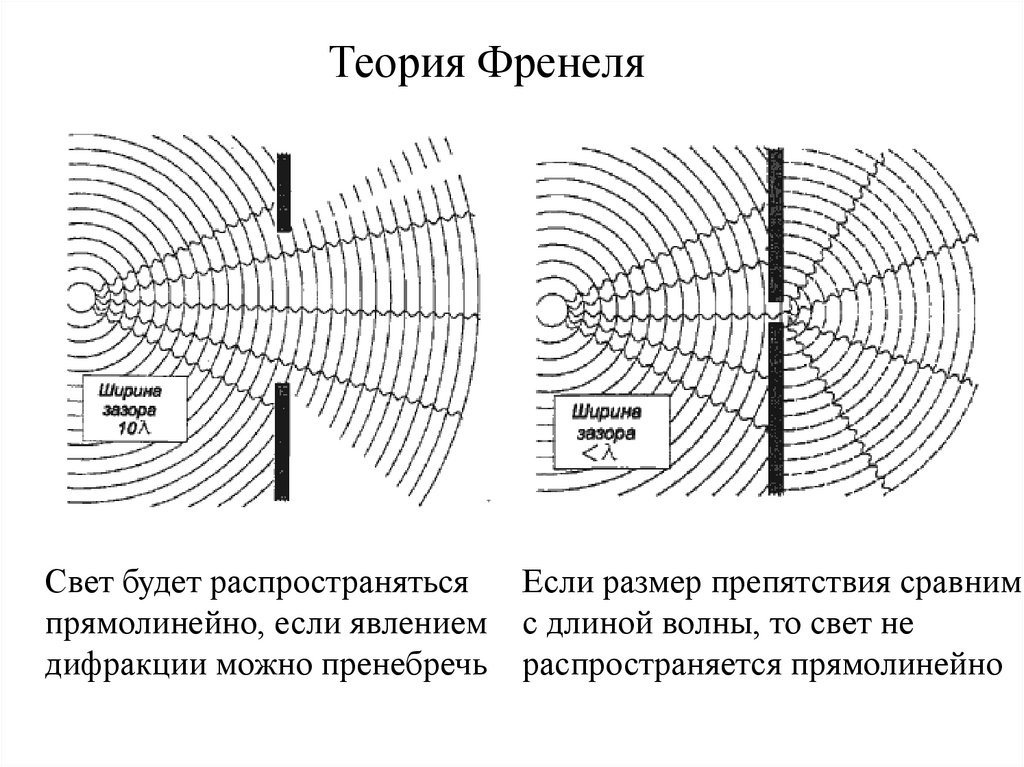
Теория ФренеляСвет будет распространяться
прямолинейно, если явлением
дифракции можно пренебречь
Если размер препятствия сравним
с длиной волны, то свет не
распространяется прямолинейно
10.
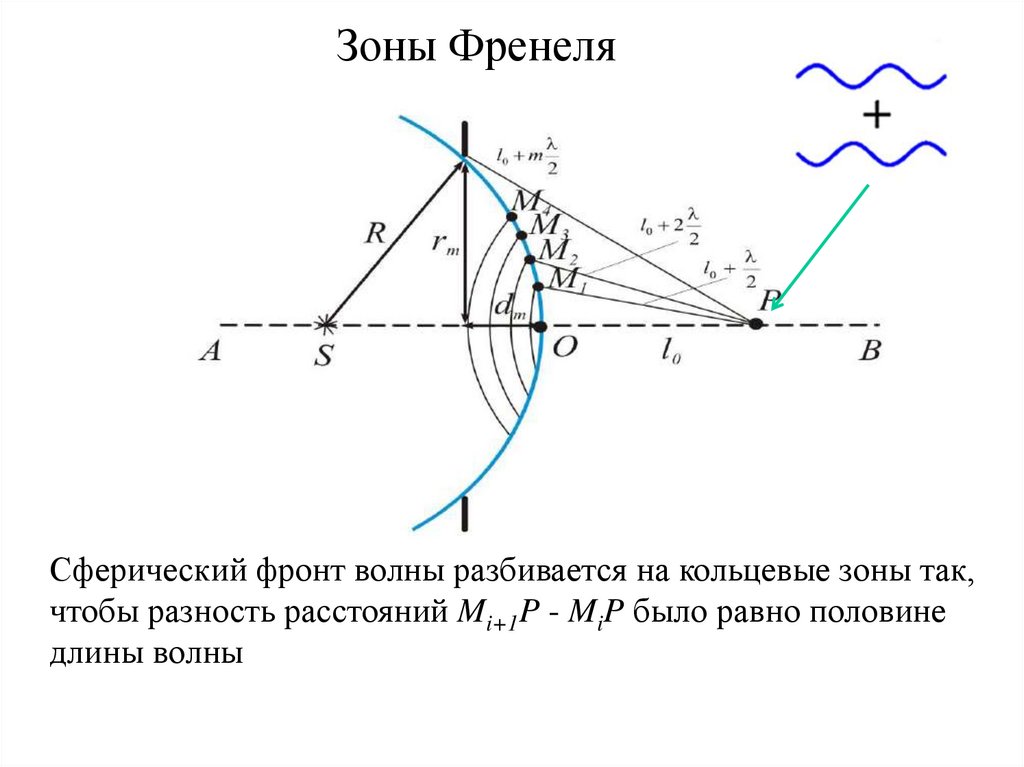
Зоны ФренеляСферический фронт волны разбивается на кольцевые зоны так,
чтобы разность расстояний Mi+1P - MiP было равно половине
длины волны
11.
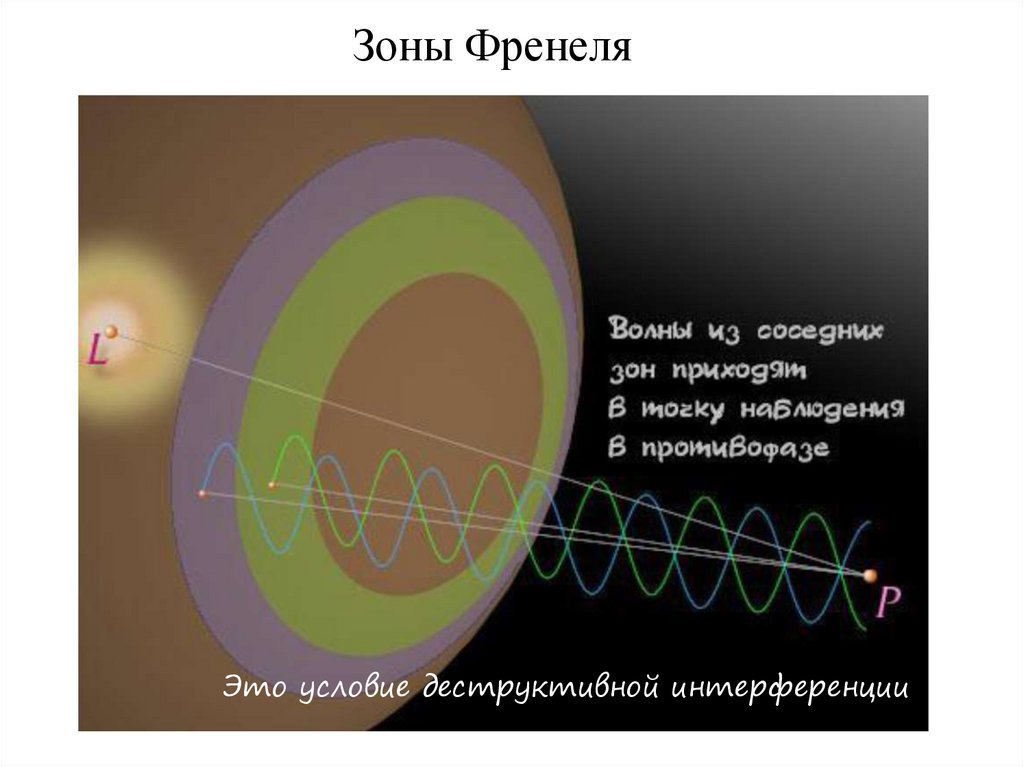
Зоны ФренеляЭто условие деструктивной интерференции
12.
Зоны Френеляl
2
2
2
rm2 R 2 R d m l0 m l0 d m
2
радиус зоны
пренебрегая квадратами l и dm, получим:
Площади зон Френеля:
Нулевая зона:
Первая кольцевая зона:
Площади всех зон Френеля равны!
13.
Зоны ФренеляПри увеличении номера зоны
амплитуда волны в точке наблюдения
от этой зоны уменьшается, так как
растет угол jm и расстояние до точки
наблюдения
-амплитуды убывают
очень медленно!
Результирующая амплитуда:
0
Запишем её так:
0
0
14.
Зоны ФренеляПолучаем:
+ для нечетного m,
- для четного
Для полностью открытого сферического фронта m
Am 0
15.
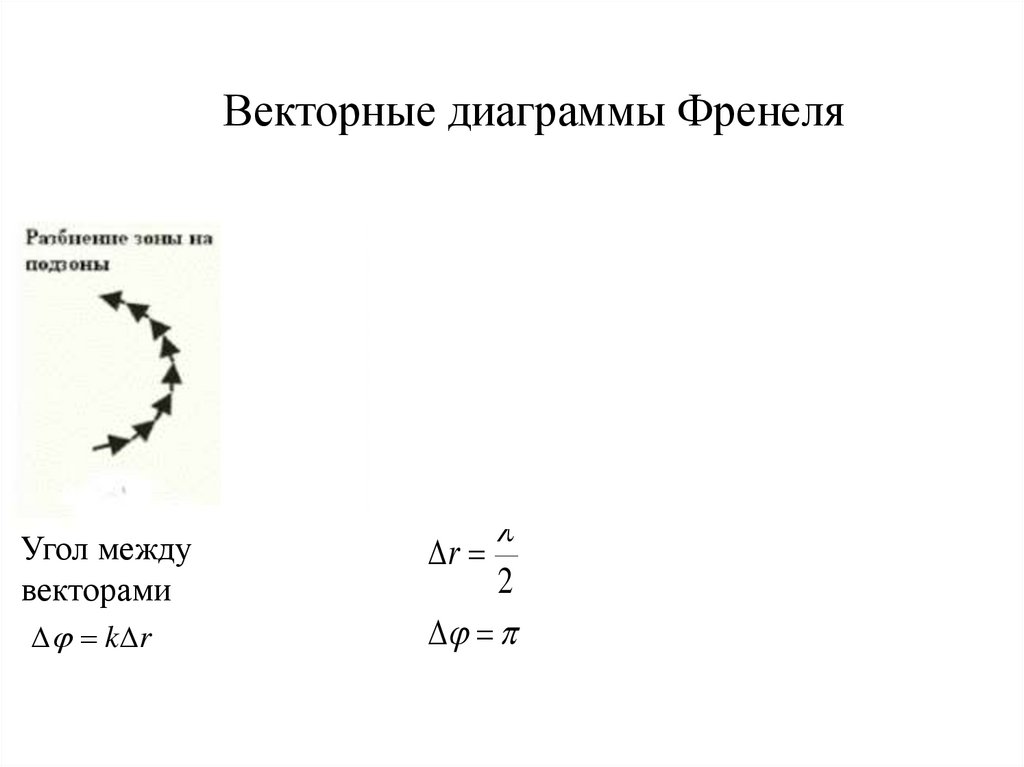
Векторные диаграммы ФренеляAm 0
Угол между
векторами
j k r
l
r
2
j
16.
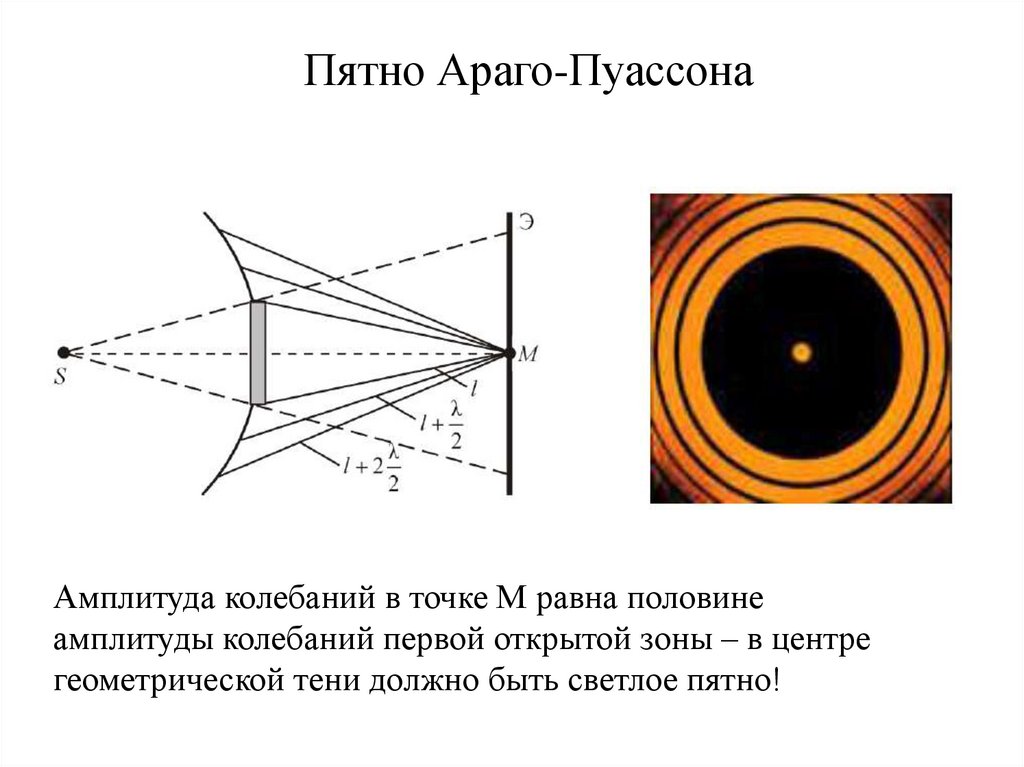
Пятно Араго-ПуассонаАмплитуда колебаний в точке М равна половине
амплитуды колебаний первой открытой зоны – в центре
геометрической тени должно быть светлое пятно!
17.
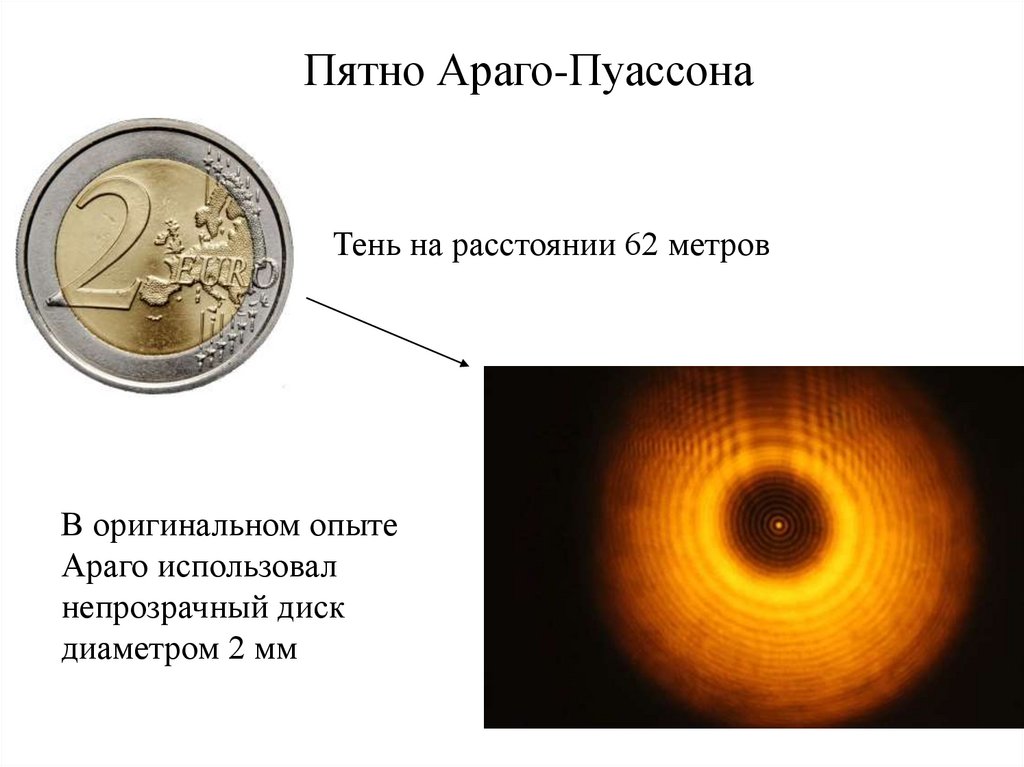
Пятно Араго-ПуассонаТень на расстоянии 62 метров
В оригинальном опыте
Араго использовал
непрозрачный диск
диаметром 2 мм
18.
Дифракция Френеля на круглом отверстииОткрыто четное число зон
1 2 A1 Am
Открыто нечетное число зон
1 2 A1 Am
19.
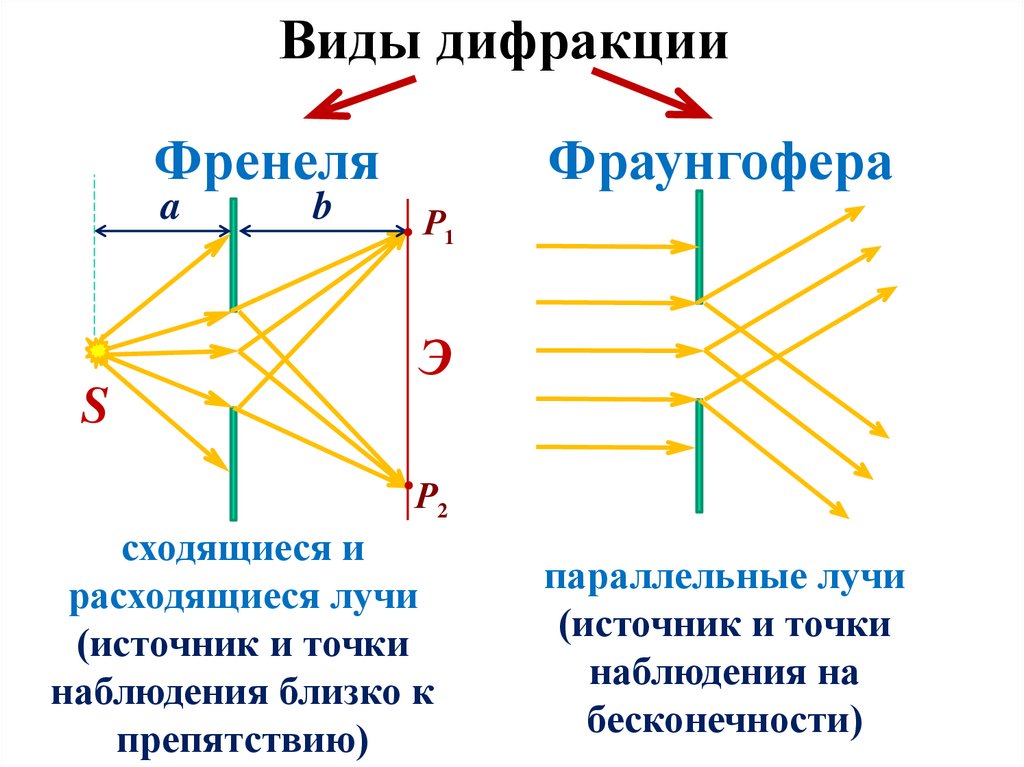
Виды дифракцииФренеля
a
b
Фраунгофера
Р1
Э
S
Р2
сходящиеся и
расходящиеся лучи
(источник и точки
наблюдения близко к
препятствию)
параллельные лучи
(источник и точки
наблюдения на
бесконечности)
20.
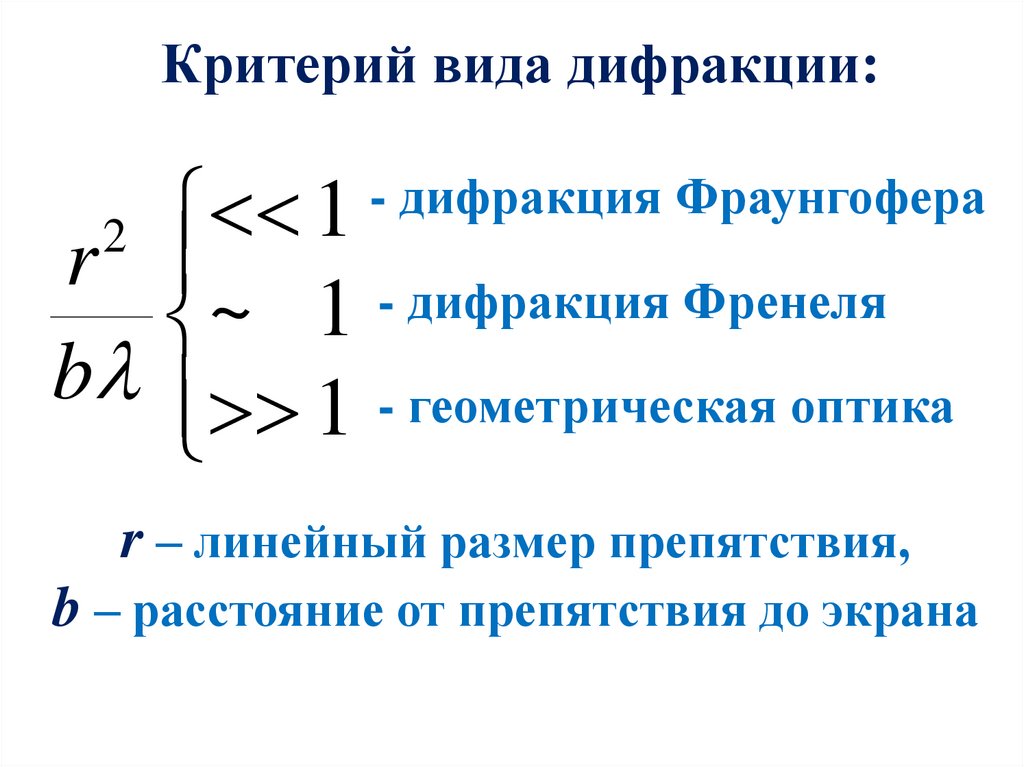
Критерий вида дифракции:1
r
- дифракция Френеля
~
1
bl 1 - геометрическая оптика
2
- дифракция Фраунгофера
r – линейный размер препятствия,
b – расстояние от препятствия до экрана
21.
Дифракция Фраунгофера на одной щелиРазность хода между точками
в и в’ равна
a sin j
Если в точке Р минимум, значит
открыто четное число зон Френеля –
2m:
l
a sin j 2m ml
2
Если в точке Р максимум, значит открыто нечетное число зон
Френеля – 2m+1:
l
1
a sin j 2m `1 m l
2
2
22.
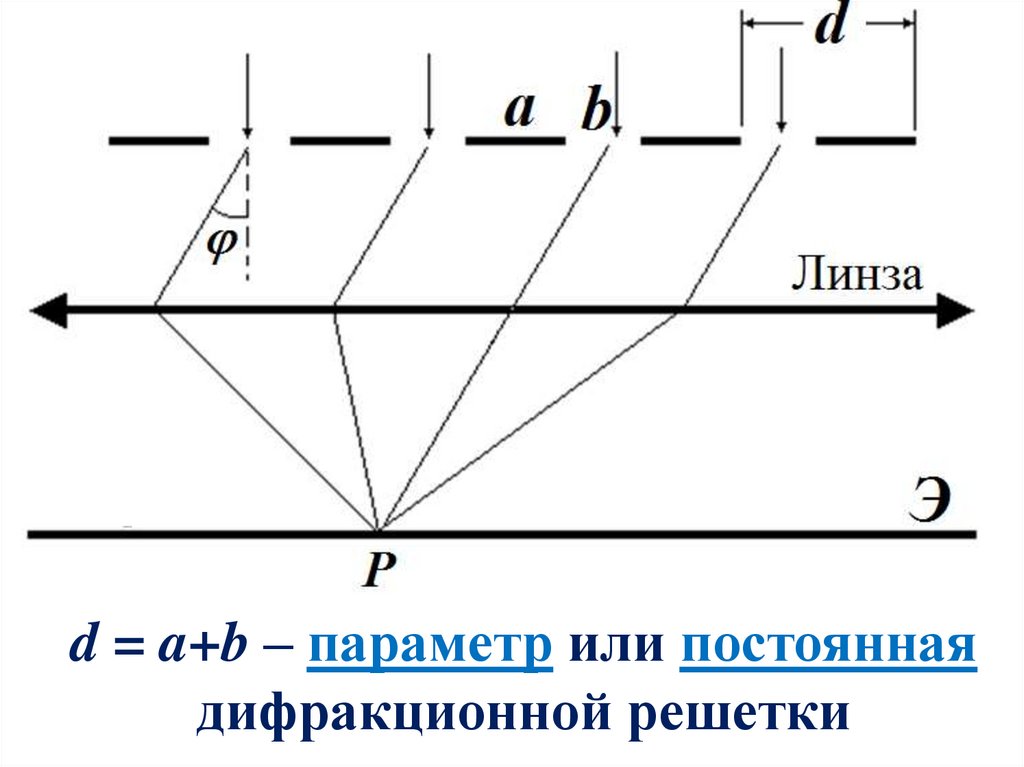
Дифракционная решеткаПравильная структура из большого числа
щелей называется дифракционной
решеткой.
23.
d = a+b – параметр или постояннаядифракционной решетки
24.
В спектре решетки есть три вида особых точек:1) Главные минимумы. Это “старые” минимумы.
Они получаются в тех же направлениях, что и
для одной щели. “Щель сама себя гасит”.
Условие: bsinj = ml (m=1,2,3…).
2) Главные максимумы. В этих направлениях
щели усиливают друг друга. Условие:
dsinj = kl (k=0,1,2,…).
3) Дополнительные минимумы. В них щели гасят
друг друга. Условие:
k
d sin j l ,( k 1, 2,...кроме 0, N , 2 N ...)
N
N – число щелей
25.
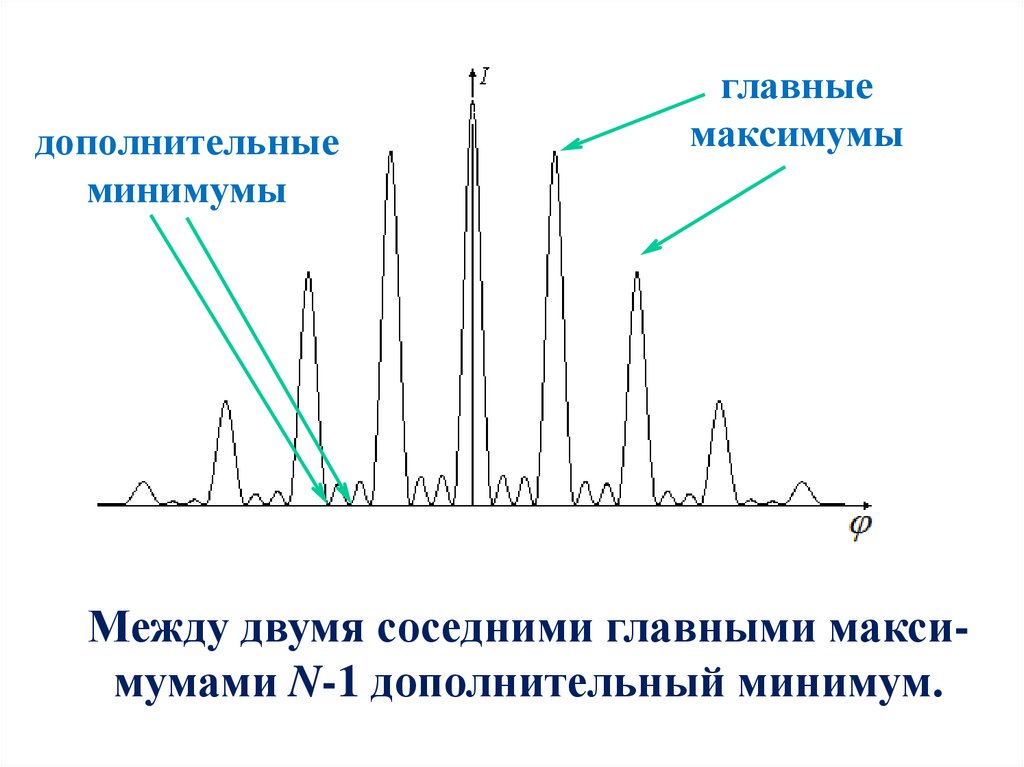
дополнительныеминимумы
главные
максимумы
Между двумя соседними главными максимумами N-1 дополнительный минимум.
26.
Разрешающая способность оптическихприборов
l
R
l
l - минимальная разность длин волн соседних
спектральных линий, воспринимаемых
раздельно
27.
Критерий РэлеяЛинии разрешены, если главный
максимум линии λ + λ совпадает с
дополнительным минимумом линии λ.
28.
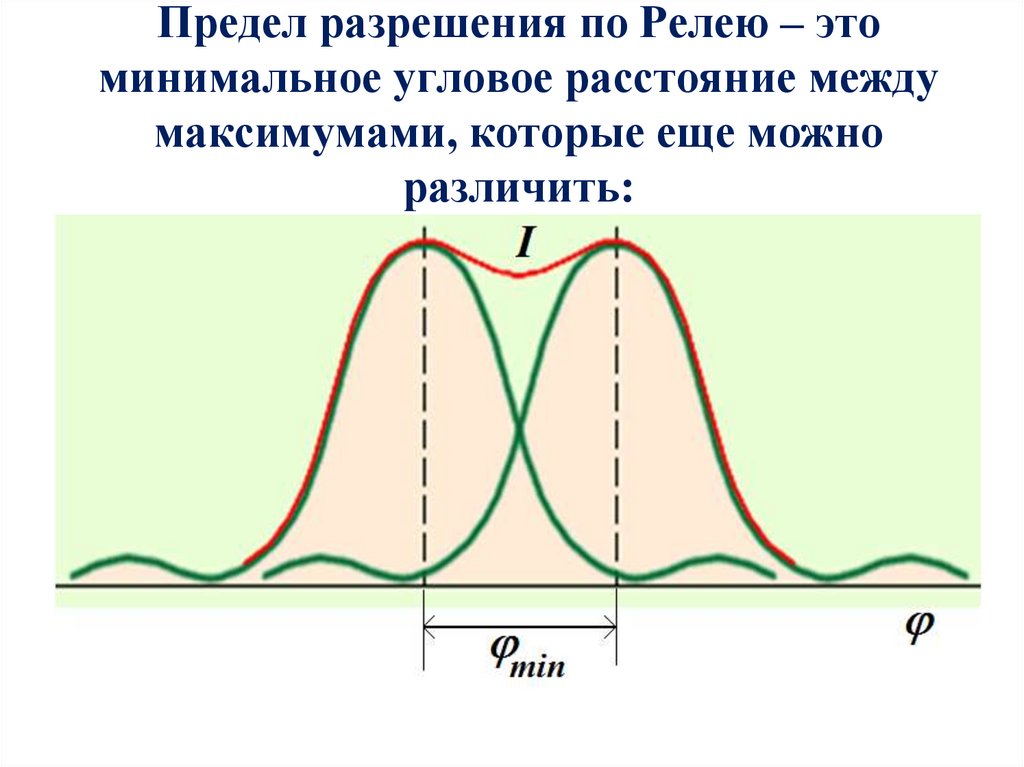
Предел разрешения по Релею – этоминимальное угловое расстояние между
максимумами, которые еще можно
различить:
29.
Разрешающая способностьдифракционной решетки:
R mN
m порядок спектра
N число щелей













 Физика
Физика








