Похожие презентации:
Задачи на построение сечений тетраэдра и параллелепипеда. Геометрия. 10 класс
1.
Конкурс педагогического мастерства – 2015Номинация «Лучшая методическая разработка»
Мультимедийное сопровождение
изучения темы «Задачи на построение сечений
тетраэдра и параллелепипеда»
Геометрия 10 класс
Учитель математики
МБОУ СОШ № 7 г. Костромы
Кишалова Ирина Ивановна
2.
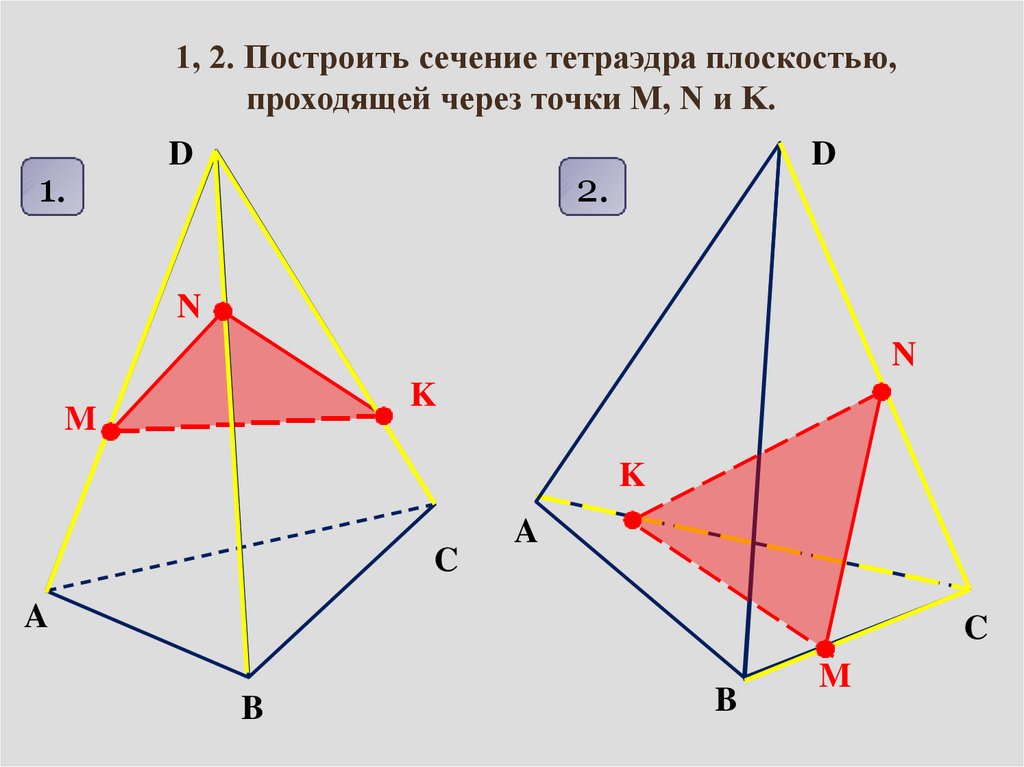
1, 2. Построить сечение тетраэдра плоскостью,проходящей через точки M, N и K.
1.
D
D
2.
N
N
K
M
K
C
A
A
C
B
B
M
3.
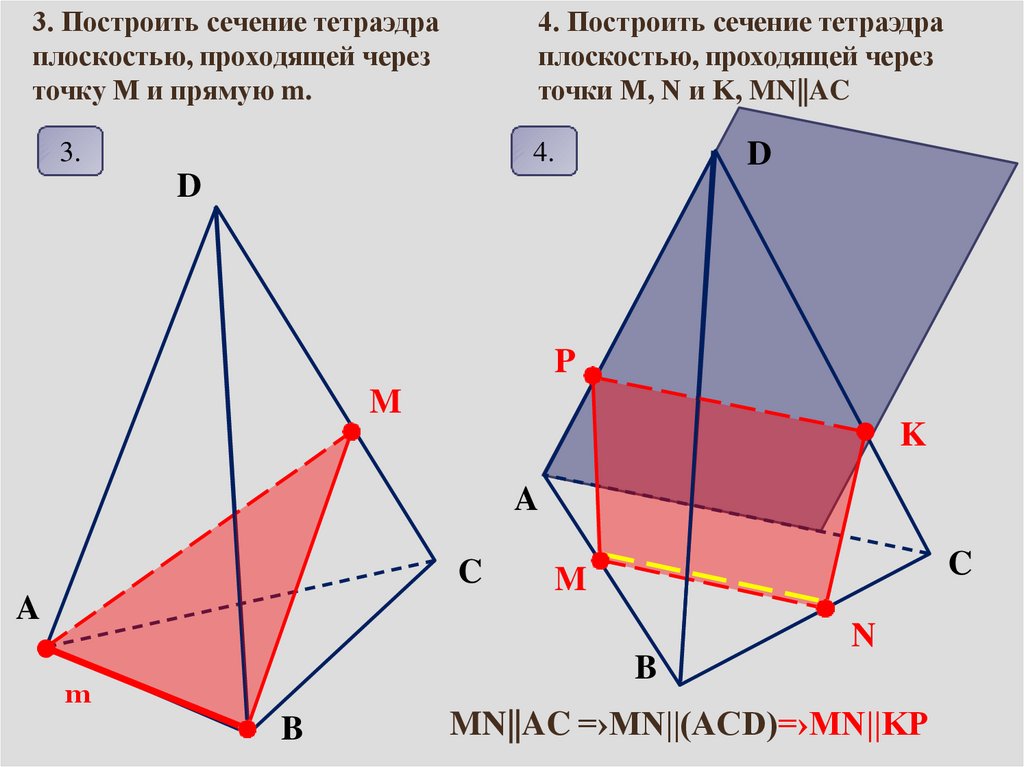
3. Построить сечение тетраэдраплоскостью, проходящей через
точку M и прямую m.
4. Построить сечение тетраэдра
плоскостью, проходящей через
точки M, N и K, MN||AC
3.
D
4.
D
P
M
K
A
C
A
C
M
N
B
m
B
MN||AC =›MN||(ACD)=›MN||KP
4.
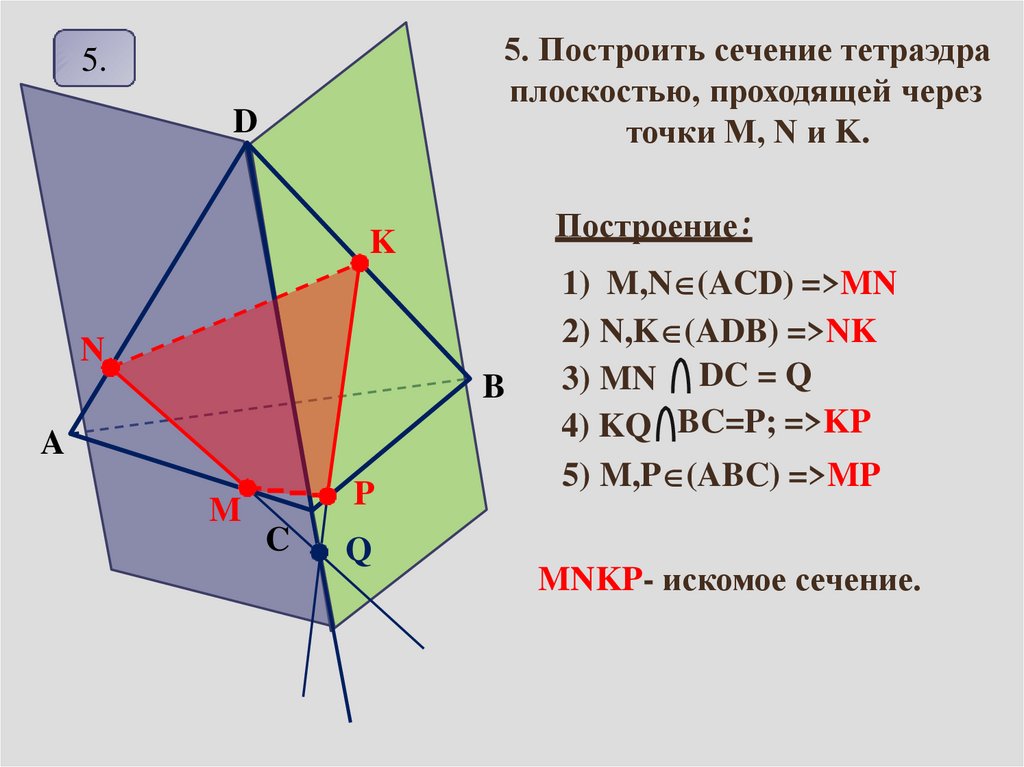
5. Построить сечение тетраэдраплоскостью, проходящей через
точки M, N и K.
5.
D
Построение:
K
N
B
A
M
P
C
Q
1) M,N (ACD) =>MN
2) N,K (ADB) =>NK
3) MN DC = Q
4) KQ BC=P; =>KP
5) M,P (ABC) =>MP
MNKP- искомое сечение.
5.
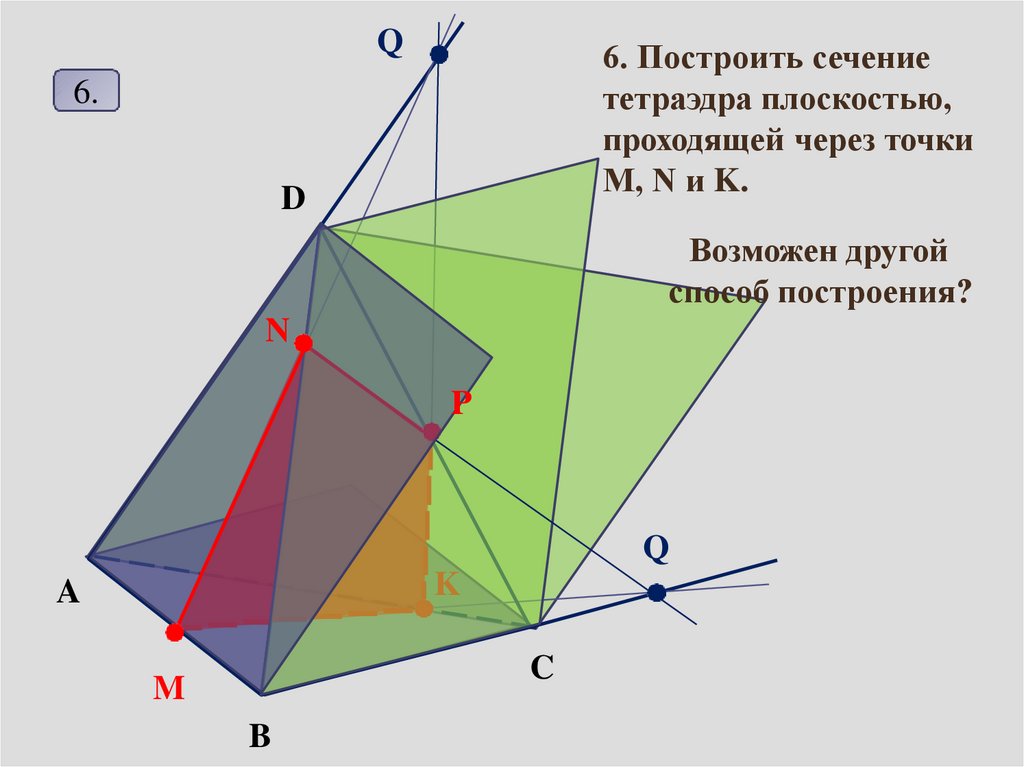
Q6. Построить сечение
тетраэдра плоскостью,
проходящей через точки
M, N и K.
6.
D
Возможен другой
способ построения?
N
P
Q
K
A
C
M
B
6.
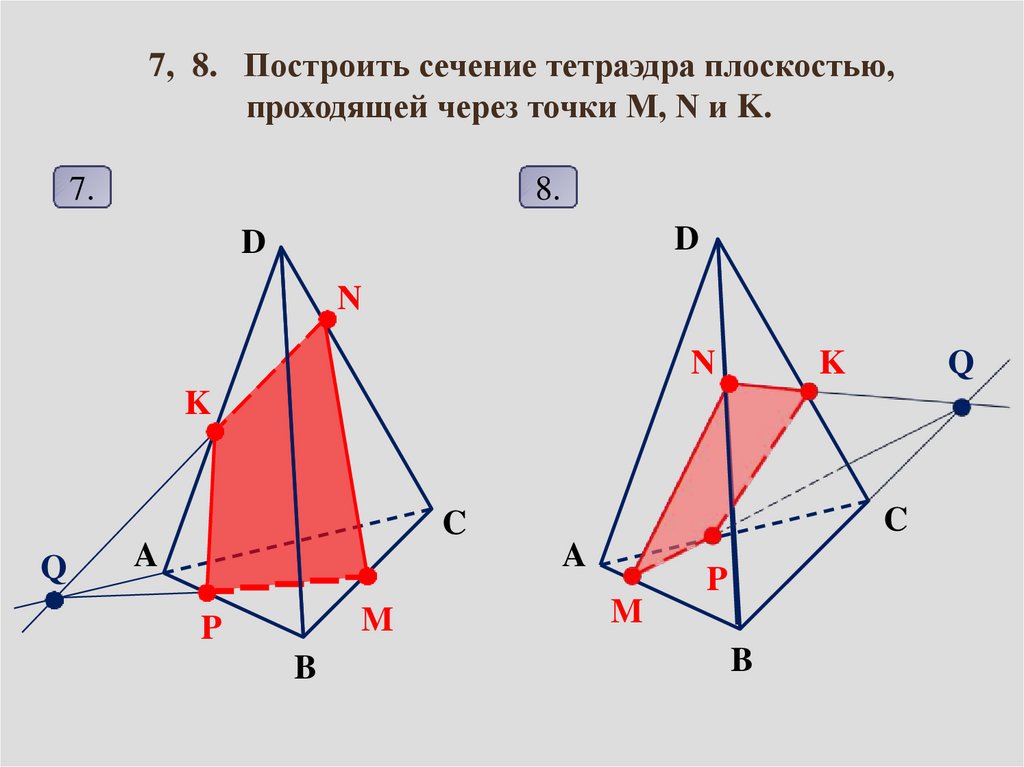
7, 8. Построить сечение тетраэдра плоскостью,проходящей через точки M, N и K.
7.
8.
D
D
N
N
K
Q
K
C
C
Q
A
A
M
P
B
P
M
B
7.
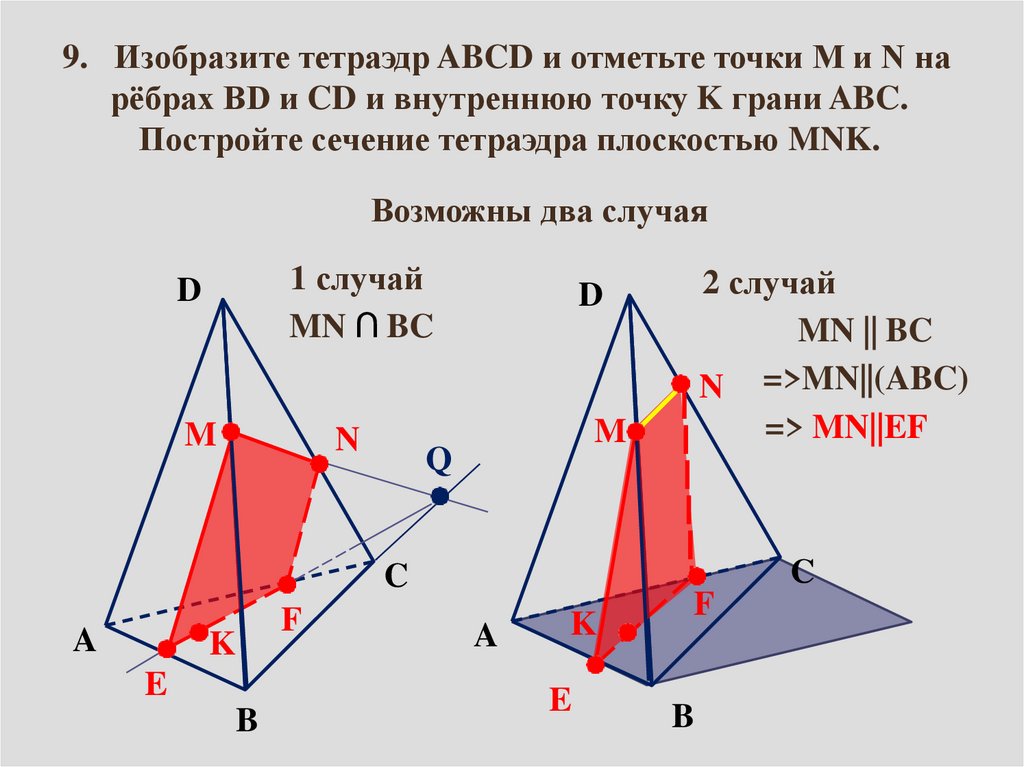
9. Изобразите тетраэдр ABCD и отметьте точки M и N нарёбрах BD и CD и внутреннюю точку K грани ABC.
Постройте сечение тетраэдра плоскостью MNK.
Возможны два случая
D
1 случай
MN ∩ BC
D
M
N
M
Q
C
C
A
F
K
E
B
2 случай
MN || BC
N =>MN||(ABC)
=> MN||EF
A
K
E
F
B
8.
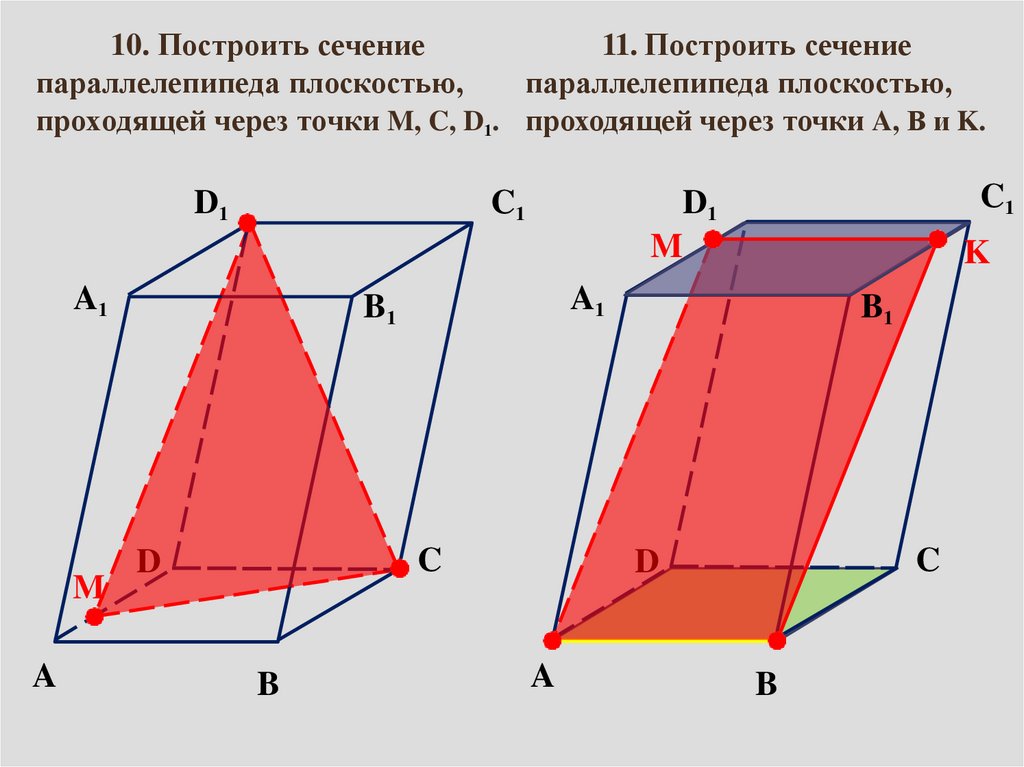
10. Построить сечение11. Построить сечение
параллелепипеда плоскостью,
параллелепипеда плоскостью,
проходящей через точки M, C, D1. проходящей через точки A, B и K.
D1
C1
A1
M
A
C
B
K
A1
B1
D
C1
D1
M
B1
C
D
A
B
9.
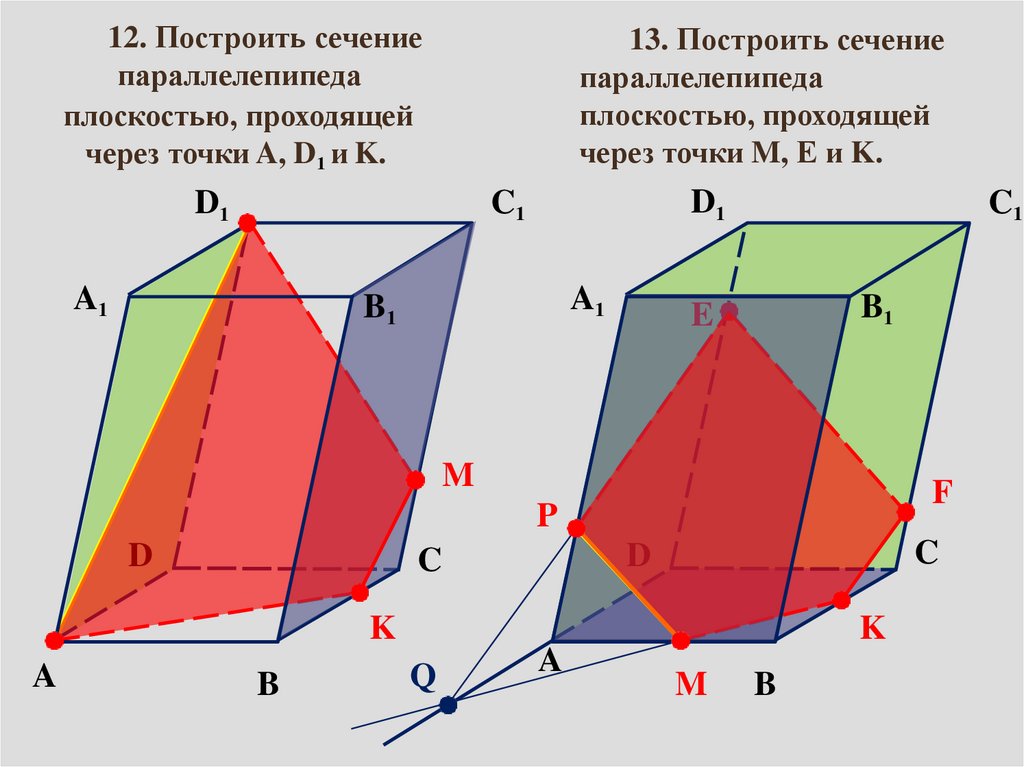
12. Построить сечениепараллелепипеда
плоскостью, проходящей
через точки A, D1 и K.
13. Построить сечение
параллелепипеда
плоскостью, проходящей
через точки M, E и K.
D1
C1
D1
A1
A1
B1
C1
B1
E
M
F
P
D
C
D
C
K
A
B
K
Q
A
M
B
10.
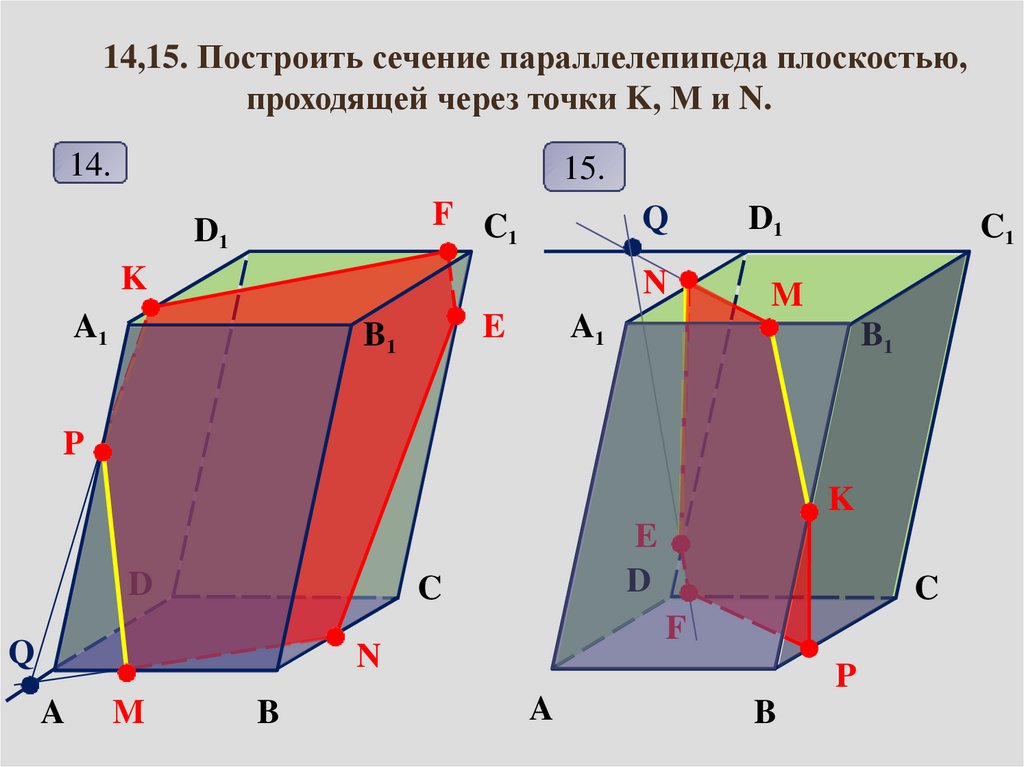
14,15. Построить сечение параллелепипеда плоскостью,проходящей через точки K, M и N.
14.
15.
F C
1
D1
K
A1
E
B1
Q
D1
N
M
C1
A1
B1
P
K
D
E
D
C
Q
F
N
A
M
B
C
P
A
B
11.
Задачи на построение сечений«Геометрия 10-11 класс»
Учебник для общеобразовательных учреждений Л.С. Атанасян, В.Ф.
Бутузов и др.
12.
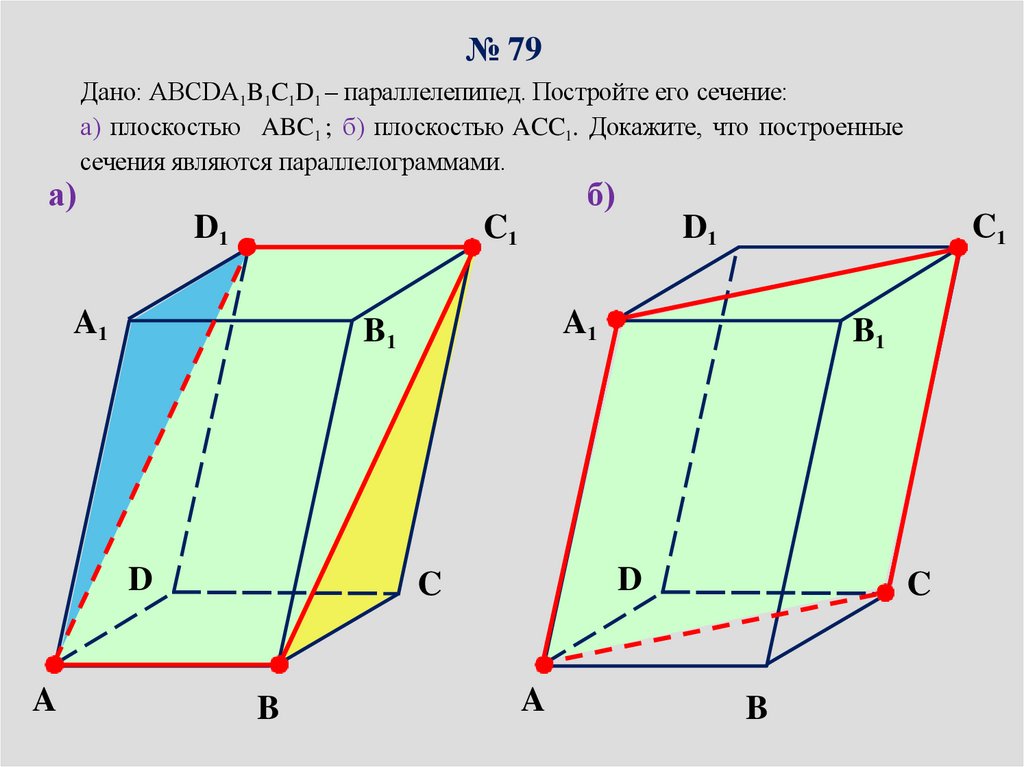
№ 79а)
Дано: ABCDA1B1C1D1 – параллелепипед. Постройте его сечение:
а) плоскостью ABC1 ; б) плоскостью ACC1. Докажите, что построенные
сечения являются параллелограммами.
б)
D1
C1
A1
A
A1
B1
D
B1
D
C
B
C1
D1
A
C
B
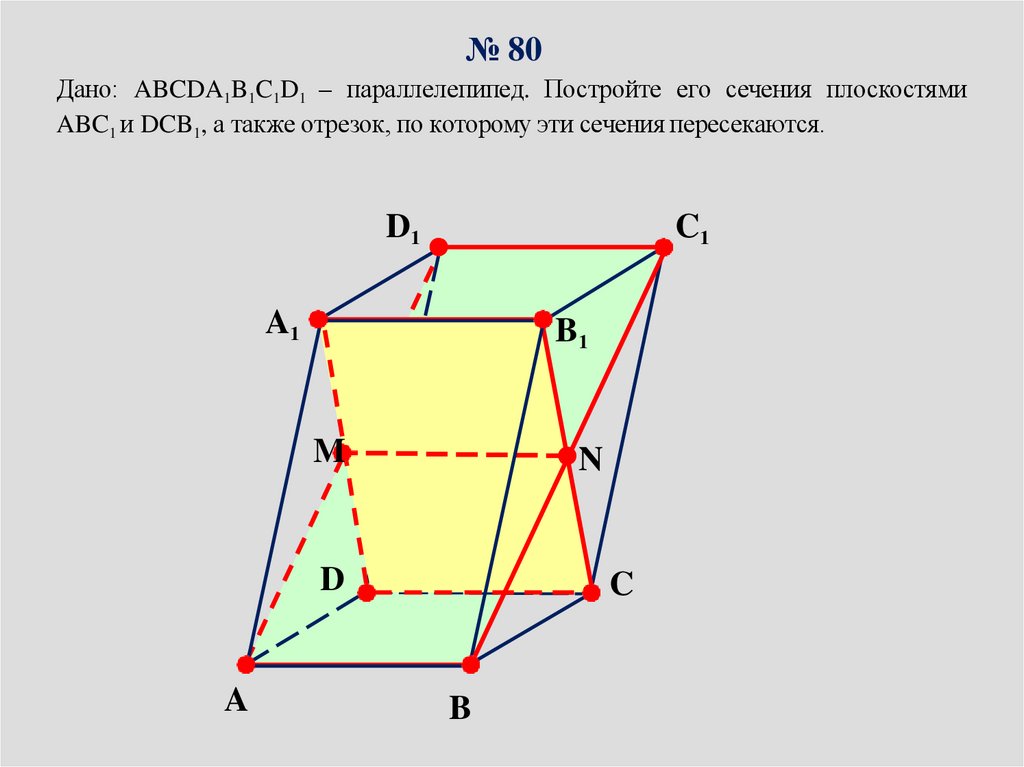
13.
№ 80Дано: ABCDA1B1C1D1 – параллелепипед. Постройте его сечения плоскостями
ABC1 и DCB1, а также отрезок, по которому эти сечения пересекаются.
D1
C1
A1
B1
M
N
D
A
C
B
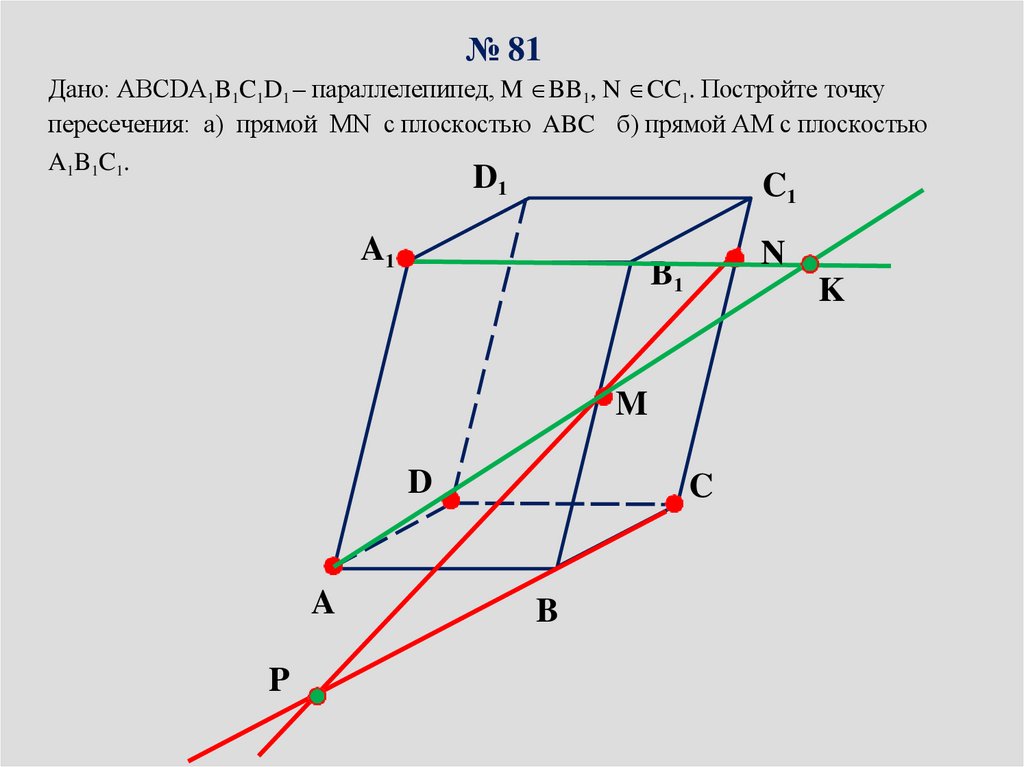
14.
№ 81Дано: ABCDA1B1C1D1 – параллелепипед, M BB1, N CC1. Постройте точку
пересечения: а) прямой MN с плоскостью ABC б) прямой АМ с плоскостью
A1B1C1.
D1
C1
A1
N
B1
K
M
D
A
P
C
B
15.
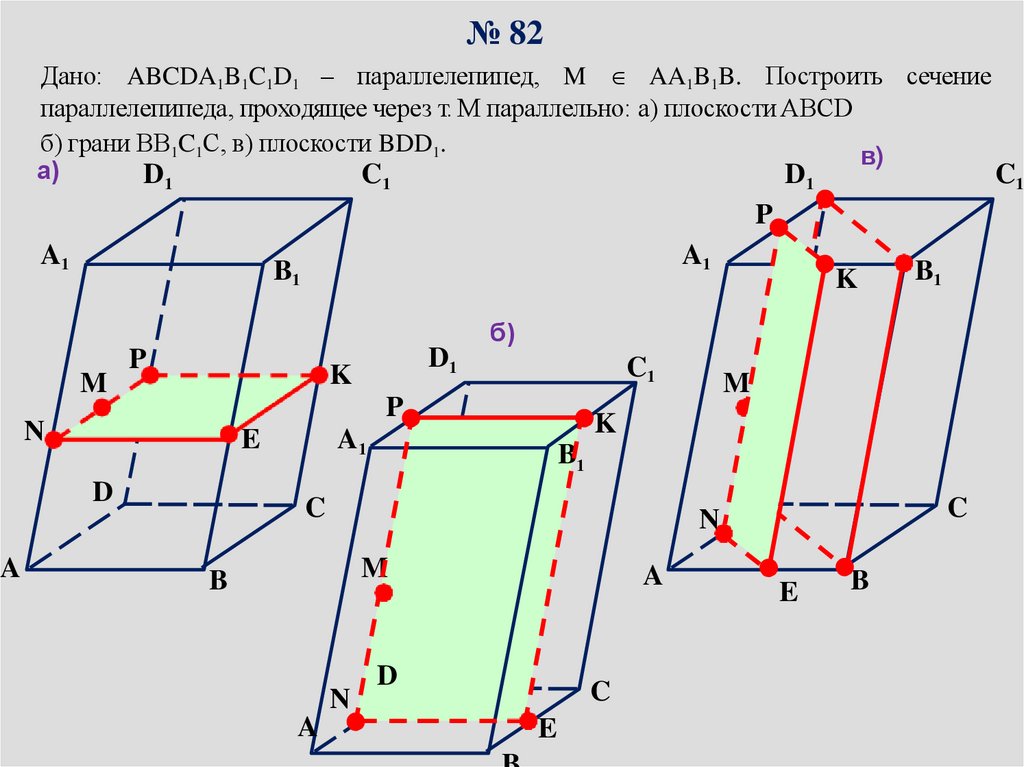
№ 82Дано: ABCDA1B1C1D1 – параллелепипед, M AA1B1B. Построить сечение
параллелепипеда, проходящее через т. М параллельно: а) плоскости ABCD
б) грани BB1C1C, в) плоскости BDD1.
в)
а)
D1
C1
D1
C1
P
A1
A1
B1
K
B1
б)
M
P
C1
P
N
E
D
A
D1
K
K
A1
B1
D
C
C
N
M
B
N
A
M
A
D
C
E
E
B
16.
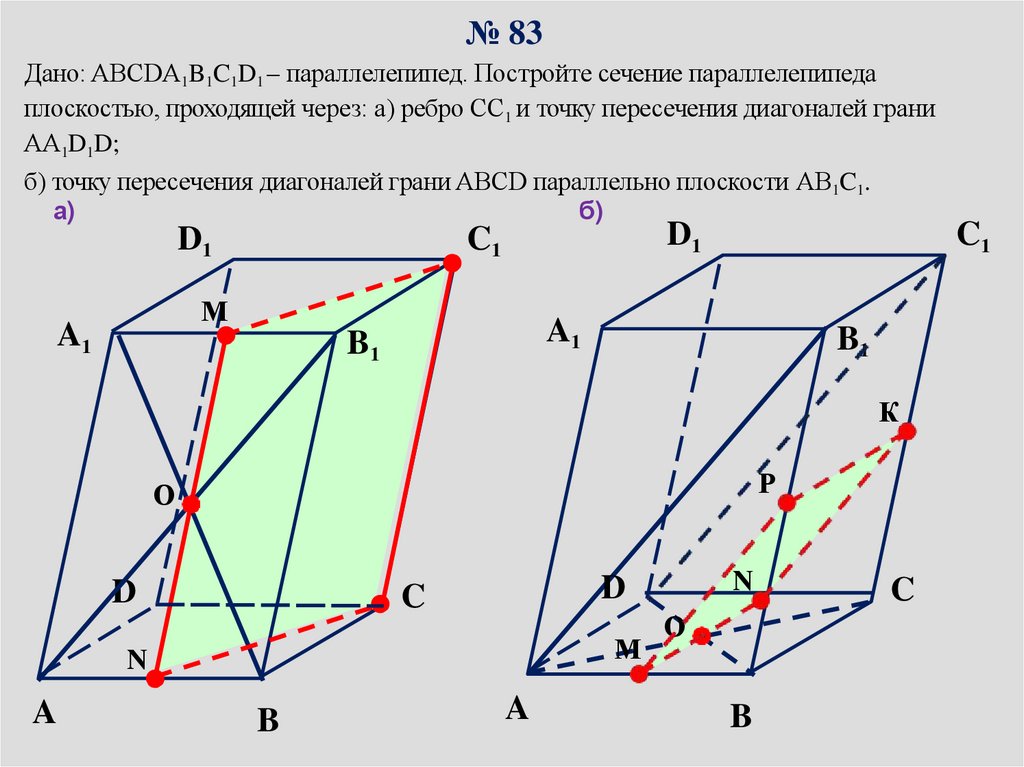
№ 83Дано: ABCDA1B1C1D1 – параллелепипед. Постройте сечение параллелепипеда
плоскостью, проходящей через: а) ребро СС1 и точку пересечения диагоналей грани
AА1D1D;
б) точку пересечения диагоналей грани ABCD параллельно плоскости АB1C1.
а)
б)
D1
D1
C1
М
A1
A1
B1
B1
К
Р
О
D
М
N
A
B
N
D
C
A
О
B
C
C1
17.
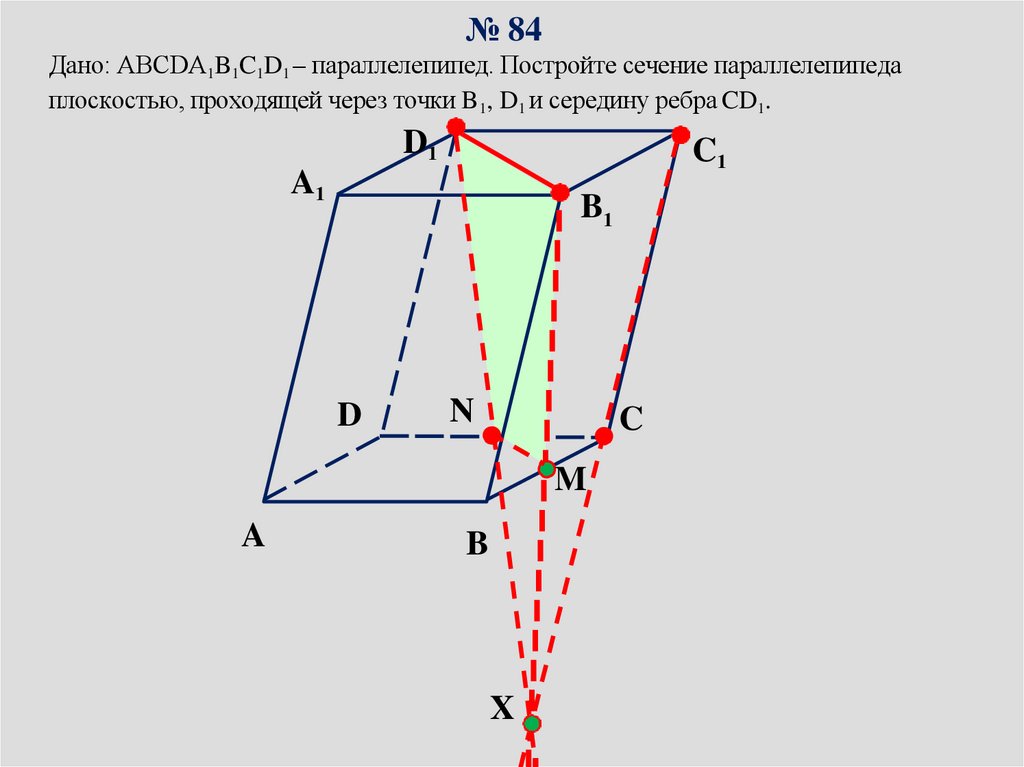
№ 84Дано: ABCDA1B1C1D1 – параллелепипед. Постройте сечение параллелепипеда
плоскостью, проходящей через точки B1, D1 и середину ребра CD1.
D1
C1
A1
B1
D
N
C
M
A
B
X
18.
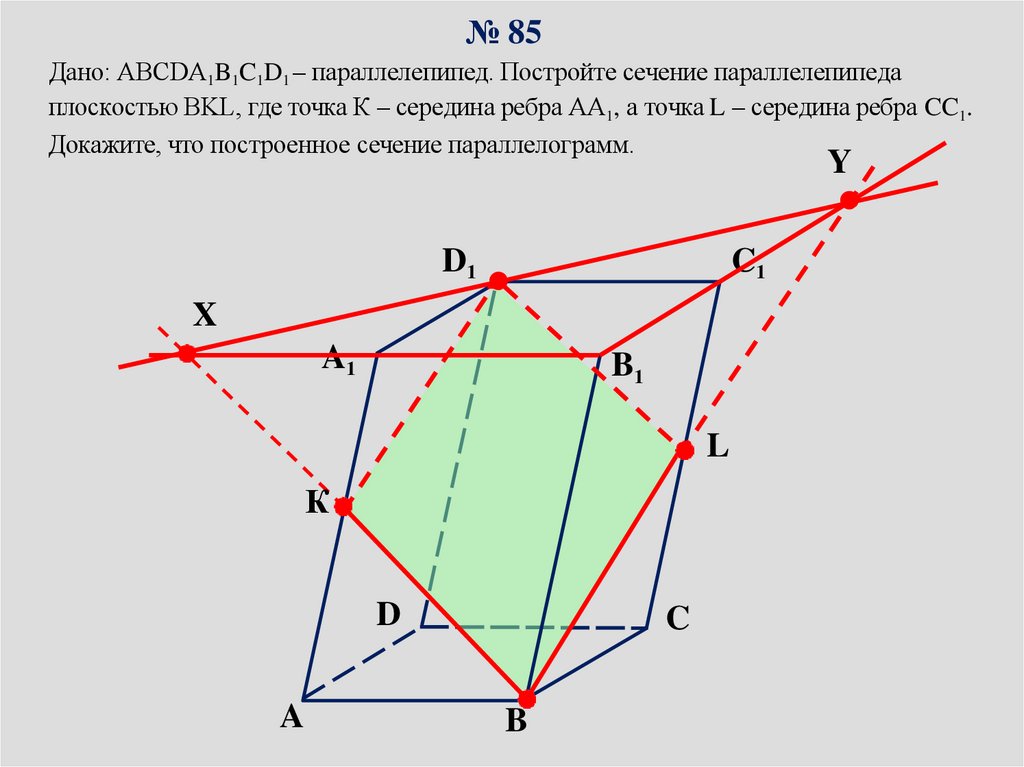
№ 85Дано: ABCDA1B1C1D1 – параллелепипед. Постройте сечение параллелепипеда
плоскостью BKL, где точка К – середина ребра АA1, а точка L – середина ребра CC1.
Докажите, что построенное сечение параллелограмм.
Y
D1
C1
X
A1
B1
L
К
D
A
C
B
19.
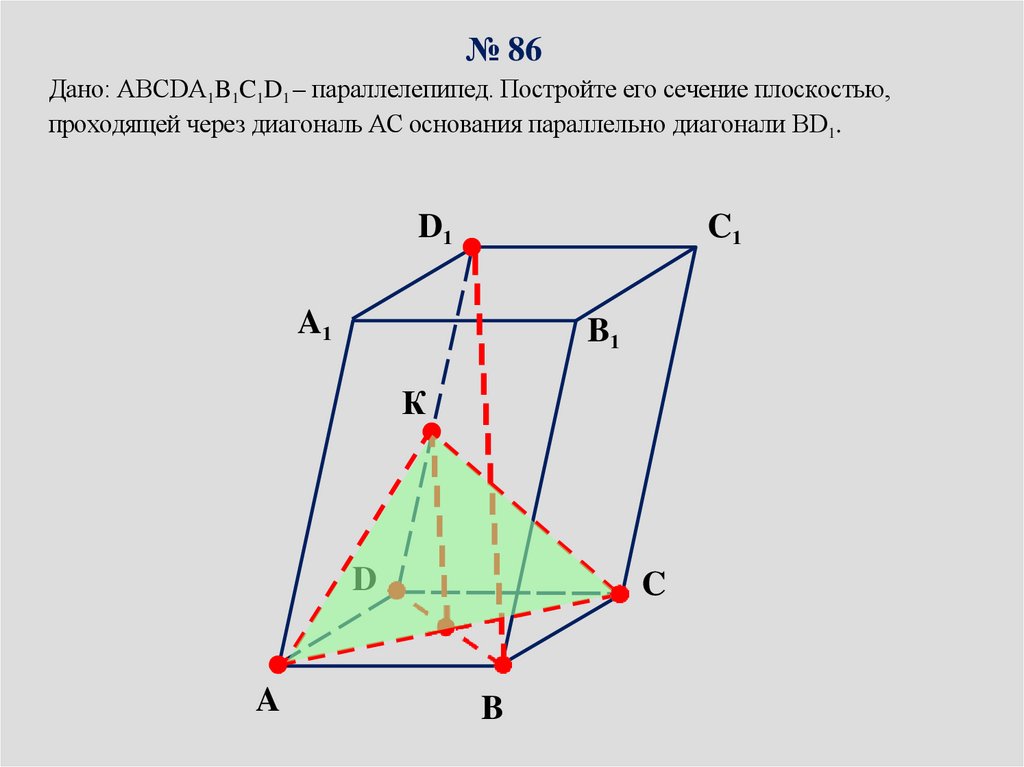
№ 86Дано: ABCDA1B1C1D1 – параллелепипед. Постройте его сечение плоскостью,
проходящей через диагональ АС основания параллельно диагонали ВD1.
D1
C1
A1
B1
К
D
A
C
B
20.
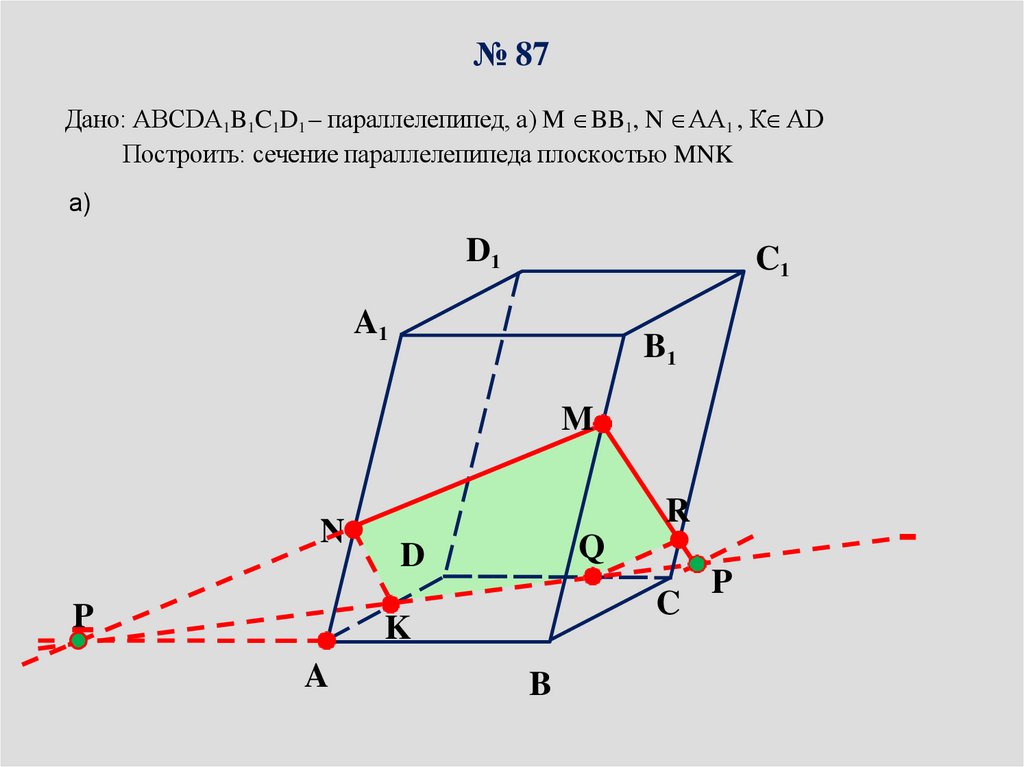
№ 87Дано: ABCDA1B1C1D1 – параллелепипед, а) M BB1, N АА1 , К АD
Построить: сечение параллелепипеда плоскостью MNK
а)
D1
C1
A1
B1
M
N
P
R
Q
D
C
K
A
B
P
21.
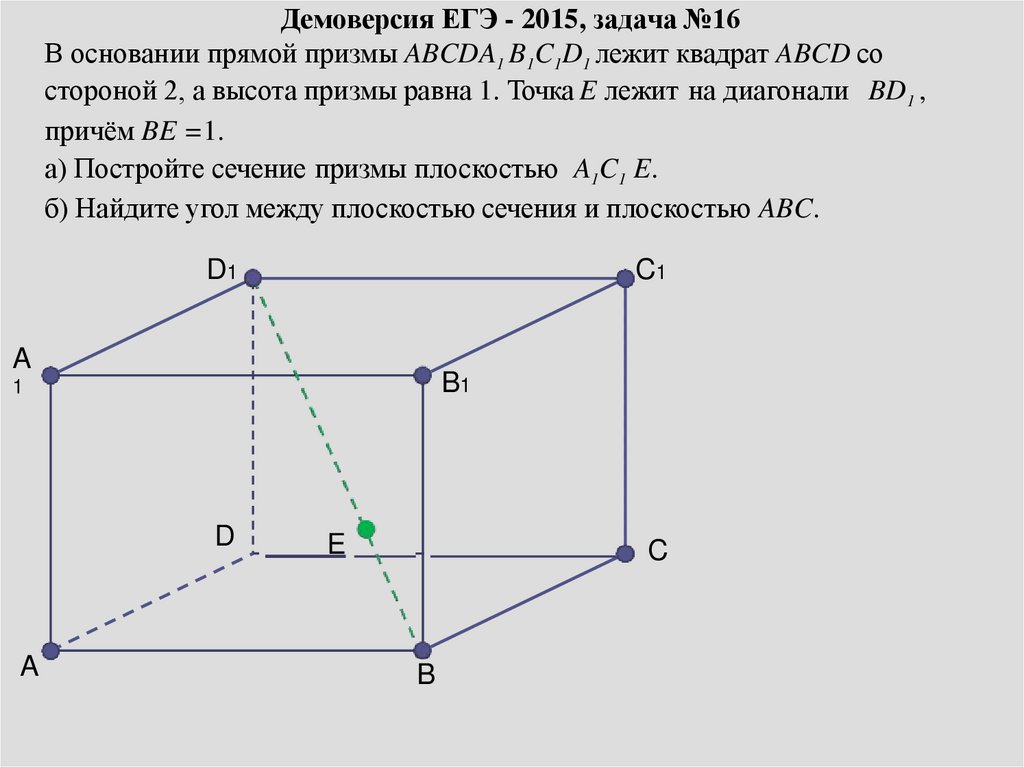
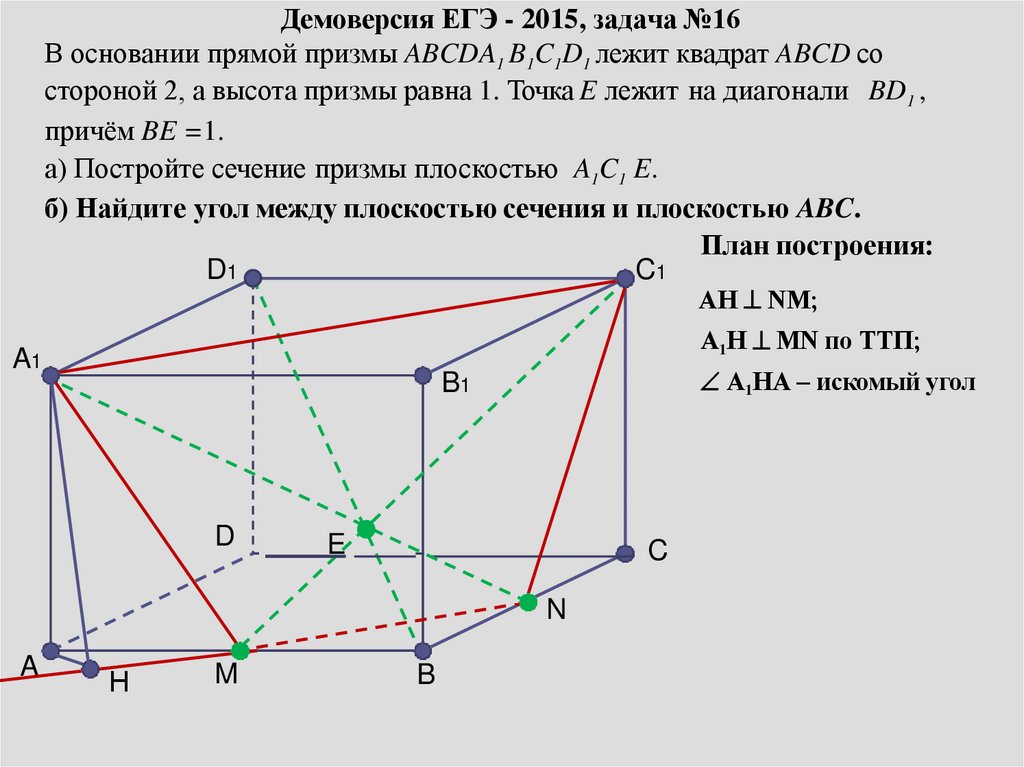
Демоверсия ЕГЭ - 2015, задача №16В основании прямой призмы ABCDA1 B1C1D1 лежит квадрат ABCD со
стороной 2, а высота призмы равна 1. Точка E лежит на диагонали BD1 ,
причём BE =1.
а) Постройте сечение призмы плоскостью A1C1 E.
б) Найдите угол между плоскостью сечения и плоскостью ABC.
D1
C1
A
B1
1
D
A
E
C
B
22.
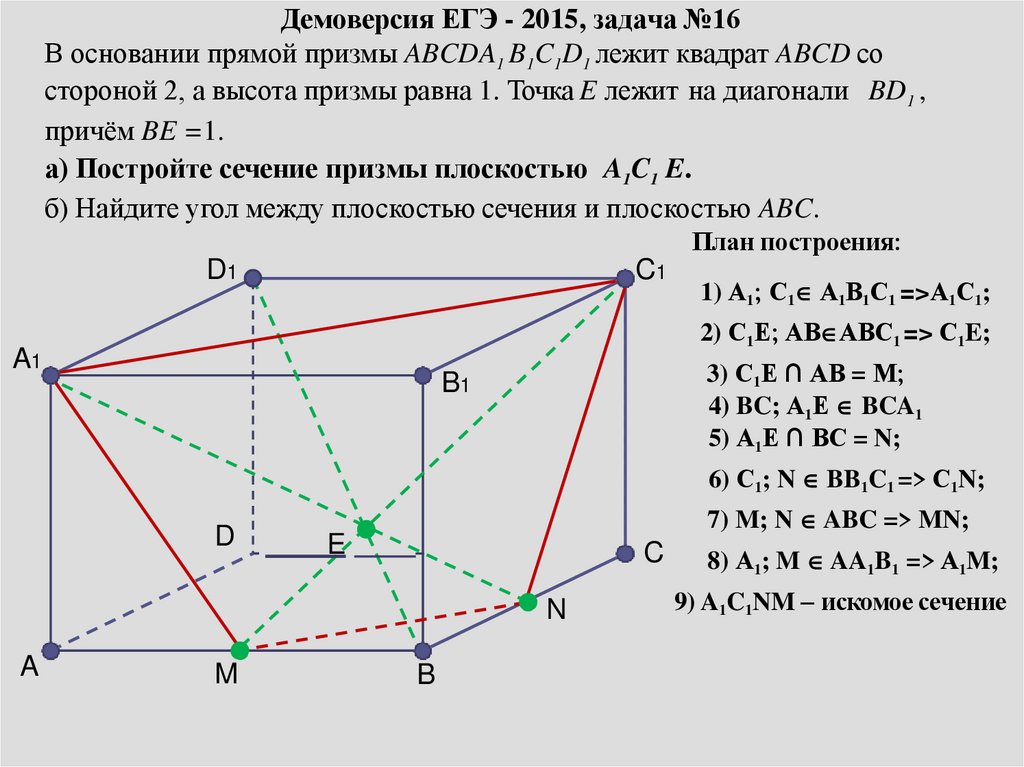
Демоверсия ЕГЭ - 2015, задача №16В основании прямой призмы ABCDA1 B1C1D1 лежит квадрат ABCD со
стороной 2, а высота призмы равна 1. Точка E лежит на диагонали BD1 ,
причём BE =1.
а) Постройте сечение призмы плоскостью A1C1 E.
б) Найдите угол между плоскостью сечения и плоскостью ABC.
План построения:
D1
C1
1) А1; С1 А1В1С1 =>А1С1;
2) С1Е; AB АBC1 => С1E;
A1
3) С1Е ∩ АВ = М;
4) BC; А1Е BCA1
5) А1Е ∩ ВС = N;
B1
6) С1; N BB1C1 => С1N;
D
7) M; N ABC => MN;
E
C
N
A
M
B
8) А1; M AA1B1 => А1M;
9) A1C1NM – искомое сечение
23.
Демоверсия ЕГЭ - 2015, задача №16В основании прямой призмы ABCDA1 B1C1D1 лежит квадрат ABCD со
стороной 2, а высота призмы равна 1. Точка E лежит на диагонали BD1 ,
причём BE =1.
а) Постройте сечение призмы плоскостью A1C1 E.
б) Найдите угол между плоскостью сечения и плоскостью ABC.
План построения:
D1
C1
АН NМ;
А1Н МN по ТТП;
A1
А1НА – искомый угол
B1
D
E
C
N
A
Н
M
B
24.
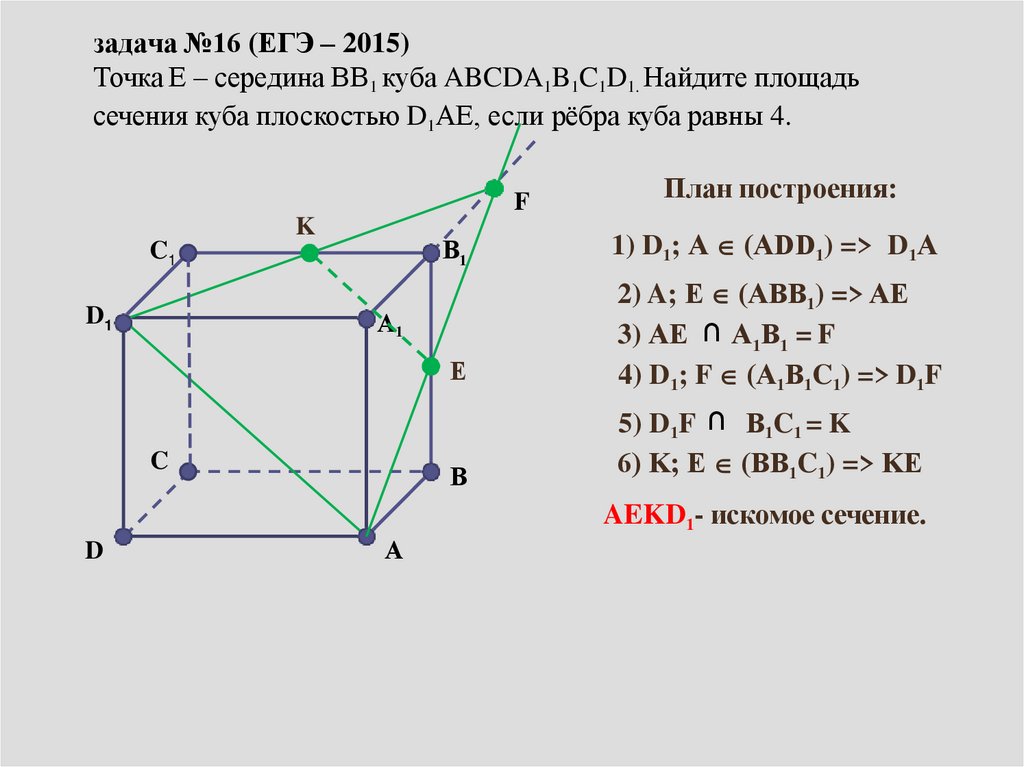
задача №16 (ЕГЭ – 2015)Точка Е – середина ВВ1 куба ABCDA1B1C1D1. Найдите площадь
сечения куба плоскостью D1AЕ, если рёбра куба равны 4.
F
K
C1
D1
В1
1) D1; А (АDD1) => D1А
Е
2) A; Е (АВВ1) => АЕ
3) АЕ ∩ А1В1 = F
4) D1; F (А1В1C1) => D1F
В
5) D1F ∩ В1C1 = K
6) K; Е (ВВ1C1) => KЕ
А1
C
План построения:
AEKD1- искомое сечение.
D
А
25.
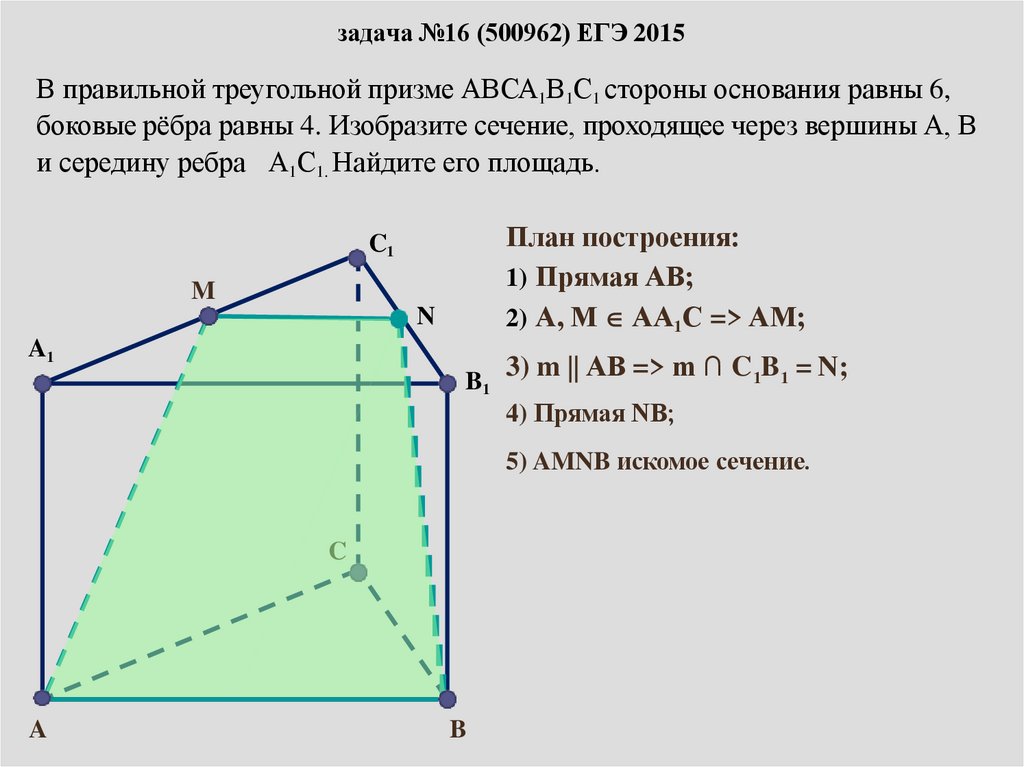
задача №16 (500962) ЕГЭ 2015В правильной треугольной призме АВСА1В1С1 стороны основания равны 6,
боковые рёбра равны 4. Изобразите сечение, проходящее через вершины А, В
и середину ребра А1С1. Найдите его площадь.
План построения:
1) Прямая АВ;
2) А, М АА1С => АМ;
C1
M
N
A1
B1
3) m АВ => m ∩ C 1B1 = N;
4) Прямая NВ;
5) AMNB искомое сечение.
C
A
B
26.
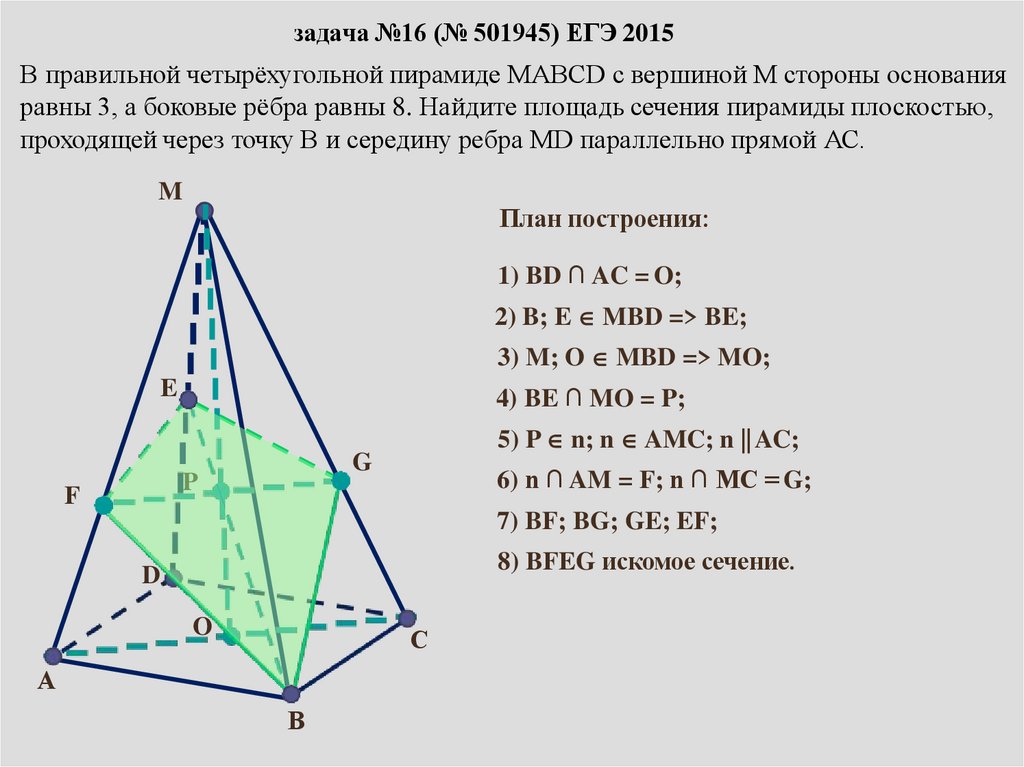
задача №16 (№ 501945) ЕГЭ 2015В правильной четырёхугольной пирамиде МАВСD с вершиной М стороны основания
равны 3, а боковые рёбра равны 8. Найдите площадь сечения пирамиды плоскостью,
проходящей через точку В и середину ребра МD параллельно прямой АС.
M
План построения:
1) BD ∩ AC = O;
2) B; E MBD => BE;
3) M; O MBD => MO;
E
4) BE ∩ MO = P;
G
P
F
5) P n; n AMC; n AC;
6) n ∩ AM = F; n ∩ MC = G;
7) BF; BG; GE; EF;
8) BFEG искомое сечение.
D
O
С
А
В
27.
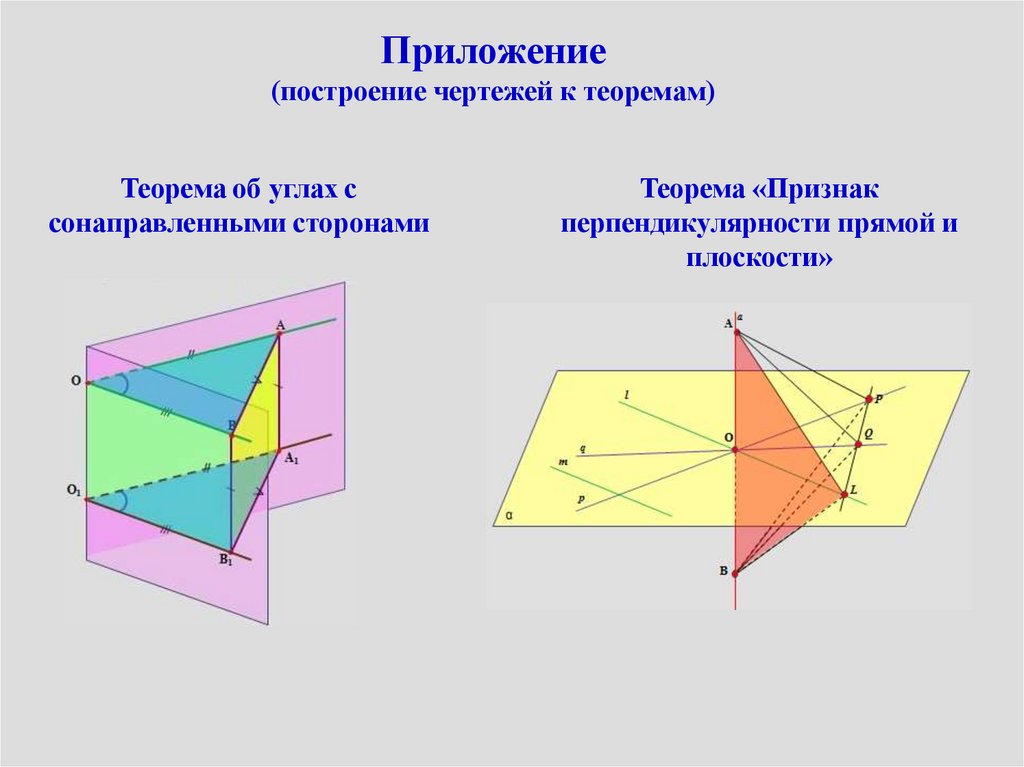
Приложение(построение чертежей к теоремам)
Теорема об углах с
сонаправленными сторонами
Теорема «Признак
перпендикулярности прямой и
плоскости»
28.
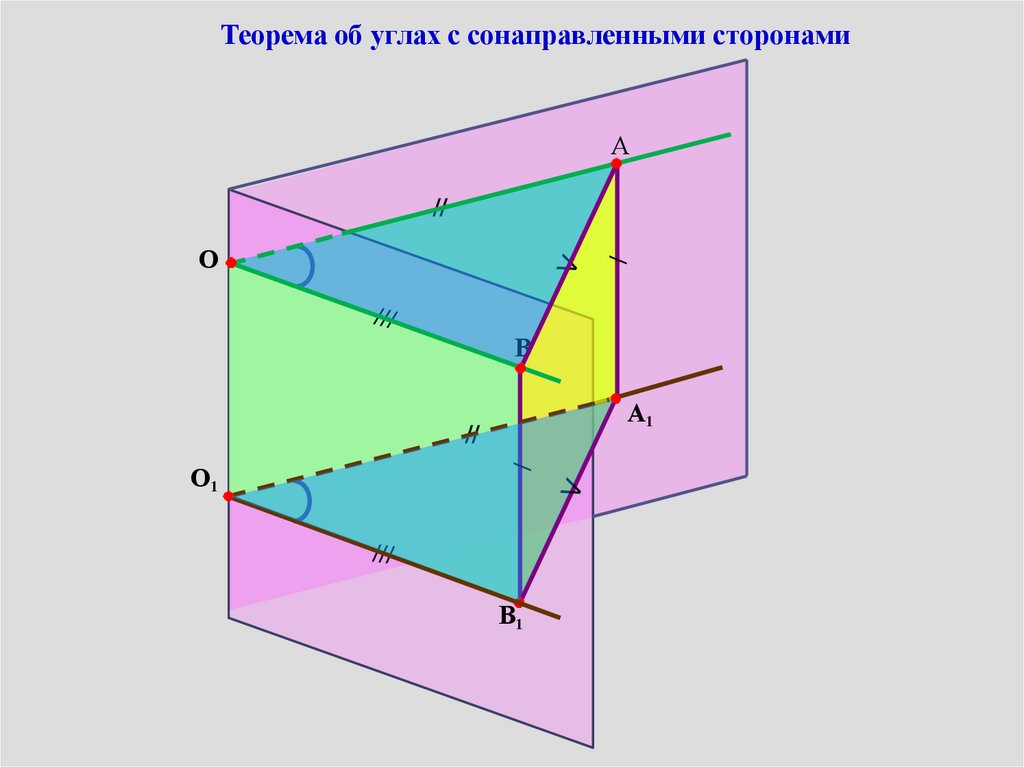
Теорема об углах с сонаправленными сторонамиА
//
О
В
А1
//
О1
В1
29.
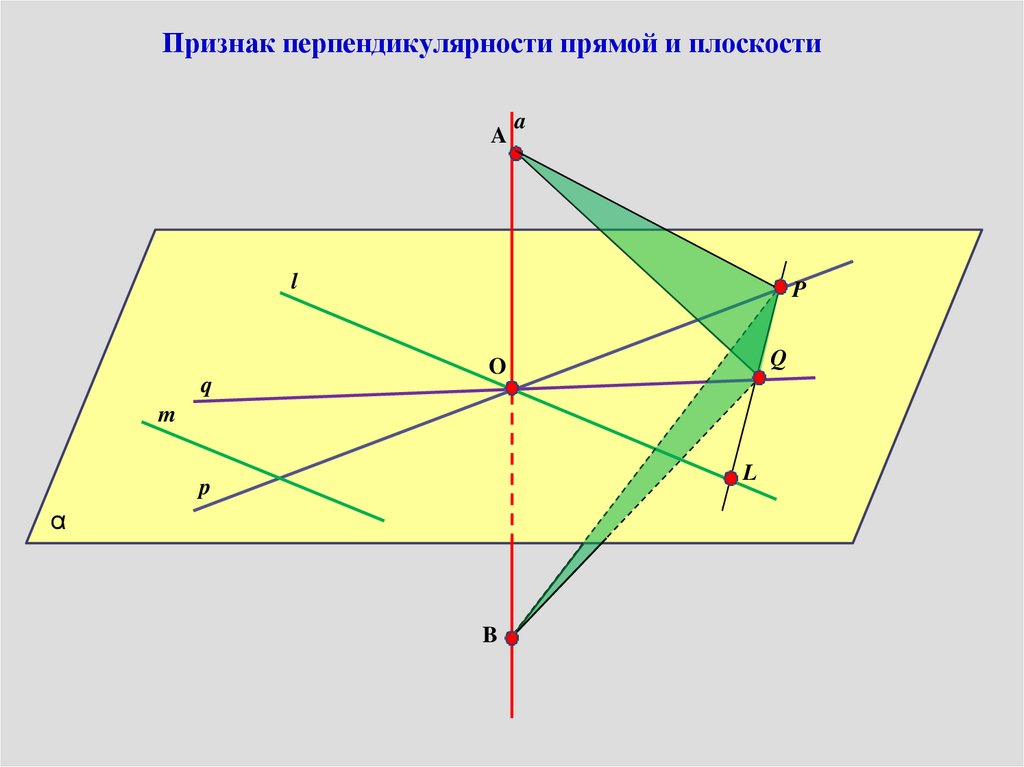
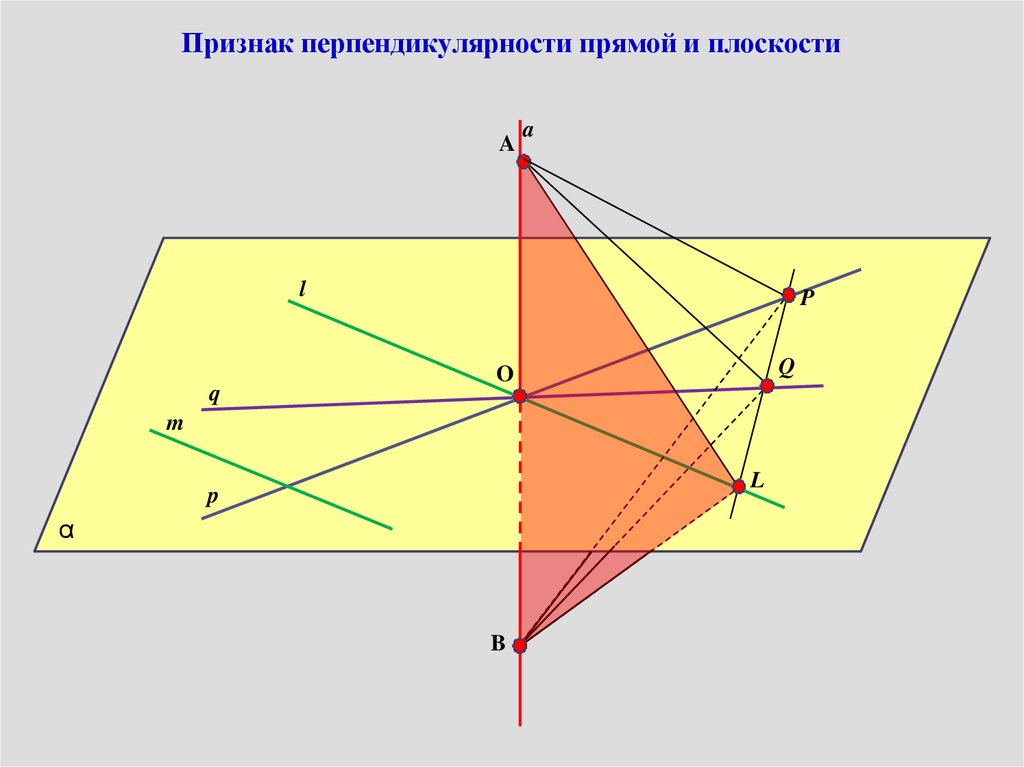
Признак перпендикулярности прямой и плоскостиA
a
l
q
P
Q
O
m
L
p
α
B
30.
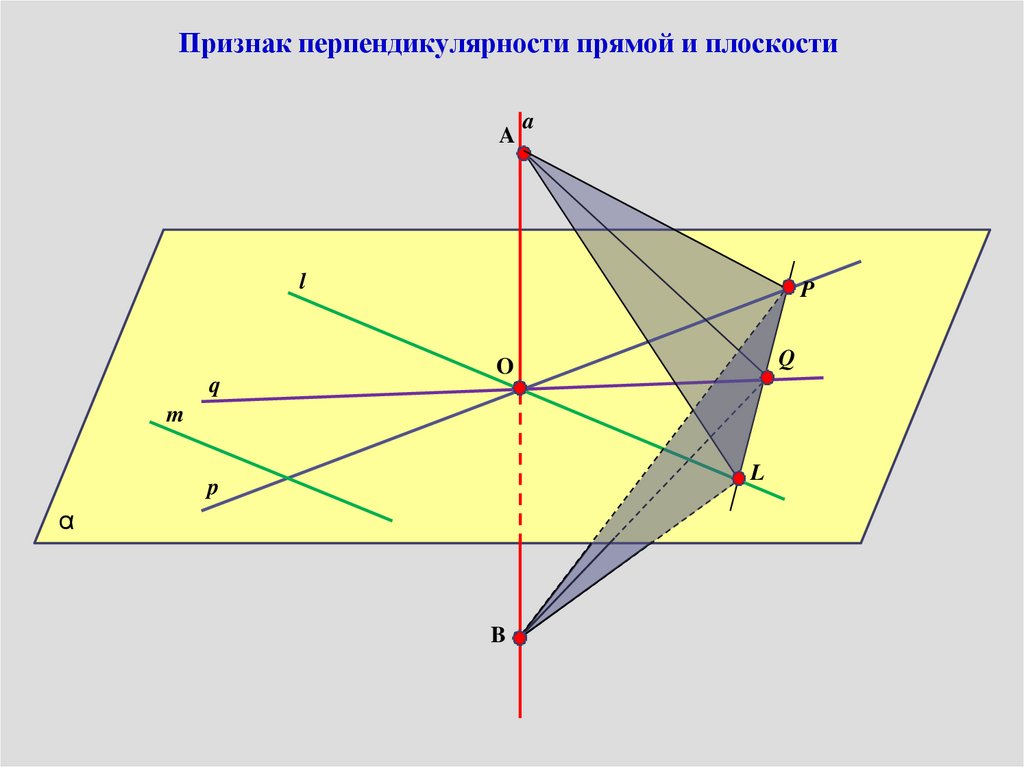
Признак перпендикулярности прямой и плоскостиA
a
l
q
P
Q
O
m
L
p
α
B
31.
Признак перпендикулярности прямой и плоскостиA
a
l
q
P
Q
O
m
L
p
α
B


 Математика
Математика








