Взаимное расположение прямой и плоскости в пространстве

1. Взаимное расположение прямой и плоскости в пространстве

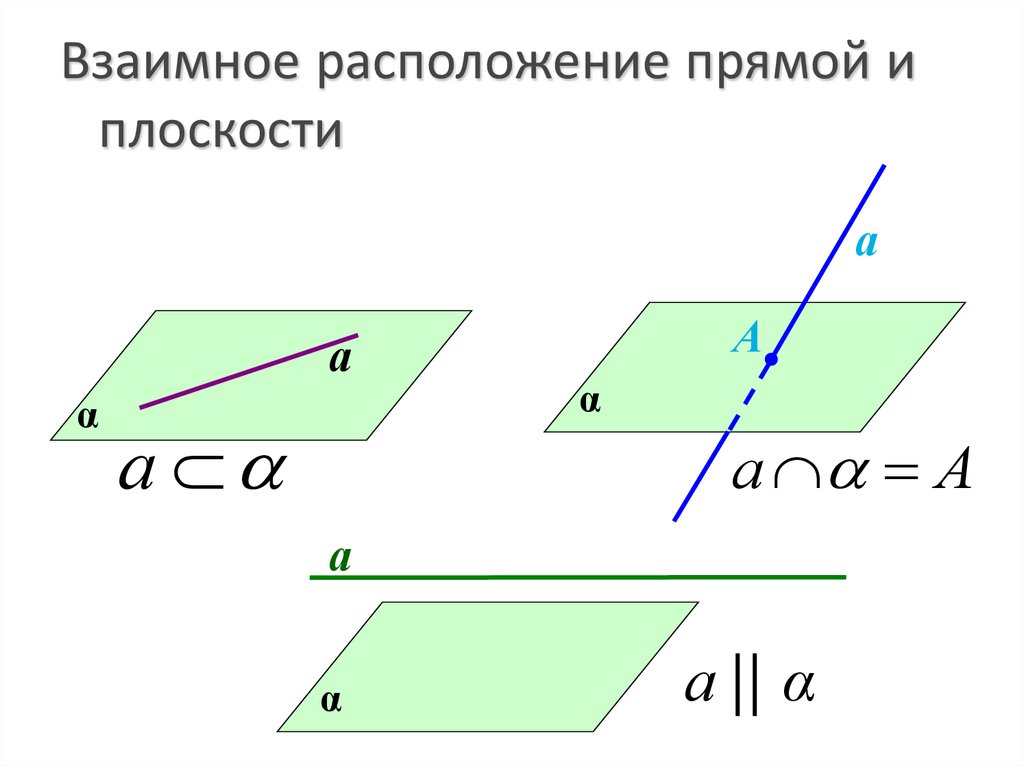
2. Взаимное расположение прямой и плоскости

а
а
α
а
А
α
а А
а
α
а || α

3. 1. Параллельность прямой и плоскости

Прямая и плоскость называются
параллельными, если они
не пересекаются.
а
α
а || α или α || а

4. Построение параллельных прямой и плоскости

Построение
параллельныхпрямой
прямойи и
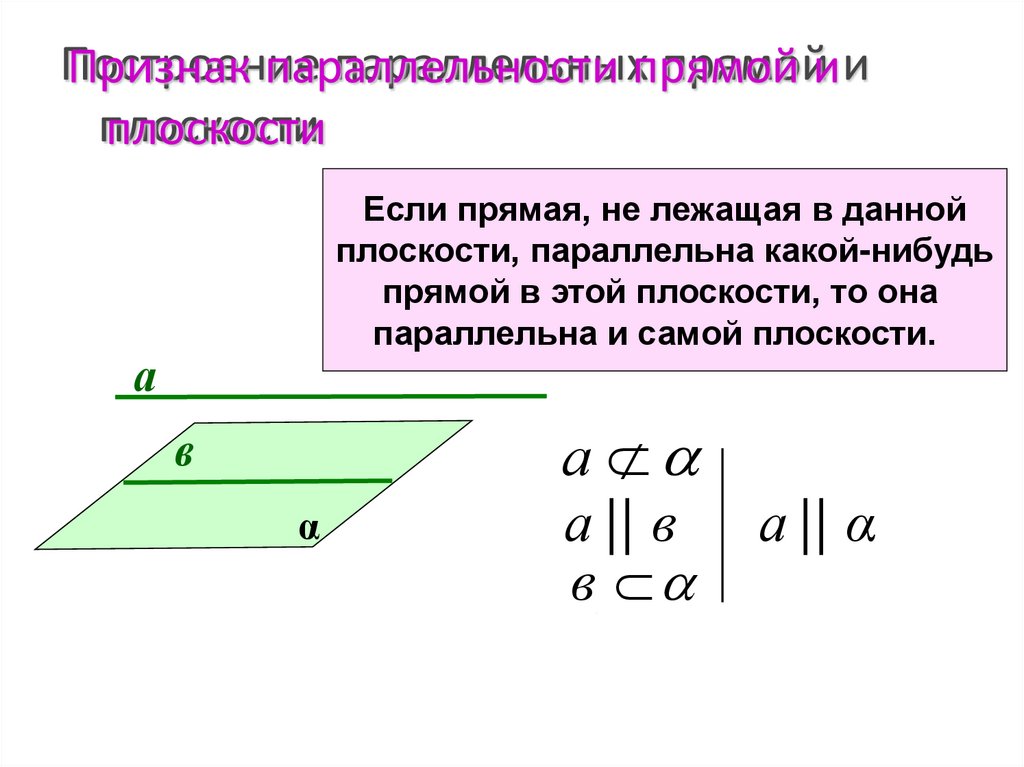
Признак параллельности
плоскости
плоскости
Если прямая, не лежащая в данной
плоскости, параллельна какой-нибудь
прямой в этой плоскости, то она
параллельна и самой плоскости.
а
в
α
а
а || в а || α
ав1

5. Утверждение 1

Если плоскость проходит
через данную прямую,
параллельную другой
плоскости, то линия
пересечения плоскостей
параллельна данной
прямой.
а
b
α
β

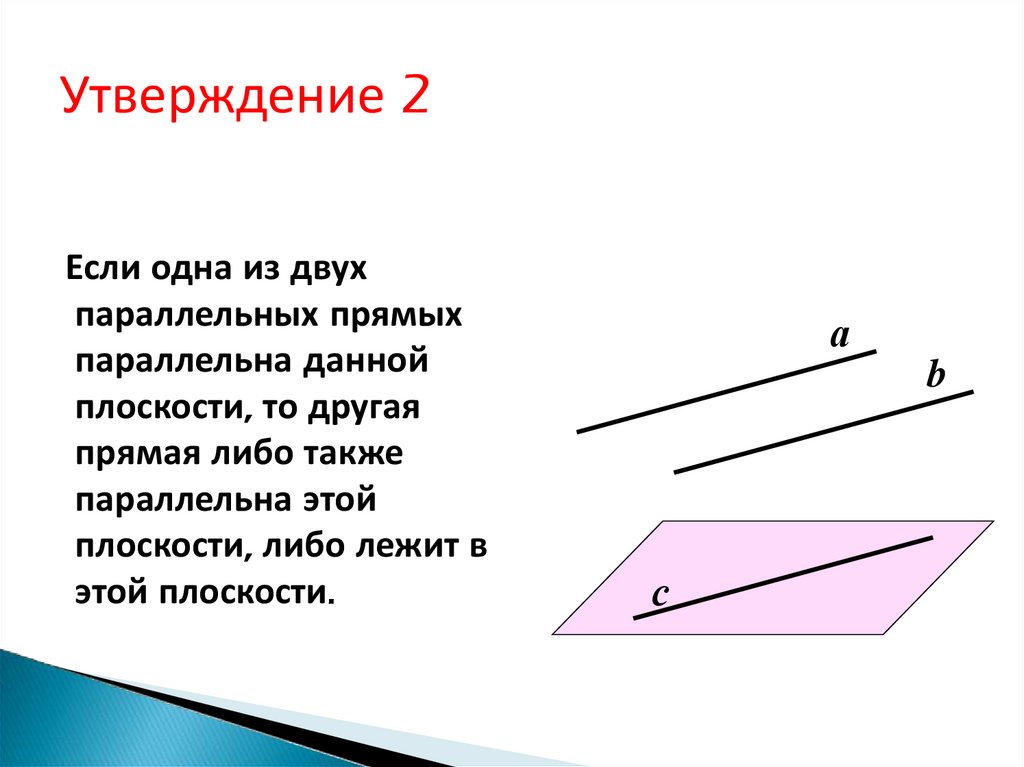
6. Утверждение 2

Если одна из двух
параллельных прямых
параллельна данной
плоскости, то другая
прямая либо также
параллельна этой
плоскости, либо лежит в
этой плоскости.
а
b
с

7. Задача 1:

8. Задача 2:

9. Самостоятельная работа

10.

2. Перпендикулярность прямой и
плоскости
a
α
Прямая
называется
перпендикулярной
к плоскости, если
она
перпендикулярна
к любой прямой,
лежащей в этой
плоскости.

11.

Теорема
a
x
a1
α
Если одна из
двух
параллельных
прямых
перпендикулярна
к плоскости, то и
другая прямая
перпендикулярна
к этой плоскости.
Провести доказательство
теоремы.

12.

Теорема (обратная)
Если две прямые
перпендикулярны
к плоскости, то
они параллельны.
α
a
b

13.

Теорема(признак перпендикулярности
прямой и плоскости)
a
q
O
p
α
m
Если прямая
перпендикулярна к
двум
пересекающимся
прямым, лежащим в
плоскости, то она
перпендикулярна к
этой плоскости.

14.

Теорема о прямой, перпендикулярной
к плоскости
Через любую
точку
пространства
проходит
прямая,
перпендикуляр
ная к данной
плоскости, и
притом только
одна.

15.

Варианты ответов:
Задание 1:
Ответьте на вопросы:
А) 0 180
Б) 0 180
В) 0 90
Г) 0 360
1. В каких пределах измеряется угол
между двумя прямыми?
2. Даны прямая а и точка А, лежащая на этой
прямой. Сколько прямых, перпендикулярных
прямой а и проходящих через точку А, можно
провести?
А) Бесконечное множество
Б) Одну
В) Ни одной
3. Даны прямая а и точка А, не лежащая на
этой прямой. Сколько прямых,
перпендикулярных а и проходящих через
точку А, можно провести?
А) Одну
Б) Ни одной
В) Бесконечное множество
4. а и в . Как расположены прямые а
и в?
А) а и в пересекаются
Б) а и в скрещиваются
В) а и в параллельны
5. а и а в. Как расположены
плоскость и прямая в?
А) в пересекает под любым углом
Б) в и параллельны
В) в и перпендикулярны
Г) в лежит в плоскости

16. Задание 2: Отметьте верные утверждения:

Две прямые в пространстве, перпендикулярные
третьей прямой, параллельны.
2. Через точку, принадлежащую данной прямой,
можно провести бесконечное множество
прямых, перпендикулярных ей.
3. Даны плоскость и параллельная ей прямая. В
плоскости можно провести бесконечное
множество прямых, перпендикулярных ей.
1.

17. Задание 3:

1. Дано: a, A , a b, A b
Построить: b
2. Дано: a || b, c a
Доказать:
c b
3. Дано: c b O, b , c , a b, a c
Доказать: а пересекает

18.

Выполнить тест в СЭО
(Группа 22 П-1)