Теоретическая механика. Динамика системы материальных точек

1. Теоретическая механика

Курс лекций для студентов электромеханического
факультета
Лектор
Иваночкин Павел Григорьевич
доктор технических наук, профессор

2.

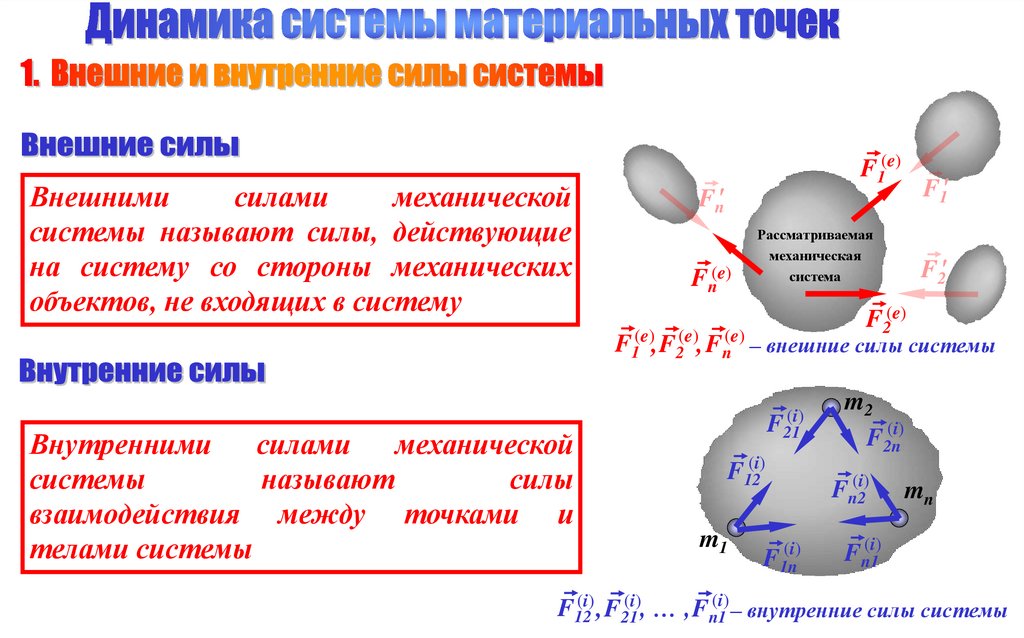
Внешними
силами
механической
системы называют силы, действующие
на систему со стороны механических
объектов, не входящих в систему
F1(e)
F1'
Fn'
Fn(e)
Рассматриваемая
механическая
система
F2'
F2(e)
F1(e), F2(e), Fn(e) – внешние силы системы
(i)
Внутренними
силами
механической
системы
называют
силы
взаимодействия между точками и
телами системы
F21
F12(i)
m1
m2
(i)
F2n
(i)
Fn2
(i)
F1n
mn
(i)
Fn1
(i)
(i)
(i)
F12
, F21
, … , Fn1
– внутренние силы системы

3.

Теорема:
Главный вектор
вектор всех внутренних сил системы и главный момент
этих сил относительно любой точки равны нулю при любом
состоянии системы
(i)
M1
F1
F2(i) M2
i i
F1 F2 0 ;
i n i
R Fk 0
k 1
i
n
i
Rx Fkx 0 ;
В проекциях на оси координат:
i
k 1
n
i
Ry Fky 0 ;
i
k 1
n
i
Rz Fkz 0.
k 1

4.

Теорема:
Главный вектор всех внутренних сил системы и главный
главный момент
момент
этих сил относительно любой точки равны нулю при любом
состоянии системы
i
i
i
i
i
i
MO F1 F1 h;
MO F2 F2 h; MO F1 MO F2 0 ;
(i)
M1
F1
F2(i) M2
k 1
r2
O
n
i n i
i
L 0 M 0 Fk rk Fk 0
h
r1
В проекциях на оси координат:
k 1
i
i
Lx M x Fk 0 ;
i
i
Ly M y Fk 0 ;
i
i
Lz M z Fk 0 ;

5.

d r1 e i
m1 2 F1 F1 ;
Fk(i)
dt
2
d r2 e i
m2 2 F2 F2 ;
dt
mk
(xk , yk , zk)
. .на. .координатные
. . . . . . . . . .оси:
.
В проекциях
2
e i
2d rk
mdk xk2 F ek F ik ;
m
F
F
;
dt
k
kx
kx
2
Fk(e)
rk
. . dt
.2 . . . . . . . . . . . .
d dyk2 r e
i
y
mkm 2 N F kyF e F kyF; i ; k 1, N
N
N
N
dt dt 2
d 2 zk
e
i
m
F
F
k
kz
kz ;
2
2
d rk dt e i
mk 2 Fk Fk , k 1, N
2
z
O
x
dt

6.

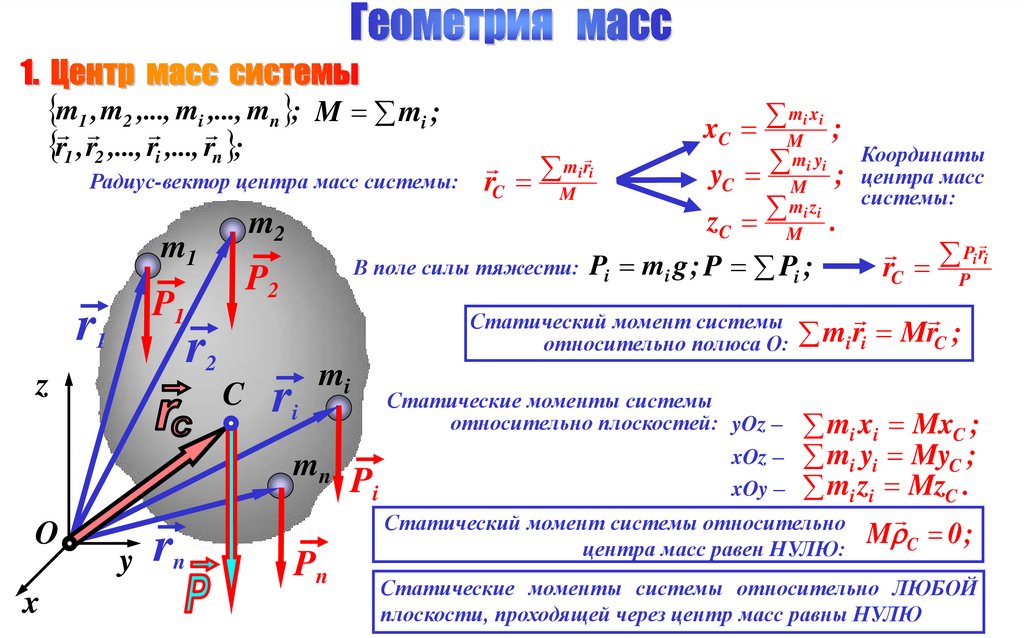
m1 , m2 ,..., mi ,..., mn ; M mi ;
r1 , r2 ,..., ri ,..., rn ;
Радиус-вектор центра масс системы:
m2
m1
r1
O
x
C
y rn
M
mi z i
M
zC
системы:
.
Pi r i
rC P
Статический момент системы
относительно полюса О: mi ri MrC ;
r2
z
C
В поле силы тяжести: Pi mi g ; P Pi ;
P2
P1
mi r i
rC M
mi x i
xC M ;
Координаты
mi yi
y
; центра масс
ri
mi
Статические моменты системы
относительно плоскостей: yOz –
mi xi MxC ;
xOz – mi yi MyC ;
mn
Pi
xOy – mi zi MzC .
Статический момент системы относительно
M
0
;
C
центра масс равен НУЛЮ:
Pn
Статические моменты системы относительно ЛЮБОЙ
плоскости, проходящей через центр масс равны НУЛЮ

7.

Z
m1
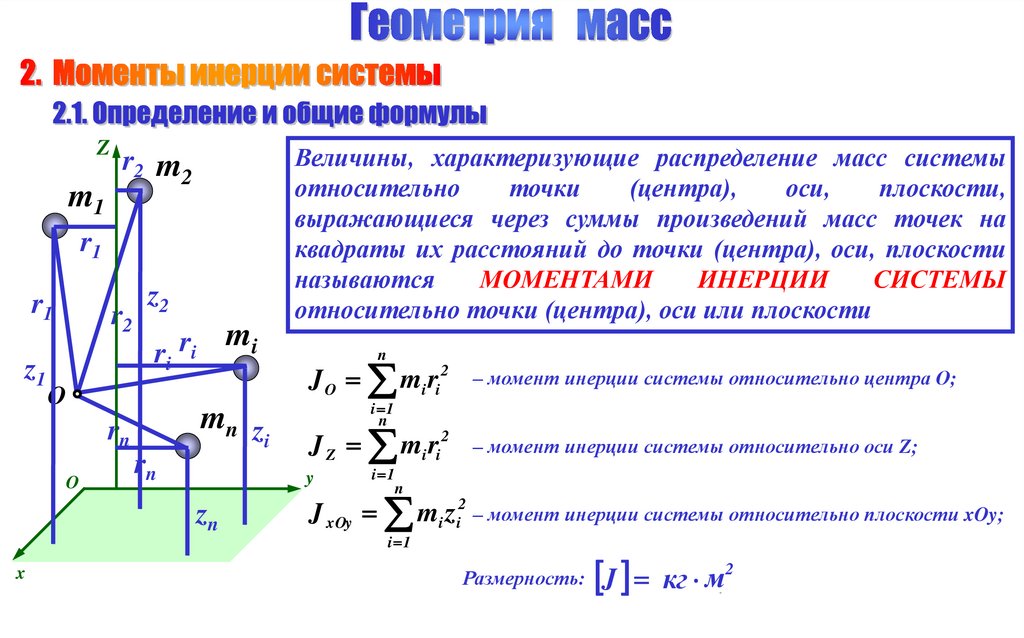
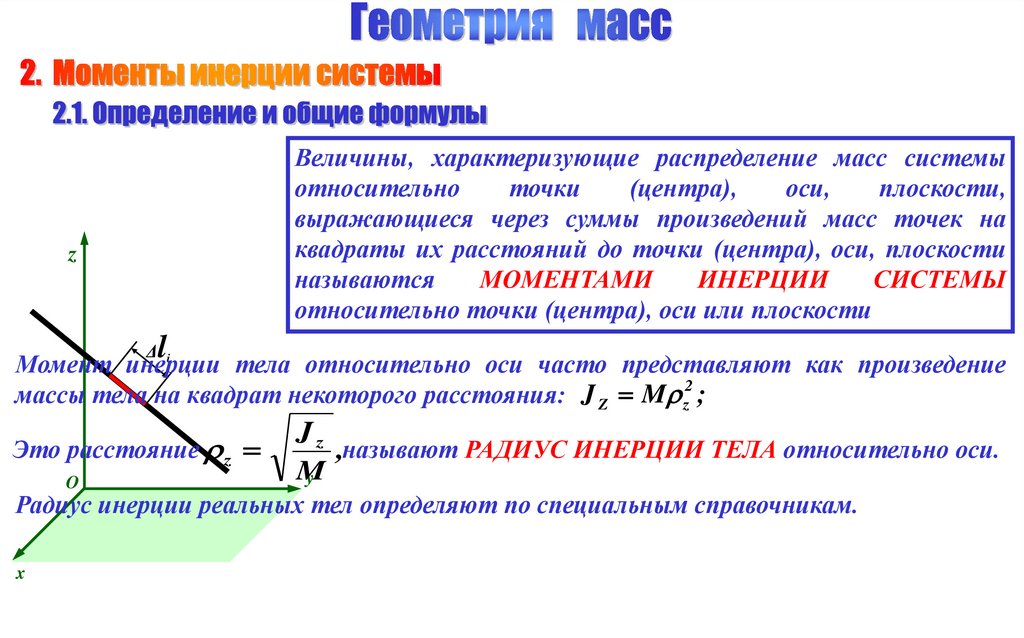
Величины, характеризующие распределение масс системы
относительно
точки
(центра),
оси,
плоскости,
выражающиеся через суммы произведений масс точек на
квадраты их расстояний до точки (центра), оси, плоскости
называются
МОМЕНТАМИ
ИНЕРЦИИ
СИСТЕМЫ
относительно точки (центра), оси или плоскости
r2 m2
r1
r1
z1
r2
z2
mi
r ri
i
O
mn z
rn
O
rn
J O mi ri2
– момент инерции системы относительно центра О;
J Z mi ri2
– момент инерции системы относительно оси Z;
i 1
n
i
y
zn
x
n
i 1
n
J xOy mi zi2 – момент инерции системы относительно плоскости xOy;
i 1
n
Размерность:
JJ кгm iмri
2
i 1

8.

∆
∆
m1
Величины, характеризующие распределение масс системы
относительно
точки
(центра),
оси,
плоскости,
выражающиеся через суммы произведений масс точек на
квадраты их расстояний до точки (центра), оси, плоскости
называются
МОМЕНТАМИ
ИНЕРЦИИ
СИСТЕМЫ
относительно точки (центра), оси или плоскости
m2
z
z2
∆
mi
Моменты инерции твердого тела:
z1
∆
mn z
y
O
zn
x
i
n 2
2
J O lim ri mi r dm – относительно центра О;
mi 0 i 1
M
n 2
2
J z lim ri mi r dm – относительно оси Z;
mi 0 i 1
M
n 2
J xOy lim zi mi z 2 dm – относительно плоскости xOy;
mi 0 i 1
M

9.

∆
∆
m1
Δv
Величины, характеризующие распределение масс системы
относительно
точки
(центра),
оси,
плоскости,
выражающиеся через суммы произведений масс точек на
квадраты их расстояний до точки (центра), оси, плоскости
называются
МОМЕНТАМИ
ИНЕРЦИИ
СИСТЕМЫ
Δσi
относительно точки (центра), оси или плоскости
m
2
Δv
2
1
z
Δ
Δ
σ
1
2
m
v
ΔlΔσ
i
Δ
O
σ
n
Δ∆ i i
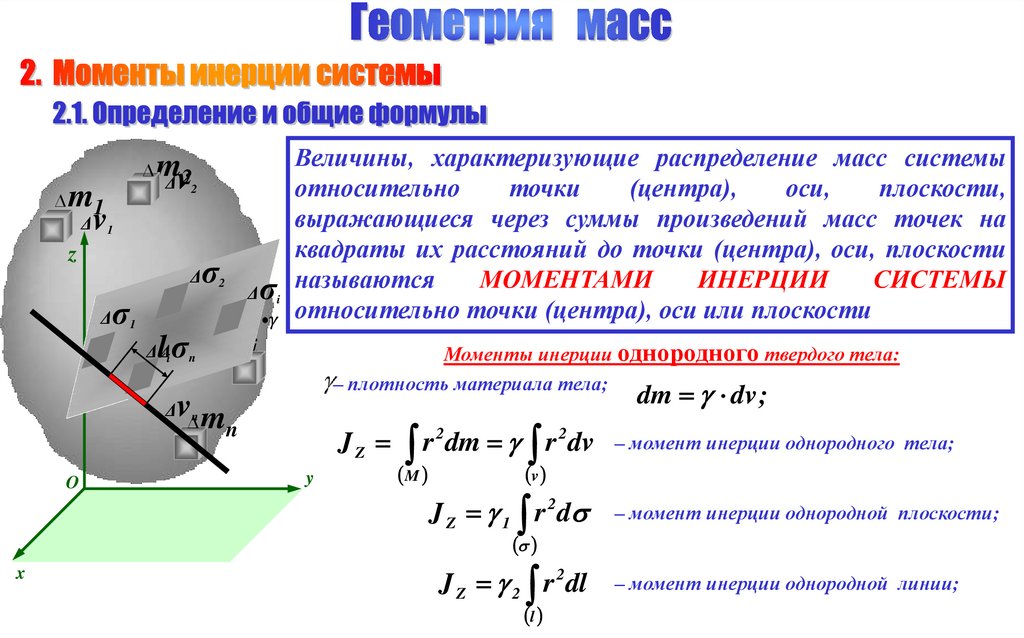
Моменты инерции однородного твердого тела:
– плотность материала тела;
dm dv ;
v∆ m
n
J Z r dm r dv
n
2
y
M
2
– момент инерции однородного тела;
v
J Z 1 r 2 d
– момент инерции однородной плоскости;
J Z 2 r 2 dl
– момент инерции однородной линии;
x
l

10.

Величины, характеризующие распределение масс системы
относительно
точки
(центра),
оси,
плоскости,
выражающиеся через суммы произведений масс точек на
квадраты их расстояний до точки (центра), оси, плоскости
называются
МОМЕНТАМИ
ИНЕРЦИИ
СИСТЕМЫ
относительно точки (центра), оси или плоскости
z
l
Момент инерции тела относительно оси часто представляют как произведение
Δ i
массы тела на квадрат некоторого расстояния: J Z M z2 ;
Это расстояние z
O
Jz
,называют РАДИУС ИНЕРЦИИ ТЕЛА относительно оси.
M
y
Радиус инерции реальных тел определяют по специальным справочникам.
x

11.

Величины, характеризующие распределение масс системы
относительно
точки
(центра),
оси,
плоскости,
выражающиеся через суммы произведений масс точек на
квадраты их расстояний до точки (центра), оси, плоскости
называются
МОМЕНТАМИ
ИНЕРЦИИ
СИСТЕМЫ
относительно точки (центра), оси или плоскости
Связь осевых моментов инерции с центральным
Момент инерции системы относительно начала координат О:
Осевые моменты инерции
системы :
n
J x mi y z ;
i 1
n
2
i
2
i
J y mi xi2 zi2 ;
i 1
n
J z mi xi2 yi2 ;
i 1
n
n
i 1
i 1
J O mi ri2 mi xi2 yi2 zi2 .
2JO J x J y J z

12.

z'
z
d
x'
O
x
d
b
n
J Oz mi x y ;
i 1
2
i
2
i
2
2
J Cz mi xi yi ;
i 1
a, b, c – координаты точки С в системе Oxyz . d2=a2+b2 – расстояние между осями Oz и Cz'.
d1
xi xi a ;
n
x1
n
z1
O1
zi zi c ;
yi yi b ;
n
n
y1 J Oz mi xi yi 2a mi xi 2b mi yi a b
i 1
n
2
2
i 1
i 1
n
n
i 1
i 1
2
2
m ;
n
i
i 1
C (a,b,c)
y'
c
M mi ; mi xi MxC 0 ; mi yi MyC 0 ; т. к. xC 0 ;yC 0 ;
a y
Момент инерции системы относительно какой-либо оси равен моменту
инерции относительно параллельной оси, проходящей через центр масс системы,
плюс произведение массы системы на квадрат расстояния между осями
i 1
J Oz J Cz Md
Для осей O1x1y1z1 :
2
J O1z1 J Cz Md12 , тогда: J O1 z1 J Oz M d12 d 2

13.

2.3.1. Стержень
С
A
dx
B
Момент инерции стержня относительно его конца (А):
l
3
2
2
A
2
2
2
l
0
x
l
J r dl x dx
;
3
M
2 ;
l
x
1
2
JA M l
3
Момент инерции стержня относительно его середины (С):
По теореме Штейнера:
l
J A JC M
2
2
1
1
1
2
2
JC J A M l M l M l 2
4
3
4
1
2
JC
M l
12

14.

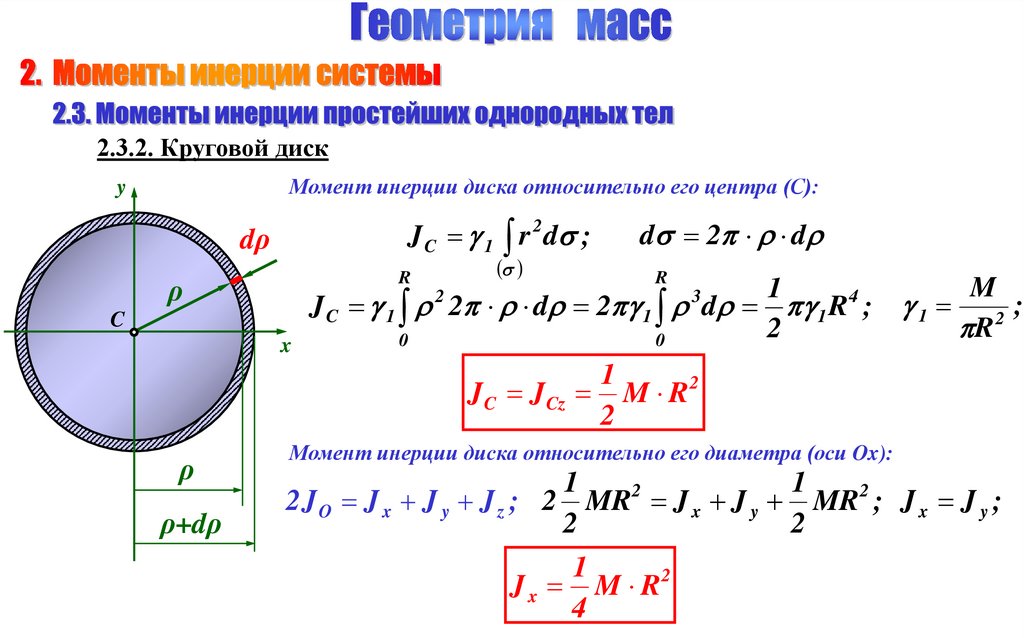
2.3.2. Круговой диск
Момент инерции диска относительно его центра (С):
y
J C 1 r d ;
2
dρ
R
ρ
x
R
1
4
J C 1 2 d 2 1 d 1 R ;
2
0
0
2
C
d 2 d
3
M
1 2 ;
R
1
2
J C J Cz M R
2
ρ
ρ+dρ
Момент инерции диска относительно его диаметра (оси Ox):
1
1
2
2
2 J O J x J y J z ; 2 MR J x J y MR ; J x J y ;
2
2
1
J x M R2
4

15.

2.3.3. Прямой круговой цилиндр
z
n
J z mi x y ;
2
i
2
i
i 1
R
Момент инерции системы не изменятся при перемещении
точек системы параллельно оси.
Если массы всех точек цилиндра сместить на его
основание, то получим диск массой М и радиусом R:
h
1
2
Jz M R
2
y
x

16.

2.3.4. Шар
Момент инерции шара относительно его центра (С):
z
J C r 2 dv ;
v
R
dρ
J C 4 d 4
4
ρ
0
С
y
dv 4 d ;
2
5
5
;
3M
;
3
4 R
3
2
JC M R
5
Момент инерции шара относительно его диаметра (оси Ox):
x
ρ
ρ+dρ
2 JC J x J y J z ; J x J y J z ;
2
2 JC 3J x ; J x JC ;
3
2
2
Jx M R
5

17. Спасибо за внимание!