Понятие конуса. Площадь поверхности конуса. Усечённый конус

1. Конус

Понятие конуса
Площадь поверхности конуса
Усечённый конус

2.

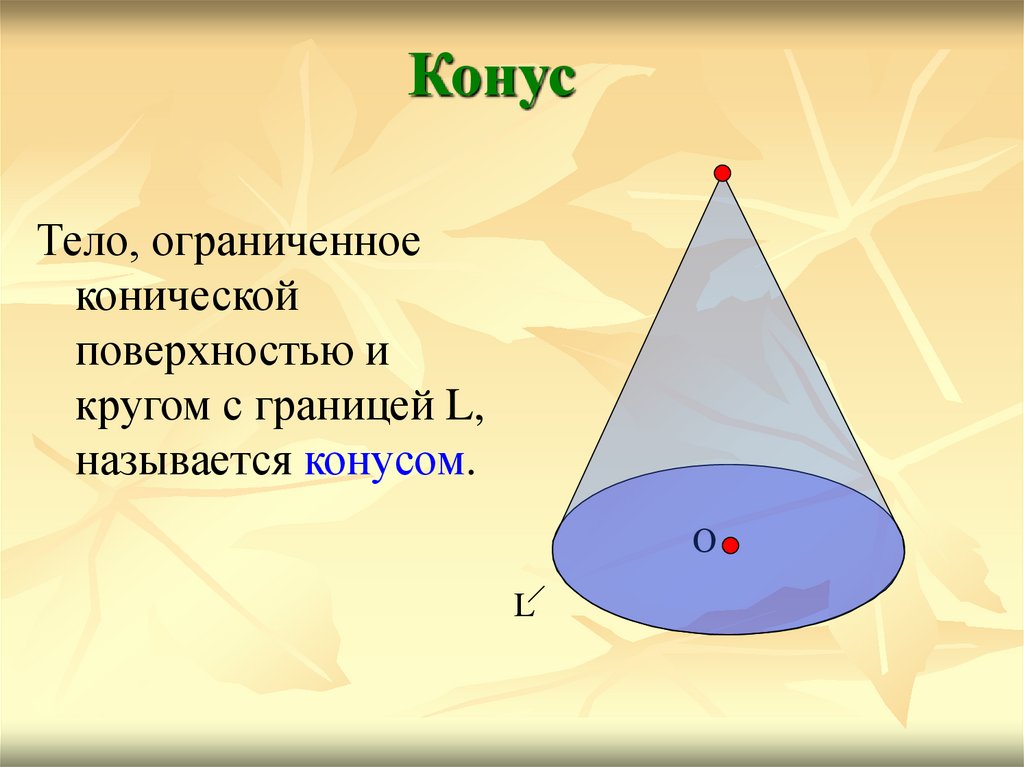
Конус
Тело, ограниченное
конической
поверхностью и
кругом с границей L,
называется конусом.
О
L

3.

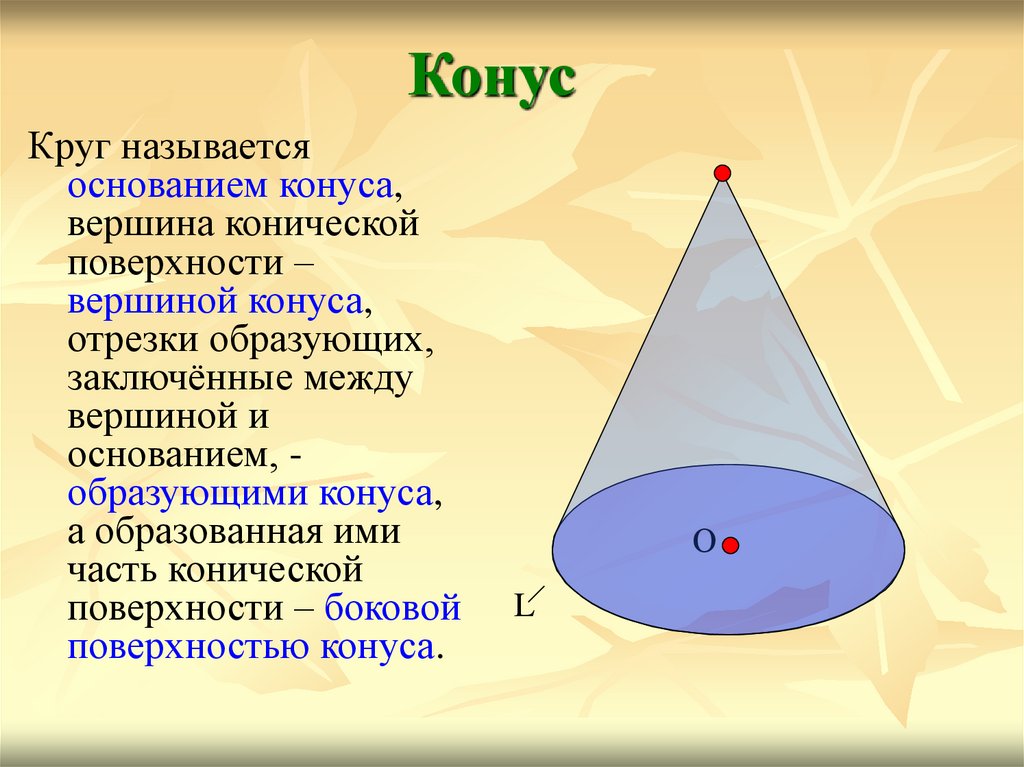
Конус
Круг называется
основанием конуса,
вершина конической
поверхности –
вершиной конуса,
отрезки образующих,
заключённые между
вершиной и
основанием, образующими конуса,
а образованная ими
часть конической
поверхности – боковой
поверхностью конуса.
О
L

4.

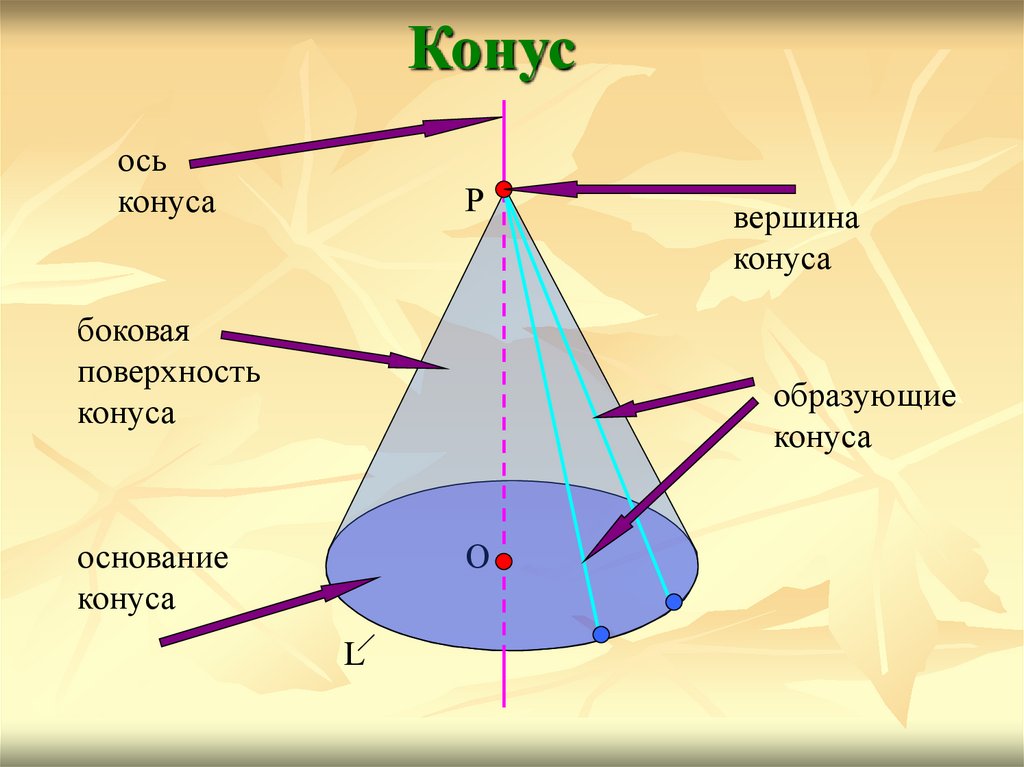
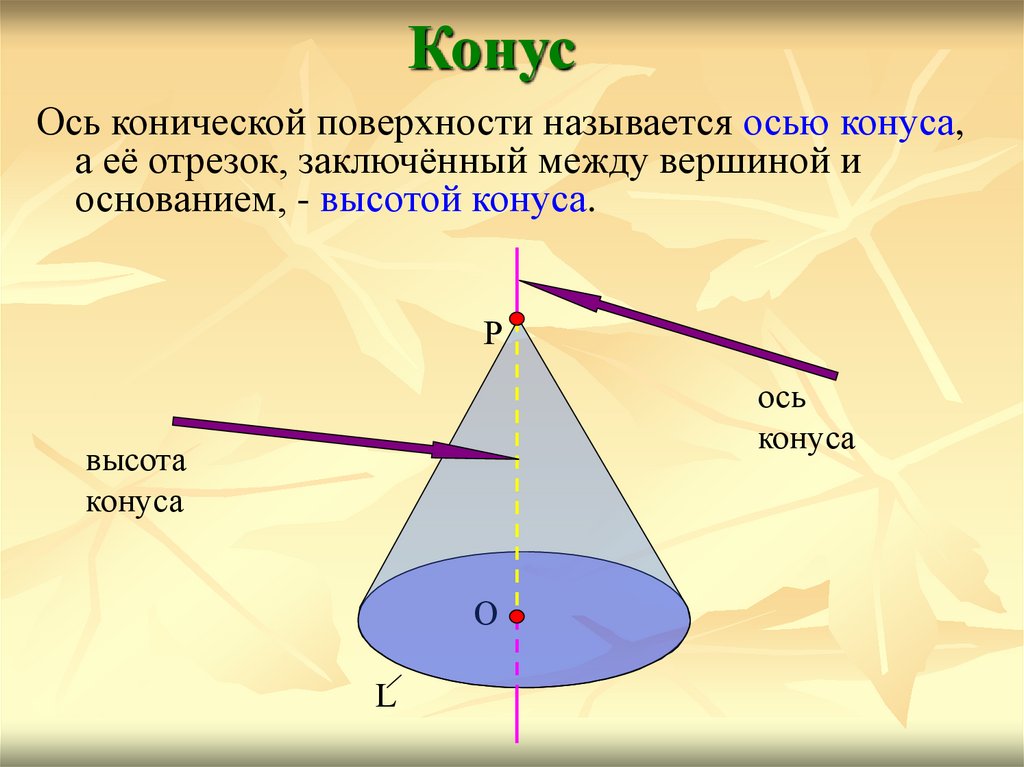
Конус
ось
конуса
Р
боковая
поверхность
конуса
вершина
конуса
образующие
конуса
основание
конуса
О
L

5.

Конус
Ось конической поверхности называется осью конуса,
а её отрезок, заключённый между вершиной и
основанием, - высотой конуса.
Р
ось
конуса
высота
конуса
О
L

6.

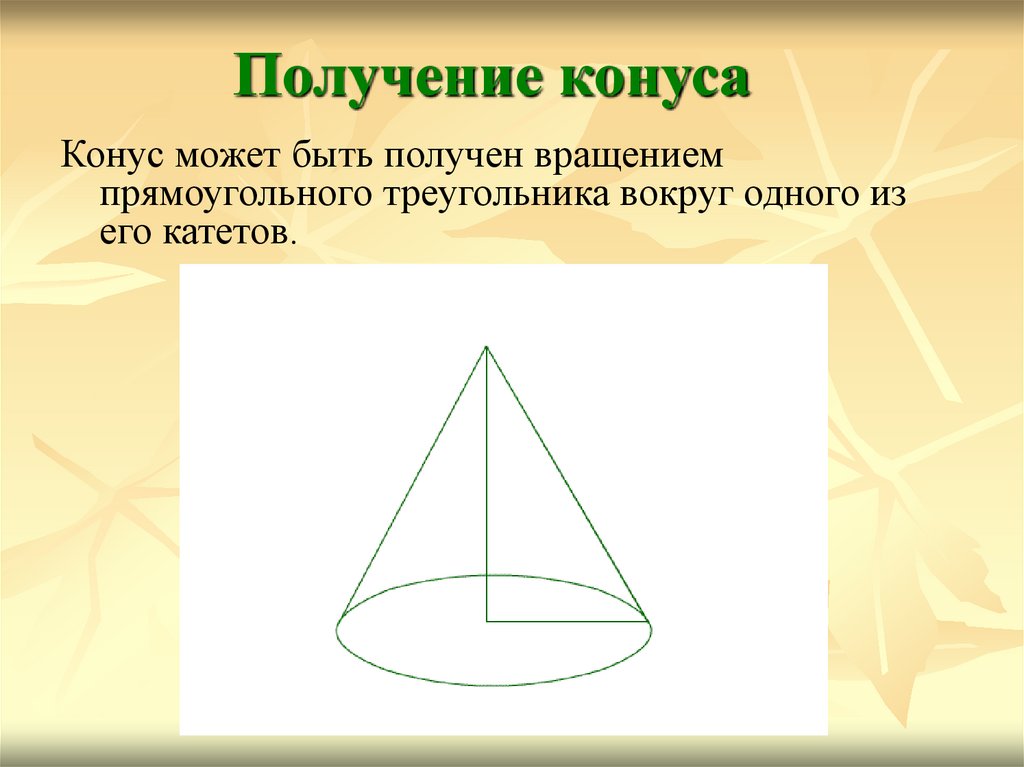
Получение конуса
Конус может быть получен вращением
прямоугольного треугольника вокруг одного из
его катетов.

7.

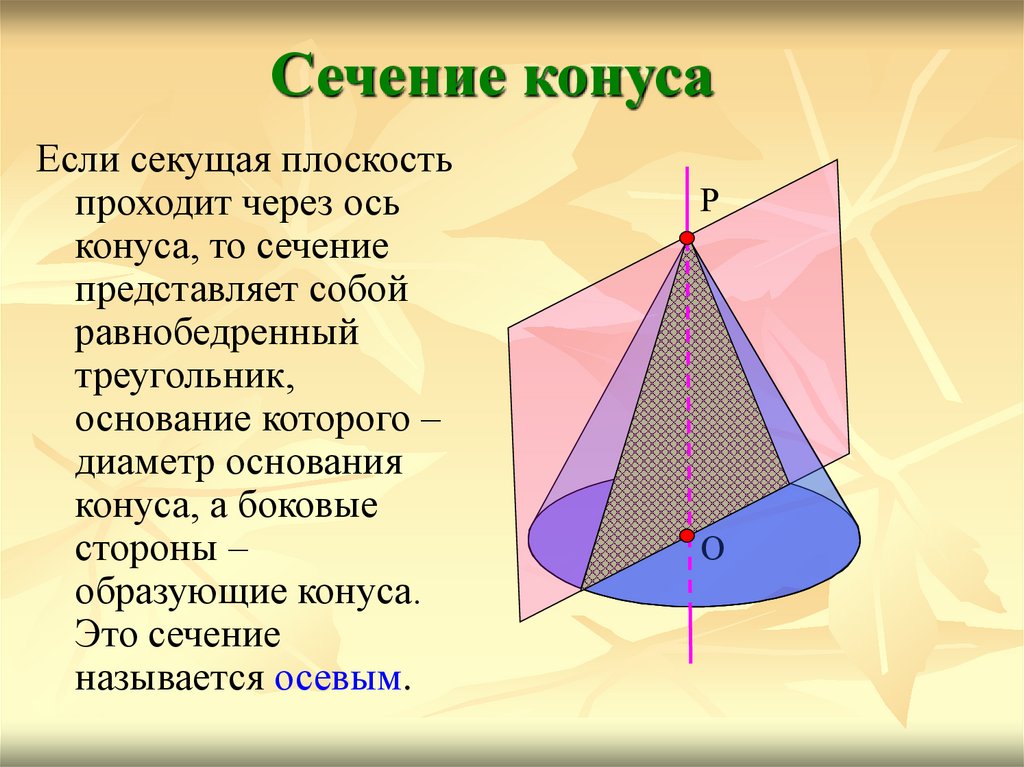
Сечение конуса
Если секущая плоскость
проходит через ось
конуса, то сечение
представляет собой
равнобедренный
треугольник,
основание которого –
диаметр основания
конуса, а боковые
стороны –
образующие конуса.
Это сечение
называется осевым.
Р
О

8.

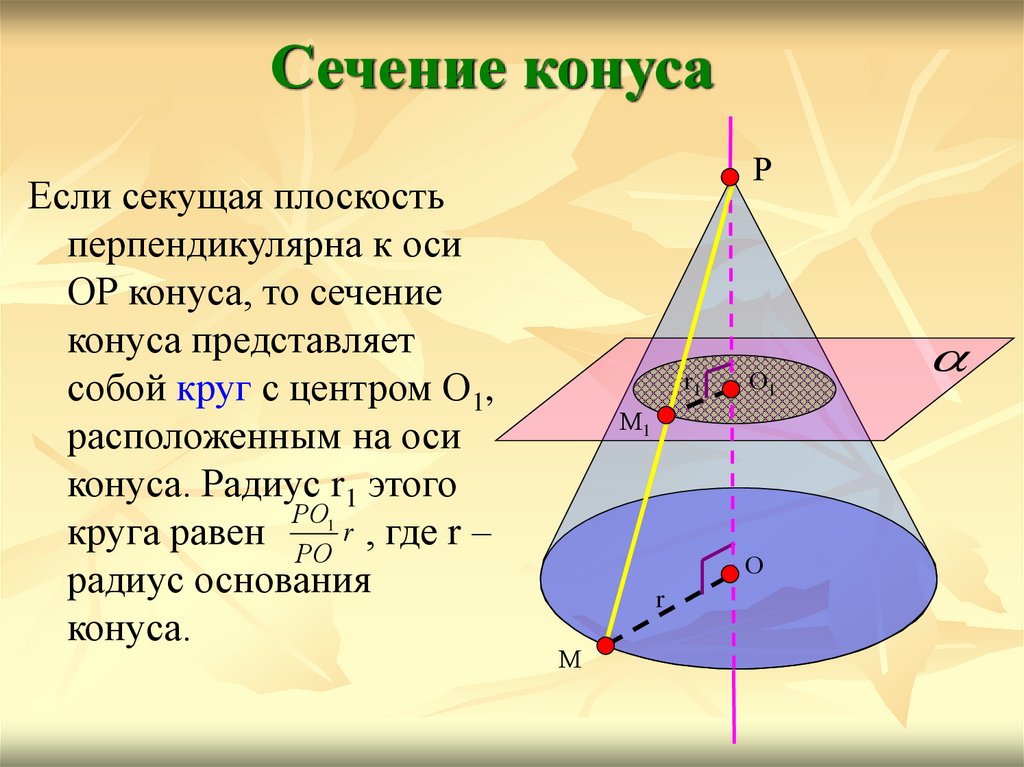
Сечение конуса
Если секущая плоскость
перпендикулярна к оси
ОР конуса, то сечение
конуса представляет
собой круг с центром О1,
расположенным на оси
конуса. Радиус r1 этого
РО1
круга равен РО r , где r –
радиус основания
конуса.
Р
r1
О1
М1
О
r
М

9.

Сечение конуса
Проводя различные сечения
одного и того же
кругового конуса, причём
любого, можно получить
эллипс, параболу и
гиперболу. При
надлежащем наклоне
секущей плоскости
удаётся получить все
типы конических сечений.
Если считать, что конус
не заканчивается в
вершине, а простирается
за неё, тогда у некоторых
сечений образуются две
ветви.

10.

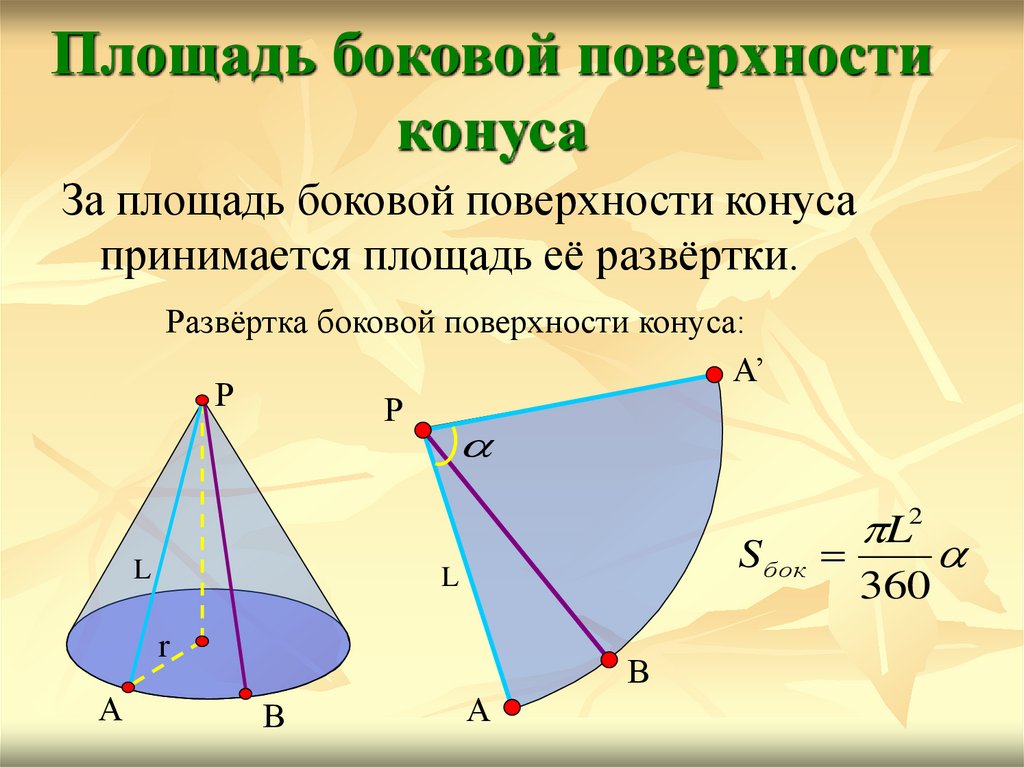
Площадь боковой поверхности
конуса
За площадь боковой поверхности конуса
принимается площадь её развёртки.
Развёртка боковой поверхности конуса:
А’
Р
Р
L
S бок
L
r
А
В
В
А
L2
360

11.

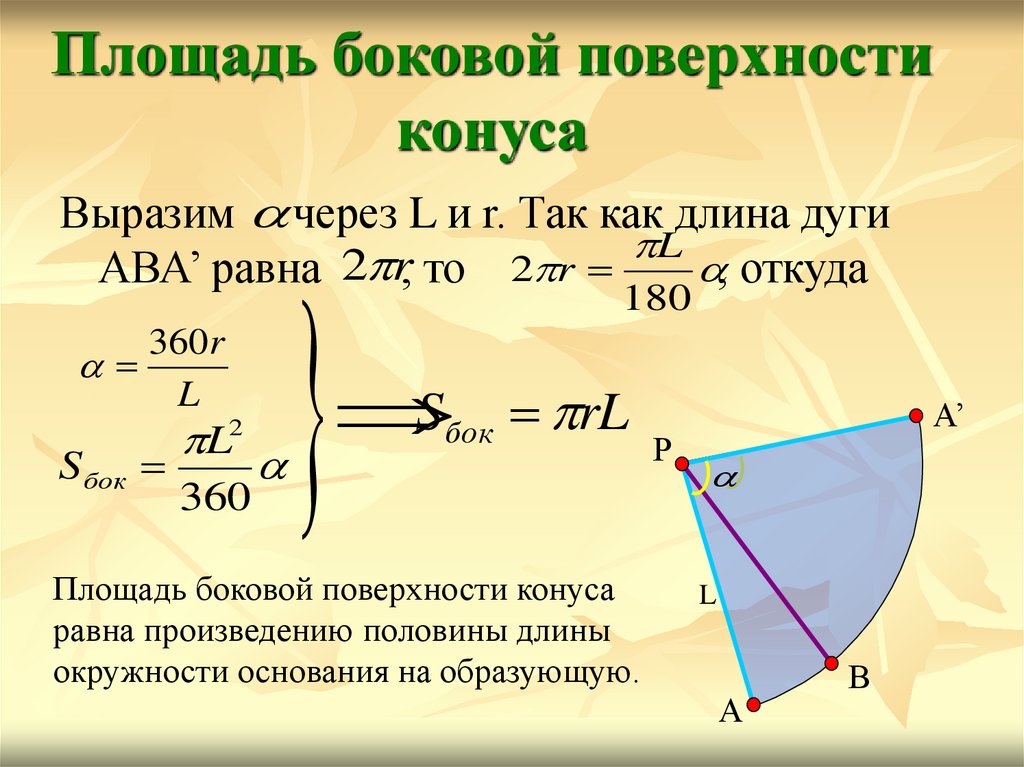
Площадь боковой поверхности
конуса
Выразим через L и r. Так как длина дуги
L
, откуда
АВА’ равна 2 r, то 2 r
360r
L
S бок
L
2
360
180
Sбок rL
Р
Площадь боковой поверхности конуса
равна произведению половины длины
окружности основания на образующую.
А’
L
А
В

12.

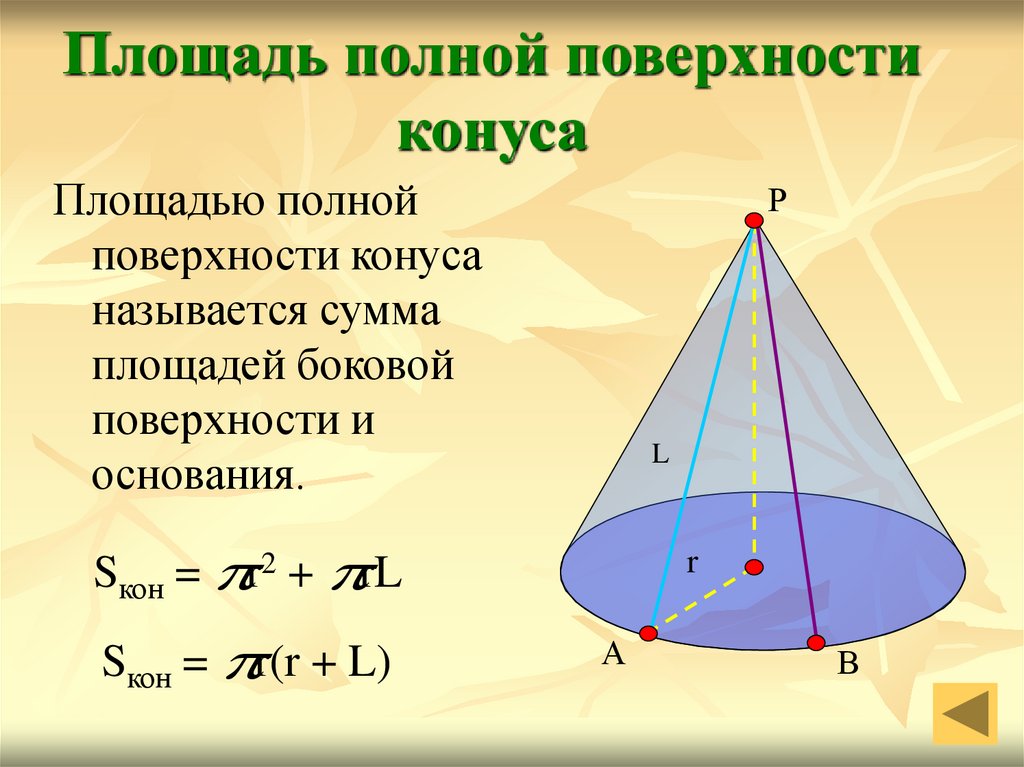
Площадь полной поверхности
конуса
Площадью полной
поверхности конуса
называется сумма
площадей боковой
поверхности и
основания.
Р
L
Sкон = r2 + rL
Sкон = r(r + L)
r
А
В

13.

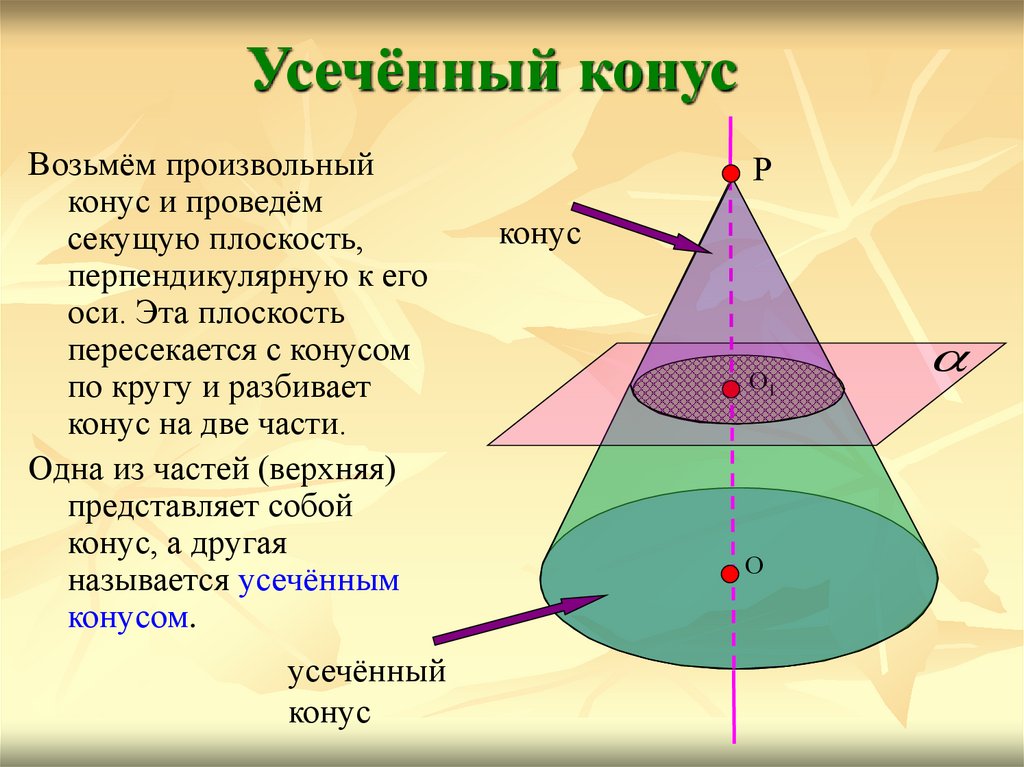
Усечённый конус
Возьмём произвольный
конус и проведём
секущую плоскость,
перпендикулярную к его
оси. Эта плоскость
пересекается с конусом
по кругу и разбивает
конус на две части.
Одна из частей (верхняя)
представляет собой
конус, а другая
называется усечённым
конусом.
усечённый
конус
Р
конус
О1
О

14.

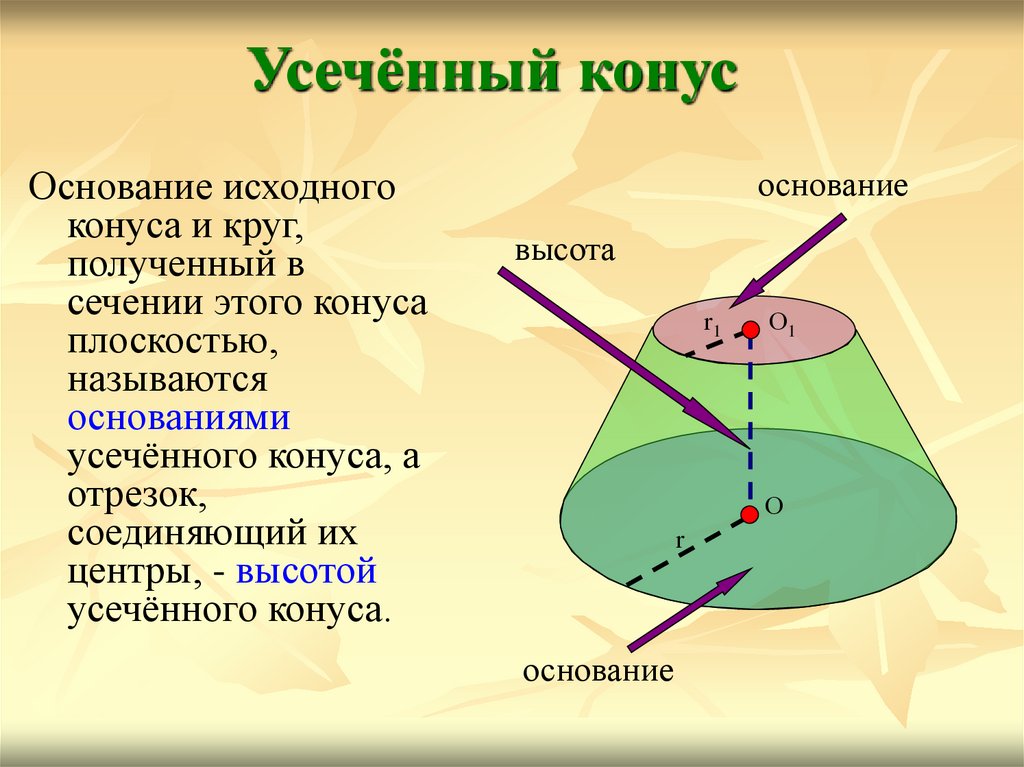
Усечённый конус
Основание исходного
конуса и круг,
полученный в
сечении этого конуса
плоскостью,
называются
основаниями
усечённого конуса, а
отрезок,
соединяющий их
центры, - высотой
усечённого конуса.
основание
высота
r1
О1
О
r
основание

15.

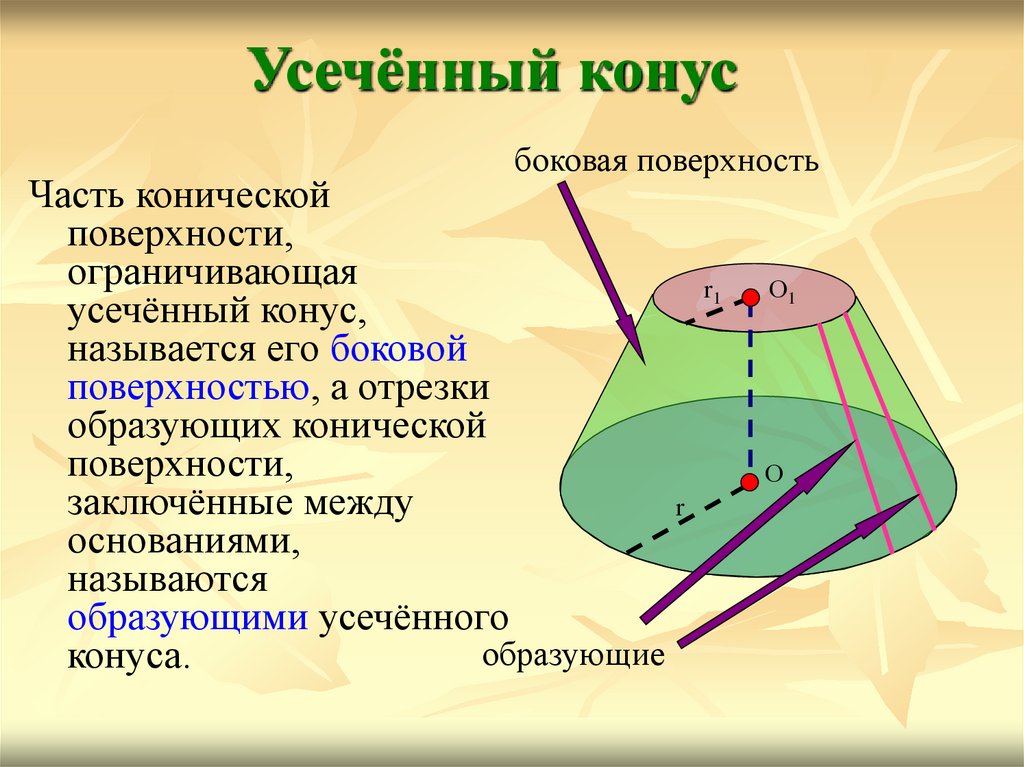
Усечённый конус
боковая поверхность
Часть конической
поверхности,
ограничивающая
r1
усечённый конус,
называется его боковой
поверхностью, а отрезки
образующих конической
поверхности,
заключённые между
r
основаниями,
называются
образующими усечённого
образующие
конуса.
О1
О

16.

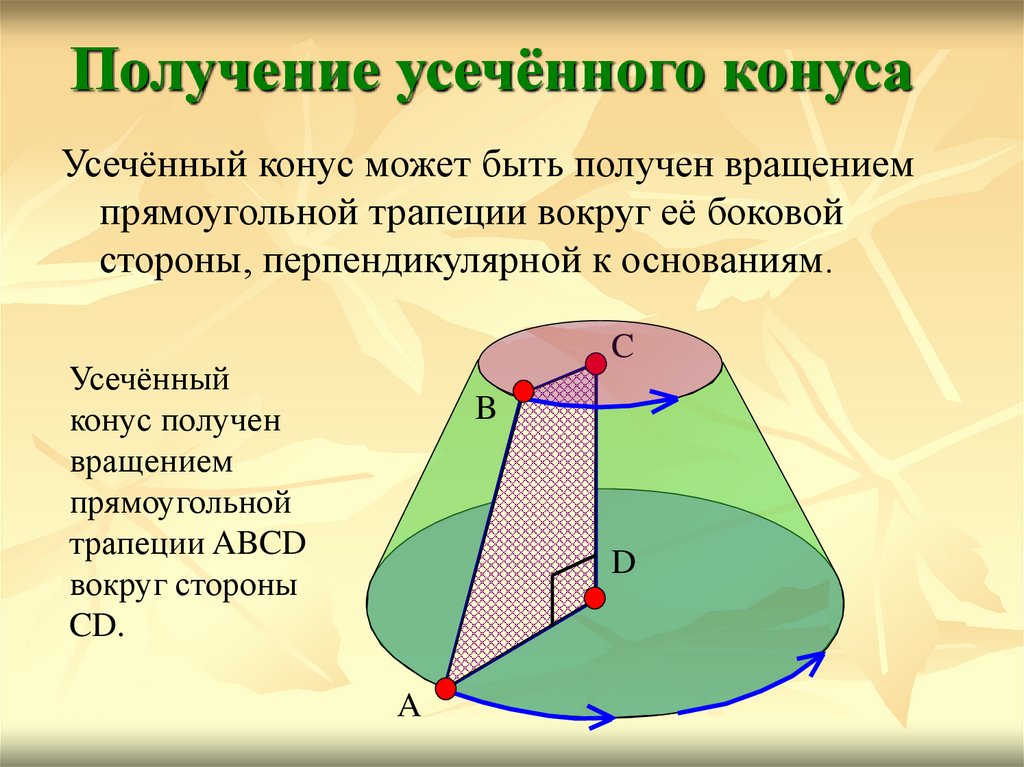
Получение усечённого конуса
Усечённый конус может быть получен вращением
прямоугольной трапеции вокруг её боковой
стороны, перпендикулярной к основаниям.
C
Усечённый
конус получен
вращением
прямоугольной
трапеции ABCD
вокруг стороны
CD.
B
D
A

17.

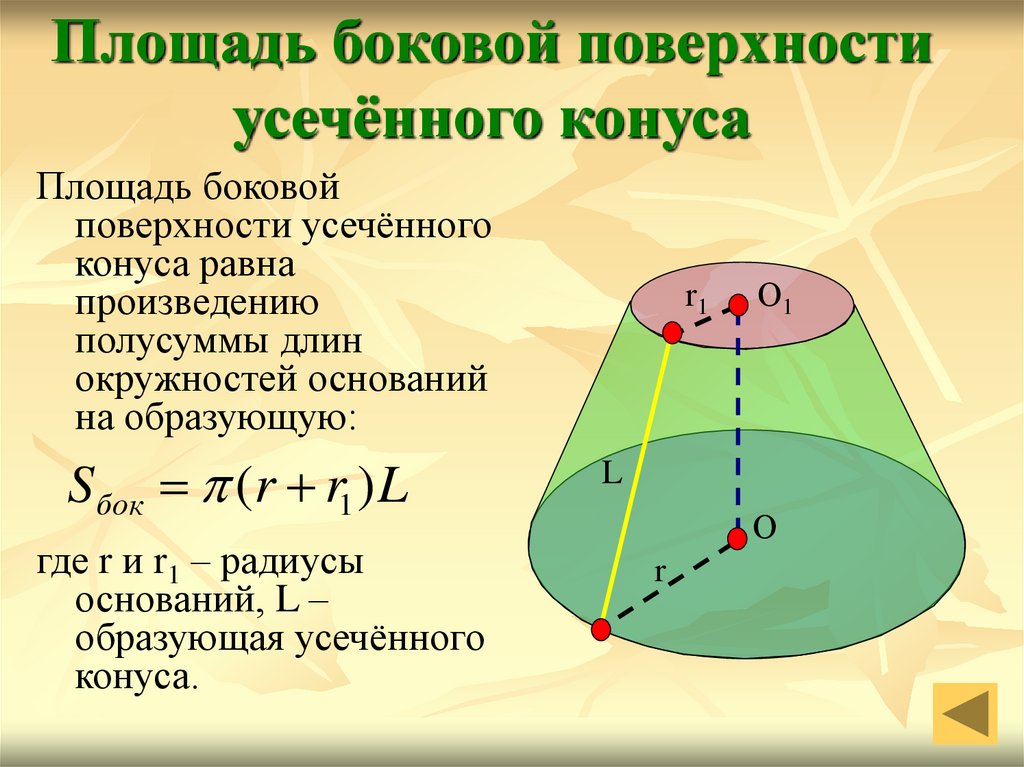
Площадь боковой поверхности
усечённого конуса
Площадь боковой
поверхности усечённого
конуса равна
произведению
полусуммы длин
окружностей оснований
на образующую:
Sбок (r r1 ) L
где r и r1 – радиусы
оснований, L –
образующая усечённого
конуса.
r1
О1
L
О
r